Advances in Digital Holographic Interferometry
Abstract
:1. Introduction
- (1)
- The method of two exposures consists of the recording of two holograms: the object under study before the exposure, which may include deformation, heating, loading of the local area, and the object after such exposure. The recording is made on the same photosensitive plate, and when using digital methods, two arrays of interference intensities of the reference and object waves are recorded on the photosensitive matrix. Hence, the result of interference of fields existing at different timepoints is observed on the plate.
- (2)
- In the real-time method, a scattered wave from an object in its original, undeformed state is registered. Instead of recording a second hologram (registration of a scattered wave from a deformed object), the resulting hologram is restored and the object is illuminated with a single reference beam. As a result, two wavefronts scattered from the object interfere with each other and form a picture of an altered state. Thus, this method allows you to observe the process of deformation of the object.
- (3)
- The time-averaging method is used to estimate periodic loads on an object. In this method, the hologram is exposed over a long period of time, thus averaging the effect of the periodic loading.
- (4)
- The strobogolographic method is similar to the real-time holographic interferometry method. At first, a hologram of an object is recorded in its original, undeformed state, after which periodic fluctuations of the object are provided. During each period of oscillation of the object, it is illuminated by a short light pulse. Thus, this method allows us to estimate the position or state of an object in an arbitrary oscillation phase.
2. Radiation Sources and Its Requirements
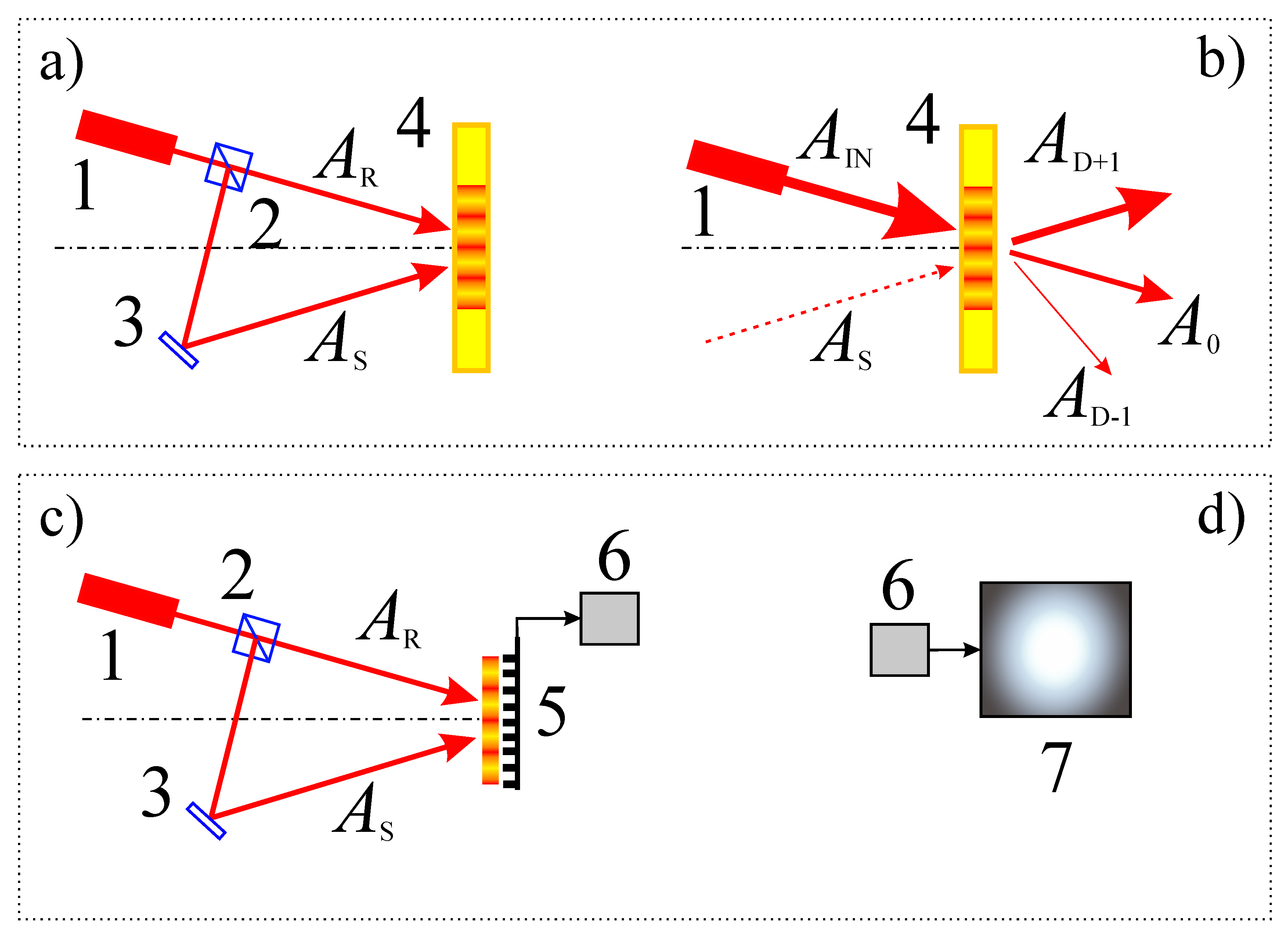
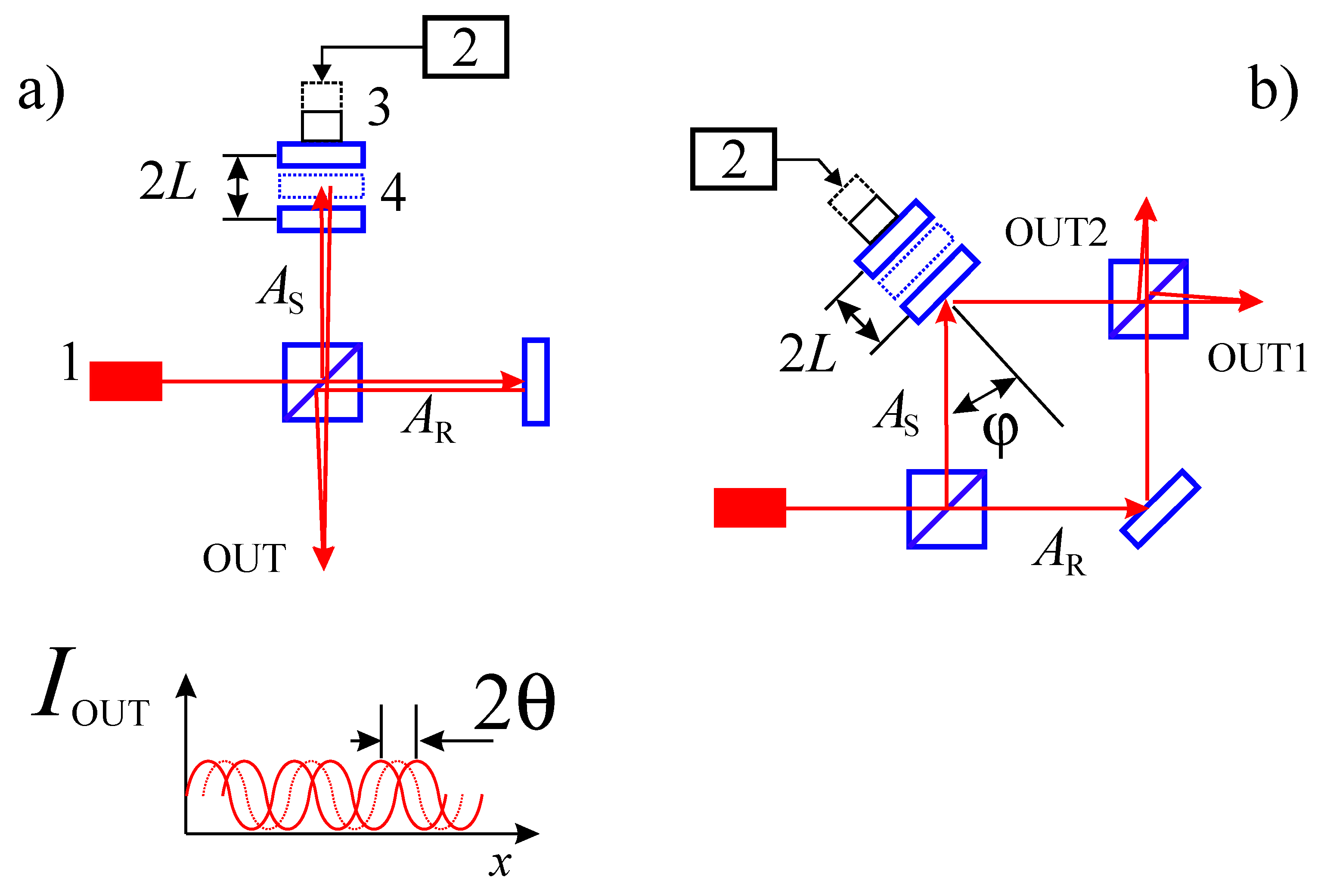
3. Overview of Digital Holographic Interferometry Schemes: Schemes Based on Michelson Interferometers, Mach–Zehnder and Other Schemes
4. Photodetectors with a Two-Dimensional Discrete Matrix
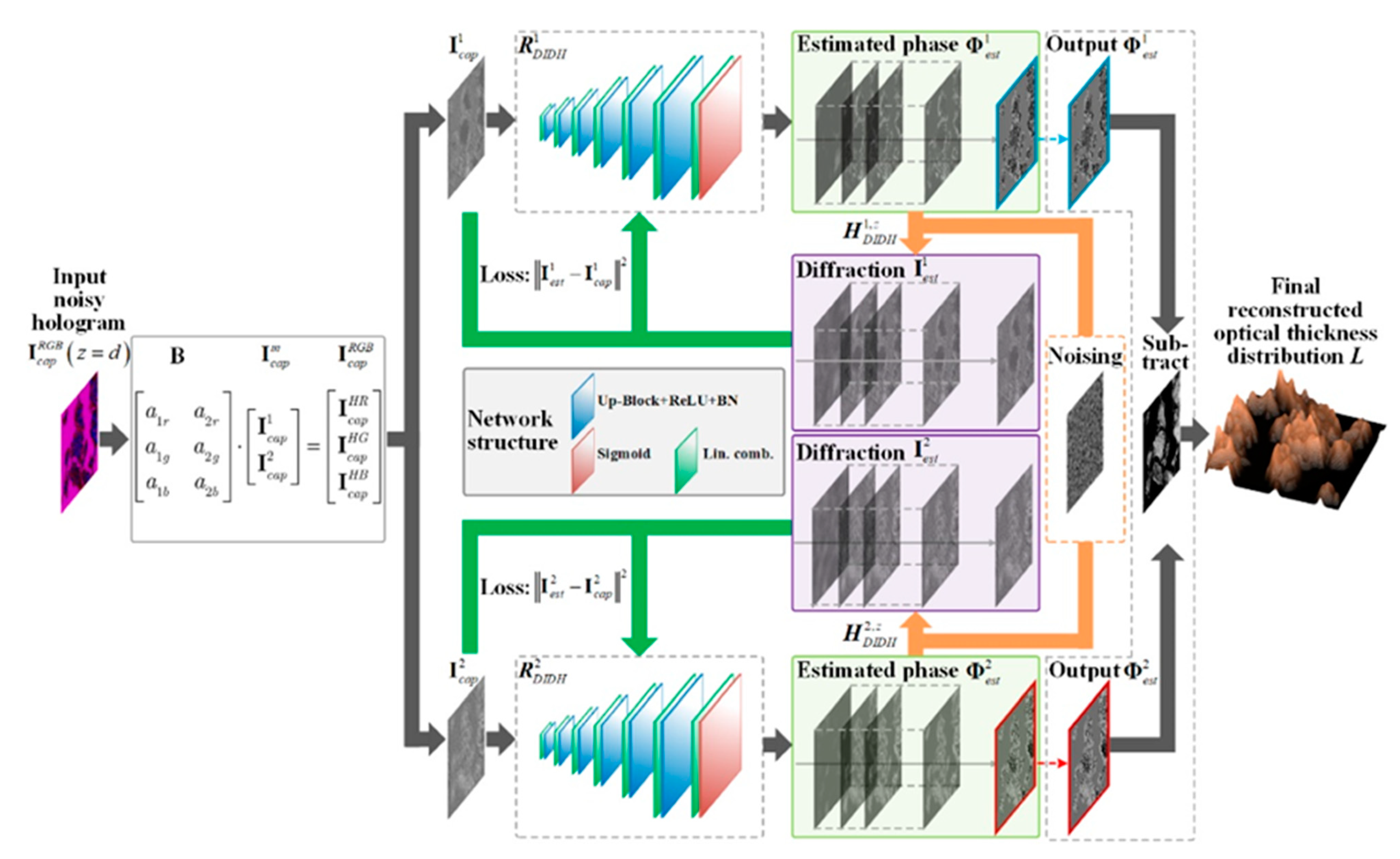
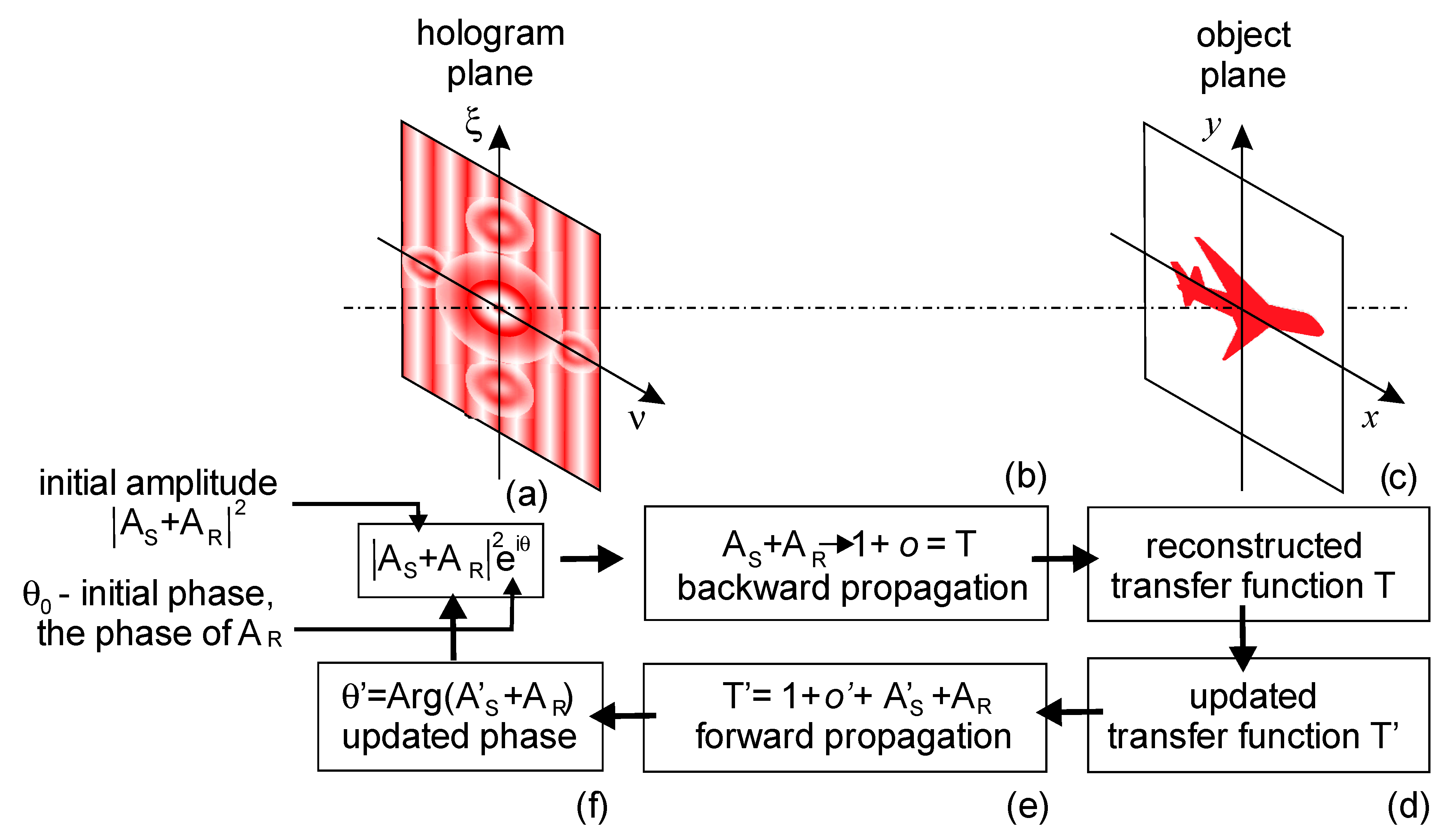
5. Methods and Algorithms for Processing and Restoring of Holograms
- Elimination of zero-order diffraction;
- Digital hologram reconstruction, extraction of the complex amplitude of the object wave in the reconstruction plane;
- Filtering of the holograms and the recovered amplitude of the object wave in the reconstruction plane.
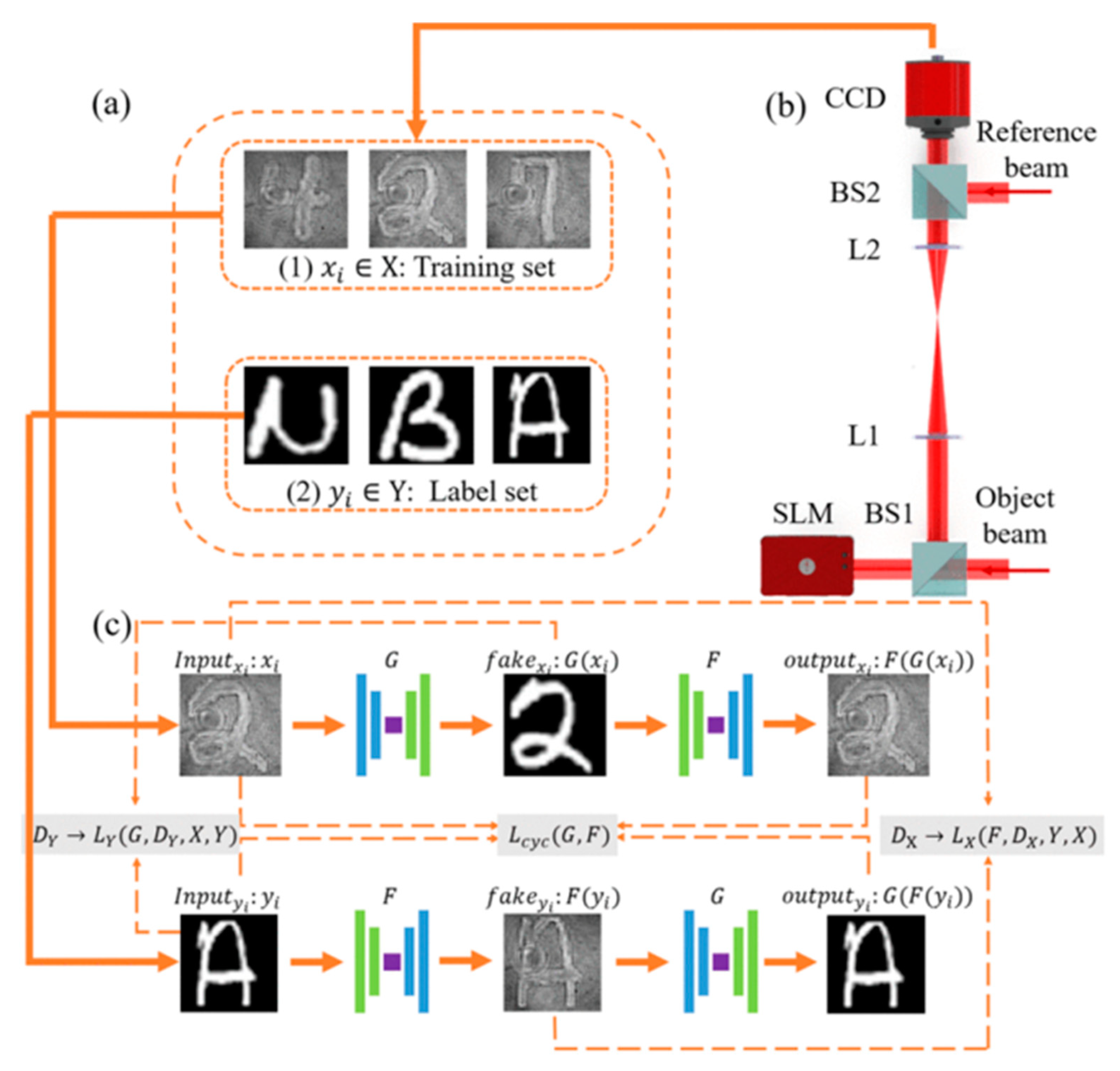
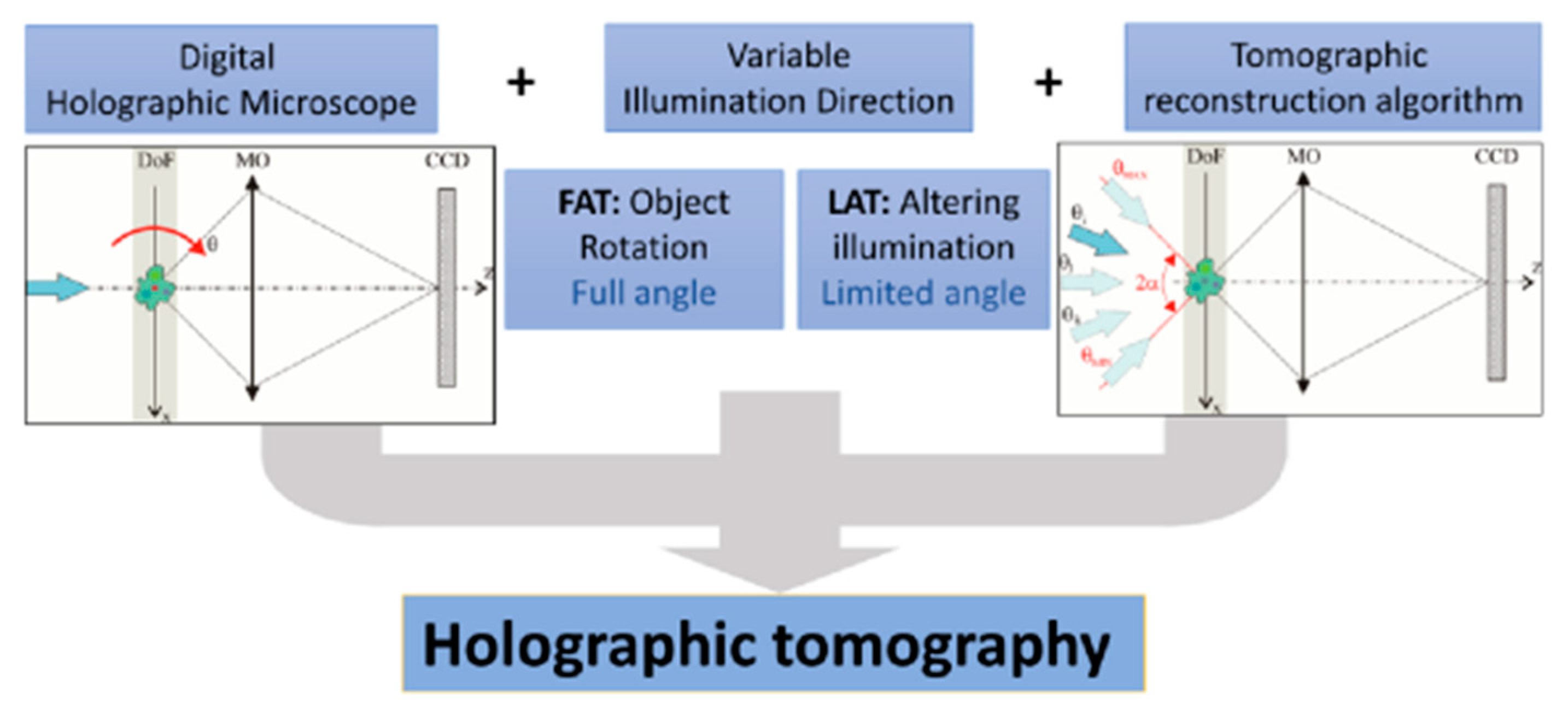
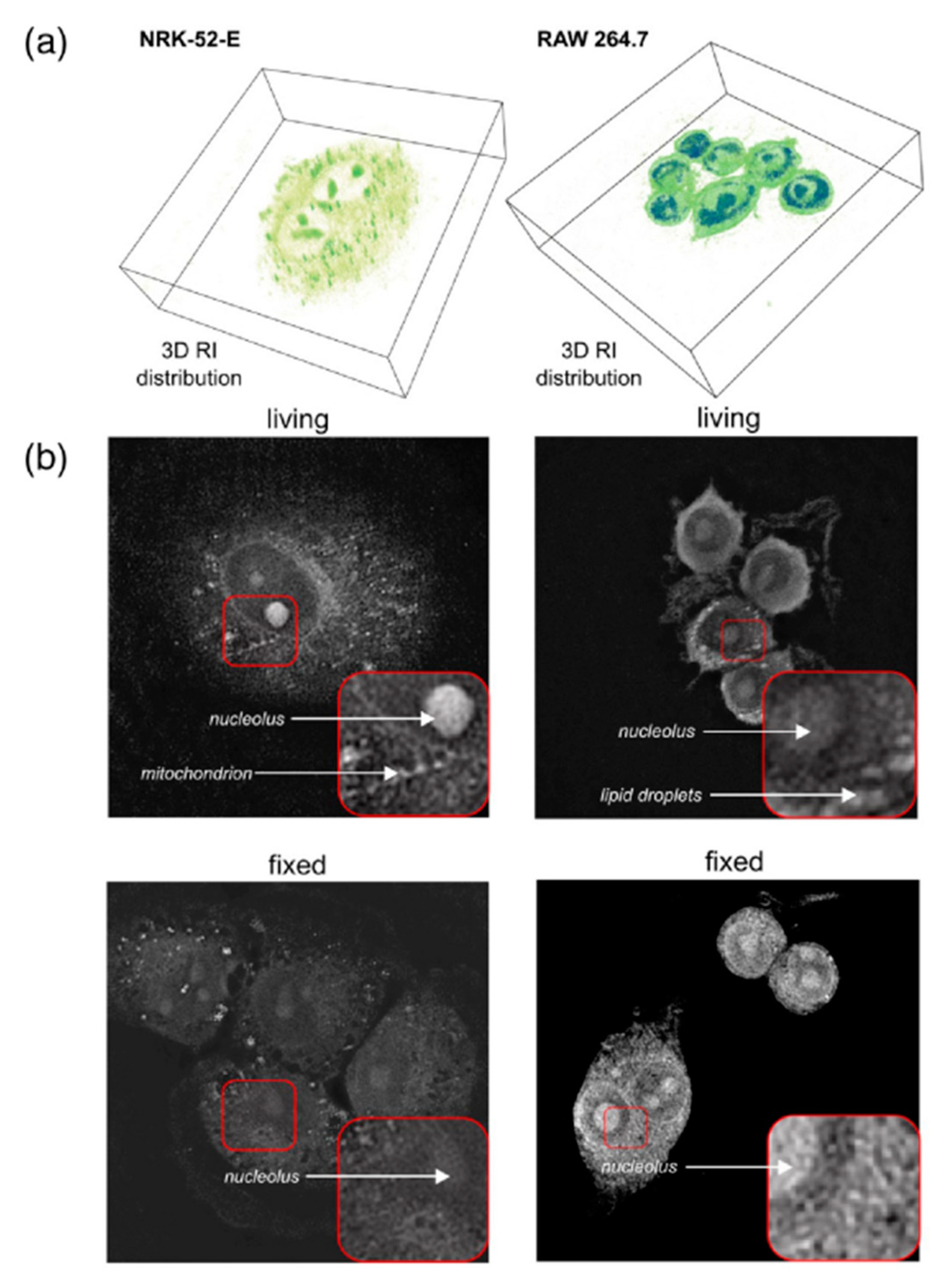
6. Digital Holography Applications
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kreis, T. Handbook of Holographic Interferometry: Optical and Digital Methods; Wiley: Hoboken, NJ, USA, 2006; p. 554. [Google Scholar]
- Hernández-Montes, M.; Mendoza-Santoyo, F.; Flores Moreno, M.; de la Torre-Ibarra, M.; Acosta, L.S.; Palacios-Ortega, N. Macro to nano specimen measurements using photons and electrons with digital holographic interferometry: A review. J. Eur. Opt. Soc.-Rapid Publ. 2020, 16, 16. [Google Scholar] [CrossRef]
- Osten, W.; Faridian, A.; Gao, P.; Körner, K.; Naik, D.; Pedrini, G.; Singh, A.K.; Takeda, M.; Wilke, M. Recent advances in digital holography. Appl. Opt. 2014, 53, G44–G63. [Google Scholar] [CrossRef] [PubMed]
- Balasubramani, V.; Kuś, A.; Tu, H.; Cheng, C.; Baczewska, M.; Krauze, W.; Kujawińska, M. Holographic tomography: Techniques and biomedical applications. Appl. Opt. 2021, 60, B65–B80. [Google Scholar] [CrossRef] [PubMed]
- Xin, L.; Xiao, W.; Che, L.; Liu, J.J.; Miccio, L.; Bianco, V.; Memmolo, P.; Ferraro, P.; Li, X.; Pan, F. Label-Free Assessment of the Drug Resistance of Epithelial Ovarian Cancer Cells in a Microfluidic Holographic Flow Cytometer Boosted through Machine Learning. ACS Omega 2021, 6, 31046–31057. [Google Scholar] [CrossRef] [PubMed]
- Goodman, J.W.; Lawrence, R.W. Digital image formation from electronically detected holograms. Appl. Phys. 1967, 11, 77–79. [Google Scholar] [CrossRef]
- Huang, T. Digital holography. Proc. IEEE 1971, 59, 1335–1346. [Google Scholar] [CrossRef]
- Kronrod, M.A.; Merzlyakov, N.S.; Yaroslavsky, L.P. Reconstruction of holograms with a computer. Sov. Phys. Tech. Phys. 1972, 17, 333–334. [Google Scholar]
- Demetrakopoulos, T.H.; Mitra, R. Digital and optical reconstruction of images from suboptical patterns. Appl. Opt. 1974, 13, 665–670. [Google Scholar] [CrossRef]
- Schnars, U.; Juptner, W. Direct recording of holograms by a CCD target and numerical reconstruction. Appl. Opt. 1994, 33, 179–181. [Google Scholar] [CrossRef]
- Vicentini, E.; Wang, Z.; Gasse, K.V.; Hänsch, T.W.; Picqué, N. Dual-comb hyperspectral digital holography. Nat. Photonics 2021, 15, 890–894. [Google Scholar] [CrossRef]
- Vicentini, E.; Chen, Z.; Huh, J.H.; Galzerano, G.; Hänsch, T.W.; Picqué, N. High-Spectral-Resolution Imaging Spectroscopy with a Dual-Comb Interferometer; Optical Society of America: Washington, DC, USA, 2020. [Google Scholar]
- Lyashenko, A.I.; Polshchikova, O.V.; Machihin, A.S.; Vlasova, A.G.; Pozhar, V.E.; Kozlov, A.B. Three-color digital holographic microscopy based on a Mach–Zehnder interferometer and a solid-state RGB laser. Quantum Electron. 2020, 50, 662–666. [Google Scholar] [CrossRef]
- Demoli, N.; Vukicevic, D.; Torzynski, M. Dynamic digital holographic interferometry with three wavelengths. Opt. Express 2003, 11, 767–774. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Vandenrijt, J.-F.; Kirkove, M.; Georges, M. Iterative phase-retrieval-assisted off-axis terahertz digital holography. Appl. Opt. 2019, 58, 9208–9216. [Google Scholar] [CrossRef]
- Guo, R.; Wang, F.; Hu, X.; Yang, W. Off-axis low coherence digital holographic interferometry for quantitative phase imaging with an LED. J. Opt. 2017, 19, 115702. [Google Scholar] [CrossRef]
- Körner, K.; Pedrini, G.; Alexeenko, I.; Steinmetz, T.; Holzwarth, R.; Osten, W. Short temporal coherence digital holography with a femtosecond frequency comb laser for multi-level optical sectioning. Opt. Express 2012, 20, 7237–7242. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Cao, L. Faithful digital holographic reconstruction using a sparse sensor array. Appl. Phys. Lett. 2020, 117, 031105. [Google Scholar] [CrossRef]
- Petrov, V.M.; Petrov, M.P.; Bryksin, V.V.; Petter, J.; Tschudi, T. Optical detection of the Casimir Force between the macroscopic objects. Opt. Lett. 2006, 21, 3167–3169. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Kuang, C.; Xu, L.; Cao, L. Multiplane digital holography based on extrapolation iterations. Opt. Commun. 2020, 481, 126526. [Google Scholar] [CrossRef]
- Guzhov, V.I.; Ilinykh, S.P.; Pozdnyakov, G.A.; Haydukov, D.S. Reconstruction of Images from Digital Holograms Obtained by Specifying Random Phase Shifts. Autometry 2019, 7, 126–135. [Google Scholar] [CrossRef]
- Tahara, T.; Ishii, A.; Ito, T.; Ichihashi, Y.; Oi, R. Single-shot wavelength-multiplexed digital holography for 3D fluorescent microscopy and other imaging modalities. Appl. Phys. Lett. 2020, 117, 031102. [Google Scholar] [CrossRef]
- Matoba, O.; Quan, X.; Xia, P.; Awatsuji, Y.; Nomura, T. Multimodal Imaging Based on Digital Holography. Proc. IEEE 2019, 105, 906–923. [Google Scholar] [CrossRef]
- Guzhov, V.I.; Ilinykh, S.P.; Marchenko, I.O. Method for increasing spatial resolution in digital holographic microscopy. Autometry 2018, 54, 301–306. [Google Scholar] [CrossRef]
- Tsuruta, M.; Fukuyama, T.; Tahara, T.; Takaki, Y. Fast Image Reconstruction Technique for Parallel Phase-Shifting Digital Holography. Appl. Sci. 2021, 11, 11343. [Google Scholar] [CrossRef]
- Greysuh, G.I.; Ezhov, E.G.; Kazin, S.V.; Stepanov, S.A. Matrix photodetectors in digital holography and holographic interferometry. In Proceedings of the XIV International Conference HOLOEXPO, Zvenigorod, Russia, 12–14 September 2017; pp. 50–52, ISBN 978-5-7038-4771-8. [Google Scholar]
- Balbekin, N.S.; Venediktov, V.Y.; Venediktov, D.V.; Petrov, N.V.; Konovalov, R.S.; Pul’kin, S.A.; Sevryugin, A.A.; Tursunov, I.; Shoev, V.I. Increasing the Interferogram Sensitivity by Digital Holography. Optoelectron. Instrum. Data Process. 2020, 56, 190–197. [Google Scholar] [CrossRef]
- Jeon, S.; Cho, J.; Jin, J.; Park, N.-C.; Park, Y.-P. Dual-wavelength digital holography with a single low-coherence light source. Opt. Express 2016, 24, 18408–18416. [Google Scholar] [CrossRef]
- Morimoto, Y.; Toru, M.; Fujigaki, M.; Kawagishi, N. Subnanometer displacement measurement by averaging of phase difference in windowed digital holographic interferometry. Opt. Eng. 2007, 46, 025603. [Google Scholar] [CrossRef]
- Min, J.; Yao, B.; Gao, P.; Guo, R.; Ma, B.; Zheng, J.; Lei, M.; Yan, S.; Dan, D.; Duan, T.; et al. Dual-wavelength slightly off-axis digital holographic microscopy. Appl. Opt. 2012, 51, 191–196. [Google Scholar] [CrossRef]
- Di, J.; Song, Y.; Xi, T.; Zhang, J.; Li, Y.; Ma, C.; Wang, K.; Zhao, J. Dual-wavelength common-path digital holographic microscopy for quantitative phase imaging of biological cells. Opt. Eng. 2017, 56, 111712. [Google Scholar] [CrossRef]
- Zaydel, A.N. Application of holographic interferometry for plasma diagnostics. Adv. Phys. Sci. 1986, 149, 105–138. [Google Scholar]
- Zhou, H.; Hussain, M.R.; Banerjee, P.P. A review of the dual-wavelength technique for phase imaging and 3D topography. Light Adv. Manuf. 2022, 3, 17. [Google Scholar] [CrossRef]
- Servin, M.; Padilla, M.; Garnica, G. Super-sensitive two-wavelength fringe projection profilometry with 2-sensitivities temporal unwrapping. Opt. Lasers Eng. 2018, 106, 68–74. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Cao, L.; Brady, D.J.; Zhang, H.; Cang, J.; Zhang, H.; Jin, G. Twin-image-free holography: A compressive sensing approach. Phys. Rev. Lett. 2018, 121, 93902–93907. [Google Scholar] [CrossRef] [PubMed]
- Bai, C.; Peng, T.; Min, J.; Li, R.; Zhou, Y.; Yao, B. Dual-wavelength in-line digital holography with untrained deep neural networks. Photonics Res. 2021, 9, 2501–2510. [Google Scholar] [CrossRef]
- Gass, J.; Dakoff, A.; Kim, M.K. Phase imaging without 2π ambiguity by multiwavelength digital holography. Opt. Lett. 2003, 28, 1141–1143. [Google Scholar] [CrossRef]
- Khmaladze, A.; Matz, R.L.; Zhang, C.; Wang, T.; Holl, M.M.B.; Chen, Z. Dual-wavelength linear regression phase unwrapping in three dimensional microscopic images of cancer cells. Opt. Lett. 2011, 36, 912–914. [Google Scholar] [CrossRef] [PubMed]
- Abdelsalam, D.G.; Magnusson, R.; Kim, D. Single-shot dual wavelength digital holography based on polarizing separation. Appl. Opt. 2011, 50, 3360–3368. [Google Scholar] [CrossRef]
- Sen, A.P.; Rout, N.K. A Comparative Analysis of the Algorithms for De-noising Images Contaminated with Impulse Noise. Sens. Imaging 2022, 23, 11. [Google Scholar] [CrossRef]
- Ghareab, D.; Ibrahim, A. Quantitative phase imaging using a combination of flat fielding and windowed Fourier filtering demodulated by a graph cuts algorithm for screening opaque and transparent objects. Opt. Contin. 2022, 1, 246–260. [Google Scholar]
- Pförtner, A.; Schwider, J. Dispersion error in white-light Linnik interferometers and its implications for evaluation procedures. Appl. Opt. 2001, 40, 6223–6228. [Google Scholar] [CrossRef]
- Claus, D.; Alekseenko, I.; Grabherr, M.; Pedrini, G.; Hibst, R. Snap-shot topography measurement via dual-VCSEL and dual wavelength digital holographic interferometry. Light Adv. Manuf. 2021, 2, 29. [Google Scholar] [CrossRef]
- Tian, X.; Tu, X.; Zhang, J.; Spires, O.; Brock, N.; Pau, S.; Liang, R. Snapshot multi-wavelength interference microscope. Opt. Express 2018, 26, 18279–18291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Muhamedsalih, H.; Al-Bashir, S.; Gao, F.; Jiang, X. Single-shot RGB polarising interferometer. Interferom. XIX 2018, 10749, 52–57. [Google Scholar]
- Jeon, J.W.; Joo, K.-N. Single-Shot Imaging of Two-Wavelength Spatial Phase-Shifting Interferometry. Sensors 2019, 19, 5094. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Popov, E.E.; Sergeev, A.A.; Pogoda, A.P.; Petrov, V.M.; Boreysho, A.S. Electro-optic Q-switched Cr: LiSAF laser. J. Phys. Conf. Ser. 2021, 2094, 022034. [Google Scholar] [CrossRef]
- Popov, E.E.; Sergeev, A.A.; Pogoda, A.P.; Boreysho, A.S. Lamp pumped LiSrAlF6: Cr laser with Bragg grating. J. Phys. Conf. Ser. 2019, 1399, 022030. [Google Scholar] [CrossRef] [Green Version]
- Jaferzadeh, K.; Hwang, S.H.; Moon, I. No-search focus prediction at the single cell level in digital holographic imaging with deep convolutional neural network. Biomed. Opt. Express 2019, 10, 4276. [Google Scholar] [CrossRef]
- Zeng, T.; Zhu, Y.; Lam, E.Y. Deep learning for digital holography: A review. Opt. Express 2021, 29, 40572–40593. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Lam, E.Y.M. End-to-end deep learning framework for digital holographic reconstruction. Adv. Photonics 2019, 1, 016004. [Google Scholar] [CrossRef]
- Ma, S.; Fang, R.; Luo, Y.; Liu, Q.; Wang, S.; Zhou, X. Phase-aberration compensation via deep learning in digital holographic microscopy. Meas. Sci. Technol. 2021, 32, 10. [Google Scholar] [CrossRef]
- Ren, Z.; Xu, Z.; Lam, E.Y. Autofocusing in digital holography using deep learning. In Three-Dimensional and Multidimensional Microscopy: Image Acquisition and Processing XXV; Spie: Bellingham, DC, USA, 2018; Volume 10499, p. 1. [Google Scholar]
- Pitkäaho, T.; Manninen, A.; Naughton, T.J. Focus prediction in digital holographic microscopy using deep convolutional neural networks. Appl. Opt. 2019, 58, A202–A208. [Google Scholar] [CrossRef]
- Yin, D.; Gu, Z.; Zhang, Y.; Gu, F.; Nie, S.; Ma, J.; Yuan, C. Digital Holographic Reconstruction Based on Deep Learning Framework With Unpaired Data. IEEE Photonics J. 2020, 12, 2. [Google Scholar] [CrossRef]
- Lam, E.Y.; Zeng, T. Computational Imaging in Digital Holographic Reconstruction with Machine Learning. In Proceedings of the IEEE International Conference on Computational Electromagnetics, Singapore, 24–26 August 2020. [Google Scholar]
- Huang, Z.; Cao, L. Bicubic interpolation and extrapolation iteration method for high resolution digital holographic reconstruction. Opt. Lasers Eng. 2020, 130, 106090. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, J.; Chen, Q.; Zuo, C. Resolution analysis in a lens-free on-chip digital holographic microscope. IEEE Trans. Comput. Imaging 2020, 6, 697–710. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Jiang, Z.; Wang, Y.; Sun, Q.; Chen, H. Single-frame reconstruction for improvement of off-axis digital holographic imaging based on image interpolation. Opt. Lett. 2020, 45, 6623–6626. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Cao, L. Generalized optimization framework for pixel super-resolution imaging in digital holography. Opt. Express 2021, 29, 28805–28823. [Google Scholar] [CrossRef]
- Souza, J.C.; Freire, R.B.R.; Santos, P.A.M. Subsampled digital holographic image reconstruction by a compressive sensing approach. Appl. Opt. 2021, 60, 1–9. [Google Scholar] [CrossRef]
- Sun, B.; Ahmed, A.; Atkinson, C.; Soria, J. A novel 4D digital holographic PIV/PTV (4D-DHPIV/PTV) methodology using iterative predictive inverse reconstruction. Meas. Sci. Technol. 2020, 31, 10. [Google Scholar] [CrossRef]
- Ren, R.; Jia, Z.; Yang, J.; Kasabov, N.K.; Huang, X. Quasi-Noise-Free and Detail-Preserved Digital Holographic Reconstruction. IEEE Access 2019, 7, 52155–52167. [Google Scholar] [CrossRef]
- Pellizzari, C.J.; Spencer, M.F.; Bouman, C.A. Phase-error estimation and image reconstruction from digital-holography data using a Bayesian framework. J. Opt. Soc. Am. A 2017, 34, 1659–1669. [Google Scholar] [CrossRef] [Green Version]
- Bazow, B.; Phan, T.; Nguyen, T.; Raub, C.; Nehmetallah, G. Simulation of digital holographic recording and reconstruction using a generalized matrix method. Appl. Opt. 2021, 60, A21–A37. [Google Scholar] [CrossRef]
- Singh, M.; Khare, K. Single-shot full resolution region-of-interest (ROI) reconstruction in image plane digital holographic microscopy. J. Mod. Opt. 2018, 65, 9. [Google Scholar] [CrossRef]
- Latychevskaia, T. Iterative phase retrieval for digital holography: Tutorial. J. Opt. Soc. Am. A 2019, 36, D31–D40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Birdi, J.; Rajora, S.; Butola, M.; Khare, K. True 3D reconstruction in digital holography. J. Phys. Photonics 2020, 2, 4. [Google Scholar] [CrossRef]
- Martínez-León, L.; Clemente, P.; Mori, Y.; Climent, V.; Lancis, J.; Tajahuerce, E. Single-pixel digital holography with phase-encoded illumination. Opt. Express 2017, 25, 4975–4984. [Google Scholar] [CrossRef] [PubMed]
- Schretter, C.; Blinder, D.; Bettens, S.; Ottevaere, H.; Schelkens, P. Regularized non-convex image reconstruction in digital holographic microscopy. Opt. Express 2017, 25, 16491–16508. [Google Scholar] [CrossRef]
- Bettens, S.; Yan, H.; Blinder, D.; Ottevaere, H.; Schretter, C.; Schelkens, P. Studies on the sparsifying operator in compressive digital holography. Opt. Express 2017, 25, 18656–18676. [Google Scholar] [CrossRef]
- Kurbatova, E.A.; Cheryomhin, P.A. Binarization of digital holograms for tasks using a micromirror modulator. In Proceedings of the XVI International Conference HOLOEXPO, Proceedings, St. Petersburg, Russia, 10–12 September 2019; pp. 356–359, ISBN 978-5-7038-5251-4. [Google Scholar]
- Kurbatova, E.A.; Rodin, V.G.; Cheryomhin, P.A. Iterative Binarization of Digital Holograms Using the Error Diffusion Method. Autometry 2020, 56, 118–125. [Google Scholar] [CrossRef]
- Kozacki, T.; Martinez-Carranza, J.; Kukolowicz, R.; Chlipala, M. Fourier horizontal parallax only computer and digital holography of large size. Opt. Express 2021, 29, 18173–18191. [Google Scholar] [CrossRef]
- Pedrini, G.; Osten, W.; Gusev, M.E. High-speed digital holographic interferometry for vibration measurement. Appl. Opt. 2006, 45, 3456–3462. [Google Scholar] [CrossRef]
- Asundi, A.; Singh, V.R. Amplitude and phase analysis in digital dynamic holography. Opt. Lett. 2006, 31, 2420–2422. [Google Scholar] [CrossRef]
- Xia, H.; Guo, R.; Yan, F.; Cheng, H. Real-Time and Quantitative Measurement of Crack-Tip Stress Intensity Factors Using Digital Holographic Interferometry. Adv. Mater. Sci. Eng. 2018, 2018, 1954573. [Google Scholar] [CrossRef] [Green Version]
- Curbeli, R.; Psota, P.; Dancova, P.; Ledl, V.; Vit, T. Digital Holographic Interferometry for the Measurement of Symmetrical Temperature Fields in Liquids. Photonics 2021, 8, 200. [Google Scholar]
- Shimobaba, T.; Takahashi, T.; Yamamoto, Y.; Endo, Y.; Shiraki, A.; Nishitsuji, T.; Hoshikawa, N.; Kakue, T.; Ito, T. Digital holographic particle volume reconstruction using a deep neural network. Appl. Opt. 2019, 58, 1900–1906. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Huang, J.; Li, S.; Zi, Y.; Qian, Y.; Cai, W.; Aldén, M.; Li, Z. Clustering-based particle detection method for digital holography to detect the three-dimensional location and in-plane size of particles. Meas. Sci. Technol. 2021, 32, 5. [Google Scholar] [CrossRef]
- Kemppinen, O.; Heinson, Y.; Berg, M. Quasi-three-dimensional particle imaging with digital holography. Appl. Opt. 2017, 56, F53–F60. [Google Scholar] [CrossRef]
- Baczewska, M.; Eder, K.; Ketelhut, S.; Kemper, B.; Kujawinska, M. Refractive index changes of cells and cellular compartments upon paraformaldehyde fixation acquired by tomographic phase microscopy. Cytom. Part A 2020, 97, 1–11. [Google Scholar] [CrossRef]
- Fukuda, T.; Wang, Y.; Xia, P.; Awatsuji, Y.; Kakue, T.; Nishio, K.; Matoba, O. Three-dimensional imaging of distribution of refractive index by parallel phase-shifting digital holography using Abel inversion. Opt. Express 2017, 25, 18066–18071. [Google Scholar] [CrossRef]
- Vaziri, R.; Beigzadeh, A.M.; Ziaie, F. Digital holographic interferometry for measuring the absorbed three-dimensional dose distribution. Eur. Phys. J. Plus 2020, 135, 436. [Google Scholar] [CrossRef]
- Pavlov, P.V.; Wolf, I.E.; Kuskov, I.E.; Bogdanov, Y.N. Computer Holography Method as a Tool for Non-Destructive Testing of Aircraft Cabin Glazing Elements. Aerosp. Forces Theory Pract. 2020, 16, 212–220. [Google Scholar]
- Lédl, V.; Psota, P.; Kaván, F.; Matoušek, O.; Mokrý, P. Surface topography measurement by frequency sweeping digital holography. Appl. Opt. 2017, 56, 7808–7814. [Google Scholar] [CrossRef]
- Simon, B.; Debailleul, M.; Houkal, M.; Ecoffet, C.; Bailleul, J.; Lambert, J.; Spangenberg, A.; Liu, H.; Soppera, O.; Haeberlé, O. Tomographic diffractive microscopy with isotropic resolution. Optica 2017, 4, 460–463. [Google Scholar] [CrossRef]
- Park, Y.; Depeursinge, C.; Popescu, G. Quantitative phase imaging in biomedicine. Nat. Photon 2018, 12, 578–589. [Google Scholar] [CrossRef]
- Lee, A.J.; Hugonnet, H.; Park, W.S.; Park, Y.K. Three-dimensional label-free imaging and quantification of migrating cells during wound healing. Biomed. Opt. Express 2020, 11, 6812–6824. [Google Scholar] [CrossRef]
- Ugele, M.; Weniger, M.; Leidenberger, M.; Huang, Y.; Bassler, M.; Friedrich, O.; Kappes, B.; Hayden, O.; Richter, L. Label-free, high-throughput detection of P. falciparum infection in sphered erythrocytes with digital holographic microscopy. Lab Chip 2018, 18, 1704–1712. [Google Scholar] [CrossRef] [PubMed]
- Mirsky, S.K.; Barnea, I.; Shaked, N.T. Dynamic Tomographic Phase Microscopy by Double Six-Pack Holography. Opt. Lasers Eng. 2022, 149, 106783. [Google Scholar] [CrossRef]
- Emery, Y.; Colomb, T.; Cuche, E. Metrology applications using off-axis digital holography microscopy J. Phys. Photonics 2021, 3, 034016. [Google Scholar] [CrossRef]
- Bettenworth, D.; Bokemeyer, A.; Poremba, C.; Ding, N.S.; Ketelhut, S.; Lenz, P.; Kemper, B. Quantitative phase microscopy for evaluation of intestinal inflammation and wound healing utilizing label-free biophysical markers. Histol. Histopathol. 2018, 33, 417–432. [Google Scholar]
- Javidi, B.; Carnicer, A.; Anand, A. Roadmap on digital holography. Opt. Express. 2021, 29, 35078–35118. [Google Scholar] [CrossRef]
- Sheridan, J.T.; Kostuk, R.K.; Gil, A.F. Roadmap on holography. J. Opt. 2020, 22, 123002. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrov, V.; Pogoda, A.; Sementin, V.; Sevryugin, A.; Shalymov, E.; Venediktov, D.; Venediktov, V. Advances in Digital Holographic Interferometry. J. Imaging 2022, 8, 196. https://doi.org/10.3390/jimaging8070196
Petrov V, Pogoda A, Sementin V, Sevryugin A, Shalymov E, Venediktov D, Venediktov V. Advances in Digital Holographic Interferometry. Journal of Imaging. 2022; 8(7):196. https://doi.org/10.3390/jimaging8070196
Chicago/Turabian StylePetrov, Viktor, Anastsiya Pogoda, Vladimir Sementin, Alexander Sevryugin, Egor Shalymov, Dmitrii Venediktov, and Vladimir Venediktov. 2022. "Advances in Digital Holographic Interferometry" Journal of Imaging 8, no. 7: 196. https://doi.org/10.3390/jimaging8070196
APA StylePetrov, V., Pogoda, A., Sementin, V., Sevryugin, A., Shalymov, E., Venediktov, D., & Venediktov, V. (2022). Advances in Digital Holographic Interferometry. Journal of Imaging, 8(7), 196. https://doi.org/10.3390/jimaging8070196




