Unified Probabilistic Deep Continual Learning through Generative Replay and Open Set Recognition
Abstract
:1. Introduction
1.1. Background and Related Work
1.1.1. Continual Learning
1.1.2. Out-of-Distribution and Open Set Recognition
2. Materials and Methods
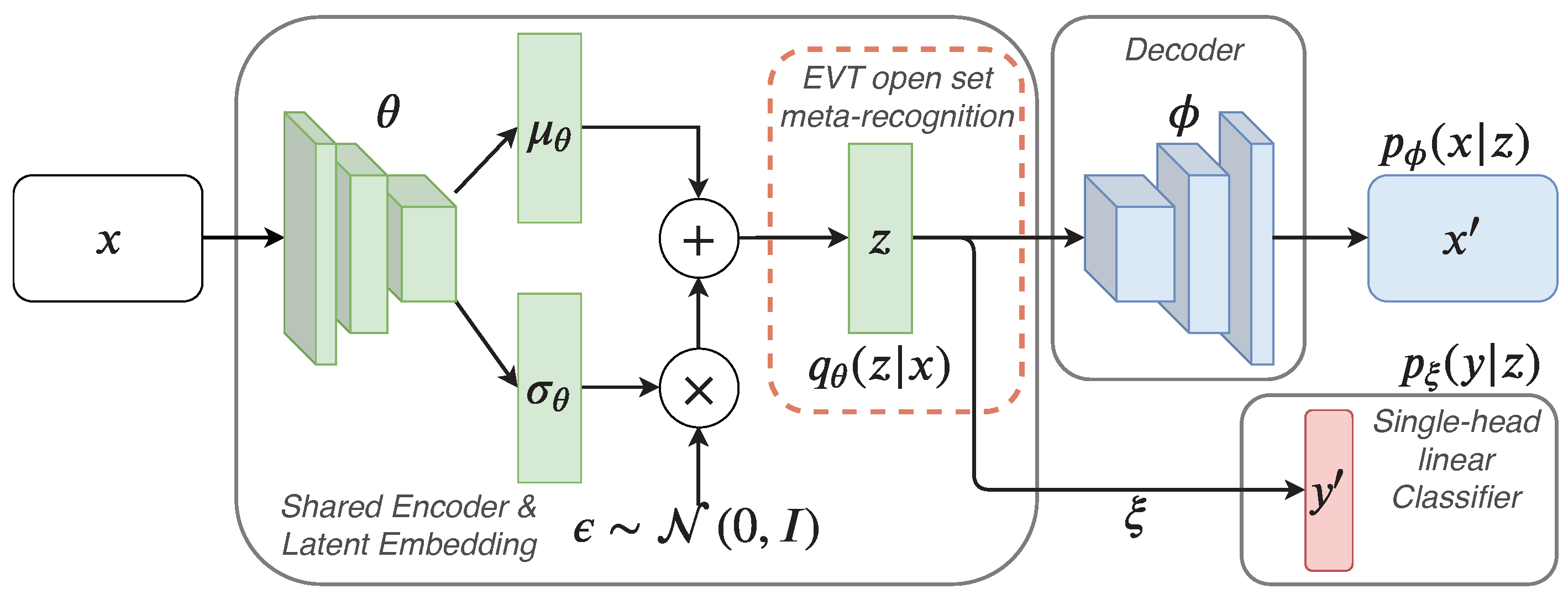
2.1. Unifying Catastrophic Interference Prevention with Open Set Recognition
2.1.1. Preliminaries: Learning Continually through Variational Auto-Encoding
2.1.2. Open Set Recognition and Generative Replay with Statistical Outlier Rejection
- For a novel data instance, Equation (6) yields the outlier probability based on the probabilistic encoder , and a false overconfident classifier prediction can be avoided.
3. Results
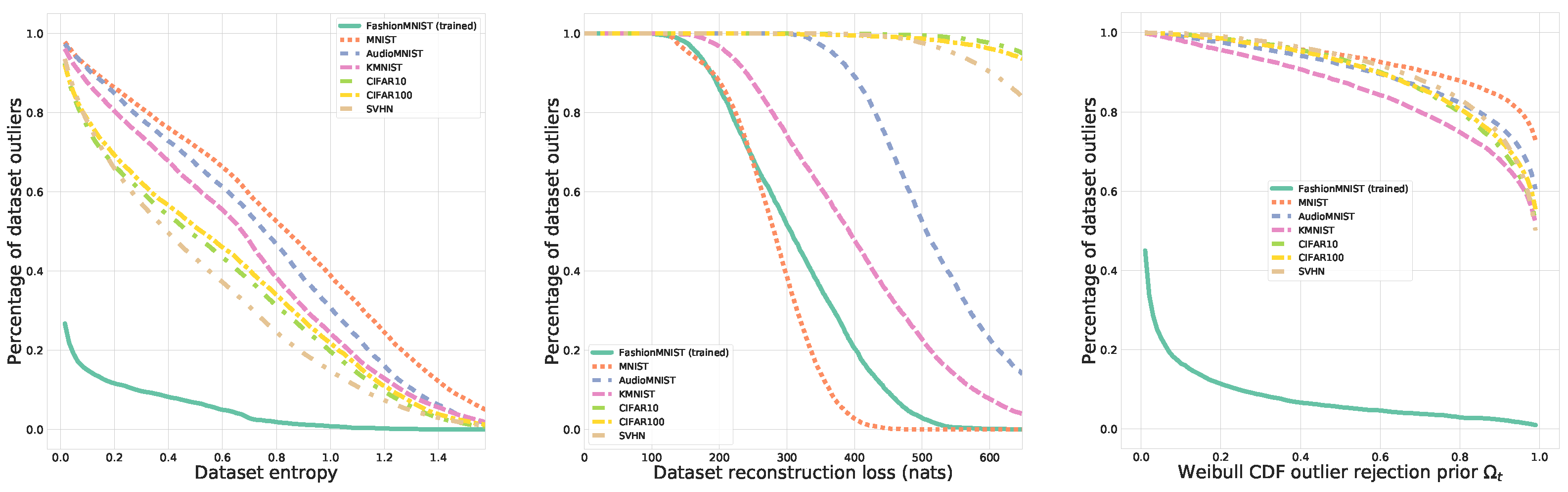
3.1. Open Set Recognition
- The classifier’s predictive entropy, as recently suggested to work surprisingly well in deep networks [58] but technically well known to be overconfident [3]. The intuition here is that the predictive entropy considers the probability of all other classes and is at a maximum if the distribution is uniform, i.e., when the confidence in the prediction is low.
- Our suggested OpenVAE aggregate posterior-based EVT approach, according to the outlier likelihood introduced Equation (6).
- Both EVT approaches generally outperform the other criteria, particularly for our suggested aggregate posterior-based OpenVAE variant, where a near perfect open-set detection can be achieved.
- Even though EVT can be applied to purely discriminative models (as in OpenMax), the generative OpenVAE model trained with variational inference consistently exhibited more accurate outlier detection. We posit that this robustness is due to OpenVAE explicitly optimizing a variational lower bound that considers the data distribution in addition to a pure optimization of features that maximize .
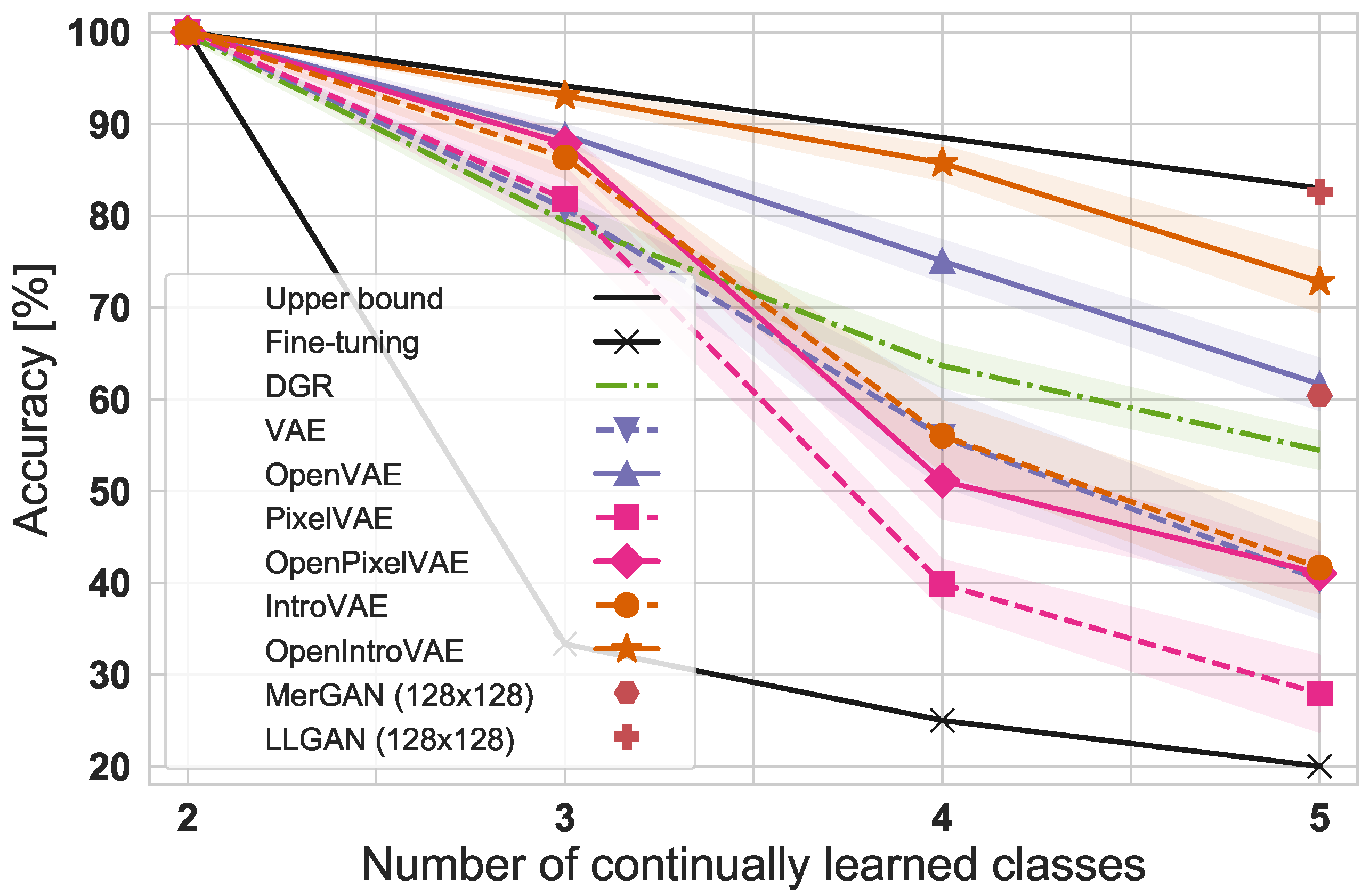
3.2. Learning Classes Incrementally in Continual Learning
4. Discussion
4.1. Presence of Unknown Data and Current Benchmarks
4.2. State of the Art in Class Incremental Learning and Exemplar Rehearsal
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
- Appendix A.1
- Derivation of the lower-bound, Equation (1) of the main body.
- Appendix A.2
- Extended discussion, qualitative and quantitative examples for the role of .
- Appendix A.3
- Description of generative model extensions: autoregression and introspection.
- Appendix A.4
- The full specification of the training procedure and hyper-parameters, including exact architecture definitions.
- Appendix A.5
- Discussion of limitations.
Appendix A.1. Lower-Bound Derivation
Appendix A.2. Further Discussion on the Role of β

| In Nats per Dimension (Nats in Brackets) | |||||
|---|---|---|---|---|---|
| 2-D Latent | Beta | KLD | Recon Loss | Class Loss | Accuracy [%] |
| train | 1.0 | 1.039 (2.078) | 0.237 (185.8) | 0.539 (5.39) | 79.87 |
| test | 1.030 (2.060) | 0.235 (184.3) | 0.596 (5.96) | 78.30 | |
| train | 0.5 | 1.406 (2.812) | 0.230 (180.4) | 0.221 (2.21) | 93.88 |
| test | 1.382 (2.764) | 0.228 (178.8) | 0.305 (3.05) | 92.07 | |
| train | 0.1 | 2.055 (4.110) | 0.214 (167.8) | 0.042 (0.42) | 99.68 |
| test | 2.071 (4.142) | 0.212 (166.3) | 0.116 (1.16) | 98.73 | |
| train | 0.05 | 2.395 (4.790) | 0.208 (163.1) | 0.025 (0.25) | 99.83 |
| test | 2.382 (4.764) | 0.206 (161.6) | 0.159 (1.59) | 98.79 | |
| In Nats per Dimension (Nats in Brackets) | |||||
|---|---|---|---|---|---|
| 60-D Latent | Beta | KLD | Recon Loss | Class Loss | Accuracy [%] |
| train | 1.0 | 0.108 (6.480) | 0.184 (144.3) | 0.0110 (0.110) | 99.71 |
| test | 0.110 (6.600) | 0.181 (142.0) | 0.0457 (0.457) | 99.03 | |
| train | 0.5 | 0.151 (9.060) | 0.162 (127.1) | 0.0052 (0.052) | 99.87 |
| test | 0.156 (9.360) | 0.159 (124.7) | 0.0451 (0.451) | 99.14 | |
| train | 0.1 | 0.346 (20.76) | 0.124 (97.22) | 0.0022 (0.022) | 99.95 |
| test | 0.342 (20.52) | 0.126 (98.79) | 0.0286 (0.286) | 99.38 | |
| train | 0.05 | 0.476 (28.56) | 0.115 (90.16) | 0.0018 (0.018) | 99.95 |
| test | 0.471 (28.26) | 0.118 (92.53) | 0.0311 (0.311) | 99.34 | |
Appendix A.3. Complementary Generative Modelling Advances
Appendix A.3.1. Improvements through Autoregressive Decoding
Appendix A.3.2. Introspection and Adversarial Training
Appendix A.4. Training Hyper-Parameters and Architecture Definitions
| Layer Type | WRN Encoder |
|---|---|
| Layer 1 | conv —48, p = 1 |
| Block 1 | conv —160, p = 1; conv —160 (skip next layer) conv —160, p = 1 conv —160, p = 1; shortcut (skip next layer) conv —160, p = 1 |
| Block 2 | conv —320, s = 2, p = 1; conv —320, s = 2 (skip next layer) conv —320, p = 1 conv —320, p = 1; shortcut (skip next layer) conv —320, p = 1 |
| Block 3 | conv —640, s = 2, p = 1; conv —640, s = 2 (skip next layer) conv —640, p = 1 conv —640, p = 1; shortcut (skip next layer) conv —640, p = 1 |
| Layer Type | WRN Decoder |
|---|---|
| Layer 1 | FC |
| Block 1 | conv_t —320, p = 1; conv_t —320 (skip next layer) conv —320, p = 1 conv — 320, p = 1; shortcut (skip next layer) conv —320, p = 1 upsample × 2 |
| Block 2 | conv_t —160, p = 1; conv_t —160 (skip next layer) conv —160, p = 1 conv — 160, p = 1; shortcut (skip next layer) conv —160, p = 1 upsample × 2 |
| Block 3 | conv_t —48, p = 1; conv_t —48 (skip next layer) conv —48, p = 1 conv —48, p = 1; shortcut (skip next layer) conv —48, p = 1 |
| Layer 2 | conv —3, p = 1 |
Appendix A.5. Limitations
- Limitations of our proposed aggregate posterior-based EVT approach and its use for open-set recognition and generative replay.
- Limitations of the employed generative model variant, i.e., caveats of autoregression or introspection.
- Limitations in terms of obtainable insights from investigated scenarios, i.e., the specific continual-learning set-up.
Appendix A.5.1. Aggregate Posterior-Based EVT Limitations
Appendix A.5.2. Limitations of the Employed Generative Model Variants
Appendix A.5.3. Limitations of the Investigated Scenarios
Appendix A.6. Full Continual Learning Results for All Intermediate Steps
| MNIST | t | UB | FT | SupVAE | OpenVAE | PixelVAE DGR | SupPixelVAE | OpenPixelVAE |
|---|---|---|---|---|---|---|---|---|
| (%) | 1 | 100.0 | 100.0 | 99.98 | 99.97 | 99.97 | 99.86 | |
| 2 | 99.82 | 00.00 | 97.28 | 99.30 | 99.54 | 96.90 | 99.64 | |
| 3 | 99.80 | 00.00 | 87.66 | 96.69 | 99.16 | 90.12 | 98.88 | |
| 4 | 99.85 | 00.00 | 54.70 | 94.71 | 98.33 | 76.84 | 98.11 | |
| 5 | 99.57 | 00.00 | 19.86 | 92.53 | 98.04 | 56.53 | 97.44 | |
| (%) | 1 | 100.0 | 100.0 | 99.97 | 99.98 | 99.97 | 99.97 | 99.86 |
| 2 | 99.80 | 99.85 | 99.75 | 99.80 | 99.71 | 99.74 | 99.82 | |
| 3 | 99.67 | 99.94 | 99.63 | 99.61 | 99.41 | 99.22 | 99.56 | |
| 4 | 99.49 | 100.0 | 99.05 | 99.15 | 98.61 | 97.84 | 98.80 | |
| 5 | 99.10 | 99.86 | 99.00 | 99.06 | 97.31 | 96.77 | 98.63 | |
| (%) | 1 | 100.0 | 100.0 | 99.97 | 99.98 | 99.97 | 99.97 | 99.86 |
| 2 | 99.81 | 49.92 | 98.54 | 99.55 | 99.60 | 98.37 | 99.69 | |
| 3 | 99.72 | 31.35 | 95.01 | 98.46 | 98.93 | 96.14 | 99.20 | |
| 4 | 99.50 | 24.82 | 81.50 | 97.06 | 98.22 | 91.25 | 98.13 | |
| 5 | 99.29 | 20.16 | 64.34 | 93.24 | 96.52 | 83.61 | 96.84 | |
| (nats) | 1 | 63.18 | 62.08 | 64.34 | 62.53 | 90.52 | 100.0 | 99.77 |
| 2 | 62.85 | 126.8 | 74.41 | 65.68 | 91.27 | 100.4 | 101.2 | |
| 3 | 63.36 | 160.4 | 81.89 | 69.29 | 91.92 | 100.3 | 101.1 | |
| 4 | 64.25 | 126.9 | 90.62 | 71.69 | 91.75 | 102.7 | 101.0 | |
| 5 | 64.99 | 123.2 | 101.6 | 77.16 | 92.05 | 102.4 | 100.5 | |
| (nats) | 1 | 63.18 | 62.08 | 64.34 | 62.53 | 90.52 | 100.0 | 99.77 |
| 2 | 88.75 | 87.93 | 89.91 | 89.64 | 115.8 | 125.7 | 124.6 | |
| 3 | 82.53 | 87.22 | 87.65 | 85.37 | 107.7 | 118.3 | 116.5 | |
| 4 | 72.68 | 74.61 | 79.49 | 74.75 | 100.9 | 107.1 | 102.3 | |
| 5 | 85.88 | 92.00 | 93.55 | 89.68 | 113.4 | 118.2 | 113.3 | |
| (nats) | 1 | 63.18 | 62.08 | 64.34 | 62.53 | 90.52 | 100.0 | 99.77 |
| 2 | 75.97 | 107.3 | 82.02 | 76.62 | 102.9 | 111.9 | 112.7 | |
| 3 | 79.58 | 172.3 | 89.88 | 82.95 | 104.8 | 114.9 | 114.6 | |
| 4 | 79.72 | 203.1 | 95.83 | 85.30 | 103.9 | 114.3 | 112.1 | |
| 5 | 81.97 | 163.7 | 107.6 | 92.92 | 106.1 | 118.7 | 111.9 |
| Fashion | t | UB | FT | SupVAE | OpenVAE | PixelVAE DGR | SupPixelVAE | OpenPixelVAE |
|---|---|---|---|---|---|---|---|---|
| (%) | 1 | 99.65 | 99.60 | 99.55 | 99.59 | 99.57 | 99.58 | 99.54 |
| 2 | 96.70 | 00.00 | 92.02 | 92.36 | 82.40 | 90.06 | 88.60 | |
| 3 | 95.95 | 00.00 | 79.26 | 83.90 | 78.55 | 83.70 | 87.66 | |
| 4 | 91.35 | 00.00 | 50.16 | 64.70 | 54.69 | 50.23 | 68.31 | |
| 5 | 92.20 | 00.00 | 39.51 | 60.63 | 60.04 | 47.83 | 74.45 | |
| (%) | 1 | 99.65 | 99.60 | 99.55 | 99.59 | 99.57 | 99.58 | 99.54 |
| 2 | 95.55 | 97.95 | 90.98 | 92.64 | 97.73 | 96.47 | 97.31 | |
| 3 | 93.35 | 99.95 | 90.26 | 83.40 | 99.09 | 97.33 | 96.88 | |
| 4 | 84.75 | 99.90 | 85.65 | 84.18 | 97.55 | 96.12 | 95.47 | |
| 5 | 97.50 | 99.80 | 96.92 | 96.51 | 98.85 | 97.91 | 98.63 | |
| (%) | 1 | 99.65 | 99.60 | 99.55 | 99.59 | 99.57 | 99.58 | 99.54 |
| 2 | 95.75 | 48.97 | 91.83 | 92.31 | 86.22 | 92.93 | 92.17 | |
| 3 | 93.02 | 33.33 | 83.35 | 86.93 | 76.77 | 84.07 | 87.30 | |
| 4 | 87.51 | 25.00 | 64.66 | 76.05 | 62.93 | 64.42 | 76.36 | |
| 5 | 89.24 | 19.97 | 58.82 | 69.88 | 72.41 | 63.05 | 80.85 | |
| (nast) | 1 | 209.7 | 209.8 | 208.9 | 209.7 | 267.8 | 230.8 | 232.0 |
| 2 | 207.4 | 240.7 | 212.7 | 212.1 | 273.6 | 232.5 | 231.8 | |
| 3 | 207.6 | 258.7 | 219.5 | 216.9 | 274.0 | 235.6 | 231.6 | |
| 4 | 207.7 | 243.6 | 223.8 | 217.1 | 273.7 | 236.4 | 231.4 | |
| 5 | 208.4 | 306.5 | 232.8 | 222.8 | 274.1 | 241.1 | 234.1 | |
| (nast) | 1 | 209.7 | 209.8 | 208.9 | 209.7 | 267.8 | 230.8 | 232.0 |
| 2 | 241.1 | 240.2 | 241.8 | 241.9 | 313.4 | 275.8 | 275.3 | |
| 3 | 213.6 | 211.8 | 215.4 | 213.0 | 269.1 | 268.3 | 262.9 | |
| 4 | 220.5 | 219.7 | 223.6 | 220.9 | 282.4 | 259.1 | 259.6 | |
| 5 | 246.2 | 242.0 | 248.8 | 244.0 | 305.8 | 283.2 | 283.5 | |
| (nast) | 1 | 209.7 | 209.8 | 208.9 | 209.7 | 267.8 | 230.8 | 232.0 |
| 2 | 224.2 | 240.4 | 226.6 | 226.9 | 293.8 | 254.3 | 255.8 | |
| 3 | 220.7 | 246.1 | 227.2 | 224.9 | 285.7 | 261.5 | 259.1 | |
| 4 | 220.4 | 238.7 | 230.4 | 226.1 | 284.9 | 263.2 | 259.5 | |
| 5 | 226.2 | 275.1 | 242.2 | 234.6 | 289.5 | 271.7 | 267.2 |
| Audio | t | UB | LB | SupVAE | OpenVAE | PixelVAE DGR | SupPixelVAE | OpenPixelVAE |
|---|---|---|---|---|---|---|---|---|
| (%) | 1 | 99.99 | 100.0 | 99.21 | 99.95 | 100.0 | 99.71 | 99.27 |
| 2 | 99.92 | 00.00 | 98.98 | 98.61 | 99.52 | 97.86 | 97.88 | |
| 3 | 100.0 | 00.00 | 92.44 | 95.12 | 93.15 | 81.38 | 95.82 | |
| 4 | 99.92 | 00.00 | 76.43 | 86.37 | 81.55 | 50.58 | 91.56 | |
| 5 | 98.42 | 00.00 | 59.36 | 79.73 | 64.60 | 29.94 | 75.25 | |
| (%) | 1 | 99.99 | 100.0 | 99.21 | 99.95 | 100.0 | 99.71 | 99.27 |
| 2 | 99.75 | 100.0 | 91.82 | 89.23 | 99.71 | 99.78 | 99.81 | |
| 3 | 98.92 | 99.58 | 95.20 | 94.43 | 98.23 | 98.41 | 99.30 | |
| 4 | 97.33 | 98.67 | 53.02 | 72.22 | 95.31 | 94.30 | 97.87 | |
| 5 | 98.67 | 100.0 | 84.93 | 89.52 | 98.18 | 97.00 | 99.43 | |
| (%) | 1 | 99.99 | 100.0 | 99.21 | 99.95 | 100.0 | 99.71 | 99.27 |
| 2 | 99.83 | 50.00 | 93.84 | 93.93 | 99.50 | 98.64 | 99.67 | |
| 3 | 99.56 | 33.19 | 94.26 | 95.70 | 95.37 | 90.10 | 97.77 | |
| 4 | 98.60 | 24.58 | 77.90 | 85.59 | 86.97 | 75.55 | 95.41 | |
| 5 | 97.87 | 20.02 | 81.49 | 87.72 | 75.50 | 63.44 | 90.23 | |
| (nast) | 1 | 433.7 | 423.2 | 435.2 | 424.2 | 434.2 | 432.6 | 433.8 |
| 2 | 422.5 | 439.4 | 423.9 | 425.2 | 434.4 | 432.5 | 433.5 | |
| 3 | 420.7 | 429.2 | 422.7 | 423.8 | 434.6 | 432.9 | 433.1 | |
| 4 | 419.9 | 428.5 | 422.8 | 423.5 | 434.2 | 433.0 | 433.0 | |
| 5 | 418.4 | 432.9 | 422.7 | 423.5 | 435.1 | 431.4 | 432.3 | |
| (nast) | 1 | 433.7 | 423.2 | 435.2 | 424.2 | 434.2 | 432.6 | 433.8 |
| 2 | 381.2 | 384.1 | 382.5 | 385.3 | 390.4 | 389.4 | 389.4 | |
| 3 | 435.9 | 436.7 | 436.3 | 436.9 | 444.7 | 442.7 | 442.4 | |
| 4 | 485.9 | 487.1 | 486.7 | 486.5 | 497.4 | 494.4 | 494.8 | |
| 5 | 421.3 | 425.2 | 423.9 | 422.9 | 431.9 | 428.0 | 429.7 | |
| (nast) | 1 | 433.7 | 423.2 | 435.2 | 424.2 | 435.2 | 432.6 | 433.8 |
| 2 | 401.9 | 411.8 | 403.2 | 403.5 | 412.4 | 410.9 | 411.5 | |
| 3 | 412.1 | 418.9 | 413.6 | 413.8 | 423.3 | 421.0 | 421.9 | |
| 4 | 430.3 | 438.4 | 432.4 | 432.6 | 441.6 | 439.8 | 439.8 | |
| 5 | 427.2 | 440.4 | 431.4 | 430.9 | 440.3 | 436.9 | 437.7 |
References
- Boult, T.E.; Cruz, S.; Dhamija, A.R.; Gunther, M.; Henrydoss, J.; Scheirer, W.J. Learning and the Unknown: Surveying Steps Toward Open World Recognition. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Chen, Z.; Liu, B. Lifelong Machine Learning. In Synthesis Lectures on Artificial Intelligence and Machine Learning; Brachman, R., Rossi, F., Stone, P., Eds.; Morgan & Claypool Publishers LLC.: San Rafael, CA, USA, 2016; Volume 10, pp. 1–145. [Google Scholar]
- Matan, O.; Kiang, R.; Stenard, C.E.; Boser, B.E.; Denker, J.; Henderson, D.; Hubbard, W.; Jackel, L.; LeCun, Y. Handwritten Character Recognition Using Neural Network Architectures. In Proceedings of the 4th United States Postal Service Advanced Technology Conference, Washington, DC, USA, 5–7 December 1990; pp. 1003–1012. [Google Scholar]
- Hendrycks, D.; Dietterich, T. Benchmarking neural network robustness to common corruptions and perturbations. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Ovadia, Y.; Fertig, E.; Ren, J.; Nado, Z.; Sculley, D.; Nowozin, S.; Dillon, J.V.; Lakshminarayanan, B.; Snoek, J. Can You Trust Your Model’s Uncertainty? Evaluating Predictive Uncertainty Under Dataset Shift. In Proceedings of the Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Nalisnick, E.; Matsukawa, A.; Teh, Y.W.; Gorur, D.; Lakshminarayanan, B. Do Deep Generative Models Know What They Don’t Know? In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- McCloskey, M.; Cohen, N.J. Catastrophic Interference in Connectionist Networks: The Sequential Learning Problem. Psychol. Learn. Motiv.-Adv. Res. Theory 1989, 24, 109–165. [Google Scholar]
- Ratcliff, R. Connectionist Models of Recognition Memory: Constraints Imposed by Learning and Forgetting Functions. Psychol. Rev. 1990, 97, 285–308. [Google Scholar] [CrossRef] [PubMed]
- Scheirer, W.J.; Rocha, A.; Sapkota, A.; Boult, T.E. Towards Open Set Recognition. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2013, 35, 1757–1772. [Google Scholar] [CrossRef] [PubMed]
- Scheirer, W.J.; Jain, L.P.; Boult, T.E. Probability Models For Open Set Recognition. IEEE Trans. Pattern Anal. Mach. Intell. (TPAMI) 2014, 36, 2317–2324. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Parisi, G.I.; Kemker, R.; Part, J.L.; Kanan, C.; Wermter, S. Continual Lifelong Learning with Neural Networks: A Review. Neural Netw. 2019, 113, 54–71. [Google Scholar] [CrossRef] [PubMed]
- Bendale, A.; Boult, T.E. Towards Open Set Deep Networks. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Ilyas, A.; Santurkar, S.; Tsipras, D.; Engstrom, L.; Tran, B.; Madry, A. Adversarial Examples are not Bugs, they are Features. In Proceedings of the Neural Information Processing Systems (NeurIPS), Vancouver, BC, Canada, 8–14 December 2019. [Google Scholar]
- Shah, H.; Tamuly, K.; Raghunathan, A.; Jain, P.; Netrapalli, P. The Pitfalls of Simplicity Bias in Neural Networks. In Proceedings of the Neural Informtation Processing Systems (NeurIPS), Online, 6–12 December 2020. [Google Scholar]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. In Proceedings of the International Conference on Learning Representations (ICLR), Scottsdale, AZ, USA, 2–4 May 2013. [Google Scholar]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- van den Oord, A.; Kalchbrenner, N.; Kavukcuoglu, K. Pixel Recurrent Neural Networks. In Proceedings of the 33rd International Conference on Machine Learning (ICML 2016), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Gulrajani, I.; Kumar, K.; Faruk, A.; Taiga, A.A.; Visin, F.; Vazquez, D.; Courville, A. PixelVAE: A Latent Variable Model for Natural Images. In Proceedings of the 5th International Conference on Learning Representations (ICLR 2017), Toulon, France, 24–26 April 2017. [Google Scholar]
- Huang, H.; Li, Z.; He, R.; Sun, Z.; Tan, T. Introvae: Introspective variational autoencoders for photographic image synthesis. In Proceedings of the Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Ulyanov, D.; Vedaldi, A.; Lempitsky, V. It Takes (Only) Two: Adversarial Generator-Encoder Networks. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zenke, F.; Poole, B.; Ganguli, S. Continual Learning Through Synaptic Intelligence. In Proceedings of the 34th International Conference on Machine Learning (ICML), Sydney, Australia, 6–11 August 2017. [Google Scholar]
- Kirkpatrick, J.; Pascanu, R.; Rabinowitz, N.; Veness, J.; Desjardins, G.; Rusu, A.A.; Milan, K.; Quan, J.; Ramalho, T.; Grabska-Barwinska, A.; et al. Overcoming catastrophic forgetting in neural networks. Proc. Natl. Acad. Sci. USA 2017, 114, 3521–3526. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Hoiem, D. Learning without forgetting. In Proceedings of the 14th European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 8–16 October 2016. [Google Scholar]
- Hinton, G.E.; Vinyals, O.; Dean, J. Distilling the Knowledge in a Neural Network. In Proceedings of the Neural Information Processing Systems (NeurIPS), Deep Learning Workshop, Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Robins, A. Catastrophic Forgetting, Rehearsal and Pseudorehearsal. Connect. Sci. 1995, 7, 123–146. [Google Scholar] [CrossRef]
- Rebuffi, S.A.; Kolesnikov, A.; Sperl, G.; Lampert, C.H. iCaRL: Incremental Classifier and Representation Learning. arXiv 2017, arXiv:1611.07725. [Google Scholar]
- Mensink, T.; Verbeek, J.; Perronnin, F.; Csurka, G.; Mensink, T.; Verbeek, J.; Perronnin, F.; Csurka, G. Metric Learning for Large Scale Image Classification: Generalizing to New Classes at Near-Zero Cost. In Proceedings of the European Conference on Computer Vision (ECCV), Florence, Italy, 7–13 October 2012. [Google Scholar]
- Bachem, O.; Lucic, M.; Krause, A. Coresets for Nonparametric Estimation—The Case of DP-Means. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015. [Google Scholar]
- O’Reilly, R.C.; Norman, K.A. Hippocampal and neocortical contributions to memory: Advances in the complementary learning systems framework. Trends Cogn. Sci. 2003, 6, 505–510. [Google Scholar] [CrossRef]
- Gepperth, A.; Karaoguz, C. A Bio-Inspired Incremental Learning Architecture for Applied Perceptual Problems. Cogn. Comput. 2016, 8, 924–934. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Lee, J.K.; Kim, J.J.; Kim, J. Continual Learning with Deep Generative Replay. In Proceedings of the Neural Information Processing Systems (NeurIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Nets. In Proceedings of the Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Farquhar, S.; Gal, Y. A Unifying Bayesian View of Continual Learning. In Proceedings of the Neural Information Processing Systems (NeurIPS), Bayesian Deep Learning Workshop, Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Farquhar, S.; Gal, Y. Towards Robust Evaluations of Continual Learning. In Proceedings of the International Conference on Machine Learning (ICML), Lifelong Learning: A Reinforcement Learning Approach Workshop, Stockholm, Sweden, 10–15 June 2018. [Google Scholar]
- Nguyen, C.V.; Li, Y.; Bui, T.D.; Turner, R.E. Variational Continual Learning. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Achille, A.; Eccles, T.; Matthey, L.; Burgess, C.P.; Watters, N.; Lerchner, A.; Higgins, I. Life-Long Disentangled Representation Learning with Cross-Domain Latent Homologies. In Proceedings of the Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Liang, S.; Li, Y.; Srikant, R. Enhancing the Reliability of Out-of-distribution Image Detection in Neural Networks. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Lee, K.; Lee, H.; Lee, K.; Shin, J. Training Confidence-Calibrated Classifiers for Detecting Out-of-Distribution Samples. In Proceedings of the International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Dhamija, A.R.; Günther, M.; Boult, T.E. Reducing Network Agnostophobia. In Proceedings of the Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- MacKay, D.J.C. A Practical Bayesian Framework. Neural Comput. 1992, 472, 448–472. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015. [Google Scholar]
- Graves, A. Practical variational inference for neural networks. In Proceedings of the Neural Information Processing Systems (NeurIPS), Granada, Spain, 12–17 December 2011. [Google Scholar]
- Higgins, I.; Matthey, L.; Pal, A.; Burgess, C.P.; Glorot, X.; Botvinick, M.; Mohamed, S.; Lerchner, A. beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Tomczak, J.M.; Welling, M. VAE with a vampprior. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Canary Islands, Spain, 9–11 April 2018. [Google Scholar]
- Hoffman, M.D.; Johnson, M.J. ELBO surgery: Yet another way to carve up the variational evidence lower bound. In Proceedings of the Neural Information Processing Systems (NeurIPS), Advances in Approximate Bayesian Inference Workshop, Barcelona, Spain, 5–10 December 2016. [Google Scholar]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-based learning applied to document recognition. Proc. IEEE 1998, 86, 2278–2323. [Google Scholar] [CrossRef] [Green Version]
- Burgess, C.P.; Higgins, I.; Pal, A.; Matthey, L.; Watters, N.; Desjardins, G.; Lerchner, A. Understanding disentangling in beta-VAE. In Proceedings of the Neural Information Processing Systems (NeurIPS), Workshop on Learning Disentangled Representations, Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Mathieu, E.; Rainforth, T.; Siddharth, N.; Teh, Y.W. Disentangling disentanglement in variational autoencoders. In Proceedings of the International Conference on Machine Learning (ICML), Long Beach, CA, USA, 10–15 June 2019; pp. 7744–7754. [Google Scholar]
- Bauer, M.; Mnih, A. Resampled Priors for Variational Autoencoders. In Proceedings of the International Conference on Artificial Intelligence and Statistics (AISTATS), Naha, Okinawa, Japan, 16–18 April 2019. [Google Scholar]
- Takahashi, H.; Iwata, T.; Yamanaka, Y.; Yamada, M.; Yagi, S. Variational Autoencoder with Implicit Optimal Priors. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Honolulu, HI, USA, 27 January–1 February 2019. [Google Scholar]
- Nilsback, M.E.; Zisserman, A. A Visual Vocabulary For Flower Classification. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR), Washington, DC, USA, 17–22 June 2006; pp. 1447–1454. [Google Scholar]
- Xiao, H.; Rasul, K.; Vollgraf, R. Fashion-MNIST: A Novel Image Dataset for Benchmarking Machine Learning Algorithms. arXiv 2017, arXiv:1708.07747. [Google Scholar]
- Becker, S.; Ackermann, M.; Lapuschkin, S.; Müller, K.R.; Samek, W. Interpreting and Explaining Deep Neural Networks for Classification of Audio Signals. arXiv 2018, arXiv:1807.03418. [Google Scholar]
- Clanuwat, T.; Bober-Irizar, M.; Kitamoto, A.; Lamb, A.; Yamamoto, K.; Ha, D. Deep Learning for Classical Japanese Literature. In Proceedings of the Neural Information Processing Systems (NeurIPS), Workshop on Machine Learning for Creativity and Design, Conference, Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Netzer, Y.; Wang, T.; Coates, A.; Bissacco, A.; Wu, B.; Ng, A.Y. Reading Digits in Natural Images with Unsupervised Feature Learning. In Proceedings of the Neural Information Processing Systems (NeurIPS), Granada, Spain, 12–17 December 2011. [Google Scholar]
- Krizhevsky, A. Learning Multiple Layers of Features from Tiny Images; Technical Report, Toronto. 2009. Available online: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf (accessed on 22 January 2022).
- Hendrycks, D.; Gimpel, K. A baseline for detecting misclassified and out-of-distribution examples in neural networks. In Proceedings of the International Conference on Learning Representations (ICLR), Toulon, France, 24–26 April 2017. [Google Scholar]
- Bendale, A.; Boult, T.E. Towards Open World Recognition. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015. [Google Scholar]
- Kemker, R.; McClure, M.; Abitino, A.; Hayes, T.; Kanan, C. Measuring Catastrophic Forgetting in Neural Networks. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Zagoruyko, S.; Komodakis, N. Wide Residual Networks. In Proceedings of the In Proceedings of the British Machine Vision Conference (BMVC), York, UK, 19–22 September 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Chaudhry, A.; Dokania, P.K.; Ajanthan, T.; Torr, P.H.S. Riemannian Walk for Incremental Learning: Understanding Forgetting and Intransigence. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018. [Google Scholar]
- Hu, W.; Lin, Z.; Liu, B.; Tao, C.; Tao, Z.; Zhao, D.; Ma, J.; Yan, R. Overcoming catastrophic forgetting for continual learning via model adaptation. In Proceedings of the International Conference on Learning Representations (ICLR), New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Wu, C.; Herranz, L.; Liu, X.; Wang, Y.; van de Weijer, J.; Raducanu, B. Memory Replay GANs: Learning to generate images from new categories without forgetting. In Proceedings of the Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 2–8 December 2018. [Google Scholar]
- Zhai, M.; Chen, L.; Tung, F.; He, J.; Nawhal, M.; Mori, G. Lifelong GAN: Continual Learning for Conditional Image Generation. In Proceedings of the International Conference on Computer Vision (ICCV), Seoul, Korea, 27 October–2 November 2019. [Google Scholar]
- Welling, M. Herding dynamical weights to learn. In Proceedings of the International Conference on Machine Learning (ICML), Montreal, QC, Canada, 14–18 June 2009. [Google Scholar]
- Prabhu, A.; Torr, P.; Dokania, P. GDumb: A Simple Approach that Questions Our Progress in Continual Learning. In Proceedings of the European Conference on Computer Vision (ECCV), Online, 23–28 August 2020. [Google Scholar]
- Liu, Y.; Su, Y.; Liu, A.A.; Schiele, B.; Sun, Q. Mnemonics Training: Multi-Class Incremental Learning without Forgetting. In Proceedings of the Computer Vision Pattern Recognition (CVPR), Online, 14–19 June 2020. [Google Scholar]
- Cha, H.; Lee, J.; Shin, J. Co2L: Contrastive Continual Learning. In Proceedings of the International Conference on Computer Vision (ICCV), online, 11–17 October 2021. [Google Scholar]
- Buzzega, P.; Boschini, M.; Porrello, A.; Abati, D.; Calderara, S. Dark Experience for General Continual Learning: A Strong, Simple Baseline. In Proceedings of the Neural Information Processing Systems (NeurIPS), Online, 6–12 December 2020. [Google Scholar]
- Kingma, D.P.; Rezende, D.J.; Mohamed, S.; Welling, M. Semi-Supervised Learning with Deep Generative Models. In Proceedings of the Neural Information Processing Systems (NeurIPS), Montreal, QC, Canada, 8–13 December 2014. [Google Scholar]
- Larsen, A.B.L.; Sonderby, S.K.; Larochelle, H.; Winther, O. Autoencoding beyond pixels using a learned similarity metric. In Proceedings of the International Conference on Machine Learning (ICML), New York, NY, USA, 19–24 June 2016. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning (ICML), Lille, France, 6–11 July 2015. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Delving deep into rectifiers: Surpassing human-level performance on imagenet classification. In Proceedings of the International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]



| Outlier Detection at 95% Validation Inliers (%) | MNIST | Fashion | Audio | KMNIST | CIFAR10 | CIFAR100 | SVHN | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Trained | Model | Test Acc. | Criterion | |||||||
| MNIST | Dual, | 99.40 | Class entropy | 4.160 | 90.43 | 97.53 | 95.29 | 98.54 | 98.63 | 95.51 |
| CNN + | Reconstruction NLL | 5.522 | 99.98 | 99.97 | 99.98 | 99.99 | 99.96 | 99.98 | ||
| VAE | OpenMax | 4.362 | 99.41 | 99.80 | 99.86 | 99.95 | 99.97 | 99.52 | ||
| Joint | 99.53 | Class entropy | 3.948 | 95.15 | 98.55 | 95.49 | 99.47 | 99.34 | 97.98 | |
| VAE | Reconstruction NLL | 5.083 | 99.50 | 99.98 | 99.91 | 99.97 | 99.99 | 99.98 | ||
| OpenVAE (ours) | 4.361 | 99.78 | 99.67 | 99.73 | 99.96 | 99.93 | 99.70 | |||
| FashionMNIST | Dual, | 90.48 | Class entropy | 74.71 | 5.461 | 69.65 | 77.85 | 24.91 | 28.76 | 36.64 |
| CNN + | Reconstruction NLL | 5.535 | 5.340 | 64.10 | 31.33 | 99.50 | 98.41 | 97.24 | ||
| VAE | OpenMax | 96.22 | 5.138 | 93.00 | 91.51 | 71.82 | 72.08 | 73.85 | ||
| Joint | 90.92 | Class Entropy | 66.91 | 5.145 | 61.86 | 56.14 | 43.98 | 46.59 | 37.85 | |
| VAE | Reconstruction NLL | 0.601 | 5.483 | 63.00 | 28.69 | 99.67 | 98.91 | 98.56 | ||
| OpenVAE (ours) | 96.23 | 5.216 | 94.76 | 96.07 | 96.15 | 95.94 | 96.84 | |||
| AudioMNIST | Dual, | 98.53 | Class entropy | 97.63 | 57.64 | 5.066 | 95.53 | 66.49 | 65.25 | 54.91 |
| CNN + | Reconstruction NLL | 6.235 | 46.32 | 4.433 | 98.73 | 98.63 | 98.63 | 97.45 | ||
| VAE | OpenMax | 99.82 | 78.74 | 5.038 | 99.47 | 93.44 | 92.76 | 88.73 | ||
| Joint | 98.57 | Class entropy | 99.23 | 89.33 | 5.731 | 99.15 | 92.31 | 91.06 | 85.77 | |
| VAE | Reconstruction NLL | 0.614 | 38.50 | 3.966 | 36.05 | 98.62 | 98.54 | 96.99 | ||
| OpenVAE (ours) | 99.91 | 99.53 | 5.089 | 99.81 | 100.0 | 99.99 | 99.98 | |||
| Outlier Detection at 95% Validation Inliers (%) | MNIST | Fashion | Audio | KMNIST | CIFAR10 | CIFAR100 | SVHN | |||
|---|---|---|---|---|---|---|---|---|---|---|
| Trained | Model | Test Acc. | Criterion | |||||||
| MNIST | Dual, | 99.41 | Class entropy | 4.276 | 91.88 | 96.50 | 96.65 | 95.84 | 97.37 | 98.58 |
| CNN + | Reconstruction | 4.829 | 99.99 | 100.0 | 99.90 | 100.0 | 100.0 | 100.0 | ||
| VAE | OpenMax | 4.088 | 87.84 | 98.06 | 95.79 | 97.34 | 98.30 | 95.74 | ||
| Joint, | 99.54 | Class entropy | 4.801 | 97.63 | 99.38 | 98.01 | 99.16 | 99.39 | 98.90 | |
| VAE | Reconstruction | 5.264 | 99.98 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | ||
| OpenVAE (ours) | 4.978 | 99.99 | 100.0 | 99.94 | 99.96 | 99.95 | 99.68 | |||
| FashionMNIST | Dual, | 90.58 | Class entropy | 75.50 | 5.366 | 70.78 | 74.41 | 49.42 | 49.17 | 38.84 |
| CNN + | Reconstruction NLL | 55.45 | 5.048 | 59.99 | 99.83 | 99.35 | 99.35 | 99.62 | ||
| VAE | OpenMax | 77.03 | 4.920 | 55.48 | 70.23 | 58.73 | 57.06 | 44.54 | ||
| Joint, | 91.50 | Class Entropy | 85.05 | 4.740 | 67.90 | 78.04 | 63.89 | 66.11 | 59.42 | |
| AE | Reconstruction | 1.227 | 5.422 | 85.85 | 39.76 | 99.94 | 99.72 | 99.99 | ||
| OpenVAE (ours) | 95.83 | 4.516 | 94.56 | 96.04 | 96.81 | 96.66 | 96.28 | |||
| AudioMNIST | Dual, | 98.76 | Class entropy | 99.97 | 61.26 | 4.996 | 96.77 | 63.78 | 65.76 | 59.38 |
| CNN + | Reconstruction NLL | 7.334 | 52.37 | 5.100 | 98.19 | 99.97 | 99.90 | 99.96 | ||
| VAE | OpenMax | 92.74 | 67.18 | 5.073 | 90.41 | 90.56 | 90.97 | 89.58 | ||
| Joint, | 98.85 | Class entropy | 99.39 | 89.50 | 5.333 | 99.16 | 94.66 | 95.12 | 97.13 | |
| VAE | Reconstruction NLL | 15.81 | 53.83 | 4.837 | 41.89 | 99.90 | 99.82 | 99.95 | ||
| OpenVAE (ours) | 99.50 | 99.27 | 5.136 | 99.75 | 99.71 | 99.59 | 99.91 | |||
| Final Accuracy [%] | |||
|---|---|---|---|
| Method | MNIST | FashionMNIST | AudioMNIST |
| MLP upper bound | 98.84 | 87.35 | 96.43 |
| WRN upper bound | 99.29 | 89.24 | 97.87 |
| EWC [22] | 55.80 [63] | 24.48 ± | 20.48 ± |
| DGR [32] | 75.47 [64] | 63.21 ± | 48.42 ± |
| VCL [36] | 72.30 [35] | 32.60 [35] | - |
| VGR [35] | 92.22 [35] | 79.10 [35] | - |
| Supervised VAE | 60.88 ± | 62.72 ± | 69.76 ± |
| OpenVAE—MLP | 87.31 ± | 66.14 ± | 81.84 ± |
| OpenVAE—WRN | 93.24 ± | 69.88 ± | 87.72 ± |
| OpenPixelVAE | 96.84 ± | 80.85 ± | 90.23 ± |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mundt, M.; Pliushch, I.; Majumder, S.; Hong, Y.; Ramesh, V. Unified Probabilistic Deep Continual Learning through Generative Replay and Open Set Recognition. J. Imaging 2022, 8, 93. https://doi.org/10.3390/jimaging8040093
Mundt M, Pliushch I, Majumder S, Hong Y, Ramesh V. Unified Probabilistic Deep Continual Learning through Generative Replay and Open Set Recognition. Journal of Imaging. 2022; 8(4):93. https://doi.org/10.3390/jimaging8040093
Chicago/Turabian StyleMundt, Martin, Iuliia Pliushch, Sagnik Majumder, Yongwon Hong, and Visvanathan Ramesh. 2022. "Unified Probabilistic Deep Continual Learning through Generative Replay and Open Set Recognition" Journal of Imaging 8, no. 4: 93. https://doi.org/10.3390/jimaging8040093
APA StyleMundt, M., Pliushch, I., Majumder, S., Hong, Y., & Ramesh, V. (2022). Unified Probabilistic Deep Continual Learning through Generative Replay and Open Set Recognition. Journal of Imaging, 8(4), 93. https://doi.org/10.3390/jimaging8040093






