Extension of the Thermographic Signal Reconstruction Technique for an Automated Segmentation and Depth Estimation of Subsurface Defects
Abstract
1. Introduction
2. Thermographic Evaluation Method
2.1. Signal Acquisition
2.2. Heat Diffusion Equation
2.3. Numerical Solution of the Heat Equation
2.4. Thermograpic Signal Reconstruction (TSR) Algorithm
3. Modification of Thermograpic Signal Reconstruction Method
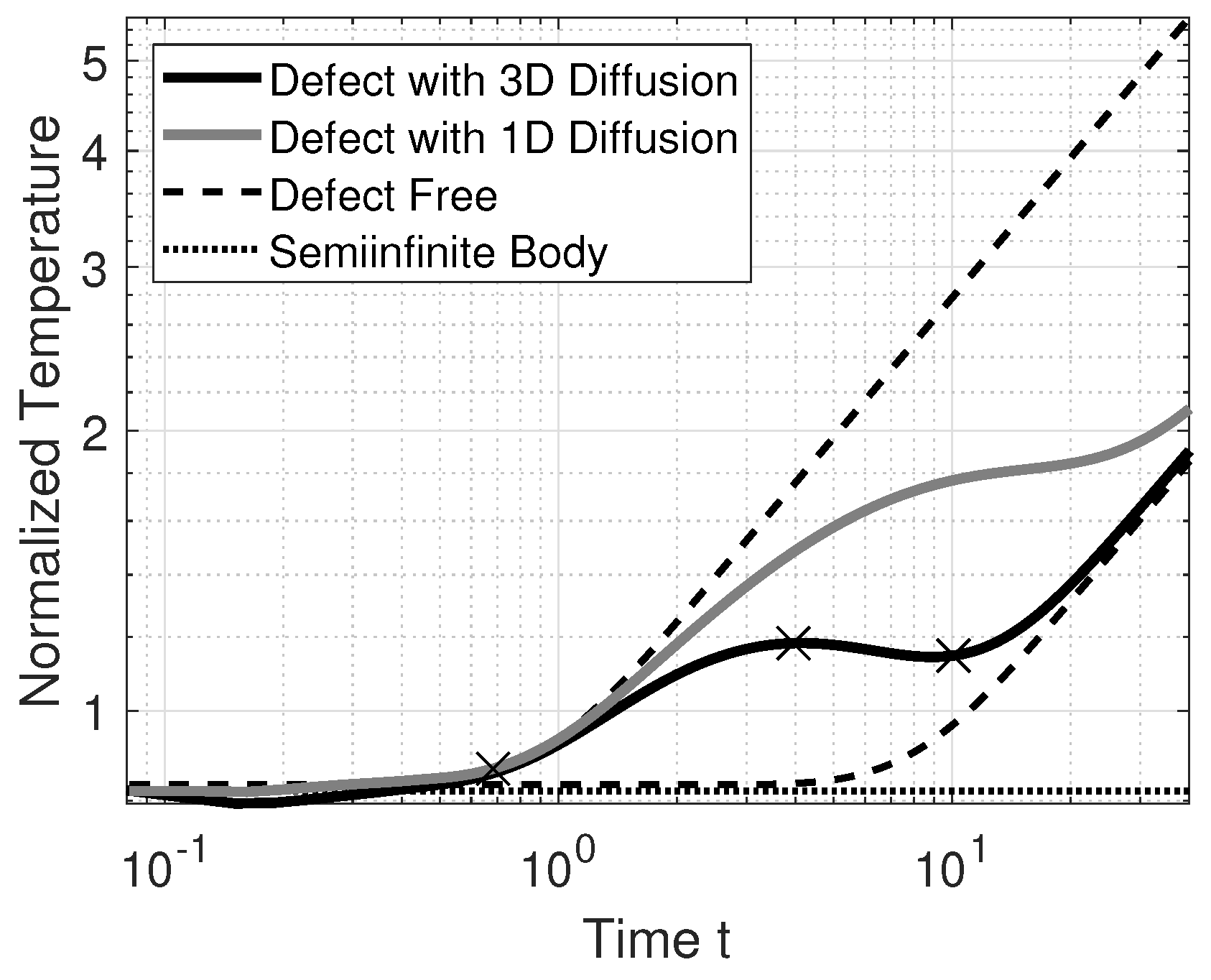
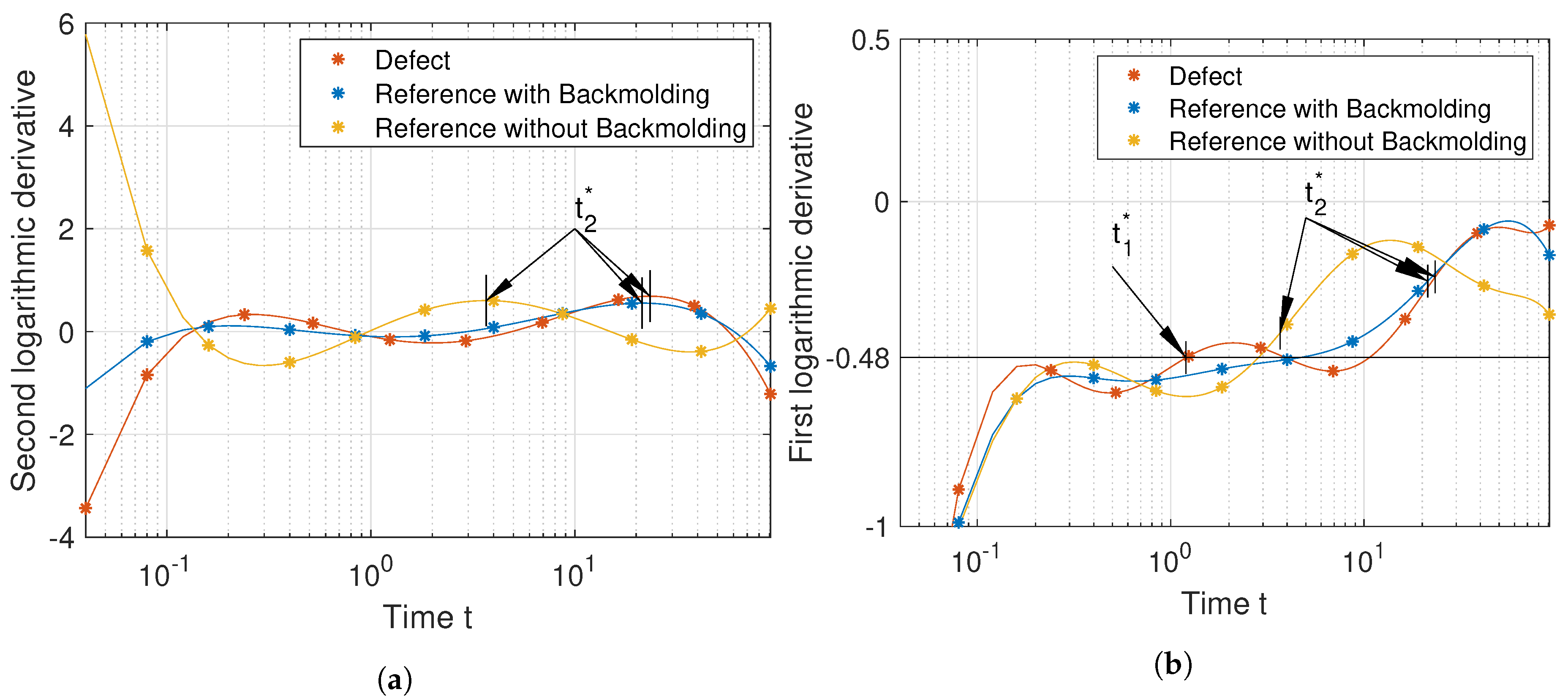
3.1. Interpreting the Characteristic Times
3.2. Implementation of the Modification
- Fit a polynomial of the form of Equation (4) to the temperature–time sequence, but use for the x-axis for improved stability of the polynomial.
- Add the value to the polynomial coefficient .
- Calculate the first derivative of this polynomial.
- Evaluate the real valued roots of this polynomial and discard roots caused by oscillation (i.e., real valued roots outside the measured time).
- If three or more roots are found this indicates a defect, and location of the first root roughly indicates the defect depth according to Equation (5).
4. Experimental Study
4.1. Measurement and Computational Complexity
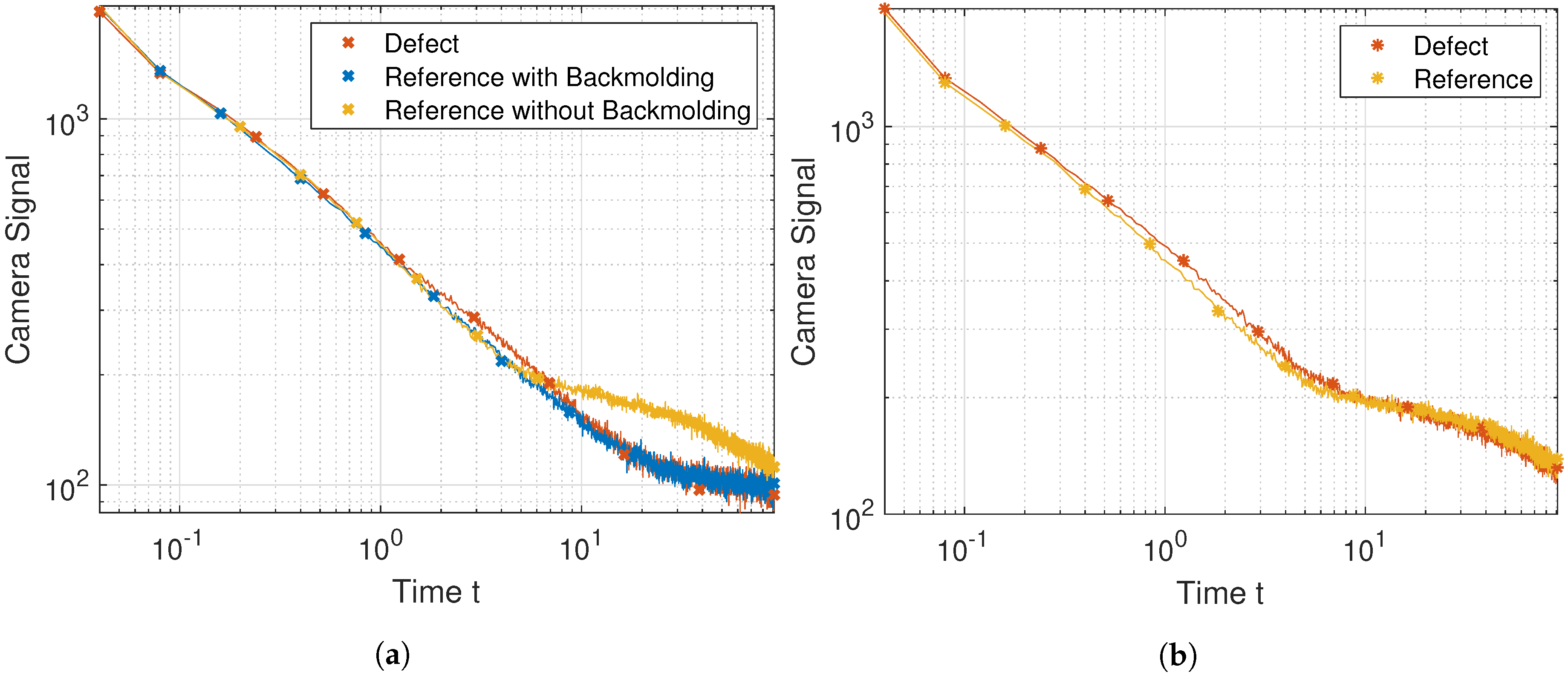
4.2. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| FRP | Fiber reinforced polymer |
| 3D-XCT | 3D-Xray computed tomography |
| UT | Ultrasonic testing |
| AT | Active Thermography |
| IR | Infrared |
| PT | Pulse thermography |
| PPT | Pulse phase thermography |
| TSR | Thermographic signal reconstruction |
| APST | Absolute peak slope time method |
| DDT | Dynamic thermal tomography |
| VWC | Virtual wave concept |
| NDE | Non-destructive evaluation |
| FBH | Flat bottomed hole |
References
- Mandelis, A. Diffusion-Wave Fields; Springer: New York, NY, USA, 2001. [Google Scholar] [CrossRef]
- Salazar, A. Energy propagation of thermal waves. Eur. J. Phys. 2006, 27, 1349–1355. [Google Scholar] [CrossRef]
- Vavilov, V.; Burleigh, D. Review of pulsed thermal NDT: Physical principles, theory and data processing. NDT E Int. 2015, 73, 28–52. [Google Scholar] [CrossRef]
- Ciampa, F.; Mahmoodi, P.; Pinto, F.; Meo, M. Recent Advances in Active Infrared Thermography for Non-Destructive Testing of Aerospace Components. Sensors 2018, 18, 609. [Google Scholar] [CrossRef] [PubMed]
- Maldague, X.; Marinetti, S. Pulse phase infrared thermography. J. Appl. Phys. 1996, 79, 2694–2698. [Google Scholar] [CrossRef]
- Maldague, X.; Galmiche, F.; Ziadi, A. Advances in pulsed phase thermography. Infrared Phys. Technol. 2002, 43, 175–181. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C. Quantitative Subsurface Defect Evaluation by Pulsed Phase Thermography: Depth Retrieval with the Phase. Ph.D. Thesis, University Laval, Quebec City, QC, Canada, 2005. [Google Scholar]
- Ibarra-Castanedo, C.; Maldague, X. Review of pulse phase thermography. In Thermosense: Thermal Infrared Applications XXXVII; Hsieh, S.J.T., Zalameda, J.N., Eds.; SPIE: Bellingham, WA, USA, 2015. [Google Scholar] [CrossRef]
- Rajic, N. Principal component thermography for flaw contrast enhancement and flaw depth characterisation in composite structures. Compos. Struct. 2002, 58, 521–528. [Google Scholar] [CrossRef]
- Zijun, W.; Tian, G.; Meo, M.; Ciampa, F. Image processing based quantitative damage evaluation in composites with long pulse thermography. NDT E Int. 2018, 99, 93–104. [Google Scholar] [CrossRef]
- Wang, Z.; Zhu, J.; Tian, G.; Ciampa, F. Comparative analysis of eddy current pulsed thermography and long pulse thermography for damage detection in metals and composites. NDT E Int. 2019, 107, 102155. [Google Scholar] [CrossRef]
- Shepard, S. System for Generating Thermographic Images Using Thermographic Signal Reconstruction. U.S. Patent No. 6,751,342, 15 June 2004. [Google Scholar]
- Shepard, S.; Frendberg Beemer, M. Advances in thermographic signal reconstruction. In Thermosense: Thermal Infrared Applications XXXVII; SPIE Proceedings; Hsieh, S.J.T., Zalameda, J.N., Eds.; SPIE: Bellingham, WA, USA, 2015; p. 94850R. [Google Scholar] [CrossRef]
- Balageas, D. In Search of Early Time: An Original Approach in the Thermographic Identification of Thermophysical Properties and Defects. Adv. Opt. Technol. 2013, 2013, 1–13. [Google Scholar] [CrossRef]
- Balageas, D.L.; Roche, J.; Leroy, F.; Liu, W.; Gorbach, A.M. The Thermographic Signal Reconstruction Method: A Powerful Tool for the Enhancement of Transient Thermograpic Images. Biocybern. Biomed. Eng. 2015, 35, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Zeng, Z.; Zhou, J.; Tao, N.; Feng, L.; Zhang, C. Absolute peak slope time based thickness measurement using pulsed thermography. Infrared Phys. Technol. 2012, 55, 200–204. [Google Scholar] [CrossRef]
- Almond, D.P.; Pickering, S.G. An analytical study of the pulsed thermography defect detection limit. J. Appl. Phys. 2012, 111, 093510. [Google Scholar] [CrossRef]
- Vavilov, V. Dynamic thermal tomography: Recent improvements and applications. NDT E Int. 2015, 71, 23–32. [Google Scholar] [CrossRef]
- Burgholzer, P.; Thor, M.; Gruber, J.; Mayr, G. Three-dimensional thermographic imaging using a virtual wave concept. J. Appl. Phys. 2017, 121, 105102. [Google Scholar] [CrossRef]
- Thummerer, G.; Mayr, G.; Haltmeier, M.; Burgholzer, P. Photoacoustic reconstruction from photothermal measurements including prior information. Photoacoustics 2020, 19, 100175. [Google Scholar] [CrossRef] [PubMed]
- Thummerer, G.; Mayr, G.; Hirsch, P.; Ziegler, M.; Burgholzer, P. Photothermal image reconstruction in opaque media with virtual wave backpropagation. NDT E Int. 2020, 112, 102239. [Google Scholar] [CrossRef]
- Burgholzer, P.; Berer, T.; Ziegler, M.; Thiel, E.; Ahmadi, S.; Gruber, J.; Mayr, G.; Hendorfer, G. Blind structured illumination as excitation for super-resolution photothermal radiometry. Quant. Infrared Thermogr. J. 2019, 1–11. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford Science Publications and Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Balageas, D.L. Thickness or diffusivity measurements from front-face flash experiments using the TSR (thermographic signal reconstruction) approach. In Proceedings of the 2010 International Conference on Quantitative InfraRed Thermography, QIRT Council, Quebec City, QC, Canada, 24–29 June 2010. [Google Scholar] [CrossRef]
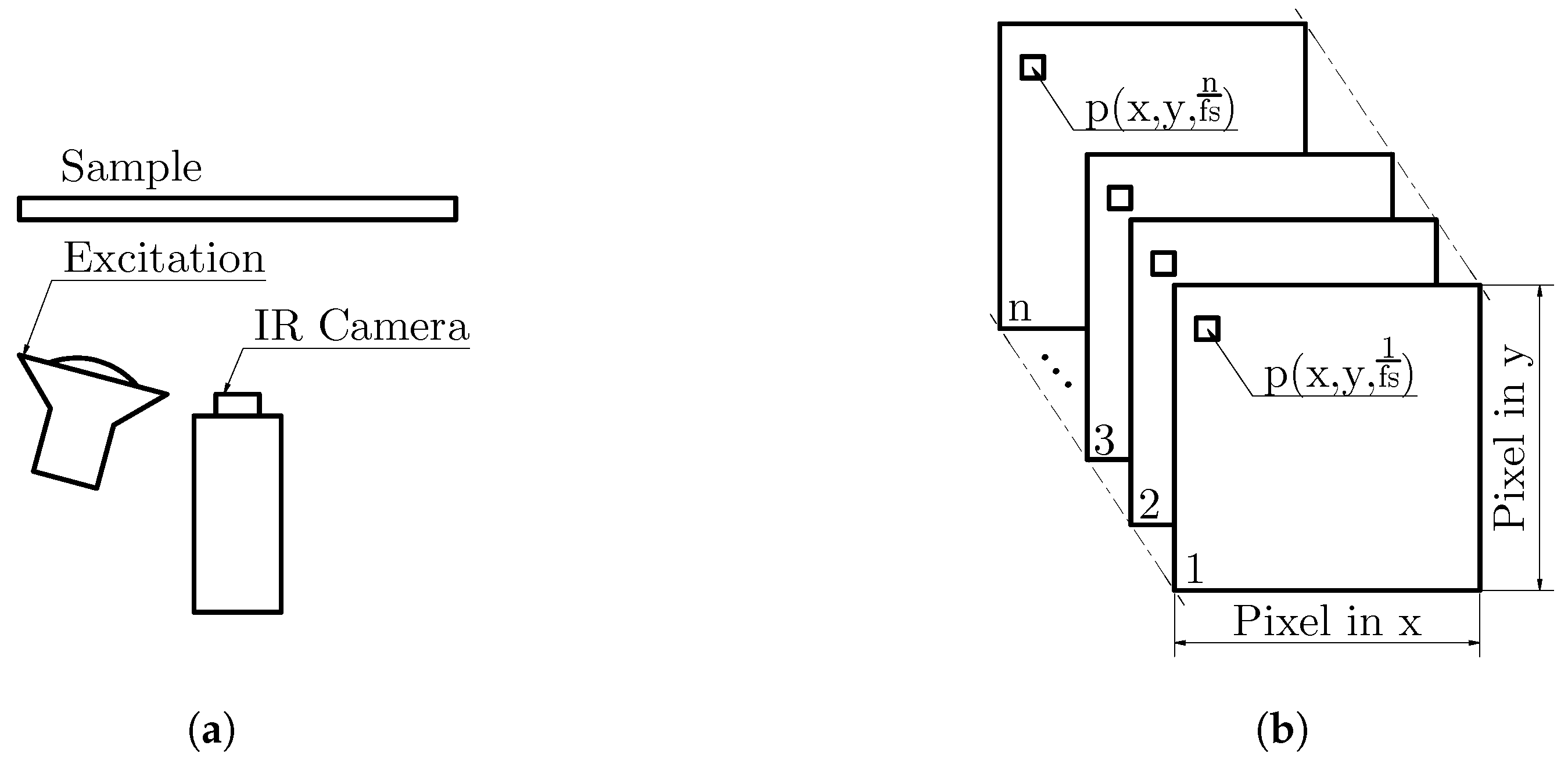
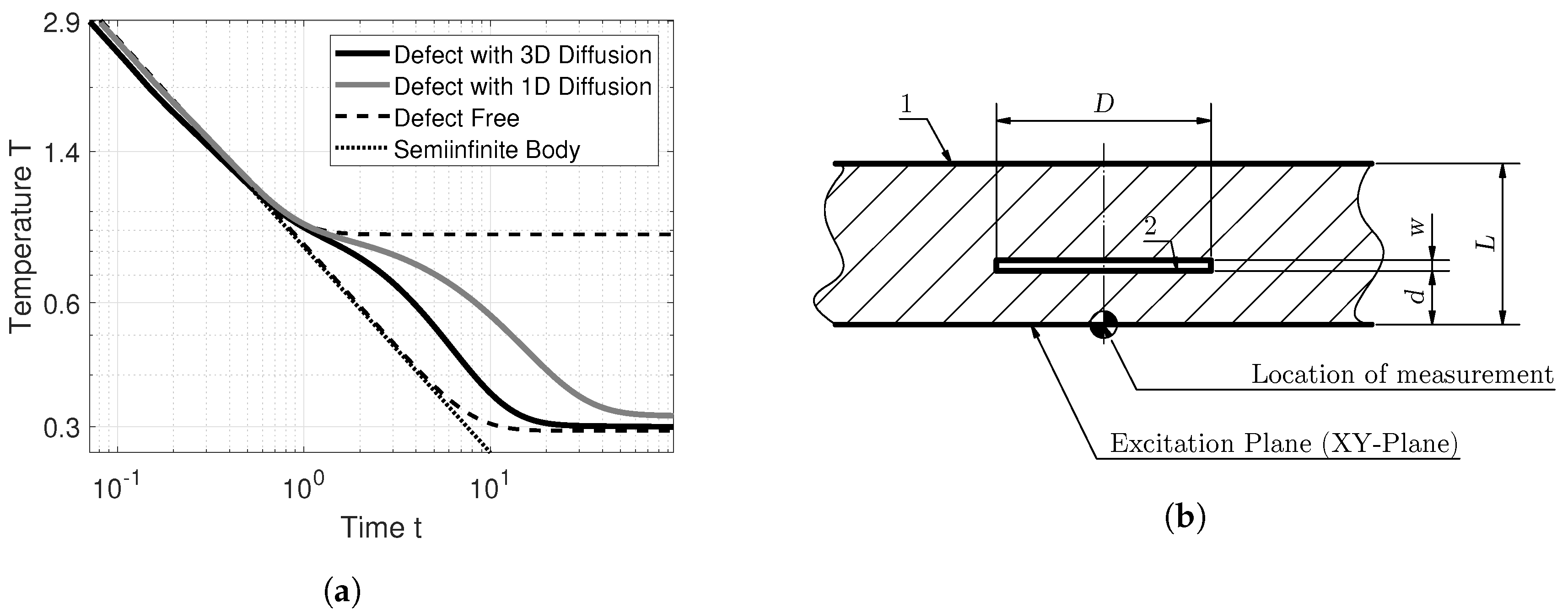




| Geometry Units in mm | Material 1, Composite | Material 2, Air | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| D | L | d | w | |||||||
| 4 | 3 | 1 | 0.2 | 1.92 | 0.64 | 1500 | 1200 | 0.0262 | 1.2 | 1 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schager, A.; Zauner, G.; Mayr, G.; Burgholzer, P. Extension of the Thermographic Signal Reconstruction Technique for an Automated Segmentation and Depth Estimation of Subsurface Defects. J. Imaging 2020, 6, 96. https://doi.org/10.3390/jimaging6090096
Schager A, Zauner G, Mayr G, Burgholzer P. Extension of the Thermographic Signal Reconstruction Technique for an Automated Segmentation and Depth Estimation of Subsurface Defects. Journal of Imaging. 2020; 6(9):96. https://doi.org/10.3390/jimaging6090096
Chicago/Turabian StyleSchager, Alexander, Gerald Zauner, Günther Mayr, and Peter Burgholzer. 2020. "Extension of the Thermographic Signal Reconstruction Technique for an Automated Segmentation and Depth Estimation of Subsurface Defects" Journal of Imaging 6, no. 9: 96. https://doi.org/10.3390/jimaging6090096
APA StyleSchager, A., Zauner, G., Mayr, G., & Burgholzer, P. (2020). Extension of the Thermographic Signal Reconstruction Technique for an Automated Segmentation and Depth Estimation of Subsurface Defects. Journal of Imaging, 6(9), 96. https://doi.org/10.3390/jimaging6090096





