Marching Cubes and Histogram Pyramids for 3D Medical Visualization
Abstract
1. Introduction
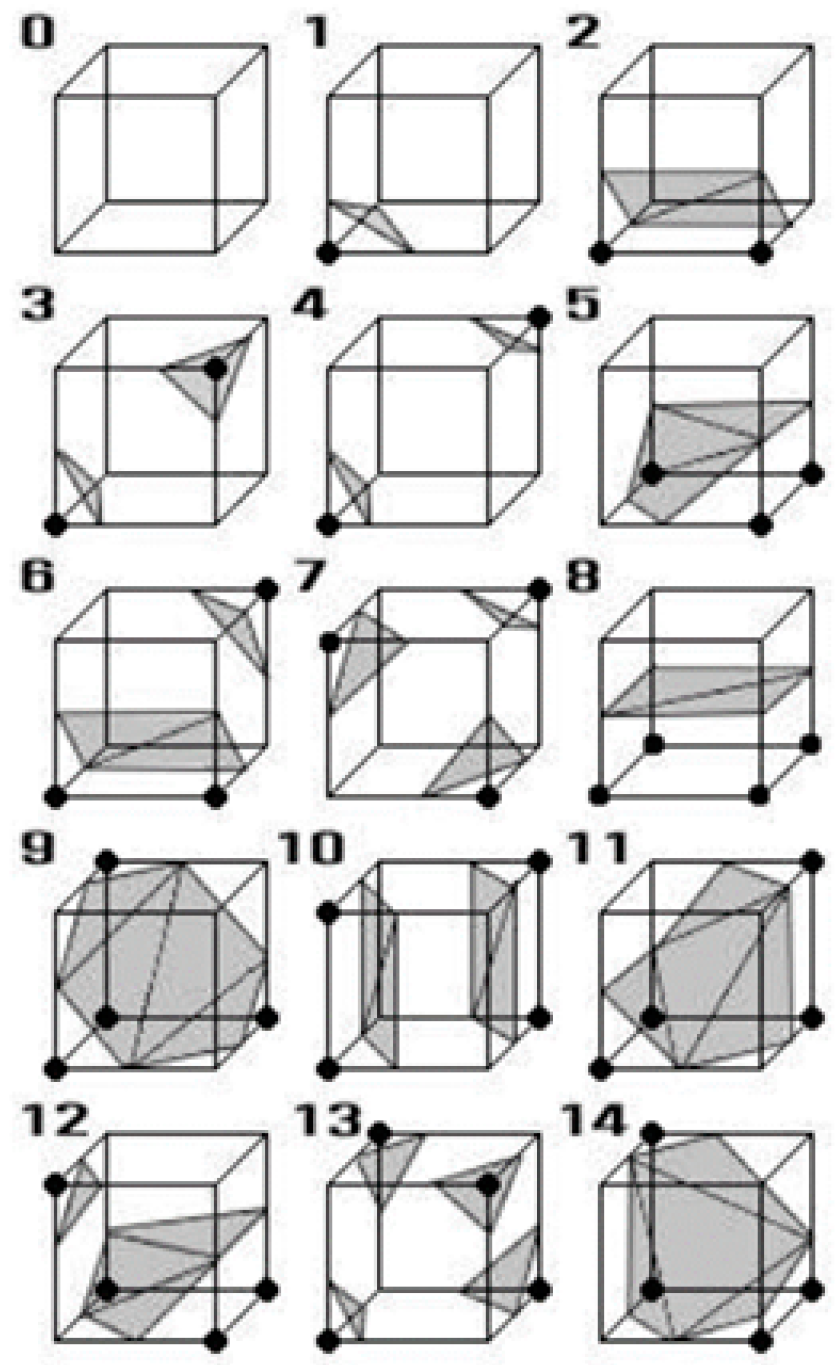
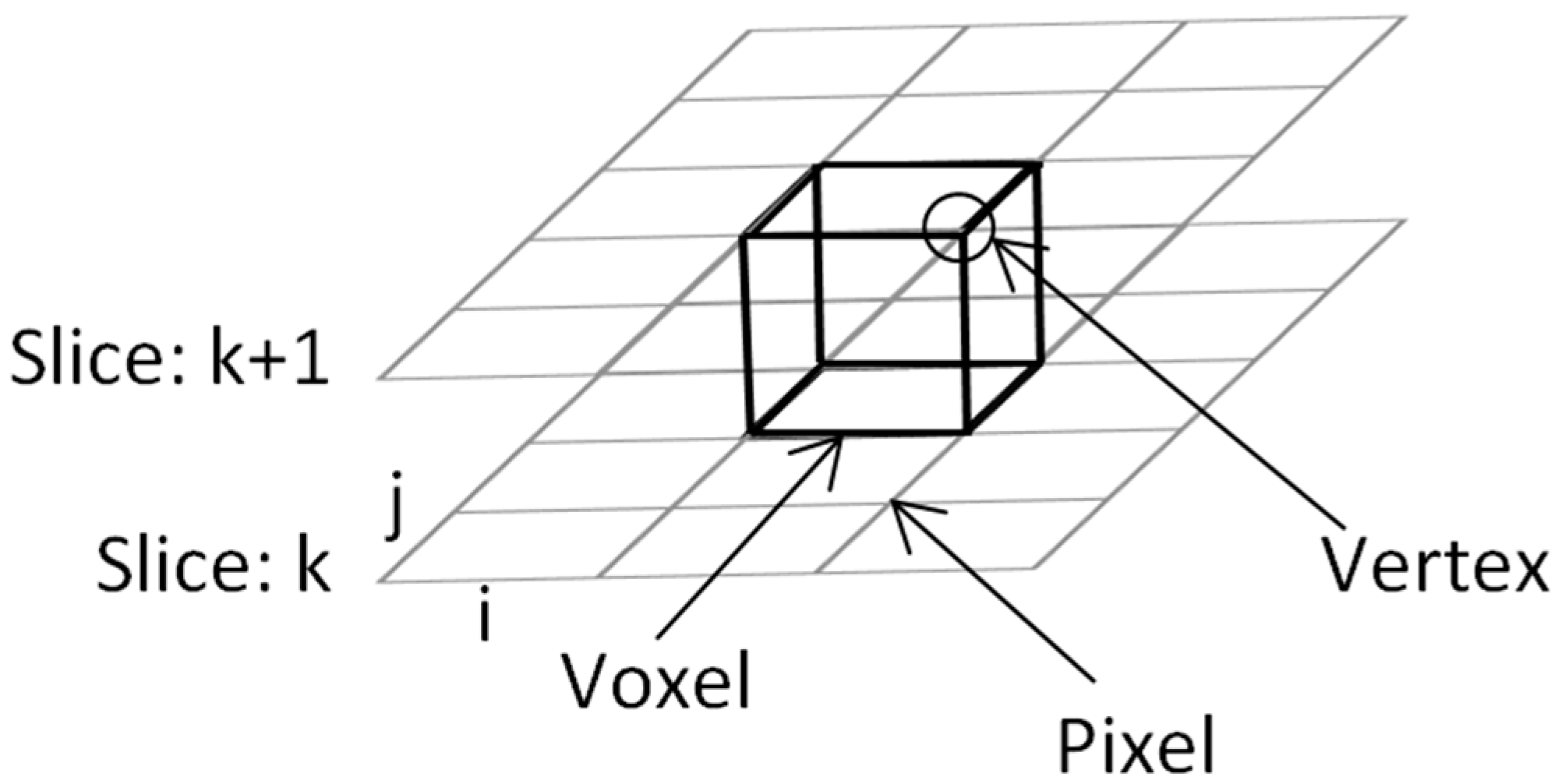
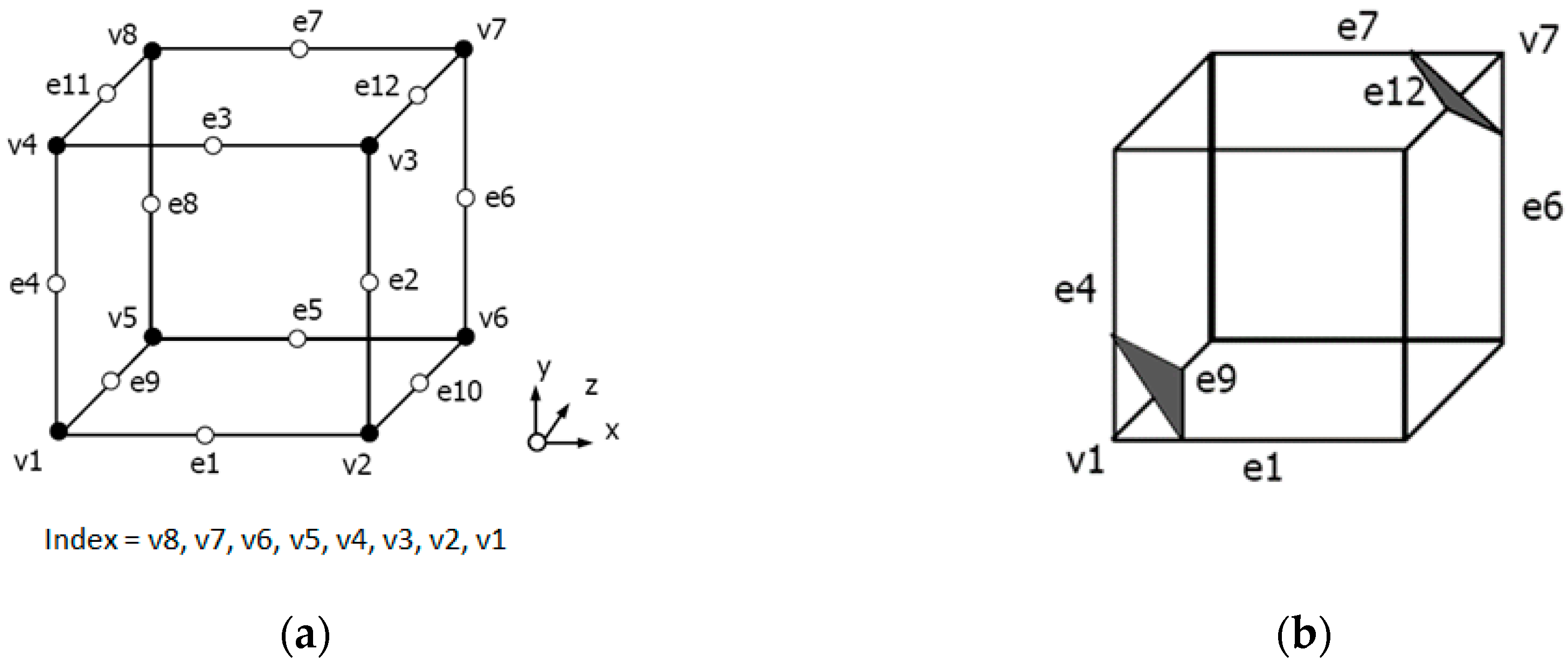
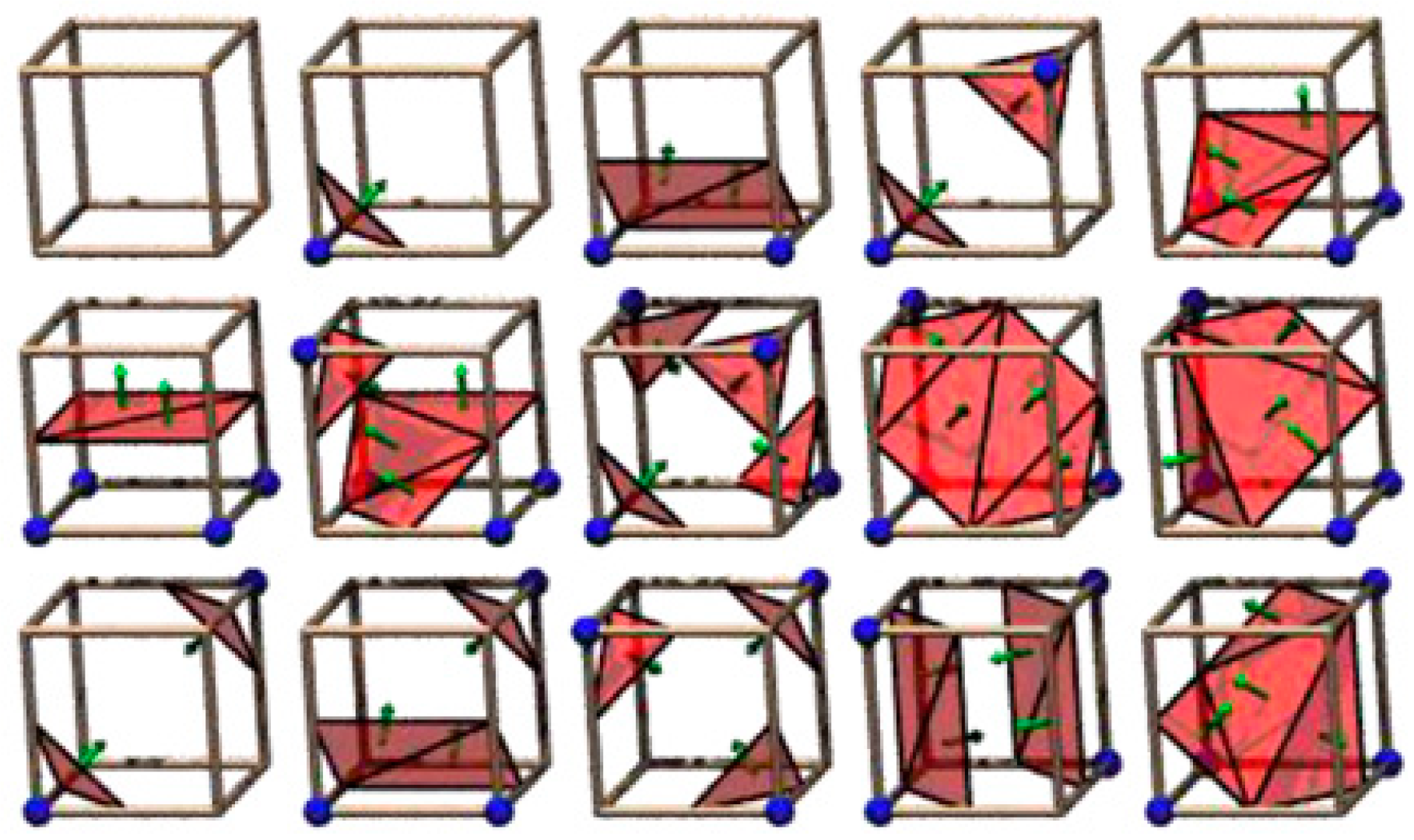
2. Marching Cubes
- The vertex will be the inner vertex if the vertex value is greater than or equal to the isosurface value; then assign “0” to the vertex.
- The vertex will be the outer vertex if the vertex value is less than the isosurface value; then assign “1” to the vertex.
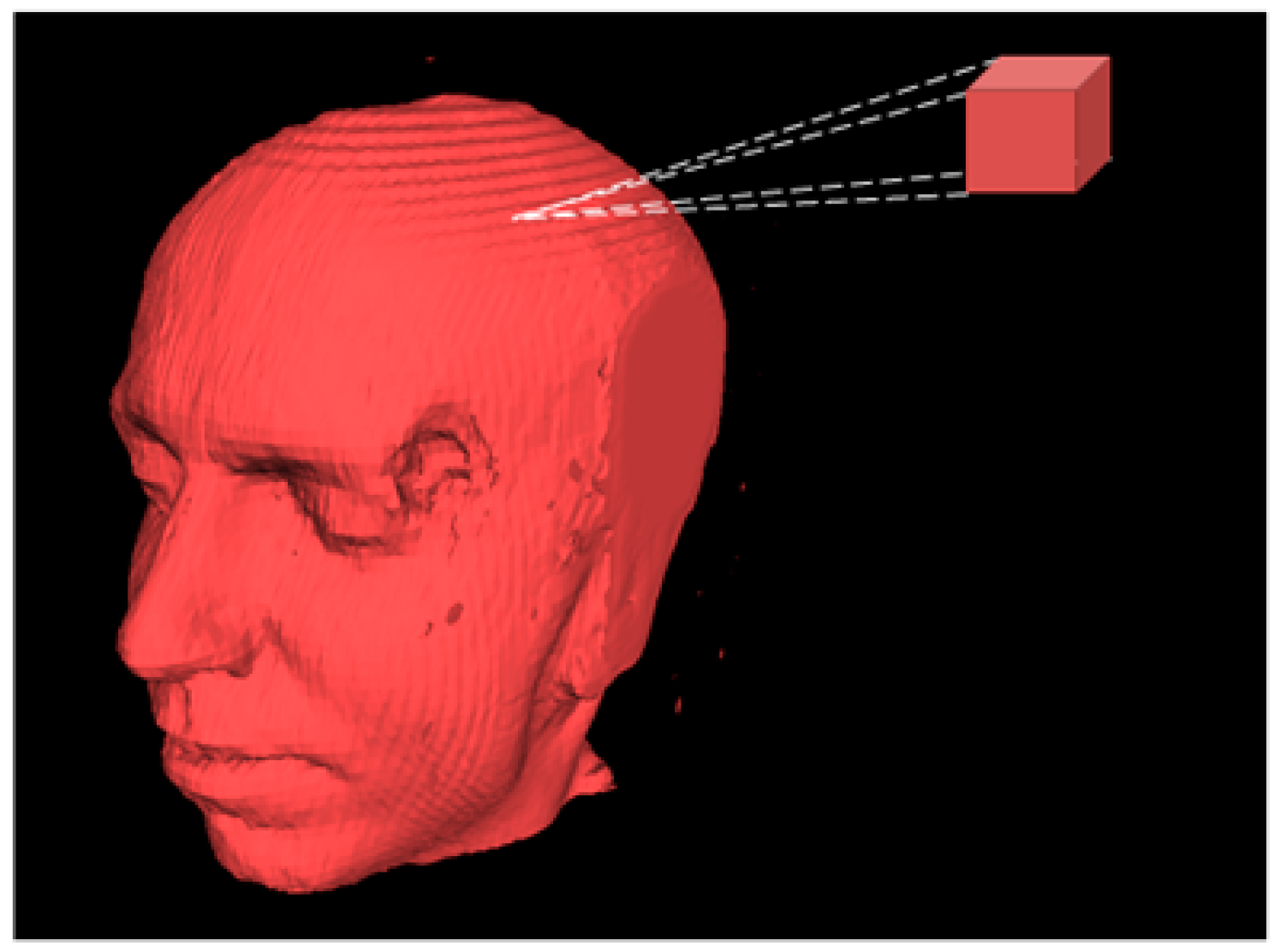
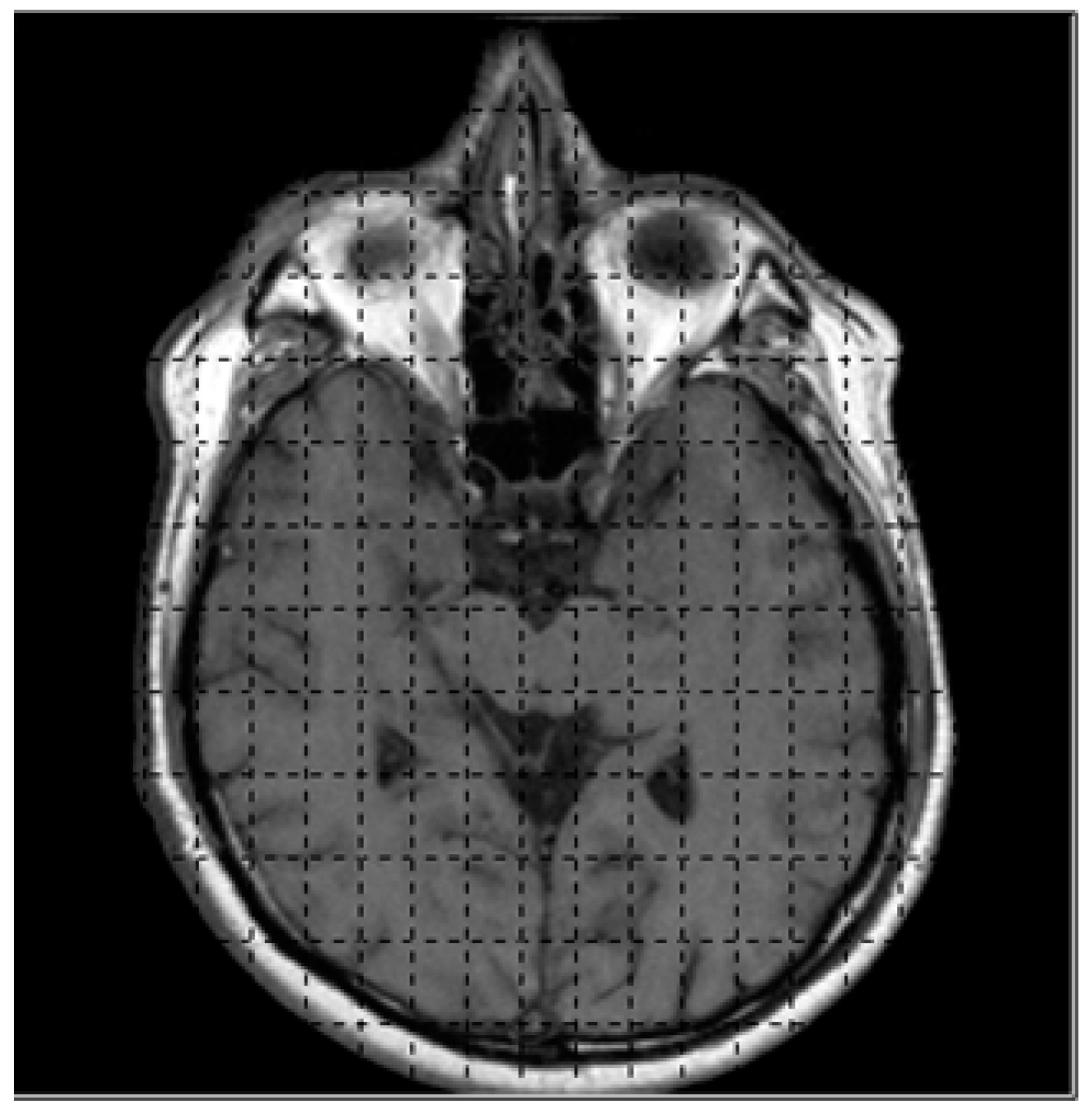
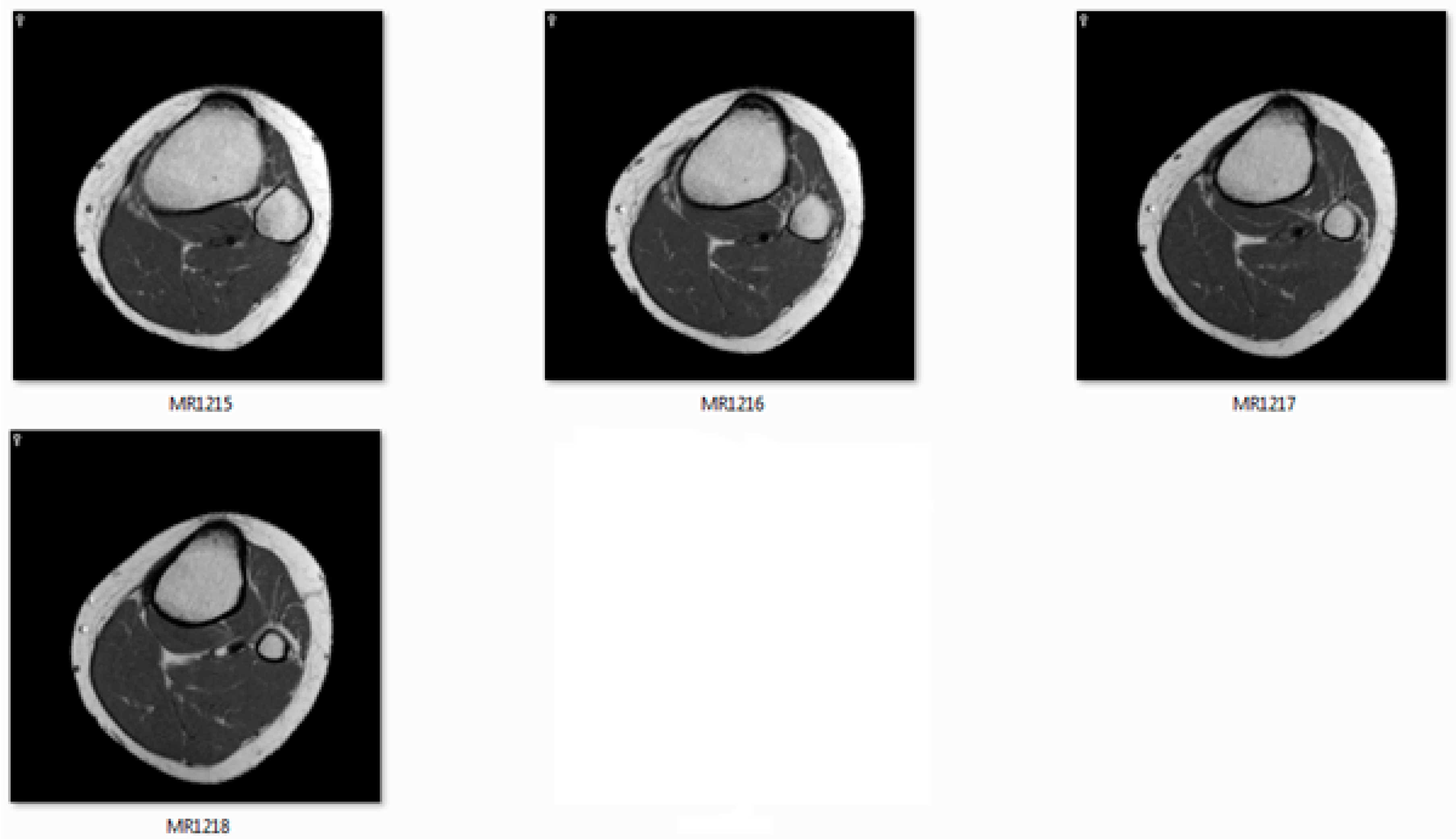
3. Reading the Intensity Value of CT Images for 3D Rendering
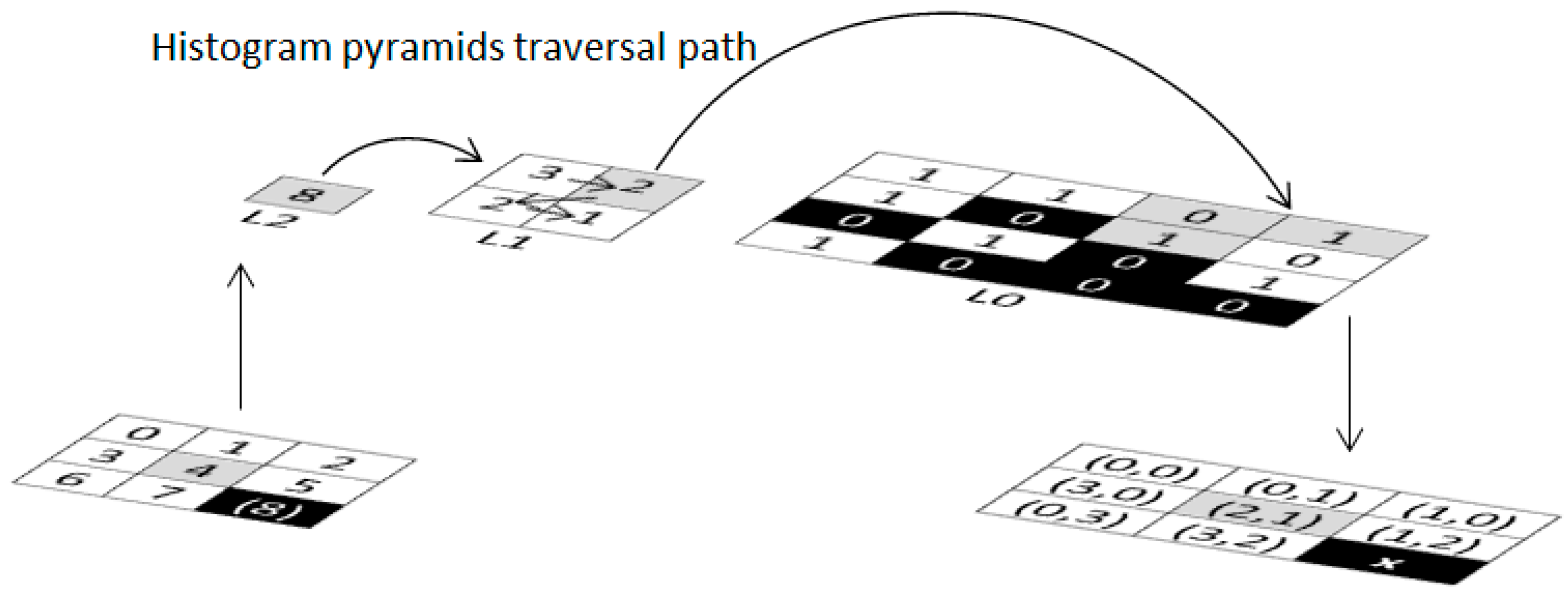
4. Histogram Pyramids
5. Implementation
6. Results
7. Conclusions and Future Works
Funding
Conflicts of Interest
References
- Nakayama, Y.; Tanida, Y. Atlas of Visualization; CRC Press: Boca Raton, FL, USA, 1997; pp. 213–214. [Google Scholar]
- Udupa, J.K. Three-dimensional visualization and analysis methodologies: A current perspective. Radiographics 1999, 19, 783–806. [Google Scholar] [CrossRef] [PubMed]
- Birkfellner, W. Applied Medical Image Processing: A Basic Course; CRC Press: Boca Raton, FL, USA, 2016; pp. 262–265. [Google Scholar]
- Helminen, H.; Alakuijala, J.; Laitinen, J.; Sallinen, S. Constant Z line texture mapping in interactive visualization of medical images. In Proceedings of the 17th International Conference of the Engineering in Medicine and Biology Society, IEEE, Montreal, QC, Canada, 20–23 September 1995; pp. 1039–1040. [Google Scholar]
- González Izard, S.; Sánchez Torres, R.; Alonso Plaza, Ó.; Juanes Méndez, J.A.; García-Peñalvo, F.J. Nextmed: Automatic Imaging Segmentation, 3D Reconstruction, and 3D Model Visualization Platform Using Augmented and Virtual Reality. Sensors 2020, 20, 2962. [Google Scholar] [CrossRef] [PubMed]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM SIGGRAPH Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Levoy, M. Display of surfaces from volume data. IEEE Comput. Graph. Appl. 1988, 8, 29–37. [Google Scholar] [CrossRef]
- Drebin, R.A.; Carpenter, L.; Hanrahan, P. Volume rendering. ACM SIGGRAPH Comput. Graph. 1988, 22, 65–74. [Google Scholar] [CrossRef]
- Sethian, J.A. Fast Marching Methods. SIAM Rev. 1999, 41, 199–235. [Google Scholar] [CrossRef]
- Long, Z.; Nagamune, K. A Marching Cubes Algorithm: Application for Three-dimensional Surface Reconstruction Based on Endoscope and Optical Fiber. Information 2015, 18, 1425–1437. [Google Scholar]
- Messmer, P.; Matthews, F.; Jacob, A.L.; Kikinis, R.; Regazzoni, P.; Noser, H. A CT Database for Research, Development and Education: Concept and Potential. J. Digit. Imaging 2007, 20, 17–22. [Google Scholar] [CrossRef] [PubMed]
- Zhong, D.; Zhang, J.; Wang, L. Fast Implicit Surface Reconstruction for the Radial Basis Functions Interpolant. Appl. Sci. 2019, 9, 5335. [Google Scholar] [CrossRef]
- Gong, S.; Newman, T.S. A corner feature sensitive marching squares. In Proceedings of the IEEE Southeastcon, IEEE, Jacksonville, FL, USA, 4–7 April 2013; pp. 1–6. [Google Scholar]
- Visutsak, P.; Pensiri, F.; Chaowalit, O. Smooth voxel surface for medical volumetric rendering. In Proceedings of the International Conference on Image and Video Processing, and Artificial Intelligence. International Society for Optics and Photonics, Shanghai, China, 23–25 August 2019; p. 113210Y. [Google Scholar]
- Marching Cubes Algorithm. Available online: http://iqc.udg.es/cat/similarity/ASA/mca.html (accessed on 28 June 2020).
- Ziegler, G.; Theobalt, C.; Seidel, H.; Kobbelt, L.; Kuhlen, T.W.; Aach, T.; Westermann, R. On-the-fly Point Clouds through Histogram Pyramids. In 11th International Fall Workshop on Vision, Modeling and Visualization; IOS Press: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Dyken, C.; Ziegler, G.; Theobalt, C.; Seidel, H.P. High-speed marching cubes using histopyramids. In Computer Graphics Forum; Blackwell Publishing Ltd.: Oxford, UK, 2008; pp. 2028–2039. [Google Scholar]
- Haque, H.F.; Rahman, A.; Ashraf, M.S.; Shatabda, S. Wavelet and pyramid histogram features for image-based leaf detection. In Emerging Technologies in Data Mining and Information Security; Springer: Singapore, 2019; pp. 269–278. [Google Scholar]
- Lavoué, G. A local roughness measure for 3D meshes and its application to visual masking. ACM Trans. Appl. Percept. (TAP) 2009, 5, 1–23. [Google Scholar] [CrossRef]
- Wang, K.; Torkhani, F.; Montanvert, A. A fast roughness-based approach to the assessment of 3D mesh visual quality. Comput. Graph. 2012, 36, 808–818. [Google Scholar] [CrossRef]
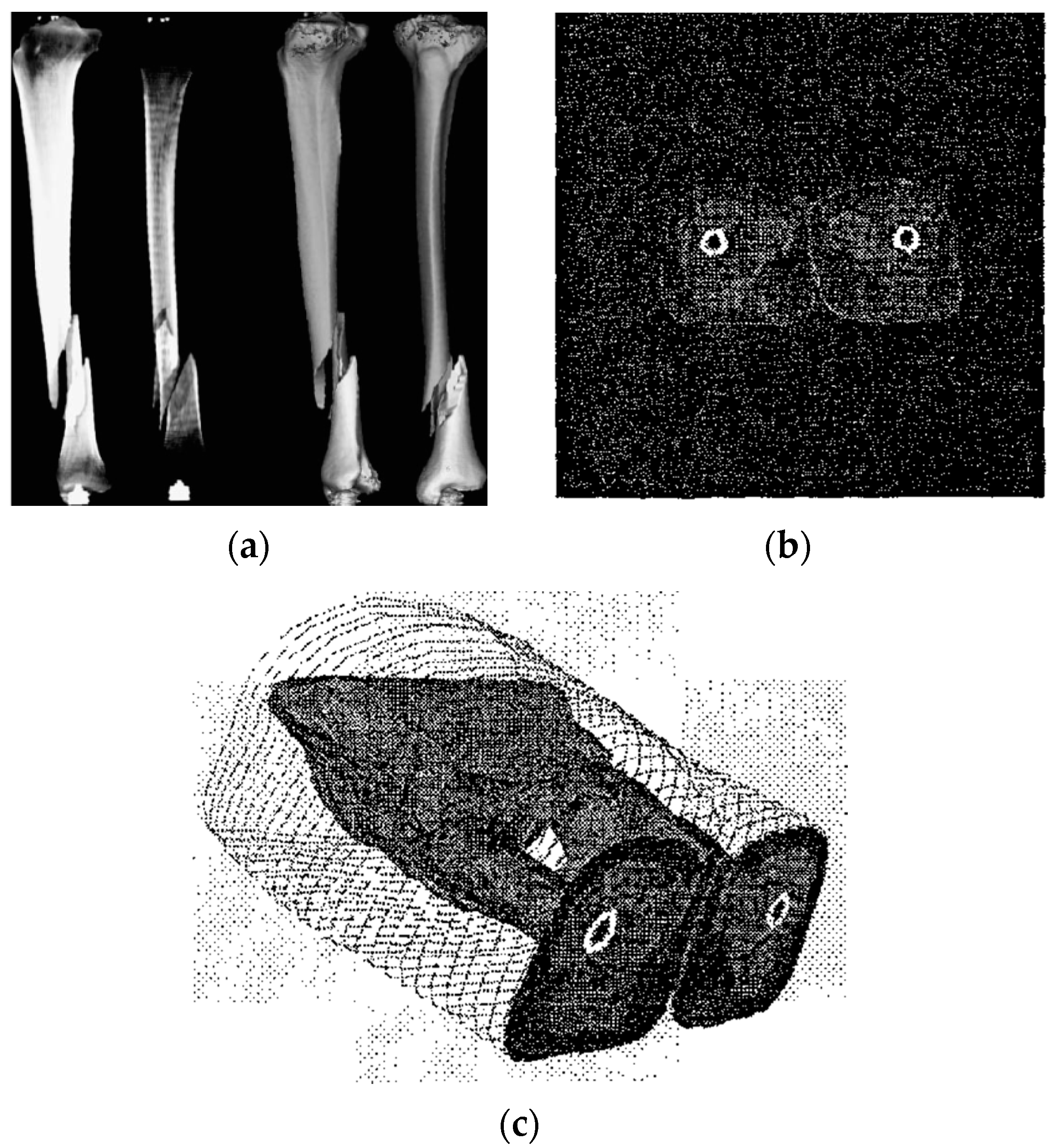




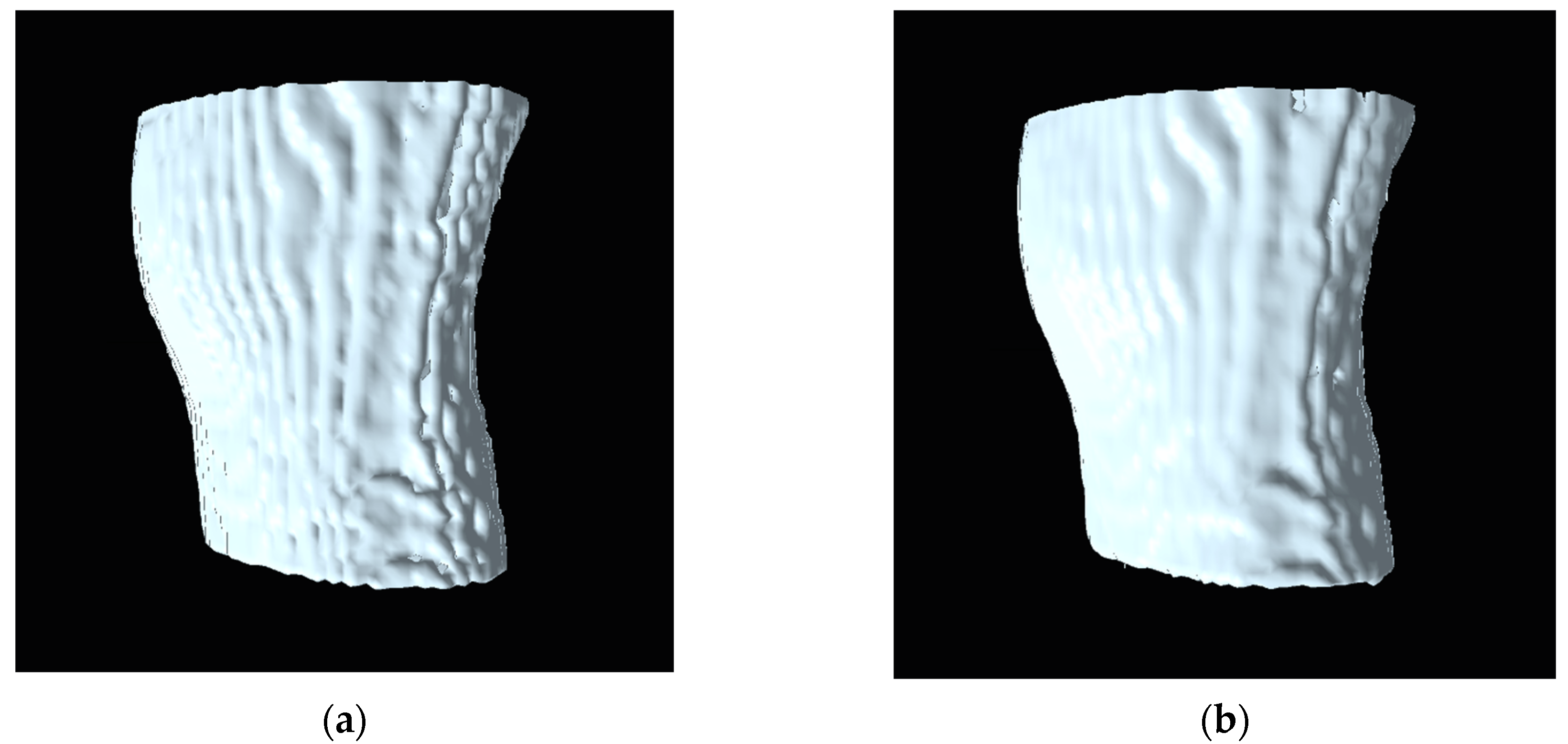


| Model | Mesh Density (Vertices) | Rendering Times (Sec.) | % Times Reduced | ||
|---|---|---|---|---|---|
| Marching Cubes [14] | Marching Cubes with Histogram Pyramids | Marching Cubes [14] | Marching Cubes with Histogram Pyramids | ||
| Sphenoid | 45,440 | 38,800 | 0.345 | 0.295 | 14.49 |
| Right-temporal | 39,600 | 32,200 | 0.338 | 0.277 | 18.04 |
| Right-maxilla | 38,560 | 31,900 | 0.324 | 0.268 | 17.28 |
| Ethmoid | 49,800 | 43,800 | 0.382 | 0.333 | 12.82 |
| Ankle bone | 63,120 | 52,900 | 0.595 | 0.500 | 15.96 |
| Teeth | 69,760 | 59,200 | 0.467 | 0.397 | 14.98 |
| - | - | - | - | Average | 15.59 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Visutsak, P. Marching Cubes and Histogram Pyramids for 3D Medical Visualization. J. Imaging 2020, 6, 88. https://doi.org/10.3390/jimaging6090088
Visutsak P. Marching Cubes and Histogram Pyramids for 3D Medical Visualization. Journal of Imaging. 2020; 6(9):88. https://doi.org/10.3390/jimaging6090088
Chicago/Turabian StyleVisutsak, Porawat. 2020. "Marching Cubes and Histogram Pyramids for 3D Medical Visualization" Journal of Imaging 6, no. 9: 88. https://doi.org/10.3390/jimaging6090088
APA StyleVisutsak, P. (2020). Marching Cubes and Histogram Pyramids for 3D Medical Visualization. Journal of Imaging, 6(9), 88. https://doi.org/10.3390/jimaging6090088





