Abstract
Computer-based fully-automated cell tracking is becoming increasingly important in cell biology, since it provides unrivalled capacity and efficiency for the analysis of large datasets. However, automatic cell tracking’s lack of superior pattern recognition and error-handling capability compared to its human manual tracking counterpart inspired decades-long research. Enormous efforts have been made in developing advanced cell tracking packages and software algorithms. Typical research in this field focuses on dealing with existing data and finding a best solution. Here, we investigate a novel approach where the quality of data acquisition could help improve the accuracy of cell tracking algorithms and vice-versa. Generally speaking, when tracking cell movement, the more frequent the images are taken, the more accurate cells are tracked and, yet, issues such as damage to cells due to light intensity, overheating in equipment, as well as the size of the data prevent a constant data streaming. Hence, a trade-off between the frequency at which data images are collected and the accuracy of the cell tracking algorithms needs to be studied. In this paper, we look at the effects of different choices of the time step interval (i.e., the frequency of data acquisition) within the microscope to our existing cell tracking algorithms. We generate several experimental data sets where the true outcomes are known (i.e., the direction of cell migration) by either using an effective chemoattractant or employing no-chemoattractant. We specify a relatively short time step interval (i.e., 30 s) between pictures that are taken at the data generational stage, so that, later on, we may choose some portion of the images to produce datasets with different time step intervals, such as 1 min, 2 min, and so on. We evaluate the accuracy of our cell tracking algorithms to illustrate the effects of these different time step intervals. We establish that there exist certain relationships between the tracking accuracy and the time step interval associated with experimental microscope data acquisition. We perform fully-automatic adaptive cell tracking on multiple datasets, to identify optimal time step intervals for data acquisition, while at the same time demonstrating the performance of the computer cell tracking algorithms.
1. Introduction
Cell migration is a fundamental process that is essential to life and it is linked to many important physiological and pathological events such as immune response, wound healing, tissue differentiation, embryogenesis, and tumour invasion [1,2,3,4,5,6,7]. Modern microscopy with image capturing devices is at the heart of techniques to study live-cell migration, such as those driven by chemotactic signalling during directed migration [8,9,10,11]. The advent of high-throughput, high-resolution microscopy, and imaging techniques means that cell outlines and migration trajectories or pathways may be visually accessible and manually traceable by a human operator (through manual tracking) to result in what is known as the gold-standard ground truth.
With the ever-increasing use of microscopy, a humongous amount of experimental data is routinely generated in many laboratories. Most of these data are collected in the absence of a monitoring segmentation and tracking algorithm. Due to the sheer magnitude of the data involved, manual tracking is often cumbersome and the development of computer algorithms for automated cell tracking is, thus, highly desirable [12,13,14,15]. In contrast, a noticeable downside of fully-automated tracking is that the recognition capability of computers is very limited (comparing to a trained human operator) despite the sizeable efforts made from the wider academic community [16,17,18,19,20].
Most of the research focuses on building fully-automated algorithms that post-process experimental outcomes without investigating the procedures underpinning data generation. The algorithms are thus blind to the underlying properties associated with quality data acquisition and a key parameter is the time step interval within the microscope. We have not explored any other parameters, since we feel these do not correlate directly with the cell tracking algorithm. Studies of this nature could be undertaken in a similar fashion. It is here that the novelty of our contribution lies, we strongly believe (and will demonstrate) that the time step interval embedded within the microscope camera setting at which experimental images are recorded is a crucial parameter that should influence the accuracy of the computer algorithms more drastically. The common choice of the time step interval between consecutive and successive camera shoot images currently published in the literature are in an ad-hoc trial-and-error approach that is generally based on the intuition and experience of microscopist or experimentalist. Typically, 5 and 10 min time step intervals are among the most common choices, for example, [21,22].
By using a novel approach for fully-automated algorithms for cell tracking, we investigate viable options during experimental microscope data acquisition to allow for accurate and high-quality acquisition of images, thereby contributing to fully-automatic big data analytics in cellular biology. Here, we focus on different choices of the time step interval within the microscope. Taking into account the drawbacks that arise from using computer algorithms (i.e., lack of superior pattern recognition and error-handling capability compared to its human counterpart), one may propose to take constant and frequent sequences of images with an exceptionally short time step interval (e.g., a few seconds apart or even multiple frames within a second). However, when an image is taken, light is shed on the cells for clear visualisation. Yet, large doses of light have the potential to damage or even kill the cells under experiment [23,24,25,26]. Recent studies show that yeast cells that appeared healthy directly after irradiation with a very low light-dose from a fluorescent microscope failed to divide when left overnight, whereas their non-imaged neighbours divided normally [27]. In fact, it has been pointed out that fixation, plasma membrane permeabilisation, and cytoskeleton destruction are among the typical light-induced cell damages in live-cell microscopy [24,28].
Evidently, a trade-off emerges on the choice of the time step interval and the quality of the images collected. Images acquired with a short time step interval would be beneficial for cell tracking algorithms, since cells will be much closer to their previous locations, but may be too harmful to the cells, as discussed above. On the other hand, a sequence of images obtained with a larger time step interval might result in less accuracy in cell tracking, since the cells could have moved further away and even out of focus or might have gone through large morphological changes.
Hence, the aim of this study is to investigate the relationship between the choice of the time step interval and the accuracy of the cell tracking algorithm, within the context of a fully-automated positive feedback loop between the quality of tracking cells and the quality of data acquisition. To the best of the authors’ knowledge, such a study has not been carried out. The majority of cell tracking algorithms published have only considered experimental data as static and given information. Here, we conduct specific experiments with known outcomes (i.e., the direction of cell migration) by either using an effective chemoattractant or employing no-chemoattractant. By acquiring images at 30 s time step intervals, we generate relatively large datasets on which we employ our cell tracking algorithms. To avoid generating extra data at say 1-, 2-min time step intervals, we use the same dataset generated with the 30-s time step interval and simply read out results at other larger time step intervals, to form different subset datasets with different time step intervals. We then evaluate the accuracy of our existing cell tracking algorithms to illustrate the effects of these different time step intervals. We establish that there exists certain fundamental relationships between the tracking accuracy and parameters that are associated with experimental microscope data acquisition.
Our fully-automated approach differs from the current-state-of-the-art cell tracking methodologies in that we investigate the dynamic interplay between segmentation and tracking (which are the hallmarks of the cell tracking algorithms) and the variable adaptive time step interval for generating quality image datasets from the microscopes. We recommend an adaptive approach, where, if the images being generated by the microscope for a particular time step interval are detected by the algorithm to be of less quality (below a certain threshold, hence poor cell tracking), the time step should then be reduced by some factor, automatically (on the fly). Conversely, if the images that are generated by the microscope at a particular time step interval are of high quality (above a certain threshold, hence too high quality cell tracking), then the time step interval can be increased by some factor, automatically. This positive interplay between the quality of the segmentation and cell tracking and the time step interval naturally leads to an adaptive optimal time step selection, such that the quality of the images is appropriate for quality segmentation and tracking and vice-versa.
This research provides a new perspective and benchmark results for the cell tracking community. Multiple experiments involving directed and random cell migration are used to capture live-cell migrations with two different cell lines in order to carry out these investigations. We include both induced (i.e., chemotactically driven) and non-induced experiments that result in directed and random cell migration, respectively. Phase-contrast microscopy is chosen to record the experimental data. This type of microscopy is generally considered to be less harmful to cells, since the intensity of lighting is an order of magnitude lower than other types, such as fluorescence microscopy. Besides the non-destructive light intensity, phase contrast is also less harmful to cells than fluorescence microscopy, because it is a label-free method [29]. We select a number of time step intervals and evaluate each result against expected cell migration pathways and the corresponding manual tracking indices, respectively. We first select two representative algorithms [30] to test automatic cell tracking and then consider a new algorithm that is based on an improved segmentation method.
2. Materials and Methods
2.1. Cell Culture and Microscopy Data
The experimental datasets used in this study consist of experimental biological data generated in the laboratories of ibidi GmbH. The data demonstrate the migration of two types of adherent, slow-moving cells: human fibrosarcoma cell line HT1080 and normal human epithelial keratinocytes (nHEK). Chemotaxis of slow-moving cells plays a crucial role in various physiological processes, including metastasis and wound healing [31,32,33]. Cell types designated as slow-moving employ the mesenchymal-like migration strategy and their average speed is in the range of approximately one cell-body length per hour (i.e., less than 1 m/min); in contrast to so-called fast-moving cells, such as immune cells that migrate using the amoeboid type of locomotion at cell speed reaching approximately 10 m/min [2,34]). The migration speed and the cell-body size provide a cue for selecting a time-lapse interval that is suitable for manual tracking, allowing for the human operator to identify one single migrating cell entity in two consecutive frames. Typically, for slow-moving cells this is of the order of several minutes, e.g., a 5- or 10-min time step interval is generally used when observing the chemotaxis of HT1080 cells [33,35]. The experiments with chemotaxis were performed while using the -Slide Chemotaxis assay (ibidi GmbH, Gräfelfing, Germany). Briefly, the HT1080 cells (DSMZ, Braunschweig, Germany) were cultured in Dulbecco’s modified Eagles Medium (DMEM, Sigma, Germany) supplemented with 10% fetal bovine serum (Sigma, Germany). The nHEK cells (CellSystems, Troisdorf, Germany) were cultured in DermaLife basal medium (Lifeline Cell Technology, Frederick, MD, USA) that was supplemented with DermaLife K LifeFactors kit. The cultures were maintained at 37 C and 5% CO. After reaching 80% confluence, the cells were trypsinised and a cell suspension of 1–2 × cells/mL was filled into the observation channels of the -Slide Chemotaxis, ibiTreat (ibidi GmbH, Gräfelfing, Germany). For experiments with the nHEK cells, the observation channel was beforehand coated with fibronectin. After attachment of the cells, the reservoirs of the chemotaxis chamber were filled with media, as follows:
- Dataset 1:
- Both reservoirs and the channel were filled with DMEM supplemented with 10% FBS to induce random migration of HT1080.
- Dataset 2:
- The lower reservoir was filled with DMEM with 10% FBS, while the channel and upper reservoir were filled with DMEM without FBS to establish a gradient inducing directed migration of HT1080.
- Dataset 3:
- The upper reservoir and the channel were filled with the DermaLife medium with 10 ng/mL epithelial growth factor (EGF; Sigma, Germany) and the lower reservoir was filled with DermaLife medium that was supplemented with a mixture of growth factors, containing 0.5 g/mL EGF and 50 ng/mL transforming growth factor -1 (Peprotech, Hamburg, Germany). At these conditions, the gradient of growth factors did not induce a chemotactic response in nHEK cells.
- Dataset 4:
- Both reservoirs and the channel were filled with the DermaLife medium with 10 ng/mL EGF to induce random migration of nHEK.
Time-lapse imaging was performed up to 24 h with a time step interval of 30 s, while using a Nikon TiE inverted microscope with a 4× phase-contrast objective (the pixel size = 1.61 m/px). We exhibit the first frames from each dataset in Figure 1.
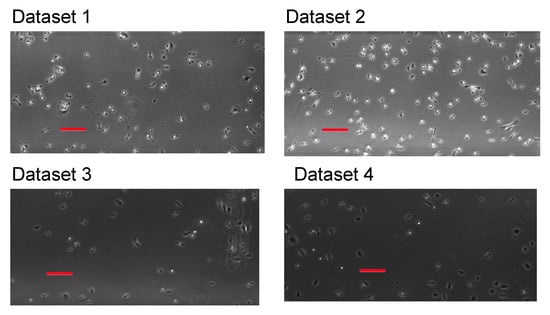
Figure 1.
The first frames from each dataset. See main text for description of the datasets. Bars are m in length.
2.2. Cell Tracking Techniques
In general, cell tracking techniques consist of two stages: segmentation and particle tracking. The first stage is to separate foreground (consisting of objects as well as potential noise and unwanted fragments in motion) and static background. Noise and fragments may be filtered by some characteristic measurements, such as their size. It is important to note that there is some uncertainty that is introduced by noise [12,13,14,15,16,18,19,20,28,30,36,37,38,39,40].
Having obtained a list of objects on every frame from the segmentation, the next stage is to temporally associate corresponding objects between consecutive frames to determine cell movement. Typically, the centroid (i.e., centre of mass) method is used to represent and locate each object (which is treated as a moving particle), again from one image to the other and these are then joined together to form trajectory pathways. Thus, this stage is often termed particle tracking, since objects are reduced to points. Taking a centroid at the current frame as a reference point, if there is a centroid on the following frame and their distance is within a pre-defined range, we say that this movement belongs to the cell that the reference point is representing. A sufficient number of movements from a single cell is recorded as a trajectory and eventually used to analyse its collective migration behaviour. This is the ultimate goal of cell tracking within the scope of this project. The pre-defined range can be seen as a parameter that defines the maximum distance a cell may move within the specified time step interval between two adjacent frames.
Furthermore, it is possible that there are multiple centroids within this pre-defined range for selection. In an ideal situation, one could determine the most appropriate target based on shape changes, similarities in size, cellular dynamics such as head-and-tail identification and statistical analysis to predict movements that are based on previous information. On the other hand, few techniques exist to reliably determine such information. Therefore, we follow arguably the most common approach that assumes the reference point moves to the closest target in that defined vicinity.
In this study, we include two different segmentation techniques following the work by [30]. The first algorithm combines edge detection and active contour [12,38], which uses the edge positions to select the objectives. The second algorithm applies background reconstruction from the entire dataset and subsequently subtract each image from the constructed background image [37,40]. A brief summary of the algorithms is provided below. Further specific details of these techniques can be found in our previous study [30]. In order to demonstrate our approach, we choose the first frame from Dataset 2 described in Section 2.1, which is shown as the top image in Figure 2. On the left-hand side column, we illustrate the first algorithm involving edge detection and active contour. The right-hand column illustrates the application of the second algorithm using the background reconstruction approach. One major issue from the chosen cell lines is that cells often develop filopodia that can be significantly stretched and elongated. This entails that cell shapes can vary drastically. Because the phase-contrast microscopy relies on changes in phase shifts and, depending on the objective lens, it only works in a certain range of phase shifts. If the shift is too big, artefacts are created. Cells may often have a noticeable bright “halo” around their outer rims and their interior may change from dark black to bright white.

Figure 2.
Illustration of two segmentation techniques: (a) the original frame from Dataset 1; (b) the work of edge detection method [12,38]; (c) active contour acting upon the result from edge detection [12,38]; (d) binary image as the result from (b,c); (e) illustrating how we stack all images to reconstruct the static background; (f) the work of background reconstruction [37,40]; and, (g) binary image resulting from the reconstruction and subtraction algorithms [30]. Bars are m in length.
These characteristics from phase-contrast microscopy impose specific errors due to the nature of the segmentation techniques. For instance, techniques, such as background reconstruction and subtraction, cannot separate internal intensity changes in a cell from changes around its membrane. For certain elongated cells, cells may be segmented into two fragments, thus causing false positives. On the other hand, an active contour method is robust at detecting changes in the intensity values and may correctly form a connected region to locate cells. Thus, internal differences in a cell can be filtered out and only the interfacial region between the cell membrane and the background is kept. However, an active contour is unlikely to separate cells that are close to each other. In conclusion, background subtraction normally results in more detections (due to fragments) than the ground truth and active contour provides less detections (due to cell proximity). We see these two pattern profiles in Figure 2. The original image has 132 cells in view, the left-hand-side edge detection and active contour found 119 objects, and the right-hand side detects 140.
2.2.1. Segmentation Algorithm 1—Edge Detection and Active Contour
Here we employ some standard segmentation methods, first of all, for each image, we identify the edges by looking at the intensity gradients in that image. This provides the information that is needed for a standard active contour to locate and identify objects of interest. These methods are widely used and their descriptions can be found in [12,38]. We demonstrate these two steps in Figure 2b,c, respectively, and Figure 2d shows the results of using this algorithm.
2.2.2. Segmentation Algorithm 2—Background Reconstruction and Subtraction
The assumption underlying the principles of this method is that we can reconstruct a background image, and then the results of subtraction to the normal images (i.e., containing cells) will yield objects of interest (or noise that may then be removed via various other methods) [30]. To reconstruct the background, we take the mode of the intensity value occurring in all frames at each pixel. Due to the fact that cells are generally moving around (hence the need for tracking), and the density is low, the mode value at each pixel is most likely to be the intensity of the background or a stationary noise that we may also categorise as background.
After having the background reconstructed, all frames can be subtracted from it and, whatever the differences are, these are either moving cells or simply noise. We can then identify and separate cells by their areas and/or trajectories following a common identification procedure [30]. We demonstrate this method in Figure 2e–g, where Figure 2f is the reconstructed background and Figure 2g represents the results after subtraction.
2.2.3. Tracking Algorithm—Nearest Neighbour Approach
We now present our tracking algorithm that relies on results from the segmentation approaches described above. It tracks through locations of centroids and links pairs of centroids from adjacent frames by assessing their distance to a threshold. This has been used in many existing works, for example, in [41,42,43,44]. We further impose a global minimisation to ensure uniqueness of our tracking process. Providing two input datasets from two segmentations, and , with and the total number of centroids in datasets A and B, respectively, and with and the positions of each centroid. We define a threshold distance , such that links between centroids whose distance from each other is greater than D is considered to be implausible. Our linking procedure is defined, as follows; first, we compute an array whose D entries are given by the Euclidean distance between the ith centroid in dataset A and the jth centroid in dataset B, such that
We create a link between the centroid and that minimises the above distance. We then remove the distances that are associated with the links and , i.e., the th row and th column of D, and apply the above procedure recursively.
3. Results
We analyse the four datasets described in Section 2.1 and summarise our findings in this section. The only effective chemoattractant is in Dataset 2, where the chemoattractant is placed at the south side of the view plane. Thus directed cell migration between north and south is expected from this dataset. On the other hand, we expect cells to adopt a random-walk from the other three datasets between north and south directions. Furthermore, all four datasets should show cells adopting a random-walk between east and west directions.
We allow cells to move freely in and out of the boundaries of the view plane; thus, the number of cells in the experiments varies. In addition, a noticeable increase to the cellular area is observed and it is likely due to developed filopodia towards the end of the experiments. We use the confluences [39], i.e., the ratio between areas of cells and total view plane, to evaluate cell density. We summarise the details of each individual experiment below.
- Dataset 1:
- Total number of frames: 2880 (24 h), confluences vary between 7.30–15.02%, random-walk pattern is expected.
- Dataset 2:
- Total number of frames: 2880 (24 h), confluences vary between 17.26–48.37%, directional migration towards south, random-walk pattern between east and west is expected.
- Dataset 3:
- Total number of frames: 2761 (23.01 h), confluences vary between 4.59–12.44%, random-walk pattern is expected.
- Dataset 4:
- Total number of frames: 2566 (21.38 h), confluences vary between 6.42–14.94%, random-walk pattern is expected.
For the first round of tests, we employ all frames (i.e., using a 30 s time step interval) from each individual dataset to track the cells. The second round of tests includes a 1-min interval, meaning we take every second frame in each dataset in our tracking algorithm and completely ignore the intermediates. Thus we only use half of the total number of frames. Tests are further repeated with 2, 3, 5, 7.5, 10, and 15 min intervals. For completeness, the choice of D within our tracking algorithm described in the previous section is 10 pixels (roughly around m) for the 30-s interval and gradually increases to around 50 pixels (approximately 83 m) for the most infrequent time step interval (i.e., 15 min). The minimum threshold on the duration of a cell trajectory is set to be of the experimental duration. In all cases, this duration is roughly h, which means a trajectory continually lasting at least h is counted as acceptable otherwise it is rejected. There is no upper bound threshold, so a trajectory may theoretically last the full length of the experiment, but this is neither practically common nor possible.
For illustrative purposes, we use the results from edge-detection-active-contour segmentation. We showcase some of the results graphically in Figure 3. We plot all the tracked trajectories of Dataset 2 from four different time step intervals: 30 s, 5, 10, and 15 min, respectively. These trajectories are shown on both white backgrounds (Figure 3(a1–c1)), as well as overlaid on the first image (Figure 3(a2–c2)) of Dataset 2 to give the reader an alternative perspective on the interplay between segmentation and cell tracking. We observe that, as the interval enlarges, less trajectories are found by the cell tracking algorithm. The length of trajectories as well as the accuracy reduce substantially. When considering the standard 10 min setting for manual tracking, we see that this choice of time step interval plays a much more vital role in determining the quality of computerised cell tracking that is different to the manual cell tracking gold-standard approach.

Figure 3.
Cell trajectories generated by the fully-automated cell tracking software with different choices of time step intervals. (a1–d1) These images show trajectories on a plain background. (a2–d2) Images demonstrate trajectories overlaid on the first image of the sequence. (a1,a2) Are generated with a 30 s time step interval; (b1,b2) generated with a 5 min time step interval; (c1,c2) generated with a 10 min time step interval; and (d1,d2) generated with a 15 min time step interval. Bars are m in length.
In Table 1, we show all results from the four datasets obtained when using the edge-detection-active-contour segmentation approach. The first column from the left indicates the different choices of the time step intervals. The second column shows the total number of trajectories found, which is equal to or greater than the required duration (i.e., of the total duration of the experiment). The third column shows the number of trajectories whose ending points are on the southern side of the starting reference point. The percentage between south moving and the total number is presented in the fourth column. In the fifth column, we show the number of east moving trajectories and their corresponding percentage in the sixth column. To fully evaluate the performance of our algorithms, we compare these tracked trajectories from our automatic cell tracked results to their corresponding counterpart results obtained manually from a trained human operator. We employ a strict approach, where, if a mistake is made (e.g., tracked to a different cell), we consider such track as a failure to provide accurate information. The details of this comparison are illustrated in the seventh column.

Table 1.
Summary of our tracking results from all four datasets using the first algorithm. Accuracy is obtained through comparison between the automatically tracked trajectories to those that have been manually tracked by a human operator.
It can be seen from Table 1 that the total number of trajectories decreases as the time step interval gets large. This is demonstrated by all four datasets that confirm our observation, as illustrated in Figure 3. We further observe that the majority of percentages from the random-walk pattern vary around with an exception of , which comes from a 15 min time step interval with a low identification count. In addition, of figures lay between 40.0–60.0%. Whereas, for directed cell migration, all of the figures show a tracking accuracy of more than . This result shows that fully-automated algorithms are capable of determining the patterns from experiments of chemotaxis. In terms of high accuracy, only within the 3 min time step interval does the algorithm achieve an accuracy of or above.
We further analyse two selected datasets (Dataset 2 and 4) using an alternative segmentation technique that is based on background reconstruction and substitution, as described earlier, in order to demonstrate that patterns are independent of the choice of the technique. It is worth noting that, because of the extra fragments, the tracking accuracy from this segmentation technique is known to be worse. We show the results in Table 2. We can see the accuracy within the 3 min time step interval is only or above. On the other hand, we see that the method is still good enough to distinguish directed cell migration from a random walk. It can be observed that the former stays above in all figures and the latter varies between 40.0–61.5%, with only one exception of .

Table 2.
Summary of our tracking results from two selected datasets using the second algorithm.
To graphically illustrate the difference between directed migration and random walk, we use the results from two datasets (Dataset 1 and 2). A star-plot format is employed here, which overlays all of the starting points of each trajectory to and only links this reference point to the ending point of each trajectory. The results from eight different intervals from these two datasets are shown in Figure 4 and Figure 5.
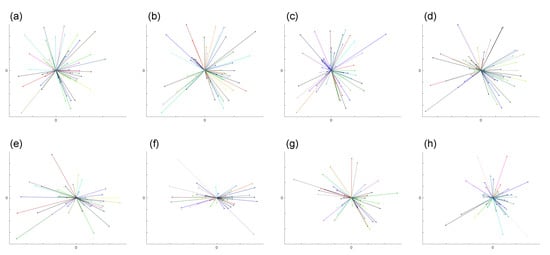
Figure 4.
The plots demonstrate graphically the random walk cell migration patterns from Dataset 1 obtained from (a–h) with time step intervals 30-s, 1-, 2-, 3-, 5-, 7.5-, 10-m and 15-min, respectively. The detailed numbers are shown in Table 1. We overlaid the starting point of each trajectory at the centre point and link the ending point, so as to illustrate the general direction of the cell.
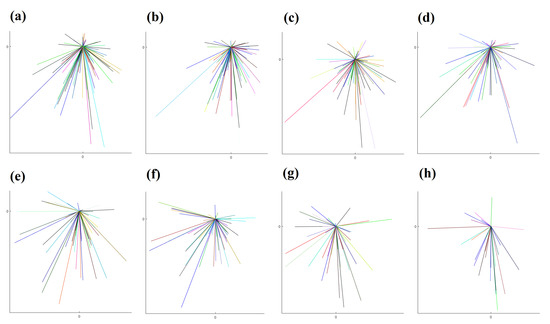
Figure 5.
The plots demonstrate graphically directed cell migration patterns from Dataset 2 obtained from (a–h) with time step intervals 30-s, 1-, 2-, 3-, 5-, 7.5-, 10-, and 15-min, respectively. Table 2 shows the detailed numbers. We overlaid the starting point of each trajectory at the centre point and link the ending point, so as to illustrate the general direction of the cell.
In terms of efficiency, any test case presented here can be fully-automatically analysed within 40 s on a moderate PC with GHZ Intel processors. Whereas, for the human operator, it could take between one to several hours to complete the manual tracking on one data test set.
4. Discussion
The interplay between cell tracking algorithms and the time step intervals (the time between when images are taken) associated with image data acquisition techniques has not been explored before in great detail. In this paper, we demonstrated the importance of the time step intervals at the data generation stage and its subsequent influence towards the accuracy of automatic cell-tracking algorithms. The authors are aware of the vast number of cell-tracking research and algorithms, such as the famous Cell Tracking Challenges [14,45] and references within. The majority of current state-of-the-art cell tracking algorithms focus primarily on how best to track cells within existing datasets. In this study, we depart from the current-state-of-the-art and propose a new novel approach, where we investigate optimal time step intervals for quality data acquisition. To demonstrate this concept, we have generated new datasets of variable quality at ibidi GmbH, Germany, where we were able to control the time step interval setting within the microscope. By carrying out manual cell tracking on these datasets, we were able to obtain the gold standard dataset to be used as a measure of accuracy for our novel fully-automated cell-tracking approach. Therefore, we were able to quantitatively investigate the optimal time step interval that yields the best quality of the dataset at a cost-effective manner and with high accuracy in cell tracking. We presented various examples by analysing the data generated from various time step intervals to illustrate the consequences and impact the time step interval has on the quality and accuracy in tracking cells. This approach supports the observation of and argument against exposing cells to too frequent light intensity during experimental data acquisition. With different cell lines, experimental settings, image acquisition devices, and different image analysing methods, an optimal choice of the time step intervals (such as minimising the light exposure while maximising tracking accuracy) is proposed and supported by various results. Therefore, this work opens research avenues and pathways for further interdisciplinary research to improve all relevant areas of cell tracking, which include segmentation, tracking, and adaptive time stepping within microscopes.
5. Conclusions
Fully-automated cell tracking has the unrivalled capability of speed for data analytics. In this paper, we establish a relationship between the accuracy in tracking cell trajectories and the time step intervals within which data is acquired that is substantially different from the standard choice of manual tracking. Using four datasets from two cell lines, we presented results which support the theory that our proposed techniques are capable of determining and characterising the migration directions in chemotaxis, thereby providing premises for quantitative statistical analysis. We further argued that, in order to achieve a higher-accuracy in cell tracking from full automation, a much more refined data acquisition approach is needed to compensate for the absence of human intelligence for manual tracking. Our results serve as a good quality control guidance for other experimental data sets.
We recognise that our fully-automated tracking techniques require additional improvement. One aspect of future work is to understand and be able to deal with cell collision. Some recent studies using statistical analysis [44] might provide a good alternative solution. We also believe a better understanding in cell migration is vital and mathematical models from computational fluid dynamics may be a valid tool [46,47].
6. Data Management
All of the computational data output is included in the present manuscript. All images that are presented in this paper are available upon request.
Author Contributions
The authors’ contributions are summarised as follows: conceptualisation, F.W.Y. and A.M.; methodology, F.W.Y., L.T., Z.v.G., K.C., and A.M.; software, F.W.Y.; validation, F.W.Y. and L.T.; resources, Z.v.G. and A.M.; writing—original draft preparation, F.W.Y. and L.T.; writing—review and editing, F.W.Y., L.T., Z.v.G., K.C., and A.M.; visualisation, F.W.Y. and L.T.; funding acquisition, Z.v.G., K.C. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research (L.T., Z.v.G., A.M.) was funded by the European Union Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 642866. This work (A.M.) was partially funded by the EPSRC grant number EP/J016780/1 and the Leverhulme Trust Research Project Grant (RPG-2014-149), the Commission for Developing Countries, and by a grant from the Simons Foundation. A.M. is a Royal Society Wolfson Research Merit Award Holder funded generously by the Wolfson Foundation. F.W.Y. is funded by EPSRC EP/R001588/1.
Acknowledgments
(F.W.Y., L.T., Z.v.G., A.M.) would like to thank the Isaac Newton Institute for Mathematical Sciences for its hospitality during the programme [Coupling Geometric PDEs with Physics for Cell Morphology, Motility and Pattern Formation] supported by EPSRC Grant Number EP/K032208/1. (F.W.Y., K.C.) would like to thank Pump Priming funding from the Centre for Mathematics in Healthcare at the University of Liverpool to enable the research collaboration. AM is a Distinguished Visiting Scholar to the Department of Mathematics, University of Johannesburg, South Africa.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ridley, A.; Schwartz, M.; Burridge, K.; Firtel, R.; Ginsberg, M.; Borisy, G.; Parsons, J.; Horwitz, A. Cell migration: Integrating signals from front to back. Science 2003, 302, 1704–1709. [Google Scholar] [CrossRef] [PubMed]
- Friedl, P.; Wolf, K. Plasticity of cell migration: A multiscale tuning model. J. Cell Biol. 2010, 188, 11. [Google Scholar] [CrossRef] [PubMed]
- Olson, M.; Sahai, E. The actin cytoskeleton in cancer cell motility. Clin. Exp. Metastasis 2009, 26, 273. [Google Scholar] [CrossRef] [PubMed]
- Stephens, L.; Milne, L.; Hawkins, P. Moving towards a better understanding of chemotaxis. Curr. Biol. 2008, 18, R485–R494. [Google Scholar] [CrossRef] [PubMed]
- Scarpa, E.; Mayor, R. Collective cell migration in development. J. Cell Biol. 2016, 212, 143. [Google Scholar] [CrossRef] [PubMed]
- Pollard, T.; Borisy, G. Cellular motility driven by assembly and disassembly of actin filaments. Cell 2003, 112, 453–465. [Google Scholar] [CrossRef]
- Pollard, T.; Cooper, J. Actin, A central player in cell shape and movement. Science 2009, 326, 1208–1212. [Google Scholar] [CrossRef]
- Stelzer, E. Light-sheet fluorescence microscopy for quantitative biology. Nat. Methods 2015, 12, 23–26. [Google Scholar] [CrossRef]
- Wagner, M.; Weber, P.; Bruns, T.; Strauss, W.; Wittig, R.; Schneckenburger, H. Light dose is a limiting factor to maintain cell viability in fluorescence microscopy and single molecule detection. Int. J. Mol. Sci. 2010, 11, 956–966. [Google Scholar] [CrossRef]
- Greger, K.; Swoger, J.; Stelzer, E. Basic building units and properties of a fluorescence single plane illumination microscope. Rev. Sci. Instrum. 2007, 78, 023705. [Google Scholar] [CrossRef]
- Keller, P.; Schmidt, A.; Santella, A.; Khairy, K.; Bao, Z.; Wittbrodt, J.; Stelzer, E. Fast, high-contrast imaging of animal development with scanned light sheet–based structured-illumination microscopy. Nat. Methods 2010, 7, 637–642. [Google Scholar] [CrossRef] [PubMed]
- Chan, T.; Vese, L. Active contours without edges. IEEE Trans. Image Process. 2001, 10, 266–277. [Google Scholar] [CrossRef] [PubMed]
- Bosgraaf, L.; van Haastert, P.; Bretschneider, T. Analysis of cell movement by simultaneous quantification of local membrane displacement and fluorescent intensities using Quimp2. Cell Motil. Cytoskelet. 2009, 66, 1560165. [Google Scholar] [CrossRef] [PubMed]
- Maska, M.; Ulman, V.; Svoboda, D.; Matula, P.; Matula, P.; Ederra, C.; Urbiola, A.; Espana, T.; Venkatesan, S.; Balak, D.; et al. A benchmark for comparison of cell tracking algorithms. Bioinformatics 2014, 30, 1609–1700. [Google Scholar] [CrossRef]
- Miura, K. Tracking movement in cell biology. Adv. Biochem. Eng./Biotechnol. 2005, 95, 267–295. [Google Scholar]
- Crocker, J.; Grier, D. Methods of digital video microscopy for colloidal studies. J. Colloid Interface Sci. 1996, 179, 298–310. [Google Scholar] [CrossRef]
- Gonzalez, R.; Woods, R.; Eddins, S. Digital Image Processing: Using MATLAB; Pearson/Prentice Hall: Upper Saddle River, NJ, USA, 2004. [Google Scholar]
- Hand, A.; Sun, T.; Barber, D.; Hose, D.; MacNeil, S. Automated tracking of migrating cells in phase-contrast video microscopy sequences using image registration. J. Microsc. 2009, 234, 62–69. [Google Scholar] [CrossRef]
- Horn, B.; Schunck, B. Determining optical flow. Artif. Intell. 1981, 17, 185–203. [Google Scholar] [CrossRef]
- Meijering, E.; Dzyubachyk, O.; Smal, I. Methods for cell and particle tracking. Methods Enzymol. 2012, 504, 183–200. [Google Scholar]
- de Rooij, J.; Kerstens, A.; Danuser, G.; Schwartz, M.; Waterman-Storer, C. Integrin-dependent actomyosin contraction regulates epithelial cell scattering. J. Cell Biol. 2005, 171, 153–164. [Google Scholar] [CrossRef]
- Peschetola, V.; Laurent, V.; Duperray, A.; Michel, R.; Ambrosi, D.; Preziosi, L.; Verdier, C. Time-dependent traction force microscopy for cancer cells as a measure of invasiveness. Cytoskeleton 2013, 70, 201–214. [Google Scholar] [CrossRef] [PubMed]
- Schneckenburger, H.; Weber, P.; Wagner, M.; Schickinger, S.; Richter, V.; Bruns, T.; Strauss, W.; Wittig, R. Light exposure and cell viability in fluorescence microscopy. J. Microsc. 2012, 245, 311–318. [Google Scholar] [CrossRef] [PubMed]
- Waldchen, S.; Lehmann, J.; Klein, T.; van de Linde, S.; Sauer, M. Light-induced cell damage in live-cell super-resolution microscopy. Sci. Rep. 2015, 5, 15348. [Google Scholar] [CrossRef] [PubMed]
- Hoebe, R.; van Oven, C.; Gadella, T.; Dhonukshe, P.; van Noorden, C.; Manders, E. Controlled light-exposure microscopy reduces photobleaching and phototoxicity in fluorescence live-cell imaging. Nat. Biotechnol. 2007, 25, 249–253. [Google Scholar] [CrossRef] [PubMed]
- Frigault, M.; Lacoste, J.; Swift, J.; Brown, C. Live-cell microscopy—Tips and tools. J. Cell Sci. 2009, 122, 753–767. [Google Scholar] [CrossRef] [PubMed]
- Carlton, P.; Boulanger, J.; Kervrann, C.; Sibarita, J.; Salamero, J.; Gordon-Messer, S.; Bressan, D.; Haber, J.; Haase, S.; Shao, L.; et al. Fast live simultaneous multiwavelength four-dimensional optical microscopy. Proc. Natl. Acad. Sci. USA 2010, 107, 16016–16022. [Google Scholar] [CrossRef]
- Artifacts of light. Nat. Methods 2013, 10, 1135. [CrossRef]
- Murphy, D. Fundamentals of Light Microscopy and Electronic Imaging; Wiley-Liss: New York, NY, USA, 2001; pp. 97–112. [Google Scholar]
- Yang, F.; Venkataraman, C.; Styles, V.; Kuttenberger, V.; Horn, E.; von Guttenberg, Z.; Madzvamuse, A. A computational framework for particle and whole cell tracking. J. Biomech. 2016, 49, 1290–1304. [Google Scholar] [CrossRef]
- Roussos, E.; Condeelis, J.; Patsialou, A. Chemotaxis in cancer. Nat. Rev. Cancer 2011, 11, 573–587. [Google Scholar] [CrossRef]
- Grinnell, F. Wound repair, keratinocyte activation and integrin modulation. J. Cell Sci. 1992, 101, 1–5. [Google Scholar]
- Zantl, R.; Horn, E. Chemotaxis of slow migrating mammalian cells analysed by video microscopy. Methods Mol. Biol. 2011, 769, 191–203. [Google Scholar] [PubMed]
- Bear, J.; Haugh, J. Directed migration of mesenchymal cells: Where signaling and the cytoskeleton meet. Curr. Opin. Cell Biol. 2014, 30, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Zengel, P.; Nguyen-Hoang, A.; Schildhammer, C.; Zantl, R.; Kahl, V.; Horn, E. μ-Slide Chemotaxis: A new chamber for long-term chemotaxis studies. BMC Cell Biol. 2011, 12, 21. [Google Scholar] [CrossRef] [PubMed]
- Debeir, O.; Milojevic, D.; Leloup, T.; van Ham, P.; Kiss, R.; Decaestecker, C. Mitotic tree construction by computer in vitro cell tracking: A tool for proliferation. In Proceedings of the EUROCON 2005 the International Conference on Computer as a Tool, Belgrade, Serbia, 21–24 November 2005; Volume 2, pp. 1–10. [Google Scholar]
- Li, K.; Miller, E.; Weiss, L.; Campbell, P.; Kanade, T. Online tracking of migrating and proliferating cells imaged with phase-contrast microscopy. In Proceedings of the 2006 Conference on Computer Vision and Pattern Recongnition Workshop, New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Sacan, A.; Ferhatosmanoglu, H.; Coskun, H. CellTrack: An open-souce software for cell tracking and motility analysis. Bioinformatics 2008, 24, 1647–1649. [Google Scholar] [CrossRef]
- Topman, G.; Sharabani-Yosef, O.; Gefen, A. A Method for Quick, Low-Cost Automated Confluency Measurements. Microsc. Microanal. 2011, 17, 915–922. [Google Scholar] [CrossRef] [PubMed]
- Xiao, M.; Zhang, L.; Kou, W.; Miao, Y.; Liu, W. A background reconstruction algorithm based on intensity extremum classification. Adv. Inf. Sci. Serv. Sci. 2012, 4, 337–345. [Google Scholar]
- Halang, P.; Vorburger, T.; Steuber, J. Serine 26 in the PomB Subunit of the Flagellar Motor Is Essential for Hypermotility of Vibrio cholerae. PLoS ONE 2015, 10, e0123518. [Google Scholar] [CrossRef]
- Caino, M.; Ghosh, J.; Chae, Y.; Vaira, V.; Rivadeneira, D.; Faversani, A.; Rampini, P.; Kossenkov, A.; Aird, K.; Zhang, R.; et al. PI3K therapy reprograms mitochondrial trafficking to fuel tumor cell invasion. Proc. Natl. Acad. Sci. USA 2015, 112, 8638–8643. [Google Scholar] [CrossRef] [PubMed]
- Popp, F.; Armitage, J.; Schuler, D. Polarity of bacterial magnetotaxis is controlled by aerotaxis through a common sensory pathway. Nat. Commun. 2014, 5, 5398. [Google Scholar] [CrossRef]
- Gilad, T.; Bray, M.; Carpenter, A.; Riklin-Raviv, T. Symmetry-based mitosis detection in time-lapse microscopy. In Proceedings of the IEEE International Symposium Biomedical Imaging: From Nano to Macro, New York, NY, USA, 16–19 April 2015; pp. 164–167. [Google Scholar]
- Ulman, V.; Maška, M.; Magnusson, K.; Ronneberger, O.; Haubold, C.; Harder, N.; Matula, P.; Matula, P.; Svoboda, D.; Radojevic, M.; et al. An objective comparison of cell-tracking algorithms. Nat. Methods 2017, 14, 1141–1152. [Google Scholar] [CrossRef]
- Guo, Z.; Lin, P.; Lowengrub, J.; Wise, S. Mass conservative and energy stable finite difference methods for the quasi-incompressible Navier–Stokes–Cahn–Hilliard system: Primitive variable and projection-type schemes. Comput. Methods Appl. Mech. Eng. 2017, 326, 144–174. [Google Scholar] [CrossRef]
- Feng, W.; Guo, Z.; Lowengrub, J.; Wise, S. A mass-conservative adaptive FAS multigrid solver for cell-centered finite difference methods on block-structured, locally-cartesian grids. J. Comput. Phys. 2018, 352, 463–497. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).