Asynchronous Semantic Background Subtraction
Abstract
:1. Introduction
Problem Statement
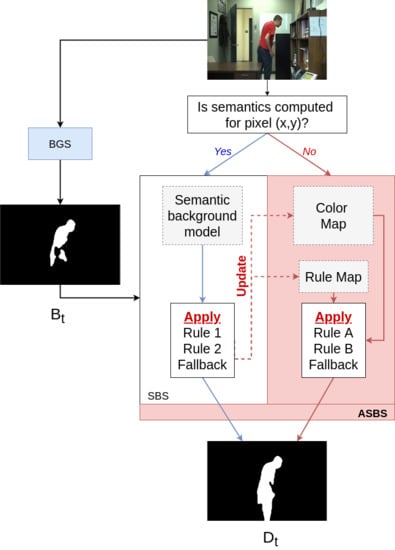
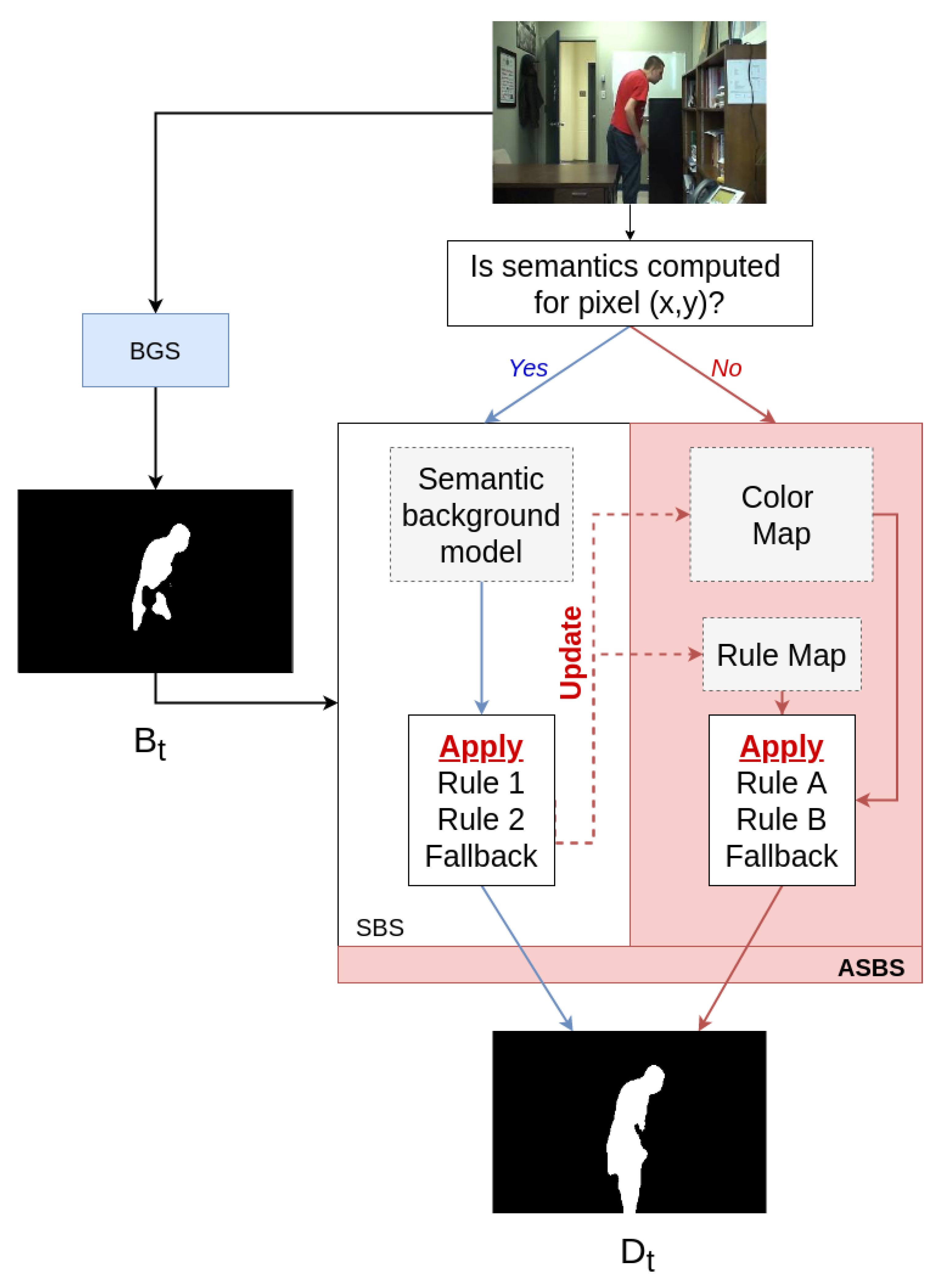
2. Description of the Semantic Background Subtraction Method
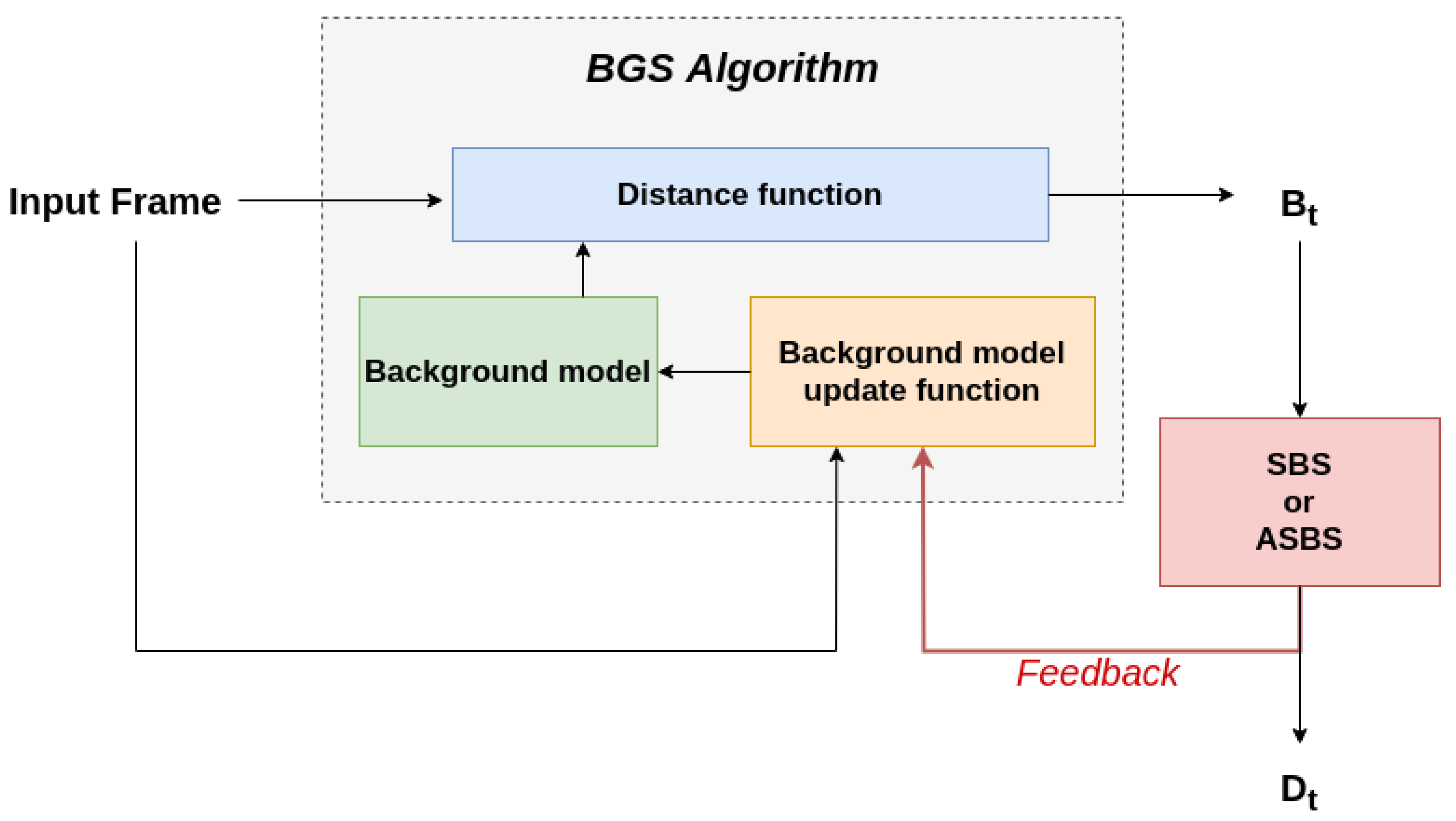
3. Asynchronous Semantic Background Subtraction
| Algorithm 1 Pseudo-code of ASBS for pixels with semantics. The rule and color maps are updated during the application of SBS (note that R is initialized with zero values at the program start). |
| Require: is the input color frame (at time t) 1: for all with semantics do 2: 3: if was activated then 4: 5: 6: else if was activated then 7: 8: 9: else 10: 11: end if 12: end for |
| Algorithm 2 Pseudo-code of ASBS for pixels without semantics, , or the fallback are applied. |
| Require: is the input color frame (at time t) 1: for all without semantics do 2: if then 3: if then 4: 5: end if 6: else if then 7: if then 8: 9: end if 10: else 11: 12: end if 13: end for |
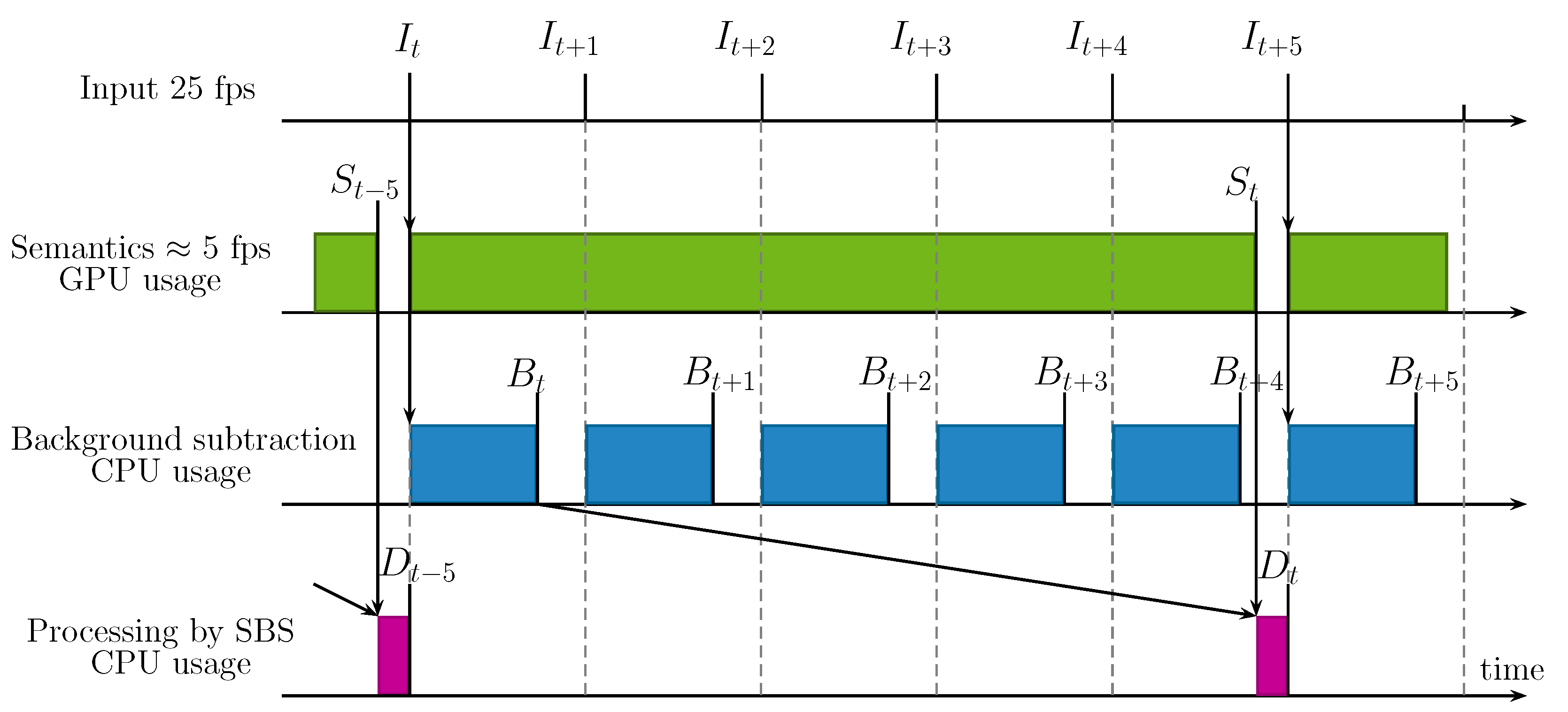
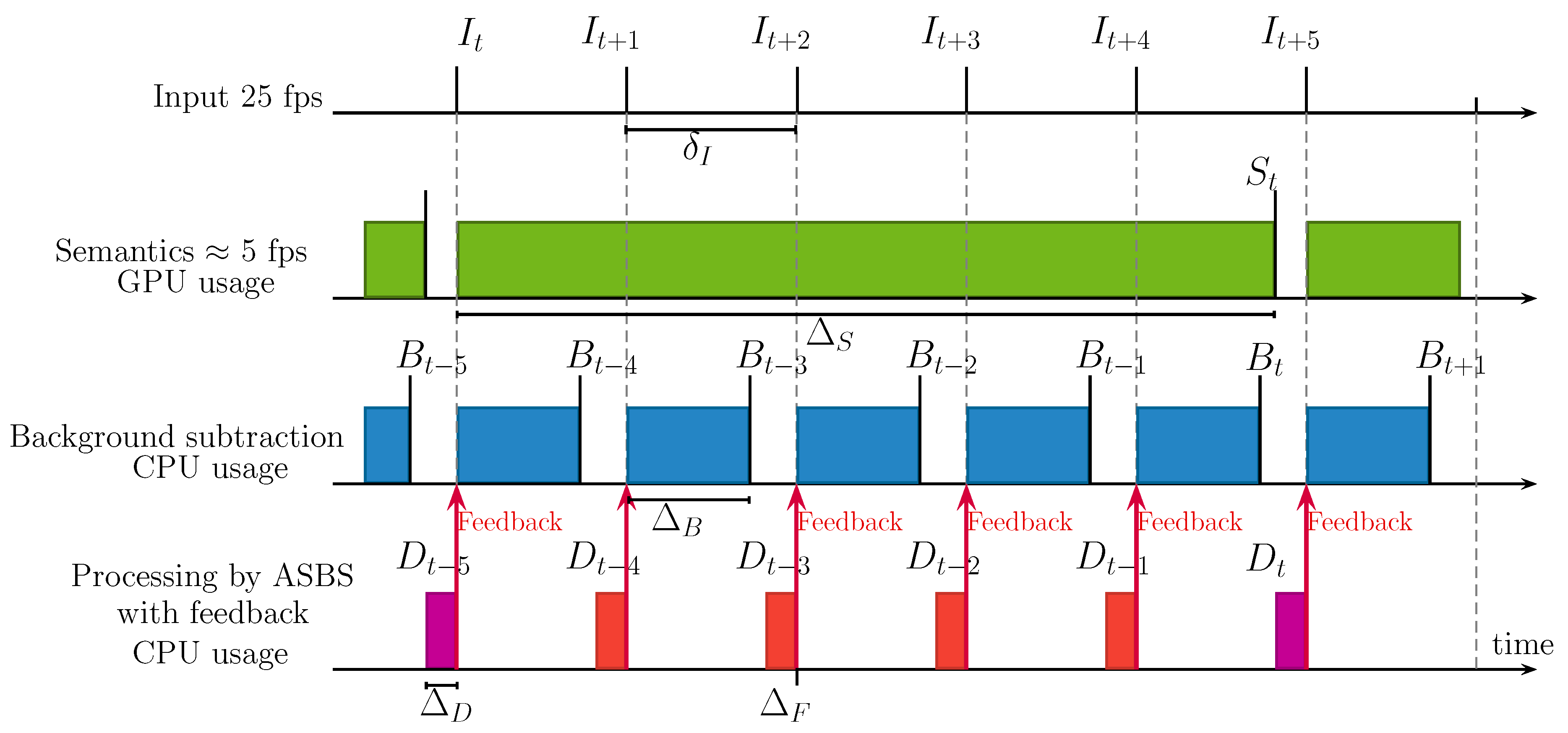
Timing Diagrams of ASBS
- , , , respectively denote an arbitrary input, semantics, background segmented by the BGS algorithm, and the background segmented by ASBS, indexed by t.
- represents the time between two consecutive input frames.
- , , are the times needed to calculate the semantics, the BGS output, and to apply SBS or ASBS, which are supposed to be the same, respectively. These times are reasonably constant.
4. Experimental Results
4.1. Evaluation Methodology
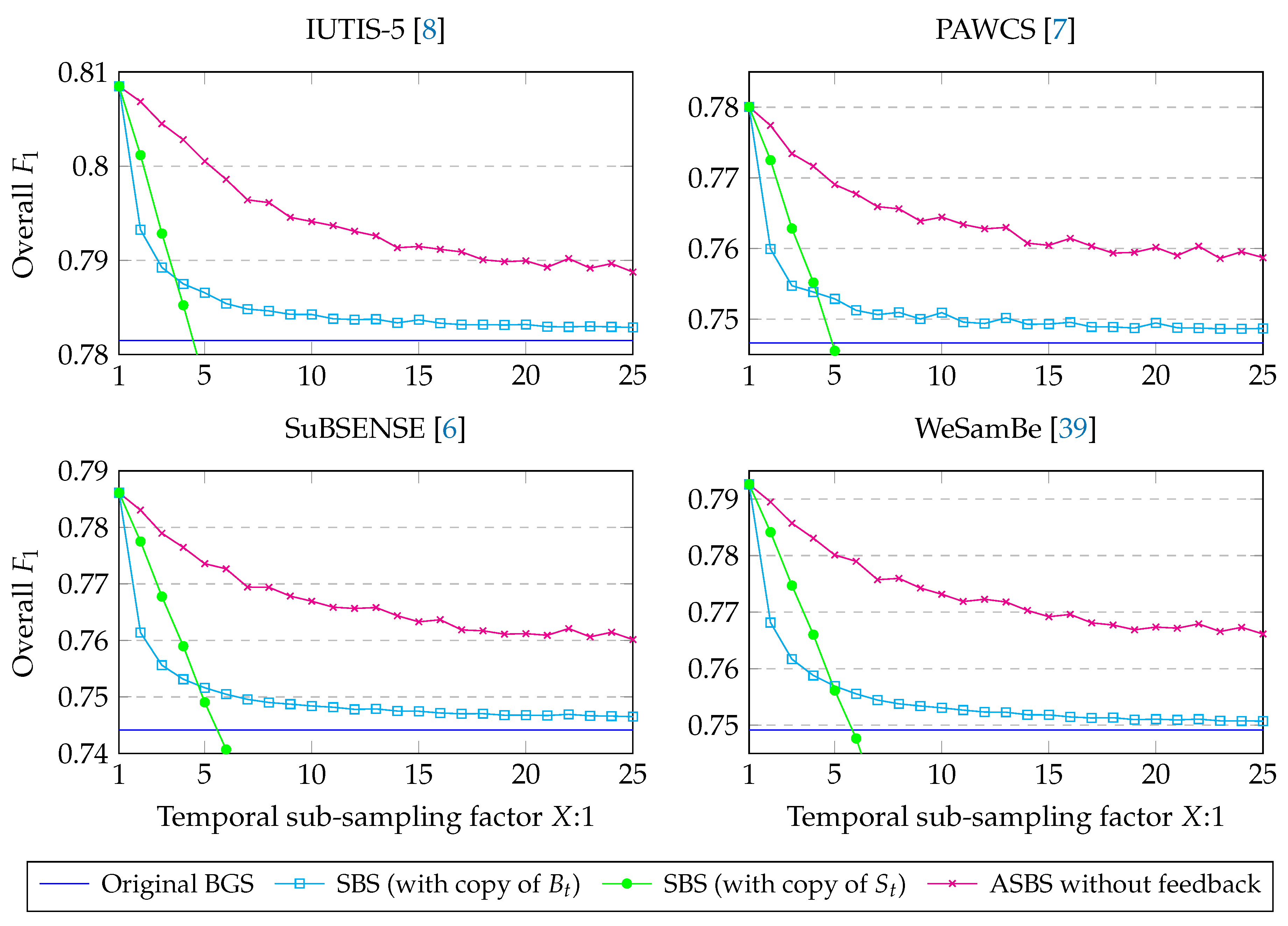
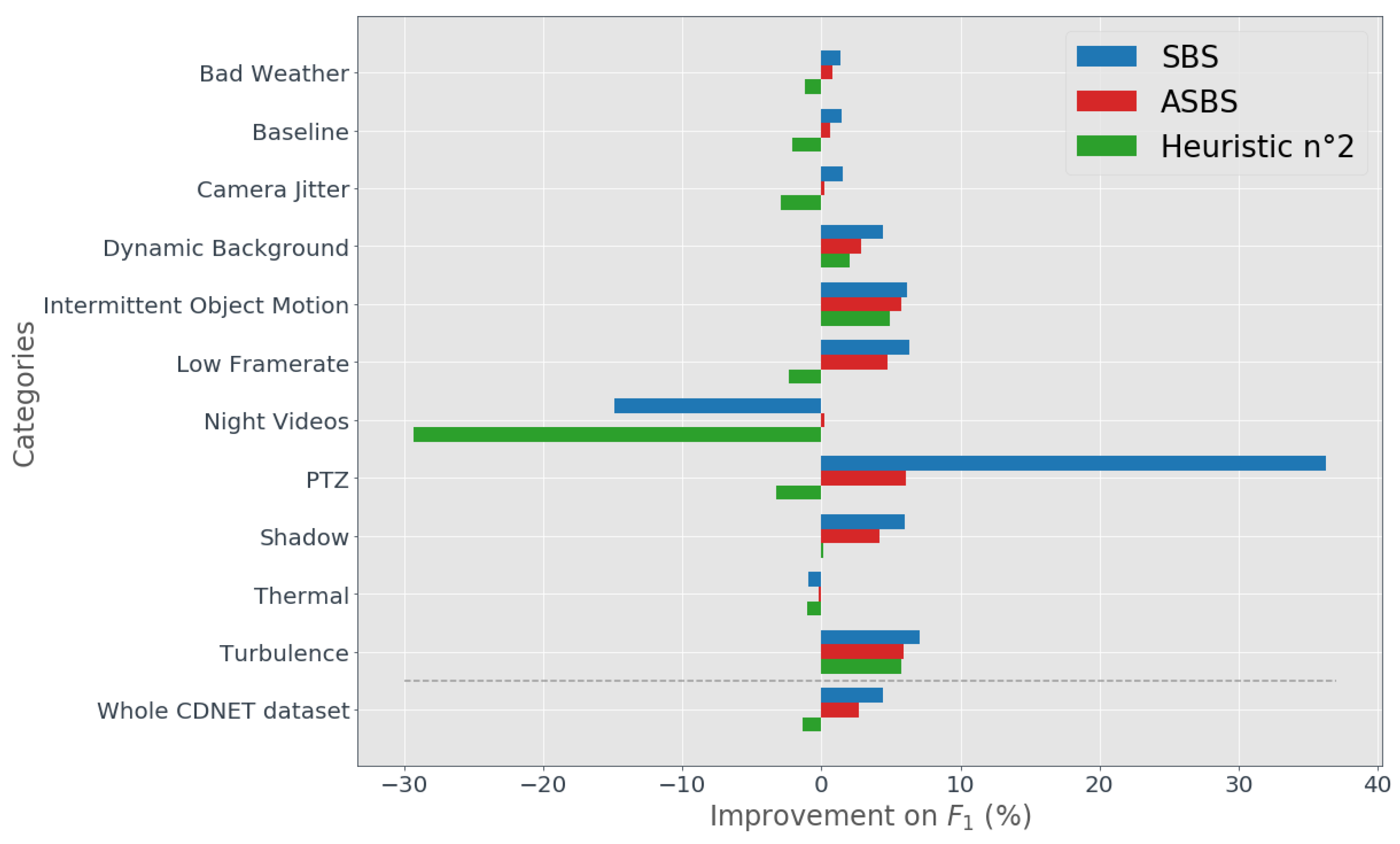
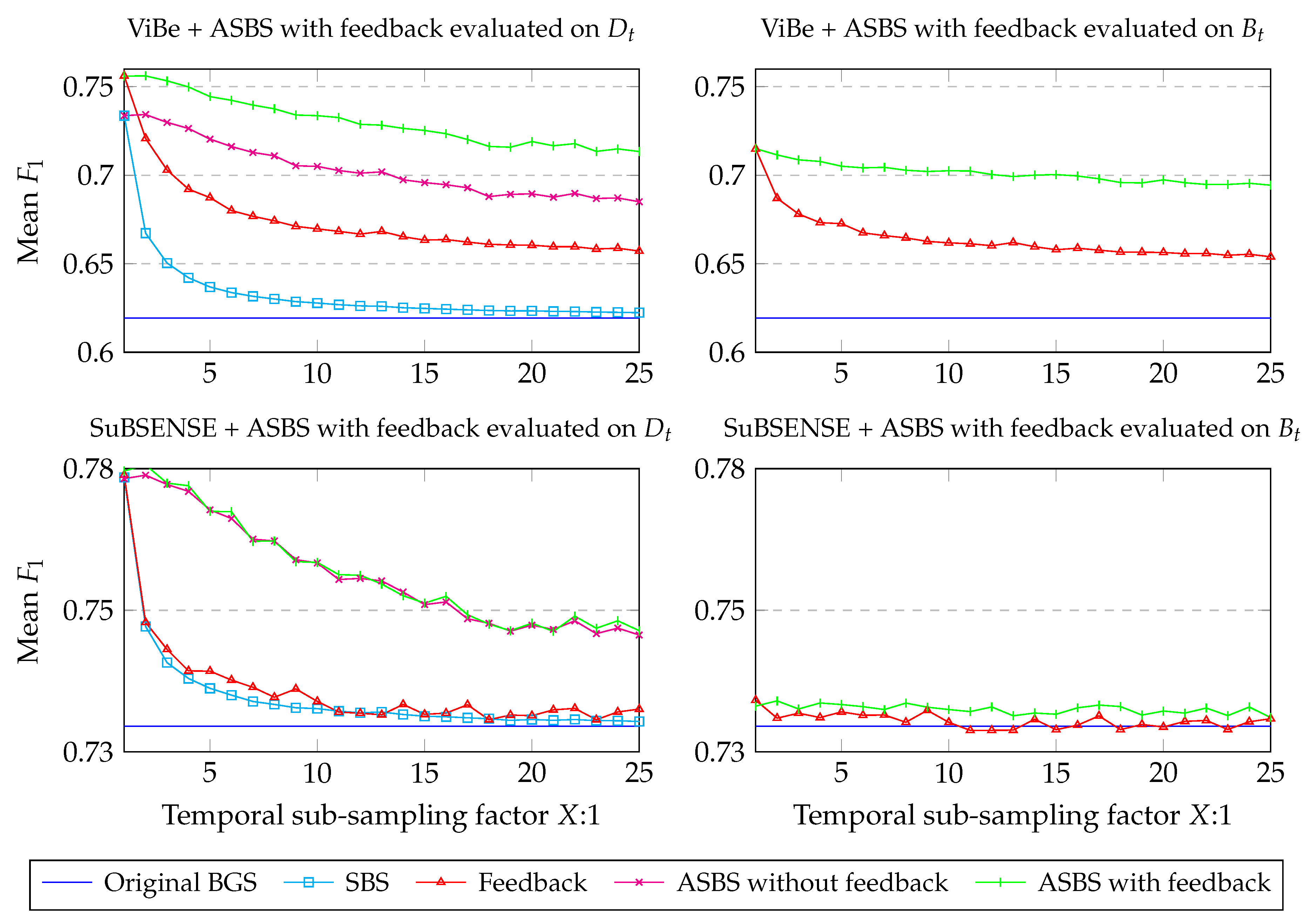
4.2. Performances of ASBS
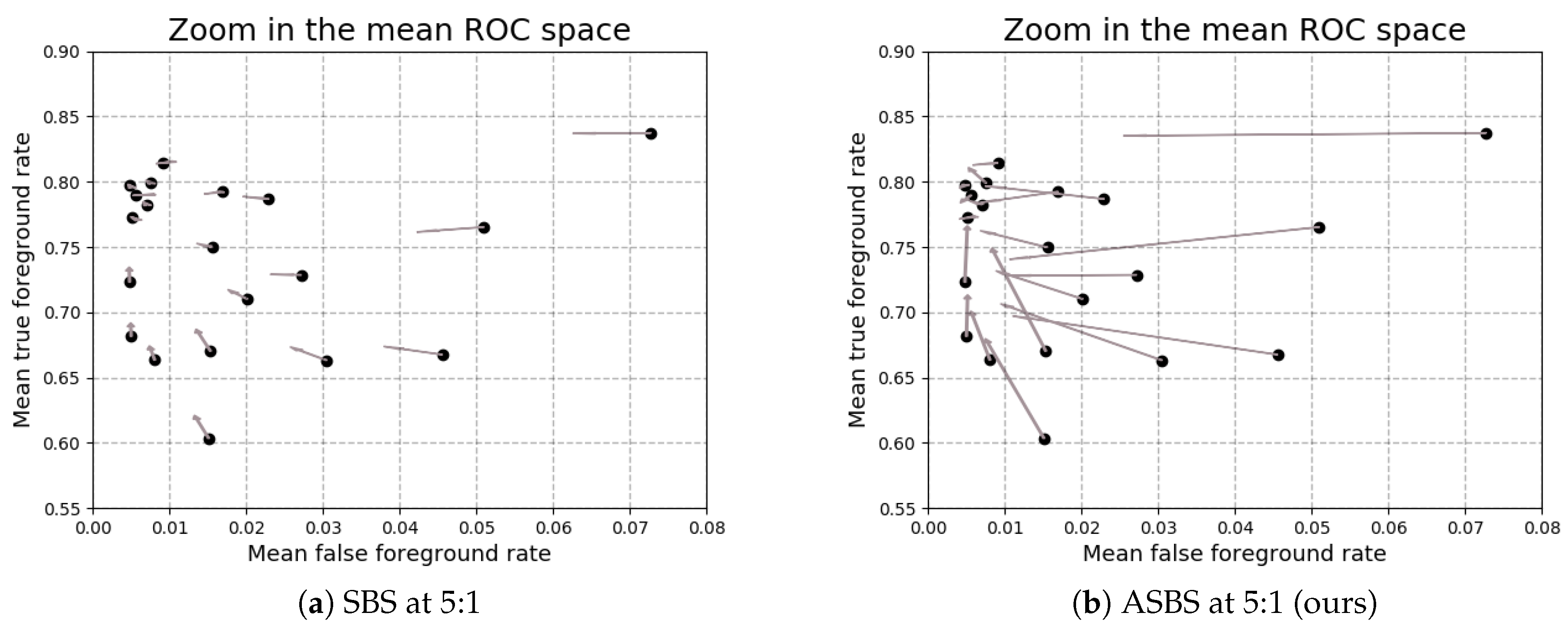
4.3. A Feedback Mechanism for SBS and ASBS
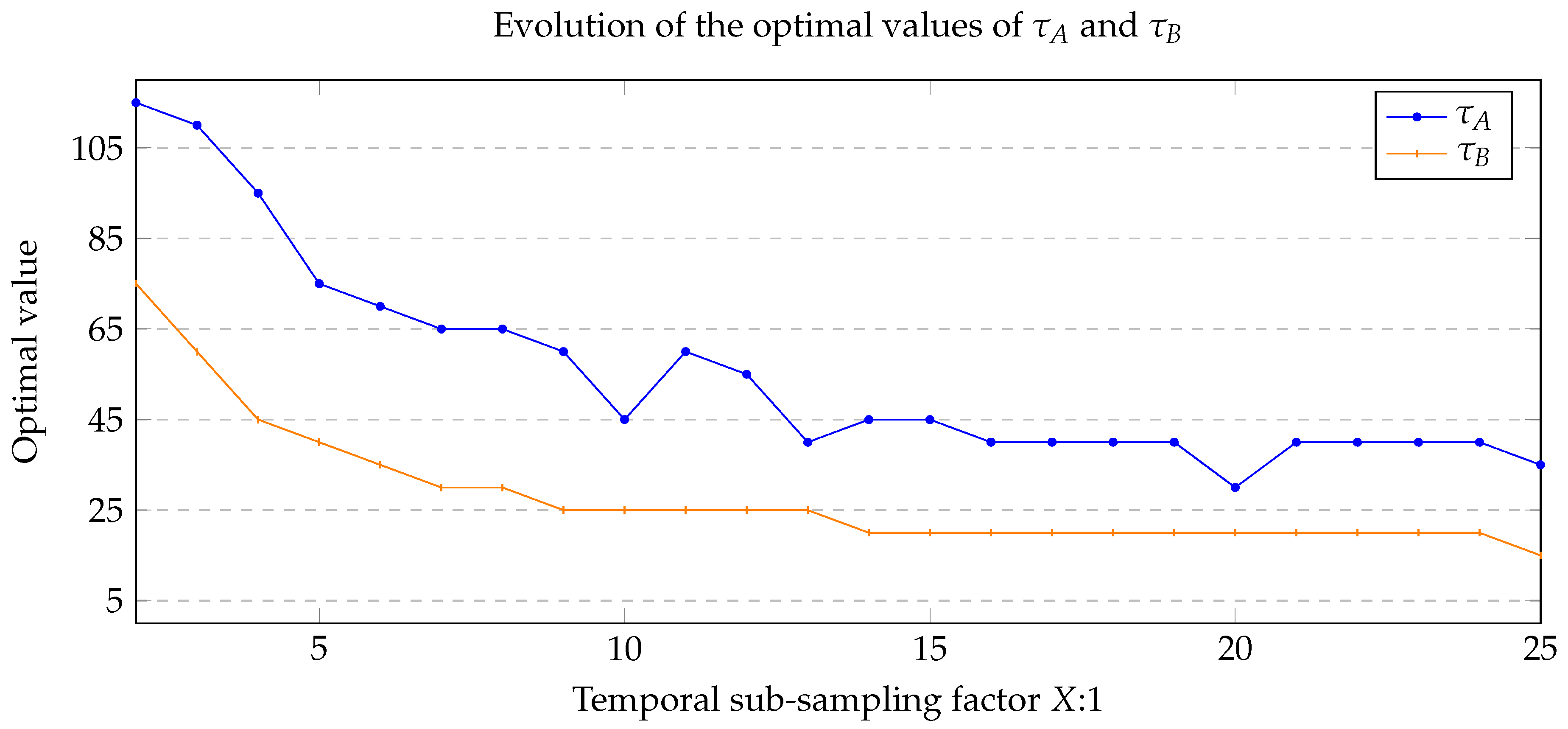
4.4. Time Analysis of ASBS
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bouwmans, T. Traditional and recent approaches in background modeling for foreground detection: An overview. Comput. Sci. Rev. 2014, 11–12, 31–66. [Google Scholar] [CrossRef]
- Stauffer, C.; Grimson, E. Adaptive background mixture models for real-time tracking. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Corfu, Greece, 20–25 September 1995; Volume 2, pp. 246–252. [Google Scholar]
- Elgammal, A.; Harwood, D.; Davis, L. Non-parametric Model for Background Subtraction. In European Conference on Computer Vision (ECCV); Lecture Notes in Computer Science; Springer: Berlin, Germany, 2000; Volume 1843, pp. 751–767. [Google Scholar]
- Maddalena, L.; Petrosino, A. A Self-Organizing Approach to Background Subtraction for Visual Surveillance Applications. IEEE Trans. Image Proc. 2008, 17, 1168–1177. [Google Scholar] [CrossRef] [PubMed]
- Barnich, O.; Van Droogenbroeck, M. ViBe: A universal background subtraction algorithm for video sequences. IEEE Trans. Image Proc. 2011, 20, 1709–1724. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- St-Charles, P.L.; Bilodeau, G.A.; Bergevin, R. SuBSENSE: A Universal Change Detection Method with Local Adaptive Sensitivity. IEEE Trans. Image Proc. 2015, 24, 359–373. [Google Scholar] [CrossRef] [PubMed]
- St-Charles, P.L.; Bilodeau, G.A.; Bergevin, R. Universal Background Subtraction Using Word Consensus Models. IEEE Trans. Image Proc. 2016, 25, 4768–4781. [Google Scholar] [CrossRef]
- Bianco, S.; Ciocca, G.; Schettini, R. Combination of Video Change Detection Algorithms by Genetic Programming. IEEE Trans. Evol. Comput. 2017, 21, 914–928. [Google Scholar] [CrossRef]
- Javed, S.; Mahmood, A.; Bouwmans, T.; Jung, S.K. Background-Foreground Modeling Based on Spatiotemporal Sparse Subspace Clustering. IEEE Trans. Image Proc. 2017, 26, 5840–5854. [Google Scholar] [CrossRef] [PubMed]
- Ebadi, S.; Izquierdo, E. Foreground Segmentation with Tree-Structured Sparse RPCA. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 2273–2280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vacavant, A.; Chateau, T.; Wilhelm, A.; Lequièvre, L. A Benchmark Dataset for Outdoor Foreground/ Background Extraction. In Asian Conference on Computer Vision (ACCV); Lecture Notes in Computer Science; Springer: Berlin, Germany, 2012; Volume 7728, pp. 291–300. [Google Scholar]
- Wang, Y.; Jodoin, P.M.; Porikli, F.; Konrad, J.; Benezeth, Y.; Ishwar, P. CDnet 2014: An Expanded Change Detection Benchmark Dataset. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Columbus, OH, USA, 23–28 June 2014; pp. 393–400. [Google Scholar]
- Cuevas, C.; Yanez, E.; Garcia, N. Labeled dataset for integral evaluation of moving object detection algorithms: LASIESTA. Comput. Vis. Image Understand. 2016, 152, 103–117. [Google Scholar] [CrossRef]
- Braham, M.; Van Droogenbroeck, M. Deep Background Subtraction with Scene-Specific Convolutional Neural Networks. In Proceedings of the IEEE International Conference on Systems, Signals and Image Processing (IWSSIP), Bratislava, Slovakia, 23–25 May 2016; pp. 1–4. [Google Scholar]
- Bouwmans, T.; Garcia-Garcia, B. Background Subtraction in Real Applications: Challenges, Current Models and Future Directions. arXiv 2019, arXiv:1901.03577. [Google Scholar]
- Lim, L.; Keles, H. Foreground Segmentation Using Convolutional Neural Networks for Multiscale Feature Encoding. Pattern Recognit. Lett. 2018, 112, 256–262. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Luo, Z.; Jodoin, P.M. Interactive Deep Learning Method for Segmenting Moving Objects. Pattern Recognit. Lett. 2017, 96, 66–75. [Google Scholar] [CrossRef]
- Zheng, W.B.; Wang, K.F.; Wang, F.Y. Background Subtraction Algorithm With Bayesian Generative Adversarial Networks. Acta Autom. Sin. 2018, 44, 878–890. [Google Scholar]
- Babaee, M.; Dinh, D.; Rigoll, G. A Deep Convolutional Neural Network for Background Subtraction. Pattern Recognit. 2018, 76, 635–649. [Google Scholar] [CrossRef]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Scene Parsing through ADE20K Dataset. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 5122–5130. [Google Scholar]
- Everingham, M.; Van Gool, L.; Williams, C.; Winn, J.; Zisserman, A. The PASCAL Visual Object Classes Challenge 2012 (VOC2012) Results. Available online: http://www.pascal-network.org/challenges/VOC/voc2012/workshop/index.html (accessed on 1 August 2019).
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Lin, T.Y.; Maire, M.; Belongie, S.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C. Microsoft COCO: Common Objects in Context. In European Conference on Computer Vision (ECCV); Lecture Notes Computer Science; Springer: Berlin, Germany, 2014; Volume 8693, pp. 740–755. [Google Scholar]
- Girshick, R.; Donahue, J.; Darrell, T.; Malik, J. Rich feature hierarchies for accurate object detection and semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 24–27 June 2014; pp. 580–587. [Google Scholar]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid Scene Parsing Network. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 6230–6239. [Google Scholar]
- He, K.; Gkioxari, G.; Dollar, P.; Girshick, R. Mask R-CNN. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017. [Google Scholar]
- Sevilla-Lara, L.; Sun, D.; Jampani, V.; Black, M.J. Optical Flow with Semantic Segmentation and Localized Layers. In Proceedings of the IEEE International Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3889–3898. [Google Scholar]
- Vertens, J.; Valada, A.; Burgard, W. SMSnet: Semantic motion segmentation using deep convolutional neural networks. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Vancouver, BC, Canada, 24–28 September 2017; pp. 582–589. [Google Scholar]
- Reddy, N.; Singhal, P.; Krishna, K. Semantic Motion Segmentation Using Dense CRF Formulation. In Proceedings of the Indian Conference on Computer Vision Graphics and Image Processing, Bangalore, India, 14–18 December 2014; pp. 1–8. [Google Scholar]
- Braham, M.; Piérard, S.; Van Droogenbroeck, M. Semantic Background Subtraction. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Beijing, China, 17–20 September 2017; pp. 4552–4556. [Google Scholar]
- Cioppa, A.; Van Droogenbroeck, M.; Braham, M. Real-Time Semantic Background Subtraction. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Abu Dhabi, UAE, 25–28 October 2020. [Google Scholar]
- Van Droogenbroeck, M.; Braham, M.; Piérard, S. Foreground and Background Detection Method. European Patent Office, EP 3438929 A1, 7 February 2017. [Google Scholar]
- Roy, S.; Ghosh, A. Real-Time Adaptive Histogram Min-Max Bucket (HMMB) Model for Background Subtraction. IEEE Trans. Circ. Syst. Video Technol. 2018, 28, 1513–1525. [Google Scholar] [CrossRef]
- Piérard, S.; Van Droogenbroeck, M. Summarizing the performances of a background subtraction algorithm measured on several videos. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Abu Dhabi, UAE, 25–28 October 2020. [Google Scholar]
- Zhou, B.; Zhao, H.; Puig, X.; Fidler, S.; Barriuso, A.; Torralba, A. Semantic understanding of scenes through the ADE20K dataset. Int. J. Comput. Vis. 2019, 127, 302–321. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Implementation of PSPNet. Available online: https://github.com/hszhao/PSPNet (accessed on 1 August 2019).
- Barnich, O.; Van Droogenbroeck, M. Code for ViBe. Available online: https://orbi.uliege.be/handle/2268/145853 (accessed on 1 August 2019).
- St-Charles, P.L. Code for SuBSENSE. Available online: https://bitbucket.org/pierre_luc_st_charles/subsense (accessed on 1 August 2019).
- Jiang, S.; Lu, X. WeSamBE: A Weight-Sample-Based Method for Background Subtraction. IEEE Trans. Circuits Syst. Video Technol. 2018, 28, 2105–2115. [Google Scholar] [CrossRef]
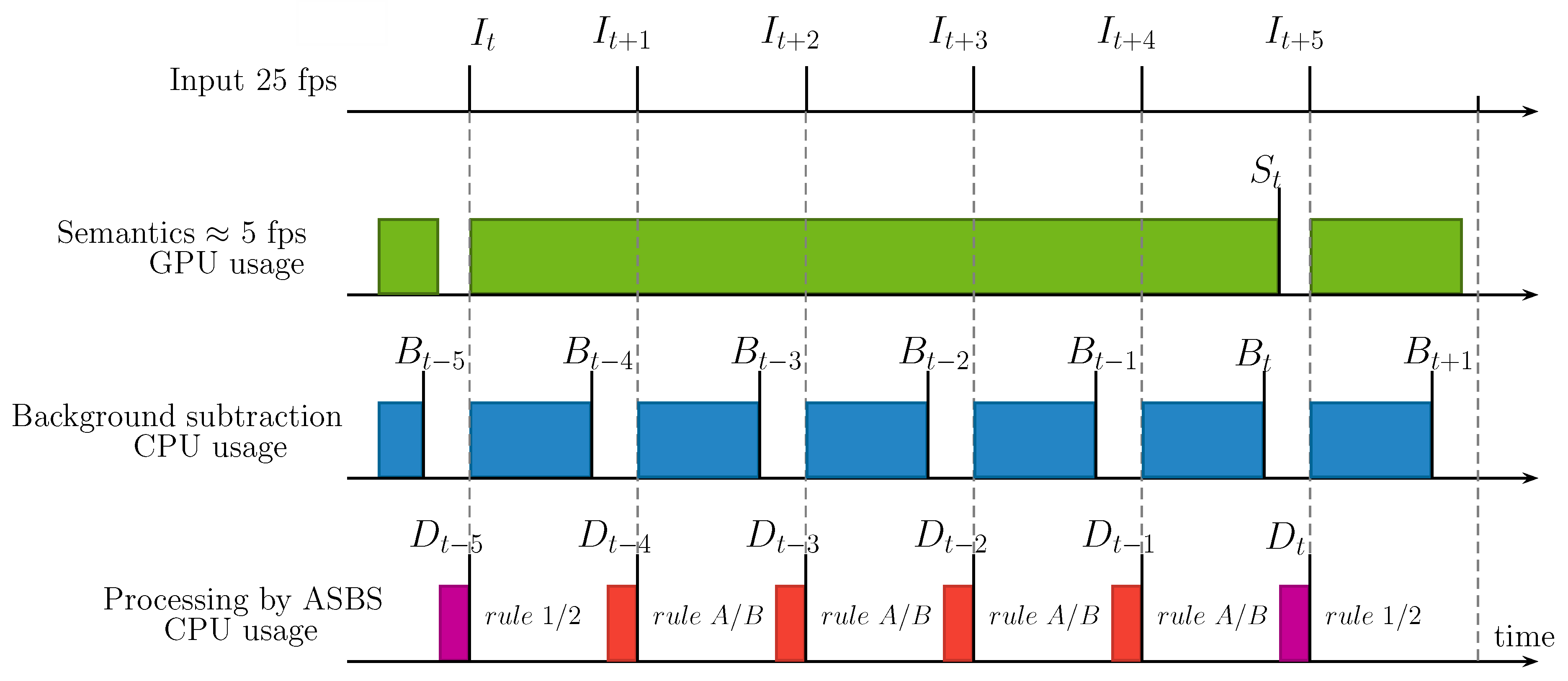

| Networks | SBS with PSPNet [25] | SBS with MaskRCNN [26] |
|---|---|---|
| Best mean |
| BG | false | false | BG |
| BG | false | true | FG |
| BG | true | false | BG |
| BG | true | true | X |
| FG | false | false | FG |
| FG | false | true | FG |
| FG | true | false | BG |
| FG | true | true | X |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cioppa, A.; Braham, M.; Van Droogenbroeck, M. Asynchronous Semantic Background Subtraction. J. Imaging 2020, 6, 50. https://doi.org/10.3390/jimaging6060050
Cioppa A, Braham M, Van Droogenbroeck M. Asynchronous Semantic Background Subtraction. Journal of Imaging. 2020; 6(6):50. https://doi.org/10.3390/jimaging6060050
Chicago/Turabian StyleCioppa, Anthony, Marc Braham, and Marc Van Droogenbroeck. 2020. "Asynchronous Semantic Background Subtraction" Journal of Imaging 6, no. 6: 50. https://doi.org/10.3390/jimaging6060050
APA StyleCioppa, A., Braham, M., & Van Droogenbroeck, M. (2020). Asynchronous Semantic Background Subtraction. Journal of Imaging, 6(6), 50. https://doi.org/10.3390/jimaging6060050