Evaluating Human Photoreceptoral Inputs from Night-Time Lights Using RGB Imaging Photometry
Abstract
1. Introduction
2. Materials and Methods
2.1. Photoreceptoral and RGB Spectrally-Weighted Radiant Quantities
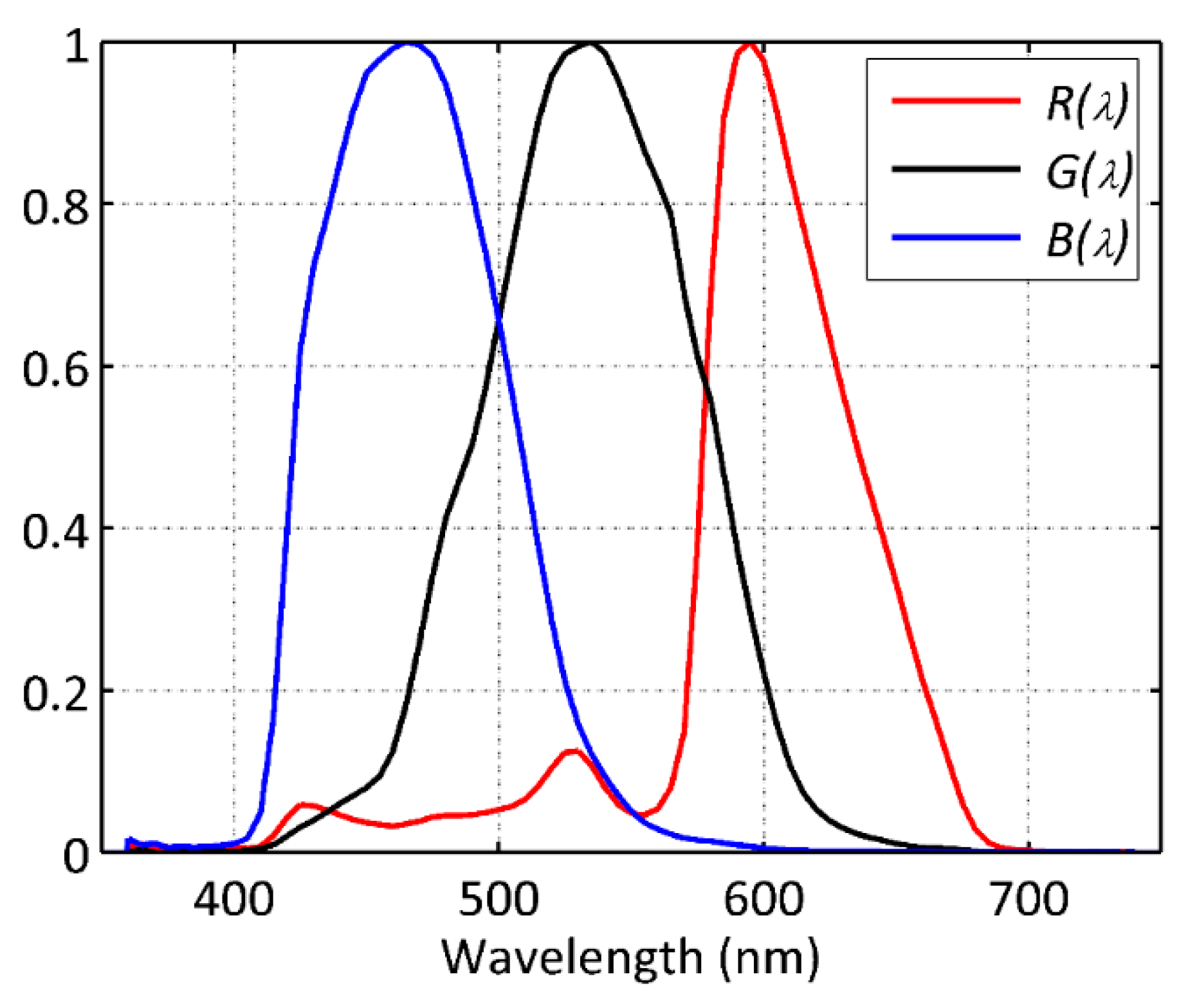
2.2. Linear Estimation of the Photoreceptoral Weighted Radiances from RGB Signals
2.3. Lamp Spectra Database
3. Results
4. Discussion
Author Contributions
Funding
Conflicts of Interest
References
- Pauley, S.M. Lighting for the human circadian clock: Recent research indicates that lighting has become a public health issue. Med. Hypotheses 2004, 63, 588–596. [Google Scholar] [CrossRef] [PubMed]
- IARC (International Agency for Research on Cancer). Painting, Firefighting, and Shiftwork: IARC Monographs on the Evaluation of Carcinogenic Risks to Humans; World Health Organization: Lyon, France, 2010; Volume 98, p. 764. [Google Scholar]
- AMA (American Medical Association). Light Pollution: Adverse health effects of nighttime lighting. In Proceedings of the American Medical Association House of Delegates, 161st Annual Meeting, Chicago, IL, USA, 16–20 June 2012; pp. 265–279. [Google Scholar]
- Haim, A.; Portnov, B. Light Pollution as a New Risk Factor for Human Breast and Prostate Cancers; Springer: Heidelberg, Germany, 2013. [Google Scholar] [CrossRef]
- Stevens, R.G.; Brainard, G.C.; Blask, D.E.; Lockley, S.W.; Motta, M.E. Breast Cancer and Circadian Disruption From Electric Lighting in the Modern World. CA Cancer J. Clin. 2014, 64, 207–218. [Google Scholar] [CrossRef]
- Fonken, L.K.; Nelson, R.J. The Effects of Light at Night on Circadian Clocks and Metabolism. Endocr. Rev. 2014, 35, 648–670. [Google Scholar] [CrossRef] [PubMed]
- Zubidat, A.E.; Haim, A. Artificial light-at-night—A novel lifestyle risk factor for metabolic disorder and cancer morbidity. J. Basic Clin. Physiol. Pharmacol. 2017, 28, 295–313. [Google Scholar] [CrossRef]
- Touitou, Y.; Reinberg, A.; Touitou, D. Association between light at night, melatonin secretion, sleep deprivation, and the internal clock: Health impacts and mechanisms of circadian disruption. Life Sci. 2017, 173, 94–106. [Google Scholar] [CrossRef]
- Russart, K.L.G.; Nelson, R.J. Light at night as an environmental endocrine disruptor. Physiol. Behav. 2018, 190, 82–89. [Google Scholar] [CrossRef]
- Provencio, I.; Rodriguez, I.R.; Jiang, G.; Hayes, W.P.; Moreira, E.F.; Rollag, M.D. A Novel Human Opsin in the Inner Retina. J. Neurosci. 2000, 20, 600–605. [Google Scholar] [CrossRef]
- Brainard, G.C.; Hanifin, J.P.; Greeson, J.M.; Byrne, B.; Glickman, G.; Gerner, E.; Rollag, M.D. Action spectrum for melatonin regulation in humans: Evidence for a novel circadian photoreceptor. J. Neurosci. 2001, 21, 6405–6412. [Google Scholar] [CrossRef]
- Hattar, S.; Liao, H.-W.; Takao, M.; Berson, D.M.; Yau, K.-W. Melanopsin-Containing Retinal Ganglion Cells: Architecture, Projections, and Intrinsic Photosensitivity. Science 2002, 295, 1065–1070. [Google Scholar] [CrossRef]
- Berson, D.M.; Dunn, F.A.; Takao, M. Phototransduction by retinal ganglion cells that set the circadian clock. Science 2002, 295, 1070–1073. [Google Scholar] [CrossRef]
- Rea, M.S.; Figueiro, M.G.; Bullough, J.D.; Bierman, A. A model of phototransduction by the human circadian system. Brain Res. Rev. 2005, 50, 213–228. [Google Scholar] [CrossRef]
- Rea, M.S.; Figueiro, M.G.; Bierman, A.; Hamner, R. Modeling the spectral sensitivity of the human circadian system. Light. Res. Technol. 2012, 44, 386–396. [Google Scholar] [CrossRef]
- Lucas, R.J.; Peirson, S.N.; Berson, D.M.; Brown, T.M.; Cooper, H.M.; Czeisler, C.A.; Figueiro, M.G.; Gamlin, P.D.; Lockley, S.W.; O’Hagan, H.B.; et al. Measuring and using light in the melanopsin age. Trends Neurosci. 2014, 37, 1–9. [Google Scholar] [CrossRef]
- CIE (Commission Internationale de l’Eclairage). Publication TN 003:2015 Report on the First International Workshop on Circadian and Neurophysiological Photometry, 2013; CIE: Vienna, Austria, 2015. [Google Scholar]
- Cinzano, P.; Falchi, F.; Elvidge, C. The first world atlas of the artificial night sky brightness. Mon. Not. R. Astron. Soc. 2001, 328, 689–707. [Google Scholar] [CrossRef]
- Cinzano, P.; Elvidge, C.D. Night sky brightness at sites from DMSP-OLS satellite measurements. Mon. Not. R. Astron. Soc. 2004, 353, 1107–1116. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Tong, K.P.; Bennie, J.; Birriel, I.; Birriel, J.J.; Cool, A.; Danielsen, A.; Davies, T.W.; den Outer, P.N.; Edwards, W.; et al. Worldwide variations in artificial skyglow. Sci. Rep. 2015, 5, 8409. [Google Scholar] [CrossRef]
- Estrada-García, R.; García-Gil, M.; Acosta, L.; Bará, S.; Sanchez de Miguel, A.; Zamorano, J. Statistical modelling and satellite monitoring of upward light from public lighting. Light. Res. Technol. 2016, 48, 810–822. [Google Scholar] [CrossRef]
- Falchi, F.; Cinzano, P.; Duriscoe, D.; Kyba, C.C.M.; Elvidge, C.D.; Baugh, K.; Portnov, B.A.; Rybnikova, N.A.; Furgoni, R. The new world atlas of artificial night sky brightness. Sci. Adv. 2016, 2, e1600377. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Kuester, T.; Sánchez de Miguel, A.; Baugh, K.; Jechow, A.; Hölker, F.; Bennie, J.; Elvidge, C.D.; Gaston, K.J.; Guanter, L. Artificially lit surface of Earth at night increasing in radiance and extent. Sci. Adv. 2017, 3, e1701528. [Google Scholar] [CrossRef]
- Duriscoe, D.M.; Anderson, S.J.; Luginbuhl, C.B.; Baugh, K.E. A simplified model of all-sky artificial sky glow derived from VIIRS Day/Night band data. J. Quant. Spectrosc. Radiat. Transf. 2018, 214, 133–145. [Google Scholar] [CrossRef]
- Kumar, P.; Rehman, S.; Sajjad, H.; Tripathy, B.R.; Rani, M.; Singh, S. Analyzing trend in artificial light pollution pattern in India using NTL sensor’s data. Urban Clim. 2019, 27, 272–283. [Google Scholar] [CrossRef]
- Miller, S.; Straka, W.; Mills, S.; Elvidge, C.; Lee, T.; Solbrig, J.; Walther, A.; Heidinger, A.; Weiss, S. Illuminating the capabilities of the suomi national polar-orbiting partnership (NPP) visible infrared imaging radiometer suite (VIIRS) day/night band. Remote Sens. 2013, 5, 6717–6766. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C. Why VIIRS data are superior to DMSP for mapping nighttime lights. Proc. Asia-Pac. Adv. Netw. 2013, 35, 62–69. [Google Scholar] [CrossRef]
- Elvidge, C.D.; Baugh, K.; Zhizhin, M.; Hsu, F.C.; Ghosh, T. VIIRS night-time lights. Int. J. Remote Sens. 2017, 38, 5860–5879. [Google Scholar] [CrossRef]
- Hsu, F.-C.; Baugh, K.E.; Ghosh, T.; Zhizhin, M.; Elvidge, C.D. DMSP-OLS Radiance Calibrated Nighttime Lights Time Series with Intercalibration. Remote Sens. 2015, 7, 1855–1876. [Google Scholar] [CrossRef]
- Jiang, W.; He, G.; Long, T.; Guo, H.; Yin, R.; Leng, W.; Liu, H.; Wang, G. Potentiality of Using Luojia 1-01 Nighttime Light Imagery to Investigate Artificial Light Pollution. Sensors 2018, 18, 2900. [Google Scholar] [CrossRef]
- Stefanov, W.L.; Evans, C.A.; Runco, S.K.; Wilkinson, M.J.; Higgins, M.D.; Willis, K. Astronaut Photography: Handheld Camera Imagery from Low Earth Orbit. In Handbook of Satellite Applications; Pelton, J.N., Madry, S., Camacho-Lara, S., Eds.; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar] [CrossRef]
- Sánchez de Miguel, A. Spatial, Temporal and Spectral Variation of the Light Pollution and its Sources: Methodology and Results. PhD Thesis, Universidad Complutense de Madrid, Madrid, Spain, 2015. [Google Scholar] [CrossRef]
- Kyba, C.C.M.; Garz, S.; Kuechly, H.; Sánchez de Miguel, A.; Zamorano, J.; Fischer, J.; Hölker, F. High-Resolution Imagery of Earth at Night: New Sources, Opportunities and Challenges. Remote Sens. 2015, 7, 1–23. [Google Scholar] [CrossRef]
- Zheng, Q.; Weng, Q.; Huang, L.; Wang, K.; Deng, J.; Jiang, R.; Ye, Z.; Gan, M. A new source of multi-spectral high spatial resolution night-time light imagery—JL1-3B. Remote Sens. Environ. 2018, 215, 300–312. [Google Scholar] [CrossRef]
- Hänel, A.; Posch, T.; Ribas, S.J.; Aubé, M.; Duriscoe, D.; Jechow, A.; Kollath, Z.; Lolkema, D.E.; Moore, C.; Schmidt, N.; et al. Measuring night sky brightness: Methods and challenges. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 278–290. [Google Scholar] [CrossRef]
- Jechow, A.; Kolláth, Z.; Lerner, A.; Hölker, F.; Hänel, A.; Shashar, N.; Kyba, C.C.M. Measuring Light Pollution with Fisheye Lens Imagery from A Moving Boat, A Proof of Concept. Available online: https://arxiv.org/abs/1703.08484 (accessed on 22 March 2017).
- Jechow, A.; Ribas, S.J.; Canal-Domingo, R.; Hölker, F.; Kolláth, Z.; Kyba, C.C.M. Tracking the dynamics of skyglow with differential photometry using a digital camera with fisheye lens. J. Quant. Spectrosc. Radiat. Transf. 2018, 209, 212–223. [Google Scholar] [CrossRef]
- Jechow, A. Observing the Impact of WWF Earth Hour on Urban Light Pollution: A Case Study in Berlin 2018 Using Differential Photometry. Sustainability 2019, 11, 750. [Google Scholar] [CrossRef]
- Kolláth, Z.; Dömény, A. Night sky quality monitoring in existing and planned dark sky parks by digital cameras. Int. J. Sustain. Light. 2017, 19, 61–68. [Google Scholar] [CrossRef]
- Jechow, A.; Hölker, F.; Kyba, C.M.M. Using all-sky differential photometry to investigate how nocturnal clouds darken the night sky in rural areas. Sci. Rep. 2019, 9, 1391. [Google Scholar] [CrossRef]
- Dobler, G.; Ghandehari, M.; Koonin, S.E.; Nazari, R.; Patrinos, A.; Sharma, M.S.; Tafvizi, A.; Vo, H.T.; Wurtele, J.S. Dynamics of the urban nightscape. Inf. Syst. 2015, 54, 115–126. [Google Scholar] [CrossRef]
- Bará, S.; Rodríguez-Arós, A.; Pérez, M.; Tosar, B.; Lima, R.C.; Sánchez de Miguel, A.; Zamorano, J. Estimating the relative contribution of streetlights, vehicles, and residential lighting to the urban night sky brightness. Light. Res. Technol. 2018. [Google Scholar] [CrossRef]
- Meier, J. Temporal profiles of urban lighting: Proposal for a research design and first results from three sites in Berlin. Int. J. Sustain. Light. 2018, 20, 11–28. [Google Scholar] [CrossRef]
- Kloog, I.; Haim, A.; Stevens, R.G.; Barchana, M.; Portnov, B.A. Light at night co-distributes with incident breast but not lung cancer in the female population of Israel. Chronobiol. Int. 2008, 25, 65–81. [Google Scholar] [CrossRef]
- Kloog, I.; Haim, A.; Stevens, R.G.; Portnov, B.A. Global co-distribution of light at night (LAN) and cancers of prostate, colon, and lung in men. Chronobiol. Int. 2009, 26, 108–125. [Google Scholar] [CrossRef]
- Portnov, B.A.; Stevens, R.G.; Samociuk, H.; Wakefield, D.; Gregorio, D.I. Light at night and breast cancer incidence in Connecticut: An ecological study of age group effects. Sci. Total Environ. 2016, 572, 1020–1024. [Google Scholar] [CrossRef]
- Rybnikova, N.A.; Haim, A.; Portnov, B.A. Is prostate cancer incidence worldwide linked to artificial light at night exposures? Review of earlier findings and analysis of current trends. Arch. Environ. Occup. Health 2016, 72, 111–122. [Google Scholar] [CrossRef]
- Rybnikova, N.; Portnov, B.A. Outdoor light and breast cancer incidence: A comparative analysis of DMSP and VIIRS-DNB satellite data. Int. J. Remote Sens. 2016, 38, 5952–5961. [Google Scholar] [CrossRef]
- Rybnikova, N.; Portnov, B.A. Population-level study links short-wavelength nighttime illumination with breast cancer incidence in a major metropolitan area. Chronobiol. Int. 2018, 35, 1198–1208. [Google Scholar] [CrossRef]
- Garcia-Saenz, A.; Sánchez de Miguel, A.; Espinosa, A.; Valentin, A.; Aragones, N.; Llorca, J.; Amiano, P.; Sanchez, V.M.; Guevara, M.; Capelo, R.; et al. Evaluating the association between artificial light-at-night exposure and breast and prostate cancer risk in Spain (MCC-Spain study). Environ. Health Perspect. 2018, 126, 047011. [Google Scholar] [CrossRef]
- Sánchez de Miguel, A.; Kyba, C.C.M.; Aubé, M.; Zamorano, J.; Cardiel, N.; Tapia, C.; Bennie, J.; Gaston, K.J. Colour remote sensing of the impact of artificial light at night (I): The potential of the International Space Station and other DSLR-based platforms. Remote Sens. Environ. 2019, 224, 92–103. [Google Scholar] [CrossRef]
- Sánchez de Miguel, A.; Aubé, M.; Zamorano, J.; Kocifaj, M.; Roby, J.; Tapia, C. Sky quality meter measurements in a colour-changing world. Mon. Not. R. Astron. Soc. 2017, 467, 2966–2979. [Google Scholar] [CrossRef]
- Tapia, C.; Sánchez de Miguel, A.; Zamorano, J. LICA-UCM Lamps Spectral Database 2.6. 2017. Available online: http://guaix.fis.ucm.es/lamps_spectra (accessed on 15 April 2019).
- CIE (Commission Internationale de l’Eclairage). CIE S 026/E:2018. CIE System for Metrology of Optical Radiation for ipRGC-Influenced Responses to Light; CIE: Wien, Austria, 2018. [Google Scholar]
- Bará, S.; Escofet, J. On lamps, walls, and eyes: The spectral radiance field and the evaluation of light pollution indoors. J. Quant. Spectrosc. Radiat. Transf. 2018, 205, 267–277. [Google Scholar] [CrossRef]
- Dobler, G.; Ghandehari, M.; Koonin, S.E.; Sharma, M.S. A hyperspectral survey of New York City lighting technology. Sensors 2016, 16, 2047. [Google Scholar] [CrossRef]
- Alamús, R.; Bará, S.; Corbera, J.; Escofet, J.; Palà, V.; Pipia, L.; Tardà, A. Ground-based hyperspectral analysis of the urban nightscape. ISPRS J. Photogramm. Remote Sens. 2017, 124, 16–26. [Google Scholar] [CrossRef]
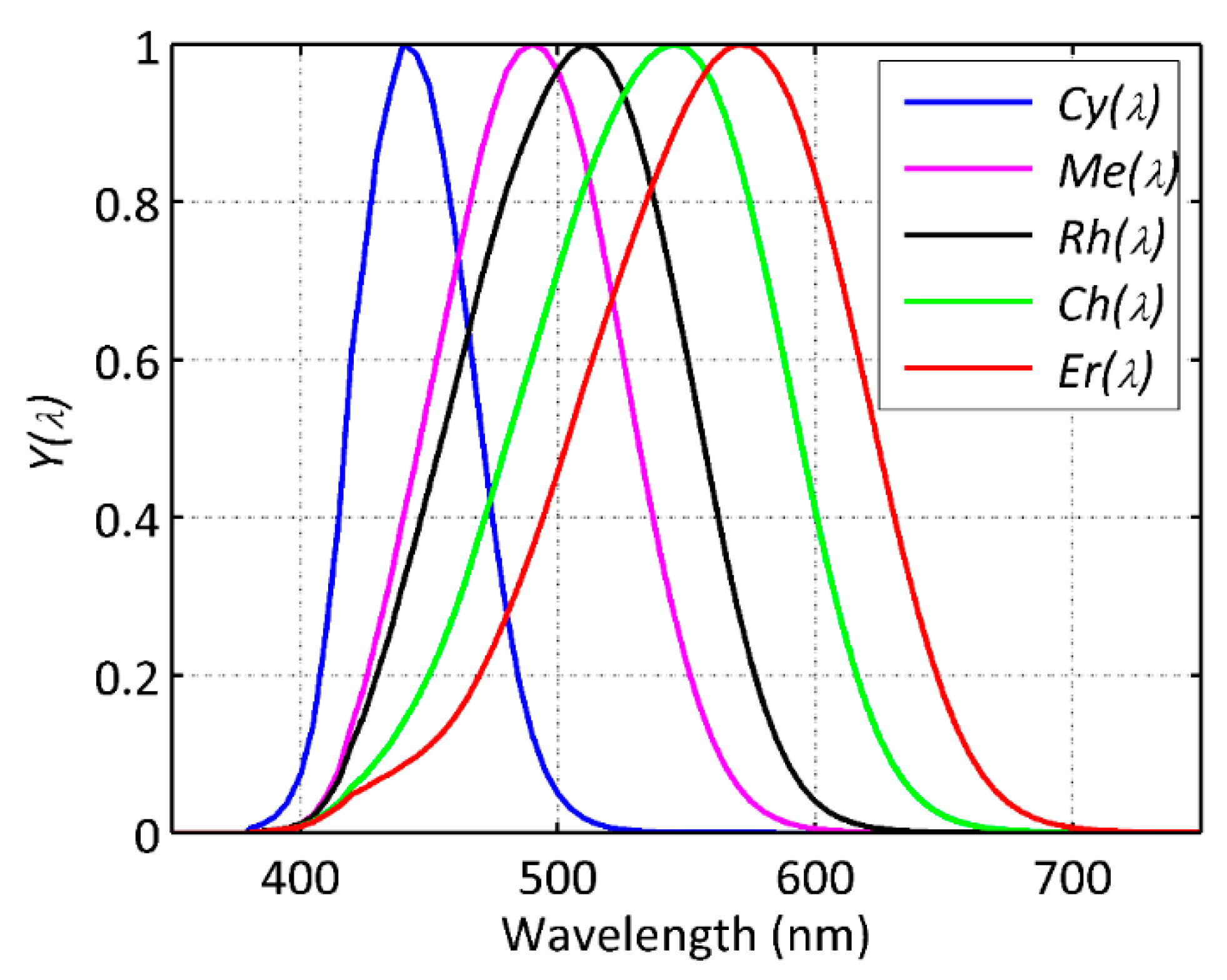
 ), LED(
), LED( ), CFL and FL(▼), CMH(◀), MH(✱), MV(
), CFL and FL(▼), CMH(◀), MH(✱), MV( ).
).
 ), LED(
), LED( ), CFL and FL(▼), CMH(◀), MH(✱), MV(
), CFL and FL(▼), CMH(◀), MH(✱), MV( ).
).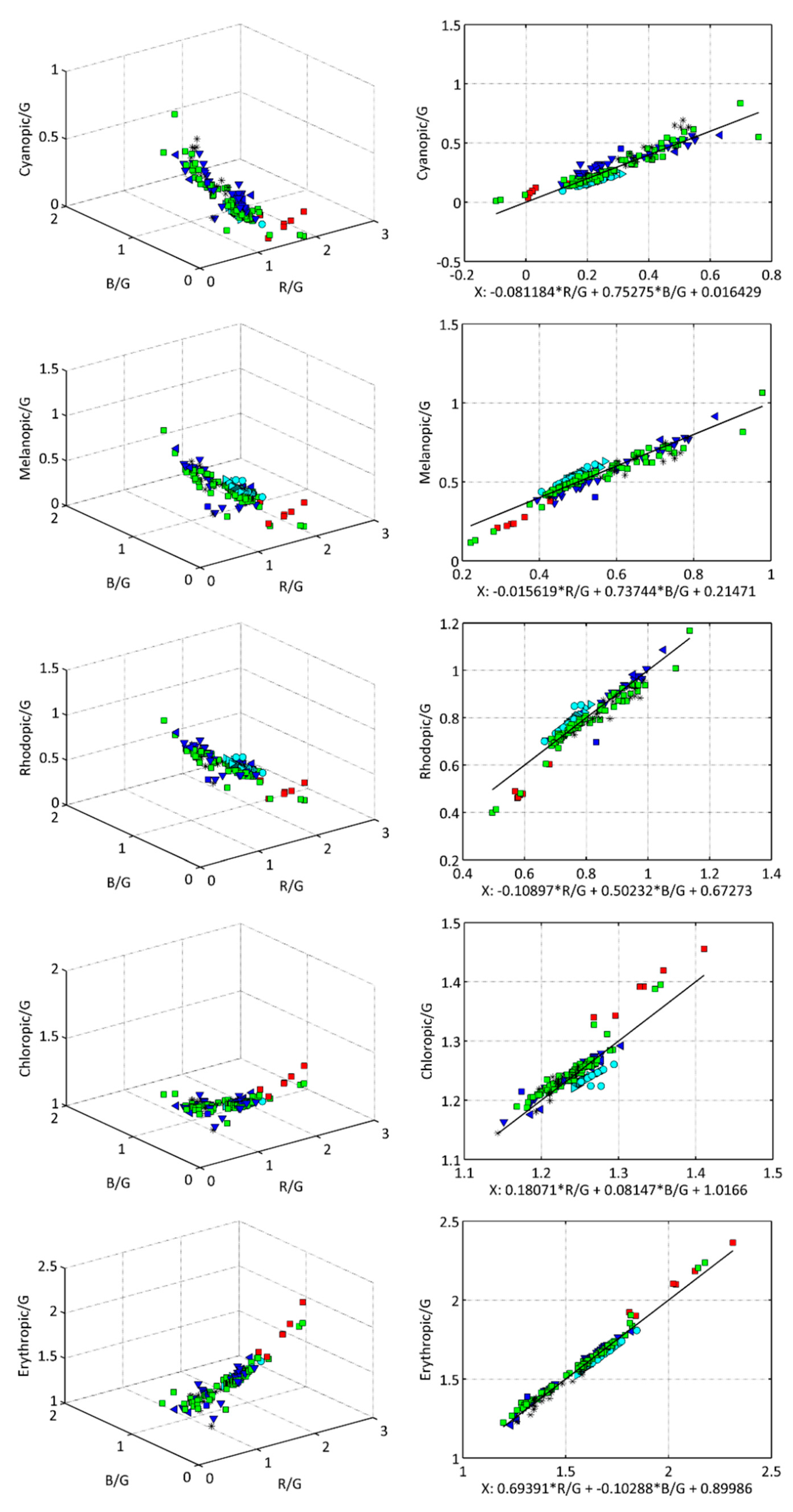
| Band/Coefficients | Residuals (std) | |||
|---|---|---|---|---|
| Cy | −0.0812(3) | 0.0164(5) | 0.7528(5) | 0.0527 |
| Me | −0.0156(3) | 0.2147(5) | 0.7374(5) | 0.0409 |
| Rh | −0.1090(5) | 0.6727(7) | 0.5023(7) | 0.0358 |
| Ch | 0.1807(7) | 1.0166(11) | 0.0815(10) | 0.0183 |
| Ery | 0.6939(8) | 0.8999(13) | −0.1029(11) | 0.0270 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez de Miguel, A.; Bará, S.; Aubé, M.; Cardiel, N.; Tapia, C.E.; Zamorano, J.; Gaston, K.J. Evaluating Human Photoreceptoral Inputs from Night-Time Lights Using RGB Imaging Photometry. J. Imaging 2019, 5, 49. https://doi.org/10.3390/jimaging5040049
Sánchez de Miguel A, Bará S, Aubé M, Cardiel N, Tapia CE, Zamorano J, Gaston KJ. Evaluating Human Photoreceptoral Inputs from Night-Time Lights Using RGB Imaging Photometry. Journal of Imaging. 2019; 5(4):49. https://doi.org/10.3390/jimaging5040049
Chicago/Turabian StyleSánchez de Miguel, Alejandro, Salvador Bará, Martin Aubé, Nicolás Cardiel, Carlos E. Tapia, Jaime Zamorano, and Kevin J. Gaston. 2019. "Evaluating Human Photoreceptoral Inputs from Night-Time Lights Using RGB Imaging Photometry" Journal of Imaging 5, no. 4: 49. https://doi.org/10.3390/jimaging5040049
APA StyleSánchez de Miguel, A., Bará, S., Aubé, M., Cardiel, N., Tapia, C. E., Zamorano, J., & Gaston, K. J. (2019). Evaluating Human Photoreceptoral Inputs from Night-Time Lights Using RGB Imaging Photometry. Journal of Imaging, 5(4), 49. https://doi.org/10.3390/jimaging5040049








