Knee-Cartilage Segmentation and Thickness Measurement from 2D Ultrasound
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Acquisition
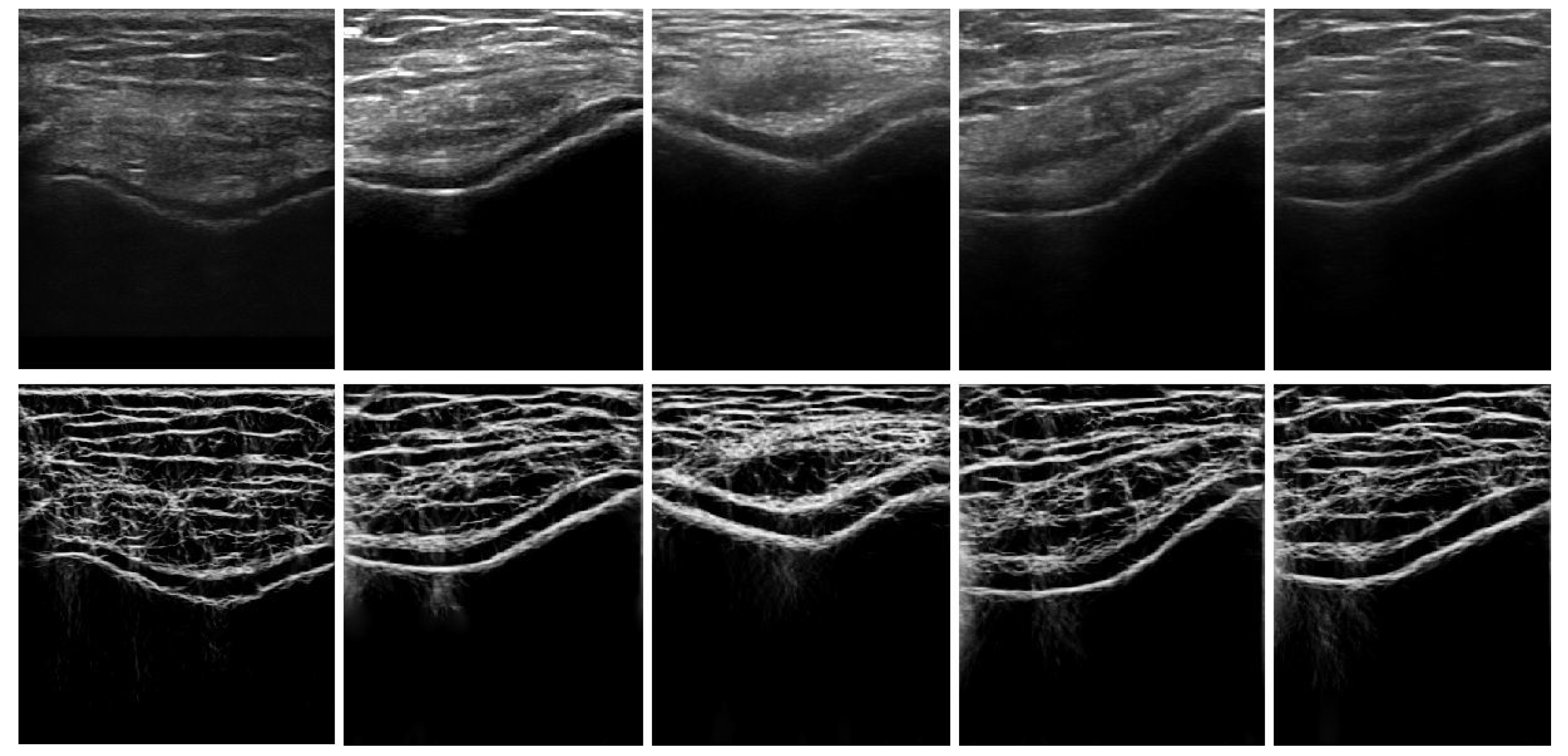
2.2. Cartilage Image Enhancement
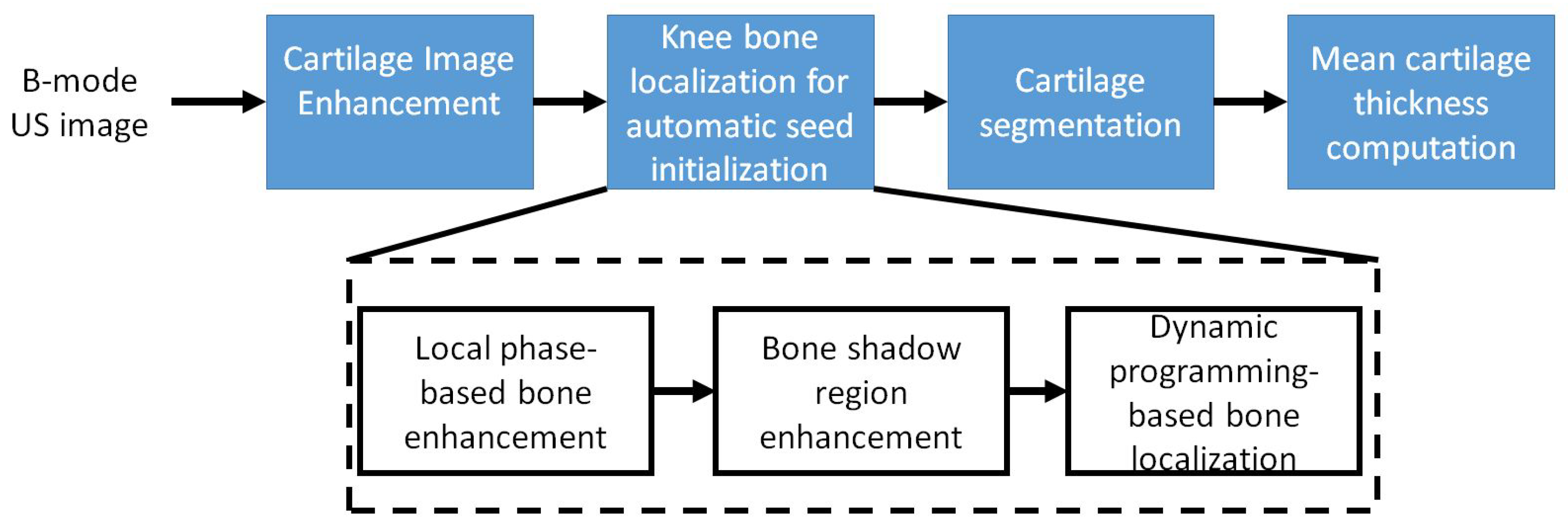
2.3. Knee-Bone Localization for Automatic Seed Initialization
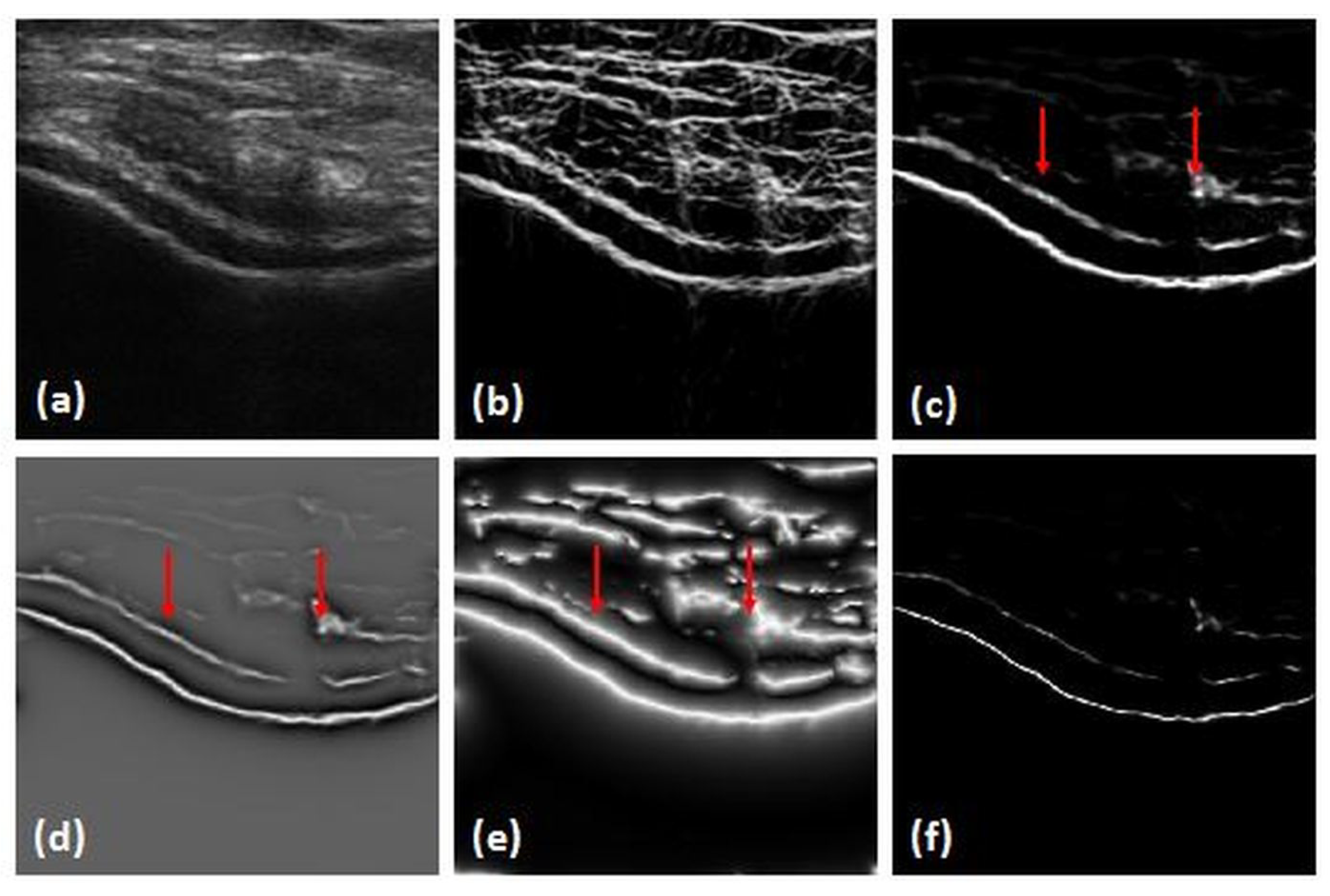
2.3.1. Local-Phase-Based Bone Enhancement
2.3.2. Bone-Shadow Enhancement
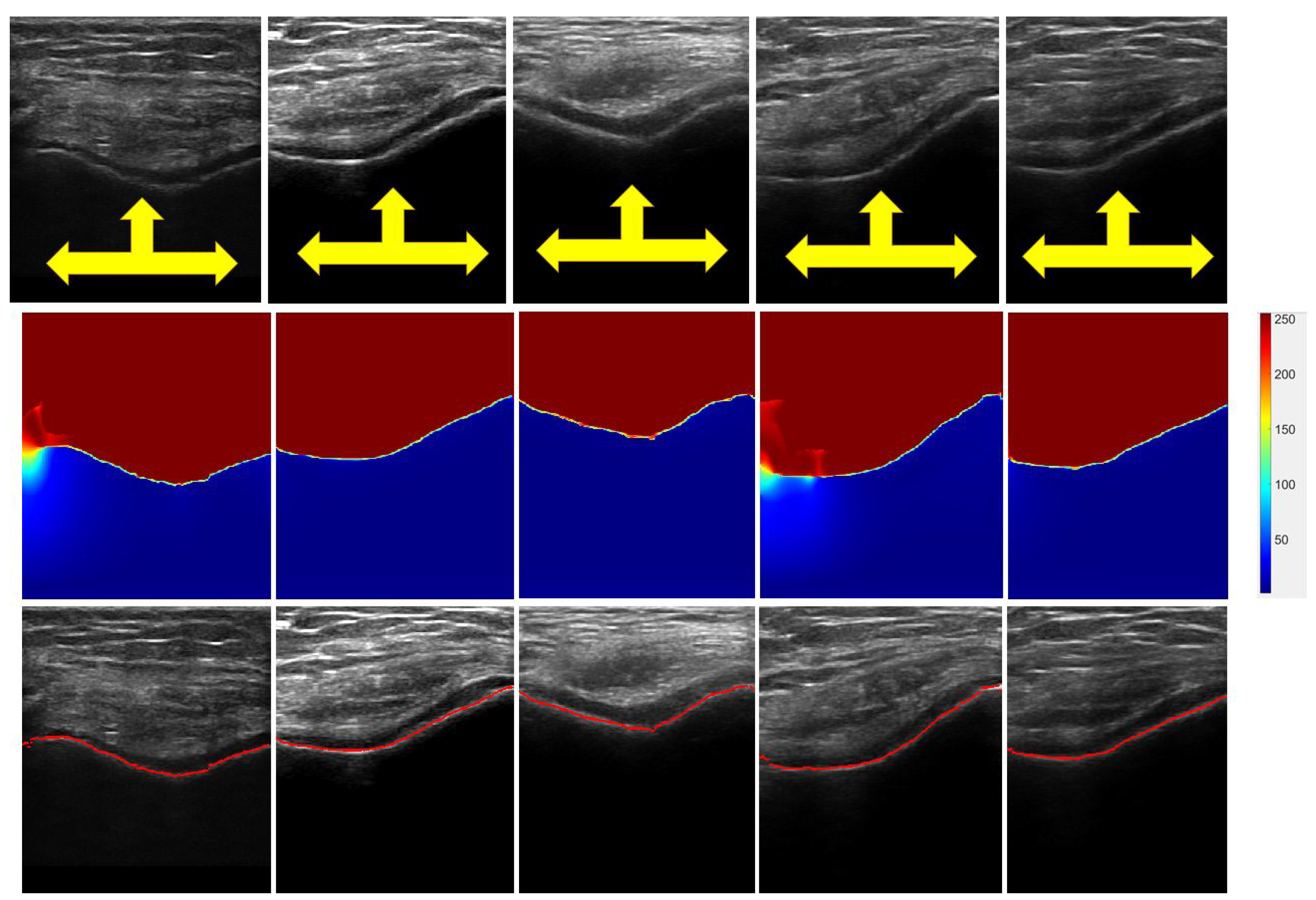
2.3.3. Bone-Surface Localization Using Dynamic Programming
2.4. Cartilage Segmentation
2.4.1. Seed Initialization
2.4.2. Random-Walker Image Segmentation
2.4.3. Watershed Image Segmentation
2.4.4. Graph-Cut Image Segmentation
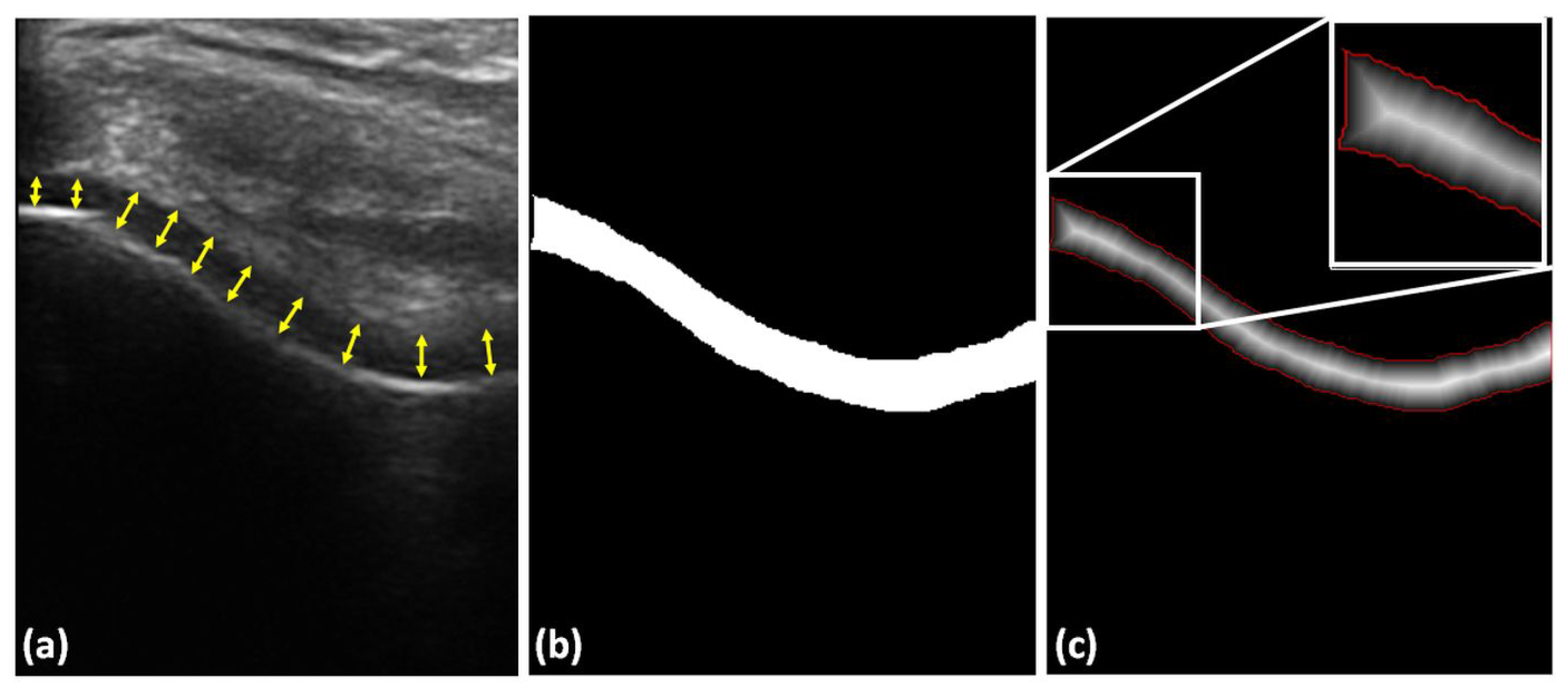
2.5. Automatic Cartilage-Thickness Computation
3. Results
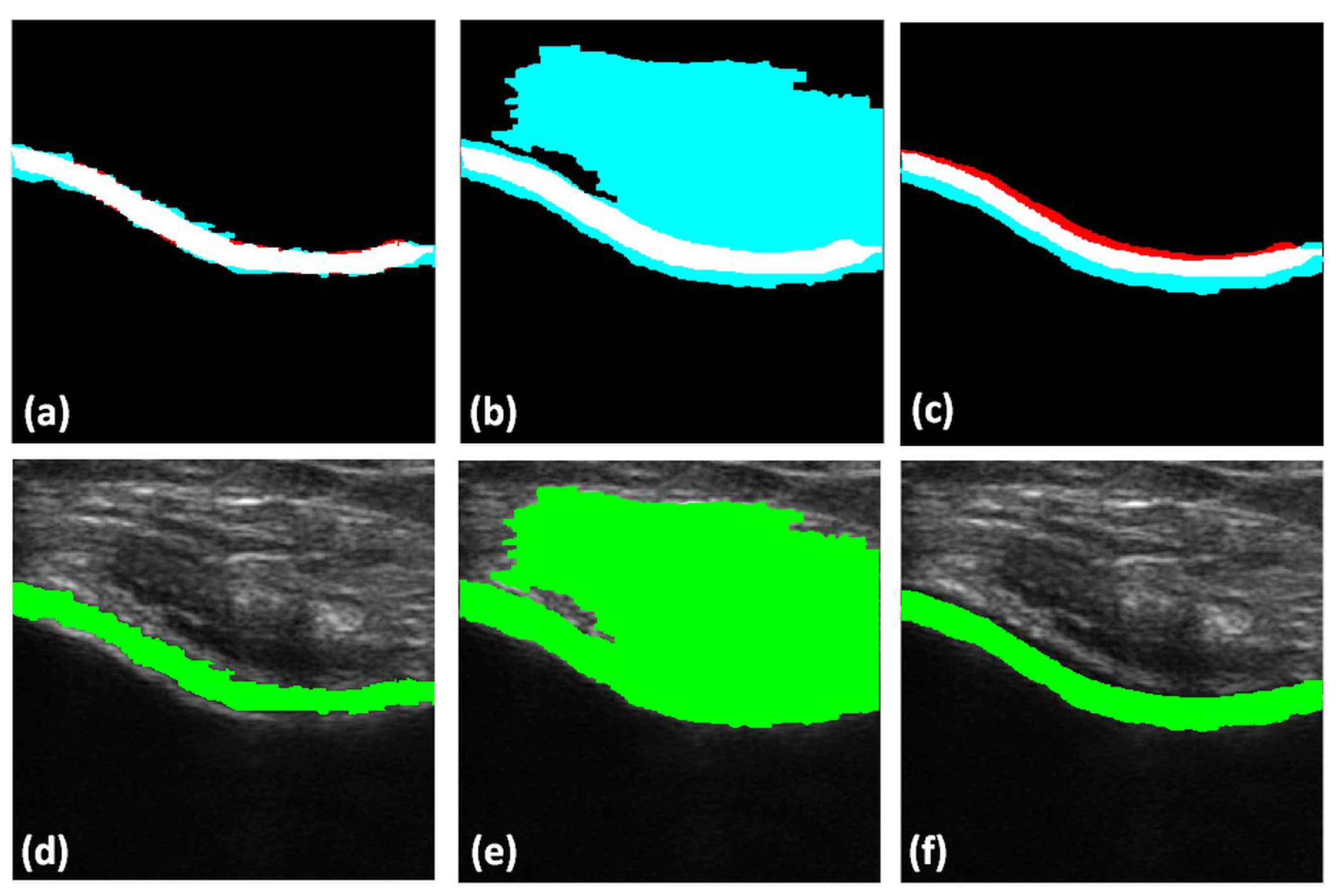
3.1. Cartilage-Segmentation Qualitative Results
3.2. Cartilage-Segmentation Quantitative Results
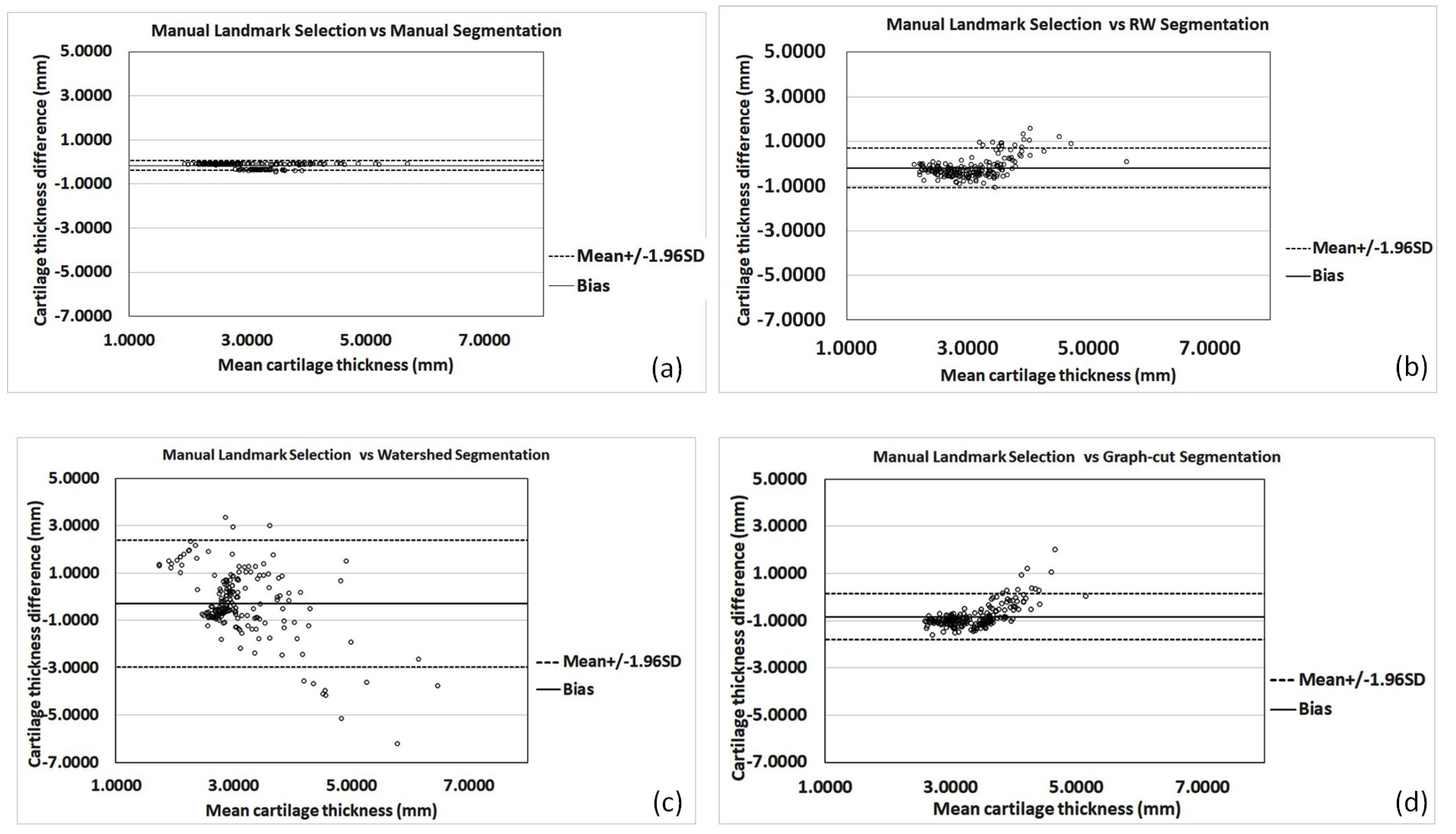
3.3. Cartilage-Thickness Measurement Quantitative Results
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Braun, H.J.; Gold, G.E. Diagnosis of osteoarthritis: Imaging. Bone 2012, 51, 278–288. [Google Scholar] [CrossRef]
- Roemer, F.W.; Crema, M.D.; Trattnig, S.; Guermazi, A. Advances in imaging of osteoarthritis and cartilage. Radiology 2011, 260, 332–354. [Google Scholar] [CrossRef]
- Aprovitola, A.; Gallo, L. Knee bone segmentation from MRI: A classification and literature review. Biocybern. Biomed. Eng. 2016, 36, 437–449. [Google Scholar] [CrossRef]
- Pedoia, V.; Li, X.; Su, F.; Calixto, N.; Majumdar, S. Fully automatic analysis of the knee articular cartilage T1ρ relaxation time using voxel-based relaxometry. J. Magn. Reson. Imaging 2016, 43, 970–980. [Google Scholar] [CrossRef] [PubMed]
- Kashyap, S.; Zhang, H.; Rao, K.; Sonka, M. Learning-Based Cost Functions for 3-D and 4-D Multi-Surface Multi-Object Segmentation of Knee MRI: Data From the Osteoarthritis Initiative. IEEE Trans. Med. Imaging 2018, 37, 1103–1113. [Google Scholar] [CrossRef]
- Fujinaga, Y.; Yoshioka, H.; Sakai, T.; Sakai, Y.; Souza, F.; Lang, P. Quantitative measurement of femoral condyle cartilage in the knee by MRI: Validation study by multireaders. J. Magn. Reson. Imaging 2014, 39, 972–977. [Google Scholar] [CrossRef]
- Swamy, M.M.; Holi, M.S. Knee joint articular cartilage segmentation, visualization and quantification using image processing techniques: A review. Int. J. Comput. Appl. 2012, 42, 36–43. [Google Scholar]
- Solloway, S.; Hutchinson, C.E.; Waterton, J.C.; Taylor, C.J. The use of active shape models for making thickness measurements of articular cartilage from MR images. Magn. Reson. Med. 1997, 37, 943–952. [Google Scholar] [CrossRef] [PubMed]
- Pakin, S.K.; Tamez-Pena, J.G.; Totterman, S.; Parker, K.J. Segmentation, surface extraction, and thickness computation of articular cartilage. In Medical Imaging 2002: Image Processing; International Society for Optics and Photonics: San Diego, CA, USA, 2002; Volume 4684, pp. 155–167. [Google Scholar]
- Maurer, C.R.; Qi, R.; Raghavan, V. A linear time algorithm for computing exact Euclidean distance transforms of binary images in arbitrary dimensions. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 265–270. [Google Scholar] [CrossRef]
- Mlejnek, M.; Vilanova, A.; Groller, M.E. Interactive thickness visualization of articular cartilage. In Proceedings of the Conference on Visualization’04, Austin, TX, USA, 10–15 October 2004; pp. 521–528. [Google Scholar]
- Heuer, F.; Sommers, M.; Reid, J.; Bottlang, M. Estimation of cartilage thickness from joint surface scans: Comparative analysis of computational methods. ASME-PUBLICATIONS-BED 2001, 50, 569–570. [Google Scholar]
- Naredo, E.; Acebes, C.; Möller, I.; Canillas, F.; de Agustín, J.J.; de Miguel, E.; Filippucci, E.; Iagnocco, A.; Moragues, C.; Tuneu, R.; et al. Ultrasound validity in the measurement of knee cartilage thickness. Ann. Rheum. Dis. 2008, 68, 1322–1327. [Google Scholar] [CrossRef]
- Myers, S.L.; Dines, K.; Brandt, D.A.; Brandt, K.D.; Albrecht, M.E. Experimental assessment by high frequency ultrasound of articular cartilage thickness and osteoarthritic changes. J. Rheumatol. 1995, 22, 109–116. [Google Scholar]
- Mathiesen, O.; Konradsen, L.; Torp-Pedersen, S.; Jørgensen, U. Ultrasonography and articular cartilage defects in the knee: An in vitro evaluation of the accuracy of cartilage thickness and defect size assessment. Knee Surg. Sports Traumatol. Arthrosc. 2004, 12, 440–443. [Google Scholar] [CrossRef]
- Aisen, A.M.; McCune, W.J.; MacGuire, A.; Carson, P.L.; Silver, T.M.; Jafri, S.Z.; Martel, W. Sonographic evaluation of the cartilage of the knee. Radiology 1984, 153, 781–784. [Google Scholar] [CrossRef]
- Grassi, W.; Lamanna, G.; Farina, A.; Cervini, C. Sonographic imaging of normal and osteoarthritic cartilage. In Seminars in Arthritis and Rheumatism; Elsevier: Amsterdam, The Netherlands, 1999; Volume 28, pp. 398–403. [Google Scholar]
- Schmitz, R.J.; Wang, H.M.; Polprasert, D.R.; Kraft, R.A.; Pietrosimone, B.G. Evaluation of knee cartilage thickness: A comparison between ultrasound and magnetic resonance imaging methods. Knee 2017, 24, 217–223. [Google Scholar] [CrossRef]
- Saarakkala, S.; Waris, P.; Waris, V.; Tarkiainen, I.; Karvanen, E.; Aarnio, J.; Koski, J. Diagnostic performance of knee ultrasonography for detecting degenerative changes of articular cartilage. Osteoarthr. Cartil. 2012, 20, 376–381. [Google Scholar] [CrossRef]
- Harkey, M.; Blackburn, J.; Davis, H.; Sierra-Arévalo, L.; Nissman, D.; Pietrosimone, B. Ultrasonographic assessment of medial femoral cartilage deformation acutely following walking and running. Osteoarthr. Cartil. 2017, 25, 907–913. [Google Scholar] [CrossRef]
- Hossain, M.B.; Lai, K.W.; Pingguan-Murphy, B.; Hum, Y.C.; Salim, M.I.M.; Liew, Y.M. Contrast enhancement of ultrasound imaging of the knee joint cartilage for early detection of knee osteoarthritis. Biomed. Signal Process. Control. 2014, 13, 157–167. [Google Scholar] [CrossRef]
- Faisal, A.; Ng, S.C.; Goh, S.L.; Lai, K.W. Knee cartilage segmentation and thickness computation from ultrasound images. Med. Biol. Eng. Comput. 2018, 56, 657–669. [Google Scholar] [CrossRef]
- Desai, P.R.; Hacihaliloglu, I. Enhancement and automated segmentation of ultrasound knee cartilage for early diagnosis of knee osteoarthritis. In Proceedings of the 2018 IEEE 15th International Symposium on Biomedical Imaging (ISBI 2018), Washington, DC, USA, 4–7 April 2018; pp. 1471–1474. [Google Scholar]
- Wang, L.; He, L.; Mishra, A.; Li, C. Active contours driven by local Gaussian distribution fitting energy. Signal Process. 2009, 89, 2435–2447. [Google Scholar] [CrossRef]
- Li, C.; Huang, R.; Ding, Z.; Gatenby, J.; Metaxas, D.N.; Gore, J.C. A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI. IEEE Trans. Image Process. 2011, 20, 2007. [Google Scholar] [PubMed]
- Hacihaliloglu, I. Localization of bone surfaces from ultrasound data using local phase information and signal transmission maps. In International Workshop and Challenge on Computational Methods and Clinical Applications in Musculoskeletal Imaging; Springer: Cham, Switzerland, 2017; pp. 1–11. [Google Scholar]
- Hacihaliloglu, I.; Abugharbieh, R.; Hodgson, A.J.; Rohling, R.N. Bone surface localization in ultrasound using image phase-based features. Ultrasound Med. Biol. 2009, 35, 1475–1487. [Google Scholar] [CrossRef]
- Hacihaliloglu, I.; Rasoulian, A.; Rohling, R.N.; Abolmaesumi, P. Local phase tensor features for 3-D ultrasound to statistical shape+ pose spine model registration. IEEE Trans. Med. Imaging 2014, 33, 2167–2179. [Google Scholar] [CrossRef]
- Belaid, A.; Boukerroui, D. α scale spaces filters for phase based edge detection in ultrasound images. In Proceedings of the 2014 IEEE 11th International Symposium on Biomedical Imaging (ISBI), Beijing, China, 29 April–2 May 2014; pp. 1247–1250. [Google Scholar]
- Hacihaliloglu, I. Enhancement of bone shadow region using local phase-based ultrasound transmission maps. Int. J. Comput. Assist. Radiol. Surg. 2017, 12, 951–960. [Google Scholar] [CrossRef]
- Karamalis, A.; Wein, W.; Klein, T.; Navab, N. Ultrasound confidence maps using random walks. Med. Image Anal. 2012, 16, 1101–1112. [Google Scholar] [CrossRef]
- Bozkurt, F.; Köse, C.; San, A. Comparison of seeded region growing and random walk methods for vessel and bone segmentation in CTA images. In Proceedings of the 2017 IEEE 10th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 30 November–2 December 2017; pp. 561–567. [Google Scholar]
- Grady, L. Random walks for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1768–1783. [Google Scholar] [CrossRef] [PubMed]
- Collins, M.D.; Xu, J.; Grady, L.; Singh, V. Random walks based multi-image segmentation: Quasiconvexity results and gpu-based solutions. In Proceedings of the 2012 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Providence, RI, USA, 16–21 June 2012; pp. 1656–1663. [Google Scholar]
- Sinop, A.K.; Grady, L. A seeded image segmentation framework unifying graph cuts and random walker which yields a new algorithm. In Proceedings of the 2007 IEEE 11th International Conference on Computer Vision (ICCV 2007), Rio de Janeiro, Brazil, 14–21 October 2007; pp. 1–8. [Google Scholar]
- Roerdink, J.B.; Meijster, A. The watershed transform: Definitions, algorithms and parallelization strategies. Fundam. Inform. 2000, 41, 187–228. [Google Scholar]
- Jia-xin, C.; Sen, L. A medical image segmentation method based on watershed transform. In Proceedings of the 2005 IEEE Fifth International Conference on Computer and Information Technology (CIT 2005), Shanghai, China, 21–23 September 2005; pp. 634–638. [Google Scholar]
- Lefèvre, S. Knowledge from markers in watershed segmentation. In Proceedings of the International Conference on Computer Analysis of Images and Patterns, Vienna, Austria, 27–29 August 2007; Springer: Berlin/Heidelberg, Germany, 2007; pp. 579–586. [Google Scholar]
- Hamarneh, G.; Li, X. Watershed segmentation using prior shape and appearance knowledge. Image Vis. Comput. 2009, 27, 59–68. [Google Scholar] [CrossRef]
- Boykov, Y.Y.; Jolly, M.P. Interactive graph cuts for optimal boundary & region segmentation of objects in ND images. In Proceedings of the 2001 Eighth IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, BC, Canada, 7–14 July 2001; Volume 1, pp. 105–112. [Google Scholar]
- Chen, X.; Udupa, J.K.; Bagci, U.; Zhuge, Y.; Yao, J. Medical image segmentation by combining graph cuts and oriented active appearance models. IEEE Trans. Image Process. 2012, 21, 2035–2046. [Google Scholar] [CrossRef] [PubMed]
- Shepherd, D.; Seedhom, B. Thickness of human articular cartilage in joints of the lower limb. Ann. Rheum. Dis. 1999, 58, 27–34. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Jin, D.; Li, C.; Janz, K.F.; Burns, T.L.; Torner, J.C.; Levy, S.M.; Saha, P.K. A robust algorithm for thickness computation at low resolution and its application to in vivo trabecular bone CT imaging. IEEE Trans. Biomed. Eng. 2014, 61, 2057–2069. [Google Scholar] [PubMed]
- Ginat, D.T.; Hung, G.; Gardner, T.R.; Konofagou, E.E. High-resolution ultrasound elastography of articular cartilage in vitro. In Proceedings of the 2006 International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 30 August–3 September 2006; pp. 6644–6647. [Google Scholar]
- Niu, H.; Liu, C.; Li, A.; Wang, Q.; Wang, Y.; Li, D.; Fan, Y. Relationship between triphasic mechanical properties of articular cartilage and osteoarthritic grade. Sci. China Life Sci. 2012, 55, 444–451. [Google Scholar] [CrossRef] [PubMed]
- Xu, H.; Chen, S.; An, K.N.; Luo, Z.P. Near field effect on elasticity measurement for cartilage-bone structure using Lamb wave method. Biomed. Eng. Online 2017, 16, 123. [Google Scholar] [CrossRef] [PubMed]


| Quantitative results when using enhanced US image . | ||||
| Method | DSC Mean ± SD | Precision | Recall | F-score |
| RW | 0.90 ± 0.01 | 0.88 | 0.92 | 0.86 |
| Watershed | 0.86 ± 0.04 | 0.82 | 0.91 | 0.86 |
| Graph-cut | 0.84 ± 0.03 | 0.81 | 0.87 | 0.84 |
| Quantitative results when using B-mode US image . | ||||
| Method | DSC Mean ± SD | Precision | Recall | F-score |
| RW | 0.79 ± 0.1 | 0.80 | 0.80 | 0.79 |
| Watershed | 0.65 ± 0.2 | 0.60 | 0.78 | 0.66 |
| Graph-cut | 0.76 ± 0.09 | 0.72 | 0.82 | 0.76 |
| Method | Image | Mean ± SD (mm) |
|---|---|---|
| Manual measurement | Original B-mode | 2.95 ± 0.66 |
| Automatic measurement | Manual Segmentation | 3.1 ± 0.68 |
| RW Segmentation | 3.14 ± 0.46 | |
| Watershed Segmentation | 3.23 ± 1.21 | |
| Graph-cut Segmentation | 3.78 ± 0.35 |
| Manual Segmentation | RW | Watershed | Graph Cut | |
|---|---|---|---|---|
| Manual landmark-based segmentation | 0.02 | 0.001 | 0.004 | 0.000003 |
| Manual Segmentation | Not Applicable | 0.57 | 0.2 | 0.00002 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Desai, P.; Hacihaliloglu, I. Knee-Cartilage Segmentation and Thickness Measurement from 2D Ultrasound. J. Imaging 2019, 5, 43. https://doi.org/10.3390/jimaging5040043
Desai P, Hacihaliloglu I. Knee-Cartilage Segmentation and Thickness Measurement from 2D Ultrasound. Journal of Imaging. 2019; 5(4):43. https://doi.org/10.3390/jimaging5040043
Chicago/Turabian StyleDesai, Prajna, and Ilker Hacihaliloglu. 2019. "Knee-Cartilage Segmentation and Thickness Measurement from 2D Ultrasound" Journal of Imaging 5, no. 4: 43. https://doi.org/10.3390/jimaging5040043
APA StyleDesai, P., & Hacihaliloglu, I. (2019). Knee-Cartilage Segmentation and Thickness Measurement from 2D Ultrasound. Journal of Imaging, 5(4), 43. https://doi.org/10.3390/jimaging5040043





