Abstract
Drones are becoming increasingly popular for remote sensing of landscapes in archeology, cultural heritage, forestry, and other disciplines. They are more efficient than airplanes for capturing small areas, of up to several hundred square meters. LiDAR (light detection and ranging) and photogrammetry have been applied together with drones to achieve 3D reconstruction. With airborne optical sectioning (AOS), we present a radically different approach that is based on an old idea: synthetic aperture imaging. Rather than measuring, computing, and rendering 3D point clouds or triangulated 3D meshes, we apply image-based rendering for 3D visualization. In contrast to photogrammetry, AOS does not suffer from inaccurate correspondence matches and long processing times. It is cheaper than LiDAR, delivers surface color information, and has the potential to achieve high sampling resolutions. AOS samples the optical signal of wide synthetic apertures (30–100 m diameter) with unstructured video images recorded from a low-cost camera drone to support optical sectioning by image integration. The wide aperture signal results in a shallow depth of field and consequently in a strong blur of out-of-focus occluders, while images of points in focus remain clearly visible. Shifting focus computationally towards the ground allows optical slicing through dense occluder structures (such as leaves, tree branches, and coniferous trees), and discovery and inspection of concealed artifacts on the surface.
1. Introduction
Airborne laser scanning (ALS) [1,2,3,4] utilizes LiDAR (light detection and ranging) [5,6,7,8] for remote sensing of landscapes. In addition to many other applications, ALS is used to make archaeological discoveries in areas concealed by trees [9,10,11], to support forestry in forest inventory and ecology [12], and to acquire precise digital terrain models (DTMs) [13,14]. LiDAR measures the round travel time of reflected laser pulses to estimate distances at frequencies of several hundred kilohertz, and for ALS is operated from airplanes, helicopters, balloons, or drones [15,16,17,18,19]. It delivers high resolution point clouds that can be filtered to remove vegetation or trees when inspecting the ground surface [20,21].
Although LiDAR has clear advantages over photogrammetry when it comes to partially occluded surfaces, it also has limitations: for small areas the operating cost is disproportionally high; the huge amount of 3D point data requires massive processing time for registration, triangulation and classification; it does not, per se, provide surface color information; and its sampling resolution is limited by the speed and other mechanical constraints of laser scanners and recording systems.
Here, we present a different approach to revealing and inspecting artifacts occluded by moderately dense structures, such as forests, that uses low-cost, off-the-shelf camera drones. Since it is entirely image-based and does not reconstruct 3D points, it has very low processing demands and can therefore deliver real-time 3D visualization results almost instantly after short image preprocessing. Like drone-based LiDAR, it is particularly efficient for capturing small areas of several hundred square meters, but it has the potential to provide a high sampling resolution and surface color information. We call this approach airborne optical sectioning (AOS) and envision applications where fast visual inspections of partially occluded areas are desired at low costs and effort. Besides archaeology, forestry and agriculture might offer additional use cases. Application examples in forestry include the visual inspection of tree population (e.g., examining trunk thicknesses), pest infestation (with infrared cameras), and forest road conditions underneath the tree crowns.
2. Materials and Methods
Cameras integrated in conventional drones apply lenses of several millimeters in diameter. The relatively large f-number (i.e., the ratio of the focal length to the lens diameter) of such cameras yields a large depth of field that makes it possible to capture the scene in focus over large distances. Decreasing the depth of field requires a lower f-number that can be achieved, for instance, with a wider effective aperture (i.e., a wider lens). Equipping a camera drone with a lens several meters rather than millimeters wide is clearly infeasible, but would enable the kind of optical sectioning used in traditional light microscopes, which applies high numerical aperture optics [22,23,24].
For cases in which wide apertures cannot be realized, the concept of synthetic apertures has been introduced [25]. Synthetic apertures sample the signal of wide apertures with arrays of smaller sub-apertures whose individual signals are computationally combined. This principle has been used for radar [26,27,28,29], telescopes [30], microscopes [31,32], and camera arrays [33].
We sample the optical signal of wide synthetic apertures (30–100 m diameter) with unstructured video images recorded by a camera drone to support optical sectioning computationally with synthetic aperture rendering [34,35]. The following section explains the sampling principles and the visualization techniques of our approach.
2.1. Wide Sythetic Aperture Sampling
Let us consider a target on the ground surface covered by a volumetric structure of random occluders, as illustrated in Figure 1. The advantage of LiDAR (cf. Figure 1a) is that the depth of a surface point on the target can theoretically be recovered if a laser pulse from only one direction is reflected by that point without being entirely occluded. In the case of photogrammetry (cf. Figure 1b), a theoretical minimum of two non-occluded directions are required for stereoscopic depth estimation (in practice, many more directions are necessary to minimize measurement inaccuracies). In contrast to LiDAR, photogrammetry relies on correspondence search, which requires distinguishable feature structures and it fails for uniform image features.
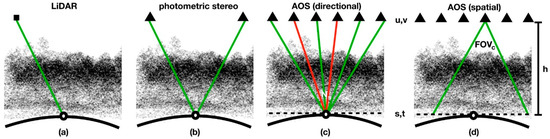
Figure 1.
For light detection and ranging (LiDAR) (a) a single ray is sufficient to sample the depth of a point on the ground surface, while photometric stereo (b) requires a minimum of two views and relies on a dense set of matchable image features. In airborne optical sectioning (AOS), for each point on the synthetic focal plane we directionally integrate many rays over a wide synthetic aperture to support optical sectioning with a low synthetic f-number (c). The spatial sampling density at the focal plane depends on the field of view, the resolution of the drone’s camera, and the height of the drone relative to the focal plane (d).
Our approach computes 3D visualizations entirely by image-based rendering [35]. However, it does not reconstruct 3D point clouds and therefore does not suffer from inaccurate correspondence matches and long processing times. As illustrated in Figure 1c, we sample the area of the synthetic aperture by means of multiple unstructured sub-apertures (the physical apertures of the camera drone). Each sample corresponds to one geo-referenced (pose and orientation) video image of the drone. Each pixel in such an image corresponds to one discrete ray r captured through the synthetic aperture that intersects the aperture plane at coordinates u,v and the freely adjustable synthetic focal plane at coordinates s,t. To compute the surface color Rs,t of each point on the focal plane, we computationally integrate and normalize all sampled rays rs,t,u,v of the synthetic aperture (with directional resolution U,V) that geometrically intersect at s,t:
Some of these directionally sampled rays might be blocked partially or fully by occluders (red in Figure 1c). However, if the surface color dominates in the integral, it can be visualized in the rendered image. This is the case if the occluding structure is sufficiently sparse and the synthetic aperture wide and sufficiently densely sampled. The wider the synthetic aperture, the lower its synthetic f-number (Ns), which in this case is the ratio of the height of the drone h (distance between the aperture plane and focal plane) to the diameter of the synthetic aperture (size of the sampled area).
A low Ns results in a shallow depth of field and consequently in a strong point spread of out-of-focus occluders over a large region of the entire integral image. Images of focused points remain concentrated in small spatial regions that require an adequate spatial resolution to be resolved.
The spatial sampling resolution fs (number of sample points per unit area) at the focal plane can be determined by back-projecting the focal plane onto the imaging plane of the drone’s camera, as illustrated in Figure 1d. Assuming a pinhole camera model and parallel focal and image planes, this leads to:
where FOVc is the field of view of the drone’s camera, n is its resolution (number of pixels on the image sensor), and h is the height of the drone. Note, that in practice, the spatial sampling resolution is not uniform, as the focal plane and image plane are not necessarily parallel, and imaging with omnidirectional cameras is not uniform on the image sensor. Furthermore, the sampling resolution is affected by the quality of the drone’s pose estimation. Appendix A explains how we estimate the effective spatial sampling resolution that considers omnidirectional images and pose-estimation errors.
2.2. Wide Synthetic Aperture Visualization
The data basis for visualization is the set of geo-referenced video images recorded by the drone during synthetic aperture sampling. They must be rectified to eliminate lens distortion. Figure 2a illustrates how a novel image is computed for a virtual camera by means of image-based rendering [35]. The parameters of the virtual camera (position, orientation, focal plane, field of view, and aperture radius) are interactively defined in the same three-dimensional coordinate system as the drone poses.
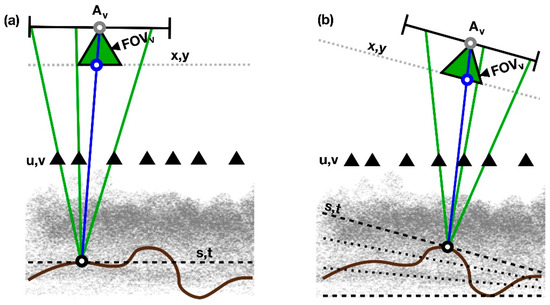
Figure 2.
For visualization, we interactively define a virtual camera (green triangle) by its pose, size of its aperture, field of view, and its focal plane. Novel images are rendered by ray integration (Equation (1)) for points s,t at the focal plane (black circle) that are determined by the intersection of rays (blue) through the camera’s projection center (grey circle) and pixels at x,y in the camera’s image plane (blue circle) within its field of view FOVv. Only the rays (green) through u,v at the synthetic aperture plane that pass through the virtual camera’s aperture Av, are integrated. While (a) illustrates the visualization for a single focal plane, (b) shows the focal slicing being applied to increase the depth of field computationally.
Given the virtual camera’s pose (position and orientation) and field of view FOVv, a ray through its projection center and a pixel at coordinates x,y in its image plane can be defined (blue in Figure 2a). This ray intersects the adjusted focal plane at coordinates s,t. With Equation (1), we now integrate all rays rs,t,u,v from s,t through each sample at coordinates u,v in the synthetic aperture plane that intersect the virtual camera’s circular aperture area Av of defined radius. The resulting surface color integral Rs,t is used for the corresponding pixel’s color. This is repeated for all pixels in the virtual camera’s image plane to render the entire image. Interactive control over the virtual camera’s parameters allows real-time renderings of the captured scene by adjusting perspective, focus, and depth of field.
The extremely shallow depth of field that results from a wide aperture blurs not only occluders, such as trees, but also points of the ground target that are not located in the focal plane. To visualize non-planar targets entirely in focus, we adjust two boundary focal planes (dashed black lines in Figure 2b) that enclose the ground target, and interpolate their plane parameters to determine a fine intermediate focal slicing (dotted black lines in Figure 2b). Repeating the rendering for each focal plane, as explained above, leads to a focal stack (i.e., a stack of x,y-registered, shallow depth-of-field images with varying focus). For every pixel at x,y in the virtual camera’s image plane, we now determine the optimal focus through all slices of the focal stack by maximizing the Sobel magnitude computed within a 3 × 3 pixel neighborhood. The surface color at the optimal focus is then used for the pixel’s color. Repeating this for all pixels leads to an image that renders the ground target within the desired focal range with a large depth of field, while occluders outside are rendered with a shallow depth of field.
3. Results
We carried out two field experiments for proof of concept. In experiment 1 (cf. Figure 3) we recovered an artificial ground target, and in experiment 2 (cf. Figure 4) the ruins of an early 19th century fortification tower. Both were concealed by dense forest and vegetation—being entirely invisible from the air.

Figure 3.
A densely forested patch is captured with a circular synthetic aperture of 30 m diameter (a), sampled with 231 video images (b) from a camera drone at an altitude of 20 m above ground. A dense 3D point cloud reconstruction from these images (c) took 8 h to compute with photogrammetry. (d) A single raw video image captured through the narrow-aperture omnidirectional lens of the drone. After image rectification, the large depth of field does not reveal features on the ground that are occluded by the trees (e). Increasing the aperture computationally decreases the depth of field and significantly blurs out-of-focus features (f). Shifting focus computationally towards the ground slices optically through the tree branches (f) makes a hidden ground target visible (g,h). Synthetic aperture rendering was possible in real-time after 15 min of preprocessing (image rectification and pose estimation). 3D visualization results are shown in Supplementary Materials Video S1.

Figure 4.
Ruins of an early 19th century fortification tower near Linz, Austria, as seen from the air (a). The structure of the remaining inner and outer ring walls and a trench become visible after optical sectioning (b). Image preprocessing (rectification and pose estimation) for AOS took 23 min. Photometric 3D reconstruction took 15 h (without tree removal) and does not capture the site structures well (c). Remains of the site as seen from the ground (d). An LiDAR scan with a resolution of 8 samples/m2 (e) does not deliver surface color but provides consistent depth. The synthetic aperture for AOS in this experiment was a 90° sector of a circle with 50 m radius and was sampled with 505 images at an altitude of 35 m above the ground (f,g). For our camera drone, this leads to effectively 74 samples/m2 on the ground. 3D visualization results are shown in Supplementary Materials Video S2.
In both experiments, we used a low-cost off-the-shelf quadcopter (Parrot Bebop 2) equipped with a fixed 14MP Complementary Metal-Oxide-Semiconductor (CMOS) camera and a 178° FOV fisheye lens. For path planning, we first outlined the dimensions and shapes of the synthetic apertures in Google Maps and then used a custom Python script to compute intermediate geo-coordinates on the flying path that samples the desired area on the synthetic aperture plane. Parrot’s ARDroneSDK3 API (developer.parot.com/docs/SDK3/) was used to control the drone autonomously along the determined path and to capture images.
For experiments 1 and 2, the distance between two neighboring recordings was 1 m and 2–4 m respectively (denser in the center of the aperture sector). In both cases, directional sampling followed a continuous scan line path, the ground speed of the drone was 1 m/s, and the time for stabilizing the drone at a sample position and recording an image was 1 s. This led to sampling rates of about 30 frames per minute and 12–20 frames per minute for experiment 1 and 2, respectively.
We applied OpenCV’s (opencv.org) omnidirectional camera model for camera calibration and image rectification and implemented a GPU visualization framework based on Nvidia’s CUDA (NVIDIA, Santa Clara, CA, USA) for image-based rendering as explained in Section 2.2. The general purpose structure-from-motion and multi-view stereo pipeline, COLMAP [36], was used for photometric 3D reconstruction, and for pose estimation of the drone.
For experiment 2, we achieved an effective spatial sampling resolution of 74 samples/m2 on the ground (see Appendix A for details) from an altitude of 35 m with a low-cost drone that uses a fixed omnidirectional camera. Since only 80° of the camera’s 178° FOV was used, just a fraction of the sensor resolution was utilized (3.5 MP of a total of 14 MP in our example). In the 60 × 60 m region of interest shown in Figure 4b (corresponding to FOVc = 80° and n = 3.5 MP), we find a ten times denser spatial sampling resolution than in the LiDAR example shown in Figure 4e (i.e., 74 samples/m2 compared to 8 samples/m2). A total of 100 focal slices were computed and processed for achieving the results shown in Figure 4b.
Photometric 3D reconstruction from the captured images requires hours (8–15 h in our experiments) of preprocessing and leads in most cases to unusable results for complex scenes, such as forests (cf. Figure 3c and Figure 4c). Currently, processing for AOS requires minutes (15–23 min in our experiments), but this can be sped up significantly with a more efficient implementation.
4. Discussion and Conclusions
Drones are becoming increasingly popular for remote sensing of landscapes. They are more efficient than airplanes for capturing small areas of up to several hundred square meters. LiDAR and photogrammetry have been applied together with drones for airborne 3D reconstruction. AOS represents a very different approach. Instead of measuring, computing, and rendering 3D point clouds or triangulated 3D meshes, it applies image-based rendering for 3D visualization. In contrast to photogrammetry, it does not suffer from inaccurate correspondence matches and long processing times. It is cheaper than LiDAR, delivers surface color information, and has the potential to achieve high spatial sampling resolutions.
In contrast to CMOS or Charge-Coupled Device (CCD) cameras, the spatial sampling resolution of LiDAR is limited by the speed and other mechanical constraints of laser deflection. Top-end drone-based LiDAR systems (e.g., RIEGL VUX-1UAV: RIEGL Laser Measurement Systems GmbH, Horn, Austria) achieve resolutions of up to 2000 samples/m2 from an altitude of 40 m. The sampling precision is affected by the precision of the drone’s inertial measurement unit (IMU) and Global Positioning System (GPS) signal, which is required to integrate the LiDAR scan lines during flight. While IMUs suffer from drift over time, GPS is only moderately precise. In contrast, pose estimation for AOS is entirely based on computer vision and a dense set of visually registered multi-view images of many hundreds of overlapping perspectives. It is therefore more stable and precise. Since AOS processes unstructured records of perspective images, GPS and IMU data is only used for navigating the drone and does not affect the precision of pose estimation.
More advanced drones allow external cameras to be attached to a rotatable gimbal (e.g., DJI M600: DJI, Shenzhen, China). If equipped with state-of-the-art 100 MP aerial cameras (e.g., Phase One iXU-RS 1000, Phase One, Copenhagen, Denmark) and appropriate objective lenses, we estimate that these can reach spatial sampling resolutions one to two orders of magnitude higher than those of state-of-the-art LiDAR drones.
However, AOS also has several limitations: First, it does not provide useful depth information, as is the case for LiDAR and photogrammetry. Depth maps that could be derived from our focal stacks by depth-from-defocus techniques [37] are as unreliable and imprecise as those gained from photogrammetry. Second, ground surface features occluded by extremely dense structures might not be resolved well—not even with very wide synthetic apertures and very high directional samplings (see Appendix B). LiDAR might be of advantage in these cases, as (in theory) only one non-occluded sample is required to resolve a surface point. This, however, also requires rigorously robust classification techniques that are able to correctly filter out vegetation under these conditions. Third, AOS relies on an adequate amount of sun light being reflected from the ground surface while LiDAR benefits from active laser illumination.
In conclusion, we believe that AOS has potential to support use cases that benefit from visual inspections of partially occluded areas at low costs and little effort. It is easy to use and provides real-time high-resolution 3D color visualizations almost instantly. For applications that require quantitative 3D measurements, however, LiDAR or photogrammetry still remain methods of first choice. We intend to explore optimal directional and spatial sampling strategies for AOS. Improved drone path planning, for instance, would lead to better usage of the limited flying time and to reduced image data. Furthermore, the fact that recorded images spatially overlap in the focal plane suggests that the actual spatial sampling resolution is higher than for a single image (as estimated in Appendix A). Thus, the potential advantage of computational super-resolution methods should be investigated. Maximizing the Sobel magnitude for determining the optimal focus through the focal stack slices is a simple first approach that leads to banding artifacts and does not entirely remove occluders (e.g., some tree trunks, see Supplementary Video S2). More advanced image filters that are based on defocus, color, and other context-aware image features will most likely provide better results.
Supplementary Materials
The following supplementary videos available online at zenodo.org/record/1304029: Supplementary Video S1: 3D visualization of experiment 1 (Figure 3) and Supplementary Video S2: 3D visualization of experiment 2 (Figure 4). The raw and processed (rectified and cropped) recordings and pose data for experiments 1 and 2 can be found at zenodo.org/record/1227183 and zenodo.org/record/1227246, respectively.
Author Contributions
Conceptualization, O.B.; Investigation, I.K., D.C.S. and O.B.; Project administration, O.B.; Software, I.K. and D.C.S.; Supervision, O.B.; Visualization, I.K. and D.C.S.; Writing—original draft, O.B.; Writing—review & editing, I.K., D.C.S. and O.B.
Funding
This research was funded by Austrian Science Fund (FWF) under grant number [P 28581-N33].
Acknowledgments
We thank Stefan Traxler, Christian Steingruber, and Christian Greifeneder of the OOE Landesmuseum (State Museum of Upper Austria) and OOE Landesregierung (State Government Upper Austria) for insightful discussions and for providing the LiDAR scans shown in Figure 4e.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
In the following we explain how the effective spatial sampling resolution is estimated for omnidirectional cameras and the presence of pose-estimation errors.
By back-projecting the slanted focal plane at the ground surface onto the camera’s image plane using the calibrated omnidirectional camera model and the pose estimation results, we count the number of pixels that sample the focal plane per square meter. This approximates Equation (2) for the non-uniform image resolutions of omnidirectional cameras.
For experiment 2, this was = 985 pixel/m2 for an altitude of h = 35 m and the n = 3.5 MP fraction of the image sensor that was affected by the scene portion of interest (FOVc = 80°). This implies that the size of each pixel on the focal plane was p = 3.18 × 3.18 cm. The average lateral pose estimation error e is determined by COLMAP as the average difference between back-projected image features after pose estimation and their original counterparts in the recorded images. For experiment 2, this was 1.33 pixels on the image plane (i.e., e = 4.23 cm on the focal plane). Thus, the effective size p’ of a sample on the focal plane that considers both the projected pixel size p, and a given pose-estimation error e, is p’ = p + 2e (cf. Figure A1). For experiment 2, this leads to p’ = 3.18 cm + 2 × 4.23 cm = 11.64 cm, which is equivalent to an effective spatial sampling resolution of = 74 samples/m2.
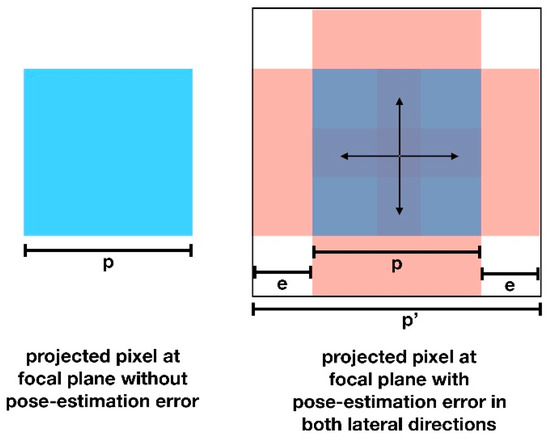
Figure A1.
The size p of a pixel projected onto the focal plane at the ground surface increases to p’ by twice the average pose-estimation error e in both lateral directions. This reduces the effective spatial sampling resolution.
Figure A2 illustrates AOS results of a known ground truth target (a multi-resolution chart of six checkerboard patterns with varying checker sizes). As in experiment 1, it was captured with a 30 m diameter synthetic aperture (vertically aligned, sampled with 135 images) from a distance of 20 m. In this case, the pixel size projected onto the focal plane was p = 1.74 × 1.74 cm (assuming a 30 × 30 m region of interest) and the pose-estimation error was e = 1.6 cm (0.94 pixels on the image plane). This leads to an effective sample size of p’ = 5.03 cm and an effective spatial sampling resolution of = 396 samples/m2. As expected, the checker size of 3 × 3 cm can still be resolved in single raw images captured by the drone, but only the 5 × 5 cm checker size can be resolved in the full-aperture AOS visualization, which combines 135 raw images at a certain pose-estimation error.
Note that the effective spatial sampling resolution does not, in general, depend on the directional sampling resolution (i.e., the number of recorded images). However, it can be expected that it increases if the pose-estimation error decreases since more images are used for structure-from-motion reconstruction.

Figure A2.
A multi-resolution chart (a) attached to a building and captured with a 30 m diameter synthetic aperture from a distance of 20 m. (b) A single raw video image captured with the drone. (c) A contrast enhanced target close-up captured in the raw image. (d) A full-aperture AOS visualization focusing on the target. (e) A contrast enhanced target close-up in the AOS visualization. All images are converted to grayscale for better comparison.
Appendix B
In the following we illustrate the influence of occlusion density, aperture size, and directional sampling resolution with respect to reconstruction quality, based on simulated data that allows for a quantitative comparison to the ground truth.
The simulation applies the same recording parameters as used for experiment 1 (Figure 3): a ground target with dimensions of 2.4 × 0.8 m, a recording altitude of 20 m, a full synthetic aperture of 30 m diameter, and an occlusion volume of 10 m³ around and above the target filled with a uniform and random distribution of 5123 (maximum) opaque voxels at various densities (simulating the occlusion by trees and other vegetation). The simulated spatial resolution (i.e., image resolution) was 5122 pixels. The simulated directional resolution (i.e., number of recorded images) was either 32, 92, or 272.
Figure A3 illustrates the influence of an increasing occlusion density at a constant spatial and directional sampling resolution (5122 × 92 in this example) and at full synthetic aperture (i.e., 30 m diameter).

Figure A3.
AOS simulation of increasing occlusion density above ground target at a 5122 × 92 sampling resolution and a full synthetic aperture of 30 m diameter. Projected occlusion voxels are green. The numbers indicate the structural similarity index (Quaternion SSIM [36]) and the PSNR with respect to the ground truth (gt).
Figure A4 illustrates the impact of various synthetic aperture diameters (30 m, 15 m, and pinhole, which approximates a single recording of the drone) and directional sampling resolutions within the selected synthetic aperture (32, 92, and 272 perspectives) at a constant occlusion density (50% in this example).

Figure A4.
AOS simulation of various synthetic aperture diameters (pinhole = single drone recording, 15 m, and 30 m) and directional sampling resolutions within the selected synthetic aperture (32, 92, and 272 perspectives). The occlusion density is 50%. Projected occlusion voxels are green. The numbers indicate the structural similarity index (Quaternion SSIM [38]) and the PSNR with respect to the ground truth.
From the simulation results presented in Figure A3 and Figure A4 it can be seen that an increasing occlusion density leads to a degradation of reconstruction quality. However, a wider synthetic aperture diameter and a higher number of perspective recordings within this aperture always lead to an improvement of reconstruction quality as occluders are blurred more efficiently. Consequently, densely occluded scenes have to be captured with wide synthetic apertures at high directional sampling rates.
References
- Rempel, R.C.; Parker, A.K. An information note on an airborne laser terrain profiler for micro-relief studies. In Proceedings of the Symposium Remote Sensing Environment, 3rd ed.; University of Michigan Institute of Science and Technology: Ann Arbor, MI, USA, 1964; pp. 321–337. [Google Scholar]
- Nelson, R. How did we get here? An early history of forestry lidar. Can. J. Remote Sens. 2013, 39, S6–S17. [Google Scholar] [CrossRef]
- Sabatini, R.; Richardson, M.A.; Gardi, A.; Ramasamy, S. Airborne laser sensors and integrated systems. Prog. Aerosp. Sci. 2015, 79, 15–63. [Google Scholar] [CrossRef]
- Kulawardhana, R.W.; Popescu, S.C.; Feagin, R.A. Airborne lidar remote sensing applications in non-forested short stature environments: A review. Ann. For. Res. 2017, 60, 173–196. [Google Scholar] [CrossRef]
- Synge, E. XCI. A method of investigating the higher atmosphere. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1930, 9, 1014–1020. [Google Scholar] [CrossRef]
- Vasyl, M.; Paul, F.M.; Ove, S.; Takao, K.; Chen, W.B. Laser radar: Historical prospective—From the East to the West. Opt. Eng. 2016, 56, 031220. [Google Scholar] [CrossRef]
- Behroozpour, B.; Sandborn, P.A.M.; Wu, M.C.; Boser, B.E. Lidar System Architectures and Circuits. IEEE Commun. Mag. 2017, 55, 135–142. [Google Scholar] [CrossRef]
- Du, B.; Pang, C.; Wu, D.; Li, Z.; Peng, H.; Tao, Y.; Wu, E.; Wu, G. High-speed photon-counting laser ranging for broad range of distances. Sci. Rep. 2018, 8, 4198. [Google Scholar] [CrossRef] [PubMed]
- Chase, A.F.; Chase, D.Z.; Weishampel, J.F.; Drake, J.B.; Shrestha, R.L.; Slatton, K.C.; Awe, J.J.; Carter, W.E. Airborne LiDAR, archaeology, and the ancient Maya landscape at Caracol, Belize. J. Archaeol. Sci. 2011, 38, 387–398. [Google Scholar] [CrossRef]
- Khan, S.; Aragão, L.; Iriarte, J. A UAV–lidar system to map Amazonian rainforest and its ancient landscape transformations. Int. J. Remote Sens. 2017, 38, 2313–2330. [Google Scholar] [CrossRef]
- Inomata, T.; Triadan, D.; Pinzón, F.; Burham, M.; Ranchos, J.L.; Aoyama, K.; Haraguchi, T. Archaeological application of airborne LiDAR to examine social changes in the Ceibal region of the Maya lowlands. PLoS ONE 2018, 13, 1–37. [Google Scholar] [CrossRef] [PubMed]
- Maltamo, M.; Naesset, E.; Vauhkonen, J. Forestry Applications of Airborne Laser Scanning: Concepts and Case Studies. In Managing Forest Ecosystems; Springer: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Sterenczak, K.; Ciesielski, M.; Balazy, R.; Zawiła-Niedzwiecki, T. Comparison of various algorithms for DTM interpolation from LIDAR data in dense mountain forests. Eur. J. Remote Sens. 2016, 49, 599–621. [Google Scholar] [CrossRef]
- Chen, Z.; Gao, B.; Devereux, B. State-of-the-Art: DTM Generation Using Airborne LIDAR Data. Sensors 2017, 17, 150. [Google Scholar] [CrossRef] [PubMed]
- Nagai, M.; Chen, T.; Shibasaki, R.; Kumagai, H.; Ahmed, A. UAV-Borne 3-D Mapping System by Multisensor Integration. IEEE Trans. Geosci. Remote Sens. 2009, 47, 701–708. [Google Scholar] [CrossRef]
- Lin, Y.; Hyyppa, J.; Jaakkola, A. Mini-UAV-Borne LIDAR for Fine-Scale Mapping. IEEE Geosci. Remote Sens. Lett. 2011, 8, 426–430. [Google Scholar] [CrossRef]
- Favorskaya, M.; Jain, L. Handbook on Advances in Remote Sensing and Geographic Information Systems: Paradigms and Applications in Forest Landscape Modeling. In Intelligent Systems Reference Library; Springer International Publishing: New York, NY, USA, 2017. [Google Scholar]
- Kwon, S.; Park, J.W.; Moon, D.; Jung, S.; Park, H. Smart Merging Method for Hybrid Point Cloud Data using UAV and LIDAR in Earthwork Construction. Procedia Eng. 2017, 196, 21–28. [Google Scholar] [CrossRef]
- Chiang, K.W.; Tsai, G.J.; Li, Y.H.; El-Sheimy, N. Development of LiDAR-Based UAV System for Environment Reconstruction. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1790–1794. [Google Scholar] [CrossRef]
- Wallace, L.; Lucieer, A.; Malenovský, Z.; Turner, D.; Vopenka, P. Assessment of Forest Structure Using Two UAV Techniques: A Comparison of Airborne Laser Scanning and Structure from Motion (SfM) Point Clouds. Forests 2016, 7, 62. [Google Scholar] [CrossRef]
- Guo, Q.; Su, Y.; Hu, T.; Zhao, X.; Wu, F.; Li, Y.; Liu, J.; Chen, L.; Xu, G.; Lin, G.; et al. An integrated UAV-borne lidar system for 3D habitat mapping in three forest ecosystems across China. Int. J. Remote Sens. 2017, 38, 2954–2972. [Google Scholar] [CrossRef]
- Streibl, N. Three-dimensional imaging by a microscope. J. Opt. Soc. Am. A 1985, 2, 121–127. [Google Scholar] [CrossRef]
- Conchello, J.A.; Lichtman, J.W. Optical sectioning microscopy. Nat. Methods 2005, 2, 920–931. [Google Scholar] [CrossRef] [PubMed]
- Qian, J.; Lei, M.; Dan, D.; Yao, B.; Zhou, X.; Yang, Y.; Yan, S.; Min, J.; Yu, X. Full-color structured illumination optical sectioning microscopy. Sci. Rep. 2015, 5, 14513. [Google Scholar] [CrossRef] [PubMed]
- Ryle, M.; Vonberg, D.D. Solar Radiation on 175 Mc./s. Nature 1946, 158, 339. [Google Scholar] [CrossRef]
- Wiley, C.A. Synthetic aperture radars. IEEE Trans. Aerosp. Electron. Syst. 1985, AES-21, 440–443. [Google Scholar] [CrossRef]
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Ouchi, K. Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics. Remote Sens. 2013, 5, 716–807. [Google Scholar] [CrossRef]
- Li, C.J.; Ling, H. Synthetic aperture radar imaging using a small consumer drone. In Proceedings of the 2015 IEEE International Symposium on Antennas and Propagation USNC/URSI National Radio Science Meeting, Vancouver, BC, Canada, 19–25 July 2015; pp. 685–686. [Google Scholar]
- Baldwin, J.E.; Beckett, M.G.; Boysen, R.C.; Burns, D.; Buscher, D.; Cox, G.; Haniff, C.A.; Mackay, C.D.; Nightingale, N.S.; Rogers, J.; et al. The first images from an optical aperture synthesis array: Mapping of Capella with COAST at two epochs. Astron. Astrophys. 1996, 306, L13–L16. [Google Scholar]
- Turpin, T.M.; Gesell, L.H.; Lapides, J.; Price, C.H. Theory of the synthetic aperture microscope. In Proceedings of the SPIE’s 1995 International Symposium on Optical Science, Engineering, and Instrumentation, San Diego, CA, USA, 9–14 July 1995; Volume 2566. [Google Scholar]
- Levoy, M.; Zhang, Z.; Mcdowall, I. Recording and controlling the 4D light field in a microscope using microlens arrays. J. Microsc. 2009, 235, 144–162. [Google Scholar] [CrossRef] [PubMed]
- Vaish, V.; Wilburn, B.; Joshi, N.; Levoy, M. Using plane + parallax for calibrating dense camera arrays. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 27 June–2 July 2004; Volume 1, pp. 2–9. [Google Scholar]
- Levoy, M.; Hanrahan, P. Light Field Rendering. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’96, New Orleans, LA, USA, 4–9 August 1996; ACM: New York, NY, USA, 1996; pp. 31–42. [Google Scholar]
- Isaksen, A.; McMillan, L.; Gortler, S.J. Dynamically reparameterized light fields. In Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’00, 2000, New Orleans, LA, USA, 23—28 July 2000; ACM: New York, NY, USA, 2000; pp. 297–306. [Google Scholar]
- Schoenberger, J.L.; Frahm, J.-M. Structure-from-Motion Revisited. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar] [CrossRef]
- Pentland, A.P. A new sense for depth of field. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 4, 523–531. [Google Scholar] [CrossRef]
- Kolaman, A.; Yadid-Pecht, O. Quaternion Structural Similarity: A New Quality Index for Color Images. IEEE Trans. Image Process. 2012, 21, 1526–1536. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).