Radio Frequency Modeling of Receive Coil Arrays for Magnetic Resonance Imaging
Abstract
:1. Introduction
2. Theory
2.1. SNR Calculation
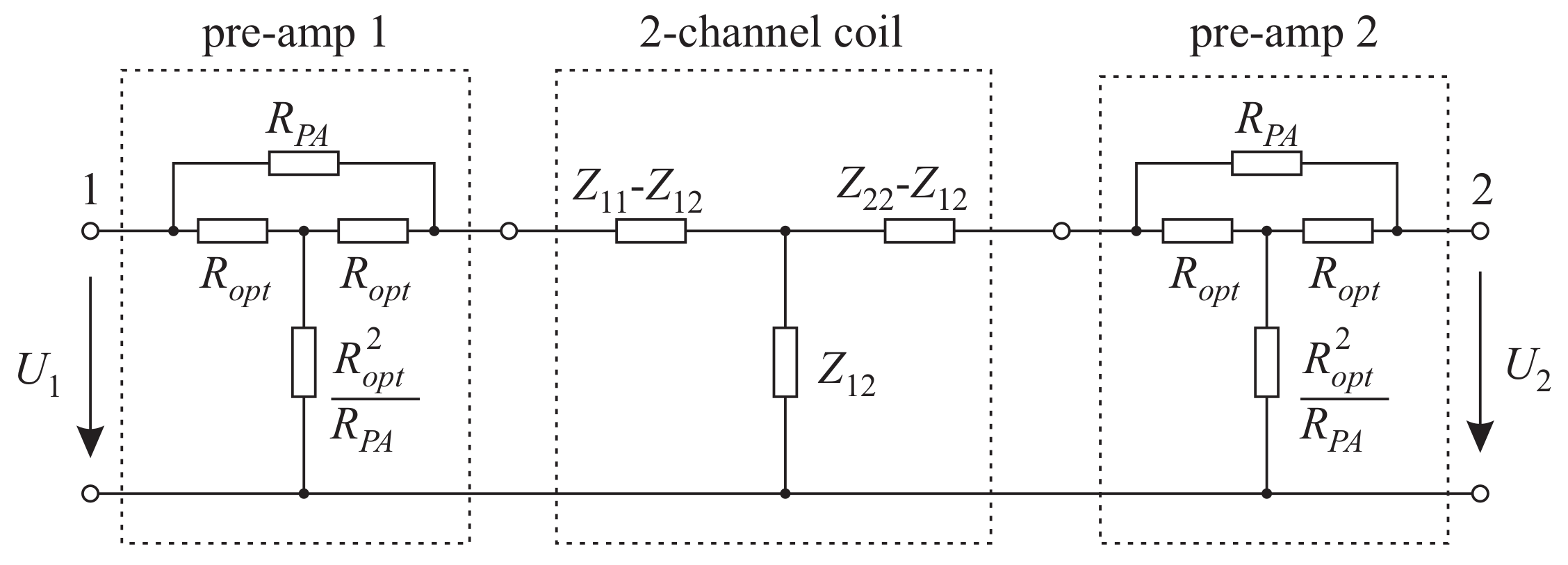
2.2. Pre-Amplifier Noise Model
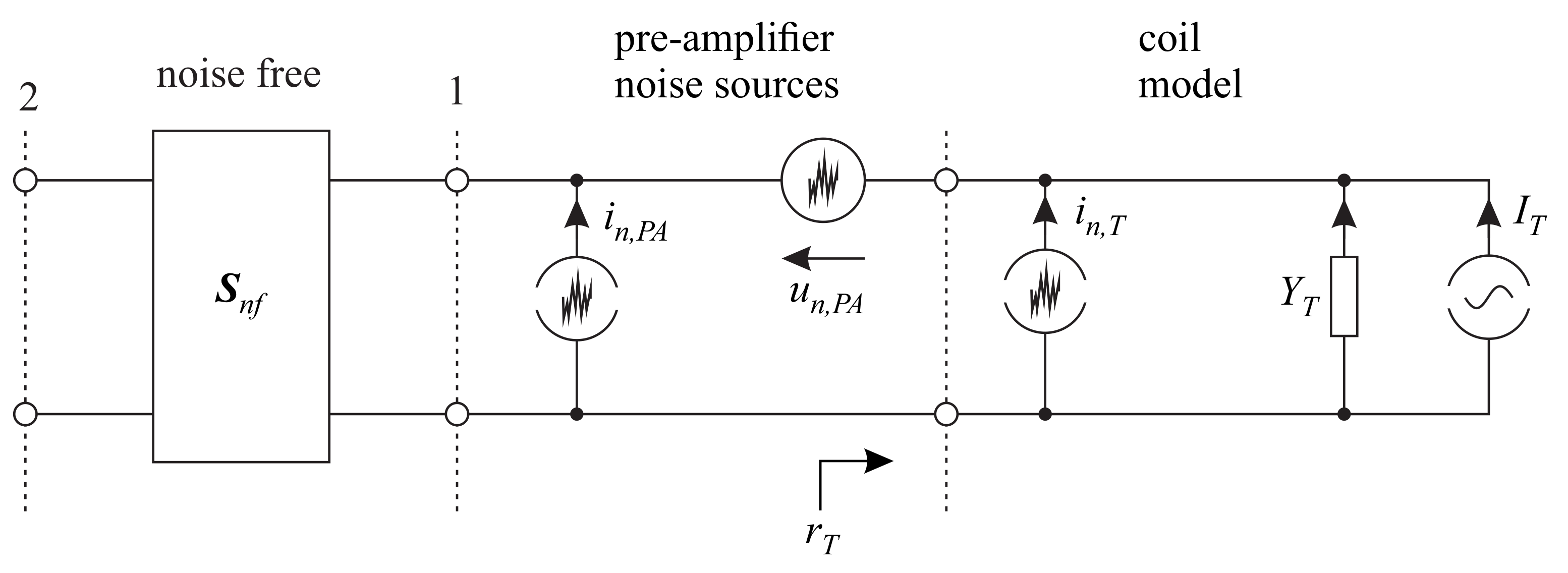
2.2.1. Single-Channel Noise Model
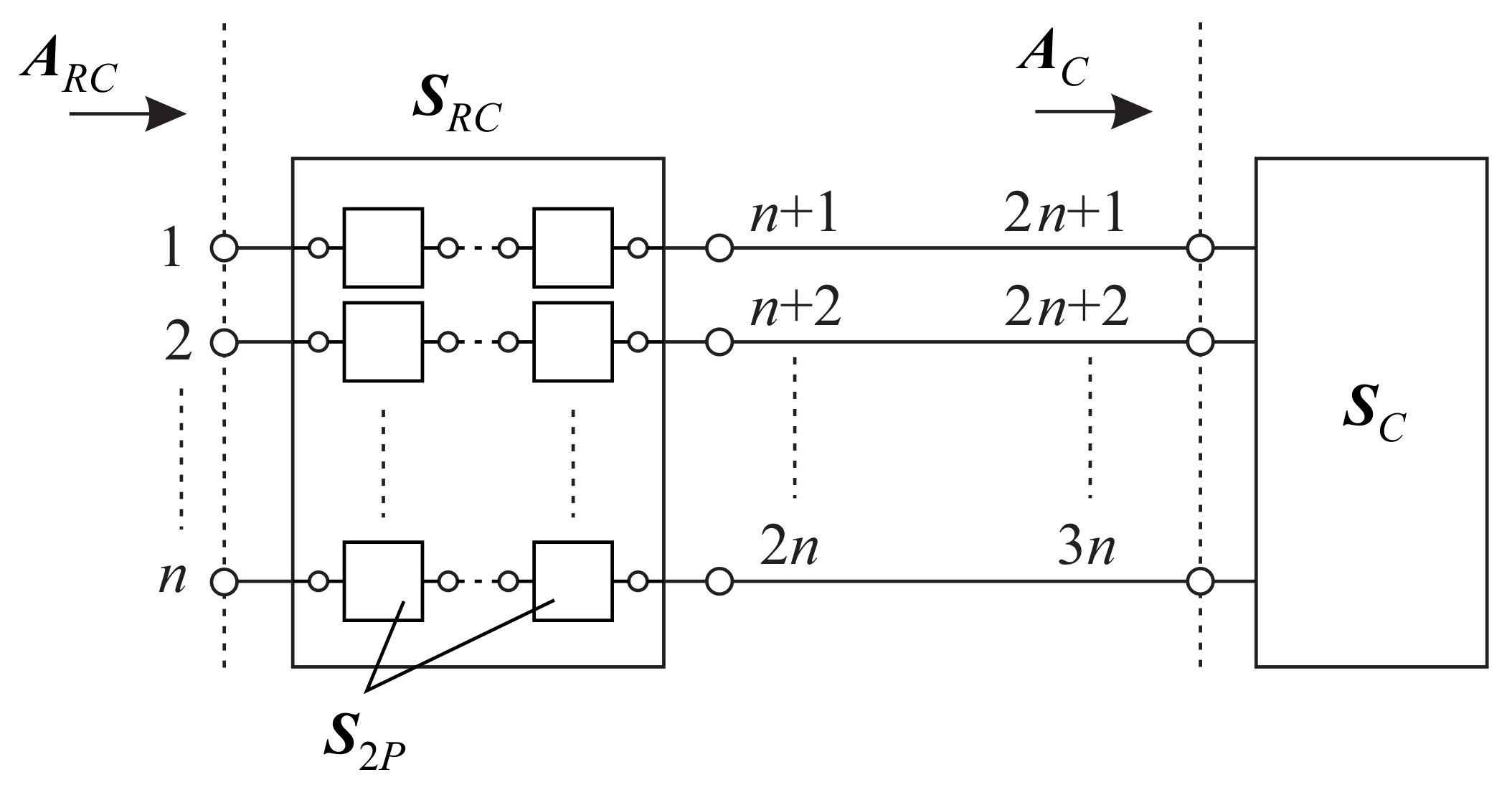
2.2.2. Multiple-Channel Noise Model
3. Methods
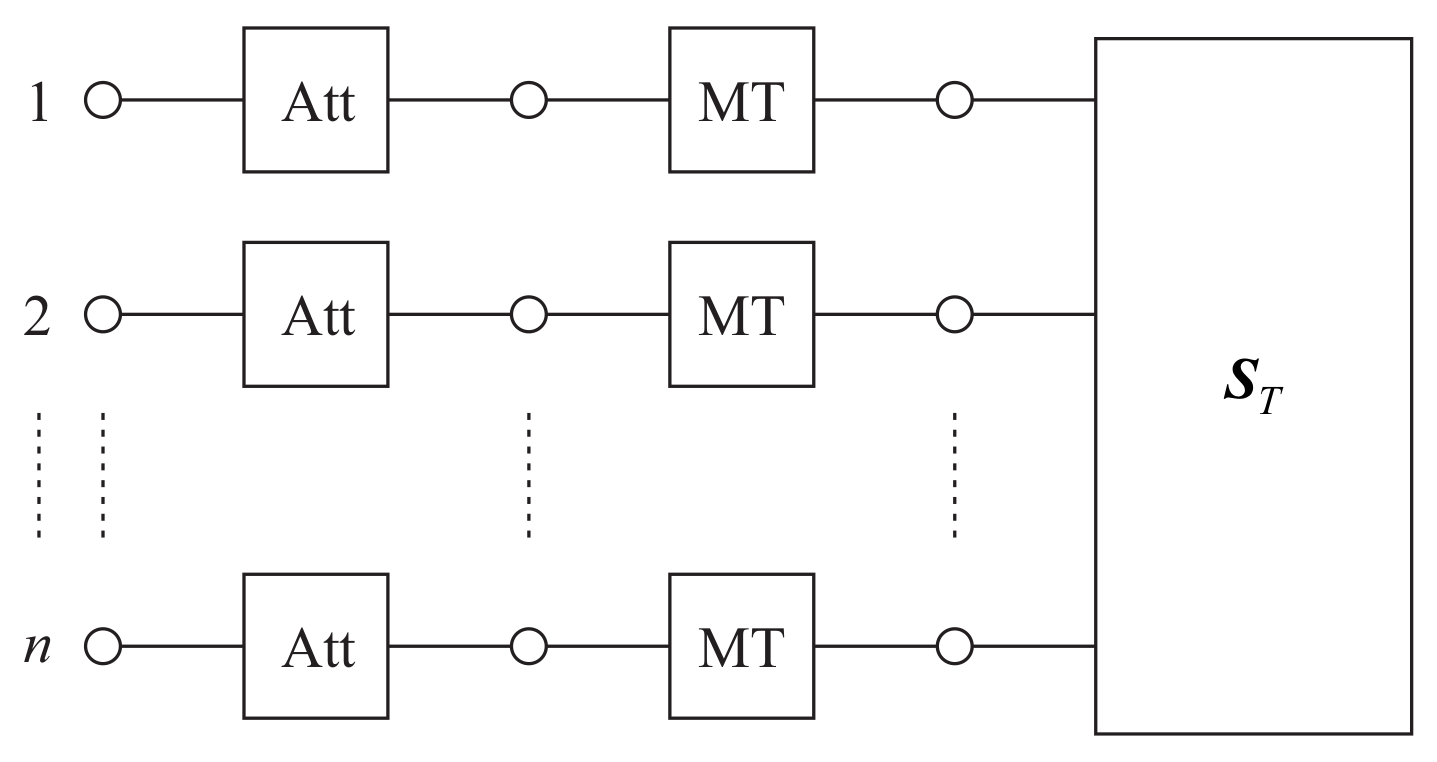
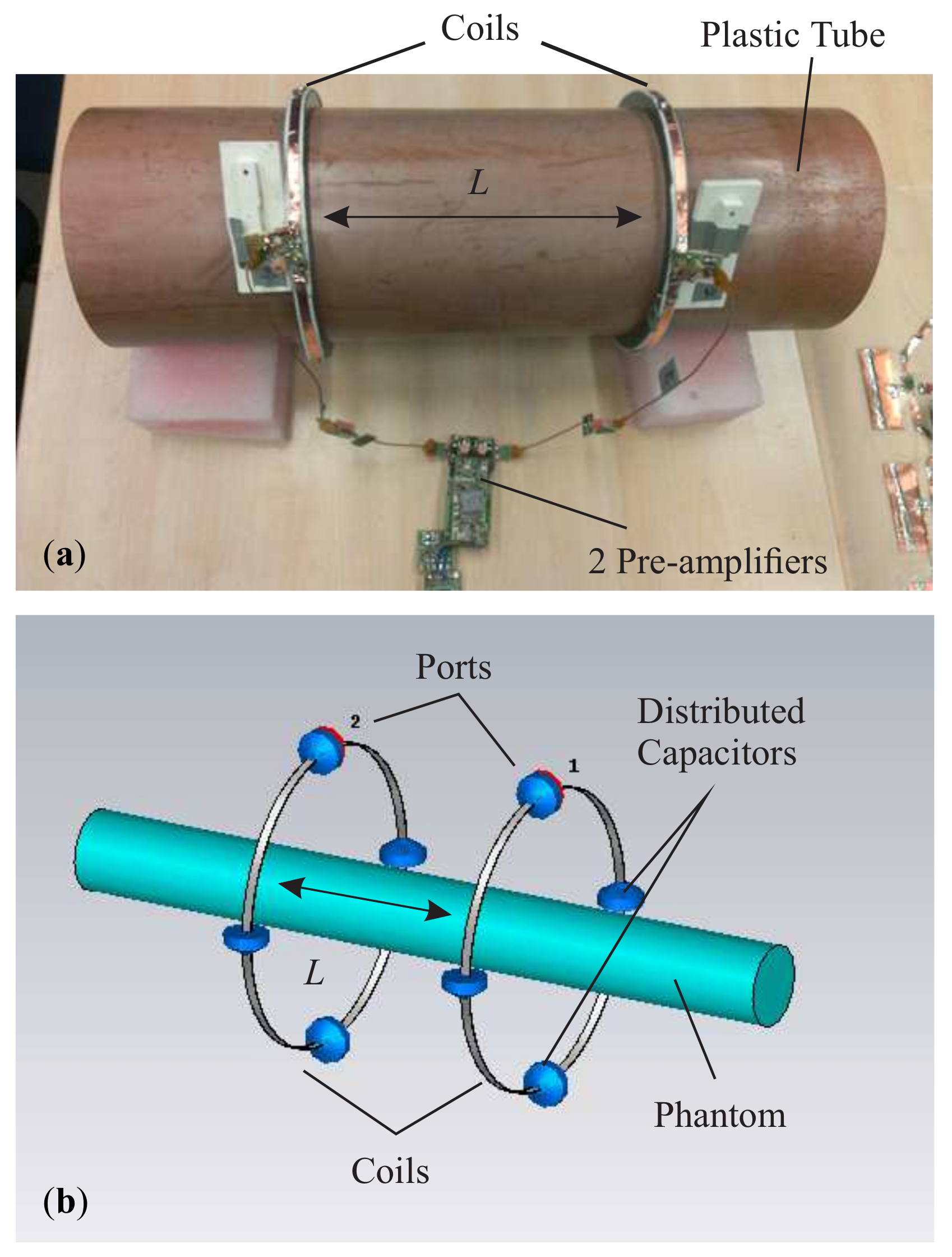
3.1. Modeling and Measurement of Receive Coil Arrays
3.1.1. Coil Array With Two and Four Elements
3.1.2. Electromagnetic Field Simulation
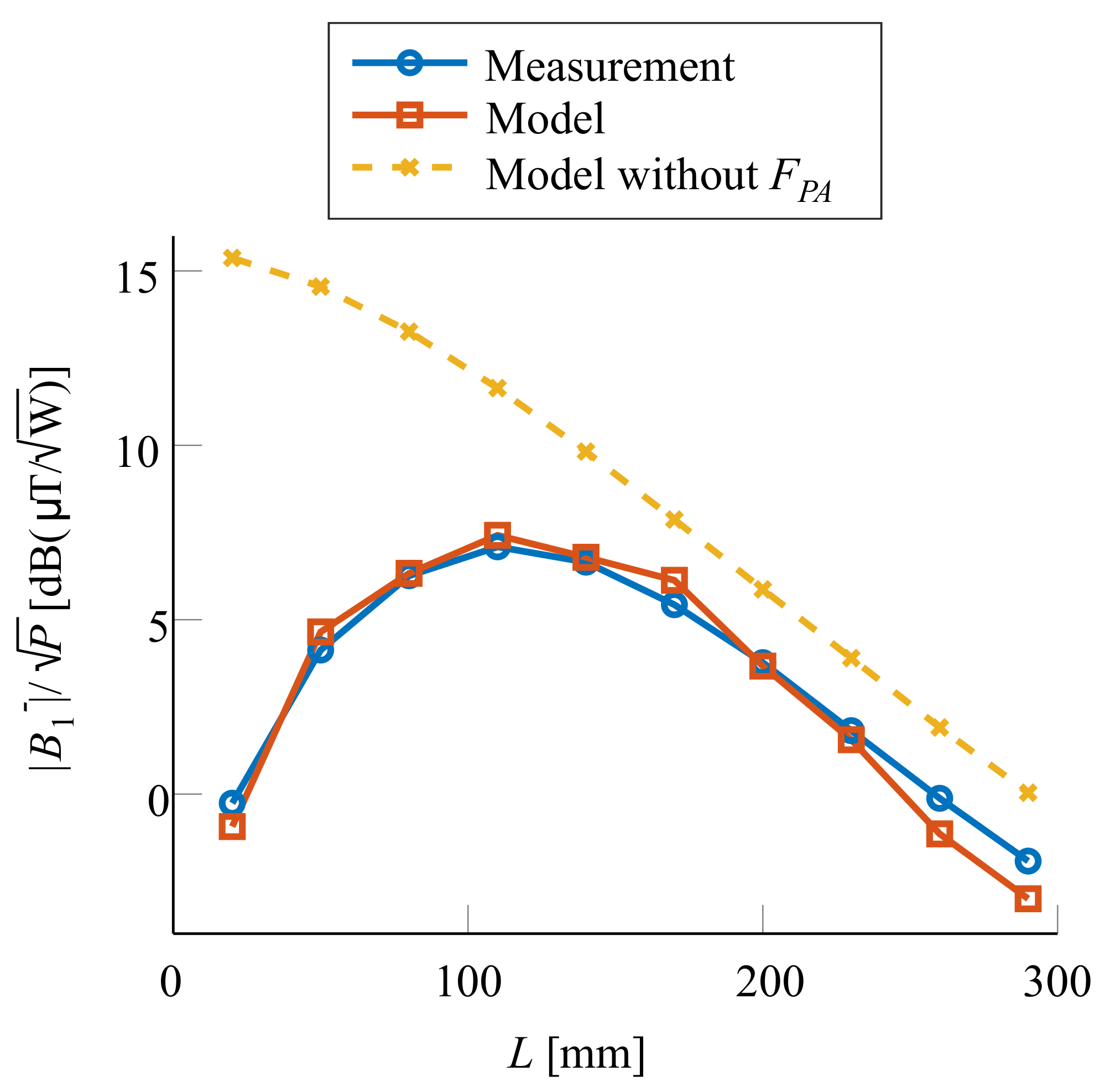
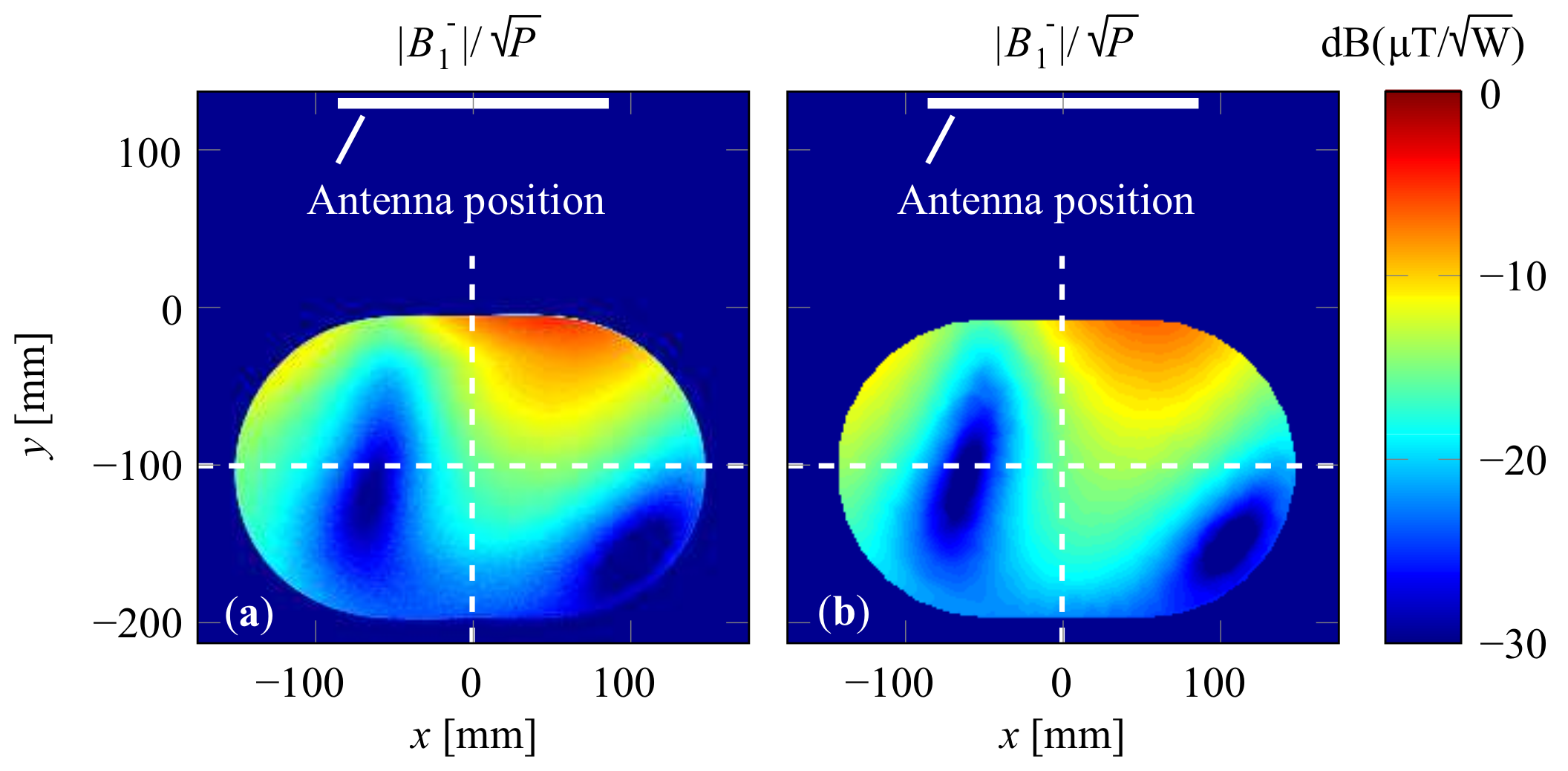
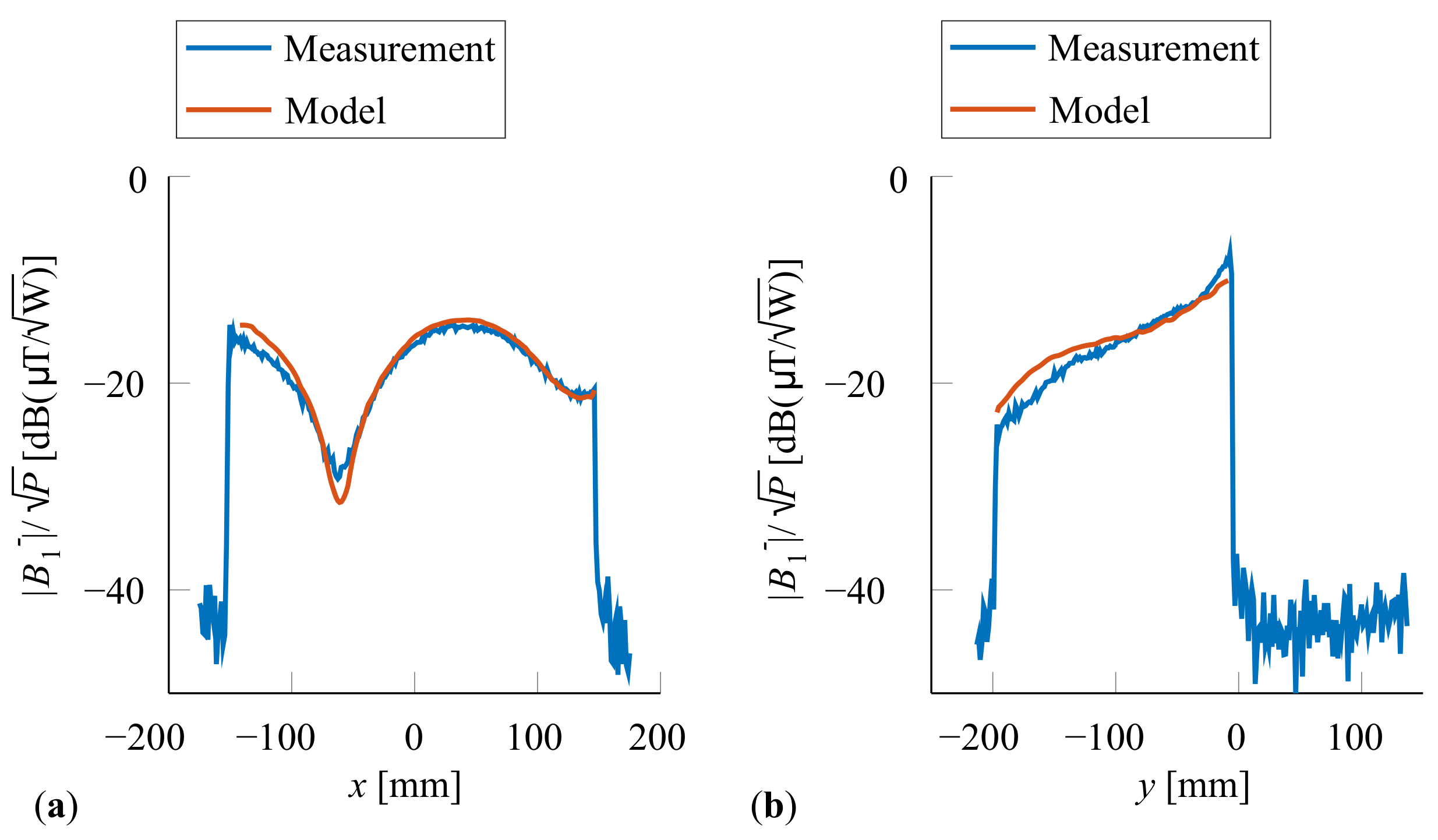
4. Results
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Schnell, W.; Renz, W.; Vester, M.; Ermert, H. Ultimate signal-to-noise-ratio of surface and body antennas for magnetic resonance imaging. IEEE Trans. Antennas Propag. 2000, 48, 418–428. [Google Scholar] [CrossRef]
- Reykowski, A. Theory and Design of Synthesis Array Coils for Magnetic Resonance Imaging. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 1996. [Google Scholar]
- Collins, C.M.; Smith, M.B. Calculations of B1 distribution, SNR, and SAR for a surface coil adjacent to an anatomically-accurate human body model. Magn. Reson. Med. 2001, 45, 692–699. [Google Scholar] [CrossRef] [PubMed]
- Collins, C.M.; Wang, Z. Calculation of radiofrequency electromagnetic fields and their effects in MRI of human subjects. Magn. Reson. Med. 2011, 65, 1470–1482. [Google Scholar] [CrossRef] [PubMed]
- Kunz, K.; Luebbers, R. The Finite Difference Time Domain Method for Electromagnetics; Taylor & Francis: Abingdon, UK, 1993. [Google Scholar]
- Hoult, D.; Richards, R. The signal-to-noise ratio of the nuclear magnetic resonance experiment. J. Magn. Reson. 1976, 24, 71–85. [Google Scholar] [CrossRef]
- Giovannetti, G.; Viti, V.; Liu, Y.; Yu, W.; Mittra, R.; Landini, L.; Benassi, A. An accurate simulator for magnetic resonance coil sensitivity estimation. Concepts Magn. Reson. Part B Magn. Reson. Eng. 2008, 33B, 209–215. [Google Scholar] [CrossRef]
- Rojas, R.; Rodriguez, A.O. Numerical Study of the SNR and SAR of MRI Coil Arrays. In Proceedings of the 2007 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 1196–1199. [Google Scholar]
- Chen, Z.; Solbach, K.; Erni, D.; Rennings, A. Improving B1 Efficiency and Signal-to-Noise-Ratio of a Surface Coil by a High-Impedance-Surface RF Shield for 7-T Magnetic Resonance Imaging. IEEE Trans. Microw. Theory Tech. 2017, 65, 988–997. [Google Scholar] [CrossRef]
- Paska, J.; Froehlich, J.; Brunner, D.O.; Pruessmann, K.P.; Vahldieck, R. Field Superposition Method for RF coil design. Proc. Int. Soc. Magn. Reson. Med. 2009, 17, 3038. [Google Scholar]
- Kozlov, M.; Turner, R. Fast MRI coil analysis based on 3-D electromagnetic and RF circuit co-simulation. J. Magn. Reson. 2009, 200, 147–152. [Google Scholar] [CrossRef] [PubMed]
- Malzacher, M.; Vester, M.; Rehner, R.; Stumpf, C.; Korf, P. SNR simulations including coupled preamplifier noise. Proc. Int. Soc. Magn. Reson. Med. 2016, 24, 2157. [Google Scholar]
- Vester, M.; Biber, S.; Rehner, R.; Brown, R.; Wiggins, G.; Sodickson, D. Mitigation of Inductive Coupling in Array Coils by Wideband Port Matching. Proc. Int. Soc. Magn. Reson. Med. 2012, 20, 2689. [Google Scholar]
- Stumpf, C.; Rehner, R.; Martius, S.; Vester, M.; Engelbrecht, R.; Schmidt, L.P. Calibration of Electromagnetic Field Simulations of MR Coil Arrays for Accurate Quantitative Comparison with the Measured Image SNR. Proc. Int. Soc. Magn. Reson. Med. 2012, 20, 2684. [Google Scholar]
- Roemer, P.B.; Edelstein, W.A.; Hayes, C.E.; Souza, S.P.; Mueller, O.M. The NMR phased array. Magn. Reson. Med. 1990, 16, 192–225. [Google Scholar] [CrossRef] [PubMed]
- Rothe, H.; Dahlke, W. Theory of noisy fourpoles. Proc. IRE 1956, 44, 811–818. [Google Scholar] [CrossRef]
- Bosma, H. On the Theory of Linear Noisy Systems; Philips Research Reports; Philips Research Laboratories: Eindhoven, The Netherlands, 1967. [Google Scholar]
- Vendelin, G.; Pavio, A.; Rohde, U. Microwave Circuit Design Using Linear and Nonlinear Techniques; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Pozar, D. Microwave Engineering; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar]
- Brown, R.; Lakshmanan, K.; Madelin, G.; Alon, L.; Chang, G.; Sodickson, D.K.; Regatte, R.R.; Wiggins, G.C. A flexible nested sodium and proton coil array with wideband matching for knee cartilage MRI at 3T. Magn. Reson. Med. 2015, 76, 1325–1334. [Google Scholar] [CrossRef] [PubMed]
- Findeklee, C.; Duensing, R.; Reykowski, A. Simulating Array SNR And Effective Noise Figure In Dependence Of Noise Coupling. Proc. Int. Soc. Magn. Reson. Med. 2011, 19, 1883. [Google Scholar]
- Stogryn, A. Equations for Calculating the Dielectric Constant of Saline Water (Correspondence). IEEE Trans. Microw. Theory Tech. 1971, 19, 733–736. [Google Scholar] [CrossRef]
- Sodickson, D.K.; Zhang, B.; Duan, Q.; Brown, R.; Lattanzi, R.; Lakshmanan, K.; Vaidya, M.V.; Yang, A.; Rehner, R.; Vester, M.; et al. Is a ’one size fits all’ many-element bore-lining remote body array feasible for routine imaging? Proc. Int. Soc. Magn. Reson. Med. 2014, 22, 618. [Google Scholar]
- Sodickson, D.; Biber, S.; Renz, W.; Schnell, W.; Vester, M. Remote Body Arrays for High-Performance Magnetic Resonance Imaging and Spectroscopy. WO 2,010,097,375 A2, 2 September 2010. [Google Scholar]
- Ernst, R.R.; Anderson, W.A. Application of Fourier Transform Spectroscopy to Magnetic Resonance. Rev. Sci. Instrum. 1966, 37, 93–102. [Google Scholar] [CrossRef]
- Jin, J. The Finite Element Method in Electromagnetics; Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]


| Noise Parameter | Mean Value | Standard Deviation |
|---|---|---|
| 0.47 | 0.02 | |
| 4.10 | 0.58 | |
| 0.10 | 0.02 | |
| −0.36 | 0.03 |
| S-Parameter | Measurement | Model |
|---|---|---|
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stumpf, C.; Malzacher, M.; Schmidt, L.-P. Radio Frequency Modeling of Receive Coil Arrays for Magnetic Resonance Imaging. J. Imaging 2018, 4, 67. https://doi.org/10.3390/jimaging4050067
Stumpf C, Malzacher M, Schmidt L-P. Radio Frequency Modeling of Receive Coil Arrays for Magnetic Resonance Imaging. Journal of Imaging. 2018; 4(5):67. https://doi.org/10.3390/jimaging4050067
Chicago/Turabian StyleStumpf, Christopher, Matthias Malzacher, and Lorenz-Peter Schmidt. 2018. "Radio Frequency Modeling of Receive Coil Arrays for Magnetic Resonance Imaging" Journal of Imaging 4, no. 5: 67. https://doi.org/10.3390/jimaging4050067
APA StyleStumpf, C., Malzacher, M., & Schmidt, L.-P. (2018). Radio Frequency Modeling of Receive Coil Arrays for Magnetic Resonance Imaging. Journal of Imaging, 4(5), 67. https://doi.org/10.3390/jimaging4050067





