Modelling of Orthogonal Craniofacial Profiles †
Abstract
:1. Introduction
2. Related Work
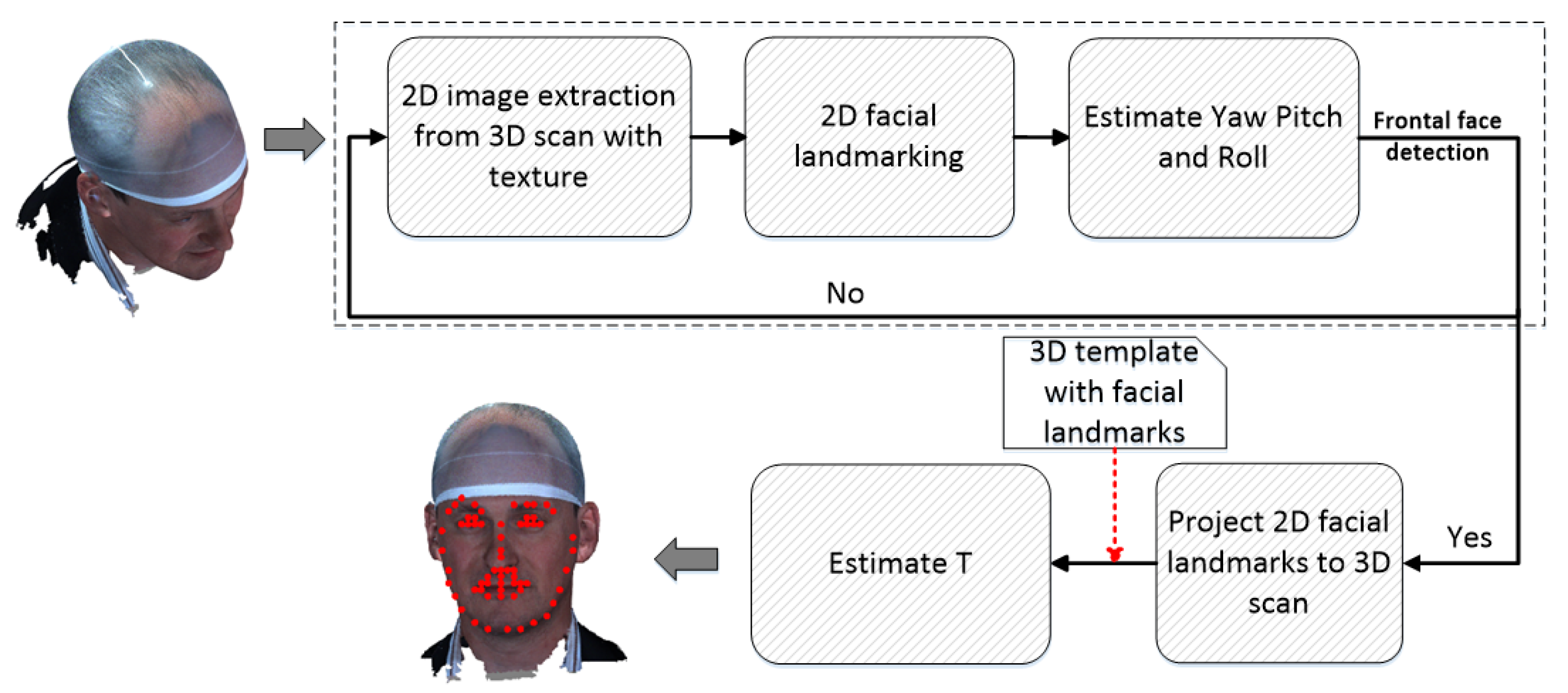
3. Model Construction Pipeline
- (i)
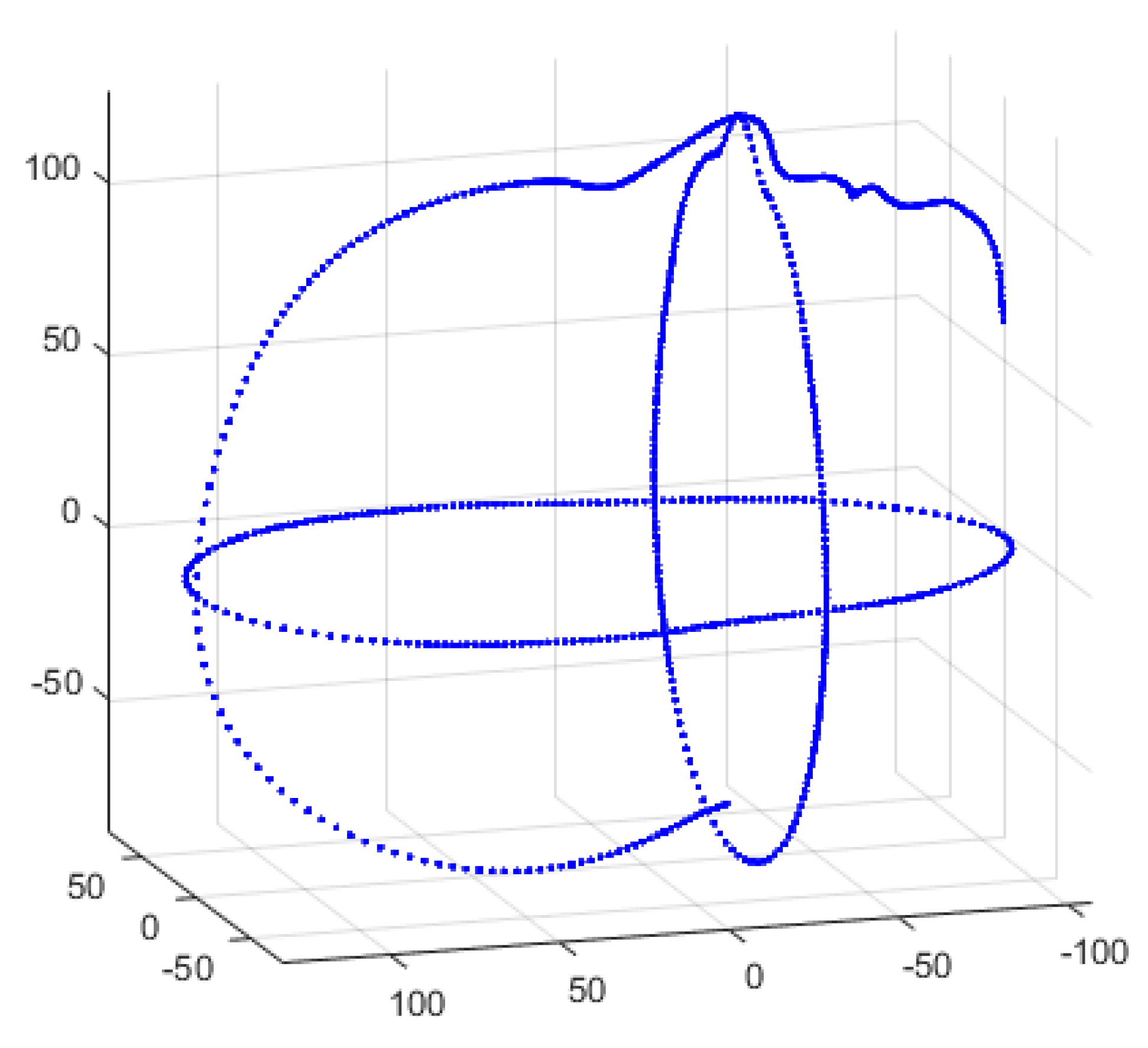
- 2D shape extraction: The raw 3D scan from the Headspace dataset undergoes pose normalization and preprocessing to remove redundant data (lower neck and shoulder area), and the 2D profile shape is extracted as closed contours from three orthogonal viewpoints: the side view, top view and frontal view (note that we automatically remove the ears in the top and frontal views, as it is difficult to get good correspondences over this section of the profiles).
- (ii)
- Dense correspondence establishment: A collection of profiles from a given viewpoint is reparametrised into a form where each profile has the same number of points joined into a connectivity that is shared across all profiles.
- (iii)
- Similarity alignment and statistical modelling: The collection of profiles in dense correspondence are subjected to Generalised Procrustes Analysis (GPA) to remove similarity effects (rotation, translation and scale), leaving only shape information. The processed meshes are statistically analysed, typically with PCA, generating a 2D morphable model expressed using a linear basis of eigen shapes. This allows for the generation of novel shape instances, over any of the three viewpoints.
3.1. 2D Shape Extraction
3.1.1. Pose Normalisation
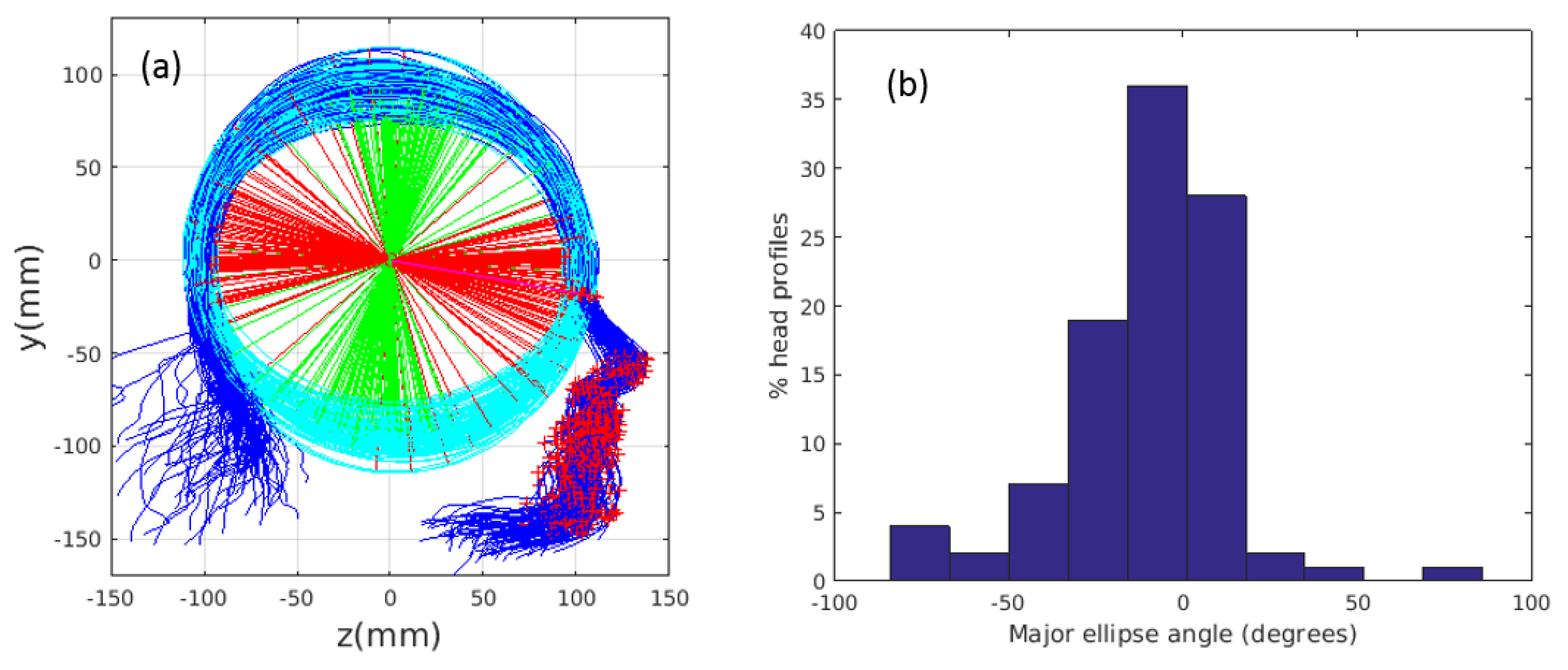
3.1.2. Cropping
3.1.3. Edge Detection
3.1.4. Automatic Annotation
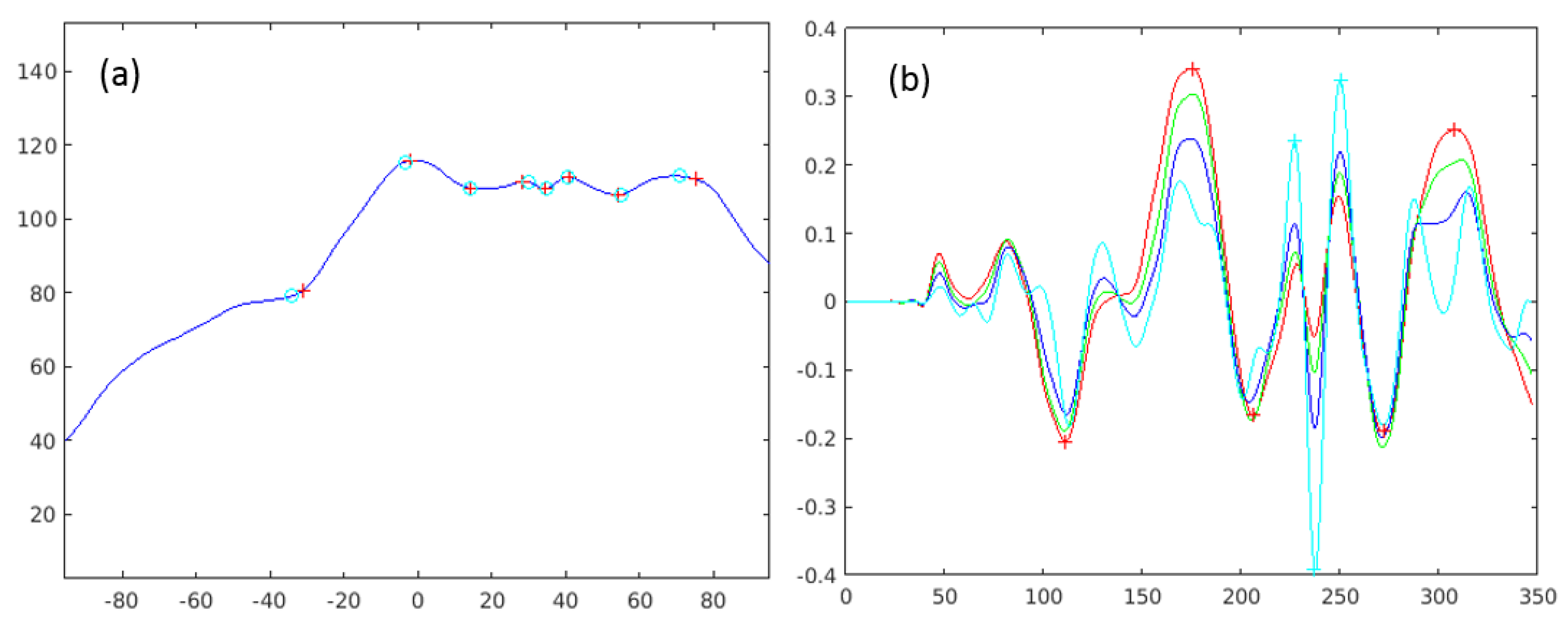
3.2. Correspondence Establishment
3.3. Similarity Alignment
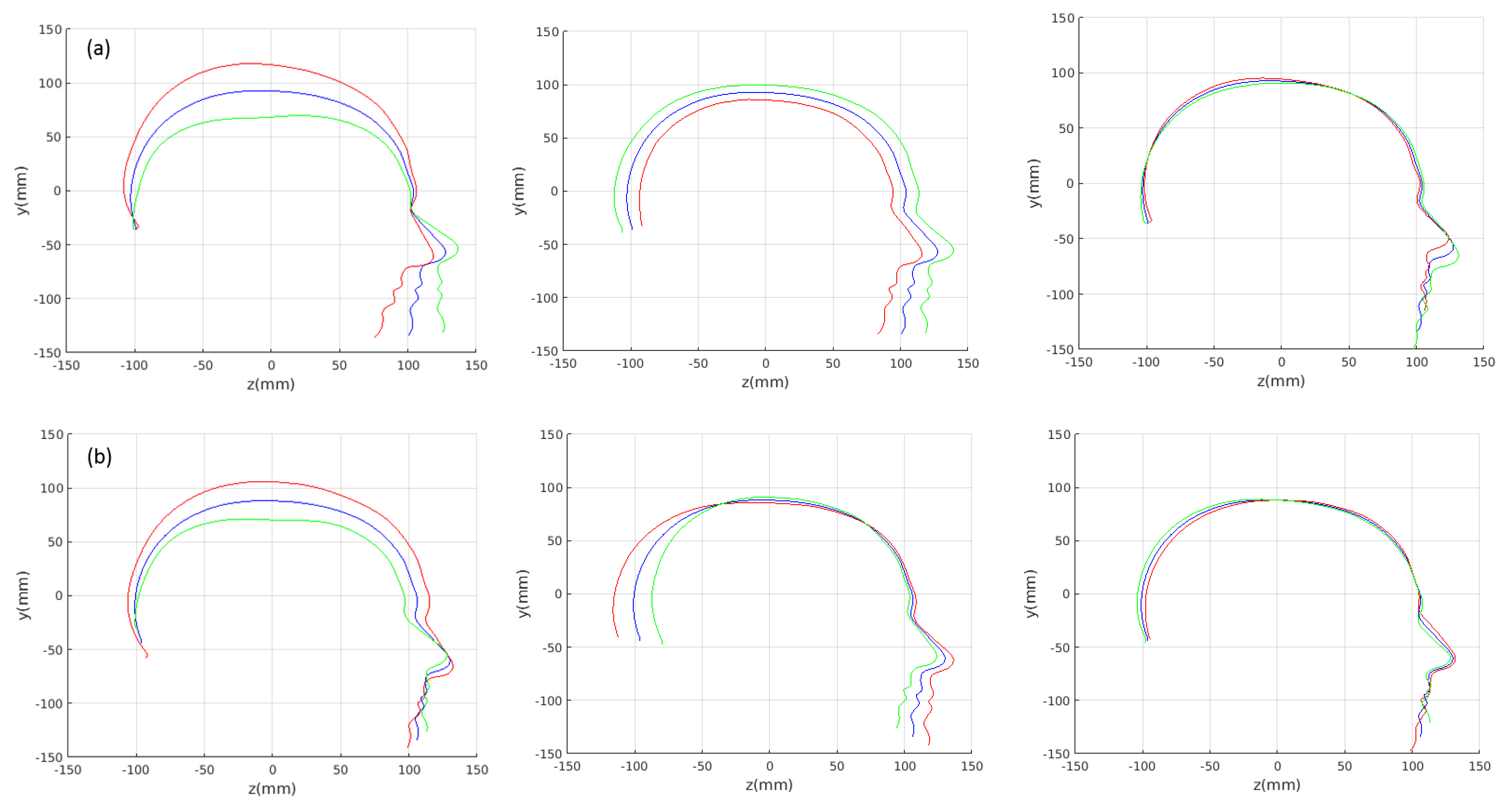
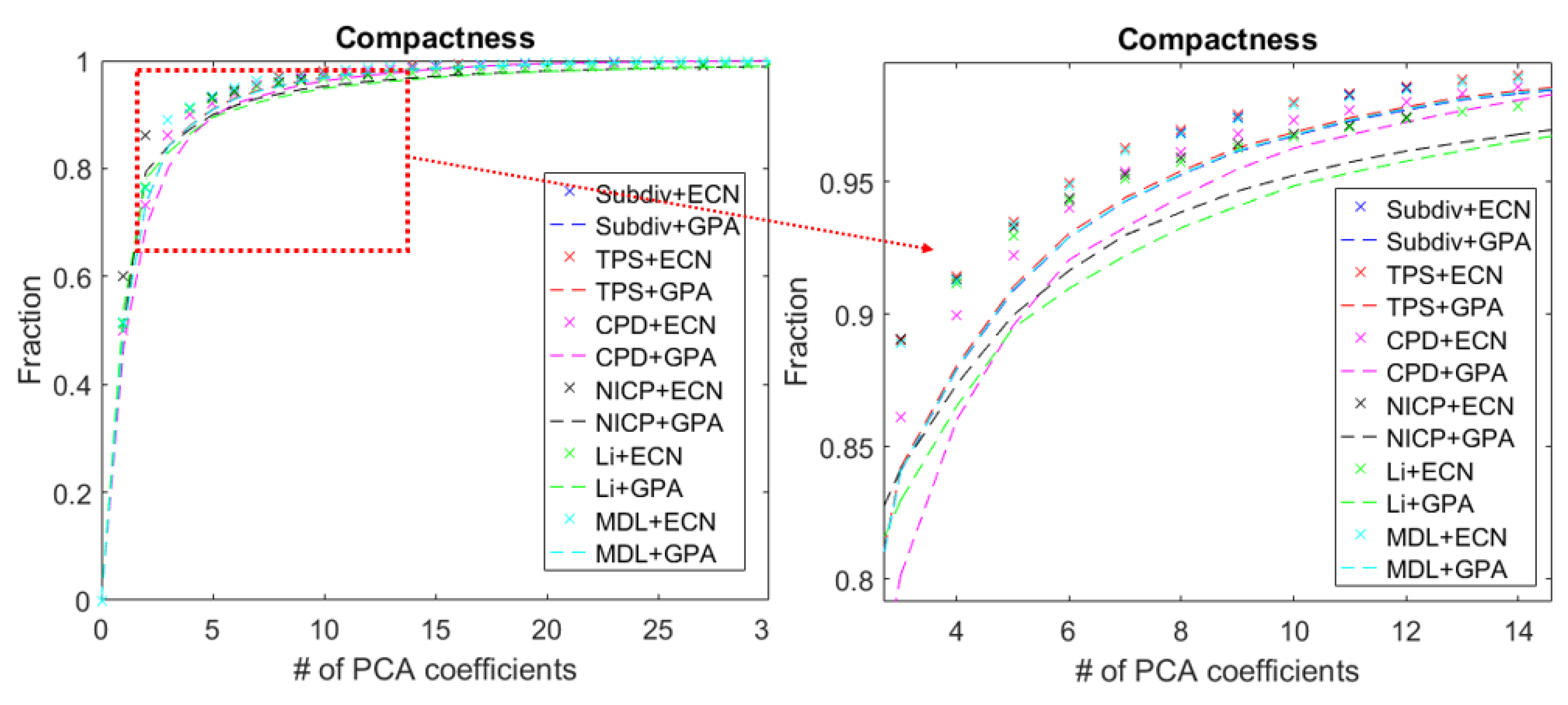
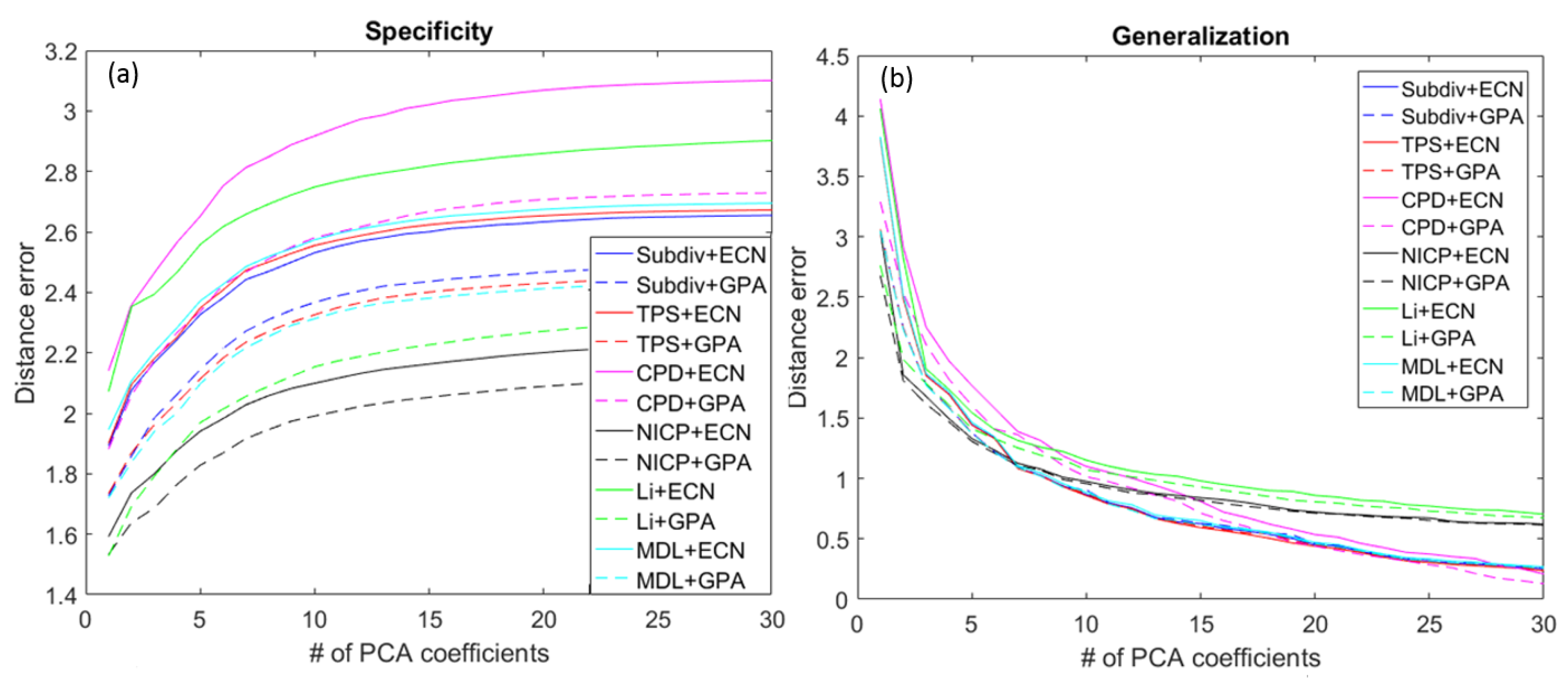
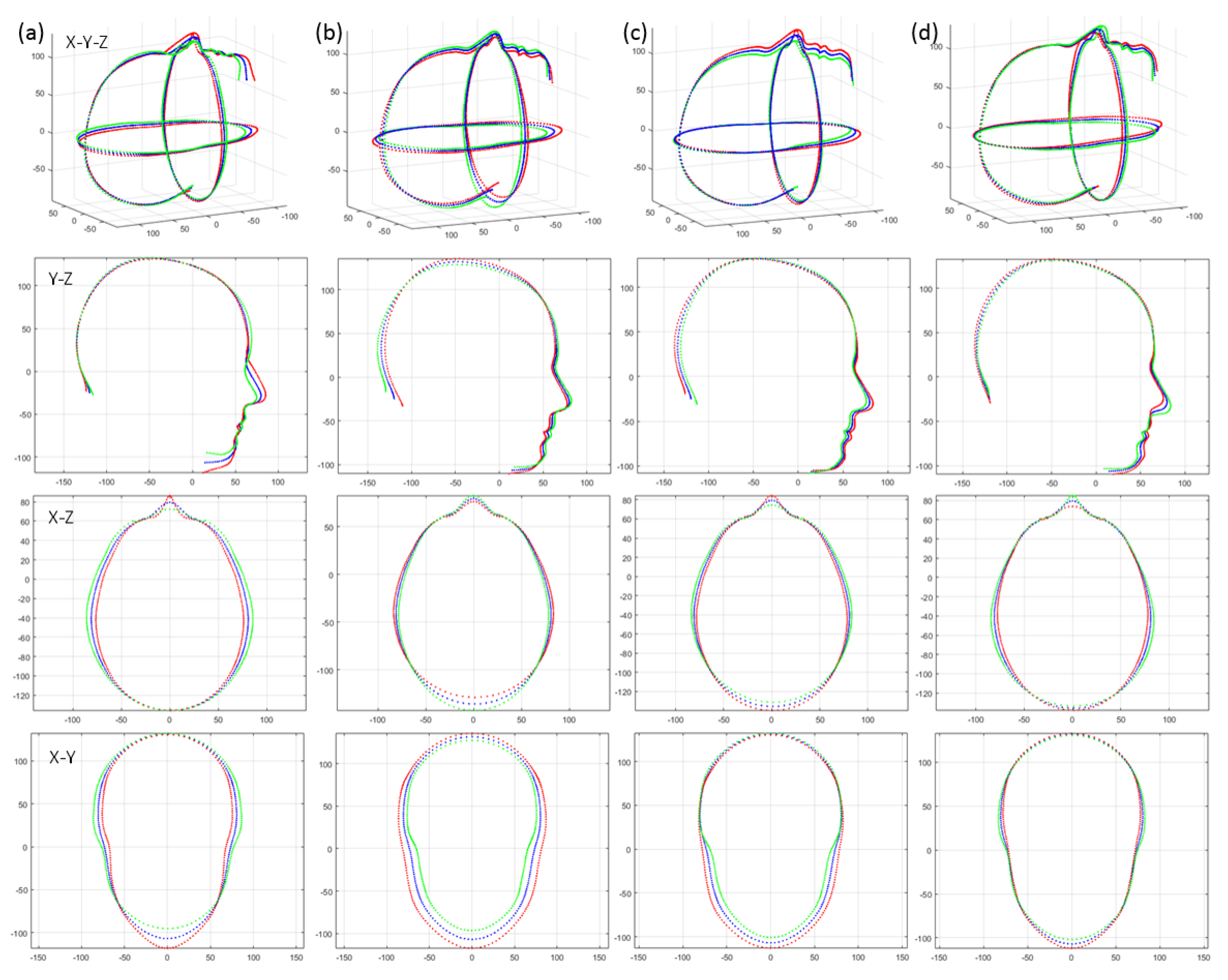
4. Morphable Model Evaluation
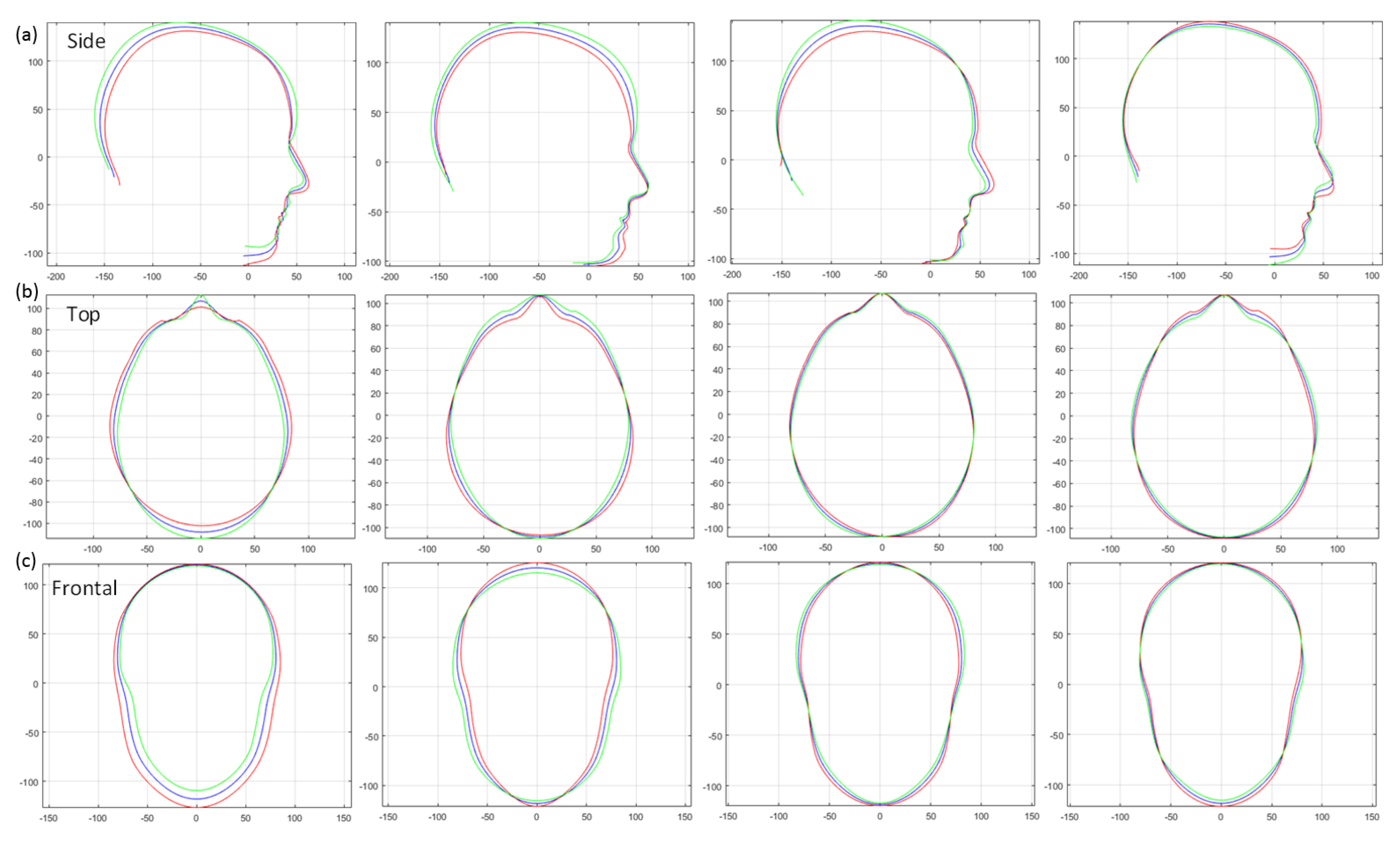
5. Single-View Models versus the Global Multi-View Model
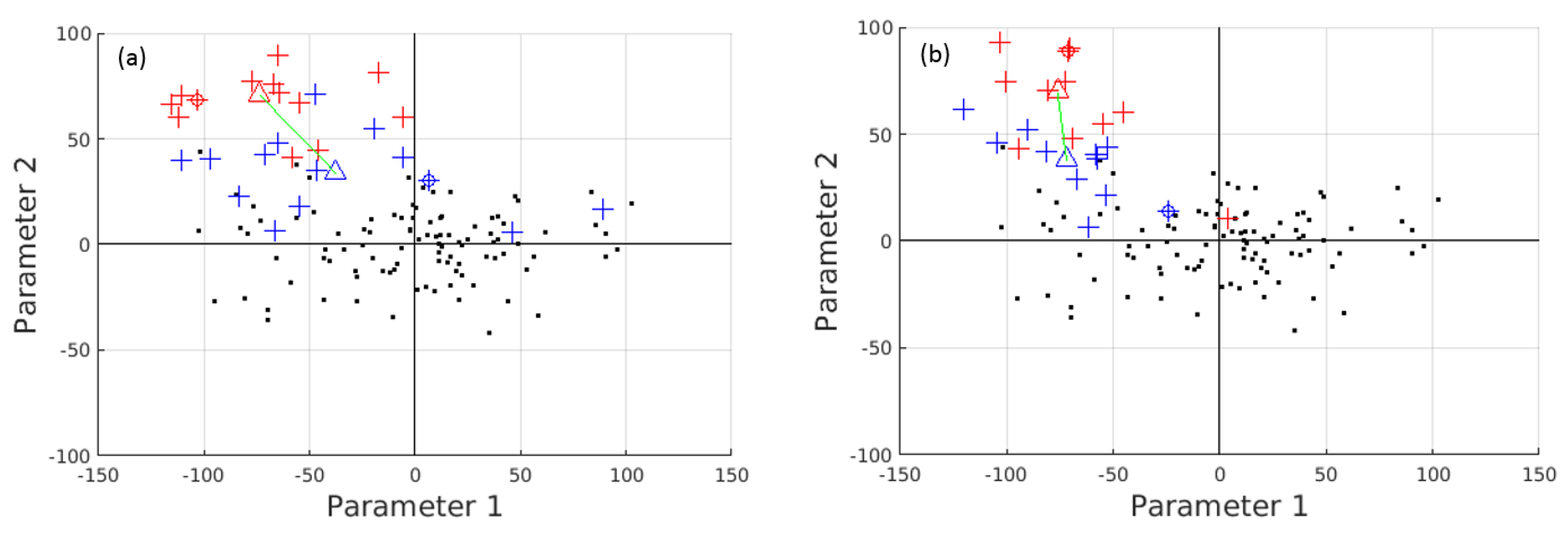
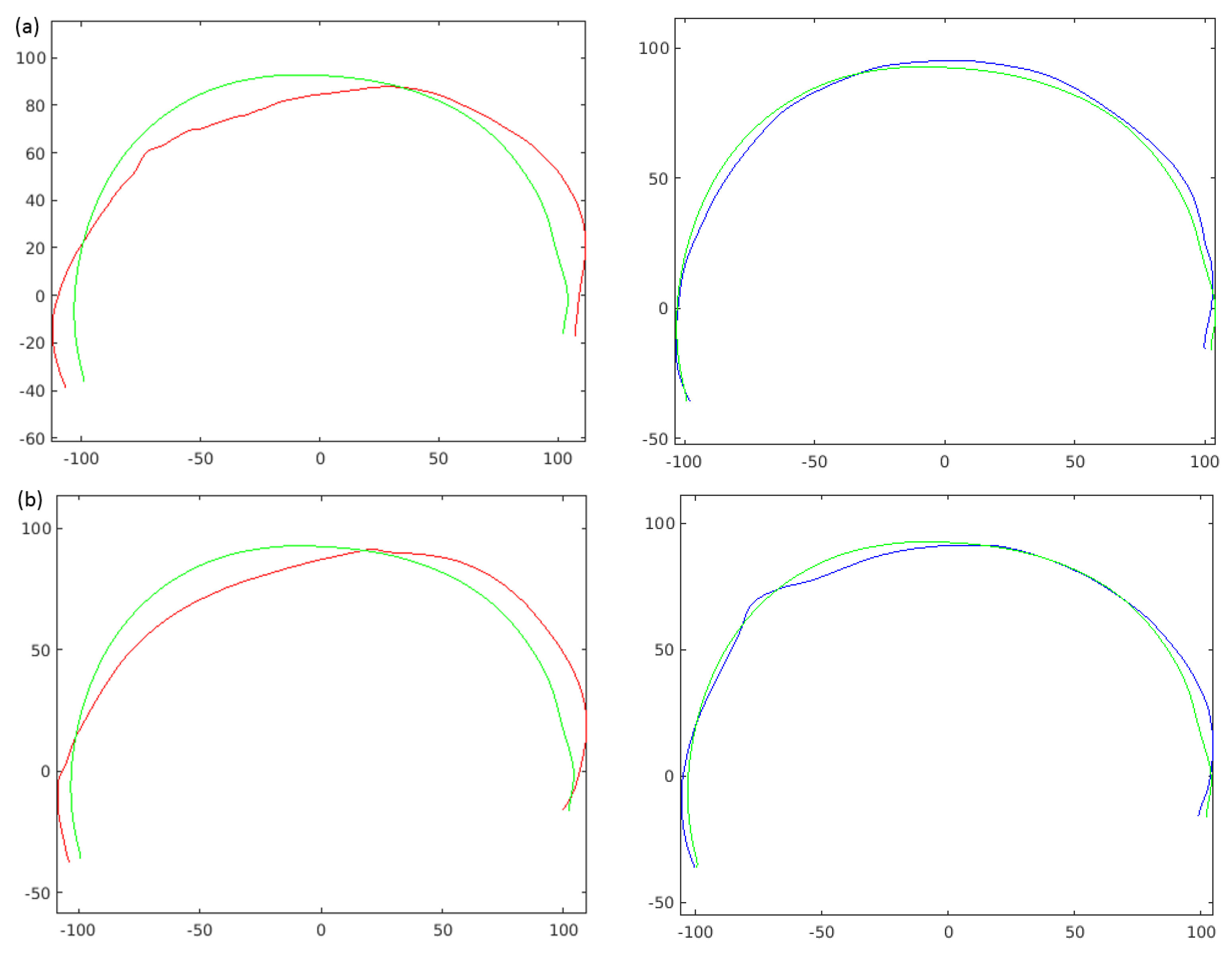
6. Craniosynostosis Intervention Outcome Evaluation
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dai, H.; Pears, N.; Duncan, C. A 2D morphable model of craniofacial profile and its application to craniosynostosis. In Proceedings of the Annual Conference on Medical Image Understanding and Analysis, Edinburgh, UK, 11–13 July 2017; pp. 731–742. [Google Scholar]
- Blanz, V.; Thomas, V. A morphable model for the synthesis of 3D faces. In Proceedings of the 26th Annual Conference on Computer Graphics and Interactive Techniques, Los Angeles, CA, USA, 8–13 August 1999; pp. 187–194. [Google Scholar]
- Blanz, V.; Thomas, V. Face recognition based on fitting a 3D morphable model. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 1063–1074. [Google Scholar] [CrossRef]
- Paysan, P.; Reinhard, K.; Brian, A.; Sami, R.; Thomas, V. A 3D face model for pose and illumination invariant face recognition. In Proceedings of the 2009 6th IEEE International Conference on Advanced Video and Signal Based Surveillance, Genoa, Italy, 2–4 September 2009; pp. 296–301. [Google Scholar]
- Amberg, B.; Sami, R.; Thomas, V. Optimal step nonrigid icp algorithms for surface registration. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007. [Google Scholar]
- Booth, J.; Ponniah, A.; Dunaway, D.; Zafeiriou, S. Large Scale Morphable Models. IJCV 2017. [Google Scholar] [CrossRef]
- Arun, K.; Huang, T.S.; Blostein, S.D. Least squares fitting of two 3D point sets. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 9, 698–700. [Google Scholar] [CrossRef] [PubMed]
- Besl, P.J.; Neil, D.M. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell. 1992, 14, 239–256. [Google Scholar] [CrossRef]
- Booth, J.; Roussos, A.; Zafeiriou, S.; Ponniah, A.; Dunaway, D. A 3d morphable model learnt from 10,000 faces. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 5543–5552. [Google Scholar]
- Hontani, H.; Matsuno, T.; Sawada, Y. Robust nonrigid ICP using outlier-sparsity regularization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012; pp. 174–181. [Google Scholar]
- Cheng, S.; Marras, I.; Zafeiriou, S.; Pantic, M. Active nonrigid ICP algorithm. In Proceedings of the 2015 11th IEEE International Conference and Workshops on Automatic Face and Gesture Recognition (FG), Ljubljana, Slovenia, 4–8 May 2015; Volume 1, pp. 1–8. [Google Scholar]
- Cheng, S.; Marras, I.; Zafeiriou, S.; Pantic, M. Statistical non-rigid ICP algorithm and its application to 3D face alignment. Image Vis. Comput. 2017, 58, 3–12. [Google Scholar] [CrossRef]
- Kou, Q.; Yang, Y.; Du, S.; Luo, S.; Cai, D. A modified non-rigid icp algorithm for registration of chromosome images. In Proceedings of the International Conference on Intelligent Computing, Lanzhou, China, 2–5 August 2016; pp. 503–513. [Google Scholar]
- Dai, H.; Pears, N.; Smith, W.; Duncan, C. A 3d morphable model of craniofacial shape and texture variation. In Proceedings of the International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; Volume 1, p. 3. [Google Scholar]
- Dai, H.; Smith, W.A.; Pears, N.; Duncan, C. Symmetry-factored Statistical Modelling of Craniofacial Shape. In Proceedings of the International Conference on Computer, Venice, Italy, 22–29 October 2017; pp. 786–794. [Google Scholar]
- Bookstein, F.L. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 11, 567–585. [Google Scholar] [CrossRef]
- Yang, J. The thin plate spline robust point matching (TPS-RPM) algorithm: A revisit. Pattern Recognit. Lett. 2011, 32, 910–918. [Google Scholar] [CrossRef]
- Lee, A.X.; Goldstein, M.A.; Barratt, S.T.; Abbeel, P. A non-rigid point and normal registration algorithm with applications to learning from demonstrations. In Proceedings of the 2015 IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015; pp. 935–942. [Google Scholar]
- Lee, J.H.; Won, C.H. Topology preserving relaxation labeling for nonrigid point matching. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 427–432. [Google Scholar] [PubMed]
- Ma, J.; Zhao, J.; Jiang, J.; Zhou, H. Non-Rigid Point Set Registration with Robust Transformation Estimation under Manifold Regularization. In Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4218–4224. [Google Scholar]
- Li, H.; Robert, W.S.; Mark, P. Global Correspondence Optimization for Non-Rigid Registration of Depth Scans. Comput. Graph. Forum 2008, 27. [Google Scholar] [CrossRef]
- Myronenko, A.; Song, X. Point set registration: Coherent point drift. IEEE Trans. Pattern Anal. Mach. Intell. 2010, 32, 2262–2275. [Google Scholar] [CrossRef] [PubMed]
- Cootes, T.F.; Gareth, J.E.; Christopher, J.T. Active appearance models. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 681–685. [Google Scholar] [CrossRef]
- Wiskott, L.; Krüger, N.; Kuiger, N.; Von Der Malsburg, C. Face recognition by elastic bunch graph matching. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 775–779. [Google Scholar] [CrossRef]
- Sauer, P.; Cootes, T.F.; Taylor, C.J. Accurate regression procedures for active appearance models. In Proceedings of the British Machine Vision Conference, Dundee, UK, 29 August–2 September 2011. [Google Scholar]
- Tresadern, P.A.; Sauer, P.; Cootes, T.F. Additive update predictors in active appearance models. In Proceedings of the British Machine Vision Conference, Aberystwyth, UK, 31 August–3 September 2010. [Google Scholar]
- Smith, B.M.; Zhang, L. Joint face alignment with nonparametric shape models. In Proceedings of the 12th European Conference on Computer Vision, Florence, Italy, 7–13 October 2012. [Google Scholar]
- Zhou, F.; Brandt, J.; Lin, Z. Exemplar-based graph matching for robust facial landmark localization. In Proceedings of the 14th IEEE International Conference on Computer Vision, Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Zhu, X.; Ramanan, D. Face detection, pose estimation, and landmark localization in the wild. In Proceedings of the Computer Vision and Pattern Recognition, Providence, RI, USA, 16–21 June 2012. [Google Scholar]
- Davies, R.H.; Twining, C.J.; Cootes, T.F.; Waterton, J.C.; Taylor, C.J. A minimum description length approach to statistical shape modeling. IEEE Trans. Med. Imag. 2002, 21, 525–537. [Google Scholar] [CrossRef] [PubMed]
- Viola, P.; Michael, J.J. Robust real-time face detection. Int. J. Comput. Vis. 2004, 57, 137–154. [Google Scholar] [CrossRef]
- Asthana, A.; Zafeiriou, S.; Cheng, S.; Pantic, M. Robust discriminative response map fitting with constrained local models. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013. [Google Scholar]
- Styner, A.M.; Kumar, T.R.; Lutz-Peter, N.; Gabriel, Z.; Gábor, S.; Christopher, J.T.; Rhodri, H.D. Evaluation of 3d correspondence methods for model building. Inf. Process. Med. Imag. 2003, 18, 63–75. [Google Scholar]
- Robertson, B.; Dai, H.; Pears, N.; Duncan, C. A morphable model of the human head validating the outcomes of an age-dependent scaphocephaly correction. Int. J. Oral Maxillofac. Surg. 2017, 46, 68. [Google Scholar] [CrossRef]


| Models | Precision | Recall | F-score |
|---|---|---|---|
| Top | 0.64 | 0.65 | 0.64 |
| Frontal | 0.73 | 0.73 | 0.73 |
| Profile | 0.77 | 0.77 | 0.77 |
| Global | 0.79 | 0.79 | 0.79 |
| Models | Precision | Recall | F-score |
|---|---|---|---|
| Top | 0.72 | 0.72 | 0.72 |
| Frontal | 0.71 | 0.71 | 0.71 |
| Profile | 0.73 | 0.73 | 0.73 |
| Global | 0.75 | 0.76 | 0.75 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, H.; Pears, N.; Duncan, C. Modelling of Orthogonal Craniofacial Profiles. J. Imaging 2017, 3, 55. https://doi.org/10.3390/jimaging3040055
Dai H, Pears N, Duncan C. Modelling of Orthogonal Craniofacial Profiles. Journal of Imaging. 2017; 3(4):55. https://doi.org/10.3390/jimaging3040055
Chicago/Turabian StyleDai, Hang, Nick Pears, and Christian Duncan. 2017. "Modelling of Orthogonal Craniofacial Profiles" Journal of Imaging 3, no. 4: 55. https://doi.org/10.3390/jimaging3040055
APA StyleDai, H., Pears, N., & Duncan, C. (2017). Modelling of Orthogonal Craniofacial Profiles. Journal of Imaging, 3(4), 55. https://doi.org/10.3390/jimaging3040055




