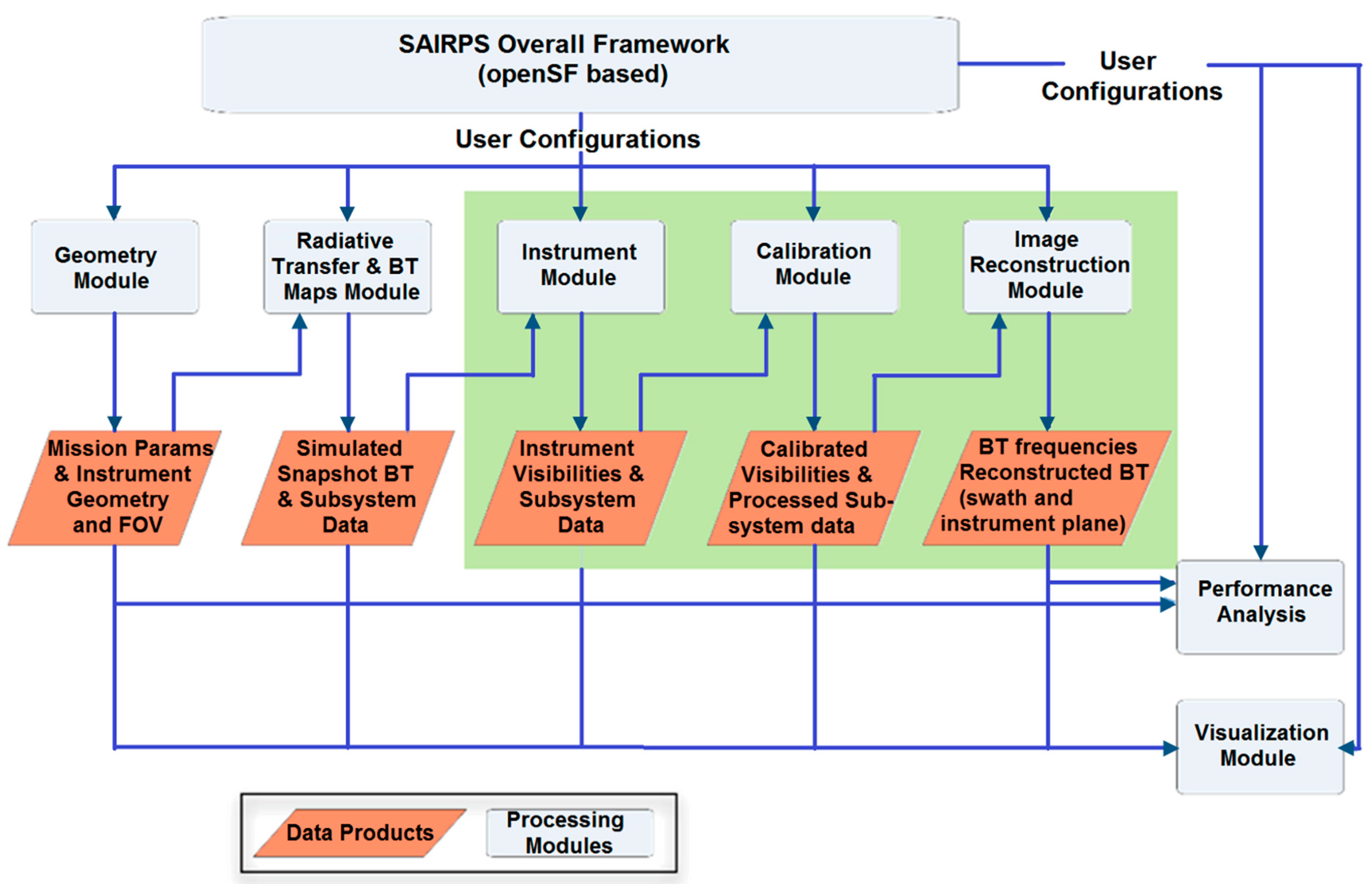
The cross-polarizations VH, HV (or YX, XY) are available only if input BT Maps include non-zero T3 and T4. Using the previous computed data—FWF, antenna patterns, receivers’ physical temperatures and the input BT map—the real and imaginary parts of the visibility samples are simulated through the following expression:
where
, the antenna spacing normalized to the electromagnetic wavelength
is called the “baseline”
, although usually the array elements lie in a plane (w = 0),
, the director cosines with respect to the X and Y axes are
and
, respectively, T
B is the brightness temperature, T
REC is the physical temperature of the receivers, F
n1,2 are the normalized antenna voltage patterns at a given polarization,
,
are the fringe-washing functions (real and imaginary parts), and Ω
m,n are the antenna solid angles [
1].
The extension of Equation (2) to the polarimetric case including the cross-polar terms was derived in [
2]:
where
and
are, respectively, the normalized co- and cross-polar radiation patterns of antenna
m at
X or
Y polarizations. In the noise injection calibration mode, since the noise is injected by switching the antennas to the outputs of the noise distribution network with S-parameters, the following expression has to be used to simulate the visibility samples:
with
the S-parameters of the Noise Injection network from input port 0 to output ports
m or
n, and with FWF
0 the complex fringe-wash function at the origin,
, and T
0 = 290 K.
2.1.1. Antenna Array Component
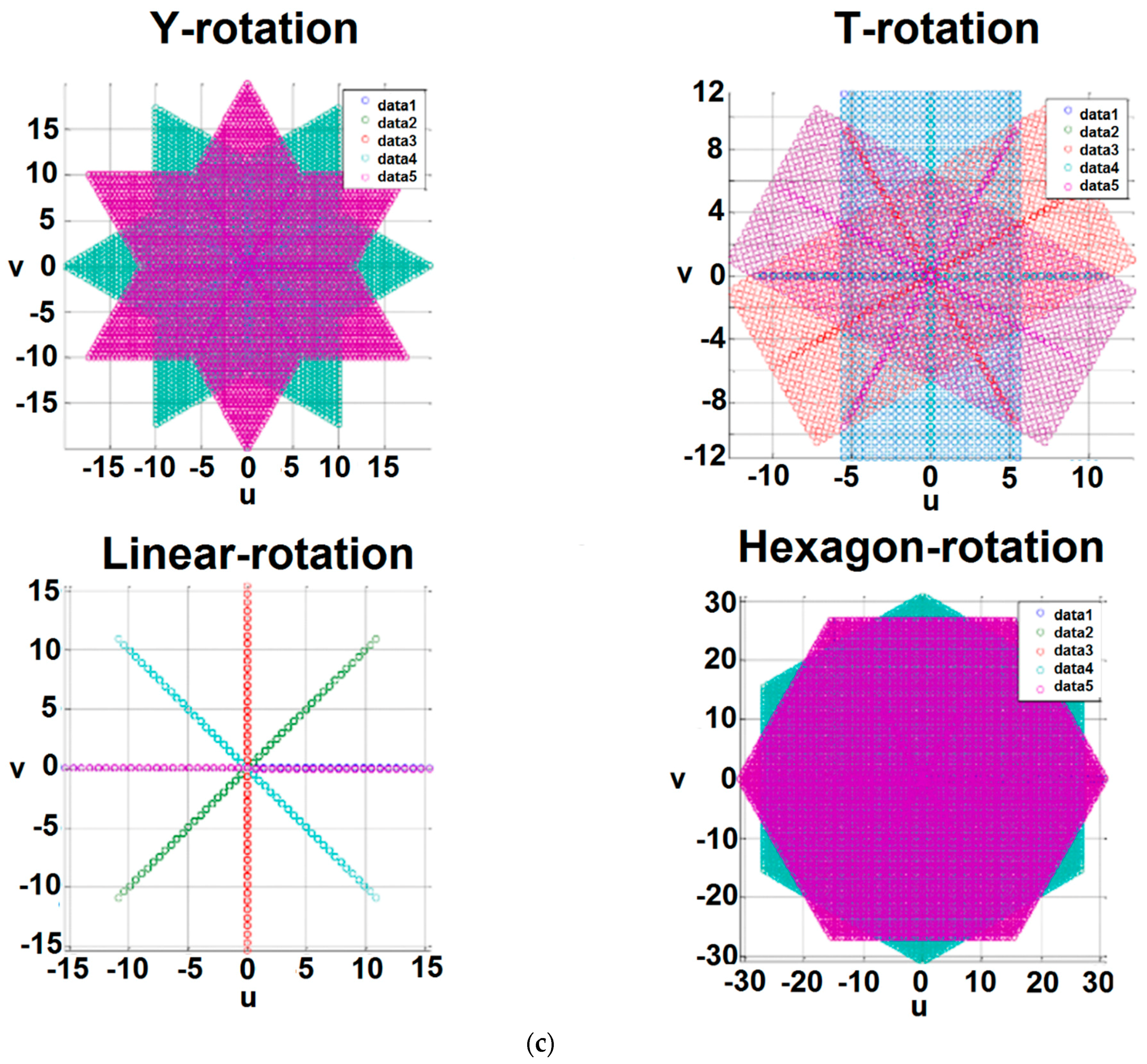
The antenna array is defined by its antenna positions as a function of time including a static array with arbitrary shape, e.g., linear, Y-shaped, T-shaped, random distribution, etc., a static array plus small deviations of the antenna positions as a function of time (e.g., thermal and mechanical oscillations), or an array with arbitrarily moving antennas, e.g., a rotating array. Antenna orientations (i.e., polarizations) can also be static or a function of time.
To make the simulator as generic as possible, the antenna positions
and polarization
(within the X-Y plane) can be described in the instrument reference frame by mathematical functions as a function of the time:
or they can be described in a tabular form to be read from an input file, from which positions at intermediate times are linearly interpolated from the values given in the tables. The angle
is defined as the rotation angle of the
nth antenna polarization frame with respect to the instrument reference frame.
From these parameters, the actual baselines (u
mn, v
mn, w
mn) being measured at each particular time (antenna positions may be moving) are determined.
Figure 3 shows sample SAIRPS antenna arrays: (a) static arrays; (b) rotating arrays; and (c) (u, v) points (baselines) measured by the rotating arrays.
In order to be able to process the visibility samples, they need to be changed first from the instrument polarization reference frame to visibilities as correlations between the antennas in their own defined polarization frames:
where the elements
,
, and
,
are the elements of the rotation matrices
defined as
.
If the instrument is in dual-polarization only (
i.e.,
and
are not measured), inverting Equation (6) is not always possible, even assuming
, since singularities appear when
:
Antenna phase center position uncertainties (Δxn, Δyn, Δzn) with respect to the antenna nominal positions (xn(t), yn(t), zn(t)) also account for (xn(t), yn(t), zn(t)) + (Δxn, Δyn, Δzn) in the “direct problem”, meaning the computation of the instrument’s observables, while the estimated (measured on the ground or known from models) antenna phase centers (xn(t), yn(t), zn(t)) are used in the “inverse problem” or image reconstruction from the instrument’s observables.
Antenna patterns (X, Y polarizations, cross-polar terms) appear in Equations (2) and (3) as the F
n m,n term. However, these equations implicitly assume that the antennas only pick up radiation from the half hemisphere around the antenna boresight. This is not the case in practice, and both the front and back lobes must be accounted for. The brightness temperature contribution coming from the platform(s) supporting the antennas has been neglected. Other contributions to the brightness temperature coming from the back of the antenna are computed by running the Radiative Transfer Module (companion paper, Part I), but looking in the opposite direction. The equations, including the back lobes, turn out to be exactly the same as Equation (2), but changing “w” to “−w” in the baseline definition,
, and, obviously, using the BT distribution present in the back side of the array. The real and imaginary parts of the visibility samples computed from the back lobes (90° < θ ≤ 180°) must be added to the ones computed from the fore lobe (0° ≤ θ ≤ 90°).
Antenna patterns, either ideal, for example or individually different (from a simulation or a measurement database), co- and cross-polar radiation voltage patterns can be used for the fore (+z) and back (−z) sides of the array. These patterns can also be defined differently for the “direct problem” (computation of the visibility samples from an input brightness temperature map) or the “inverse problem” (image reconstruction from “measured” visibility samples) to allow the estimate of the impact of an imperfect antenna pattern characterization in the radiometric accuracy of the retrieved BT image.
Individual antenna patterns can be either modeled or read from Auxiliary Data Files (ADFs). In SAIRPS the model used consists of an average pattern plus individual random deviations in amplitude and phase over the mean value, and a pointing error described (θ
0, ϕ
0) by two parameters,
where
n is a parameter used to adjust the antenna beamwidth or, equivalently, the directivity (
D = 10log(2(n + 1)), (θ
0, ϕ
0) is the direction of the maximum of the antenna pattern (not necessarily the array boresight +z),
Aa and
Af are the magnitudes of the amplitude (with respect to 1) or phase (radians) ripples,
na and
nf are the frequencies of the amplitude and phase ripples, and Φ
a and Φ
f are the phases of the amplitude and phase ripples to randomize them and avoid all ripples being in phase at the antenna maximum;
is an arbitrary small number to avoid singularities.
If antenna patterns are read from ADFs (real and imaginary parts), the default angular spacing is set to 1° (i.e., 181 × 361 points in θ and ϕ, one sample/° for both hemispheres); however, if the width of the synthetic beam is narrower, the sampling of the antenna pattern must satisfy the Nyquist criterion, which is at least two samples per angular resolution, or otherwise antenna pattern uncertainties may be underestimated. For example, for a SAIR in a geostationary satellite with a 0.016° angular resolution (10 km), the antenna pattern must be sampled at least every 0.008°.
Once the fore and back sides of the antenna pattern are computed (or read from an ADF), the solid angle is computed by integration of the co- and cross-polar radiation pattern over both hemispheres (4π stereo-radians).
Individual antenna imperfect matching and ohmic losses (ηΩm = average plus deviations ΔηΩm) must also be taken into account to properly compute the overall frequency response and noise figure of each receiving channel. The antenna ohmic losses are modeled as a perfectly matched attenuator of parameters, and , right after an ideal lossless antenna. The antenna physical temperature (Tph (t)) is also used to compute the actual noise introduced by the antenna ohmic losses, since the noise power at the antenna output is given by a different antenna temperature: , and the added noise at the antenna input is given by .
Coupling between different antenna elements produces two effects: a distortion of the antenna pattern itself that appears as ripples with a spatial frequency equal to the baseline between the two antennas being coupled, and a cross-correlation offset coming from the backwards noise radiated by the receiver that is coupled to a neighbor antenna. The second effect will be analyzed in
Section 2.1.2. The antenna array coupling is characterized by the S-parameters of a multi-port circuit in which each antenna is a port.
In order to account for the proper distance and orientation dependence of the mutual coupling, the antenna coupling model implemented is based on the coupling between linear dipoles in arbitrary positions and orientations, but scaled by a user-defined factor to simulate the absolute value of the coupling.
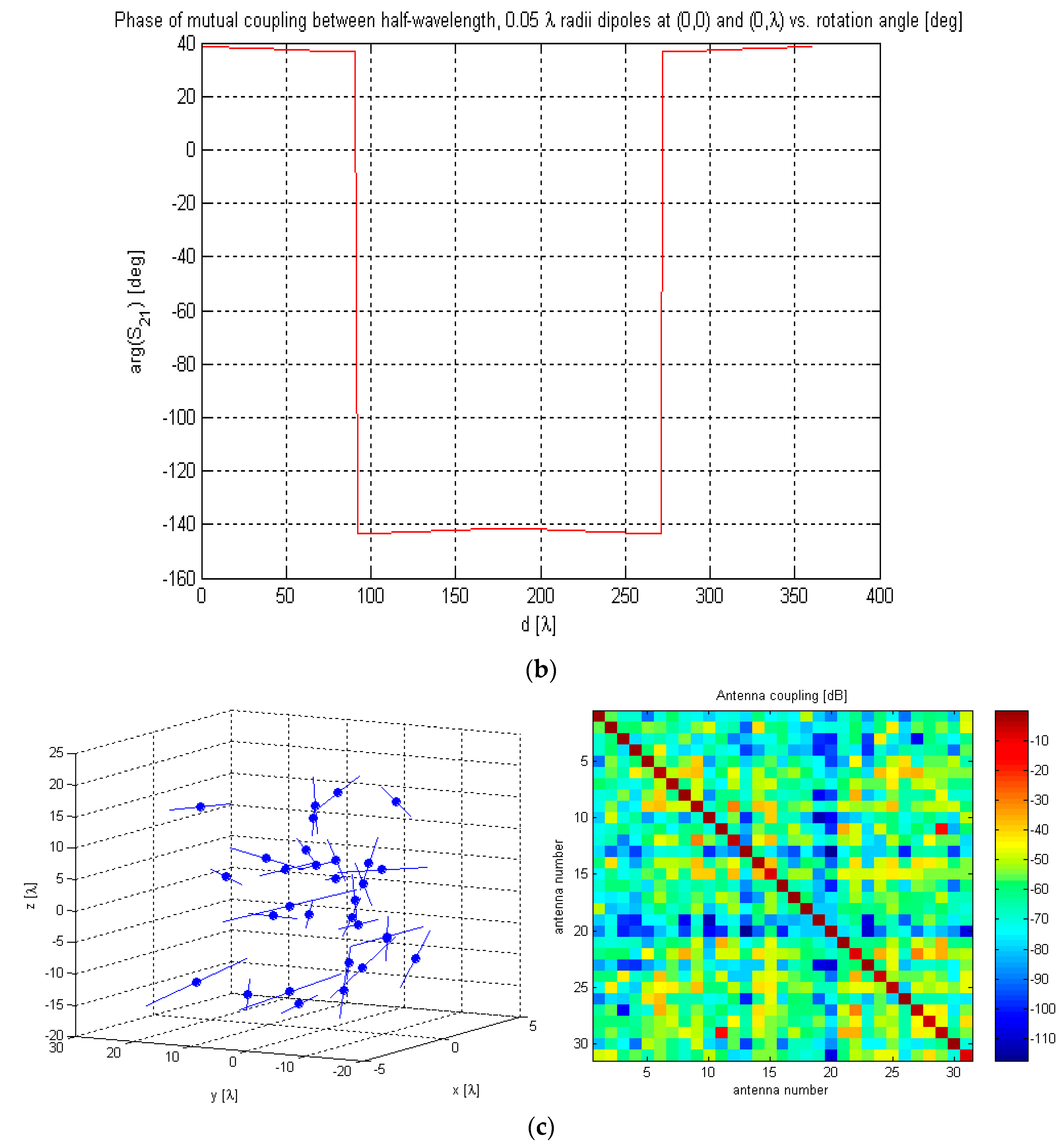
Figure 4 shows the simulated antenna coupling (S
21) between two parallel or collinear half-wavelength dipoles as a function of the distance in terms of the wavelength. As expected, the mutual coupling between collinear dipoles (in red) is much weaker and decreases faster than between the parallel dipoles (in blue).
Figure 5 shows the simulated antenna coupling (S
21) in amplitude and phase between two co-planar half-wavelength dipoles at (0,0) and (0,λ) as a function of the angle between their axes. As expected, coupling is at maximum when they are parallel and at minimum (zero) when they are perpendicular. This model allows us to simulate in a realistic way complex three-dimensional (3D) arrays with arbitrary configurations and antenna orientations such as the one shown in
Figure 5c.
The measured visibility samples under antenna coupling conditions can be computed through the mutual coupling matrix
, as defined in [
3,
4]:
where the element
Vmn of the visibility matrix
corresponds to the cross-correlation between the signals collected by antennas m and n, and the
matrix is defined as:
where
Zin and
ZL are the input and load impedances of the antennas (assumed all to be the same for the sake of simplicity), and
is the Z-parameter matrix and it is given by:
where
and
are the identity and the S-parameter matrices, and
is the characteristic impedance.
Equation (10) shows that antenna coupling actually produces a mix of the visibility samples whose main effect is moving energy from the shortest baselines (larger amplitude) to the longest ones (smaller amplitude). This effect can also be understood as a visibility offset given by:
An alternative way to interpret Equation (10) is as a linear combination of the isolated antenna patterns with a phase term equal to the baseline and amplitude proportional to the mutual impedance [
4]. For a linear array of antennas spaced
d wavelengths along the
z axis (e.g., at positions 0,
d, 2
d, 3
d…), antenna coupling consists of a modification of the antenna patterns, following the approximate formula below:
where
is the
mth normalized antenna voltage pattern with/without the effect of mutual coupling, and
Z1m is the mutual impedance between elements 1 and m, and
d is the basic antenna spacing (in wavelengths).
The second term in the brackets in Equation (13) represents the oscillations in the antenna pattern due to the mutual coupling effects.
2.1.2. Receiver Component
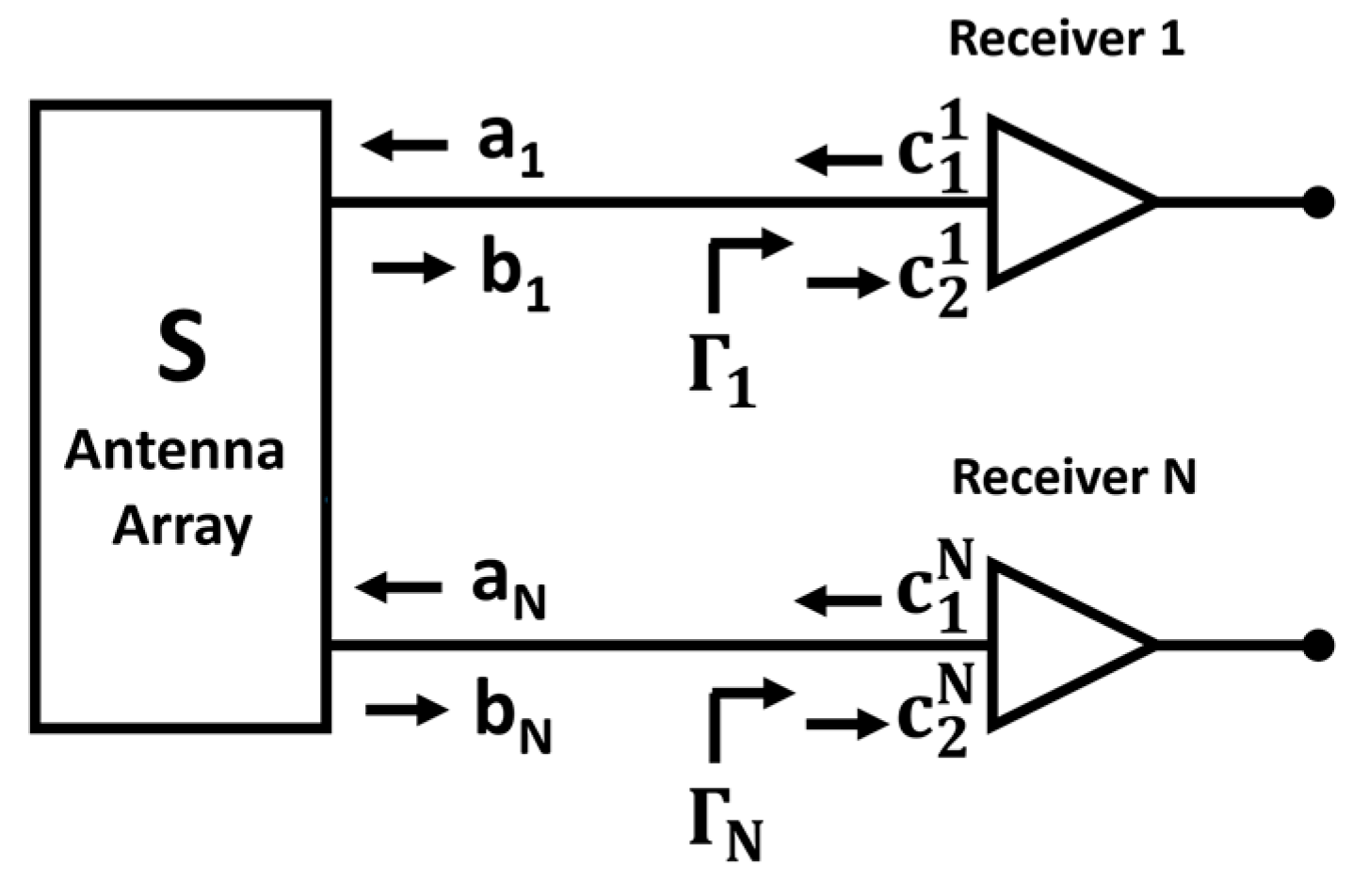
The receiver model is sketched in
Figure 6. It is composed of: (1) a switch that selects the input to the receiver channels from the antenna ports (either X or Y polarization, the receiver is duplicated for both polarizations), uncorrelated noise injection at port U (50 Ω matched load), and correlated noise injection at port C; (2) the radio frequency (RF) path composed of a first RF band-pass filter (RF-BPF1), an isolator, an LNA, and a second RF band-pass filter (RF-BPF2), an RF amplifier (RFAmp), and a coupler; (3) an I/Q mixer and local oscillator (LO); and (4) the intermediate frequency (IF) in-phase and quadrature (I/Q) paths, both composed by an IF band-pass filter (IF-BPF), a first IF amplifier (IFAmp1), a slope corrector, a second IF amplifier (IFAmp2), and the analog-to-digital converter (ADC with an arbitrary number of bits, sampling frequency, jitter,
etc.). Note that depending on the selected values for the central frequencies, bandwidths, and receiver topology (e.g., lack of an image rejection filter), results may have no sense. The user must be educated in RF engineering and check that the resulting fringe-washing function (Equation (25)) is correct.
In this generic model, receivers’ central frequency and bandwidths for the elements can be arbitrarily defined, as in the most general case, and input data can be read from ADFs with the complex S-parameter matrices as a function of frequency.
Modeling of Receiving Chains Frequency Response
To calculate the fringe-washing functions and for the real and imaginary parts of the visibility function computed between antenna elements 1 and 2, the frequency response of receiving chains must be computed first (different for X and Y polarizations, and for the real and imaginary parts, since after the mixer the in-phase and quadrature branches are separated; see Equation (2a) and (2b)). Regardless of how the frequency response is evaluated, by cascading the S-parameters of each subsystem (noise parameters for the active subsystems are also included) or using end-to-end frequency response ADFs, the long-term gain drifts are included by means of the temperature sensitivity coefficients (nominal temperature = 25°), or as different frequency response ADFs for different temperatures. The correlated noise generated by passive components is evaluated using the S-parameters, and the noise generated by the active subsystems is modeled by the minimum noise figure, the optimum input reflection coefficient, and the equivalent noise "resistance", as a function of frequency, at each physical temperature.
The short-term gain fluctuations (ΔG) due to flicker noise, which limit the ultimate stability that can be achieved, are modeled in a similar way to jitter, and are used in the snapshot, time-evolution, and MonteCarlo simulation modes. The local oscillator is modeled by its central frequency, phase noise and thermal floor noise level, which are converted into a jitter error, and a correlator offset through the mixer finite isolation, respectively. ADCs are modeled by the number of bits, quantization levels uniformly or non-uniformly distributed, and a mathematical transfer function to model saturation, clipping, etc., and skew and jitter errors. The correlator is modeled according to the number of bits, their distribution, and the mathematical transfer function that relates input and output, sampling frequency, jitter, etc.
The failure of a receiver is modeled by forcing a zero in all baselines in which this receiver intervenes, and the failure of a correlator by forcing a zero in only the two baselines computed by that correlator (it and its Hermitian one).
The RF subsystems (amplifiers, filters, isolators, mixer, IF filter and IF attenuator) are typically described by their S-parameters, while the IF sections (filter, amplifiers,
etc.) at VHF and UHF are described by the insertion losses (or gain) and voltage standing wave ratio (VSWR). Since, in the pass-band, the VSWR is typically quite small (<1.10), and propagation effects can be neglected, the S-parameters will be:
and
By transforming the S-parameters into the transmission (ABDC) matrices [
5]:
the response of the different subsystems can be easily computed by multiplication of the transmission matrices. Finally, the end-to-end S-parameters are computed as:
since subsystems in the receiver block diagram may or may not be present. In case they are not present, their ABCD matrix becomes A = D = 1, B = C = 0 at all frequencies. For the mixer, different gains are considered in both outputs (I and Q), as well as in input and output reflection coefficients and the phase difference between both outputs (quadrature error). This allows us to compute the equivalent S-parameters of the mixer, using the same formulas above, and the different responses of the I and Q branches.
The first two subsystems after the mixer (the IF filter and the IF slope corrector) also use the S-parameter representation since they are based on a 50 Ω reference impedance. The same formulas are used to compute the cascaded S-parameters, but they are shifted to the RF band, in order to get the equivalent overall RF response, and the values for RF frequency values lower than that of the local oscillator are the conjugates of those at their image frequency.
The RF and IF filters are critical because they shape the frequency response to a large extent. They can either be read from a data file, or they can be computed from an analytical model, by default an eighth-order Chebychev band-pass filter, with nominal ripple (e.g., 0.5 dB), user-defined lower and higher band frequencies, user-defined Q-factor of the resonators (e.g., 1000), component tolerance, including inverter constants, and temperature sensitivity of the components. The IF filter is described in a similar way, but in this case it can be a third-order Chebyschev lumped element band-pass filter, with a user-defined Q-factor of the resonators (e.g., 100), component tolerance, and a temperature coefficient of inductors, capacitors and the Q-factor. The S-parameters of each filter are then computed, applying random number generators for each individual parameter, along with the temperature coefficient.
Noise Modeling
The simplest way to compute the receivers’ noise temperature consists of computing the available power gain of each RF subsystem from its S-parameters:
where Γ
s is the corresponding source reflection coefficient, and Γ
0 the output reflection coefficient, computed as:
For all the passive subsystems, the equivalent noise temperature is given by:
where
Tph is the physical temperature.
Then, for the active subsystems, LNA, RF and IF amplifiers, the noise temperature is directly read from the instrument database. Finally, the overall noise temperature is computed at each frequency using the Friis formula [
5]:
Note that, because the input switch can have different S-parameters in each of the states, , , and can be different, and the noise temperatures as seen from the correlated noise input, from the uncorrelated noise input, and from the antenna input can be different as well.
However, the modeling of the noise in an interferometric radiometer has to be much more accurate: backwards noise and the cross-correlation between the forward and backward noise waves are required. A full noise wave analysis is required to evaluate the correlation between outgoing noise waves
c1 and
c2 in two ports, and it is detailed in [
6]. These noise waves add to the outgoing signal waves
b1 and
b2 (
Figure 7), as follows:
The power of the noise waves
c1 and
c2 and their correlation is given by Equations (23a)–(23d) from [
6] (except for the Boltzmann’s constant term, omitted below).
and
where
T0 = 290 K,
Z0 is the normalization impedance,
Tmin is the minimum noise temperature that will be attained when the device is charged with Γ
opt at the input, Γ
opt is the input reflection coefficient which provides the best noise performance, and
Rn is the equivalent noise "resistance". These four parameters (Γ
opt is complex) are the ones that describe the noise performance of an active device, and they can be mapped into the four noise wave parameters
,
, and
(which is also complex). In order to refer
and
at the input, it suffices to divide Equation (23b) by
, and Equation (23c) by
(see Equation (10) in [
6]).
The finite antenna coupling and the cross-correlation between the outgoing noise waves (Equation (23c)) introduces an offset in the visibility samples (
Figure 8). All noise waves are referred at the antenna reference frame (after an ideal lossless antenna, but before the attenuator that models the antenna ohmic losses, so that the wave amplitudes do not need to be re-scaled).
All effects, including imperfect matching both at the antenna side and at the receiving chain side can be obtained by:
where
is either the S-parameter matrix of the antenna array (same as in Equation (12)) or the noise injection S-parameters when the input switch is in noise injection calibration mode,
is a diagonal matrix with the reflection coefficients of each port, diag(
) is an operator that converts the elements of the vector
in a diagonal matrix, and
,
, and
are the equivalent noise temperatures associated with
,
, and
. Note that neither the antennas’ nor the receivers’ input need to be perfectly matched and that
will be slightly different when the input switch is connected to the antennas or to the noise distribution network.
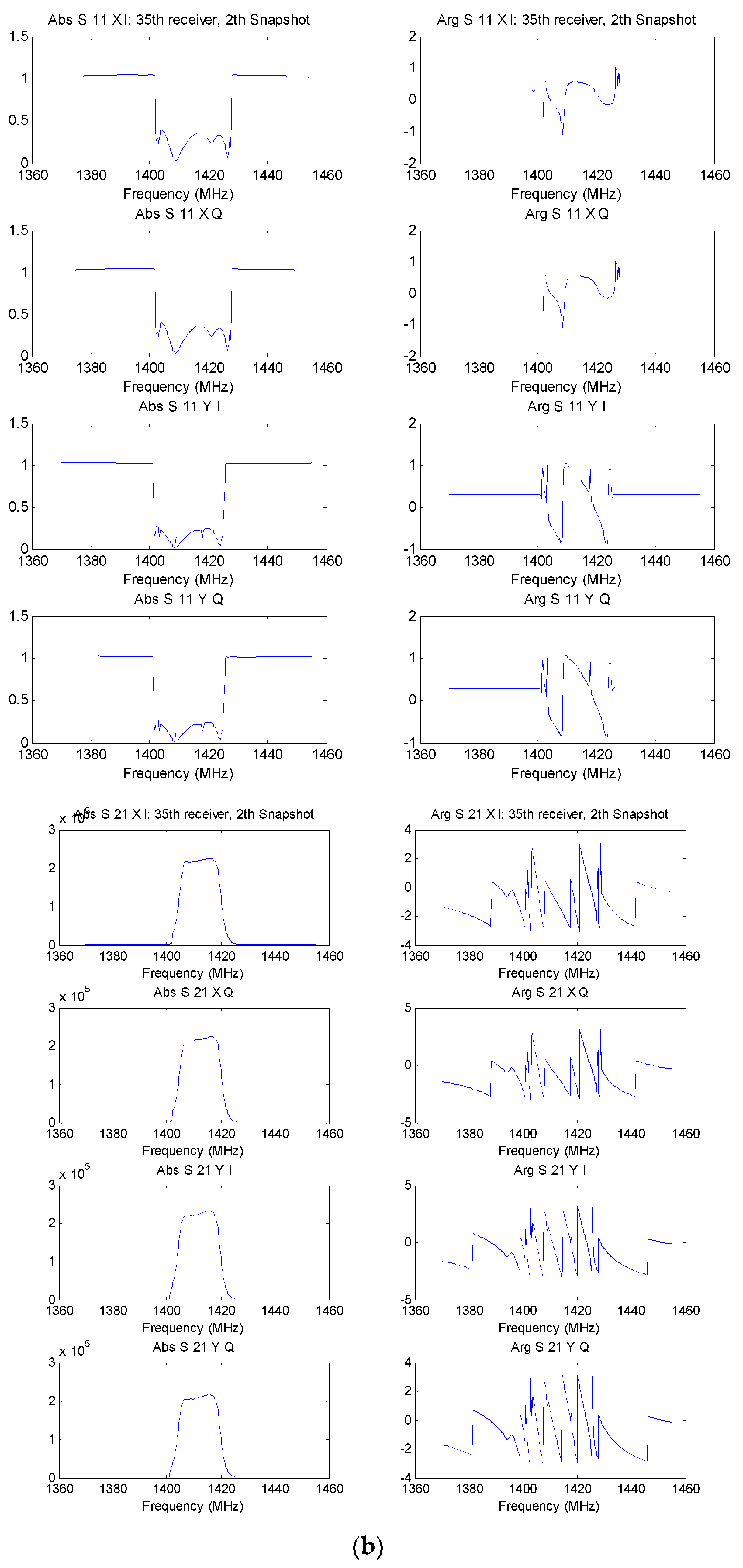
Figure 9 shows an example of the receivers’ modeling of a SMOS-like instrument (Soil Moisture and Ocean Salinity mission) at the L-band: (a) the noise figure as a function of the frequency for the
I- and
Q-channels; (b) the
S11 and
S21 parameters (amplitude and phase, X- and Y-polarizations,
I- and
Q-channels); and (c) the end-to-end frequency responses (amplitude and phase) for X- and Y-polarizations,
I- and
Q-channels.
Modeling the Fringe Washing Function
Since the
I- and the
Q-branches may have slightly different frequency responses, the fringe-wash functions (FWF) (
in Equation (2a) and
Equation (2b)) are computed for all possible pairs of receivers (total N
rec·(N
rec-1)/2 pairs: 1-2, 1-3, 1-4, … 1-N
rec; 2-3, 2-4, … 2-N
rec; 3-4, 3-5…3-N
rec…) from a number of complex samples of the individual receiver frequency responses:
where
Hn m,n is the frequency response of receiver
m or
n, respectively (
I- or
Q-branches), normalized to unity, and
are the noise bandwidths. The symbol
F−1 is the inverse Fourier transform and
u() is the step unit function. Note that the quadrature channel frequency transfer function used in
includes a 90° phase shift introduced in the local oscillator.
Figure 10 shows sample fringe-washing functions for the
X- and
Y-polarizations,
II and
QI pairs, computed using Equation (25).
An FFT algorithm is used to compute all the FWFs, and the result is limited to the main lobe of the function, which has a “sinc-like” shape. For the sake of computational efficiency in the computation of the visibility samples (“direct problem”), the fringe-wash function is approximated by:
The parameters
A,
B,
C,
D,
E and
F are computed from:
in the image reconstruction algorithm (“inverse problem”), the fringe-wash function is estimated from calibration measurements at three different lags (−
Ts, 0,
Ts), mimicking the fitting in Equation (27). On the other hand, since the shape of the FWF is an even function, and the relative bandwidth is very small, it can be simply ignored and set to 1. Note that the phase and amplitude at the origin are the values that need to be calibrated.
2.1.3. Correlator Model
In the computation of the samples of the visibility function, the non-ideal digital correlator effects must also be included. Quantization distorts and spreads the cross-correlation spectrum, decreasing the radiometer resolution. Sampling also impacts the spectrum of the cross-correlation. Even above the Nyquist sampling rate, quantization spreads the spectrum. In the case of a one-bit two-level correlator, the effect is well described in the SMOS analysis [
7]. More general cases are discussed in [
8].
Figure 11, for example, shows the transfer function
g(
x) of an arbitrary analog-to-digital (ADC) converter, with gain compression, and uneven spacing in the input and output variables.
The impact of quantization effects in the measured cross-correlation can be numerically computed from:
where
is the ideal correlation coefficient of the two variables
x and
y (before the non-linear ADC functions
and
),
is the correlation coefficient of
x and
y after the non-linear functions
and
are applied to
x and
y, respectively, and X
p and Y
p are the positions where the steps of the transfer function occur (
Figure 11). In some particular and simplified cases, Equation (29) can be obtained analytically, for instance in the case of quantifying with two levels (one bit,
and
). In this case, Equation (28) becomes the well-known solution stated [
8]:
Figure 12a shows different transfer functions computed from Equation (28) for different quantization schemes using four bits (equally spaced thresholds, with gain compression or randomly distributed), one bit/two levels, and the ideal 1:1 transfer function.
Figure 12b shows the root mean square error as a function of the ADC window normalized to the standard deviation of the input signals for different numbers of equally spaced quantification levels. Once the transfer functions are computed for each correlator, they are stored in look-up tables for the sake of time efficiency.
Furthermore, skew due to clock inaccuracies and jitter due to delay offset are modeled:
. The skew is a constant timing error that produces a decrease of the cross-correlation amplitude (
Figure 13). Since the in-phase and quadrature branches may have (do have) different sampling errors, skew also produces a phase and quadrature error as detailed in [
7]:
where
is the skew error between the
Im and
In channels (or
Qm and
Qn) used to compute the real part of the visibility sample, and
is the skew error between the
Qm and
In channels (or
Im and
Qn) used to compute the imaginary part of the visibility sample.
On the other hand, the jitter is a random variable effect that can be statistically modeled as a zero-mean random Gaussian variable of variance depending on time (
), where “n” and “m” are two different samples. Thus, it can be associated with two different and independent processes [
9,
10]:
the aperture jitter, which is related to the random sampling time variations in the ADC caused by thermal noise in the sample and hold circuit. The aperture jitter is commonly modeled as an independent Gaussian variable with zero-mean and a standard deviation of .
The clock jitter, which is a parameter of the clock generator that drives the ADC with the clock signal. The clock jitter is modeled as a Wiener process, i.e., a continuous-time, non-stationary random process with independent Gaussian increments with a standard deviation equal to .
Finally, jitter effects are included in the FWF as:
where
is the cross-correlation function (FWF) modified by the jitter,
is the cross-correlation function (FWF), and * denotes the convolution operator. Finally, the combined effect of skew and jitter effects can be modeled as
.
The question is now how to compute the jitter from the phase noise spectrum of the local oscillator.
Figure 14 (from [
11]) shows a typical phase noise spectrum, where the different areas are modeled by a constant slope term,
ai. This spectrum can be approximated by:
where
u() represents Heaviside’s step function.
The rms clock jitter (
) can be computed as:
The last effect that can occur is the offset induced by the local oscillator thermal noise leakage to IF through the finite LO-IF isolation. If the baseband clock is distributed, and then a dedicated Phase Locked Loop (PLL) is used in each receiver, then this effect is most likely going to be negligible, since the noises are uncorrelated. If a common LO is distributed (at least by groups), then thermal noise leaks due to the finite LO-IF isolation (>10–20 dB for a typical mixer):
in all channels, and therefore produces an offset at the output. In Equation (34),
Tph is the physical temperature of the LO,
G is the gain of the LO driver (assuming that the LO needs to be amplified for distribution to different channels, if not
G = 1), and
Isolation is the LO-IF isolation of the mixer.
For a generic SAIR, the effect of an arbitrary type of correlator can be modeled based on the results in [
12].
Figure 15a,b represent the quantization effect in the time domain (left) and its corresponding spectrum (right), which, as expected, spills above its original band. Finally,
Figure 16 shows the FWF
vs. sampling frequency. Note that the FWF when sampling at the Nyquist frequency, is different compared to the FWF when sampling at a much higher frequency, due to the fold-over of the “tails” of the signal’s spectrum after quantization which expand beyond
(
Figure 15b).
The thermal noise and its dependence on the correlator type are discussed below.