Imaging for High-Throughput Phenotyping in Energy Sorghum
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.1.1. Energy Sorghum Material
2.1.2. Camera
2.1.3. Imaging Environment
2.2. Methods
2.2.1. Image-Distance Calibration
2.2.2. Image Analysis
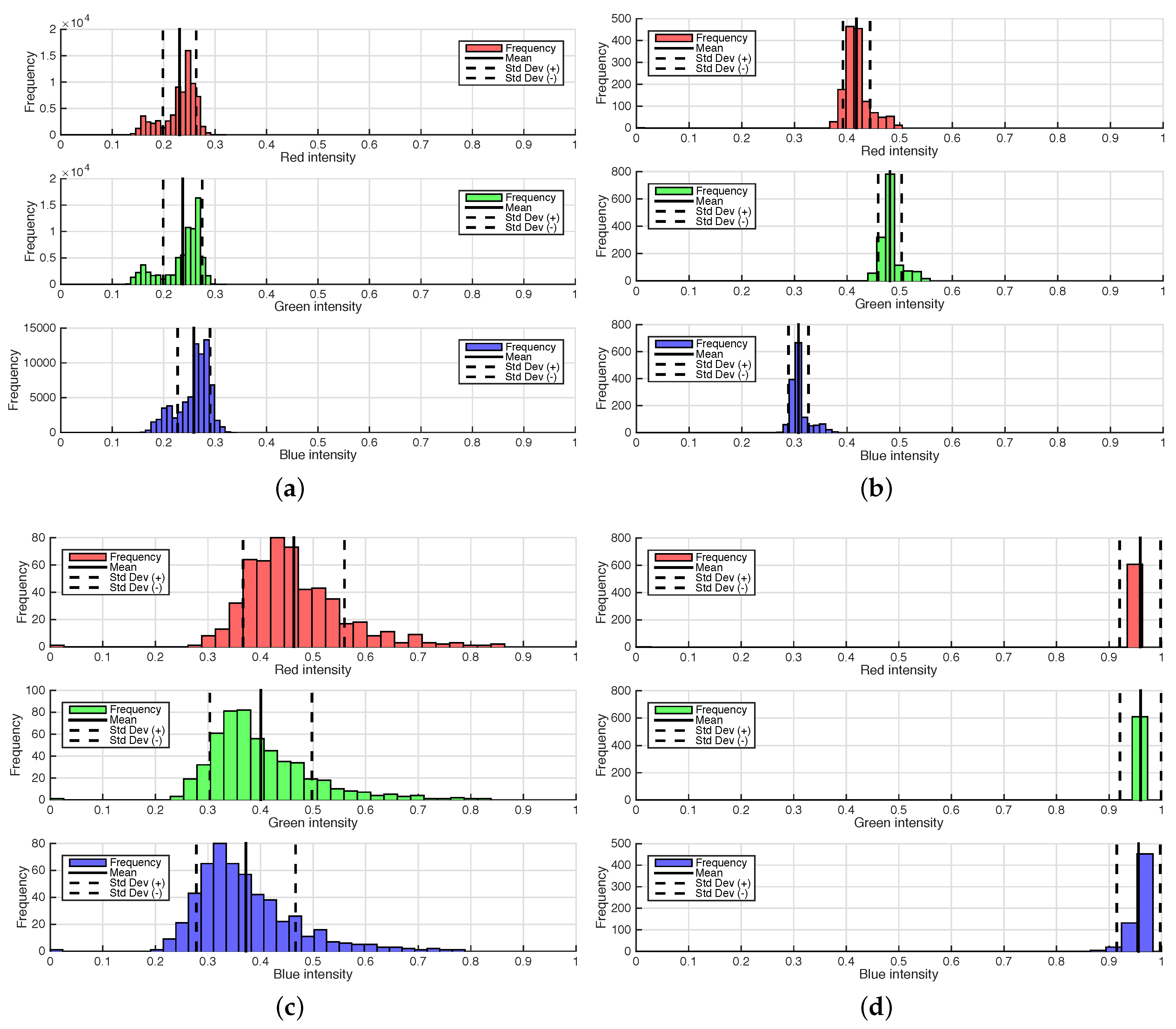
K-Means Algorithm

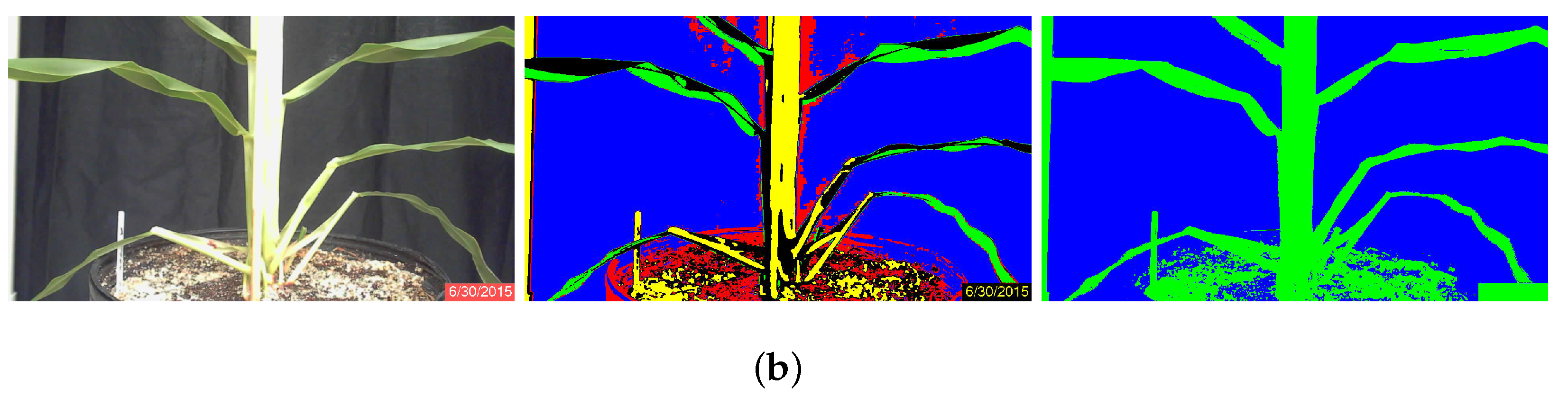
Minimum Distance Algorithm

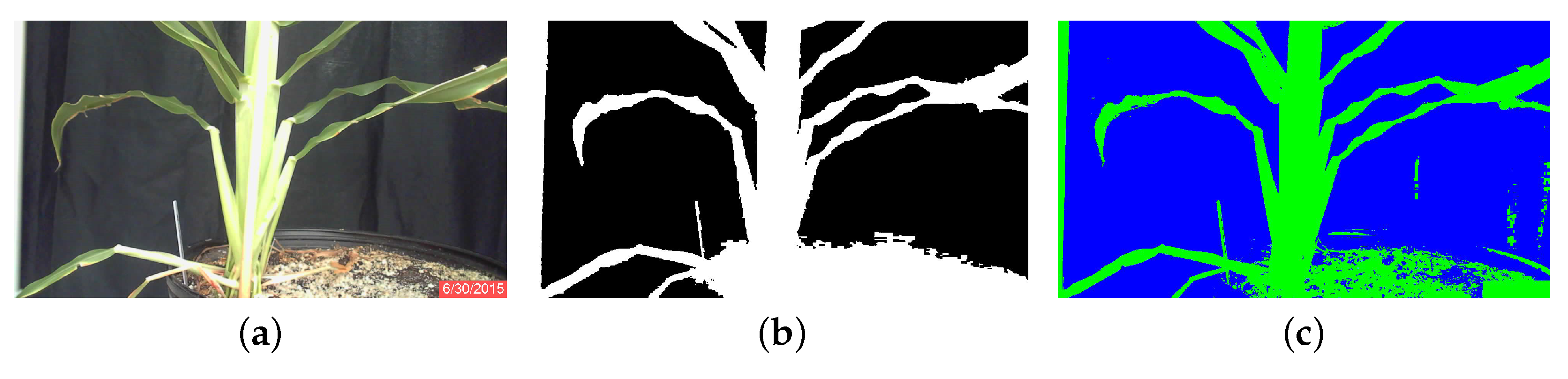
Stalk Thickness Calculation Algorithm
Depth Camera Accuracy

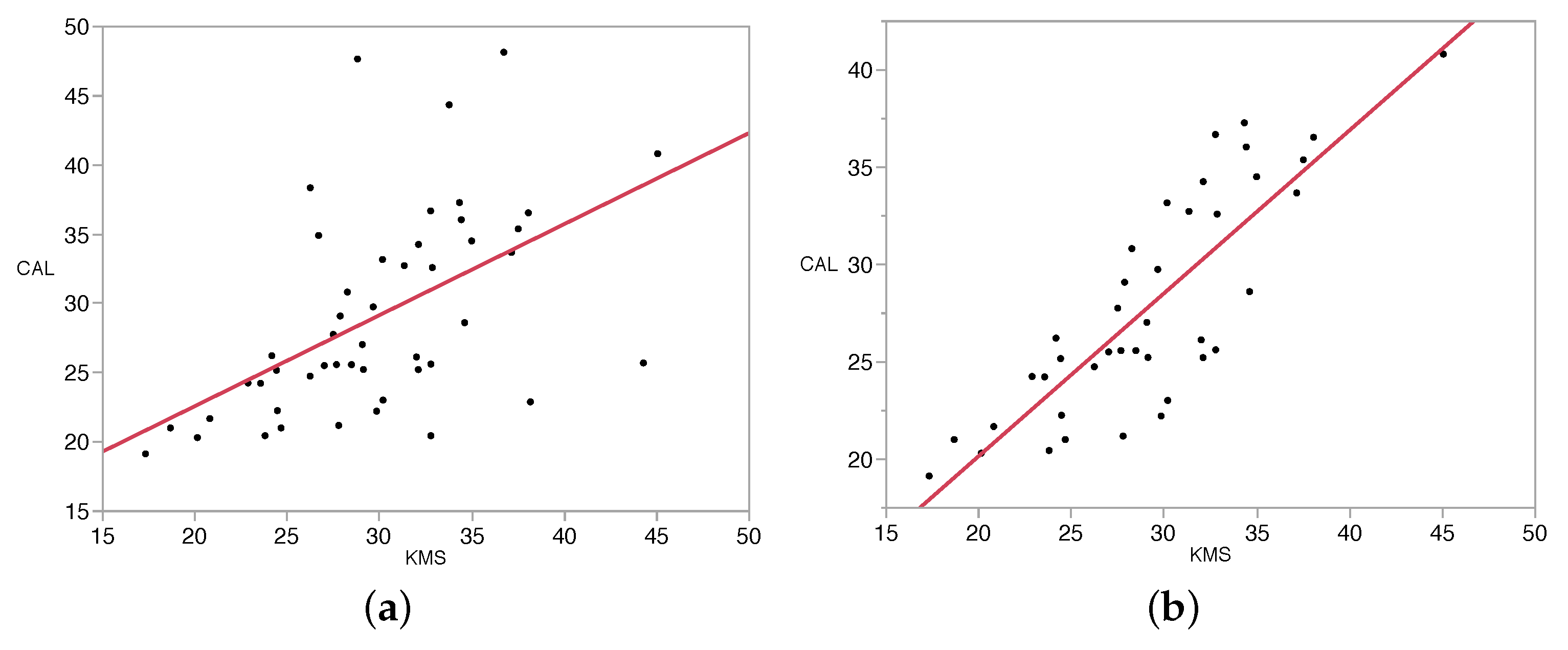
3. Results and Discussion
| Measured Value (mm) | Percent Error (%) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Date | Plant ID | Caliper Reading (mm) | KMU | MDU | KMS | MDS | KMU | MDU | KMS | MDS |
| 30 June | 1A | 25.58 | 24.12 | 32.27 | 28.47 | 27.47 | 5.71 | 26.17 | 11.29 | 7.41 |
| 2A | 33.17 | 28.96 | 40.13 | 30.15 | 29.18 | 12.69 | 20.98 | 9.12 | 12.04 | |
| 3A | 30.82 | 31.18 | 31.41 | 28.25 | 26.88 | 1.17 | 1.91 | 8.32 | 12.77 | |
| 4A | 32.59 | 35.75 | 35.11 | 32.85 | 27.31 | 9.70 | 7.74 | 0.80 | 16.20 | |
| 1B | 29.75 | 21.84 | 30.62 | 29.65 | 31.45 | 26.59 | 2.92 | 0.35 | 5.70 | |
| 2B | 28.61 | 27.57 | 37.41 | 34.60 | 32.96 | 3.64 | 30.78 | 20.95 | 15.19 | |
| 3B | 27.76 | 21.65 | 26.22 | 27.49 | 25.36 | 22.01 | 5.56 | 0.96 | 8.65 | |
| 4B | 25.62 | 60.49 | 39.14 | 32.77 | 26.98 | 136.10 | 52.79 | 27.90 | 5.29 | |
| 7 July | 1A | 40.81 | 19.07 | 58.85 | 45.05 | 49.09 | 53.27 | 44.20 | 10.38 | 20.28 |
| 2A | 48.14 | 34.41 | 41.70 | 36.72 | 38.83 | 28.52 | 13.38 | 23.73 | 19.34 | |
| 3A | 34.91 | 20.73 | 35.05 | 26.69 | 26.85 | 40.62 | 0.40 | 23.55 | 23.08 | |
| 4A | 44.34 | 29.50 | 36.88 | 33.76 | 34.52 | 33.47 | 16.82 | 23.86 | 22.15 | |
| 1B | 38.35 | 15.44 | 31.84 | 26.24 | 29.48 | 59.74 | 16.97 | 31.58 | 23.13 | |
| 2B | 32.73 | 21.52 | 32.23 | 31.33 | 29.43 | 34.25 | 1.51 | 4.29 | 10.07 | |
| 3B | 29.09 | 25.07 | 30.90 | 27.86 | 30.43 | 13.82 | 6.22 | 4.23 | 4.61 | |
| 4B | 47.65 | 20.16 | 28.48 | 28.80 | 29.31 | 57.69 | 40.23 | 39.56 | 38.49 | |
| 14 July | 1A | 36.54 | 35.44 | 34.25 | 38.05 | 32.10 | 3.01 | 6.27 | 4.13 | 12.16 |
| 2A | 36.04 | 40.80 | 40.50 | 34.42 | 32.92 | 13.21 | 12.38 | 4.51 | 8.64 | |
| 3A | 35.38 | 41.10 | 41.98 | 37.50 | 36.87 | 16.17 | 18.65 | 5.99 | 4.22 | |
| 4A | 33.68 | 41.59 | 35.09 | 37.14 | 36.47 | 23.49 | 4.20 | 10.27 | 8.29 | |
| 1B | 36.68 | 35.40 | 36.81 | 32.76 | 31.55 | 3.49 | 0.37 | 10.69 | 14.00 | |
| 2B | 34.51 | 31.20 | 36.08 | 34.98 | 35.55 | 9.59 | 4.54 | 1.36 | 3.00 | |
| 3B | 22.22 | 35.39 | 38.57 | 29.83 | 30.71 | 59.27 | 73.59 | 34.23 | 38.23 | |
| 4B | 37.28 | 44.04 | 34.63 | 34.32 | 31.37 | 18.13 | 7.11 | 7.94 | 15.85 | |
| 21 July | 1A | 20.45 | 28.60 | 31.55 | 32.77 | 31.88 | 39.85 | 54.29 | 60.24 | 55.91 |
| 2A | 25.51 | 22.77 | 25.98 | 27.00 | 26.77 | 10.74 | 1.84 | 5.82 | 4.94 | |
| 3A | 25.17 | 24.36 | 26.34 | 24.41 | 24.77 | 3.22 | 4.65 | 3.04 | 1.59 | |
| 4A | 34.26 | 31.41 | 32.74 | 32.10 | 32.20 | 8.32 | 4.43 | 6.32 | 6.01 | |
| 1B | 21.01 | 16.10 | 57.74 | 18.67 | 17.11 | 23.37 | 174.81 | 11.16 | 18.58 | |
| 2B | 24.75 | 37.99 | 25.20 | 26.23 | 27.25 | 53.49 | 1.83 | 5.98 | 10.11 | |
| 3B | 25.70 | 43.96 | 39.39 | 44.28 | 44.75 | 71.05 | 53.28 | 72.30 | 74.13 | |
| 4B | 22.89 | 37.24 | 36.41 | 38.16 | 38.99 | 62.69 | 59.07 | 66.71 | 70.32 | |
| 4 August | 1A | 21.01 | 24.12 | 23.31 | 24.66 | 23.14 | 14.80 | 10.97 | 17.35 | 10.12 |
| 2A | 25.22 | 28.96 | 29.13 | 32.09 | 32.09 | 14.83 | 15.50 | 27.24 | 27.24 | |
| 3A | 25.58 | 31.18 | 26.33 | 27.66 | 26.99 | 21.89 | 2.94 | 8.13 | 5.51 | |
| 4A | 27.03 | 35.75 | 24.83 | 29.06 | 29.70 | 32.26 | 8.15 | 7.49 | 9.88 | |
| 1B | 20.45 | 21.84 | 21.55 | 23.79 | 23.54 | 6.80 | 5.39 | 16.31 | 15.11 | |
| 2B | 23.02 | 27.57 | 27.43 | 30.18 | 30.48 | 19.77 | 19.17 | 31.08 | 32.41 | |
| 3B | 22.26 | 21.65 | 21.28 | 24.46 | 25.90 | 2.74 | 4.42 | 9.88 | 16.33 | |
| 4B | 26.22 | 60.49 | 22.49 | 24.16 | 24.31 | 130.70 | 14.21 | 7.88 | 7.29 | |
| 11 August | 1A | 24.23 | 19.07 | 23.31 | 23.55 | 23.64 | 21.30 | 3.78 | 2.83 | 2.42 |
| 2A | 25.23 | 34.41 | 29.13 | 29.12 | 27.96 | 36.39 | 15.46 | 15.42 | 10.81 | |
| 3A | 24.25 | 20.73 | 26.33 | 22.87 | 21.86 | 14.52 | 8.59 | 5.69 | 9.86 | |
| 4A | 26.13 | 29.50 | 24.83 | 31.99 | 30.26 | 12.90 | 4.99 | 22.43 | 15.80 | |
| 1B | 19.14 | 15.44 | 21.55 | 17.32 | 17.40 | 19.33 | 12.60 | 9.51 | 9.07 | |
| 2B | 20.31 | 21.52 | 27.43 | 20.13 | 20.32 | 5.96 | 35.07 | 0.91 | 0.02 | |
| 3B | 21.19 | 25.07 | 21.28 | 27.78 | 28.26 | 18.31 | 0.41 | 31.08 | 33.38 | |
| 4B | 21.68 | 20.16 | 22.49 | 20.80 | 20.96 | 7.01 | 3.76 | 4.06 | 3.34 | |
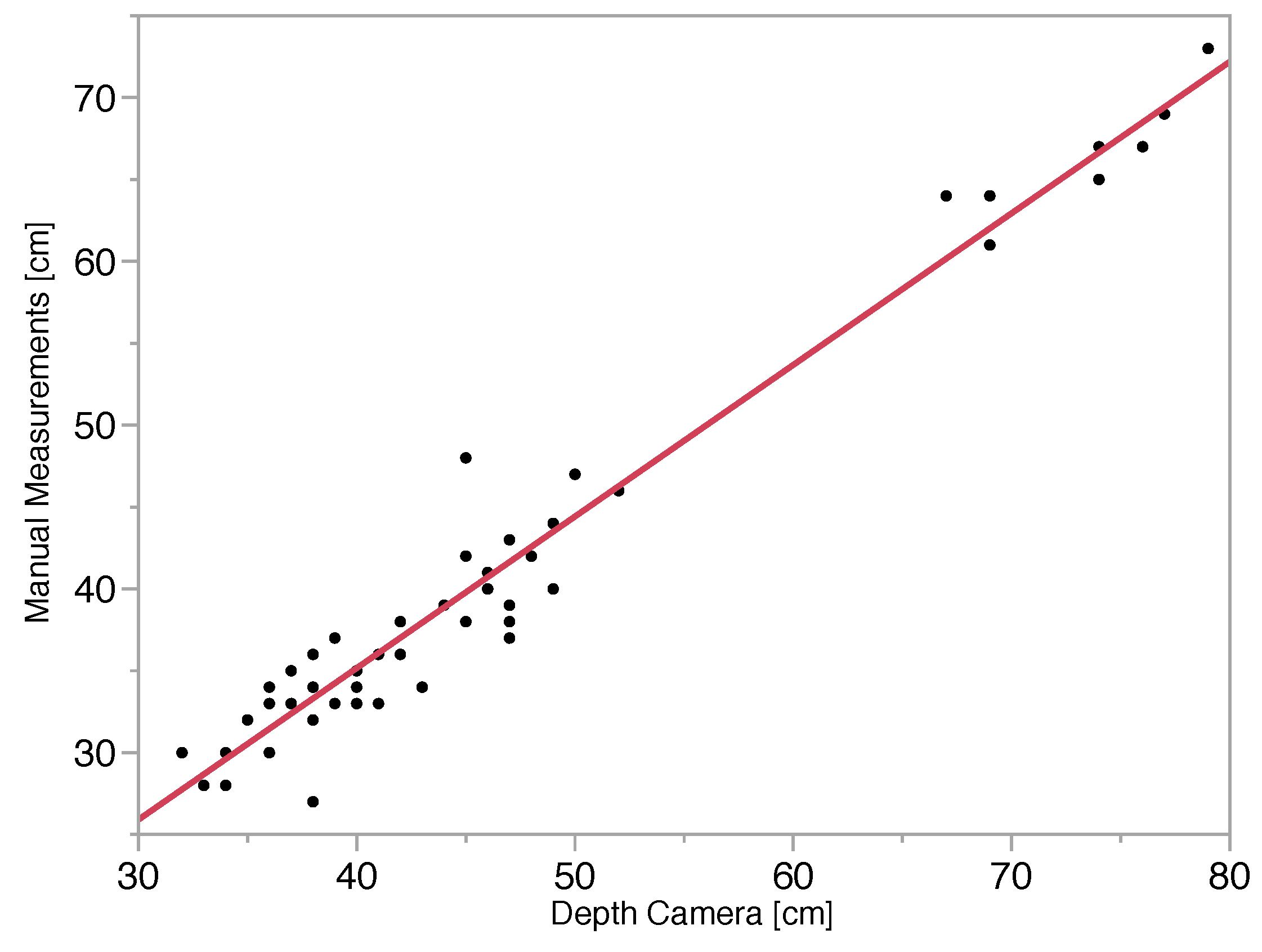
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Davies, J. Better distribution holds the key to future food security for all. Poult. World 2015, 170, 1–19. [Google Scholar]
- Koçar, G.; Civas, N. An overview of biofuels from energy crops: Current status and future prospects. Renew. Sustain. Energy Rev. 2013, 28, 900–916. [Google Scholar] [CrossRef]
- Chapman, S.C.; Chakraborty, S.; Dreccer, M.F.; Howden, S.M. Plant adaptation to climate change—Opportunities and priorities in breeding. Crop Pasture Sci. 2012, 63, 251–268. [Google Scholar] [CrossRef]
- Calviño, M.; Messing, J. Sweet sorghum as a model system for bioenergy crops. Curr. Opin. Biotechnol. 2012, 23, 323–329. [Google Scholar] [CrossRef] [PubMed]
- Cobb, J.N.; DeClerck, G.; Greenberg, A.; Clark, R.; McCouch, S. Next-generation phenotyping: Requirements and strategies for enhancing our understanding of genotype–phenotype relationships and its relevance to crop improvement. Theor. Appl. Genet. 2013, 126, 867–887. [Google Scholar] [CrossRef] [PubMed]
- Regassa, T.H.; Wortmann, C.S. Sweet sorghum as a bioenergy crop: Literature review. Biomass Bioenergy 2014, 64, 348–355. [Google Scholar] [CrossRef]
- Busemeyer, L.; Mentrup, D.; Möller, K.; Wunder, E.; Alheit, K.; Hahn, V.; Maurer, H.P.; Reif, J.C.; Würschum, T.; Müller, J.; et al. BreedVision—A Multi-Sensor Platform for Non-Destructive Field-Based Phenotyping in Plant Breeding. Sensors 2013, 13, 2830–2847. [Google Scholar] [CrossRef] [PubMed]
- Kicherer, A.; Herzog, K.; Pflanz, M.; Wieland, M.; Rüger, P.; Kecke, S.; Kuhlmann, H.; Töpfer, R. An Automated Field Phenotyping Pipeline for Application in Grapevine Research. Sensors 2015, 15, 4823–4836. [Google Scholar] [CrossRef] [PubMed]
- Klodt, M.; Herzog, K.; Töpfer, R.; Cremers, D. Field phenotyping of grapevine growth using dense stereo reconstruction. BMC Bioinf. 2015, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Upadhyaya, H.; Wang, Y.H.; Sharma, S.; Singh, S.; Hasenstein, K. SSR markers linked to kernel weight and tiller number in sorghum identified by association mapping. Euphytica 2012, 187, 401–410. [Google Scholar] [CrossRef]
- Mullet, J.; Morishige, D.; McCormick, R.; Truong, S.; Hilley, J.; McKinley, B.; Anderson, R.; Olson, S.; Rooney, W. Energy Sorghum—A genetic model for the design of C4 grass bioenergy crops. J. Exp. Bot. 2014, 65, 1–11. [Google Scholar] [CrossRef] [PubMed]
- van der Weijde, T.; Alvim Kamei, C.L.; Torres, A.F.; Wilfred, V.; Oene, D.; Visser, R.G.F.; Trindade, L.M. The potential of C4 grasses for cellulosic biofuel production. Front. Plant Sci. 2013, 4, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Trouche, G.; Bastianelli, D.; Cao Hamadou, T.V.; Chantereau, J.; Rami, J.F.; Pot, D. Exploring the variability of a photoperiod-insensitive sorghum genetic panel for stem composition and related traits in temperate environments. Field Crops Res. 2014, 166, 72–81. [Google Scholar] [CrossRef]
- Chéné, Y.; Rousseau, D.; Lucidarme, P.; Bertheloot, J.; Caffier, V.; Morel, P.; Belin, É.; Chapeau-Blondeau, F. On the use of depth camera for 3D phenotyping of entire plants. Comput. Electron. Agric. 2012, 82, 122–127. [Google Scholar] [CrossRef]
- Vollmann, J.; Walter, H.; Sato, T.; Schweiger, P. Digital image analysis and chlorophyll metering for phenotyping the effects of nodulation in soybean. Comput. Electron. Agric. 2011, 75, 190–195. [Google Scholar] [CrossRef]
- Chaivivatrakul, S.; Tang, L.; Dailey, M.N.; Nakarmi, A.D. Automatic morphological trait characterization for corn plants via 3D holographic reconstruction. Comput. Electron. Agric. 2014, 109, 109–123. [Google Scholar] [CrossRef]
- Roscher, R.; Herzog, K.; Kunkel, A.; Kicherer, A.; Töpfer, R.; Förstner, W. Automated image analysis framework for high-throughput determination of grapevine berry sizes using conditional random fields. Comput. Electron. Agric. 2014, 100, 148–158. [Google Scholar] [CrossRef]
- Aksoy, E.E.; Abramov, A.; Wörgötter, F.; Scharr, H.; Fischbach, A.; Dellen, B. Modeling leaf growth of rosette plants using infrared stereo image sequences. Comput. Electron. Agric. 2015, 110, 78–90. [Google Scholar] [CrossRef]
- Fahlgren, N.; Gehan, M.A.; Baxter, I. Lights, camera, action: High-throughput plant phenotyping is ready for a close-up. Curr. Opin. Plant Biol. 2015, 24, 93–99. [Google Scholar] [CrossRef] [PubMed]
- Kolukisaoglu, Ü.; Thurow, K. Future and frontiers of automated screening in plant sciences. Plant Sci. 2010, 178, 476–484. [Google Scholar] [CrossRef]
- Lobet, G.; Draye, X.; Périlleux, C. An online database for plant image analysis software tools. Plant Methods 2013, 9. [Google Scholar] [CrossRef] [PubMed]
- Colombi, T.; Kirchgessner, N.; Le Marié, C.; York, L.; Lynch, J.; Hund, A. Next generation shovelomics: Set up a tent and REST. Plant Soil 2015, 388, 1–20. [Google Scholar] [CrossRef]
- Bucksch, A.; Burridge, J.; York, L.M.; Das, A.; Nord, E.; Weitz, J.S.; Lynch, J. Image-Based High-Throughput Field Phenotyping of Crop Roots. Plant Physiol. 2014, 166, 470–486. [Google Scholar] [CrossRef] [PubMed]
- Rooney, W.L.; (Soil and Crop Science Professor, Texas A&M University, College Station, TX, USA) Stalk diameter measure location in energy sorghum. Personal communication, 2015.
- Corke, P. Robotics, Vision and Control: Fundamental Algorithms in MATLAB; Springer Science & Business Media: Berlin, Germany, 2011; Volume 73. [Google Scholar]
- Ghimire, S.; Wang, H. Classification of image pixels based on minimum distance and hypothesis testing. Comput. Stat. Data Anal. 2012, 56, 2273–2287. [Google Scholar] [CrossRef]
- Liang, B.; Zhang, J. KmsGC: An Unsupervised Color Image Segmentation Algorithm Based on K-Means Clustering and Graph Cut. Math. Probl. Eng. 2014, 2014, 464875. [Google Scholar] [CrossRef]
- Sert, E.; Okumus, I.T. Segmentation of mushroom and cap width measurement using modified K-means clustering algorithm. Adv. Electr. Electron. Eng. 2014, 12, 354–360. [Google Scholar] [CrossRef]
- Yu, W.; Wang, J.; Ye, L. An Improved Normalized Cut Image Segmentation Algorithm with K-means Cluster. Appl. Mech. Mater. 2014, 548–549, 1179–1184. [Google Scholar] [CrossRef]
- Neter, J.; Kutner, M.H.; Nachtsheim, C.J.; Wasserman, W. Applied Linear Statistical Models, 4th ed.; McGraw-Hill: Boston, MA, USA, 1996. [Google Scholar]
- Cline, D. Statistical Analysis; STAT 601 Class Notes; Texas A&M University: College Station, TX, USA, 2015. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Batz, J.; Méndez-Dorado, M.A.; Thomasson, J.A. Imaging for High-Throughput Phenotyping in Energy Sorghum. J. Imaging 2016, 2, 4. https://doi.org/10.3390/jimaging2010004
Batz J, Méndez-Dorado MA, Thomasson JA. Imaging for High-Throughput Phenotyping in Energy Sorghum. Journal of Imaging. 2016; 2(1):4. https://doi.org/10.3390/jimaging2010004
Chicago/Turabian StyleBatz, Jose, Mario A. Méndez-Dorado, and J. Alex Thomasson. 2016. "Imaging for High-Throughput Phenotyping in Energy Sorghum" Journal of Imaging 2, no. 1: 4. https://doi.org/10.3390/jimaging2010004
APA StyleBatz, J., Méndez-Dorado, M. A., & Thomasson, J. A. (2016). Imaging for High-Throughput Phenotyping in Energy Sorghum. Journal of Imaging, 2(1), 4. https://doi.org/10.3390/jimaging2010004






