High-Throughput ORB Feature Extraction on Zynq SoC for Real-Time Structure-from-Motion Pipelines
Abstract
1. Introduction
1.1. FPGA vs. ASIC Rationale
Contributions
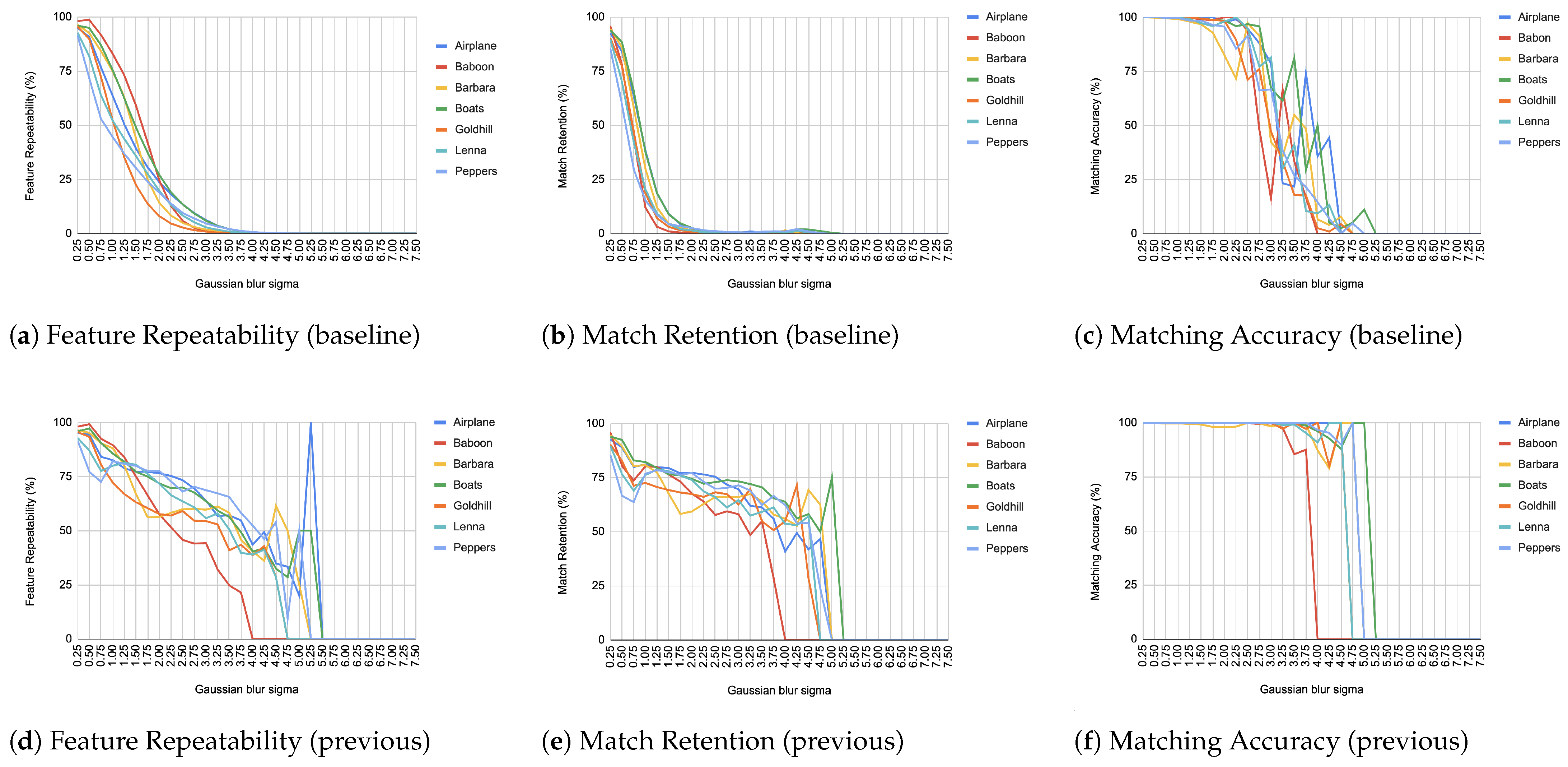
- An optimized version of the ORB algorithm is presented, enabling real-time structure from motion for monocular vision. The system achieves 60 fps at full-HD resolution.
- A low-latency, double-data-rate (DDR) memory scheme is implemented for the Harris–Stephens corner detector, minimizing propagation delay in the data path.
- A comprehensive evaluation of the architecture is provided, including feature repeatability, matching retention, and accuracy—demonstrating the precision of the proposed ORB core.
2. Related Work
2.1. Feature Detection and Description Algorithms
2.2. Structure from Motion (SFM) Pipelines
2.3. FPGA-Based Implementations
3. Materials and Methods
3.1. Methodology
3.1.1. Choice of ORB
3.1.2. Modifications for SfM
3.1.3. Optimization for FPGA
3.2. Implementation
- A new pixel is inserted ().
- The FAST algorithm is applied to the central pixel of the sliding window (comparing the yellow with the orange pixels).
- The descriptor for the central pixel ( yellow) is created.
- The pixel (red) is checked if it constitutes a feature, and if it is, its descriptor is exported.
3.2.1. FAST Algorithm and Descriptor Extraction
3.2.2. Harris Response Calculation
- Clock edge 1 (rising): Insertion of a new pixel in the image patch (shift the image patch by one position).
- Clock edge 2 (falling): Derivative calculation part 1. Prewitt masks are applied to each pixel within the red square (depicted in Figure 2) to calculate the partial derivatives in the x and y directions. In this step, four values are produced for each pixel. These are the sums of the pixel intensities of the column on its right and on its left as well as the sums of the pixel intensities of the rows above and below.
- Clock edge 3 (rising): Derivative calculation part 2. In this step, the difference between the sums along the x and y directions and the application of the absolute value are performed. Now, each pixel within the red square has its partial derivatives computed.
- Clock edge 4 (falling): Computation of the products , and ·, required for the calculation of the second moment matrix used in the Harris criterion, from the derivatives of the previous step. The , and · derivative values are calculated not only for the central pixel k14_14 but also for its neighboring pixels (within the red square). This is required when weighting the derivatives based on the distance from the center pixel by applying a Gaussian kernel.
- Clock edge 5 (rising): Multiplication of , and · of each pixel by the corresponding element in the Gaussian kernel. Multiplication refers to integer numbers. More details on convolution with the Gaussian kernel are provided in Section 3.2.4.
- Clock edge 6 (falling): Division of the results of the previous step by applying the appropriate number of bit shifts to the right. This step is required to produce image convolution results from a normalized Gaussian kernel.
- Clock edge 7 (rising): Gaussian sum part 1. The results of the convolution between the values of , and · and the Gaussian kernel for the central pixel require the addition of the nine elements of the 3 × 3 matrices obtained from the previous steps. In this step, a sum takes place for each row, producing three intermediate results.
- Clock edge 8 (falling): Gaussian sum part 2. The sum of the intermediate results of the previous step is calculated to obtain the weighted values gk(, gk(), and gk(·) for the central pixel k14_14. The separation of the sum into two steps is critical since the addition of nine elements would violate the maximum propagation delay in the datapath to support 60 fps full-HD video frames.
- Clock edge 9 (rising): Calculation of the determinant and the of the matrix produced in the previous step.
- Clock edge 10 (falling): Multiplication between the trace of M and 0.05 (the constant k is selected as 0.05). The operation is accomplished by approximating the 0.05 with 51/1024. First, multiplication by 51 takes place; afterwards, by shifting 10 times the product to the right, the quotient of the division is produced.
- Clock edge 11 (rising): Computation of the Harris response (R) by subtracting the result in the previous step from the determinant of M.
3.2.3. Feature Point Extraction
3.2.4. Hardware Friendly Floating Point Multiplication and Gaussian Convolution
- 1.
- A power of two is selected and multiplied by the element of the Gaussian kernel, herein 0.09235312. In the design, the power of two used is 1024. This means .
- 2.
- The product is rounded to the nearest integer, which is .
- 3.
- The multiplication performed in hardware is between 95 and the square of the partial derivative (350). Both multiplicands are integers. The product is .
- 4.
- Finally, 10 right shifts are applied to produce the result of the initial multiplication. In this case, , so is 32.
3.2.5. Room for Improvement
4. Results and Discussion
4.1. Software Validation
- 1.
- A match must be at least 75% better than the second-best match (Lowe’s ratio test [12]).
- 2.
- The match must be at least 75% identical (a quality threshold that we define).
4.2. Comparing Against a Widely Accepted Implementation
4.3. Hardware Validation
4.4. Resource Usage
4.5. Video Input from Camera and the Noise Issue
5. Future Work
- 1.
- Feature matching.
- 2.
- Geometric verification.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AXI4 | Advanced eXtensible Interface |
| BRAM | Block RAM |
| BRIEF | Binary Robust Independent Elementary Features |
| rBRIEF | Rotated Binary Robust Independent Elementary Features |
| CPU | Central Processing Unit |
| DDR | Double Data Rate |
| DMA | Direct Memory Access |
| DOAJ | Directory of open access journals |
| FAST | Features from Accelerated Segment Test |
| FIFO | First-In, First-Out |
| FPGA | Field Programmable Gate Array |
| fps | frames per second |
| HDMI | High-Definition Multimedia Interface |
| ILA | Integrated Logic Analyzer |
| IP | Intellectual Property |
| LUT | Look-Up Table |
| MDPI | Multidisciplinary Digital Publishing Institute |
| ORB | Oriented FAST and rotated BRIEF |
| RANSAC | Random Sample Consensus |
| SfM | Structure from Motion |
| SLAM | Simultaneous Localization And Mapping |
| SoC | System On a Chip |
| UHD | Ultra-High Definition |
| VHDL | VHSIC Hardware Description Language |
| VHSIC | Very-High-Speed Integrated Circuit |
References
- Song, S.; Chandraker, M.; Guest, C.C. High Accuracy Monocular SFM and Scale Correction for Autonomous Driving. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 730–743. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, X.; Liu, X.; Lu, S.; Tang, H. Facing challenges: A survey of object tracking. Digit. Signal Process. 2025, 161, 105082. [Google Scholar] [CrossRef]
- Wei, Y.M.; Kang, L.; Yang, B.; Wu, L.D. Applications of structure from motion: A survey. J. Zhejiang Univ.-Sci. C 2013, 14, 486–494. [Google Scholar] [CrossRef]
- Giordan, D.; Godone, D.; Baldo, M.; Piras, M.; Grasso, N.; Zerbetto, R. Survey Solutions for 3D Acquisition and Representation of Artificial and Natural Caves. Appl. Sci. 2021, 11, 6482. [Google Scholar] [CrossRef]
- Glette, K.; Torresen, J.; Hovin, M. Intermediate Level FPGA Reconfiguration for an Online EHW Pattern Recognition System. In Proceedings of the 2009 NASA/ESA Conference on Adaptive Hardware and Systems, San Francisco, CA, USA, 29 July–1 August 2009; pp. 19–26. [Google Scholar]
- Wan, Z.; Yu, B.; Li, T.Y.; Tang, J.; Zhu, Y.; Wang, Y. A Survey of FPGA-Based Robotic Computing. IEEE Circuits Syst. Mag. 2021, 21, 48–74. [Google Scholar] [CrossRef]
- Chelton, W.N.; Benaissa, M. Fast Elliptic Curve Cryptography on FPGA. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2008, 16, 198–205. [Google Scholar] [CrossRef]
- Kastensmidt, F.; Rech, P. FPGAs and Parallel Architectures for Aerospace Applications: Soft Errors and Fault-Tolerant Design; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Rublee, E.; Rabaud, V.; Konolige, K.; Bradski, G. ORB: An efficient alternative to SIFT or SURF. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011. [Google Scholar]
- Harris, C.; Stephens, M. A Combined Corner and Edge Detector. In Proceedings of the Alvey Vision Conference, Manchester, UK, 31 August–2 September 1988; pp. 15.1–15.6. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the International Conference on Computer Vision (ICCV), Kerkyra, Greece, 20–27 September 1999; Volume 2, pp. 1150–1157. [Google Scholar]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Bay, H.; Ess, A.; Tuytelaars, T.; Van Gool, L. Speeded Up Robust Features. In Computer Vision and Image Understanding; ETH Zurich: Zürich, Switzerland; Katholieke Universiteit Leuven: Leuven, Belgium, 2008; Volume 110, pp. 346–359. [Google Scholar]
- Moulon, P.; Monasse, P.; Perrot, R.; Marlet, R. OpenMVG: Open Multiple View Geometry. In Reproducible Research in Pattern Recognition (RRPR 2016); Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2016; Volume 10214. [Google Scholar]
- Schönberger, J.; Zheng, E.; Pollefeys, M.; Frahm, J.M. Pixelwise View Selection for Unstructured Multi-View Stereo. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016. [Google Scholar]
- Schönberger, J.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 26 June–1 July 2016. [Google Scholar]
- Adorjan, M. OpenSfM: A Collaborative Structure-from-Motion System. Bachelor’s Thesis, Vienna University of Technology, Vienna, Austria, 2016. Registration Number 0927290. [Google Scholar]
- AliceVision. Available online: https://github.com/alicevision/AliceVision/releases (accessed on 2 April 2025).
- Komorkiewicz, M.; Kryjak, T.; Chuchacz-Kowalczyk, K.; Skruch, P.; Gorgoń, M. FPGA based system for real-time structure from motion computation. In Proceedings of the 2015 Conference on Design and Architectures for Signal and Image Processing (DASIP), Krakow, Poland, 23–25 September 2015; pp. 1–7. [Google Scholar]
- Weberruss, J.; Kleeman, L.; Drummond, T. ORB feature extraction and matching in hardware. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Seattle, WA, USA, 26–30 May 2015. [Google Scholar]
- Weberruss, J.; Kleeman, L.; Boland, D.; Drummond, T. FPGA acceleration of multilevel ORB feature extraction for computer vision. In Proceedings of the 2017 27th International Conference on Field Programmable Logic and Applications (FPL), Ghent, Belgium, 4–8 September 2017; pp. 1–8. [Google Scholar]
- Fang, W.; Zhang, Y.; Yu, B.; Liu, S. FPGA-based ORB feature extraction for real-time visual SLAM. In Proceedings of the 2017 International Conference on Field Programmable Technology (ICFPT), Melbourne, Australia, 11–13 December 2017; pp. 275–278. [Google Scholar]
- de Lima, R.; Martinez-Carranza, J.; Morales-Reyes, A.; Cumplido, R. Improving the construction of ORB through FPGA-based acceleration. Mach. Vis. Appl. 2017, 28, 525–537. [Google Scholar] [CrossRef]
- Kalms, L.; Ibrahim, H.; Göhringer, D. Full-HD Accelerated and Embedded Feature Detection Video System with 63fps Using ORB for FREAK. In Proceedings of the 2018 International Conference on ReConFigurable Computing and FPGAs (ReConFig), Cancun, Mexico, 3–5 December 2018; pp. 1–6. [Google Scholar]
- Liu, R.; Yang, J.; Chen, Y.; Zhao, W. ESLAM: An Energy-Efficient Accelerator for Real-Time ORB-SLAM on FPGA Platform. In Proceedings of the 56th Annual Design Automation Conference (DAC ’19), Las Vegas, NV, USA, 2–6 June 2019. [Google Scholar]
- Sun, R.; Qian, J.; Jose, R.H.; Gong, Z.; Miao, R.; Xue, W.; Liu, P. A Flexible and Efficient Real-Time ORB-Based Full-HD Image Feature Extraction Accelerator. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2020, 28, 565–575. [Google Scholar] [CrossRef]
- Taranco, R.; Arnau, J.-M.; Gonzalez, A. A Low-Power Hardware Accelerator for ORB Feature Extraction in Self-Driving Cars. In Proceedings of the 2021 Symposium on Computer Architecture and High Performance Computing (SBAC-PAD), Porto Alegre, Brazil, 17–20 September 2021; pp. 11–21. [Google Scholar]
- Vemulapati, V.; Chen, D.; ORB-based SLAM accelerator on SoC FPGA. Preprint. 2022. Available online: https://arxiv.org/abs/2207.08405 (accessed on 4 April 2025).
- Wasala, M.; Szolc, H.; Kryjak, T. An Efficient Real-Time FPGA-Based ORB Feature Extraction for an UHD Video Stream for Embedded Visual SLAM. Electronics 2022, 11, 2259. [Google Scholar] [CrossRef]
- Belmessaoud, N.M.; Bentoutou, Y.; El-Mezouar, M.C. FPGA implementation of feature detection and matching using ORB. Microprocess. Microsyst. 2022, 94, 104666. [Google Scholar] [CrossRef]
- Zhang, Q.; Sun, H.; Deng, Q.; Yu, H.; Ha, Y. NORB: A Stream-Based and Non-Blocking FPGA Accelerator for ORB Feature Extraction. In Proceedings of the 2023 30th IEEE International Conference on Electronics, Circuits and Systems (ICECS), Marrakech, Morocco, 17–20 December 2023; pp. 1–4. [Google Scholar]
- Qi, X.; Liu, Y.; Hao, S.; Liu, Z.; Huang, K.; Yang, M.; Zhou, L.; Zhou, J. A High-Performance ORB Accelerator with Algorithm and Hardware Co-design for Visual Localization. In Proceedings of the 2024 IEEE International Symposium on Circuits and Systems (ISCAS), Tokyo, Japan, 19–22 May 2024; pp. 1–5. [Google Scholar]
- Noble, F.K. Comparison of OpenCV’s feature detectors and feature matchers. In Proceedings of the 2016 23rd International Conference on Mechatronics and Machine Vision in Practice (M2VIP), Nanjing, China, 28–30 November 2016; pp. 1–6. [Google Scholar]
- Tafti, A.P.; Baghaie, A.; Kirkpatrick, A.B.; Holz, J.D.; Owen, H.A.; D’Souza, R.M.; Yu, Z. A comparative study on the application of SIFT, SURF, BRIEF and ORB for 3D surface reconstruction of electron microscopy images. Comput. Methods Biomech. Biomed. Eng. Imaging Vis. 2018, 6, 17–30. [Google Scholar] [CrossRef]
- Tareen, S.A.K.; Saleem, Z. A comparative analysis of SIFT, SURF, KAZE, AKAZE, ORB, and BRISK. In Proceedings of the 2018 International Conference on Computing, Mathematics and Engineering Technologies (iCoMET), Sukkur, Pakistan, 3–4 March 2018; pp. 1–10. [Google Scholar]
- Yakovleva, O.; Nikolaieva, K. Research of descriptor based image normalization and comparative analysis of SURF, SIFT, BRISK, ORB, KAZE, AKAZE descriptors. Adv. Inf. Syst. 2020, 4, 89–101. [Google Scholar] [CrossRef]
- Calonder, M.; Lepetit, V.; Ozuysal, M.; Trzcinski, T.; Strecha, C.; Fua, P. BRIEF: Computing a local binary descriptor very fast. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 34, 1281–1298. [Google Scholar] [CrossRef] [PubMed]
- ScikitImage. Available online: https://github.com/scikit-image/scikit-image (accessed on 30 September 2024).
- Vourvoulakis, J.; Lygouras, J.; Kalomiros, J. Acceleration of RANSAC algorithm for images with affine transformation. In Proceedings of the 2016 IEEE International Conference on Imaging Systems and Techniques (IST), Chania, Greece, 4–6 October 2016; pp. 1–5. [Google Scholar]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamatakis, P.; Vourvoulakis, J. High-Throughput ORB Feature Extraction on Zynq SoC for Real-Time Structure-from-Motion Pipelines. J. Imaging 2025, 11, 178. https://doi.org/10.3390/jimaging11060178
Stamatakis P, Vourvoulakis J. High-Throughput ORB Feature Extraction on Zynq SoC for Real-Time Structure-from-Motion Pipelines. Journal of Imaging. 2025; 11(6):178. https://doi.org/10.3390/jimaging11060178
Chicago/Turabian StyleStamatakis, Panteleimon, and John Vourvoulakis. 2025. "High-Throughput ORB Feature Extraction on Zynq SoC for Real-Time Structure-from-Motion Pipelines" Journal of Imaging 11, no. 6: 178. https://doi.org/10.3390/jimaging11060178
APA StyleStamatakis, P., & Vourvoulakis, J. (2025). High-Throughput ORB Feature Extraction on Zynq SoC for Real-Time Structure-from-Motion Pipelines. Journal of Imaging, 11(6), 178. https://doi.org/10.3390/jimaging11060178






