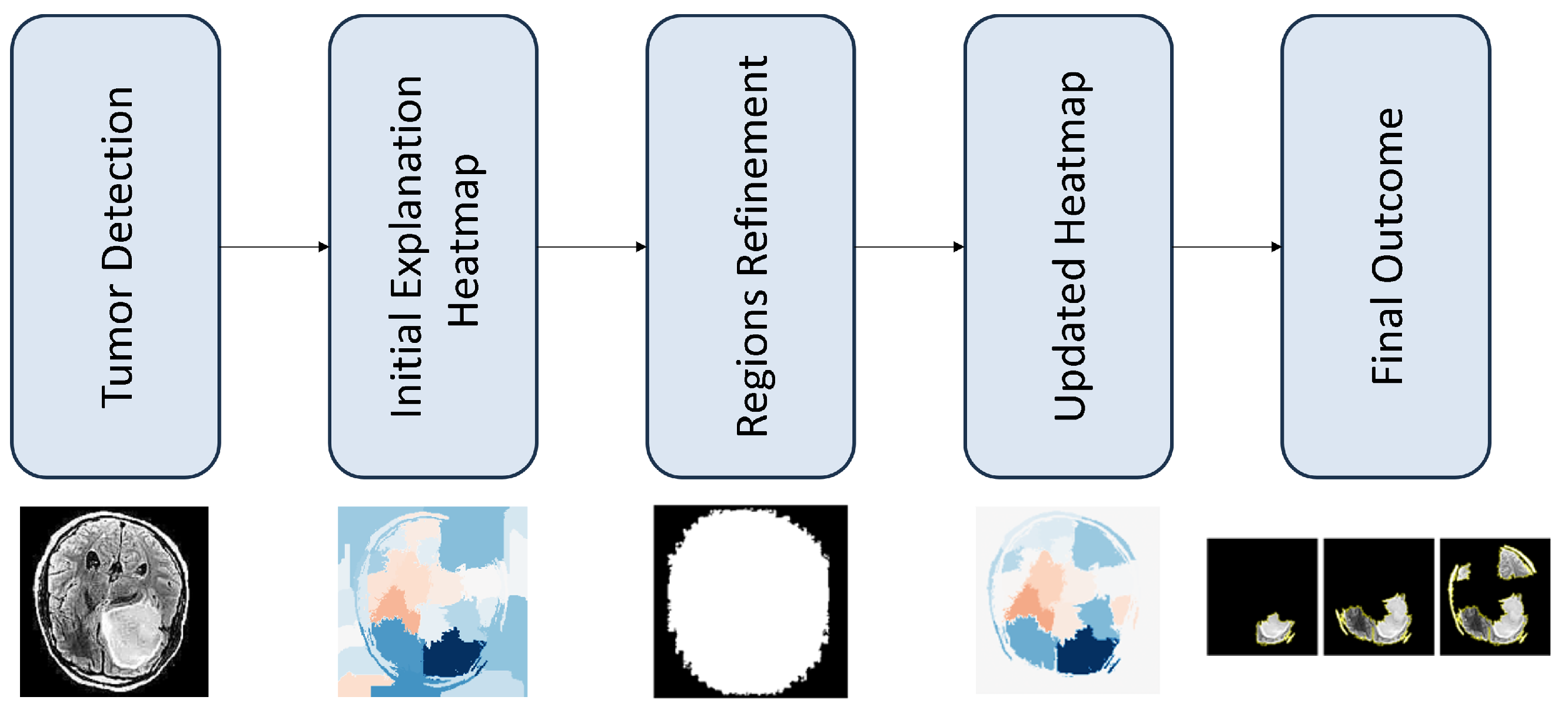
The proposed scheme was evaluated using a publicly available dataset, which is described in the end of this article. The objective of the methodology was to refine the LIE-generated heatmaps by removing topology-related inconsistencies. All of the experiments conducted were employed using Python utilizing public libraries (Tensorflow, Skimage, Sklearn, Shapely, Lime, and Matplotlib). The computations were performed in Google Colab with GPU acceleration enabled.
At this point, we need to stress that the setup was arranged to provide robust conclusions about the impact of combining different image segmentation algorithms and edge detection techniques within the LIMEs framework. Our approach aimed to refine and enhance the interpretability of model predictions. The optimal configuration of these methodologies will be explored in future work to further improve the reliability and accuracy of tumor detection.
The following sections present the datasets employed in this study and the approach followed to form training and evaluation sets. Then, we present the details of selecting the classification model that performed best in the specific dataset. Finally, we discuss the obtained results and their implications for improving the interpretability of the deep learning models examined in our study.
4.2. Performance Metrics
Each deep learning model’s performance was evaluated using typical metrics like accuracy, precision, recall, and F1 score. These metrics rely on key elements such as True Positive (TP) values, True Negative (TN) values, False Positive (FP) values, and False Negative (FN) values. These metrics are defined as follows:
In addition to these metrics, we introduced a new metric to evaluate how well the segments from LimeImageExplainer matched the presence of tumors. Using the VGG Image Annotator, manual annotations of the tumor were performed on 271 images out of the 471 infected instances in the test set. These images were selected for their relative ease of annotation. This custom metric aims to quantify the percentage of the brain tumor included in the explanation’s segments, and we will refer to it as “Tumor Segment Coverage”.
To be more specific, after the use of the VGG Image Annotator, a new mask that represents the location of the tumor was created. This means that a pixel of the original image
belongs in the Tumor Mask if and only if this pixel is inside of the tumor polygon that is created. With this mask, to find the Tumor Segment Coverage (TSC), we calculated the percentage of pixels that were both part of the mask and the tumor annotation.
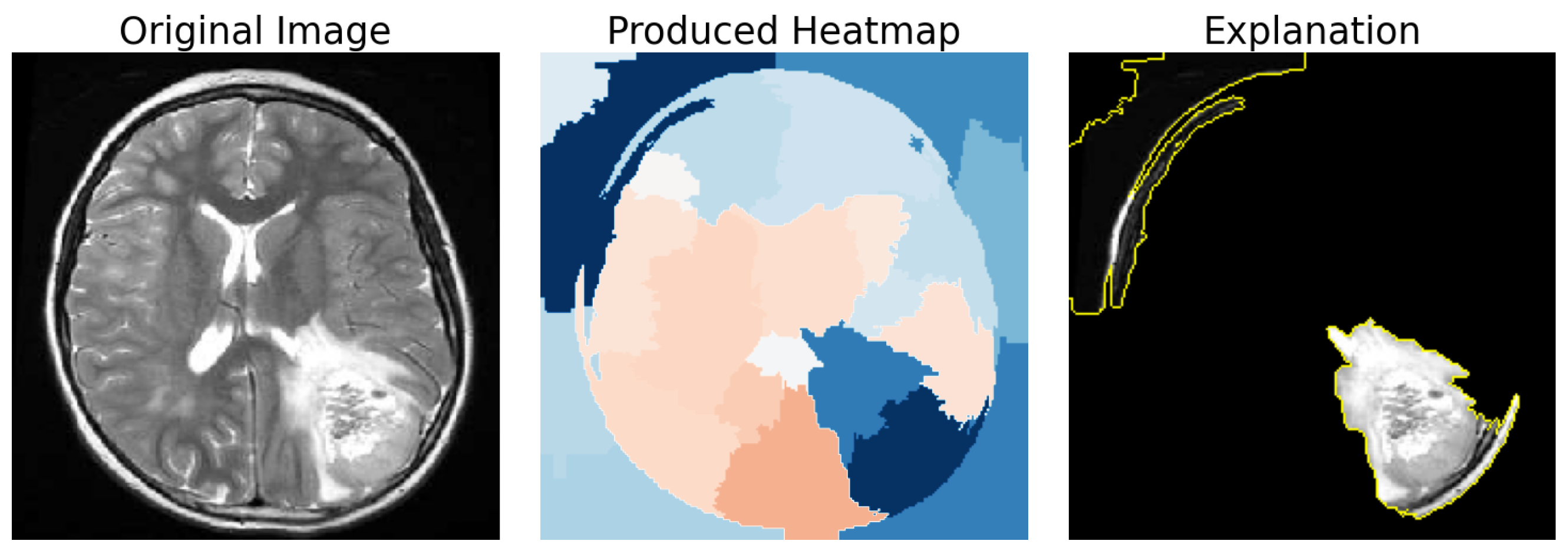
Figure 7 demonstrates such a case with a Tumor Segment Coverage of 51.75%.
In addition we used another metric called “Brain Segment Coverage” (BSC), and it defines the percentage of brain mask covered by the explanation’s segments. This means that, after we produced the refined explanation, we calculated the percentage of the pixels that were part of the explanation and also belonged in the brain mask that was created using an edge detector, as explained in
Section 3.4.
Figure 8 demonstrates such a case with a brain coverage score of 21.92%.
4.3. Segmentation-Based Refinement Impact
This section demonstrates the possible impact, for the proposed refinment methodology, as discused in
Section 3.4. In particular, we started by selecting the best classification model and then produced explanations for the MRI images using the LIE. We then examined the results produced after the use of our refinement method.
Table 1 and
Figure 9 demonstrate the performance scores for the models’ predictions for every fold. ResNet50V2 appears to be the most prominent classifier in terms of its F1 score.
To compare the pre-trained models, we conducted a statistical Mann–Whitney test on their F1 scores, considering both the scores obtained during cross-validation and after. The test showed that ResNet50v2 outperformed both InceptionV3 (p = 0.02) and NasNetLarge (p = 0.008). However, there was no significant difference between InceptionV3 and NasNetLarge (p = 0.39). Given these results, we chose ResNet50v2 for further analysis in the explainability part.
As mentioned before, the LimeImageExplainer was employed to provide explanations for model predictions before and after the proposed refinement. We used three segmentation algorithms in order to separate the image into segments: QuickShift, Slic, and Felzenszwalb. We also used five edge detection techniques, as mentioned in
Section 3.3. There were two quantitative criterion used for the performance of the adopted approaches: (a) BSC and (b) TSC. The former validates whether the applied image processing techniques correctly identify the brain areas. The latter demonstrates how practical is, for the medical experts, the
n most important image segments.
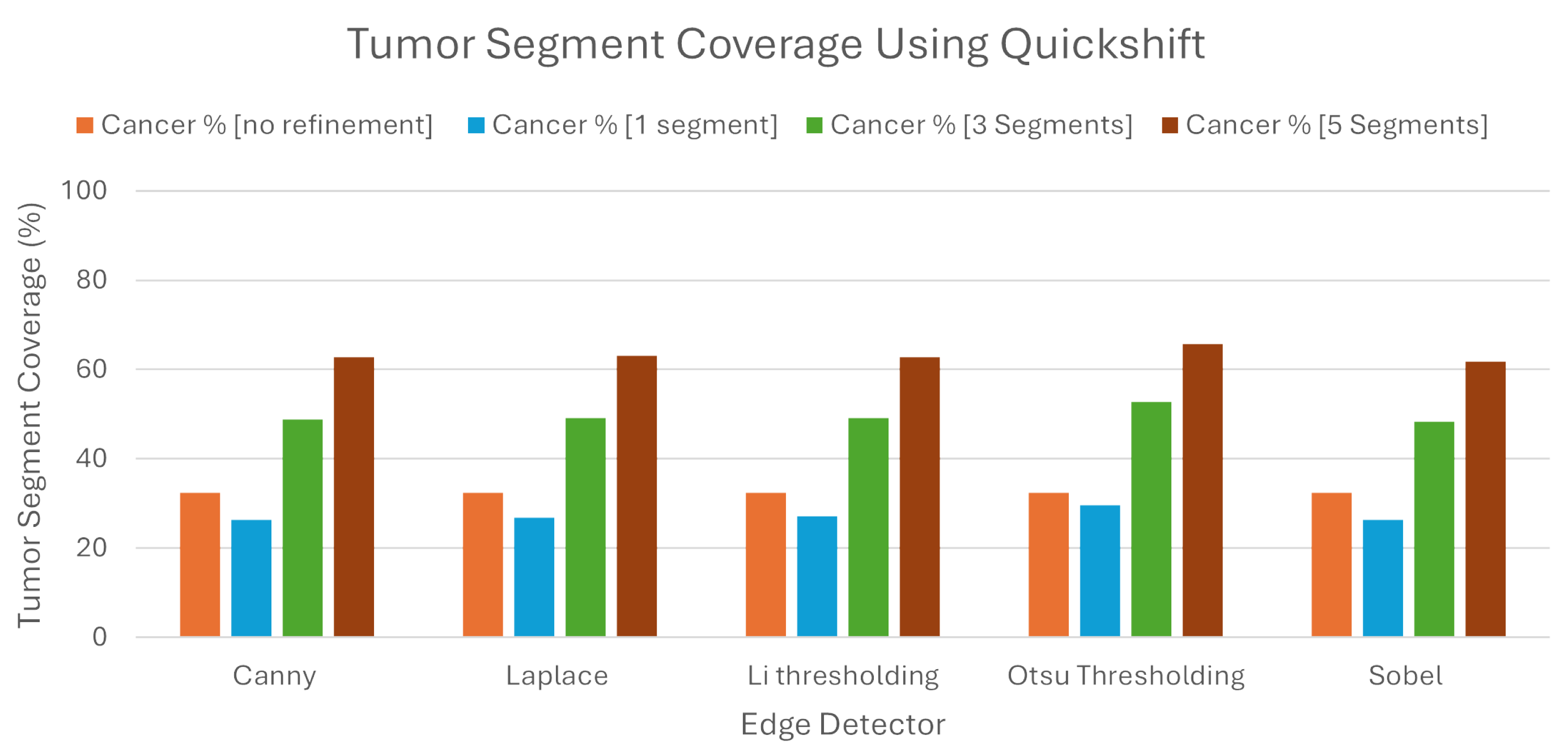
We can see from the
Figure 10, that when we used Quickshift as the segmentation algorithm, the LIE produced explanations that had 32.41% TSC on average, without the proposed refinement. We must note here that the LIE took the three most important areas.
Following the introduction of the refinement mechanism, using again the three most important segments, a substantial improvement was observed, with the TSC average increasing to 49.68% across the five edge detection techniques. We must also note here that Otsu’s thresholding produced the best explanations compared to the rest of the edge detection algorithms, as the TSC with this technique averaged 52.74%, when the rest averaged below 49.2%.
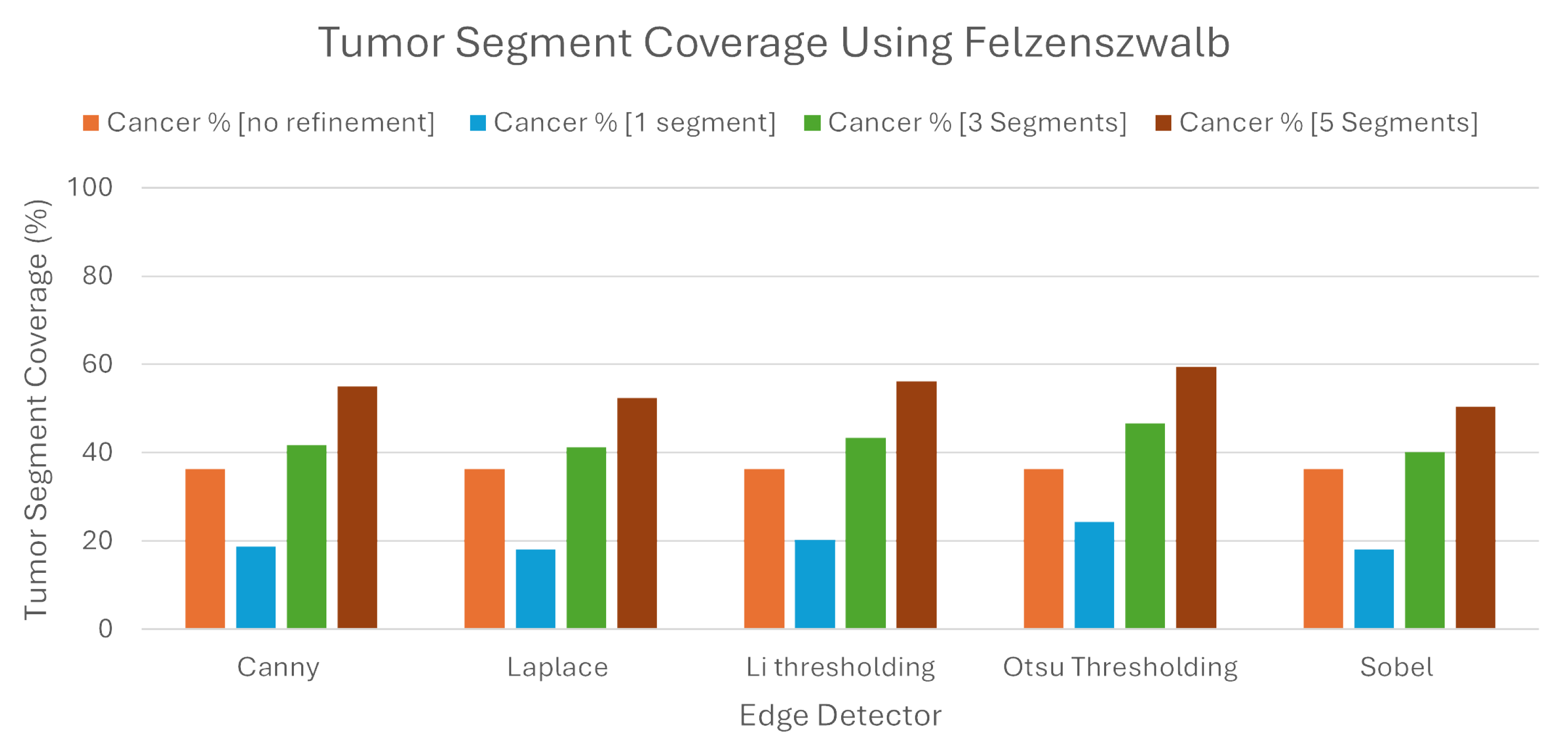
To determine the best number of segments for generating meaningful explanations, we explored the impact of selecting the best single, three, and five segments using the refined LIE. Examining the Tumor Segment Coverage, we found that relying on a single segment yielded an average TSC of 27.26%, and employing five segments resulted in a TSC average of 63.22%. All of the results are presented in
Table 2. As we can see, Otsu’s thresholding gave the best results in all of the experiments using Quickshift.
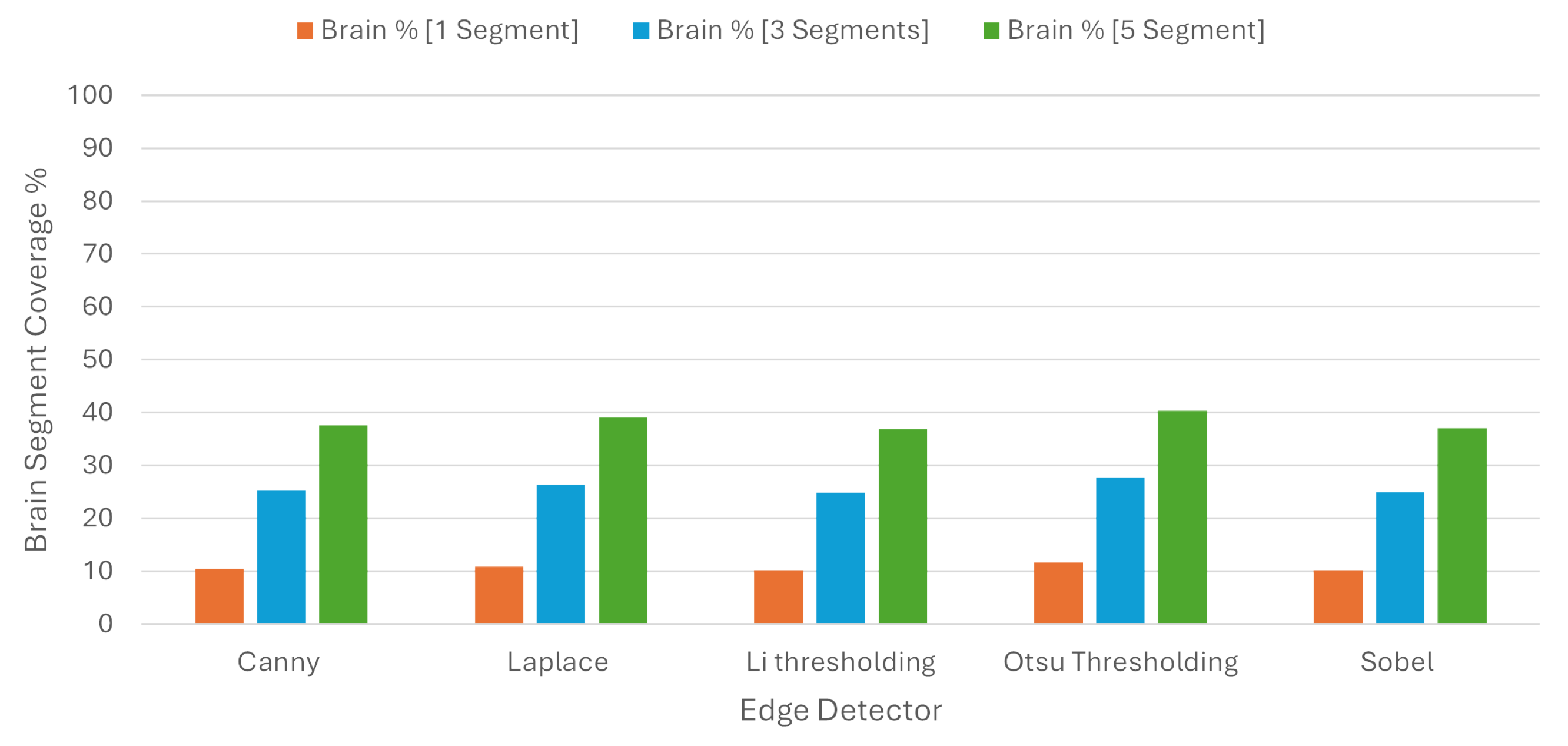
In order to check the balance between coverage and specificity, we used the BSC, where one segment covered 10.71%, three segments covered 25.85%, and five segments covered 38.23% of the brain region on average. These results are presented in
Table 3 and in
Figure 11.
Regarding Felzenszwalb, our refinement seemed to work slightly better than the algorithm without it. To be more specific, when the LIE produced explanations, the average TSC was 36.43%. We must note here that this average was higher than the percentage found regarding Quickshift as the image segmenter. As noted before, the same average with Quickshift was 32.41%.
While this algorithm produced better explanations without the proposed refinement, when we tried to intervene, the new explanations produced had, once again, better TSC percentages, but the results were quite dissapointing. Our refinement showed roughly a 6% higher TSC, with the average being 42.64%.
As we can also see from the
Table 4 and the
Figure 12, the selection of one and five segments did not bring better results compared to the Quickshift experiment. Selecting the best segment had average TSC of 19.96%, while selecting the best five segments had only a 54.72% TSC. The same percentages in the previous experiment were approximately 10% higher in both selections. The one thing that must be noted here is that, once again, Otsu’s thresholding brought better results in the production of explanations compared to the other methods.
Consistent with the previous results, there was no improvement regarding the BSC. To be more explicit, for every experiment that we made regarding the number of segments, the percentage of the brain used was higher in all of them. As we can see from
Table 5 and
Figure 13, when we chose one, three, and five segments, the BSC percentages were 17.34 %, 36.23%, and 45.57%, respectively, while the same percentages using Quickshift were 10.71%, 25.85%, and 38.23%.
Not only werethe explanations produced less informative, but they used more brain area; so, in this case, this algorithm was not a better approach than Quickshift. The one thing that we should mention once more here is that, again, the proposed refinement produced better explanations than the original algorithm.
For the last experiment, Slic was used in order to separate the image into areas. This algorithm had the best results in all of the experiments and methods used. We must say here that we only compared this algorithm with Quickshift, having in mind that Felzenszwalb performed worse, so there was no need to compare it.
We can clearly see in
Table 6 and
Figure 14 that all of the results were elevated. Without the proposed refinement, the LIE itself was capable of producing explanations that had a 46.53% TSC on average. This percentage was more than 10% higher than both of percentages Quickshift and Felzenszwalb.
With the refinement and the selection of the three most important segments, the TSC on the produced explanations rose to 63.77%. This percentage was even higher than the previous experiments when we picked the five most important segments. This means that this algorithm with the combination of our refinement was capable of producing better explanations even with a lower number of segments picked. Indeed, even when we picked only the best segment, the TSC percentage coverage was 34.9% on average, which is a value that is higher than the average TSC percentage when we used the Quickshift algorithm without the refinement and the best three segments (32.41%). The explanations produced with the selection of the five best segments had 74.42% TSC on average, leveraging the highest TSC on all of the experiments conducted.
Examining the BSC of the explantions, as shown in the
Figure 15 and the
Table 7, we can see that the percentages were slightly higher than Quickshift when selecting the best three and five segments. To be more precise, selecting three and five segments resulted in BSC average percentages of 27.7% and 44.67%, respectively, and in the same cases when using Quickshift, the same percentages were 25.85% and 38.23%.
In contradiction with previous statements, the selection of the best segment had a BSC of 10.3% on average, which is lower than the percentage found from every experiment conducted before in this study. This average, combined with the fact that the average TSC when selecting the best segment was 46.53%, assures that the refinement may produce better explanations than the original algorithm, even with the selection of less segments.
4.4. Statistical Evaluation
In this section, an investigation has been conducted to identify the existence of specific combinatory approaches that outperform others. In particular, we evaluated whether certain combinations of the LIE segmentation algorithms and brain area detectors would produce, statistically speaking, better results. As such, a thorough analysis on the performance of all of our segments/refinement combinations was performed. The performance criterion was considered as the accurate detection of tumor regions. Recall that a desirable outcome would be a high overlap of tumor areas with the n top-ranked areas according to the LIE outcomes.
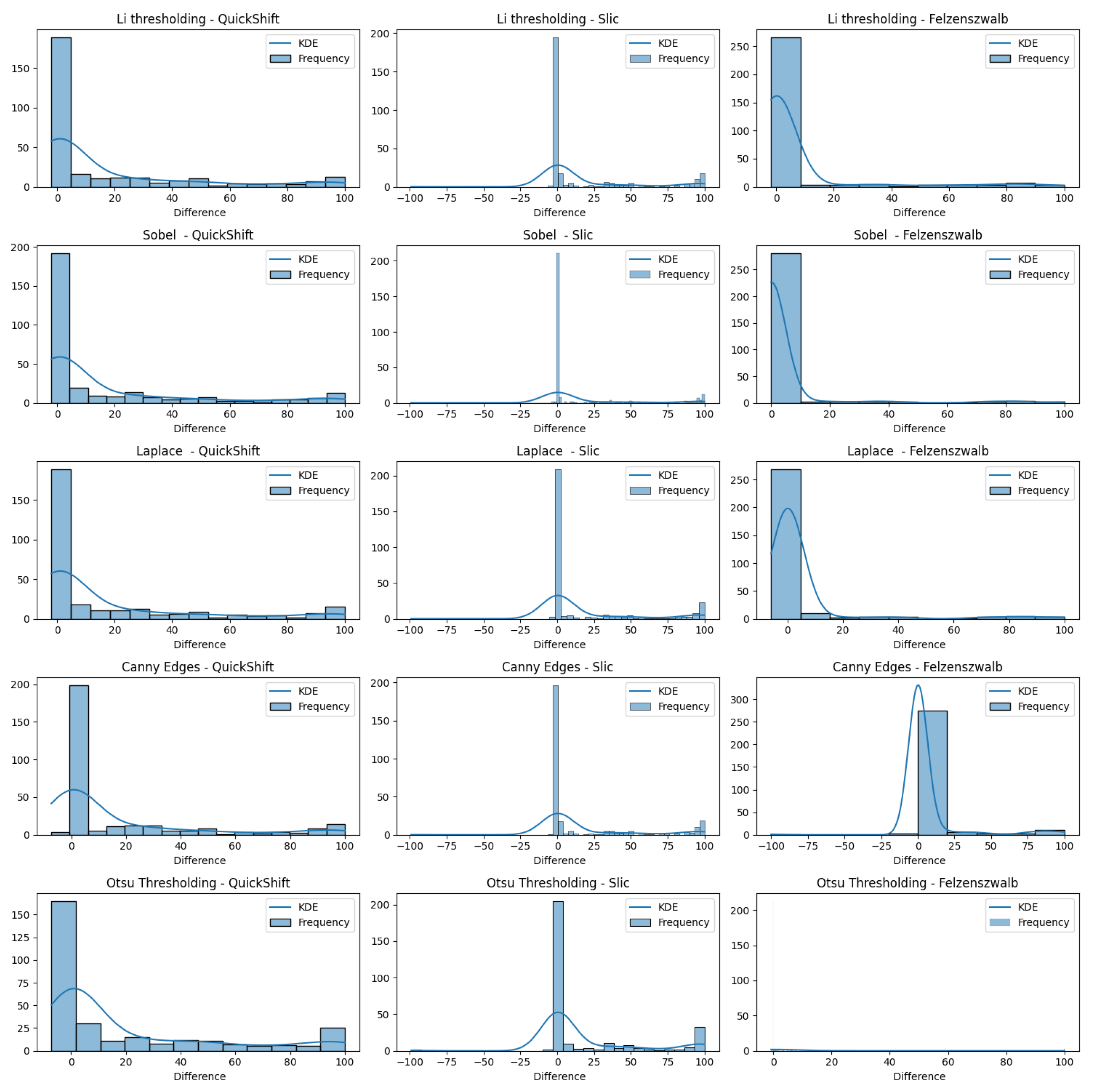
In
Figure 16, we present varius histograms summarizing the difference in tumor segment coverage, for each image, before and after using our refinement method. A positive result indicates that the refinement approach resulted in a higher percentage of tumor-related areas to appear on the top-3 segments provided by the LIE. Each histogram represents a different combination of segment and brain region detector, providing a comprehensive view of the performance across all tested configurations.
It is important to note that a significant subset of images exhibited minimal variation in terms of the TSC, with changes of less than 1%. To better assess the effects of our refinement mechanism, we concentrated on the subset of images that demonstrated a more substantial variation in the TSC, exceeding 1%.
Figure 17 demonstrates this case.
The results indicate that all of the edge detectors, in combination with the QuickShift segmentation algorithm, led to a positive improvement regarding the tumor area detection. A similar situation was observed when using Felzenszwalb as the segmenter, with the exception of the Canny edges detector for the refinement; less than 10 images obtained worse results. This is happening due to the weakness of the edge detector to create a brain mask that covers the brain area in some images (see
Section 4.5). Something else that should be noticed is that, even when we saw a positive impact regarding the TSC difference, the improvement in the majority of the images ranged only from 0 to 10%.
Now, when we used Slic as the image segmenter, the histograms were quite different. We can see in each of the histograms regarding Slic that there was one or two images that had a negative impact that ranged from 50 to 100%, not being able to produce a proper explanation. The reason that this is happening, as mentioned before, is the inability of the edge detectors to produce a proper brain mask that covers the brain area. We can also see that there were about 15 images that had a negative impact ranging from 0.1 to 5%, but they were just being placed in the bin ranging from −25 to 0. Having this in mind, we can also see that the majority of the explanations had positive impacts, and most of them had an improvement in their TSCs ranging from 75 to 100%, excluding the case using Otsu’s thresholding as the edge detector.
The analysis reveals that all proposed combinations led to a general positive impact on tumor area detection. Also, our refinement approach enhanced the accuracy and reliability of identifying tumor regions, thereby validating the effectiveness of our method. When applying our refinement proccess, the regions of interest contained tumor areas in a higher percentage than before, enhancing the overall interpretability and usefulness of the model’s predictions in a clinical setting.
We also conducted a Kruskal–Wallis statistical test regarding the differences before and after the refinement method for each of the combinations used in order to check if there was a specific combination that would produce better results than the rest.
The finding of this statistical analysis did not show us which combination is better than the rest, but which combinations should be avoided. Checking previous results presented in
Section 4.3, we would say that the best algorithm is Slic when talking only about the segmenter. After looking at the results presented in
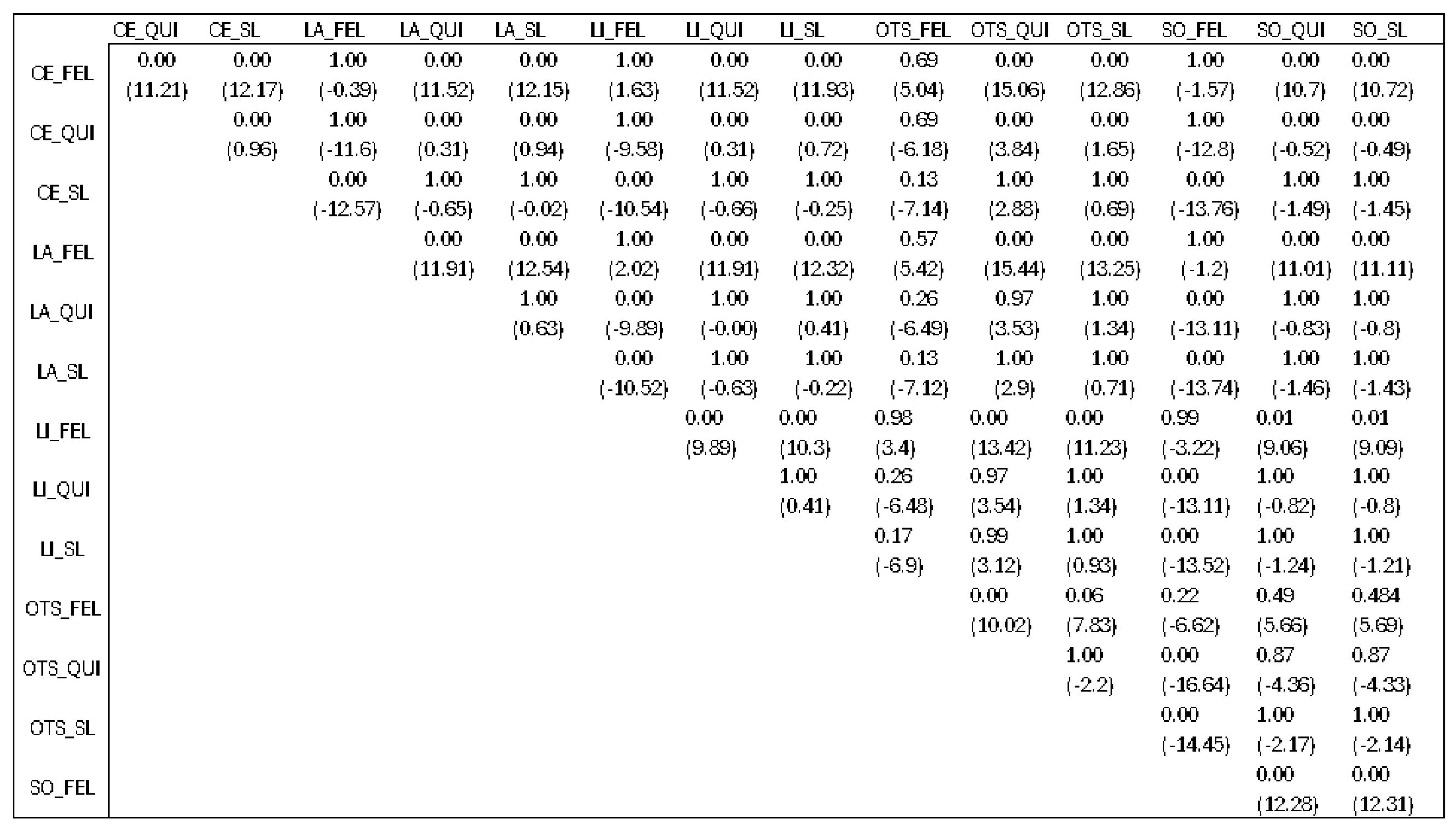
Figure 18 with
p-values and mean differences (denoted in the parenthesis) between different combinations, we can come to a conclusion.
The first characters before the underscore denote the edge detection techniques, Canny edges (CEs), Laplacian edges (LAs), Tthresholding LI (LI), Otsu’s thresholding (OTS), and Sobel (SO). The characters after the underscore denote the segmentation algorithm used from the LIE, Slic (SL), Quickshift (QUI), and Felzenszwalb (FEL).
There was not a specific technique that outperformed the rest, but the combinations that had Felzenszwalb as the image segmenter were worse than the others. This means that, statistically speaking, if we pick Slic or Quickshift as image segmenters, we would not have a big difference for the explanations produced. But, if we choose Felzenszwalb as the segmenter, the explanations that will be produced will not give us a clear understanding behind the model’s decision.
4.5. Advantages and Limitations
The obtained results, see
Section 4.3, suggest that there is potential in refining LIMEs explanations using image processing approaches. In order to quantify the improvement in interpretability of the black box models, two performance metrics must be considered simultaneously: TSC and BSC. Both values are likely to increase if we maintain more segments for the analysis. Yet, presenting a large area of healthy brain tissue as an explanation for a positive tumor detection is counterintuitive. This scenario is further explained in the text bellow.
The Slic algorithm appears to be the most appropriate image segmentation technique. The average TSC score was higher than the rest of the image segmentors. As shown in
Table 6 and
Table 7, both the TSC and BSC scored higher when using five segments, with average scores of 74.42% and 44.67%, respectively. Despite the high TSC score, the BSC score of 44.67% advises against using five segments. Practically speaking, almost half of the brain tissue (BSC score of 44.67%) was presented as important for the decision, and approximately one-fourth of the tumor was not included in the suggested areas (1 − TSC = 25.58%).
Considering the above situation, utilizing the top-3 segments appears to be a better alternative. TheTSC and BSC scores were 63.77% and 27.7%, respectively. In other words, the areas presented for explanation cover one-forth of the brain tissue, and approximately one-third of the tumor is not included in the suggested areas (1 − TSC = 36.23%). As such, the use of three segments emerges as an appropriate choice, finding a balance between avoiding the overuse of non-informative brain regions and offering insightful explanations.
While the proposed refinement mechanism has shown improvement in explainability, certain limitations should be acknowledged. First of all, the accuracy and precision of the initial segmentation accomplished by the chosen algorithms directly affects how effective the refinement technique is. Any inaccuracies or inconsistencies in the segmentation output can propagate through the refinement process, compromising the quality of the explanation and possibly resulting in incorrect interpretations.
Factors influencing segmentation quality include the algorithm’s parameter settings, image characteristics (i.e., resolution, contrast), and the presence of noise or artifacts in the input images. In scenarios where the segmentation algorithms fail to accurately define tumor boundaries or distinguish between tumor and non-tumor regions, the subsequent refinement process may struggle to isolate relevant segments, resulting in explanations that are incomplete or erroneous.
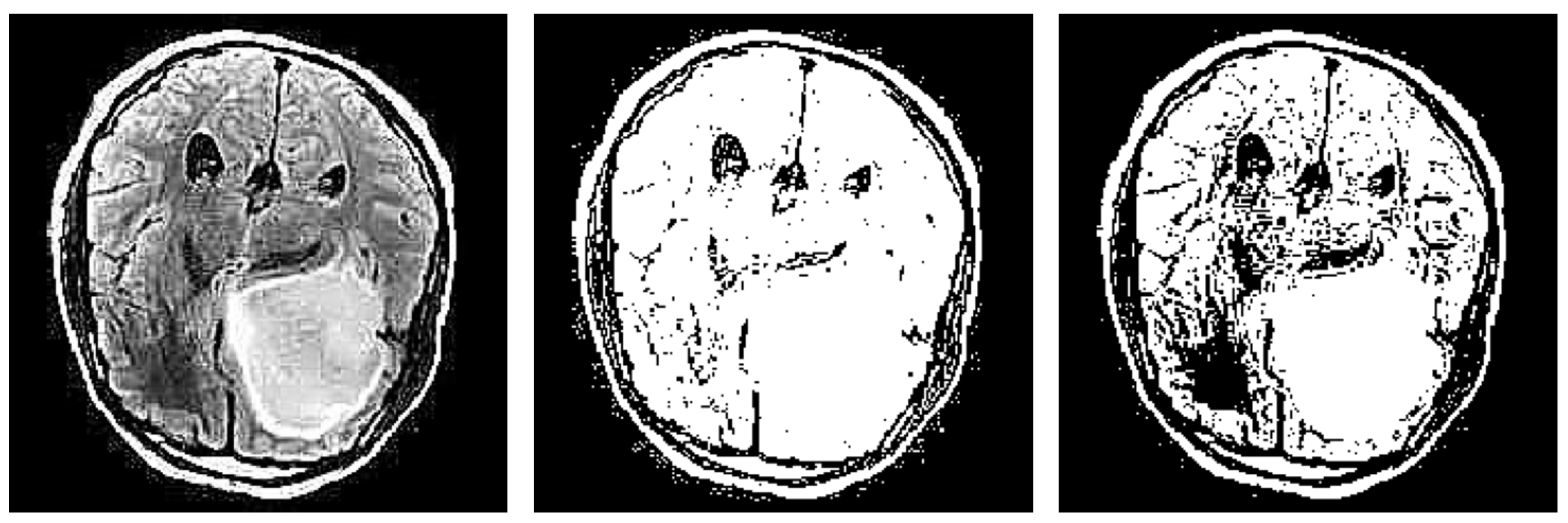
Another notable drawback observed in the proposed refinement mechanism is the potential inconsistency in creating the brain mask (see examples in
Figure 19). The method relies on the edges detected by the different techniques and subsequently extracting the largest contour as the brain mask. However, in some instances, this process may yield inconsistent results.
One issue arises when the detected edges fail to accurately define the boundaries of the brain, resulting in incomplete or fragmented contours. Consequently, the extracted brain mask may cover only a portion of the actual brain region or extend beyond its boundaries, leading to false interpretations during explanation generation.
To address these challenges, future iterations of the refinement mechanism could explore alternative approaches for brain mask generation, such as incorporating machine learning-based segmentation methods or integrating feedback mechanisms to iteratively refine the mask based on user input. The utilization of multimodal imaging and omics data could further refine the explainability of these models by offering a more detailed and comprehensive understanding of tumor characteristics. This approach may also aid in the identification of biomarkers, enhancing the precision of brain tumor analysis. Additionally, robust preprocessing techniques and parameter tuning may help improve the reliability and consistency of edge detection algorithms, thereby enhancing the overall effectiveness of the refinement process.