1. Introduction
Nigeria covers an area of about 924,000 km
2 in West Africa. This area lies within latitudes of 4° N to 14° N and longitudes of 3° E to 14° E. Nigeria bears the highest population in Africa and stands as the seventh most populous in the world. The current population could be estimated as 198,583,016, based on population growth rate of 3.2 per annum and the year 2006 census population figure of 140,431,790 [
1]. Because of this vast population, Nigeria has many populated urban areas, semi-urban areas and municipalities that generate solid waste. The municipal solid waste (MSW) from the majority of the cities has not been characterized in terms of composition and ‘socio-econo-demographic’ effects. Food wastes (leftover food, vegetable wastes, leaves, etc.) constitute a significant proportion of the household-derived MSW, thus organic composition, and by extension the overall composition of MSW, should vary in Nigeria with food culture. In essence, household MSW should be characterized in more and more municipalities for more efficient management. The Nigerian MSW has a high content of compostable organic matter. The typical organic composition values and per capita waste generation for the following studied sites are: 36–57% and 0.54 kg/cap/day for Makurdi [
2], 63.6% and 0.634 kg/capita/day for Abuja [
3], - and 0.54 kg/capita/day for Abuja [
4], 56% and - kg/capita/day for Nsukka [
5], and 51.27% and 0.13 kg/capita/day for Ogbomoso [
6]. The above organic compositions with high percentages of food material are typical of low and medium income countries [
7]. The meaning is that the Nigerian MSW is amenable to stabilization through a controlled biological digestion process. The uncontrolled biological digestion processes that occur in the ineffectively managed Nigerian dumpsites pose a serious threat to environmental sustainability and safety due to the release of landfill gas. Landfill gas is a major greenhouse gas, composed of 45–60% CH
4, 40–55% CO
2, and trace components.
The call for sustainable development is loud and almost none of the available reviews of the Nigerian biomass mix failed to highlight the significant proportion of the MSW that is compostable. The other major components of the Nigerian MSW are also useful as recyclables and reusables. Being a country in dire energy crises [
8], Nigeria must embrace its abundant waste biomass resources for grid-connected and distributed bio-power production. Going forward towards sustainability, the foregoing underscores MSW as relevant, based on its high content of compostable materials. Clean technologies are available, which can be adopted, to harness the MSW bioenergy through anaerobic digestion, fermentation, and landfill gas capture. The abundant resources cannot be viably integrated into the Nigerian energy future unless it is fully characterized across the Nigerian landscape. The advocated characterization should reliably ascertain variation of MSW composition with socio-econo-demographic and cultural parameters in order to create a sizeable data bank for planning waste management schemes and bio-energy integration at the sub-national and national levels. Additionally, improved accuracy in composition and per capita generation analyses of MSW are necessary for an efficient management scheme that would allocate the biomass as renewable energy feedstock, while also exploiting the recyclables and reusables.
The generic issue of enhance reliability and accuracy in composition analysis of MSW, as pursued in this work, is motivated by the need to improve certainty in planning, since accurate data is sensitive to effective waste handling. Waste management operations in developing countries receive the highest share in municipalities’ budget, with 80–90% usually allocated for waste collection [
9]. Yet only about 40–70% of all urban solid waste are being collected [
10]. Factors responsible for the inefficient services partly border on non-existent for precise and updated waste planning data. It is a fact that continuous improvement on accuracy of MSW statistics has helped to achieved sustainable cities and societies in select developed locations of the world. This is evidenced in several waste to wealth initiatives that have seen conversion of solid waste to heat, electricity, compost, and bio-fuels in those places [
11]. For instance, International Solid Waste Association reported in 2012 that out of over 600 waste-energy-facilities built worldwide, 472 are in EU, 100 in Japan, with the remaining 86 in the United States. Further enquiries readily reveal that the afore-mentioned places have one of the most improved methods of waste data collection and analysis [
12]. In addition, the world urban population is growing faster than urbanization itself. The current three billion world city residents generate approximately 1.3 billion tons of solid waste annually. It is projected that by 2025, the global urban population would have about 4.3 billion people generating 2.2 billion tons of solid waste every year. The cost implication also shows that the
$205.4 billion that is being spent annually in urban solid waste management would increase to
$375.5 billion by 2025 [
10]. These are precursors to extensive planning schemes that would begin with accurate mining of waste generation and composition data across cities of the world. Accurate waste composition data as an essential ingredient of integrated solid waste management offers more benefits, which is summarized by [
13] as aiding in comprehensive assessment of environmental and economic impacts of the different solid waste streams, promoting social acceptability through increased public participation, and providing ideas on prevention and minimization of waste generation.
An approach based on zero-intercept first-order polynomial regression is proposed for improved accuracy of composition analysis and compared with the usual averaging technique. Awka municipality, which—to the best of the knowledge available to the authors—has not been studied, is selected as the case study location for sampling and illustration of the proposed analytical method. Being that the location has not been studied, the numerical results from this work are potential additions to the available data bank.
The other components of MSW are the recyclables, the reusables, and the others. The recyclables and the reusables include plastic, ceramic, and metal bottles, metal scraps, and reusable papers (e.g., outdated newspapers, marked and collated scripts used for roadside packaging, and sales of bean cake and other food items), while “others” mainly suggests the non-recyclables and the non-reusables like diapers, tissue paper, ash, and sand and dust. Scavenging is a black market economy that mops up plastics, ceramics, and metal bottles (the reusables) and metal scraps (recyclables) from MSW at the source or the collection bins. This activity is widespread in Nigeria, as noted by [
3,
14]. The economic and environmental benefits of scavenging were quantified by Agunwamba [
14], who concluded that more benefits could accrue if their activities are regulated. Scavenging is expected to enhance the organic composition of MSW at the dumpsites; the organic composition of dumpsite MSW for Uyo municipality is 73.7% [
15], which is above the range of values listed above for household composition.
There are crises in the management of MSW in Nigeria which Agunwamba [
16] had summarized in the following points; absence of adequate policies, absence of enabling legislation, and absence of an environmentally stimulated and enlightened public. The result of these factors are seen as street waste bins, waste collection centers, and dumpsites that are always overfilled and unattended. The crises in the MSW management that persist till date is a reflection of non-implementation of the core policies of Nigeria in MSW management, as articulated by the Federal Ministry of Environment [
17].
2. The Case Study Area
The Awka municipality is selected as the case study location in this work. Awka—located in the south eastern part of Nigeria between latitudes 6.12° N and 6.21° N and between longitudes 7.06° E and 7.44° E—is the capital city of Anambra state. It is located 321.4 km from Abuja, the federal capital territory of Nigeria. Awka is generally known to have a moderate climatic condition. It has two notable seasons across the year; rainy and dry seasons. From June to December, the air temperature in Awka fluctuates from 27 to 30 degrees, while from January to April, the air temperature surges to a higher fluctuation range of 32 to 34 degrees Celsius. Prior to being named the state capital in August 1991, Awka was a semi-urban city, predominantly occupied by local indigenes with few non-indigenes that migrated mainly from nearby towns for greener pastures. But after assuming state capital status, several institutions—Federal, state, and private institutions—sprang up, causing population growth and rapid urban expansion. It has a population of 301,657 according to the 2006 census.
The low income areas are predominantly located to the left of the popular Nnamdi Azikiwe (Zik’s) avenue—the portion of Enugu to Onitsha old road that falls within the Awka metropolis (
Figure 1). These areas predominantly have low cost accommodation, such as one room apartments with shared facilities and multiple room apartments also with shared facilities. It has unplanned housing patterns and poor infrastructure. Over time, lands were plotted, with little government supervision, in the near-right of the Nnamdi Azikiwe Avenue. Today, this area can be classified as the dwelling place for the majority of middle income class earners (civil servants, traders, etc.) who are predominantly non-indigenes. The major residential streets that fall within this area include Emma Nnaemeka, Works Road, Court Road, Kwata, Kenneth Dike, Umukabia, Araba, etc. This middle class area has moderate amenities like streets properly numbered. It also has several story buildings divided into flats.
The high income class are found in estates carefully plotted by government. They enjoy good facilities like tarred roads, good drainage system, more power supply, safe water supply, and better security. The houses are mostly bungalows, duplexes, and mansions. Udoka estate, Ngozika Estate, and Government Reserves Areas (GRAs) are the sub-areas under this class. In order to have a statistically balanced study, the study sample participants were drawn from the three income groupings.
3. Methodology
According to the year 2006 census, the number of regular households in Awka South local government area—as sourced from the national population commission Awka office—is 38,546, with a total population of 17,0723. The regular household is about 96.08% of all kinds of households in the area. Awka South is approximately the same as the municipality, called Awka, that constitutes the capital of Anambra state. Assuming a fixed household size (the ratio of population to household number or the number of occupants per household) of 17,0723/38,546 people per household and a fixed geometric population growth rate of
r = 3.2% per annum (the national value) [
1], the current number of households of the municipality is projected as;
which gives
households.
Use is made of the simple sample size formula;
where
N is the population size and e is the level of precision. In this study,
and
= 10%, giving the sample size of 100 households. Based on this sample size, 120 households were randomly drawn equally from the three major income areas to participate in the study; Udoka and Ngozika housing estates for high income earners, Umukabia, Works Road, and Kenneth Dike areas for middle income earners and Umudioka, Umubelele, and Amenyi for the low income residents. The judgment of income status was not just predicated by place of residence but was also confirmed with a questionnaire. The three major income groupings are not formally classified in Nigeria. They are classified here for quantitative reasons bearing in mind the current economic recession in Nigeria, which has drastically reduced purchasing power of households. They are as follows; (1) the low income stratum—this batch of households are considered to earn not more than ₦100,000, (2) the middle income stratum—this batch of households are considered to earn more than ₦100,000 but not more than ₦250,000, and (3) the high income stratum—this batch of households are considered to earn more than ₦250,000. This is shown in
Table 1.
Ten days sampling was conducted. On the first day, numbered questionnaires were distributed to participants who were also numbered according to the questionnaires. The questionnaires were structured to extract the econo-demographic indices of the households. The reason for the research was explained to the participants and ethics of confidentiality guaranteed them. A waste bag was given to each participant. On the second day, the generated household waste and the questionnaires were gathered and taken to the study center. The mass and loose volume of the household waste, as collected, were measured first. The wastes were then sorted accordingly and the components weighed. The components of the wastes were re-mixed, compacted by human power, and the compact volume measured. The result for each participant were recorded on the logging table created on the correspondingly numbered questionnaire. The structure of the logging table is shown in
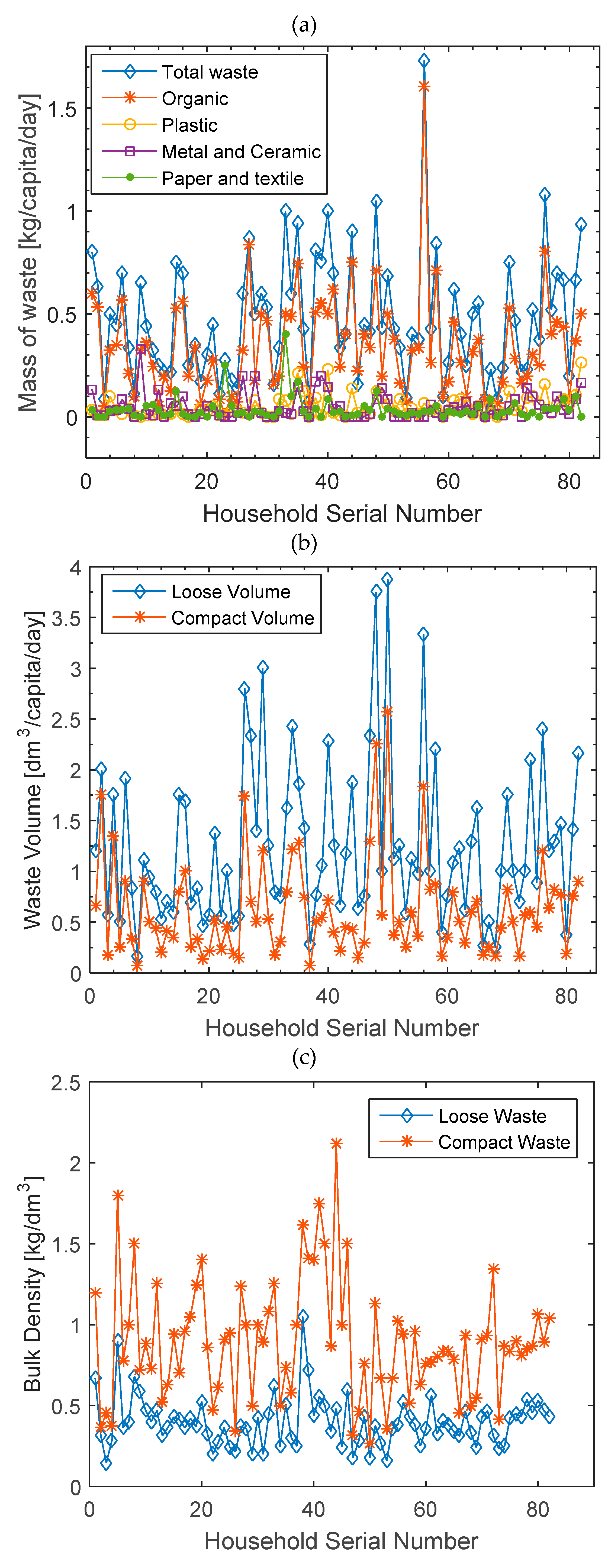
Table 2. The procedure was repeated until 10-day data was sampled. Eighty two participants were consistent and their data were used in the analysis. This represents 11% level precision, which is only a slight deviation from the assumed 10%. The contributions of the economic strata in the sampled data are 36.6% from low income, 32.9% from middle income, and 30.5% from the high income. Therefore 82 by 10 sampled data sets were available for this study. This is large enough to justify assumption of normality, which is the foundation of regression analysis proposed in this work.
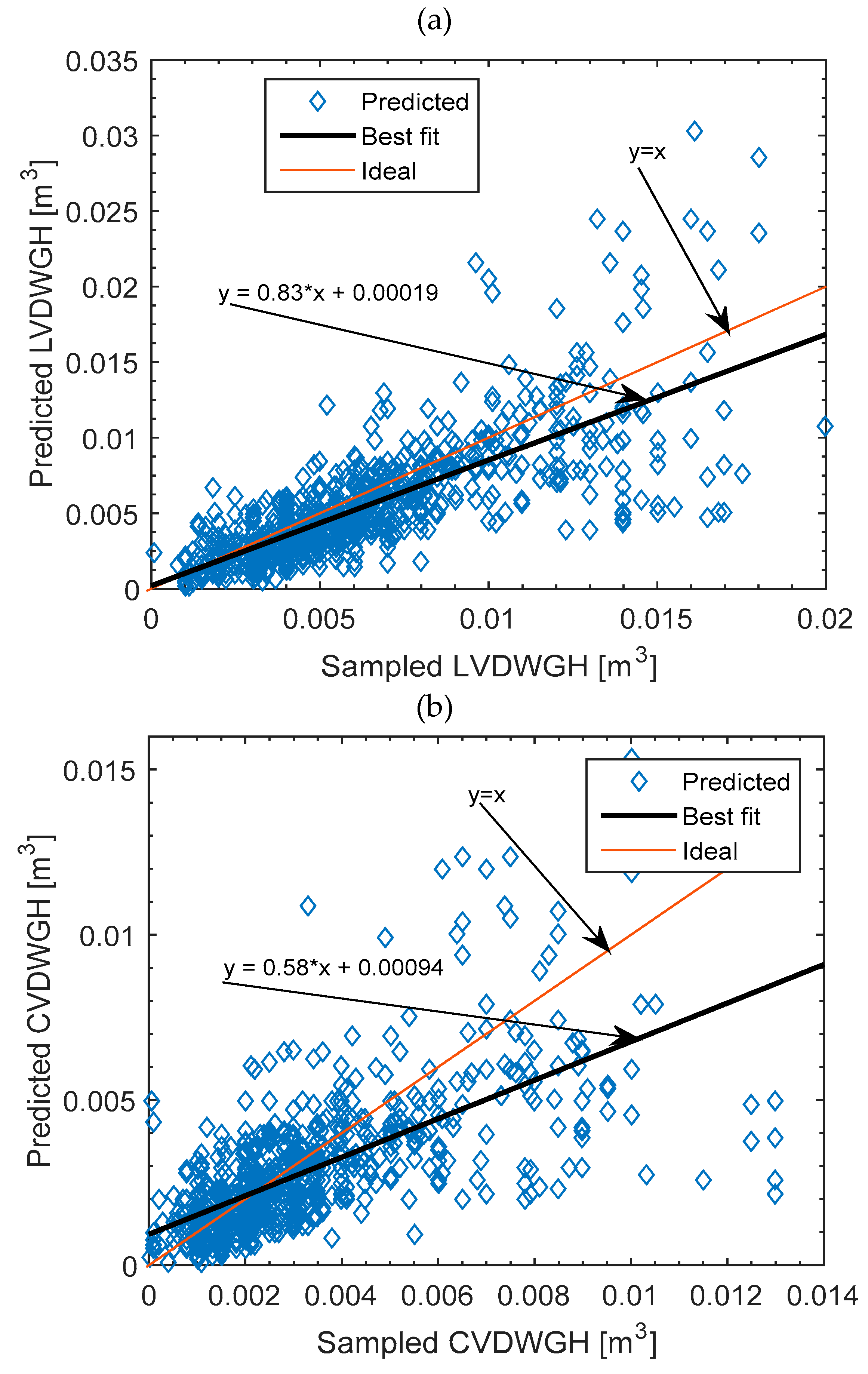
Composition of MSW is usually given in terms of descriptive statistics. This approach usually involves measures of location and central tendency (mostly mean), measures of dispersion (mostly standard deviation), and error or uncertainty. This tradition should be improved with mathematical and statistical tools. It proposed in this work that accuracy could be improved if composition of MSW is established through statistical regression analysis that minimizes the sum of square residuals. Zero-intercept first-order polynomial regression was suggested by Ozoegwu et al [
18] for estimating biomass wastes generated in various stages of processing cassava into food. The fractions established through the method—for converting harvest data of cassava to waste biomass potential—were shown to be more accurate than fractions established through the descriptive approach. Since composition analysis of MSW is similar to estimation of the non-food biomass proportion of harvested cassava, it is believed that adaption of the zero-intercept first-order polynomial regression approach to MSW composition analysis will give better results. It must be noted that non-zero-intercept first-order multi-variate polynomial regression approach has been used to correlate MSW generation by households with socio-econo-demographic parameters like income, household size, education status, etc., as can be seen in the following works [
19,
20,
21,
22,
23], but to the best of the knowledge of the authors, no work has applied regression to the composition analysis. Zero-intercept is imposed in regressive waste composition analysis to avoid the unrealistic cases of a non-zero constituent at zero waste generation. Similarly, zero-intercept is imposed in regressive waste per capita generation analysis to avoid the unrealistic case of non-zero per capita generation at zero household size. In the proposed zero-intercept first-order polynomial regression, the sampled waste generation is considered the independent variable, where the components (organic, plastic, metals, paper and textile, etc.) and volume (loose and compact volume) are considered dependent variables. Also, the daily per capita waste generations, the daily per capita constituent waste generations, and the daily per capita waste volumes are dependent on the household size in the proposed method.
The traditional descriptive approach is formulated for this study as follows. Suppose the total mass of waste generation of the
th household (
) in
th day (
) is represented as
and the mass of the
th component (
) for the day represented as
, the descriptive approach gives the mean, standard deviation, and uncertainty of the composition
as follows
It must be noted that in the descriptive approach, the elements of the sample, represented by a random variable , are assumed to be independently drawn from the population(s).
The proposed zero-intercept first-order polynomial regression approach is formulated for this study as follows. This approach to MSW composition analysis assumes that
are the measured values of the random variable
, which under deterministic conditions has a fixed value
. The element
is a component of a vector
of dimension
and the element
is a component of a vector
of dimension
, such that
with the solution
where
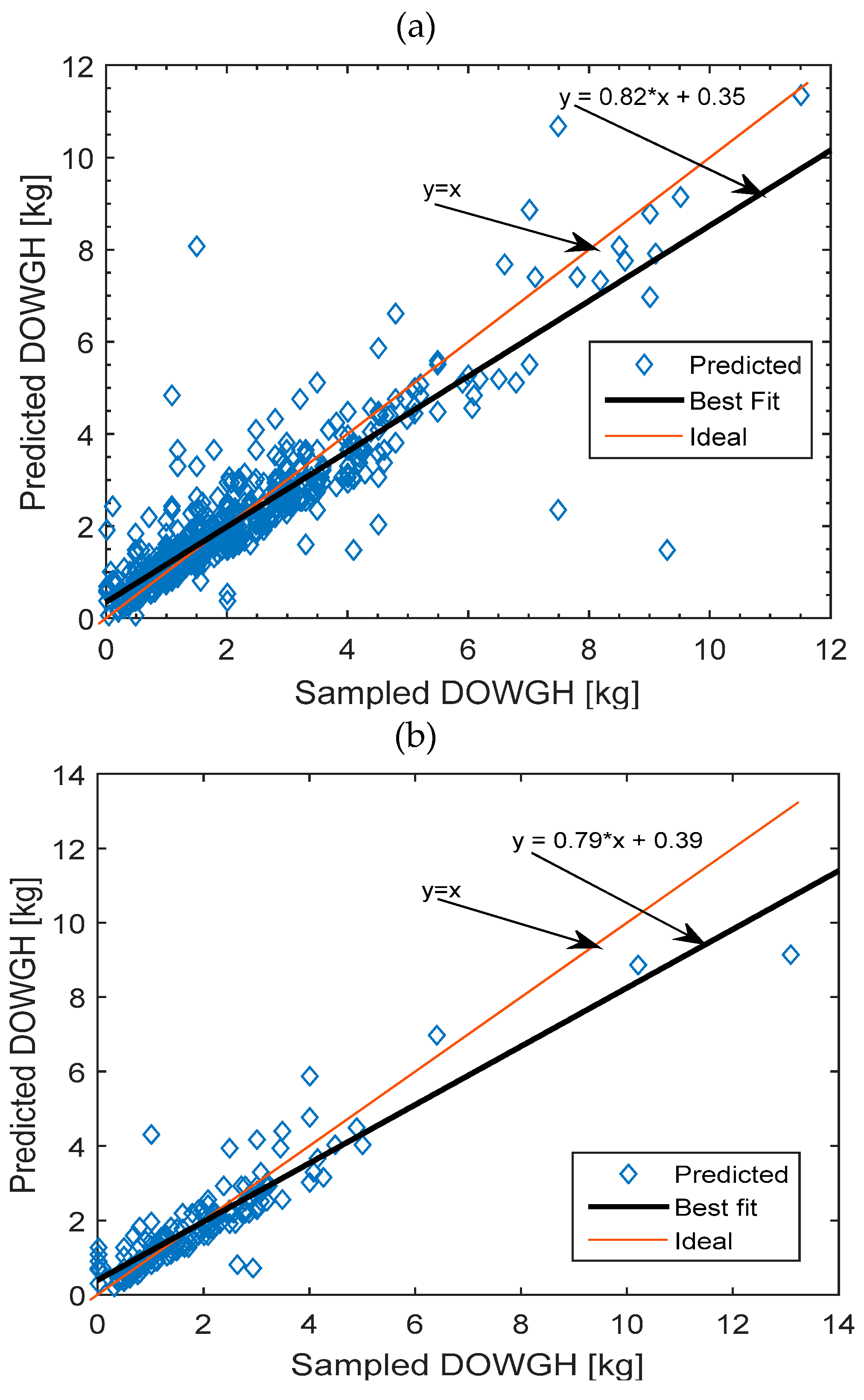
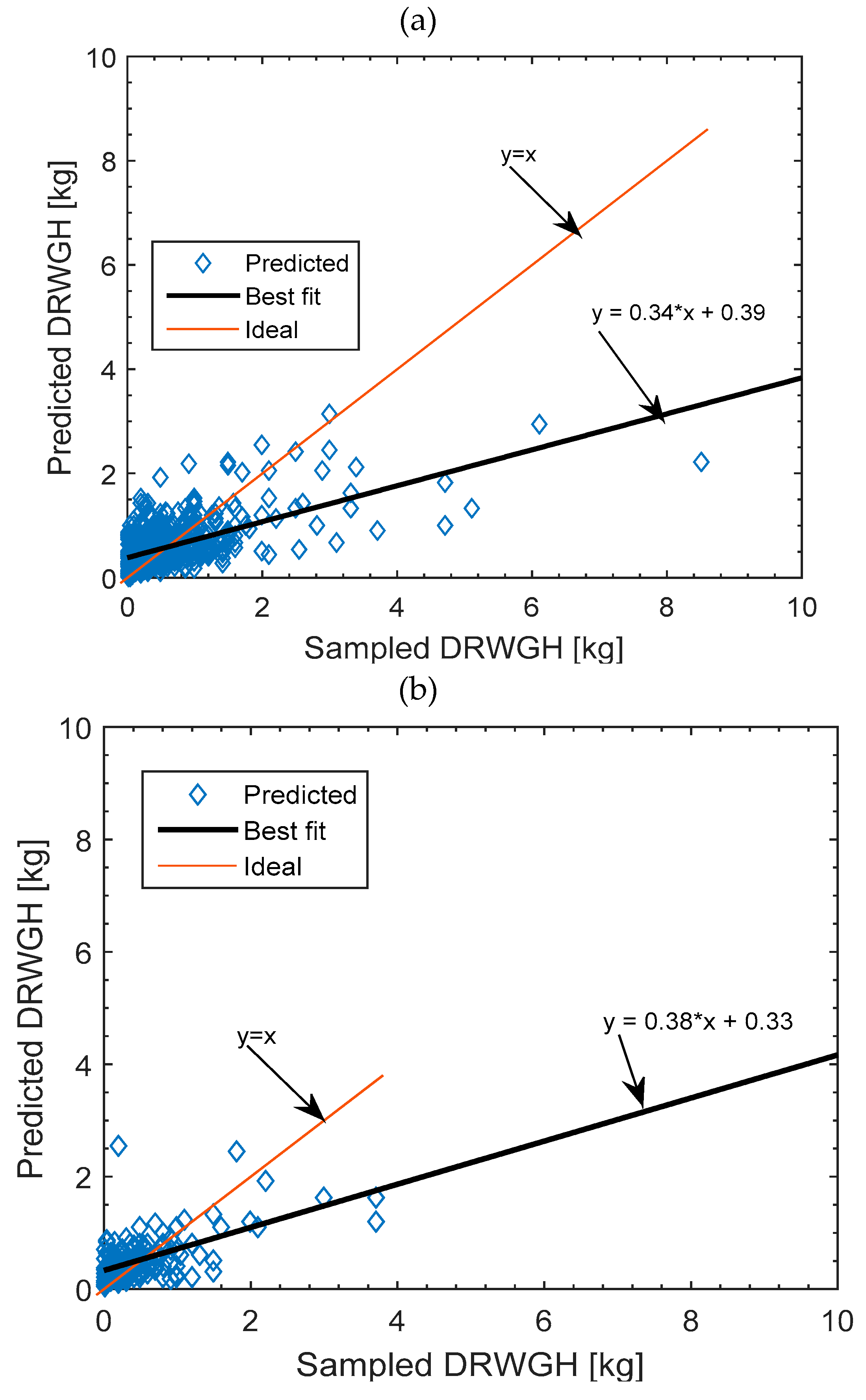
The results from the two approaches— and , respectively, are compared in what follows, using the following statistical indices; the coefficient of determination R2, root mean square error (RMSE), mean bias error (MBE), mean absolute bias error (MABE), t-Test statistic, and correlation coefficient (r).
5. The City-Wide Waste Generation
The daily per capita quantities established in the foregoing section are used to calculate the daily city-wide quantities. Such city-wide estimates are necessary for resource and capital allocation to MSW management. The daily per capita quantities of interest are those that jointly cover for the three income groups and relate to the overall management. They are
=
kg/capita/day,
=
kg/capita/day,
kg/capita/day,
kg/capita/day,
= 0.9021 dm
−3/capita/day, and
= 0.4508dm
−3/capita/day. Adopting a population of 17,0723 (according to the year 2006 census) and assuming a fixed geometric population growth rate of
r = 3.2% per annum (the national value) [
1], the projected population for a future year “20XY” is
households. Since only households were sampled, correction factors are needed to transform results to overall generation capacity of Awka. Household waste is about 40–60% of urban waste [
3]. The survey by [
2] showed that 82% of the solid waste generated in a rapidly growing urban area in Central Nigeria came from households. Since Awka is not an industrial area, it is assumed that household contribution to the MSW is in the high side of the known range for Nigerian locations, therefore, 75% of MSW is assumed to come from households. The Awka city-wide generation for the year 2016 becomes
where
=
or
and
=
,
,
,
,
, or
. Therefore, the daily total MSW generation is 130.0348 tonne/day, the daily compostable MSW generation is 95.7872 tonne/day, the daily recyclable MSW generation is 25.8884 tonne/day, the daily paper and textile MSW generation is 7.8601 tonne/day, the daily loose volume of MSW is 281.3730 m
3/day, and the daily compact volume of MSW is 140.6085 m
3/day. These data would aid managers in allocation of resources to the city waste management. For example, given the capacity of evacuation trucks, the needed number of trucks can be recommended to depend on the number of through puts allowed for complete evacuation.