An Unscented Kalman Filter-Based Robust State of Health Prediction Technique for Lithium Ion Batteries

Abstract

Electric vehicles (EVs) have emerged as a promising solution for sustainable transportation. The high energy density, long cycle life, and low self-discharge rate of lithium-ion batteries make them an ideal choice for EVs. Recently, these batteries have been prone to faster decay in life span, leading to sudden failure of the battery. To avoid uncertainty among EV users with sudden battery failures, a robust health monitoring and prediction scheme is required for the EV battery management system. In this regard, the Unscented Kalman Filter (UKF)-based technique has been developed for accurate and reliable prediction of battery health status. The UKF approximates nonlinearity using a set of sigma points and propagates them via the nonlinear function to enhance battery health estimation accuracy. Furthermore, the UKF-based health estimation scheme considers the state of charge (SOC) and internal resistance of the battery. Here, the UKF-based health prediction technique is compared with the Extended Kalman filter (EKF) scheme. The robustness of the UKF and EKF-based health prognostic techniques were studied under varying initial SOC values. Under these abrupt changing conditions, the proposed UKF technique performed effectively in terms of state of health (SOH) prediction. Accurate SOH determination can help EV users to decide when the battery needs to be replaced or if adjustments need to be made to extend its life. Ultimately, accurate and reliable battery health estimation is essential in vehicular applications and plays a pivotal role in ensuring lithium-ion battery sustainability and minimizing environmental impacts.

1. Introduction

The use of Li-ion batteries has become increasingly popular in recent times, particularly for EVs and renewable energy systems [1]. Electric vehicles are increasing in popularity as a means of reducing harmful gas emissions and reducing dependence on fossil fuels [2]. However, the success of EVs depends heavily on the performance and reliability of their energy storage systems. Li-ion batteries are the most used energy storage system in EVs due to their long cycle life, high energy density, and low self-discharge rate [3]. The energy density and life cycle of different kinds of batteries, like lead-acid and nickel-metal hydride batteries, are lower, which makes them less suitable for use in EVs [4]. Li-ion battery modeling is of utmost importance to predict crucial battery parameters like SOC, R₀, SOH, battery lifetime, and charge/discharge characteristics. Accurate battery modeling is essential for estimating the SOC, R₀, and SOH of Li-ion batteries. In this regard, several battery-modeling methods have been proposed, varying from simple empirical models to complex physics-based models, such as the equivalent circuit model, electrochemical model, thermal-electrochemical model, and three-dimensional model [5,6]. The precision of battery modeling is based on the complexity of the model, the quality of the data used for model calibration, and the accuracy of the battery model parameters [7,8]. Among the different modeling methods, the equivalent circuit model is the most broadly used because a simplified electrical circuit can mimic the accurate dynamic behavior of a battery [9]. With regard to battery modeling, the equivalent circuit model is broadly used due to its simplicity and accuracy in estimating the different parameters of the batteries [10]. Furthermore, these models can characterize the battery’s internal nonlinear dynamics with simple circuit elements such as resistors and capacitors. The utilization of equivalent circuit models is a valuable approach for the estimation of SOC and internal resistance of lithium-ion batteries due to the capability of providing a satisfactory trade-off between the accuracy of results and computational complexity [11]. The SOC estimation is crucial because it reflects the amount of energy stored in the battery at any given time [12]. Therefore, accurate SOC estimation is necessary for optimizing battery performance and predicting its remaining capacity.

With regard to SOC estimation, several methodologies have been suggested, including coulomb counting, model-based methods, open circuit voltage (OCV), and Kalman filter-based observers [13]. The coulomb counting method is a commonly employed technique for the determination of SOC of batteries that involves the measurement of the electric charge passing into or out of the battery over a given period. However, this method has some drawbacks, such as sensor measurement errors due to noise, which can lead to inaccuracies in the estimated SOC [14]. The OCV method is also used for the estimation of the SOC of a battery. However, it may not be practical for real-time estimation because obtaining an accurate measurement of the OCV typically requires the battery to reach a stable state, which can take several hours to achieve. Among these techniques, Kalman filter-based techniques are widely used because they provide accurate SOC estimation and also robustness to measurement noise [15,16,17,18]. With regard to different variants of the Kalman filter, the basic Kalman filter (KF) and EKF are the two most broadly used techniques for SOC estimation [19,20]. EKF is a popular technique because it provides an accurate estimation of linear and nonlinear systems. However, EKF is susceptible to modeling errors and measurement noise under high nonlinear dynamics of the battery [21,22,23].

Further, the SOH of a battery reflects its degradation over time and is a critical feature in determining the remaining useful life of a battery [24]. The exact estimation of SOH is essential for estimating the remaining capacity and optimizing battery performance. In EVs, knowing the SOH can help determine when a battery needs to be replaced or if it can still provide a sufficient range. Several factors can affect the SOH of a battery, including aging, temperature, and charging/discharging rates [25]. There are several techniques for estimating SOH, such as coulomb counting, voltage-based methods, electrochemical impedance spectroscopy (EIS), and model-based methods such as KF and EKF [24]. Among these techniques, model-based methods are widely used because they provide accurate SOH estimation and are relatively easy to implement [26], while the KF and EKF are less capable against sensor noise and varying dynamics of the battery, which limits the usage of these techniques in real-time SOH estimation [27].

To overcome the aforementioned limitations with regard to existing techniques, in this paper, the UKF-based technique has been propounded for the accurate estimation of the SOH of the battery to enhance its overall performance and lifespan. The proposed technique is also capable of handling nonlinearities of current and voltage sensor measurements, which leads to accurate health status predictions. The UKF approximates nonlinearity using a set of sigma points and propagates them via the nonlinear function to estimate the covariance and mean of the predicted state and measurement. This leads to more accurate and reliable estimates of the battery’s health, which is important for enhancing battery performance and prolonging battery life. To assess the effectiveness of the UKF as an algorithm for SOH estimation, its performance was evaluated across a range of diverse operating conditions. Moreover, to verify the robustness of the suggested UKF-based health estimation technique, the initial value of the SOC was varied. With this variation in initial SOC, the proposed technique performed better compared to existing KF-based variants (KF, EKF).

The primary contributions of this paper are listed below:

• A robust UKF technique was developed to monitor the health degradation of lithium-ion batteries.
• The proposed technique was validated, considering varying initial conditions to verify the robustness in the health monitoring of the battery,
• The UKF technique was compared with the widely used EKF algorithm for battery health monitoring and prediction.
• The health monitoring techniques (UKF and EKF) were validated under different nonlinearities to verify the accuracy of health prediction.

The subsequent sections of this paper are organized as follows: Section 2 and Section 3 depict the LIB modeling and UKF-based SOC estimation, respectively. Section 4 discusses the SOH prediction analytical formula for LIBs, and Section 5 elaborates on the analyses. Finally, Section 6 highlights the conclusion of the work.

2. Lithium Ion Battery Modeling

To estimate different crucial battery parameters, such as SOC, R_0, and SOH, a reliable and accurate battery model is an indispensable component. In this regard, this section elaborates on different battery modeling techniques. While Li-ion batteries have applications in various domains, they are increasingly being used in vehicular applications. However, a major challenge in estimating the internal states of lithium-ion batteries lies in their high degree of nonlinearity, which poses a significant obstacle to accurate estimation [28]. To make the battery’s state estimation less difficult, the concept of battery modeling is introduced, and it plays a vital role in state estimations [1]. The modeling of batteries is commonly employed to monitor battery capacity voltage (V)–current(I) characteristics and charging-discharging status. Lithium-ion battery modeling is divided into various models. The equivalent circuit model is considered the most widely used technique due to its practicality for real-time implementation. It has been shown to be effective in accurately estimating the internal dynamics of batteries [28]. The equivalent circuit model is typically preferred for battery modeling due to its ability to address various battery management system challenges, including power flow control problems and others [23].

There are many combinations of equivalent circuit models currently available. Among them, the 1-RC battery model (Figure 1) has been widely used because it can replicate the battery’s dynamic behavior accurately [15]. The complexity of these models is low and their durability is high, which makes them more suitable for real-time applications. The 1-RC model comprises a series resistance and is connected with the parallel combination of resistance and a capacitor. Series resistance depicts the internal resistance of the battery, whereas the parallel combination of the resistor and capacitor represents the change transfer reaction in the battery.

Mathematical equations for the 1-RC battery model are as follows:

$$\frac{d{V}_p}{dt}=-\frac{V_p}{C_1{R}_1}+\frac{I_{bat}}{C_1}$$

(1)

$$V_t=V_{oc}-V_p-I_{bat}{R}_0$$

(2)

$$V_{oc}(\mathrm{s})-V_t(\mathrm{s})={\mathrm{I}}_{bat}(\mathrm{s})(R_0+\frac{R_1}{1+s{R}_1{C}_1})$$

(3)

The final discrete equation can be formulated by using the bilinear transformation technique as follows:

$$V\left(k\right)+a_{1}V\left(k-1\right)=b_{0}I\left(k\right)+b_{1}I\left(k-1\right)$$

(4)

where the term V depicts the output vector at time k. The parameters $a_1$, $b_0$, and $b_1$ are predictable using the help of the recursive least square (RLS) method, where $a_1$, $b_0$, and $b_1$ are parameters that set the value of $R_0$, $R_1$, and $C_1$ in the 1RC model as follows [27]:

$$R_1=\frac{2(a_1{b}_0+b_1)}{1-a_1^2}$$

(5)

$$C_1=\frac{T{(1+a_1)}^2}{4(a_1{b}_0+b_1)}$$

(6)

$$R_0=\frac{b_0-b_1}{1+a_1}$$

(7)

where $V_{oc}$ refers to the open circuit voltage, which is measured when the battery is not connected to the load. The circuit parameters $C_1$ and $R_1$ are the polarization capacitance and resistance of the battery, respectively, and $V_p$ is the voltage parallel to $R_1$ and $C_1$. The resistance $R_0$ represents the internal resistance of the battery. $I_{bat}$ is the charging/discharging current of the battery. $V_t$ depicts the terminal voltage of the battery and S and K are the constants used in determining the behavior of the battery [22].

3. UKF-Based SOC Estimation Scheme

To study the performance and efficiency of batteries for various applications, it is necessary to employ performance metrics such as SOC. The SOH of the battery is highly dependent on an accurate estimation of SOC. In this context, the accurate and reliable estimation of SOC is very important [3] because the SOC method can offer an effective charging/discharging strategy and gives more accurate results, which may lead to an increase in battery efficiency. Essentially, the SOC acts like a fuel indicator in EVs. Hence, the accurate estimation of SOC is essential to operate LIBs under safe conditions and to enhance their performance and efficiency [10,11].

The UKF is a nonlinear variant of the KF that allows for battery state estimation when state dynamics are nonlinear [9]. It is particularly useful for SOC estimation in BMS, where the battery model is highly nonlinear. The fundamental concept of the UKF is to approximate the nonlinear dynamics of a system by utilizing a cautiously selected set of sigma points [15]. These sigma points are then used to propagate the state and covariance estimates with the help of nonlinear system equations. This results in a new set of sigma points that approximate the posterior state and covariance distributions [13]. The battery SOC and R₀ were estimated using the UKF technique. This is because the proposed UKF technique comprises recursive equations which are estimated repetitively during battery charging/discharging. This shows that the internal dynamic parameters of the battery can be estimated. The following equation presents the battery state space model:

$$x\left(k+1\right)=A{x}_k+B{I}_k+w_k$$

(8)

$$y_k=C{x}_k+v_k$$

(9)

where the matrices A, B, and C in (8) and (9) describe the battery’s internal dynamics, while x_k and I_k depict the internal state and charge/discharge current of the battery. The parameters v_k and w_k are measurement noise and process noise, respectively. The term y_k depicts the output of the system and is calculated using (9) as a linear combination of the system state and input. The different parameters associated with the battery state space model (Equations (8) and (9)) are detailed below:

$$x_k={\left[SOC{\mathrm{V}}_p{R}_0\right]}^{\mathrm{T}}$$

(10)

$$A\left(k\right)=\left[\begin{array}{lll}1& 0& 0\\ 0& {\mathrm{e}}^{-\frac{\Delta t}{R_1{C}_1}}& 0\\ 0& 0& 1\end{array}\right]$$

(11)

$$B\left(k\right)={\left[\begin{array}{c}0\\ R_1\left(1-{\mathrm{e}}^{-\frac{\Delta t}{R_1{C}_1}}\right)\\ 0\end{array}\right]}^{\mathrm{T}}$$

(12)

$$C\left(k\right)=\left[\frac{f\left(SOC\right)}{x_1}-1-I_k\right]$$

(13)

The UKF algorithm typically consists of the following steps. Initialization: initialize the covariance matrix P and State Vector X:

X (0) = X0

(14)

P (0) = P0

(15)

Equations (14) and (15) represent the initial state and initial covariance matrix, which is used to model the uncertainty or error in the state estimate and to propagate this uncertainty through the prediction and update steps of the filter [13]. By appropriately modeling the uncertainty using the covariance matrix, the UKF can provide a more accurate and robust estimate of the state [15].

Prediction: use the battery model to predict the next state x(k + 1) and covariance matrix P(k + 1|k) based on the current state x(k) and control input u(k):

$$X\left(k+1|k\right)=f(X(k),u(k))=X(\mathrm{k})-\left(\frac{1}{RC}\right)\ast X(k)\ast \mathrm{d}\mathrm{t}+\left(\frac{1}{RC}\right)\ast i(k)\ast \mathrm{d}\mathrm{t}$$

(16)

$$R\left(k+1|k\right)=F(k)+P\left(\frac{k}{k}\right)\ast F{(k)}^T+Q(k)$$

(17)

Equations (16) and (17) depict the state and covariance prediction, respectively, in which x(k + 1|k) is the predicted state vector at time k + 1 and f is the state transition function that describes how the state vector evolves, based on the control input u and any other known inputs. X(k) depicts the current state vector at time k. The parameter u(k) represents the control input or known input to the system at time k, which influences the dynamics of the system. In this case, there is a current input, I(k), that is known at time k. The first term, X(k) * dt, on the RHS of Equation (16), represents the change in the state variable x(k) due to self-discharge. The second term, I(k) * dt, on the RHS of Equation (16), represents the change in charge/discharge current. The term F(k) is the state transition matrix and it shows how each state changes over time. F(k)T is the transpose matrix, used to ensure that the resulting covariance matrix has the correct dimensions. Finally, the term Q(k) is the process noise covariance matrix, which represents the uncertainty or error as SOC rated with the prediction step.

Unscented transformation: the unscented transform is a mathematical technique employed in the Unscented Kalman Filter (UKF) algorithm to propagate the mean and covariance of a random variable through a nonlinear function [14]. In the UKF algorithm, the state estimation is based on a group of sigma points, which are generated using the unscented transform [17]. The unscented transform generates sigma points by taking the mean and covariance of the random variable as inputs and distributing a set of sigma points around the mean based on the covariance matrix. The number of sigma points generated is 2n + 1, where n is the number of dimensions of the random variable [19]. After the generation of sigma points, they are passed through the nonlinear function to obtain the predicted sigma points for the next time step [21]. The predicted sigma points obtained from the non-linear function are utilized to estimate the mean and covariance of the random variable for the subsequent step as well as to update the covariance matrix using the measurement data [29].

$$\mathrm{sigma}\_\mathrm{points}=unscented\_transform\left(X\left(\frac{k+1}{k}\right),P\left(\frac{k+1}{k}\right)\right)$$

(18)

Equation (18) portrays the process of generating the sigma points for the next time step in the UKF algorithm. The input to the unscented transform is the predicted mean and covariance of the state variables at time step k + 1, denoted by X(k + 1|k) and P(k + 1|k), respectively [29].

State update: the state update equations for the Unscented Kalman Filter (UKF) are used to estimate the state variables of a dynamic system, based on measurements and a system model.

$$Y(k+1)=h(\mathrm{SP})=X(k+1|k)$$

(19)

Equation (19) gives the predicted measurement, which is obtained by passing predicted state X(k + 1|k) through h( ), where h( ) is the measurement function.

$$Y(k+1)=h(k+1)\ast \mathrm{sigma}\_po\mathrm{int}s$$

(20)

Equation (20) gives the transformed measurement covariance, which is obtained by transforming the sigma points through h( ). In this step, UKF captures the non-linearities in the system which cannot be achieved by KF.

$$P_{yy}(k+1)=Y(k+1)+Y{(k+1)}^T+R(k+1)$$

(21)

Equation (21) is the predicted measurement covariance, which predicts the measurement covariance P_yy(k + 1) at the subsequent time step based on the transformed measurement covariance Y(k + 1) and the measurement noise covariance R(k + 1) [25]. R(k + 1) is the measurement noise covariance matrix, which is a diagonal matrix that describes the statistical properties of the noise that is present in the measurement. The inclusion of R(k + 1) in the predicted measurement covariance P_yy(k + 1) ensures that the filter takes into account the presence of measurement noise when updating the state estimate.

$$P_{xy}(k+1)=P\left(\frac{k+1}{k}\right)\ast Y{(k+1)}^T$$

(22)

Equation (22) is the cross-covariance matrix P_xy(k + 1) and measures the correlation between the predicted state and the predicted measurement [29]. It represents the relationship between how the predicted state affects the predicted measurement. The notation P_xy is used because it represents the cross-covariance matrix between the state variable ‘x’ and measured variable ‘y’ [8].

$$K(k+1)=P_{xy}(k+1)\ast \mathrm{inv}(P_{xy}(k+1))$$

(23)

Equation (23) represents Kalman gain, which is a critical element in the Kalman filter algorithm. It is a vector that determines the degree to which the predicted state estimate (x(k + 1|k)) is adjusted by the observed measurement (z(k + 1)) [15]. The Kalman gain is calculated by multiplying the cross-covariance matrix P_xy(k + 1) by the inverse of the predicted measurement covariance matrix P_yy(k + 1) [18]. The Kalman gain K(k + 1) combines the information from the predicted state estimate and the predicted measurement to produce a more accurate estimate of the true state.

3.1. Measurement Update

$$X(k+1)=X\left(\frac{k+1}{k}\right)+K(k+1)\ast (z(k+1)-y(k+1))$$

(24)

Equation (24) represents the state update step in the Kalman filter. It updates the predicted state estimate x(k + 1|k) with the actual measurement z(k + 1) using the Kalman gain K(k + 1). The residual error between the actual measurement and the predicted measurement y(k + 1), which is generated by passing the sigma points through the measurement function, is weighted by the Kalman gain [9,12]. This weight determines how much the measurement should be used to correct the predicted state estimate. The resulting correction is added to the predicted state estimate to obtain the updated state estimate x(k + 1) [14].

3.2. Covariance Update

$$P(k+1)=P\left(\frac{k+1}{k}\right)-K(k+1)\ast P_{yy}(k+1)\ast K{(k+1)}^T$$

(25)

Equation (25) calculates the updated estimate of the error covariance matrix after incorporating the measurement at time k + 1. It uses the Kalman gain (K(k + 1)) calculated in the previous step, the predicted error covariance matrix at time k + 1|k (P(k + 1|k)), and the predicted measurement covariance matrix (P_yy(k + 1)) [18]. Equation (25) essentially calculates the amount of uncertainty that remains in the state estimate after incorporating the measurement. The term K(k + 1) * P_yy(k + 1) * K(k + 1)^T represents the portion of the error covariance matrix that is reduced due to the measurement. Subtracting this term from the predicted error covariance matrix (P(k + 1|k)) gives the updated error covariance matrix (P(k + 1)) that reflects the reduction in uncertainty due to the measurement [25].

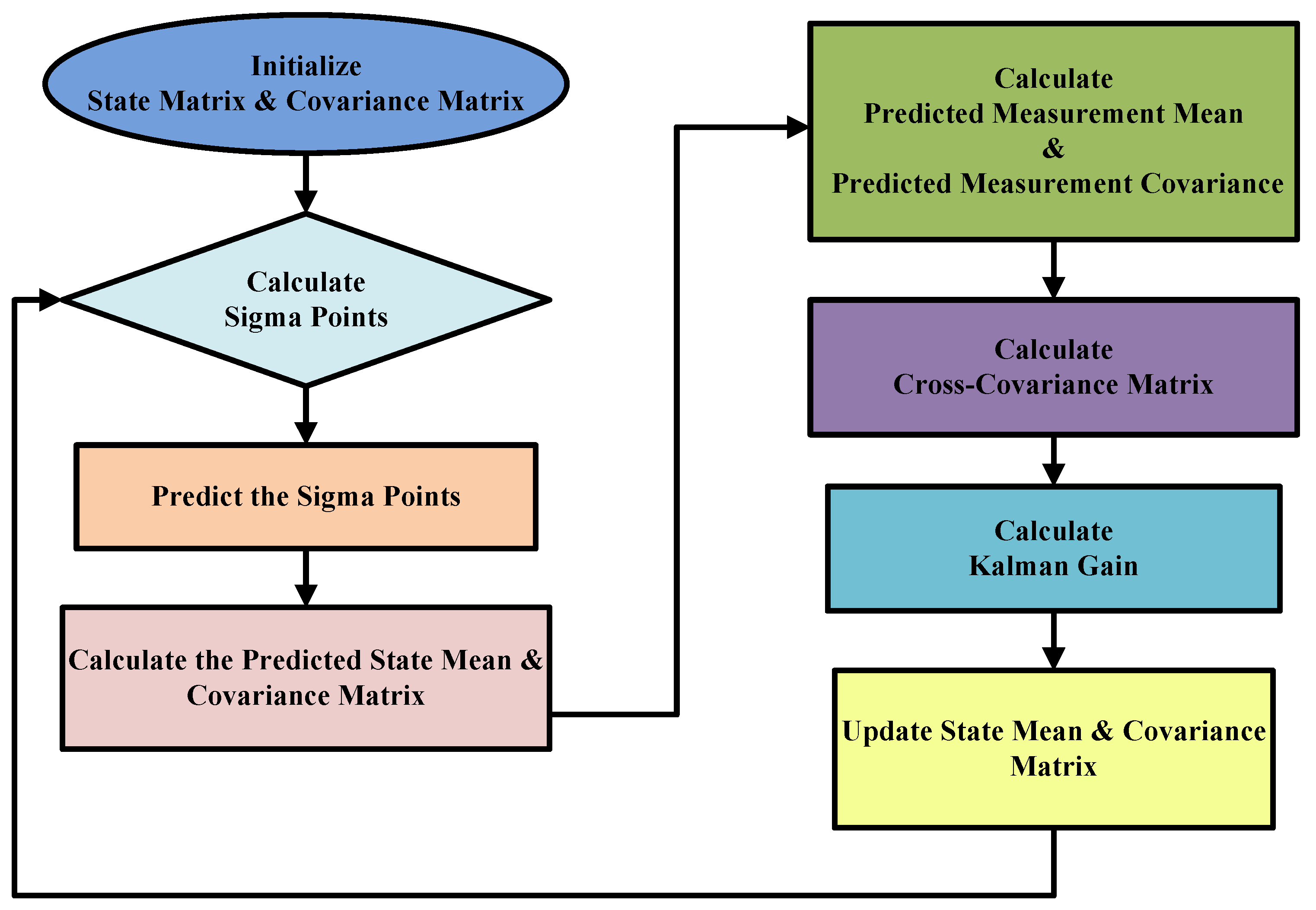
After the initialization step, Equations (17)–(25) are applied repeatedly to continually update the battery’s state estimate as new measurements become available. The exact number of times these equations need to be applied will depend on the specific problem being considered and the desired level of accuracy or precision. The overall flowchart of the UKF-based technique is depicted in Figure 2.

Using the above technique, SOC can be estimated. The SOH of lithium-ion batteries is highly dependent on accurate SOC prediction. The subsequent section describes the technique for SOC-dependent SOH estimation.

4. SOH Estimation Technique for LIBs

In this section, different SOH estimation techniques are elaborated. Li-ion batteries have become an essential part of modern life, especially in powering EVs. Li-ion batteries used in electric vehicles undergo cycles of charging and discharging during operation, which causes the battery to age over time. Furthermore, they can experience a decline in performance and capacity [24]. The deterioration of a battery’s capacity over time is commonly known as “capacity fade”, which can have a significant impact on the overall SOH [30,31,32]. The SOH of a lithium-ion battery is a measure of its present condition and how much it has degraded from its original state. Accurate monitoring of the SOH of a battery is crucial for predicting its remaining useful life, optimizing its performance, and ensuring its safe and reliable operation. There are several metrics used to assess the SOH of Li-ion batteries, including the columbic efficiency, capacity, cycle count, internal resistance, and self-discharge. Each of these metrics provides valuable information about the battery’s current state, and they can be used together to gain a comprehensive understanding of the battery’s health [24].

The basic SOH estimation analytical expression is given as:

$$\mathrm{SOH}=\frac{C_a}{C_{rated}}\ast 100\%$$

(26)

Equation (26) is used to calculate a lithium-ion battery’s SOH. The SOH of a battery is a measure of its current condition and how much it has degraded from its original state [30]. The actual capacity (C_a) of a battery refers to the quantity of stored energy it can deliver at a particular point in time. This value can be measured by charging the battery fully and then discharging it completely while measuring the amount of energy delivered [30]. The capacity decreases over time as the battery undergoes charging and discharging cycles and is affected by temperature and usage patterns. The rated capacity (C_rated) of a battery is the amount of energy it is designed to store and deliver under ideal conditions [31]. The manufacturer typically provides this value and is based on the battery’s chemistry and design.

For improved SOH estimation, the following analytical expression has been derived [24]:

$$\mathrm{SOH}=\frac{R_{end}-R_{pre}}{R_{end}-R_{new}}\ast 100\%$$

(27)

Equation (27) is an important technique widely used to compute the SOH of lithium-ion batteries. The term Rend represents the battery’s initial or “as-new” R₀, R_pre is the current R₀, and R_new is the R₀ of a brand-new battery of the same type. R₀ is a measure of the opposition to the flow of current within the battery. As Li-ion batteries age, their R₀ tends to increase due to the decomposition of unwanted materials and changes in the battery’s physical structure [24]. A higher R₀ can result in a decrease in the battery’s capacity and overall performance. Equation (27) calculates the SOH by comparing the current R₀ of the battery (R_pre) to its initial or “as-new” R₀ (R_end). The difference between R_end and R_pre is then divided by the difference between R_end and the R₀ of a brand-new battery of the same type (R_new) [20]. This ratio is then multiplied by 100 to obtain the SOH percentage. By monitoring the R₀ and implementing the derived Equation (27) in the battery management system, EV users can estimate an accurate SOH of a battery. Additionally, the derived formulation is useful for battery users and manufacturers for reliable health monitoring of EV batteries and allows EV users to make prompt decisions about battery replacement time [24].

5. Results and Discussion

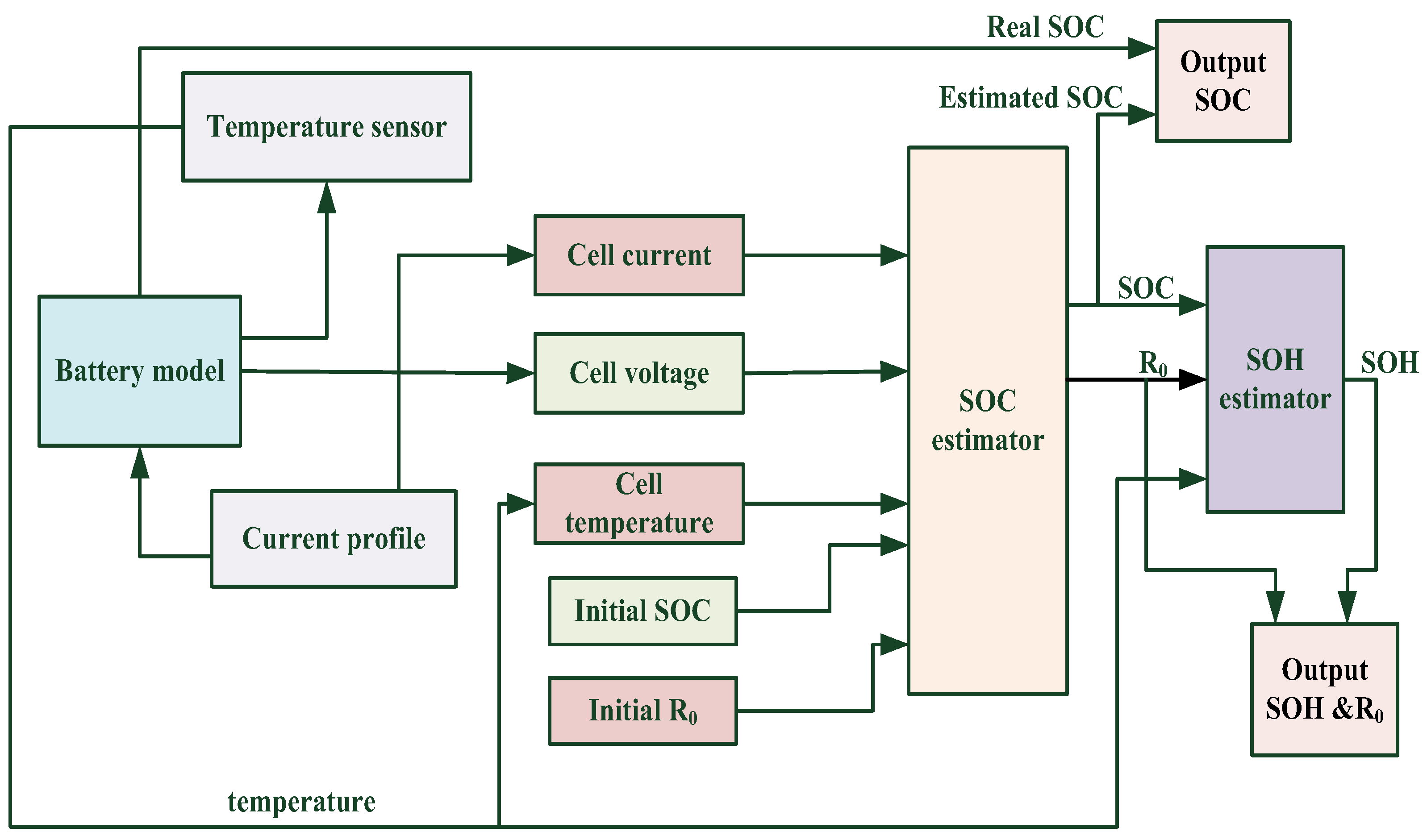
The SOC-dependent SOH estimation is elaborated on in this section. The various observations, such as SOH and R₀ of the battery, were carefully estimated with different initial SOC values. Furthermore, the robustness of the SOH estimation using the UKF technique was studied and compared with well-established techniques in the literature (EKF Technique). Figure 3 illustrates the steps involved in estimating the SOH of a battery. Accurate modeling of a battery is crucial in estimating its SOH, especially in the case of lithium-ion batteries. A precise model can provide insight into the internal behavior and characteristics of the battery, enabling accurate prediction of its remaining useful life. In this context, by using the battery model (Figure 1), it is possible to simulate the performance of the battery for a range of operating conditions and estimate its SOH based on the comparison with the model’s simulated performance. Temperature sensors are instrumental in the estimation of SOH for Li-ion batteries, as they offer critical insights into the internal temperature of the battery, which has a notable influence on its performance, degradation, and safety. The internal temperature of a Li-ion battery can greatly impact its capacity and cycle life. For example, at high temperatures, the battery can undergo thermal runaway, leading to irreparable damage or even explosion.

Voltage measurement and current measurement sensors are essential components in the SOH estimation of Li-ion batteries. They are employed to measure the battery’s voltage and current during EV operation, which provides critical information about the battery’s state and performance and helps in the estimation of important parameters such as battery capacity, SOC, R₀, and operating temperature. Furthermore, these parameters are of utmost importance for estimating the battery’s remaining capacity, which is critical for SOH estimation. The estimation of the SOC of a battery has been accomplished using measurement data obtained from the voltage and current sensors. The estimated SOC plays a vital role in predicting the SOH of the battery by tracking its SOC over time, as depicted in Figure 3. In addition, the estimated SOC obtained through the UKF method, along with the temperature and R₀ information, was utilized to estimate the SOH of the battery.

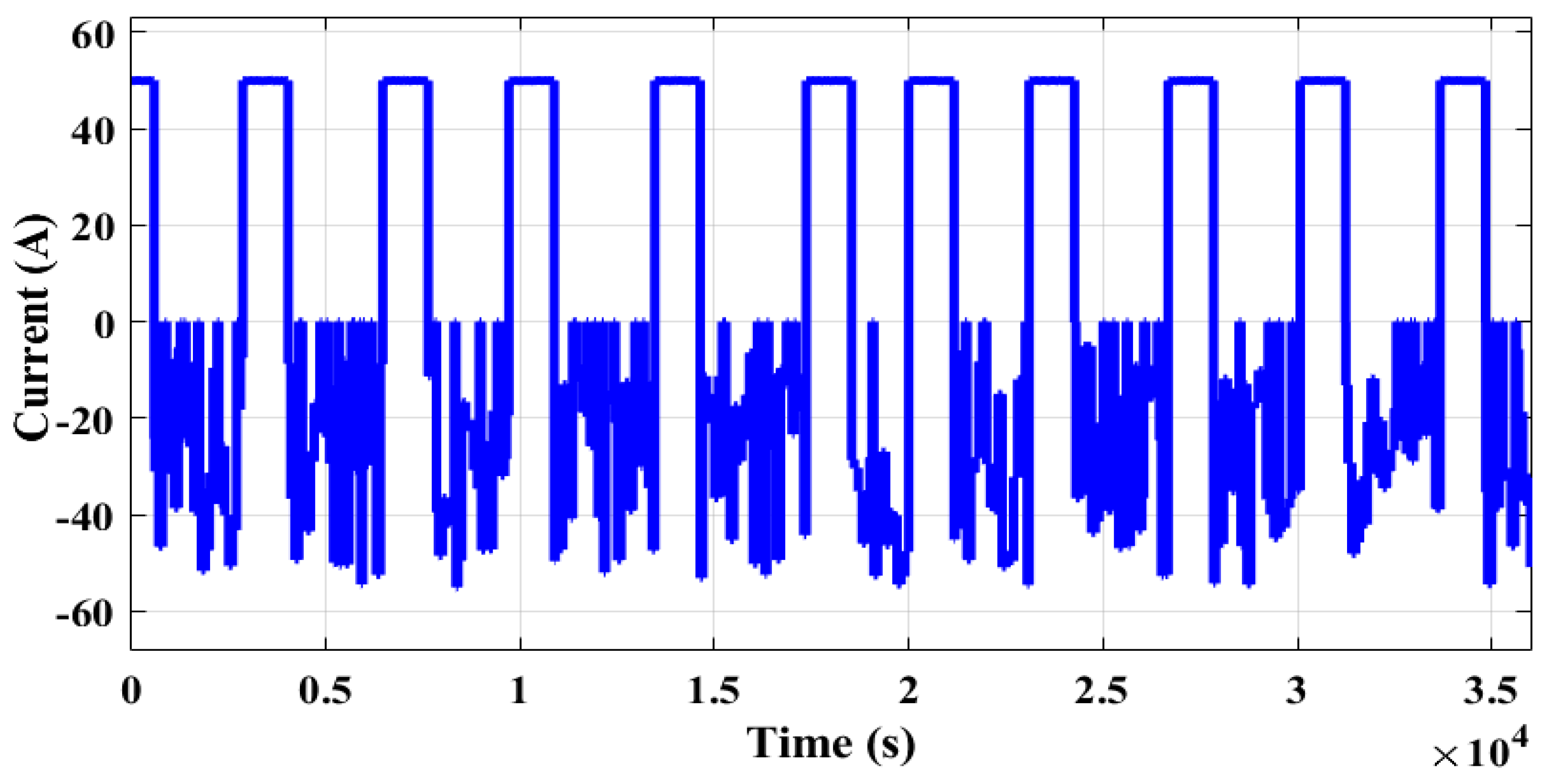
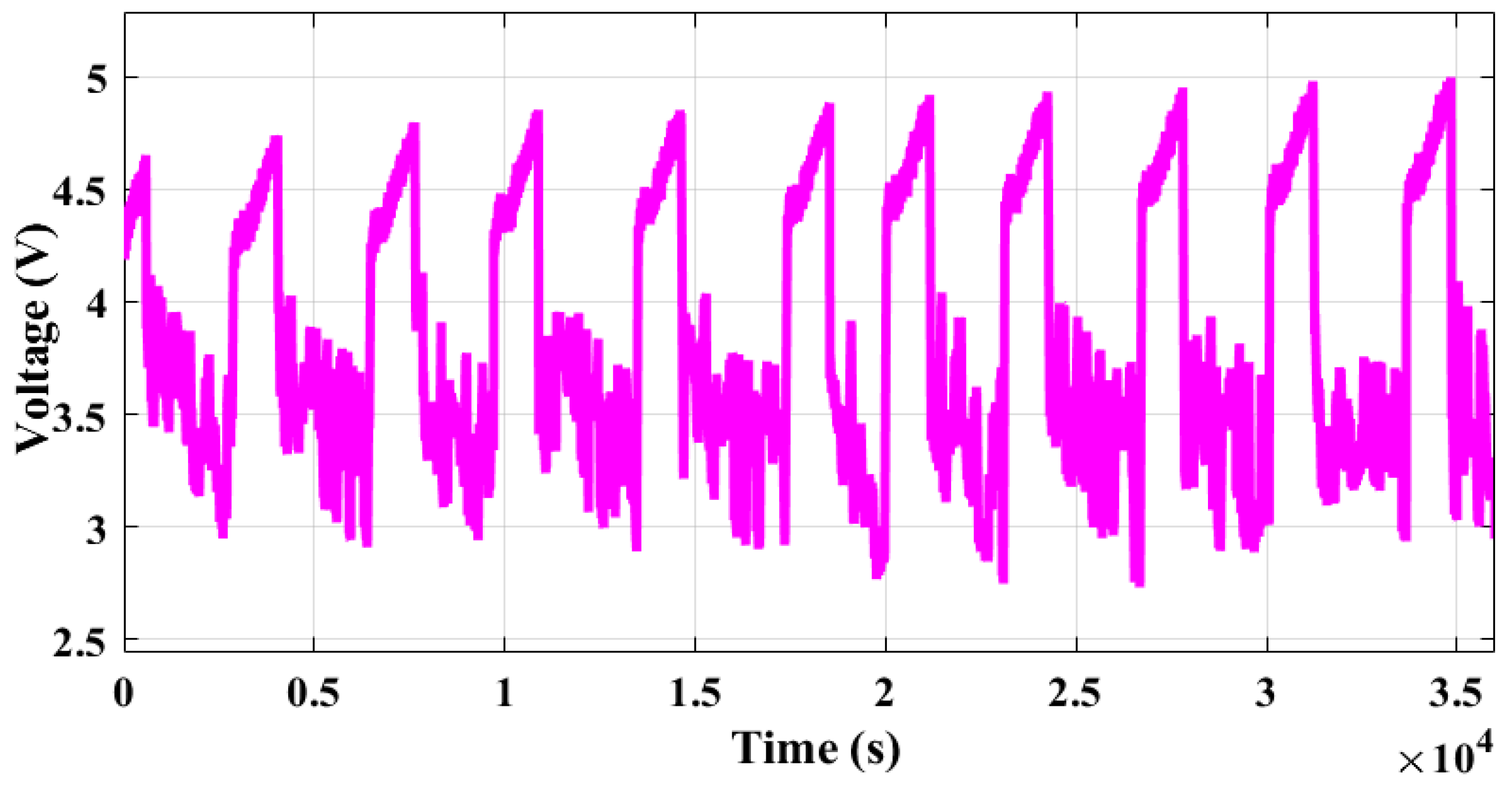
Initially, the battery was operated with the current profile as depicted in Figure 4. The current profile represents the amount of current that is being drawn or supplied to the battery over time during EV operation. The current profile (Figure 4) is given to the battery model (discussed in Section 2). The battery voltage dynamics (Figure 5) were observed for the given input charge/discharge drive profile. The voltage profile of the battery was acquired using a voltage sensor that is positioned across the battery terminals. The voltage sensor may introduce some noise into the measurements; this error is also added to the measured voltage and given as input to the SOC estimator. 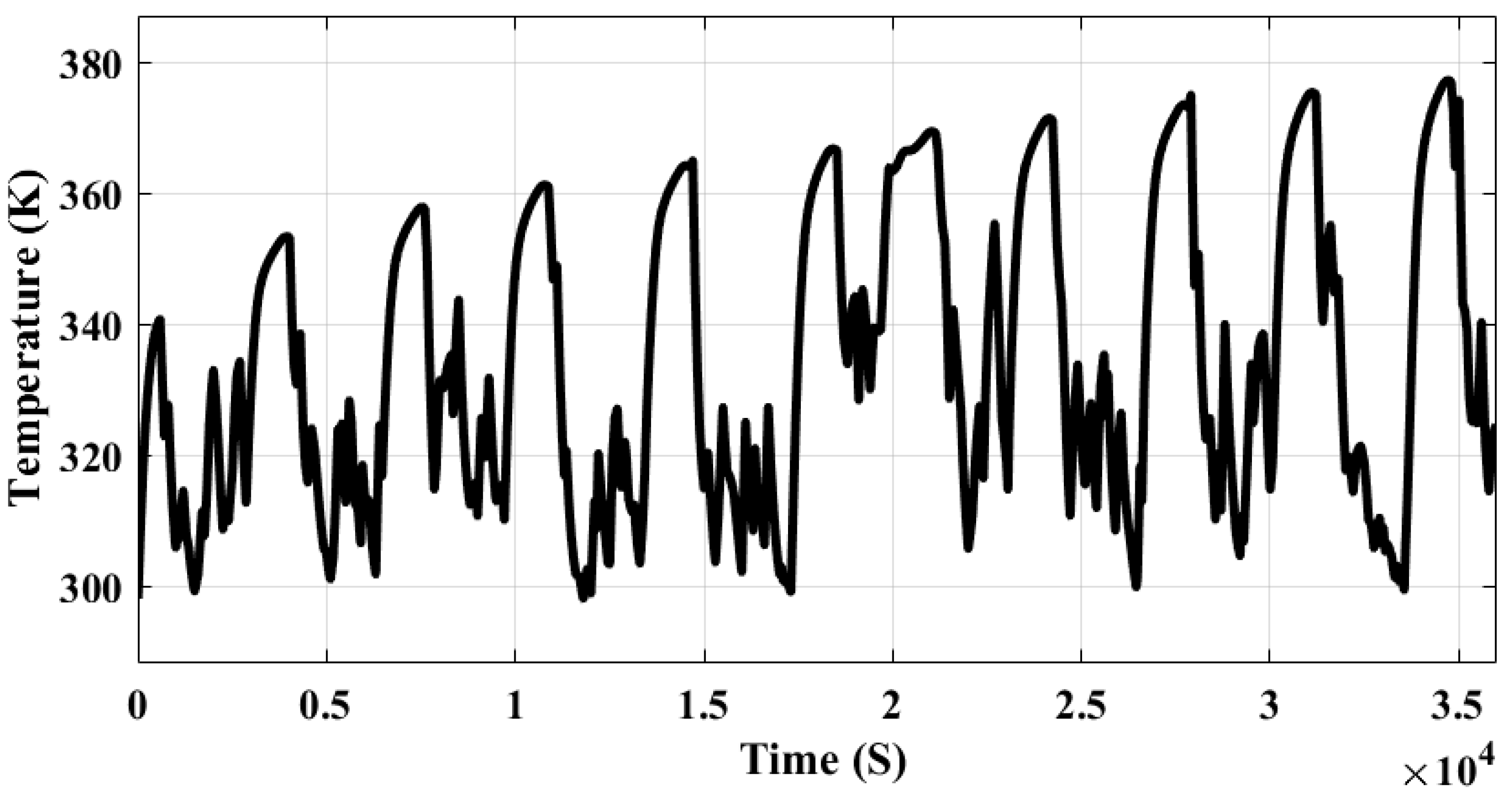Figure 6 illustrates the battery temperature measurements obtained during the operation of the EV. The temperature of the battery is monitored over time by a temperature sensor. From Figure 6, it can be observed that the temperature increases while charging and decreases while discharging. This phenomenon can be explained by the fact that during a charging cycle, the temperature of the battery may increase due to the conversion of electrical energy into chemical energy within the battery. Conversely, during a discharge cycle, chemical energy is converted into electrical energy, leading to a decrease in temperature.

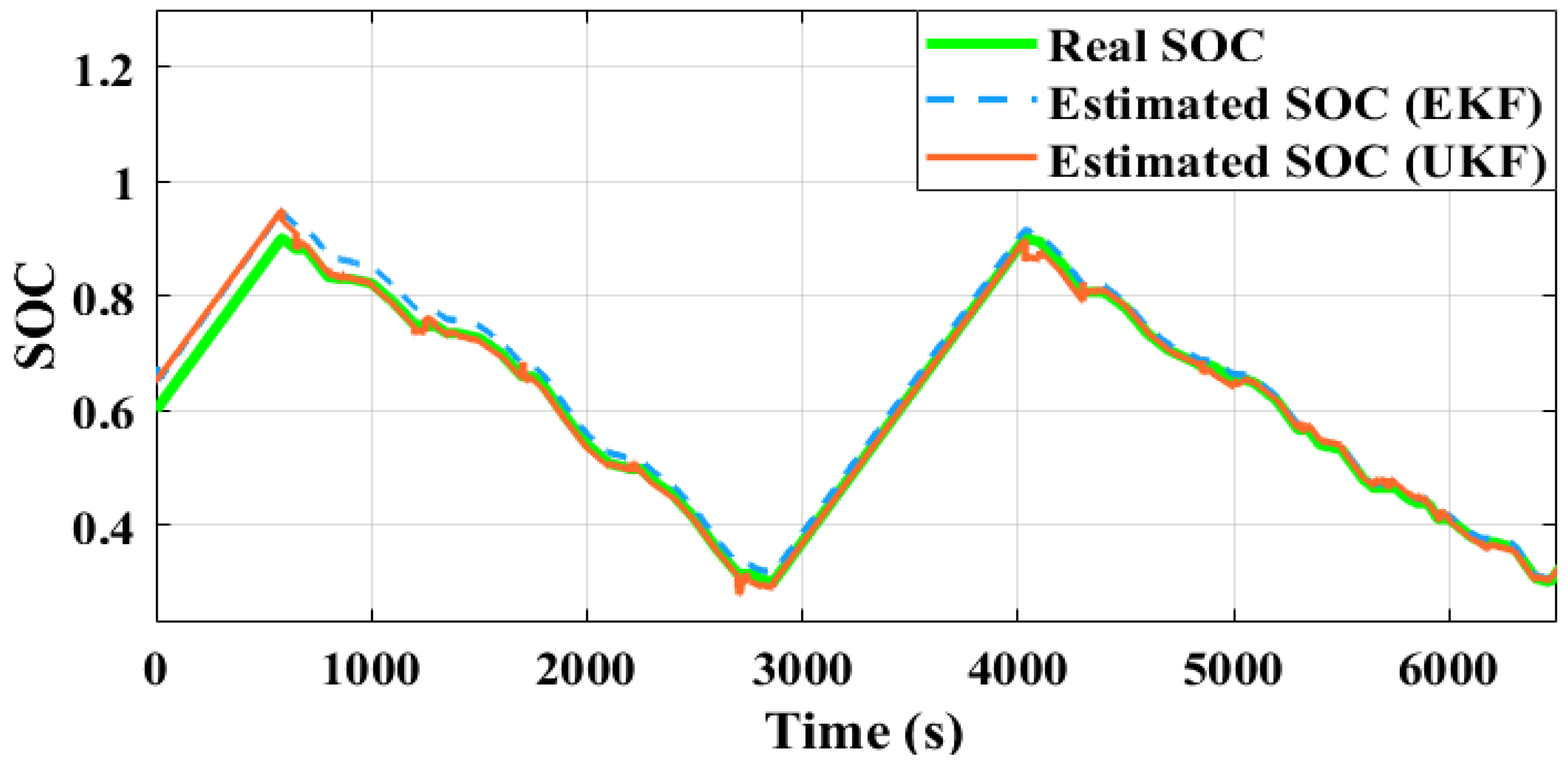
The SOH estimation process elaborated on in Figure 3 demands an accurate SOC estimation to predict battery degradation accurately. Initially, the actual SOC of the battery is measured with commonly used methods, such as the coulomb counting technique or the current integration technique, based on the EV drive profile (Figure 1). The measured real SOC is depicted in Figure 7. The estimated SOC using the coulomb counting technique has a critical limitation, such as current sensor noise accumulation and initial SOC being updated at a regular interval of time. This makes the accurate SOC estimation uncertain, further affecting the accuracy of the battery degradation prediction. This demands an accurate and reliable SOC estimation technique.

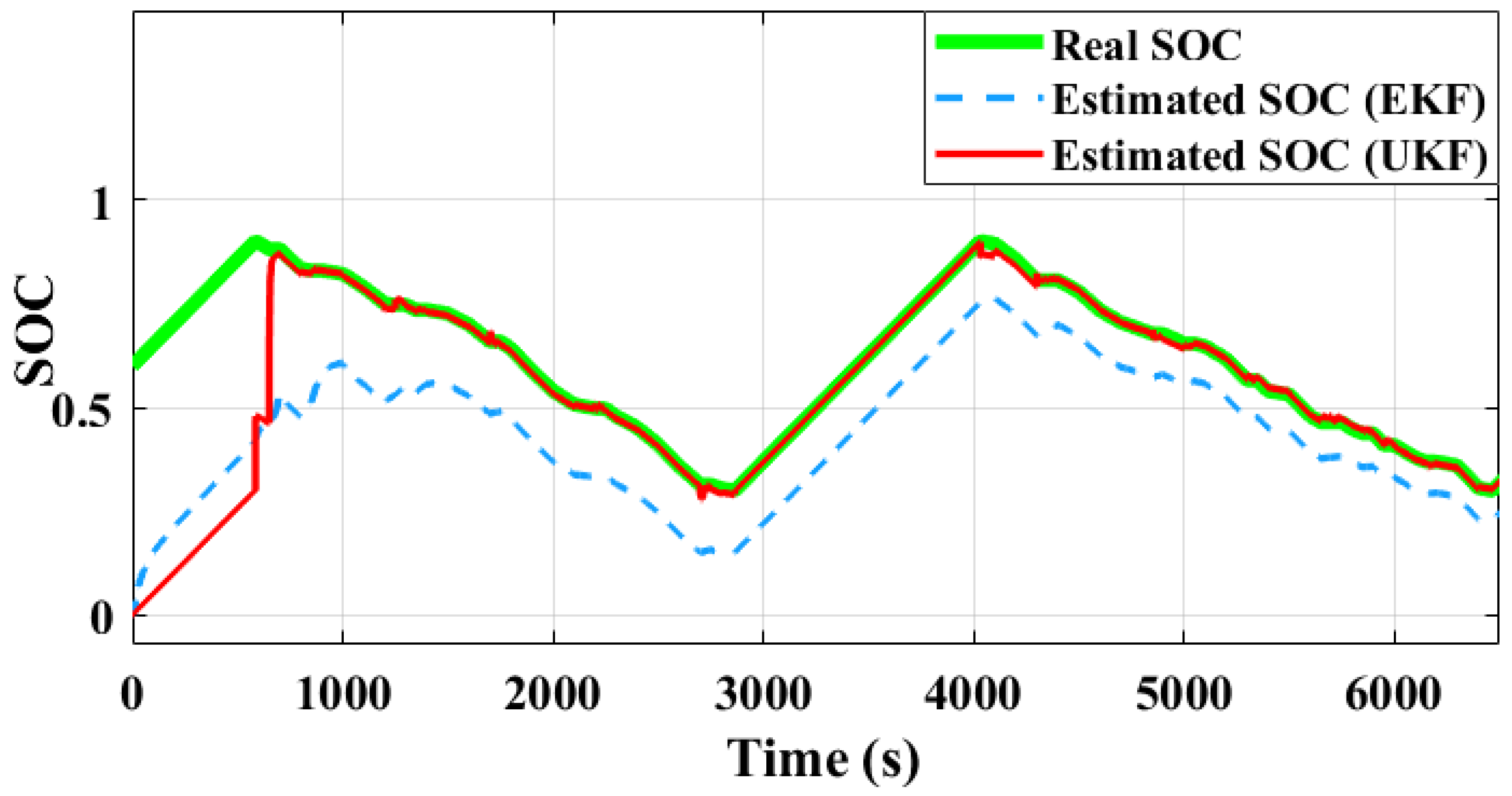
To overcome the above limitations, different KF variants have been adopted. Using the input drive profile (Figure 4) and output voltage profile (Figure 5), the proposed UKF technique, as discussed in Section 3, was utilized for estimating the SOC of the battery, which is illustrated in Figure 7. From Figure 7, it can be seen that the UKF algorithm performs better in comparison to widely used techniques such as the EKF algorithm for estimating the SOC of a battery. The enlarged depiction presented in Figure 8 provides enhanced clarity concerning the effectiveness of the SOC estimation technique based on the UKF algorithm. This means that the UKF algorithm provides more accurate and reliable SOC estimates than the EKF algorithm. The UKF algorithm is more adept at managing non-linearities, noise, and uncertainties associated with input parameters.

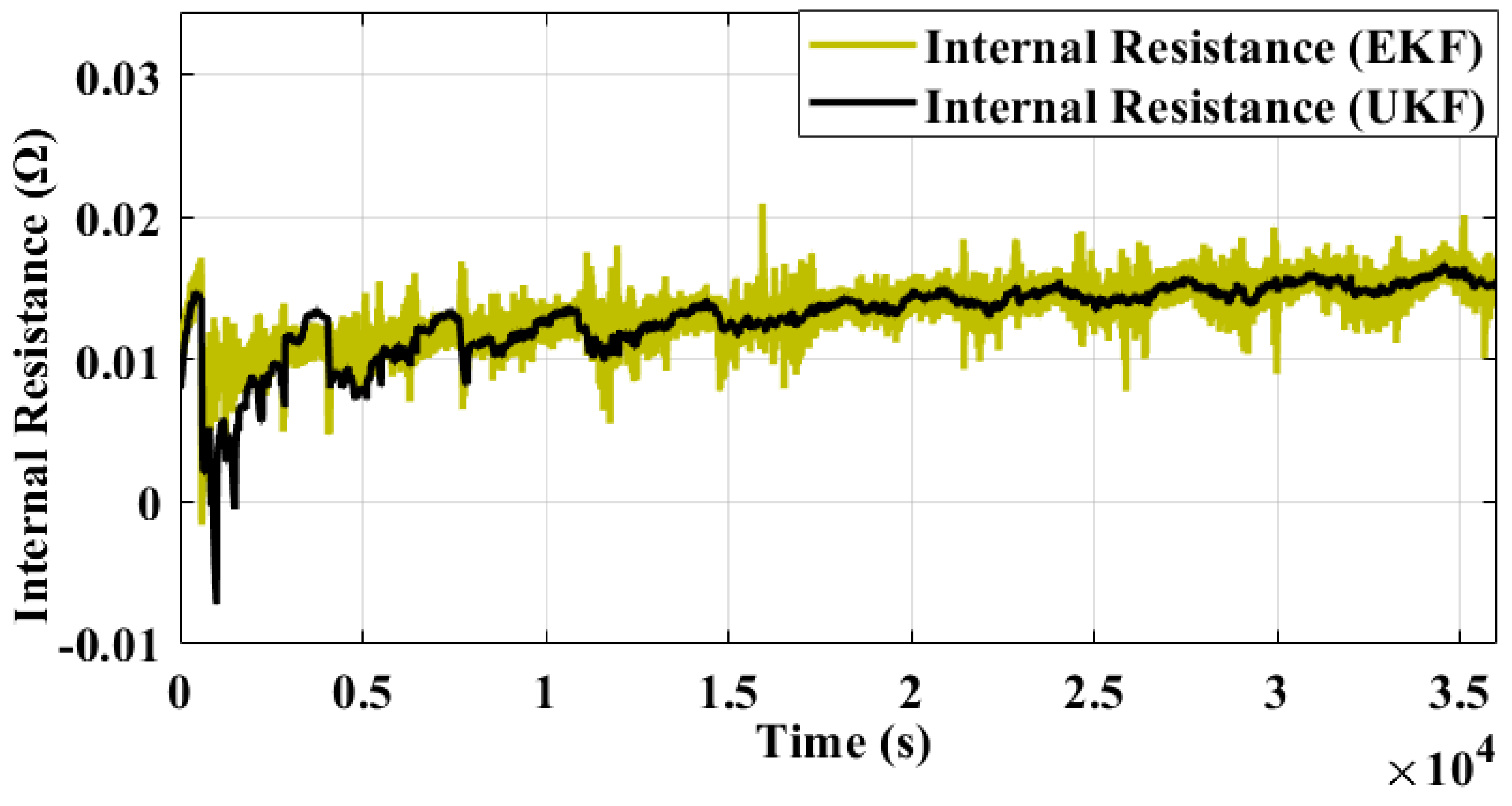
The UKF-based SOC estimator produced an output (estimated R₀) along with an estimated SOC as shown in Figure 9. To verify the accuracy of the estimated R₀, measurements were taken using both UKF and EKF algorithms. It can be observed that the estimated R₀ increased with time, which is a common trend in battery aging. Additionally, it was observed that the R₀ obtained from EKF had more noise compared to UKF, indicating that the EKF algorithm may be more sensitive to noise and other sources of error in the input data. 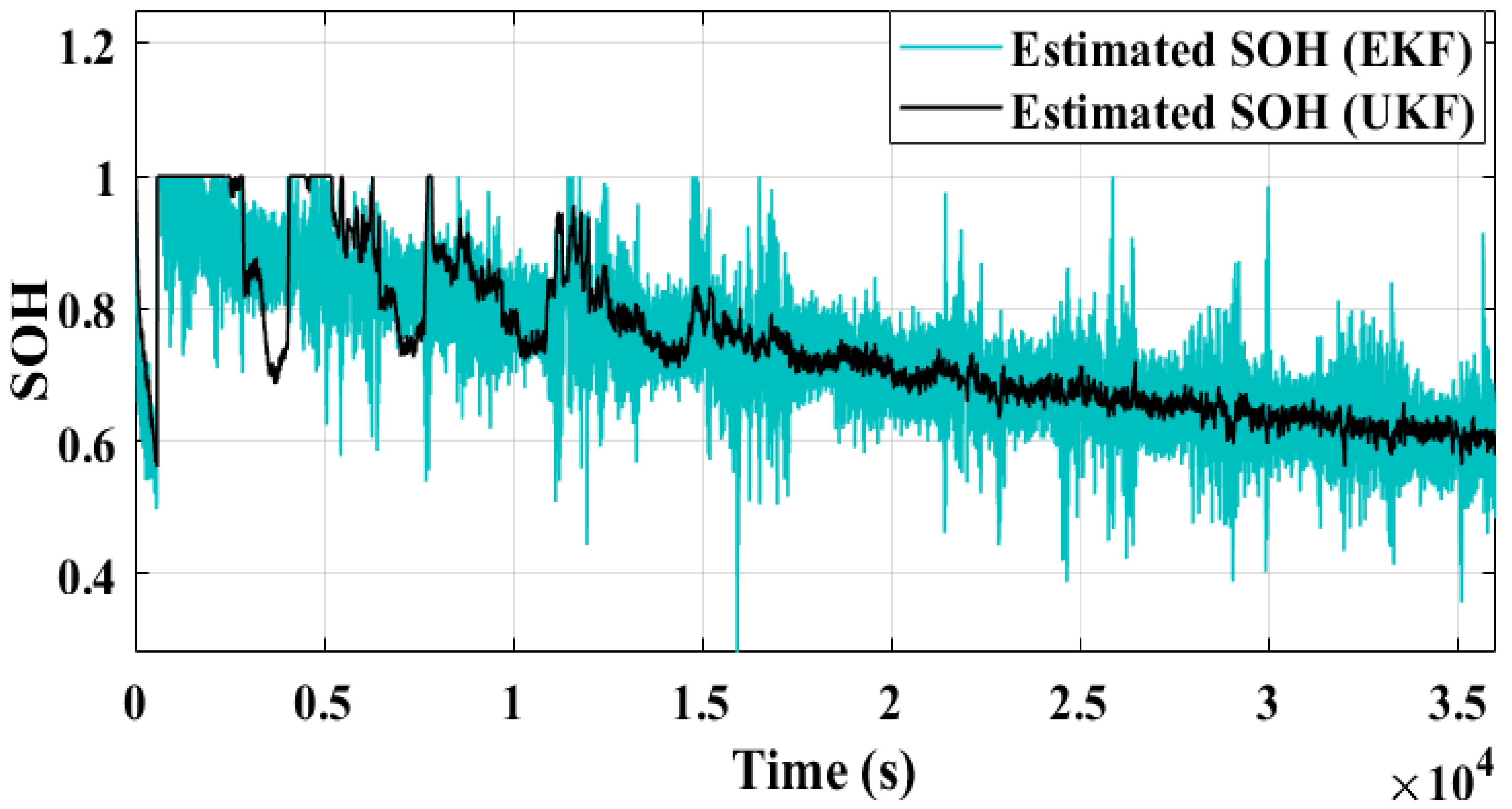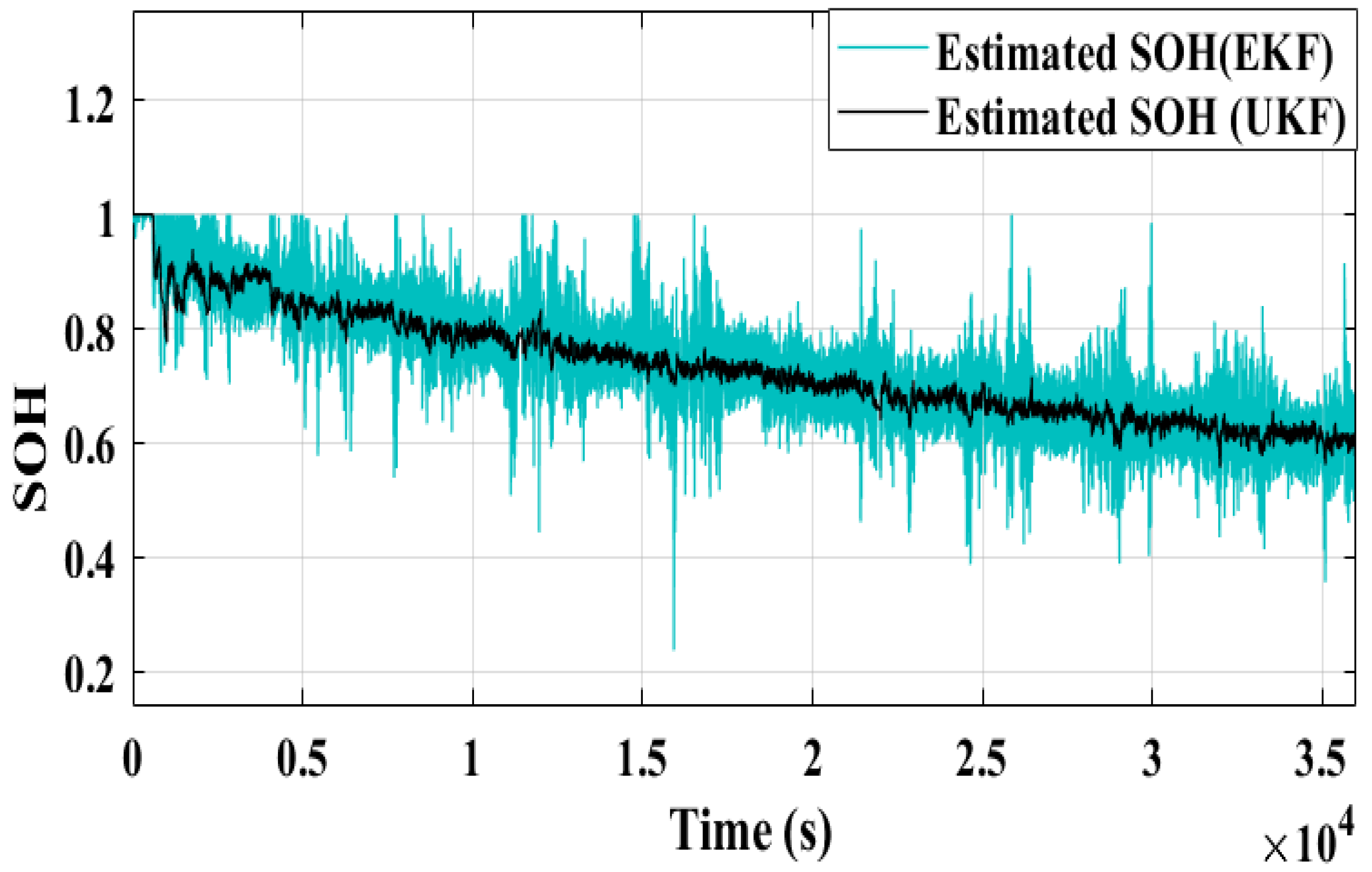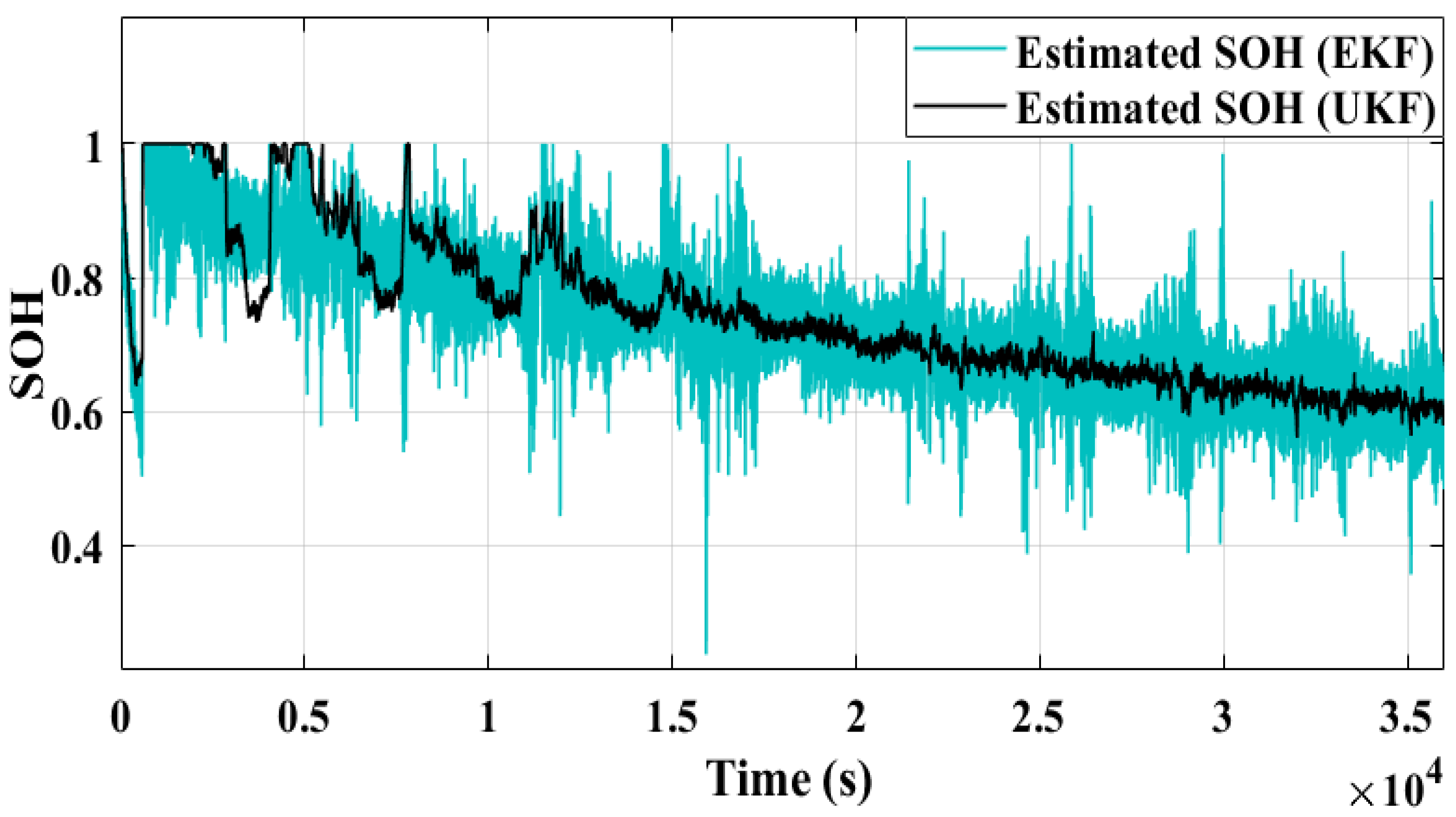With the estimated SOC (using UKF), R₀ (Figure 9), and temperature measurements, the SOH (using Equation (27)) of the battery has been estimated and is depicted in Figure 10. It can be seen (Figure 10) that the SOH decreases with time, which is due to various degradation mechanisms. To verify the accuracy of the SOH estimator, measurements were taken using both UKF and EKF algorithms as shown in Figure 10. It can also be seen that the EKF algorithm produces more noise in the SOH estimation compared to UKF, indicating that EKF may be more sensitive to noise and other sources of error in the input data The smooth measurements of R₀ (Figure 9) and SOH (Figure 10) using the UKF technique depict that it is more robust against unknown sensor noise/input and nonlinearities in system dynamics.

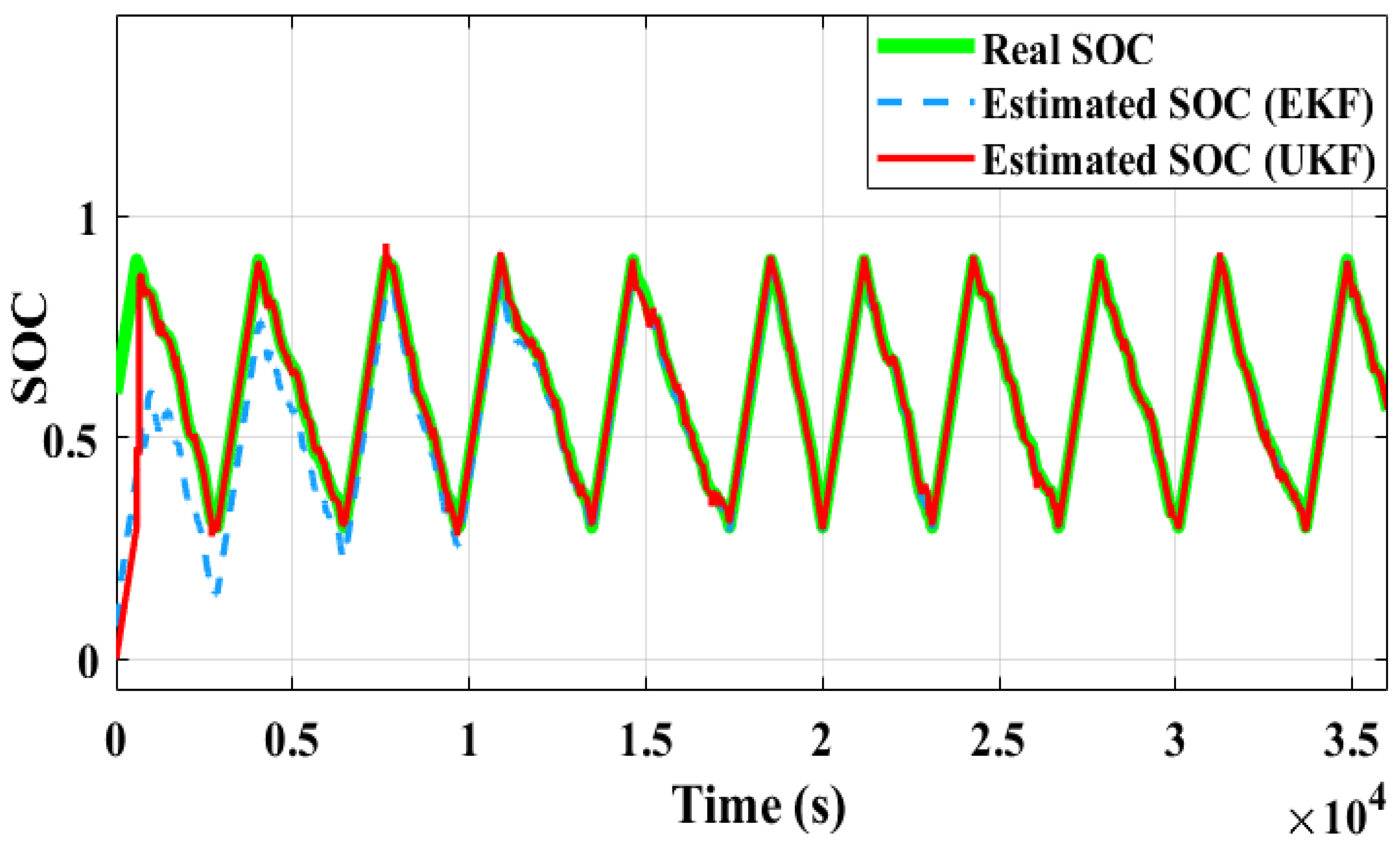
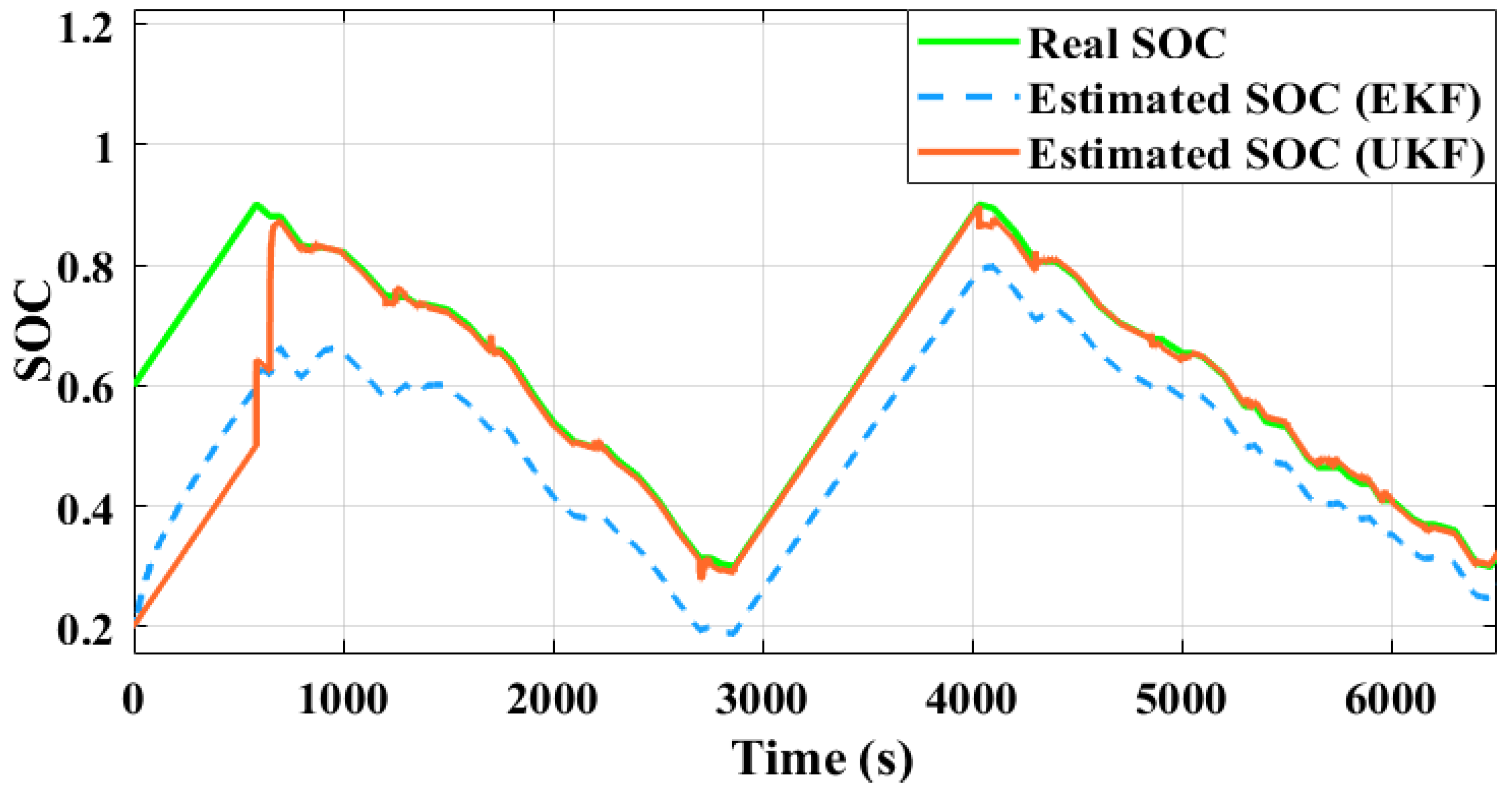
To check the robustness of SOH estimation using the UKF technique, the initial SOC value was varied to different values. The proposed UKF-based technique robustness was validated under two different scenarios. During case I, the initial value was fixed as SOC = 0, and the SOC and R₀ of the battery were estimated using UKF and EKF. This estimated SOC and R₀ are depicted in Figure 11, Figure 12 and Figure 13, respectively. Based on the observations from Figure 11 and Figure 12, it can be concluded that the UKF technique provides more accurate and faster tracking of the real SOC compared to the EKF technique. Using the estimated SOC, estimated R₀ (Figure 13), and temperature measurements, the SOH (Using Equation (27)) of the battery has been predicted, as shown in Figure 14.

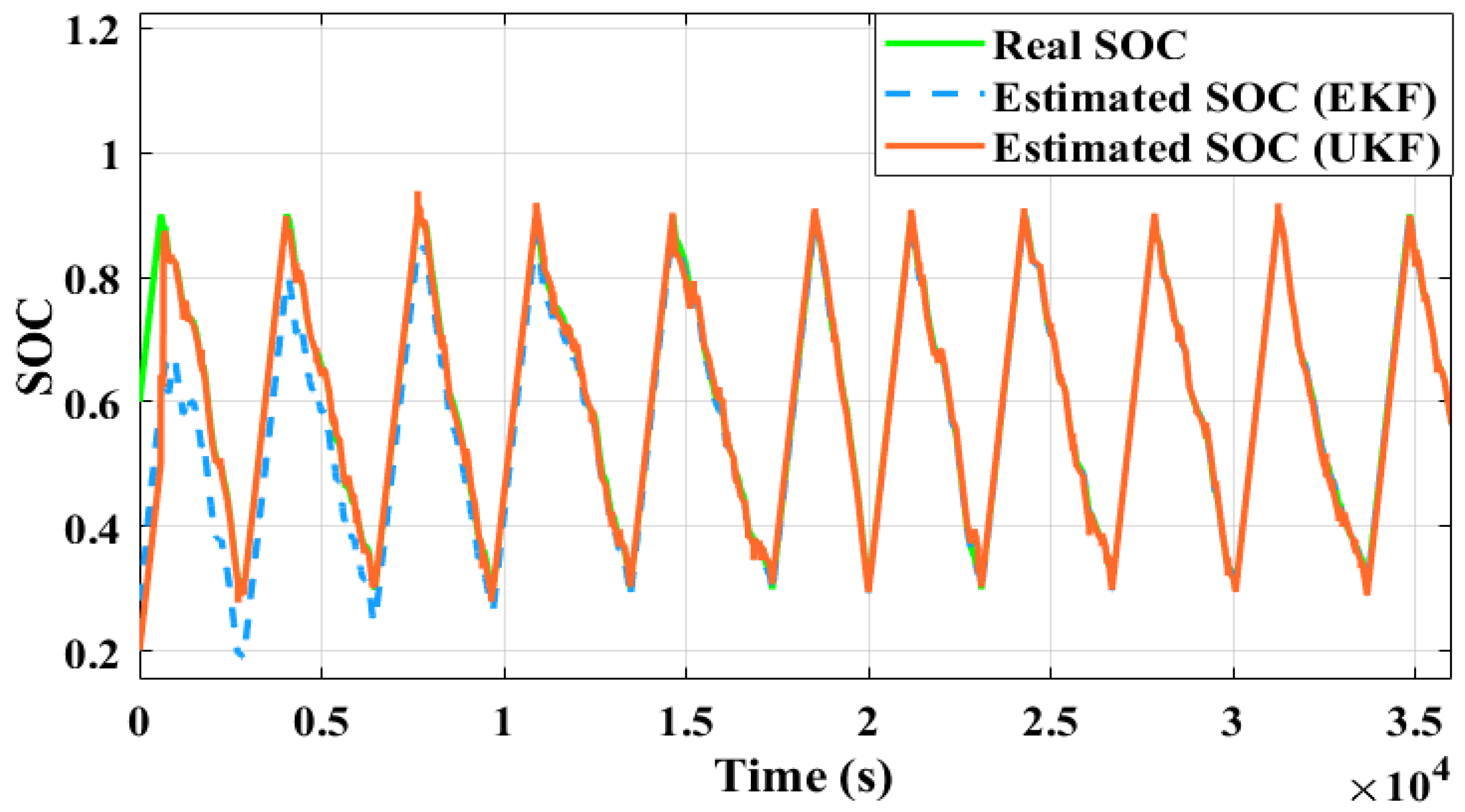
This SOH prediction further depicts that the EKF algorithm produces more noise in the SOH estimation compared to UKF, indicating that EKF may be more sensitive to noise and other sources of error in the input data. A similar analysis was carried out considering case II (initial SOC = 0.2). Under the fluctuating condition of an initial SOC of 0.2, the SOC and R₀ estimation using the UKF technique were found to be superior to the EKF technique, as demonstrated in Figure 15, Figure 16 and Figure 17. The magnified view presented in Figure 16 provides clear evidence of the effectiveness of the proposed technique (UKF) for SOC estimation. Furthermore, the SOH of the battery was estimated considering the estimated SOC and R₀. The estimated SOH for case II is illustrated in Figure 18 and it can be seen that the UKF technique provides robustness against noise and other uncertainties in comparison to the UKF base method. From Figure 13, Figure 14, Figure 17 and Figure 18, it is clear that the initial SOC value estimator will affect the estimation of other battery parameters, such as SOH and R₀. If the initial SOC value is inaccurate, the estimator may produce distorted estimates of SOH and R₀ in the initial phase. This is because the estimator needs to gather enough information about the battery behavior to produce accurate estimates of the health parameters (SOH and R₀). Finally,

Table 1. Comparative analysis among different techniques (UKF, EKF) with varying initial conditions.

Initial SOC	Tracking Time (Real SOC)
	UKF	EKF
SOC0 = 0	700 s	8000 s
SOC0 = 0.2	730 s	8469 s
SOC0 = 0.4	780 s	8678 s

depicts the superiority of the proposed technique (UKF) in terms of tracking speed to real SOC.

6. Conclusions

This paper provides a robust battery health monitoring and prediction scheme for an electric vehicle battery management system. The UKF-based technique has been developed to monitor the health status of the battery. Furthermore, we have shown that the UKF is an effective tool for the SOH estimation of Lithium-ion batteries under diverse operating conditions. The UKF technique was compared with the widely used EKF-based health estimation scheme. The results depict that the proposed technique performed well in comparison to the EKF-based scheme. The study also found that the UKF technique produced accurate and reliable results in estimating the SOH of the battery, even when the battery was subjected to varying initial conditions in terms of the state of charge. Furthermore, the obtained results depict that the proposed UKF-based technique tracks real SOC very quickly in comparison to the EKF-based estimation scheme under varying initial conditions (varying SOC). This shows that the proposed technique (UKF) has a higher computation speed. Overall, the study demonstrates that the use of the UKF technique for SOH estimation has the potential to enhance the efficiency and durability of Lithium-ion batteries. The utilization of the UKF technique can aid in mitigating the risk of unforeseen battery failures and reduce maintenance costs associated with battery systems in electric vehicles.