New Mass Transport Correlation for Vanadium Redox-Flow Batteries Based on a Model-Assisted Parameter Estimation
Abstract
1. Introduction
2. Overview of Mass Transport Correlations for Felt Electrodes
| Reference | Correlation(s) | Electrolyte | Electrode | Schmidt Number |
|---|---|---|---|---|
| Kinoshita et al. [29] | Sh = 1.29 Re0.72 Sh = 1.01 Re0.61 0.01 < Re < 0.4 | 6 to 62 mM Br2 in 2 M ZnBr2 + 1M ZnCl2 + 3 M KCl | Carbon felt, type CH, Fiber Materials Inc. Fiber diameter: 25.4 µm | ~900 * |
| Schmal et al. [30] | Sh = 7 Re0.4 0.04 ≤ Re ≤ 0.2 | 0.1 to 10 mM K3Fe(CN)6 in 1 M KOH | Carbon fiber, Le Carbone Lorraine AGT/FT10 000 Fiber diameter: 8 µm | ~1600 (estimated to be similar to Vatistas et al.) |
| Vatistas et al. [56] | Sh = 4.26 Re0.64 ** 0.003 < Re < 0.19 | 1 or 3 mM K3Fe(CN)6 in 3 or 9 mM K4Fe(CN)6 + 0.5 M KOH | Carbon felt, GFD 5, SIGRI GmbH Fiber diameter: 8 µm | 1393–2264 † |
| You et al. [57] | Sh = 1.68 Re0.9 0.08 < Re < 1.43 | 50 mM FeCl2 in 0.75 M FeCl3 + 2 M HCl | Carbon felt, type n.a. Fiber diameter: 10 µm | 1522 |
| Barton et al. [58] flow through (FT) and interdigitated (ID) | Sh = 0.004 Re0.75 Sc0.51 0.005 < Re < 0.4 (FT) Sh = 0.018 Re0.68 Sc0.50 0.0006 < Re < 0.05 (ID) | 0.5 M FeCl2 + 0.5 M FeCl3 in 2 M HCl | Carbon paper, Sigracet 29AA, SGL Carbon Fiber diameter: 7 µm | 3800–24,000 |
| Kok et al. [59] | Sh = 0.9 Re0.4 Sc0.4 (rounded) 10−6 < Re < 1 | n.a. | Carbon felt, GFD, SGL Carbon Fiber diameter: 8.2 µm | n.a. |
| Reference | Correlation | Electrolyte | Electrode | Schmidt Number |
|---|---|---|---|---|
| Carta et al. [54] | Shdh = 3.19 Re 0.69 1 < Redh < 15 | 2 mM K3Fe(CN)6 in 100 mM K4Fe(CN)6 + 1 M KNO3 and 1 mM CuSO4 in 0.1 M H2SO4 | Carbon felt, SIGRI GmbH Fiber diameter: 11 µm | 1203 and 1365 |
| Xu et al. [55] | Shdh = 2 + 1.534 Redh0.912 0.3 < Redh < 2.4 | 0.125 M to 1.0 M V @90% SoC in 3M H2SO4 | GFA, SGL Carbon GmbH Fiber diameter: n.a. | n.a. |
3. Setup of the Mathematical Model
4. Experimental Setup
5. Results and Discussion
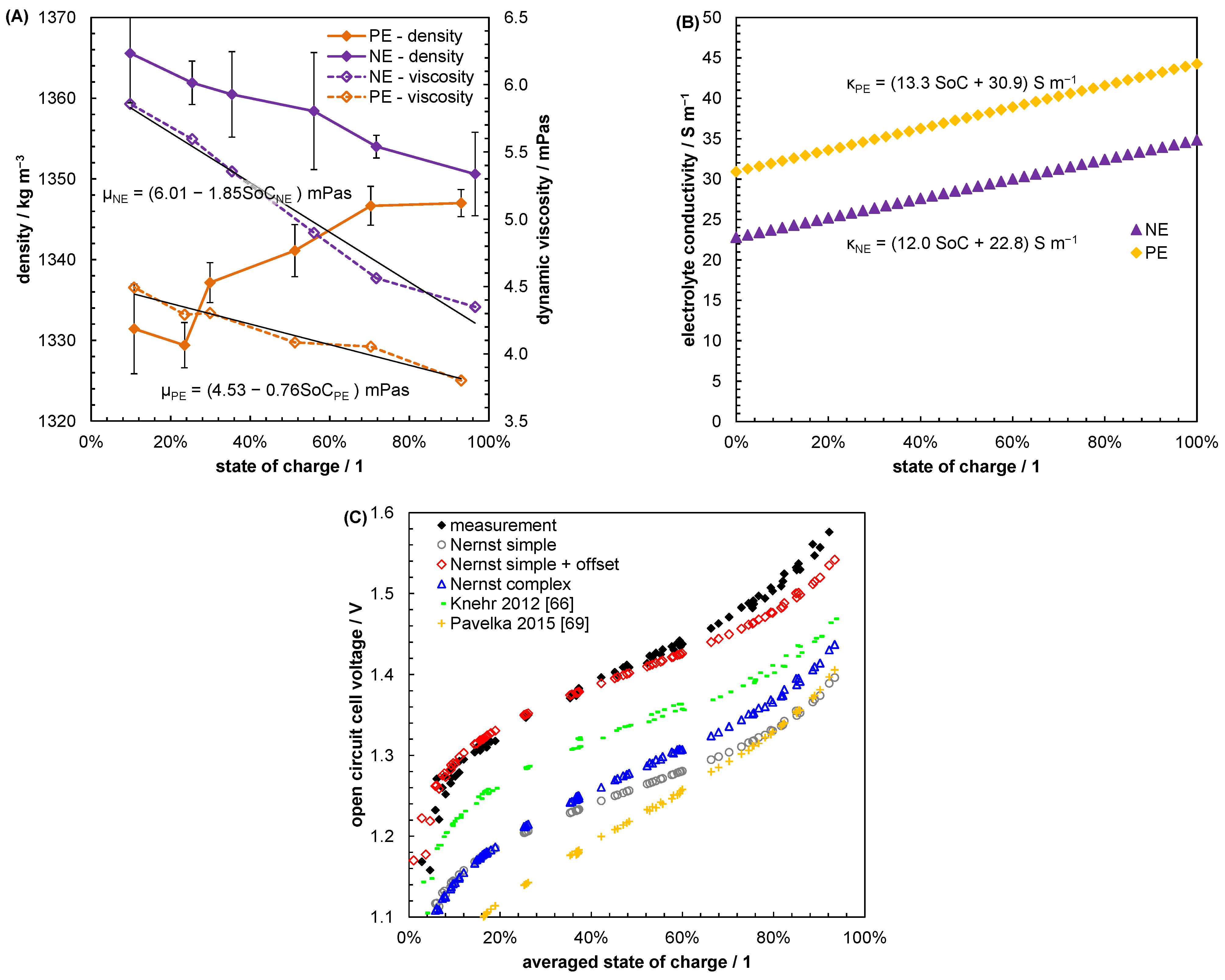
5.1. Evaluating Reasonable Diffusion Coefficients from Literature Data
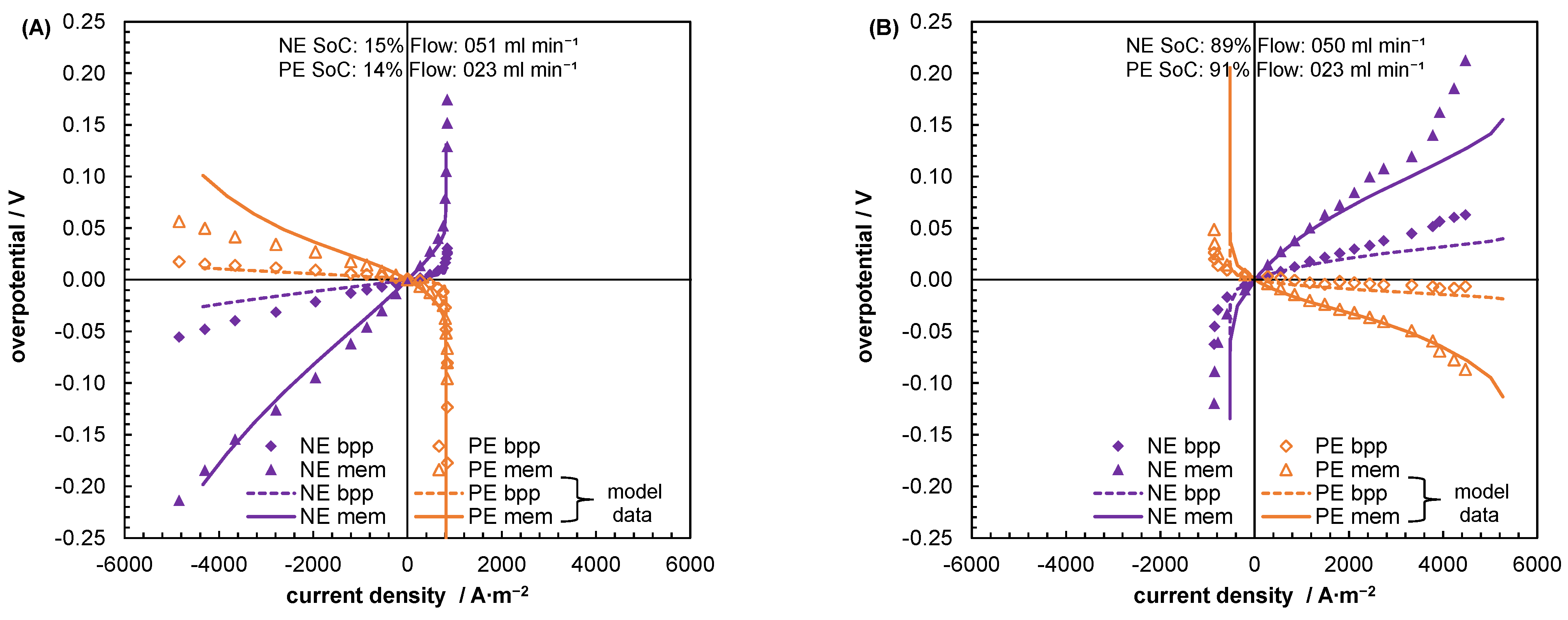
5.2. Mass Transport Parameter Estimation and Model Validation
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Symbol | Name | Unit |
|---|---|---|
| a | Specific surface area of the electrode | m2 m−3 |
| aSh, bSh, cSh | Empirical coefficients for the calculation of the Sherwood number | - |
| cin | Concentration of vanadium species in cell inlet | mol m−3 |
| cbulk | Concentration in the bulk of the electrolyte | mol m−3 |
| CR | Compression rate of the electrode | % |
| cref | Reference concentration according to standard conditions | 1000 mol m−3 |
| csurf | Concentration on the fiber surface of the carbon-felt electrode | mol m−3 |
| D | Diffusion coefficient | m2 s−1 |
| df | Diameter of the graphite fibers | m |
| dh | Hydraulic diameter of the carbon felt | m |
| Eeq | Equilibrium potential of a single reaction | V |
| EOCV | Open circuit potential of a full cell | V |
| Eref | Standard electrode potential | V |
| F | Faradaic constant (96,485) | 96,485 C mol−1 |
| H | Height of the electrode | m |
| i | Charge transfer current density | A m−2 |
| i0 | Exchange current density | A m−2 |
| J | Mass flux | mol m−2 s−1 |
| j | Local current density | A m−2 |
| jeff | Effective current density applied to the whole cell | A m−2 |
| jL | Current density in the liquid phase of the electrode area | A m−2 |
| jS | Current density in the solid phase of the electrode | A m−2 |
| k0 | Reaction rate constant | m s−1 |
| Ks | Acid dissociation constant | - |
| km | Mass transfer coefficient | m s−1 |
| R | Ideal gas constant | 8.314 J mol−1 K−1 |
| rbpp | Bipolar plate resistance | Ω m2 |
| Re | Reynolds number | - |
| rmem,ch | Membrane resistance during charging | Ω m2 |
| rmem,dis | Membrane resistance during discharging | Ω m2 |
| Sh | Sherwood number | - |
| SoC | State of Charge | % |
| T | Temperature | K |
| t | Thickness of the compressed electrode | m |
| t0 | Uncompressed thickness of the electrode | m |
| u | Electrolyte flow velocity | m s−1 |
| U | Cell voltage | V |
| Flow rate through the electrode | m3 s−1 | |
| W | Width of the electrode | m |
| w | Areal weight of the electrode | kg m−2 |
| x | Horizontal dimension in the NE electrode | m |
| x’ | Horizontal dimension in the PE electrode | m |
| y | Vertical dimension | m |
| z | Elementary charge | - |
| αan | Anodic charge transfer coefficient | - |
| αcat | Cathodic charge transfer coefficient | - |
| δ | Diffusion layer thickness | m |
| ε | Porosity of the electrode | % |
| κel | Electrolyte conductivity | S m−1 |
| κoffest | Electrolyte conductivity, offset parameter | S m−1 |
| κslope | Electrolyte conductivity, slope parameter | S m−1 |
| µel | Electrolyte viscosity | Pa s |
| µoffset | Electrolyte viscosity, offset parameter | Pa s |
| µslope | Electrolyte viscosity, slope parameter | Pa s |
| ν | Stoichiometric coefficient | - |
| νan | Reaction order for the anodic reaction | - |
| νcat | Reaction order for the cathodic reaction | - |
| ρcarbon | Carbon fiber density of the carbon felt electrode | kg m−3 |
| ρL | Specific electrical resistance of the liquid phase | Ω m |
| ρS | Specific electrical resistance of the solid phase/carbon felt electrode | Ω m |
| ρel | Density of the electrolyte | kg m−3 |
| φL | Potential in the liquid phase of the electrode | V |
| φS | Potential in the solid phase of the electrode | V |
| Index/Subscript | Name |
|---|---|
| bulk | Variable or parameter related to the bulk phase of the electrolyte in the electrode |
| el | Electrolyte parameter |
| i | Index of the vanadium species |
| in | Inlet conditions |
| k | Index of acid species |
| L | Liquid phase |
| NE | Negative electrolyte |
| offset | Offset value of a parameter for an SoC of 0% |
| PE | Positive electrolyte |
| r | Index of the reaction |
| S | Solid phase |
| slope | Slope of a parameter in dependence of SoC |
| surf | Variable or parameter related to the surface of the carbon fibers |
References
- Minke, C.; Kunz, U.; Turek, T. Techno-Economic Assessment of Novel Vanadium Redox Flow Batteries with Large-Area Cells. J. Power Sources 2017, 361, 105–114. [Google Scholar] [CrossRef]
- Sánchez-Díez, E.; Ventosa, E.; Guarnieri, M.; Trovò, A.; Flox, C.; Marcilla, R.; Soavi, F.; Mazur, P.; Aranzabe, E.; Ferret, R. Redox Flow Batteries: Status and Perspective towards Sustainable Stationary Energy Storage. J. Power Sources 2021, 481, 228804. [Google Scholar] [CrossRef]
- Huang, Z.; Mu, A.; Wu, L.; Yang, B.; Qian, Y.; Wang, J. Comprehensive Analysis of Critical Issues in All-Vanadium Redox Flow Battery. ACS Sustain. Chem. Eng. 2022, 10, 7786–7810. [Google Scholar] [CrossRef]
- Ghimire, P.C.; Bhattarai, A.; Lim, T.M.; Wai, N.; Skyllas-Kazacos, M.; Yan, Q. In-Situ Tools Used in Vanadium Redox Flow Battery Research—Review. Batteries 2021, 7, 53. [Google Scholar] [CrossRef]
- Soloveichik, G.L. Flow Batteries: Current Status and Trends. Chem. Rev. 2015, 115, 11533–11558. [Google Scholar] [CrossRef]
- Noack, J.; Roznyatovskaya, N.; Herr, T.; Fischer, P. The Chemistry of Redox-Flow Batteries. Angew. Chem. Int. Ed. 2015, 54, 9776–9809. [Google Scholar] [CrossRef]
- Winsberg, J.; Hagemann, T.; Janoschka, T.; Hager, M.D.; Schubert, U.S. Redox-Flow Batteries: From Metals to Organic Redox-Active Materials. Angew. Chem. Int. Ed. Engl. 2017, 56, 686–711. [Google Scholar] [CrossRef]
- Zhang, C.; Zhang, L.; Ding, Y.; Peng, S.; Guo, X.; Zhao, Y.; He, G.; Yu, G. Progress and Prospects of Next-Generation Redox Flow Batteries. Energy Storage Mater. 2018, 15, 324–350. [Google Scholar] [CrossRef]
- Ke, X.; Prahl, J.M.; Alexander, J.I.D.; Wainright, J.S.; Zawodzinski, T.A.; Savinell, R.F. Rechargeable Redox Flow Batteries: Flow Fields, Stacks and Design Considerations. Chem. Soc. Rev. 2018, 47, 8721–8743. [Google Scholar] [CrossRef]
- König, S. Model-Based Design and Optimization of Vanadium Redox Flow Batteries. Ph.D. Thesis, Karlsruhe Institute of Technology, Karlsruhe, Germany, 2017. [Google Scholar] [CrossRef]
- Puleston, T.; Clemente, A.; Costa-Castelló, R.; Serra, M. Modelling and Estimation of Vanadium Redox Flow Batteries: A Review. Batteries 2022, 8, 121. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Crawford, A.J.; Thomsen, E.C.; Shamim, N.; Li, G.; Huang, Q.; Reed, D.M. An Overview of the Design and Optimized Operation of Vanadium Redox Flow Batteries for Durations in the Range of 4–24 Hours. Batteries 2023, 9, 221. [Google Scholar] [CrossRef]
- Huang, Z.; Mu, A.; Wu, L.; Wang, H. Vanadium Redox Flow Batteries: Flow Field Design and Flow Rate Optimization. J. Energy Storage 2022, 45, 103526. [Google Scholar] [CrossRef]
- You, D.; Zhang, H.; Chen, J. A Simple Model for the Vanadium Redox Battery. Electrochim. Acta 2009, 54, 6827–6836. [Google Scholar] [CrossRef]
- Wandschneider, F.T.; Röhm, S.; Fischer, P.; Pinkwart, K.; Tübke, J.; Nirschl, H. A Multi-Stack Simulation of Shunt Currents in Vanadium Redox Flow Batteries. J. Power Sources 2014, 261, 64–74. [Google Scholar] [CrossRef]
- Pugach, M.; Kondratenko, M.; Briola, S.; Bischi, A. Numerical and Experimental Study of the Flow-by Cell for Vanadium Redox Batteries. Energy Procedia 2017, 142, 3667–3674. [Google Scholar] [CrossRef]
- Zugschwert, C.; Dundálek, J.; Leyer, S.; Hadji-Minaglou, J.-R.; Kosek, J.; Pettinger, K.-H. The Effect of Input Parameter Variation on the Accuracy of a Vanadium Redox Flow Battery Simulation Model. Batteries 2021, 7, 7. [Google Scholar] [CrossRef]
- Huang, S.; Lu, Y. Numerical Parametric Investigation of Nonaqueous Vanadium Redox Flow Batteries. Batteries 2022, 8, 75. [Google Scholar] [CrossRef]
- Vudisi, P.K.; Jayanti, S.; Chetty, R. Model for Rating a Vanadium Redox Flow Battery Stack through Constant Power Charge–Discharge Characterization. Batteries 2022, 8, 85. [Google Scholar] [CrossRef]
- Eifert, L.; Banerjee, R.; Jusys, Z.; Zeis, R. Characterization of Carbon Felt Electrodes for Vanadium Redox Flow Batteries: Impact of Treatment Methods. J. Electrochem. Soc. 2018, 165, A2577. [Google Scholar] [CrossRef]
- Hassan, A.; Tzedakis, T. Enhancement of the Electrochemical Activity of a Commercial Graphite Felt for Vanadium Redox Flow Battery (VRFB), by Chemical Treatment with Acidic Solution of K2Cr2O7. J. Energy Storage 2019, 26, 100967. [Google Scholar] [CrossRef]
- Pezeshki, A.M.; Clement, J.T.; Veith, G.M.; Zawodzinski, T.A.; Mench, M.M. High Performance Electrodes in Vanadium Redox Flow Batteries through Oxygen-Enriched Thermal Activation. J. Power Sources 2015, 294, 333–338. [Google Scholar] [CrossRef]
- Nibel, O.; Taylor, S.M.; Pătru, A.; Fabbri, E.; Gubler, L.; Schmidt, T.J. Performance of Different Carbon Electrode Materials: Insights into Stability and Degradation under Real Vanadium Redox Flow Battery Operating Conditions. J. Electrochem. Soc. 2017, 164, A1608. [Google Scholar] [CrossRef]
- Eifert, L.; Jusys, Z.; Behm, R.J.; Zeis, R. Side Reactions and Stability of Pre-Treated Carbon Felt Electrodes for Vanadium Redox Flow Batteries: A DEMS Study. Carbon 2020, 158, 580–587. [Google Scholar] [CrossRef]
- Becker, M.; Turek, T. Combination of Impedance Spectroscopy and Potential Probe Sensing to Characterize Vanadium Redox-Flow Batteries. J. Power Sources 2020, 446, 227349. [Google Scholar] [CrossRef]
- Belfiore, L.A. Laminar Boundary Layer Mass Transfer around Solid Spheres, Gas Bubbles, and Other Submerged Objects. In Transport Phenomena for Chemical Reactor Design; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; pp. 275–360. ISBN 978-0-471-47162-2. [Google Scholar]
- Belfiore, L.A. Dimensional Analysis of the Equations of Change for Fluid Dynamics Within the Mass Transfer Boundary Layer. In Transport Phenomena for Chemical Reactor Design; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2003; pp. 361–368. ISBN 978-0-471-47162-2. [Google Scholar]
- Perry, R.H.; Green, D.W. Mass Transfer. In Perry’s Chemical Engineers’ Handbook; Mcgraw-Hill Professional: New York, NY, USA, 1997; pp. 5–59. ISBN 978-0-07-049841-9. [Google Scholar]
- Kinoshita, K.; Leach, S.C. Mass-Transfer Study of Carbon Felt, Flow-Through Electrode. J. Electrochem. Soc. 1982, 129, 1993–1997. [Google Scholar] [CrossRef]
- Schmal, D.; Van Erkel, J.; Van Duin, P.J. Mass Transfer at Carbon Fibre Electrodes. J. Appl. Electrochem. 1986, 16, 422–430. [Google Scholar] [CrossRef]
- Bayanov, I.M.; Vanhaelst, R. The Numerical Simulation of Vanadium RedOx Flow Batteries. J. Math. Chem. 2011, 49, 2013–2031. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, H.; Xing, F. A Three-Dimensional Model for Negative Half Cell of the Vanadium Redox Flow Battery. Electrochim. Acta 2011, 58, 238–246. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S.; Leung, P.K. Numerical Investigations of Flow Field Designs for Vanadium Redox Flow Batteries. Appl. Energy 2013, 105, 47–56. [Google Scholar] [CrossRef]
- Zheng, Q.; Zhang, H.; Xing, F.; Ma, X.; Li, X.; Ning, G. A Three-Dimensional Model for Thermal Analysis in a Vanadium Flow Battery. Appl. Energy 2014, 113, 1675–1685. [Google Scholar] [CrossRef]
- Wang, Y.; Cho, S.C. Analysis and Three-Dimensional Modeling of Vanadium Flow Batteries. J. Electrochem. Soc. 2014, 161, A1200–A1212. [Google Scholar] [CrossRef]
- Yu, Y.; Zuo, Y.; Zuo, C.; Liu, X.; Liu, Z. A Hierarchical Multiscale Model for Microfluidic Fuel Cells with Porous Electrodes. Electrochim. Acta 2014, 116, 237–243. [Google Scholar] [CrossRef]
- Chen, C.L.; Yeoh, H.K.; Chakrabarti, M.H. An Enhancement to Vynnycky’s Model for the All-Vanadium Redox Flow Battery. Electrochim. Acta 2014, 120, 167–179. [Google Scholar] [CrossRef]
- Wandschneider, F.T.; Kuettinger, M.; Noack, J.; Fischer, P.; Pinkwart, K.; Tuebke, J.; Nirschl, H. A Coupled-Physics Model for the Vanadium Oxygen Fuel Cell. J. Power Sources 2014, 259, 125–137. [Google Scholar] [CrossRef]
- Rudolph, S.; Schröder, U.; Bayanov, I.M.; Hage, D. Measurement, Simulation and in Situ Regeneration of Energy Efficiency in Vanadium Redox Flow Battery. J. Electroanal. Chem. 2014, 728, 72–80. [Google Scholar] [CrossRef]
- Yu, V.K.; Chen, D. Peak Power Prediction of a Vanadium Redox Flow Battery. J. Power Sources 2014, 268, 261–268. [Google Scholar] [CrossRef]
- Wandschneider, F.T.; Finke, D.; Grosjean, S.; Fischer, P.; Pinkwart, K.; Tübke, J.; Nirschl, H. Model of a Vanadium Redox Flow Battery with an Anion Exchange Membrane and a Larminie-Correction. J. Power Sources 2014, 272, 436–447. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S. Fundamental Models for Flow Batteries. Prog. Energy Combust. Sci. 2015, 49, 40–58. [Google Scholar] [CrossRef]
- Khazaeli, A.; Vatani, A.; Tahouni, N.; Panjeshahi, M.H. Numerical Investigation and Thermodynamic Analysis of the Effect of Electrolyte Flow Rate on Performance of All Vanadium Redox Flow Batteries. J. Power Sources 2015, 293, 599–612. [Google Scholar] [CrossRef]
- Gandomi, Y.A.; Aaron, D.S.; Zawodzinski, T.A.; Mench, M.M. In Situ Potential Distribution Measurement and Validated Model for All-Vanadium Redox Flow Battery. J. Electrochem. Soc. 2016, 163, A5188–A5201. [Google Scholar] [CrossRef]
- Li, Y.; Skyllas-Kazacos, M.; Bao, J. A Dynamic Plug Flow Reactor Model for a Vanadium Redox Flow Battery Cell. J. Power Sources 2016, 311, 57–67. [Google Scholar] [CrossRef]
- Crawford, A.; Thomsen, E.; Reed, D.; Stephenson, D.; Sprenkle, V.; Liu, J.; Viswanathan, V. Development and Validation of Chemistry Agnostic Flow Battery Cost Performance Model and Application to Nonaqueous Electrolyte Systems. Int. J. Energy Res. 2016, 40, 1611–1623. [Google Scholar] [CrossRef]
- Zago, M.; Casalegno, A. Physically-Based Impedance Modeling of the Negative Electrode in All-Vanadium Redox Flow Batteries: Insight into Mass Transport Issues. Electrochim. Acta 2017, 248, 505–517. [Google Scholar] [CrossRef]
- Fu, J.; Wang, T.; Wang, X.; Sun, J.; Zheng, M. Dynamic Flow Rate Control for Vanadium Redox Flow Batteries. Energy Procedia 2017, 105, 4482–4491. [Google Scholar] [CrossRef]
- Yue, M.; Zheng, Q.; Xing, F.; Zhang, H.; Li, X.; Ma, X. Flow Field Design and Optimization of High Power Density Vanadium Flow Batteries: A Novel Trapezoid Flow Battery. Aiche J. 2018, 64, 782–795. [Google Scholar] [CrossRef]
- Koenig, S.; Suriyah, M.R.; Leibfried, T. Validating and Improving a Zero-Dimensional Stack Voltage Model of the Vanadium Redox Flow Battery. J. Power Sources 2018, 378, 10–18. [Google Scholar] [CrossRef]
- Wang, T.; Fu, J.; Zheng, M.; Yu, Z. Dynamic Control Strategy for the Electrolyte Flow Rate of Vanadium Redox Flow Batteries. Appl. Energy 2018, 227, 613–623. [Google Scholar] [CrossRef]
- Kim, Y.; Choi, Y.Y.; Yun, N.; Yang, M.; Jeon, Y.; Kim, K.J.; Choi, J.-I. Activity Gradient Carbon Felt Electrodes for Vanadium Redox Flow Batteries. J. Power Sources 2018, 408, 128–135. [Google Scholar] [CrossRef]
- Zhang, B.W.; Lei, Y.; Bai, B.F.; Xu, A.; Zhao, T.S. A Two-Dimensional Mathematical Model for Vanadium Redox Flow Battery Stacks Incorporating Nonuniform Electrolyte Distribution in the Flow Frame. Appl. Therm. Eng. 2019, 151, 495–505. [Google Scholar] [CrossRef]
- Carta, R.; Palmas, S.; Polcaro, A.M.; Tola, G. Behaviour of a Carbon Felt Flow by Electrodes Part I: Mass Transfer Characteristics. J. Appl. Electrochem. 1991, 21, 793–798. [Google Scholar] [CrossRef]
- Xu, Q.; Zhao, T.S. Determination of the Mass-Transport Properties of Vanadium Ions through the Porous Electrodes of Vanadium Redox Flow Batteries. Phys. Chem. Chem. Phys. 2013, 15, 10841–10848. [Google Scholar] [CrossRef] [PubMed]
- Vatistas, N.; Marconi, P.F.; Bartolozzi, M. Mass-Transfer Study of the Carbon Felt Electrode. Electrochim. Acta 1991, 36, 339–343. [Google Scholar] [CrossRef]
- You, X.; Ye, Q.; Cheng, P. The Dependence of Mass Transfer Coefficient on the Electrolyte Velocity in Carbon Felt Electrodes: Determination and Validation. J. Electrochem. Soc. 2017, 164, E3386–E3394. [Google Scholar] [CrossRef]
- Barton, J.L.; Milshtein, J.D.; Hinricher, J.J.; Brushett, F.R. Quantifying the Impact of Viscosity on Mass-Transfer Coefficients in Redox Flow Batteries. J. Power Sources 2018, 399, 133–143. [Google Scholar] [CrossRef]
- Kok, M.D.R.; Jervis, R.; Tranter, T.G.; Sadeghi, M.A.; Brett, D.J.L.; Shearing, P.R.; Gostick, J.T. Mass Transfer in Fibrous Media with Varying Anisotropy for Flow Battery Electrodes: Direct Numerical Simulations with 3D X-Ray Computed Tomography. Chem. Eng. Sci. 2019, 196, 104–115. [Google Scholar] [CrossRef]
- Shah, A.A.; Watt-Smith, M.J.; Walsh, F.C. A Dynamic Performance Model for Redox-Flow Batteries Involving Soluble Species. Electrochim. Acta 2008, 53, 8087–8100. [Google Scholar] [CrossRef]
- Becker, M.; Bredemeyer, N.; Tenhumberg, N.; Turek, T. Kinetic Studies at Carbon Felt Electrodes for Vanadium Redox-Flow Batteries under Controlled Transfer Current Density Conditions. Electrochim. Acta 2017, 252, 12–24. [Google Scholar] [CrossRef]
- Kroner, I.; Becker, M.; Turek, T. Determination of Rate Constants and Reaction Orders of Vanadium-Ion Kinetics on Carbon Fiber Electrodes. ChemElectroChem 2020, 7, 4314–4325. [Google Scholar] [CrossRef]
- Corcuera, S.; Skyllas-Kazacos, M. State-of-Charge Monitoring and Electrolyte Rebalancing Methods for the Vanadium Redox Flow Battery. Eur. Chem. Bull. 2012, 1, 511–519. [Google Scholar] [CrossRef]
- Becker, M.; Bredemeyer, N.; Tenhumberg, N.; Turek, T. Polarization Curve Measurements Combined with Potential Probe Sensing for Determining Current Density Distribution in Vanadium Redox-Flow Batteries. J. Power Sources 2016, 307, 826–833. [Google Scholar] [CrossRef]
- Küster, F.W.; Thiel, A. Rechentafeln Für Die Chemische Analytik; Walter de Gruyter & Co. KG: Berlin, Germany; New York, NY, USA, 2002; p. 239. ISBN 3-11-017566-5. [Google Scholar]
- Knehr, K.W.; Agar, E.; Dennison, C.R.; Kalidindi, A.R.; Kumbur, E.C. A Transient Vanadium Flow Battery Model Incorporating Vanadium Crossover and Water Transport through the Membrane. J. Electrochem. Soc. 2012, 159, A1446–A1459. [Google Scholar] [CrossRef]
- Paasch, G.; Micka, K.; Gersdorf, P. Theory of the Electrochemical Impedance of Macrohomogeneous Porous Electrodes. Electrochim. Acta 1993, 38, 2653–2662. [Google Scholar] [CrossRef]
- Schafner, K.; Becker, M.; Turek, T. Membrane Resistance of Different Separator Materials in a Vanadium Redox Flow Battery. J. Membrane Sci. 2019, 586, 106–114. [Google Scholar] [CrossRef]
- Pavelka, M.; Wandschneider, F.; Mazur, P. Thermodynamic Derivation of Open Circuit Voltage in Vanadium Redox Flow Batteries. J. Power Sources 2015, 293, 400–408. [Google Scholar] [CrossRef]
- Yamamura, T.; Watanabe, N.; Yano, T.; Shiokawa, Y. Electron-Transfer Kinetics of Np3+/Np4+, NpO2+/NpO2+, V2+/V3+, and VO2+/VO2+ at Carbon Electrodes. J. Electrochem. Soc. 2005, 152, A830. [Google Scholar] [CrossRef]
- Lawton, J.S.; Tiano, S.M.; Donnelly, D.J.; Flanagan, S.P.; Arruda, T.M. The Effect of Sulfuric Acid Concentration on the Physical and Electrochemical Properties of Vanadyl Solutions. Batteries 2018, 4, 40. [Google Scholar] [CrossRef]
- Jiang, Z.; Klyukin, K.; Alexandrov, V. Structure, Hydrolysis, and Diffusion of Aqueous Vanadium Ions from Car-Parrinello Molecular Dynamics. J. Chem. Phys. 2016, 145, 114303. [Google Scholar] [CrossRef]
- Oriji, G.; Katayama, Y.; Miura, T. Investigations on V(IV)/V(V) and V(II)/V(III) Redox Reactions by Various Electrochemical Methods. J. Power Sources 2005, 139, 321–324. [Google Scholar] [CrossRef]
- Gattrell, M.; Park, J.; MacDougall, B.; Apte, J.; McCarthy, S.; Wu, C.W. Study of the Mechanism of the Vanadium 4+/5+ Redox Reaction in Acidic Solutions. J. Electrochem. Soc. 2004, 151, A123–A130. [Google Scholar] [CrossRef]
- Lemmermann, T.; Becker, M.; Stehle, M.; Drache, M.; Beuermann, S.; Bogar, M.S.; Gohs, U.; Fittschen, U.E.A.; Turek, T.; Kunz, U. In Situ and in Operando Detection of Redox Reactions with Integrated Potential Probes during Vanadium Transport in Ion Exchange Membranes. J. Power Sources 2022, 533, 231343. [Google Scholar] [CrossRef]
- Di Noto, V.; Vezzù, K.; Crivellaro, G.; Pagot, G.; Sun, C.; Meda, L.; Rutkowska, I.A.; Kulesza, P.J.; Zawodzinski, T.A. A General Electrochemical Formalism for Vanadium Redox Flow Batteries. Electrochim. Acta 2022, 408, 139937. [Google Scholar] [CrossRef]
- Becker, M. Validation of a two-dimensional model for vanadium redox-flow batteries. Ph.D. Thesis, Clausthal University of Technology, Clausthal-Zellerfeld, Germany, 2020. [Google Scholar]
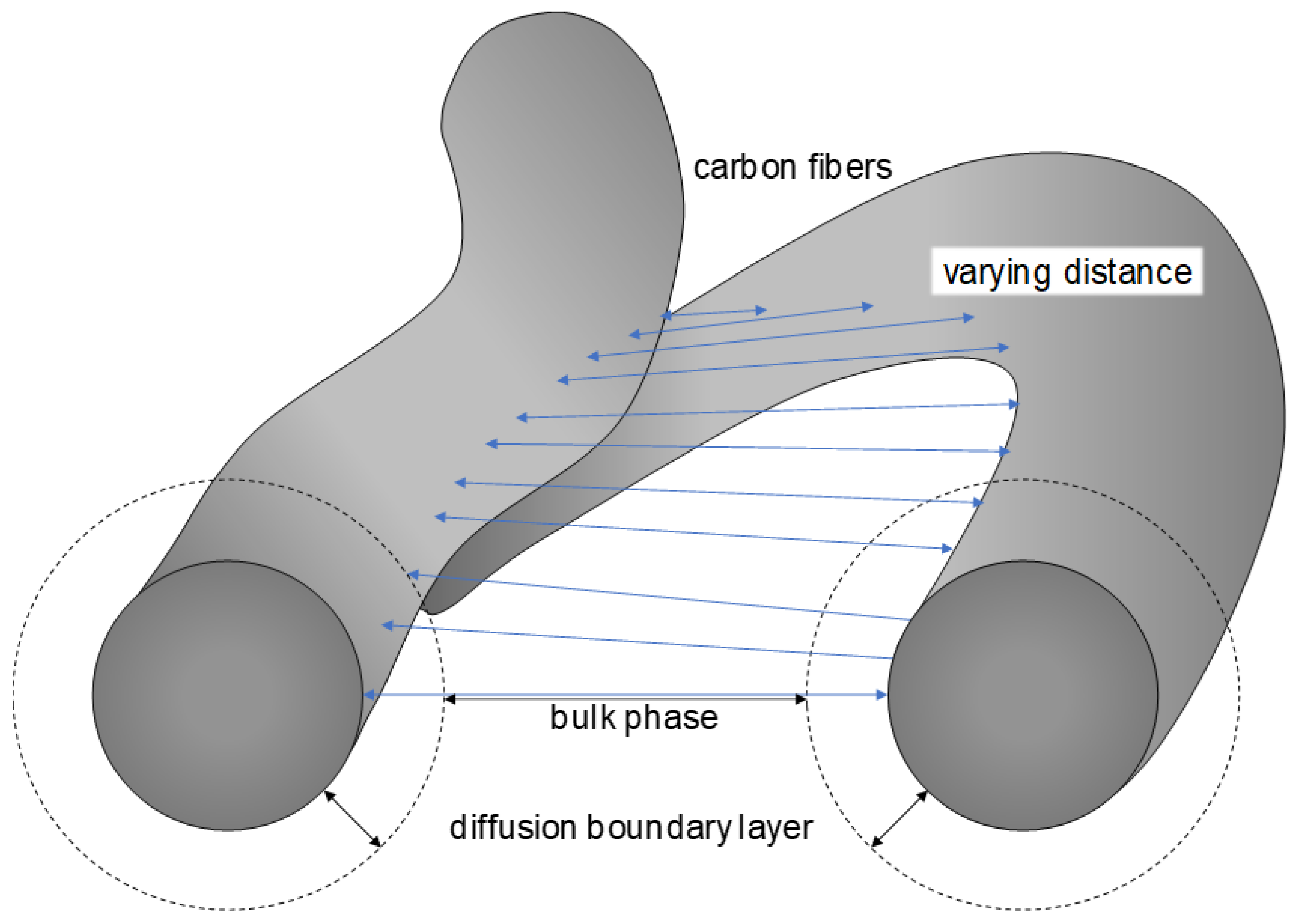


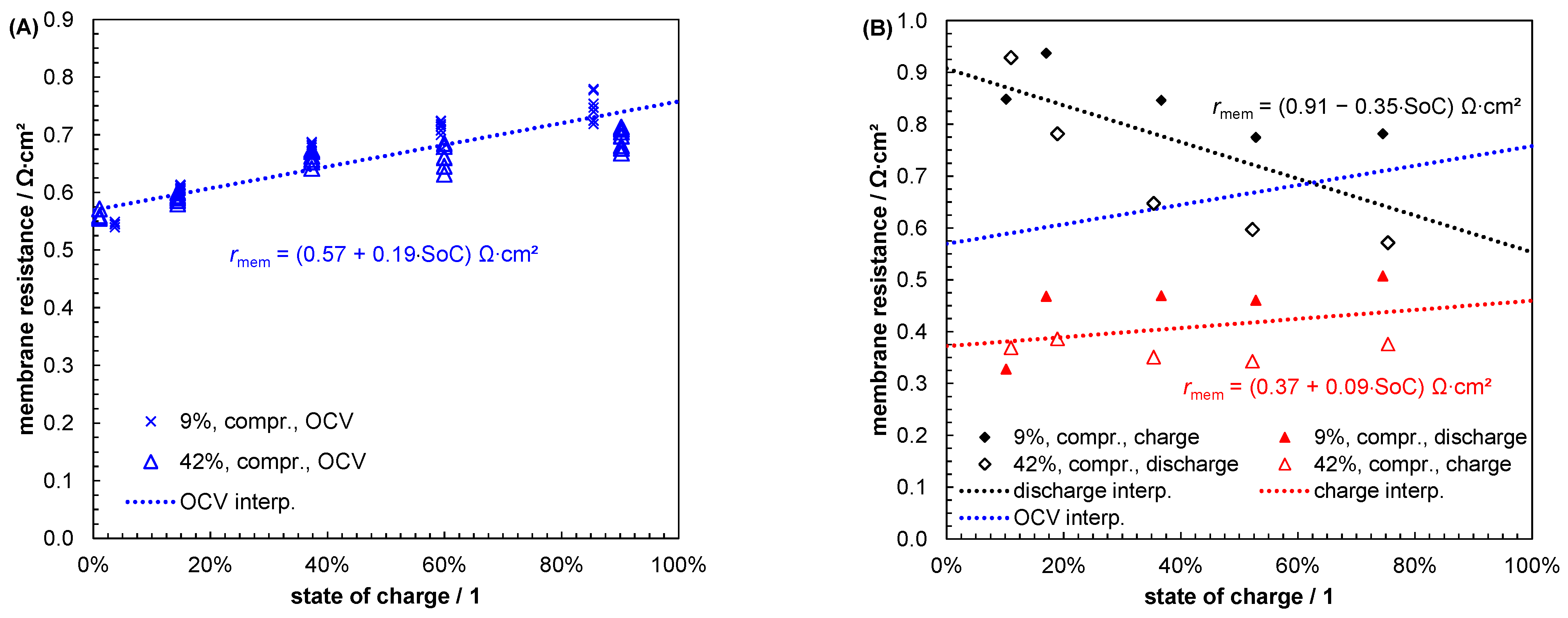
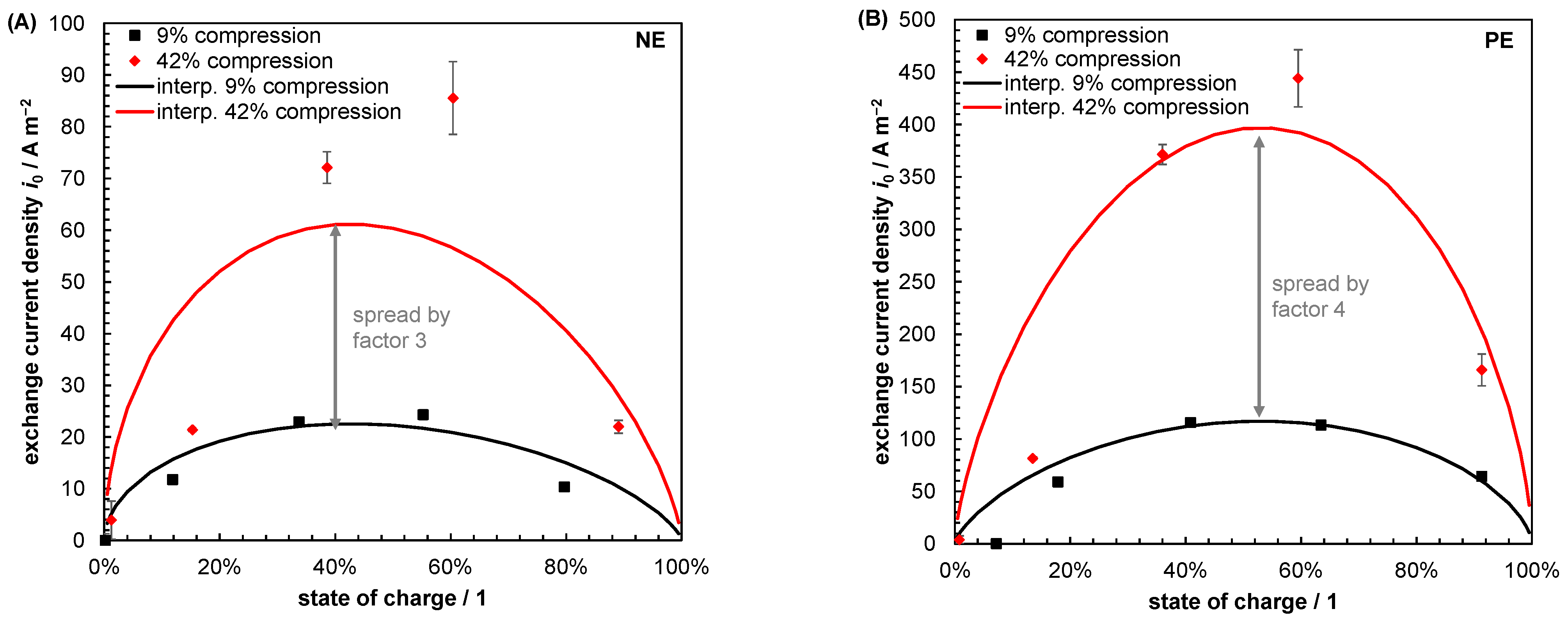

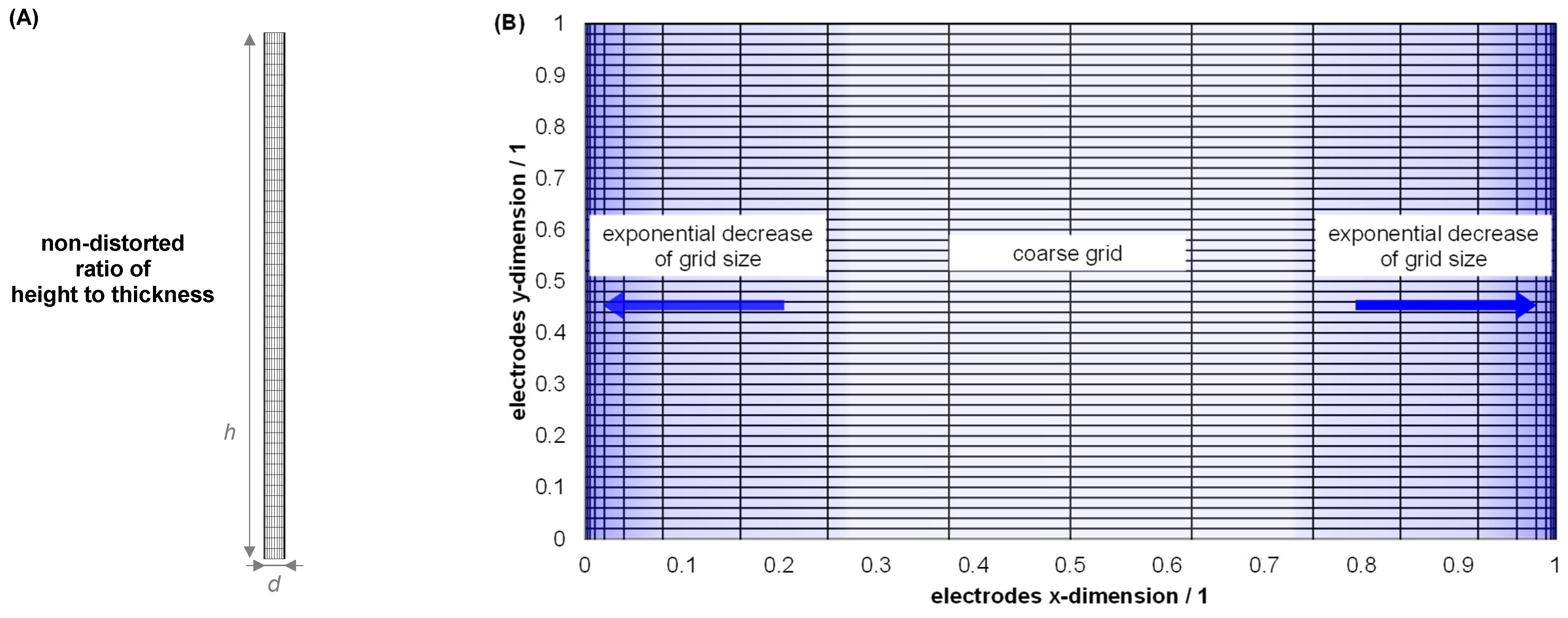

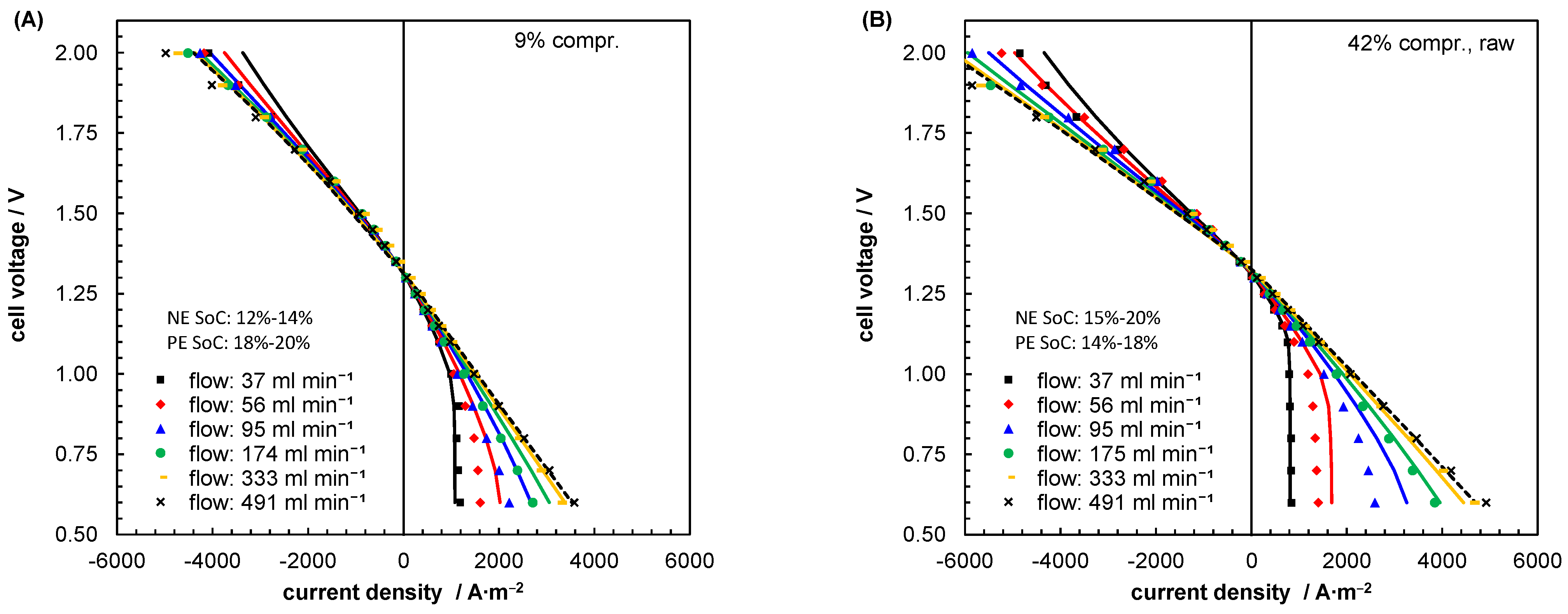
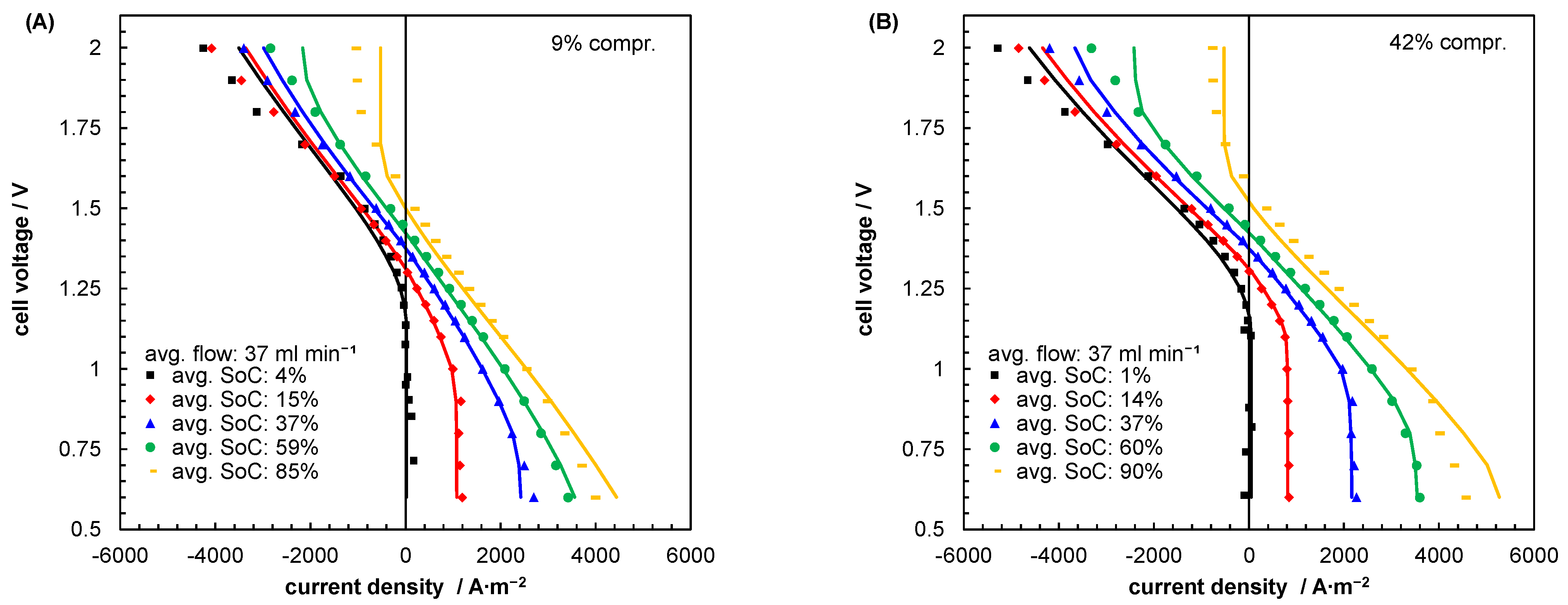
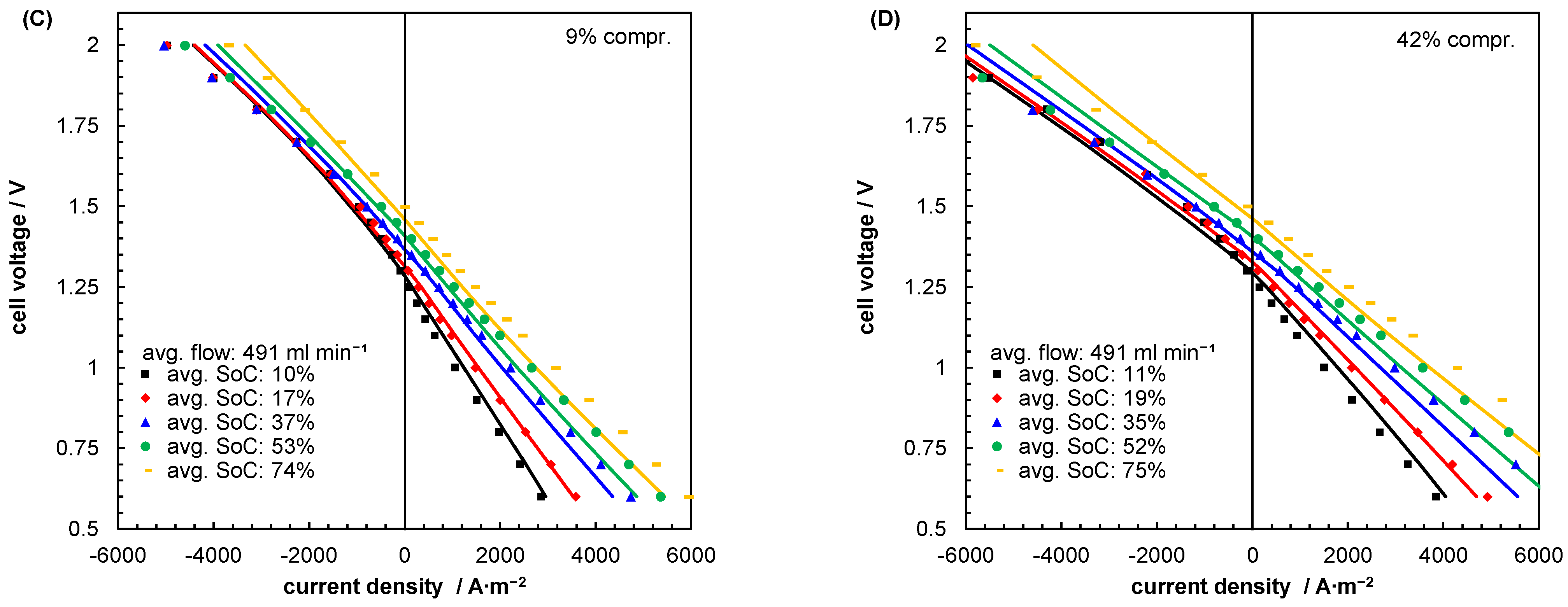


| Index/Order | Equation | |
|---|---|---|
| Reaction | (13) | |
| Vanadium species | (14) | |
| Stoichiometric coefficient | (15) | |
| Anodic reaction order [25] | (16) | |
| Cathodic reaction order [25] | (17) |
| Described Process | Equation | |
|---|---|---|
| Potential gradient in solid phase | (18) | |
| Potential gradient in liquid phase | (19) | |
| Specific electrical resistance of the electrolyte | (20) |
| Described Process | Equation | |
|---|---|---|
| Gradient of current density in solid phase | (21) | |
| Gradient of current density in liquid phase | (22) | |
| Transfer current density | (23) | |
| Overpotential | (24) | |
| Equilibrium potential | (25) | |
| Exchange current density | (26) |
| Described Process | Equation | |
|---|---|---|
| Mass transport equation | (27) | |
| Inner mass transport | (28) | |
| Sherwood correlation | (29) | |
| Reynolds number | (30) | |
| Schmidt number | (31) | |
| Diffusion layer thickness | (32) |
| Description | Equation | |
|---|---|---|
| Specific surface area of the electrode | (33) | |
| Porosity of the electrode | (34) | |
| Compression rate of the electrode | (35) | |
| State of charge of positive and negative electrolyte | (36) | |
| Electrolyte viscosity | (37) | |
| Electrolyte conductivity | (38) |
| Description | Equation | |
|---|---|---|
| Current density distributed over the height of the cell | (39) | |
| Current density applied to the cell | (40) | |
| Liquid phase current density at the bipolar plate interface of the NE | for 0 < y < H | (41) |
| Solid phase current density at the membrane interface of the NE | for 0 < y < H | (42) |
| Solid phase potential at the bipolar plate interface of the NE | for 0 < y < H | (43) |
| No mass transport through the bipolar plate of the NE | for 0 < y < H | (44) |
| No mass transport through the membrane from the NE | for 0 < y < H | (45) |
| Inlet concentration for the NE | for 0 < x < t | (46) |
| Description | Equation | |
|---|---|---|
| Liquid phase potential at the membrane interface of the PE | for 0 < y < H | (47) |
| Solid phase current density at the membrane interface of the PE | for 0 < y < H | (48) |
| Solid phase current density at the bipolar plate interface of the PE | for 0 < y < H | (49) |
| Liquid phase current density at the membrane interface of the PE | for 0 < y < H | (50) |
| No mass transport through the bipolar plate of the PE | for 0 < y < H | (51) |
| No mass transport through the membrane from the PE | for 0 < y < H | (52) |
| Total cell voltage | (53) | |
| Inlet concentration for the PE | for 0 < x < t | (54) |
| k0,NE | k0,PE | ρS | rbpp | ε | |
|---|---|---|---|---|---|
| m·s−1 | m·s−1 | Ω·m | Ω·m2 | % | |
| 9% compression rate | 3.0·10−7 | 1.6·10−6 | 2.2·10−3 | 0.9·10−5 | 94.4 |
| 42% compression rate | 8.3·10−7 | 5.3·10−6 | 1.9·10−3 | 0.65·10−5 | 91.2 |
| Vanadium Species | Diffusion Coefficient | Schmidt Number |
|---|---|---|
| m2·s−1 | Dimensionless | |
| V2+ | 2.3·10−10 | 13,398 |
| V3+ | 0.6·10−10 | 74,198 |
| VO2+ | 1.6·10−10 | 20,972 |
| VO2+ | 1.6·10−10 | 17,454 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Becker, M.; Turek, T. New Mass Transport Correlation for Vanadium Redox-Flow Batteries Based on a Model-Assisted Parameter Estimation. Batteries 2023, 9, 253. https://doi.org/10.3390/batteries9050253
Becker M, Turek T. New Mass Transport Correlation for Vanadium Redox-Flow Batteries Based on a Model-Assisted Parameter Estimation. Batteries. 2023; 9(5):253. https://doi.org/10.3390/batteries9050253
Chicago/Turabian StyleBecker, Maik, and Thomas Turek. 2023. "New Mass Transport Correlation for Vanadium Redox-Flow Batteries Based on a Model-Assisted Parameter Estimation" Batteries 9, no. 5: 253. https://doi.org/10.3390/batteries9050253
APA StyleBecker, M., & Turek, T. (2023). New Mass Transport Correlation for Vanadium Redox-Flow Batteries Based on a Model-Assisted Parameter Estimation. Batteries, 9(5), 253. https://doi.org/10.3390/batteries9050253







