Preparation of Electrospun Membranes and Their Use as Separators in Lithium Batteries
Abstract
1. Introduction
2. Materials and Methods
2.1. Membranes Production by Electrospinning Manufacturing
2.2. Microstructural Characterization and Porosity
2.3. Regression Modelling of Microstructural Properties
2.4. Thermochemical Characterization
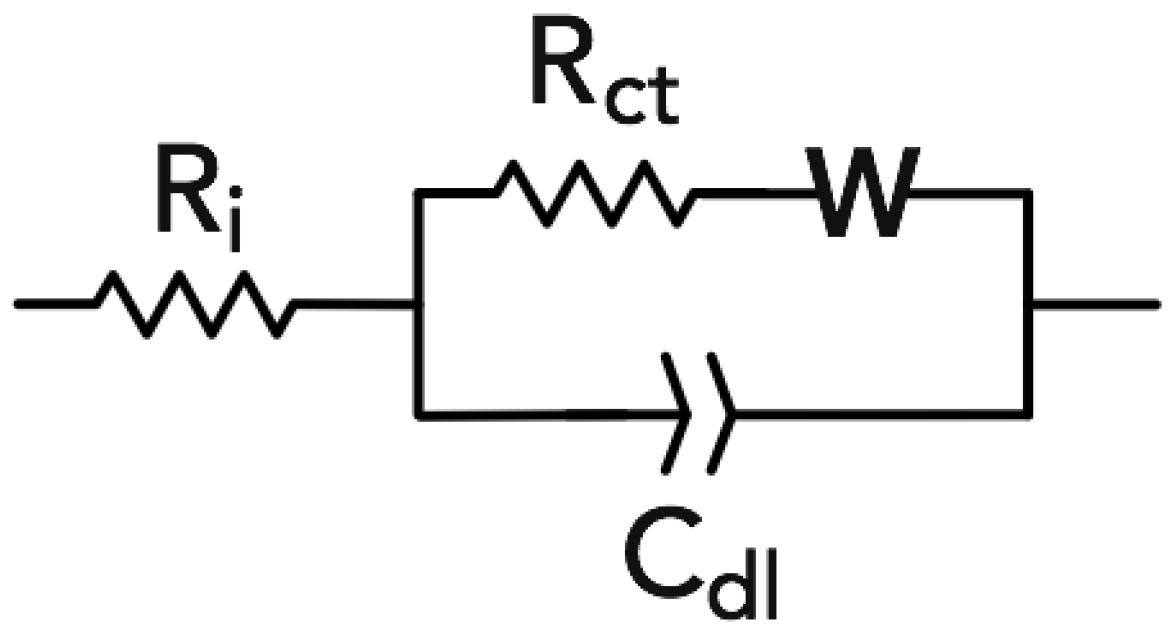
2.5. Electrochemical Tests
3. Results
3.1. Membranes Production
3.2. Thickness and Porosity
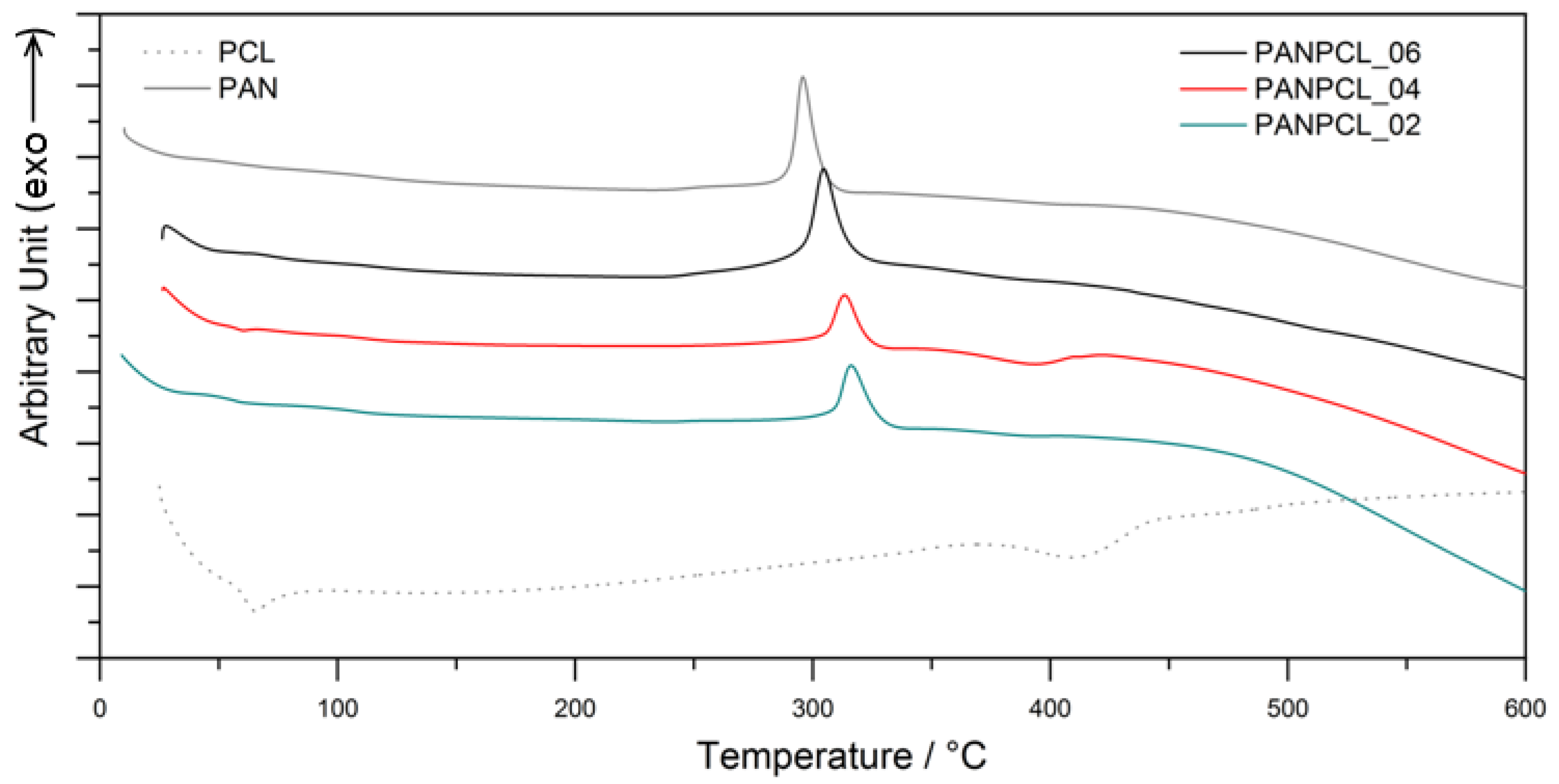
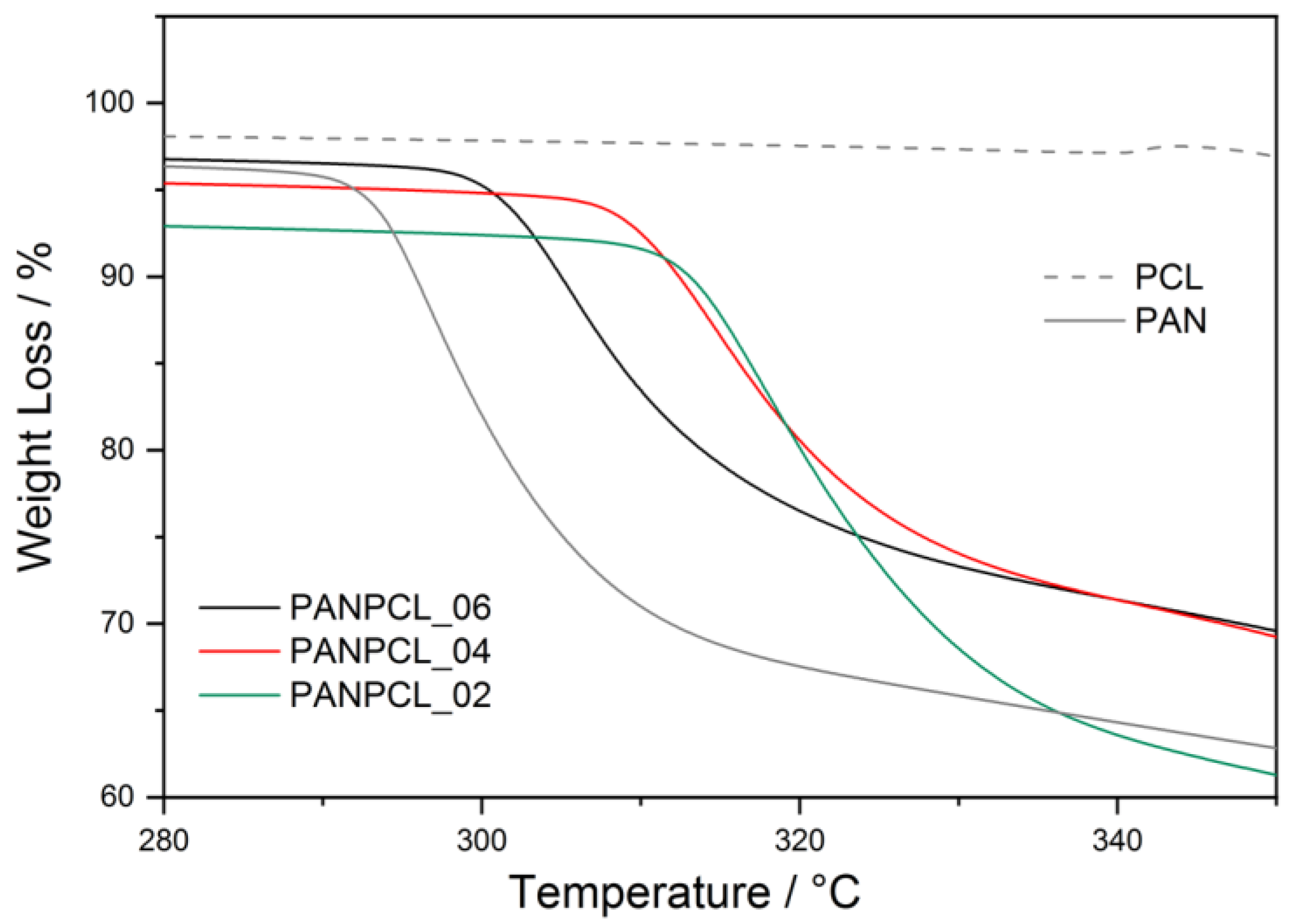
3.3. Thermochemical Characterization
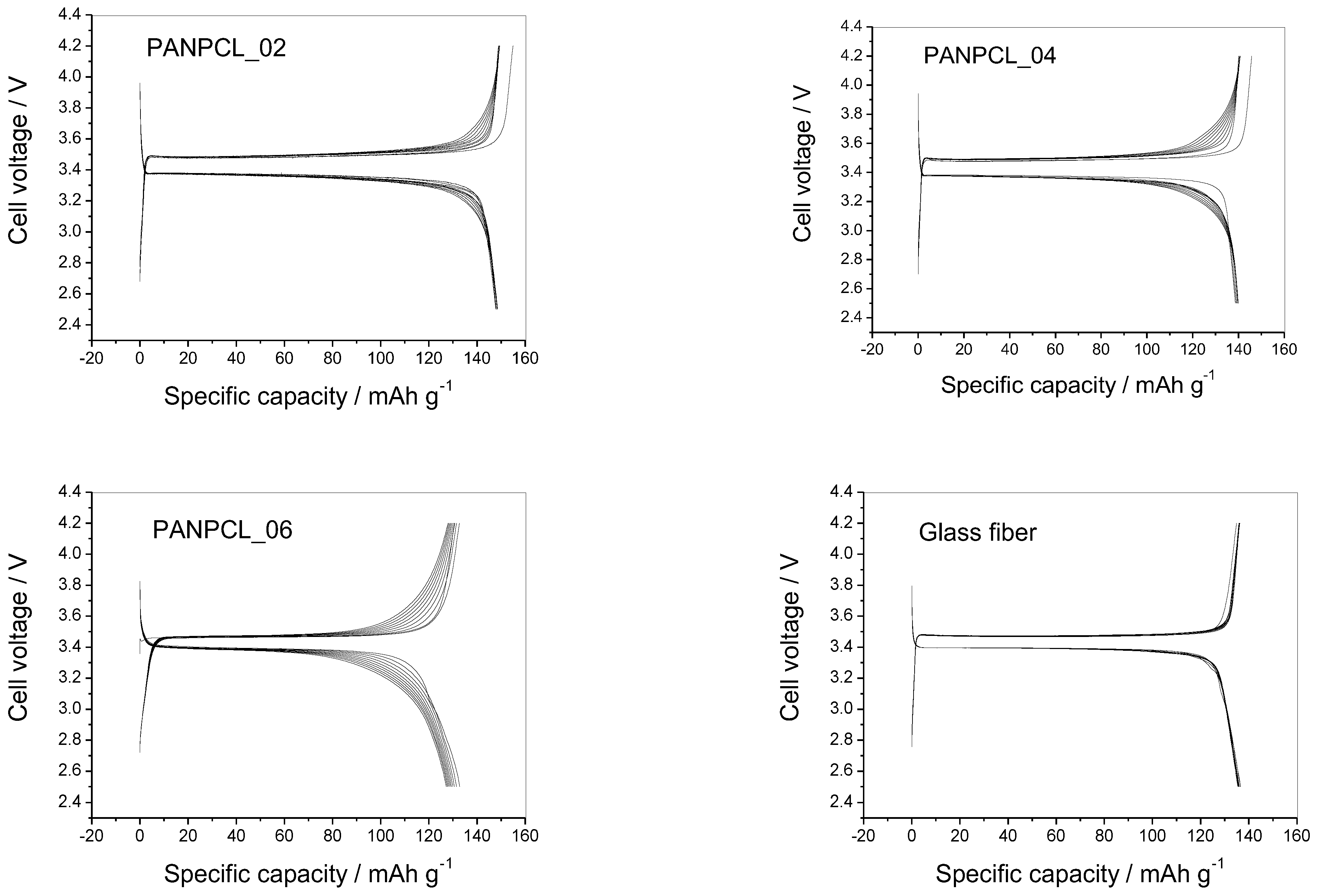
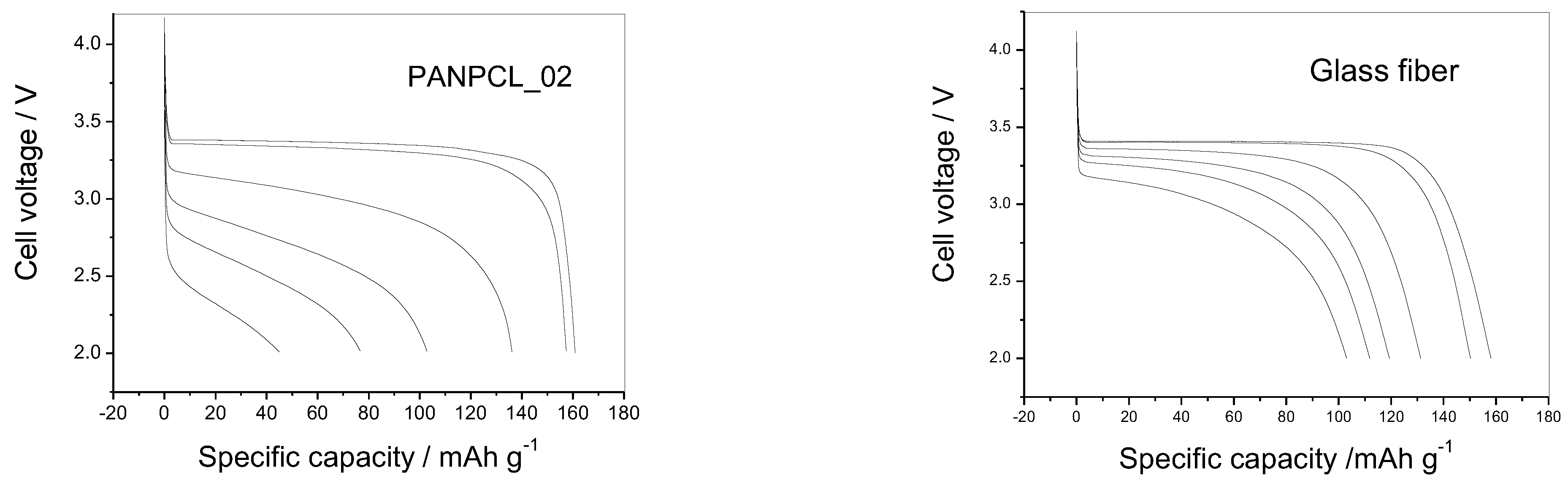
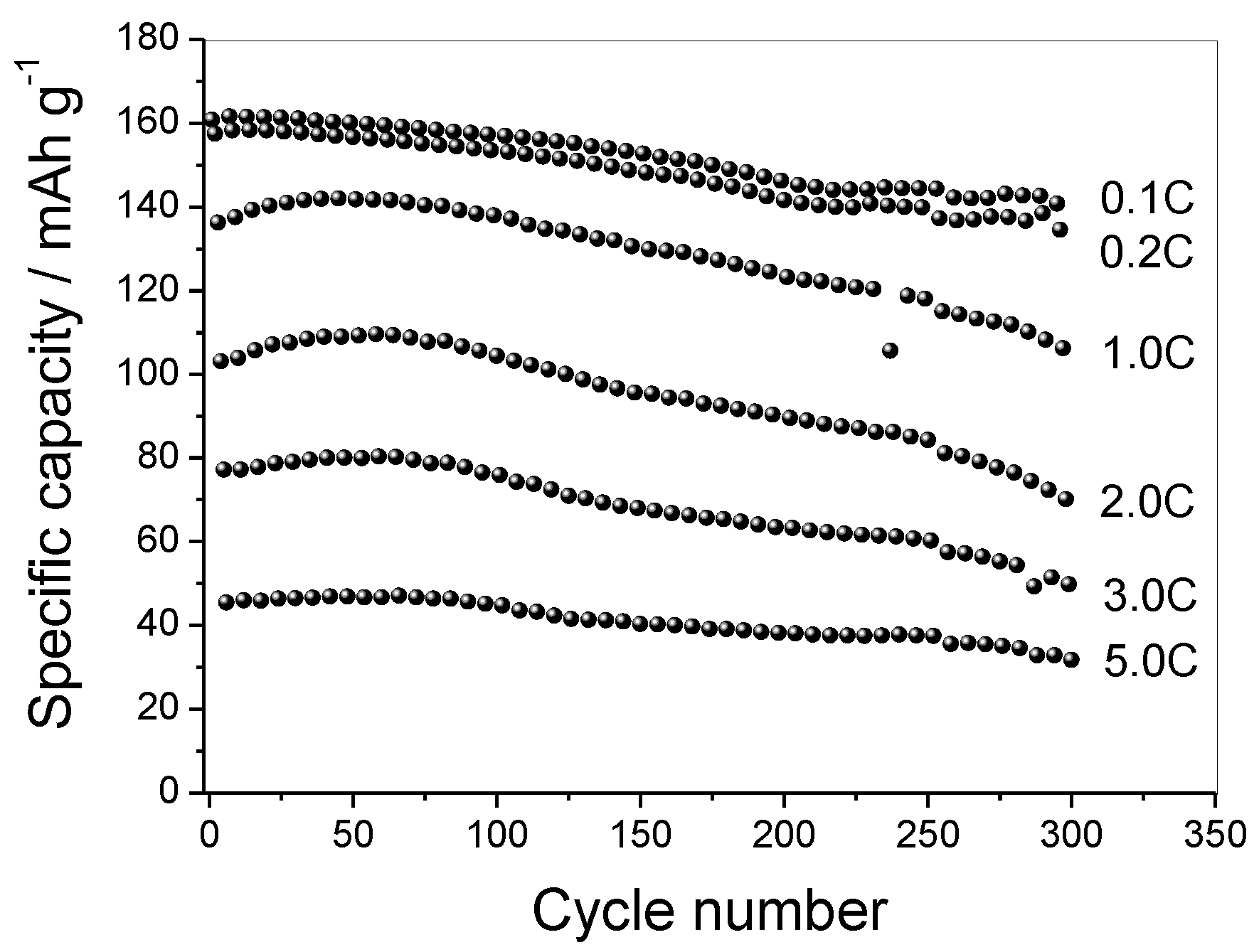
3.4. Electrochemical Test
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yang, J.; Hu, C.; Wang, H.; Yang, K.; Liu, J.B.; Yan, H. Review on the research of failure modes and mechanism for lead-acid batteries. Int. J. Energy Res. 2017, 41, 336–352. [Google Scholar] [CrossRef]
- Das, S.K.; Mahapatra, S.; Lahan, H. Aluminium-ion batteries: Developments and challenges. J. Mater. Chem. A 2017, 5, 6347–6367. [Google Scholar] [CrossRef]
- Ji, B.; Zhang, F.; Wu, N.; Tang, Y. A dual-carbon battery based on potassium-ion electrolyte. Adv. Energy Mater. 2017, 7, 1700920. [Google Scholar] [CrossRef]
- Lourenssen, K.; Williams, J.; Ahmadpour, F.; Clemmer, R.; Tasnim, S. Vanadium redox flow batteries: A comprehensive review. J. Energy Storage 2019, 25, 100844. [Google Scholar] [CrossRef]
- Huie, M.M.; Bock, D.C.; Takeuchi, E.S.; Marschilok, A.C.; Takeuchi, K.J. Cathode materials for magnesium and magnesium-ion based batteries. Coord. Chem. Rev. 2015, 287, 15–27. [Google Scholar] [CrossRef]
- Prosini, P.P.; Cento, C.; Rufoloni, A.; Rondino, F.; Santoni, A. A lithium-ion battery based on LiFePO4 and silicon nanowires. Solid State Ion 2015, 269, 93–97. [Google Scholar] [CrossRef]
- La Monaca, A.; De Giorgio, F.; Soavi, F.; Tarquini, G.; Di Carli, M.; Prosini, P.P.; Arbizzani, C. 1,3-Dioxolane: A strategy to improve electrode interfaces in Latium ion and lithium-sulfur batteries. ChemElectroChem 2018, 5, 1272–1278. [Google Scholar] [CrossRef]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research development on sodium-ion batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef]
- Opra, D.; Gnedenkov, S.; Sokolov, A.; Podgorbunsky, A.; Ustinov, A.Y.; Mayorov, V.Y.; Kuryavyi, V.; Sinebryukhov, S. Vanadium-doped TiO2-B/anatase mesoporous nanotubes with improved rate and cycle performance for rechargeable lithium and sodium batteries. J. Mater. Sci. Technol. 2020, 54, 181–189. [Google Scholar] [CrossRef]
- Rangarajan, S.S.; Sunddararaj, S.P.; Sudhakar, A.; Shiva, C.K.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Lithium-Ion Batteries—The Crux of Electric Vehicles with Opportunities and Challenges. Clean Technol. 2022, 4, 908–930. [Google Scholar] [CrossRef]
- Yoshio, M.; Brodd, R.J.; Kozawa, A. Lithium-Ion Batteries: Science and Technologies; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Scrosati, B.; Garche, J. Lithium Batteries: Status, Prospects and Future. J. Power Sources 2010, 195, 2419–2430. [Google Scholar] [CrossRef]
- Bashir, T.; Ismail, S.A.; Song, Y.; Irfan, R.M.; Yang, S.; Zhou, S.; Zhao, J.; Gao, L. A review of the energy storage aspects of chemical elements for lithium-ion based batteries. Energy Mater. 2021, 1, 100019. [Google Scholar] [CrossRef]
- Luiso, S.; Fedkiw, P. Lithium-ion battery separators: Recent developments and state of art. Curr. Opin. Electrochem. 2020, 20, 99–107. [Google Scholar] [CrossRef]
- Li, Y.; Li, Q.; Tan, Z. A review of electrospun nanofiber-based separators for rechargeable lithium-ion batteries. J. Power Sources 2019, 443, 227262. [Google Scholar] [CrossRef]
- Orendorff, C.J. The Role of Separators in Lithium-Ion Cell Safety. Electrochem. Soc. Interface 2012, 21, 61–65. [Google Scholar] [CrossRef]
- Lee, H.; Yanilmaz, M.; Toprakci, O.; Fu, K.; Zhang, X. A Review of Recent Developments in Membrane Separators for Rechargeable Lithium-Ion Batteries. Energy Environ. Sci. 2014, 7, 3857–3886. [Google Scholar] [CrossRef]
- Mecerreyes, D.; Porcarelli, L.; Casado, N. Innovative Polymers for Next-Generation Batteries. Macromol. Chem. Phys. 2020, 221, 1900490. [Google Scholar] [CrossRef]
- Choi, S.W.; Jo, S.M.; Lee, W.S.; Kim, Y.R. An electrospun poly(vinylidene fluoride) nanofibrous membrane and its battery applications. Adv. Mater. 2003, 15, 2027–2032. [Google Scholar] [CrossRef]
- Yang, C.; Jia, Z.; Guan, Z.; Wang, L. Polyvinylidene fluoride membrane by novel electrospinning system for separator of Li-ion batteries. J. Power Sources 2009, 189, 716–720. [Google Scholar] [CrossRef]
- Bansal, D.; Meyer, B.; Salomon, M. Gelled membranes for Li and Li-ion batteries prepared by electrospinning. J. Power Sources 2008, 178, 848–851. [Google Scholar] [CrossRef]
- Kianfar, P.; Bongiovanni, R.; Ameduri, B.; Vitale, A. Electrospinning of Fluorinated Polymers: Current State of the Art on Processes and Applications. Polym. Rev. 2023, 63, 127–199. [Google Scholar] [CrossRef]
- Miao, Y.-E.; Zhu, G.-N.; Hou, H.; Xia, Y.-Y.; Liu, T. Electrospun polyimide nanofiber-based nonwoven separators for lithium-ion batteries. J. Power Sources 2013, 226, 82–86. [Google Scholar] [CrossRef]
- Hao, J.; Lei, G.; Li, Z.; Wu, L.; Xiao, Q.; Wang, L. A novel polyethylene terephthalate nonwoven separator based on electrospinning technique for lithium ion battery. J. Membr. Sci. 2013, 428, 11–16. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, Y.; Xu, T.; John, A.E.; Li, Y.; Li, W.; Zhu, B. Poly(m-phenylene isophthalamide) separator for improving the heat resistance and power density of lithium-ion batteries. J. Power Sources 2016, 329, 8–16. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Han, Y.; Zhang, L.; Li, S.; Tang, B.; Xu, S.; Xu, Z. b Ether modified poly(ether ether ketone) nonwoven membrane with excellent wettability and stability as a lithium ion battery separator. J. Power Sources 2018, 378, 176–183. [Google Scholar] [CrossRef]
- Qi, W.; Lu, C.; Chen, P.; Han, L.; Yu, Q.; Xu, R. Electrochemical performances and thermal properties of electrospun Poly(phthalazinone ether sulfone ketone) membrane for lithium-ion battery. Mater. Lett. 2012, 66, 239–241. [Google Scholar] [CrossRef]
- Xiao, W.; Zhao, L.; Gong, Y.; Liu, J.; Yan, C. Preparation and performance of poly(vinyl alcohol) porous separator for lithium-ion batteries. J. Membr. Sci. 2015, 487, 221–228. [Google Scholar] [CrossRef]
- Cho, T.H.; Tanaka, M.; Onishi, H.; Kondo, Y.; Nakamura, T.; Yamazaki, H.; Tanase, S.; Sakai, T. Battery performances and thermal stability of polyacrylonitrile nano-fiber-based nonwoven separators for Li-ion battery. J. Power Sources 2008, 181, 155–160. [Google Scholar] [CrossRef]
- Xu, T.; Binjie, X.; Zan, L.; Weihong, G.; Fuli, Z. Electrospun sandwich polysulfonamide/polyacrylonitrile/polysulfonamide composite nanofibrous membranes for lithium-ion batteries. RSC Adv. 2019, 9, 11220–11229. [Google Scholar] [CrossRef]
- Di Carli, M.; Caso, M.F.; Aurora, A.; Della Seta, L.; Prosini, P.P. Electrospinning nanofibers as separators for lithium-ion batteries. AIP Conf. Proc. 2019, 2145, 020009. [Google Scholar] [CrossRef]
- Khodaverdi, F.; Vaziri, A.; Javanbakht, M.; Jahanfar, M. Improvement of PAN separator properties using PVA/malonic acid by electrospinning in lithium ion-batteries. J. Appl. Polym. Sci. 2021, 138, 50088. [Google Scholar] [CrossRef]
- Oh, S.H.; Park, I.K.; Kim, J.M.; Lee, J.H. In vitro and in vivo characteristics of PCL scaffolds with pore size gradient fabricated by a centrifugation method. Biomaterials 2007, 28, 1664–1671. [Google Scholar] [CrossRef] [PubMed]
- Deng, A.; Yang, Y.; Du, S. Tissue Engineering 3D Porous Scaffolds Prepared from Electrospun Recombinant Human Collagen (RHC) Polypeptides/Chitosan. Nanofibers Appl. Sci. 2021, 11, 5096. [Google Scholar] [CrossRef]
- Eichhorn, S.J.; Sampson, W.W. Statistical geometry of pores and statistics of porous nanofibrous assemblies. J. R. Soc. Interface 2005, 2, 309–318. [Google Scholar] [CrossRef]
- Soliman, S.; Pagliari, S.; Rinaldi, A.; Forte, G.; Fiaccavento, R.; Pagliari, F.; Franzese, O.; Minieri, M.; Di Nardo, P.; Licoccia, S.; et al. Multiscale three-dimensional scaffolds for soft tissue engineering via multimodal electrospinning. Acta Biomater. 2010, 6, 1227–1237. [Google Scholar] [CrossRef]
- Seyedmahmoud, R.; Rainer, A.; Mozetic, P.; Giannitelli, S.M.; Basoli, F.; Trombetta, M.; Traversa, E.; Licoccia, S.; Rinaldi, A. A primer of statistical methods for correlating parameters and properties of electrospun poly(L-lactide) scaffolds for tissue engineering—Part 2: Regression. J. Biomed. Mater. Res. Part A 2015, 103, 103–114. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, J.S.; Hunter, W.G. Statistics for Experimenters: Design, Innovation, and Discovery, 2nd ed.; Wiley: New York, NY, USA, 2006; ISBN 978-0-471-71813-0. [Google Scholar]
- Szewczyk, P.K.; Stachewicz, U. The impact of relative humidity on electrospun polymer fibers: From structural changes to fiber morphology. Adv. Colloid Interface Sci. 2020, 286, 102315. [Google Scholar] [CrossRef]
- Zhang, H.; Quan, L.; Gao, A.; Tong, Y.; Shi, F.; Xu, L. Thermal Analysis and Crystal Structure of Poly(Acrylontirile-Co-Itaconic Acid) Copolymers Synthesized in Water. Polymers 2020, 12, 221. [Google Scholar] [CrossRef]
- Su, T.T.; Jiang, H.; Gong, H. Thermal Stabilities and the Thermal Degradation Kinetics of Poly (ε-Caprolactone). Polym. Plast. Technol. Eng. 2008, 47, 398–2403. [Google Scholar] [CrossRef]
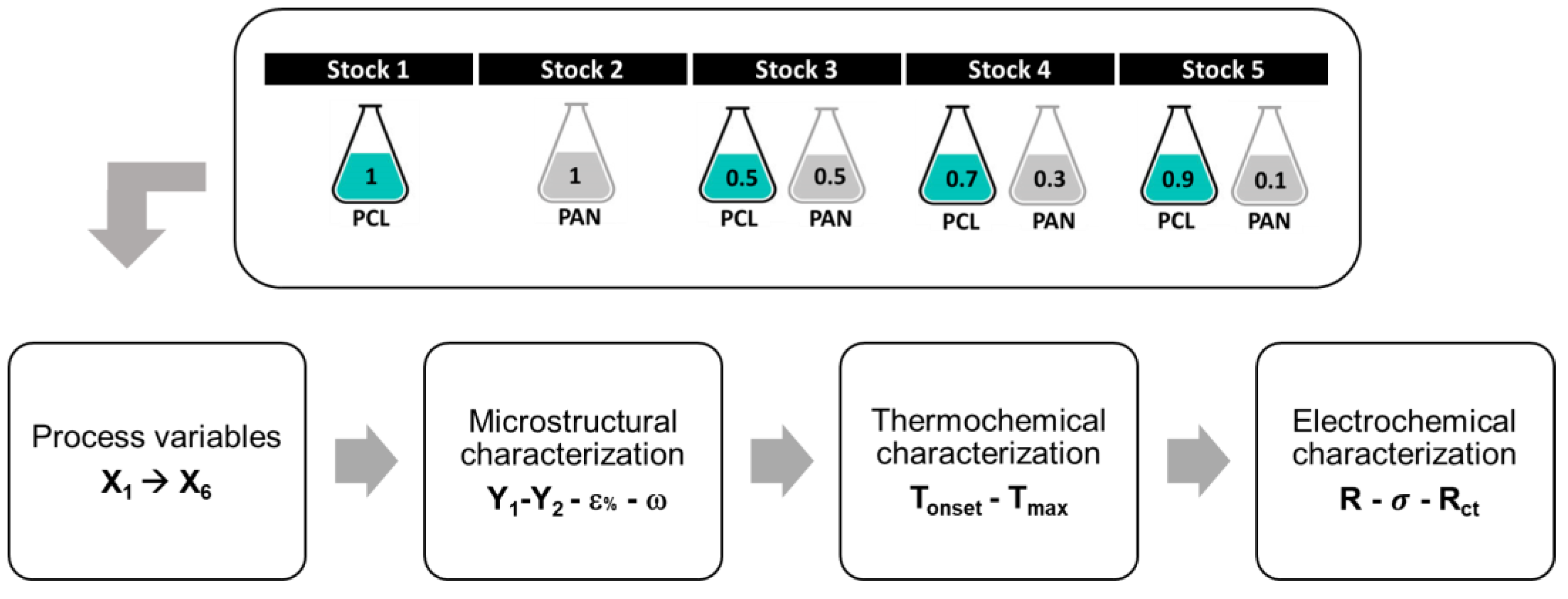



| X1 | X2 | X3 | X4 | X5 | X6 | Y1 | Y2 | ||
|---|---|---|---|---|---|---|---|---|---|
| Label | PAN (wt.%) | Flow Rate (mL h−1) | Deposition Time (min) | Emitter Voltage (V) | Collector Voltage (V) | R.H. (%) | T (°C) | Mean FD (µm) | Std. Dev. FD (µm) |
| PANPCL_00 | 50 | 6 | 15 | 5 | −25 | 35 | 26.1 | 0.37 | 0.18 |
| PANPCL_01 | 50 | 6 | 15 | 5 | −25 | 55 | 21.7 | 0.76 | 0.36 |
| PANPCL_02 | 50 | 6 | 30 | 5 | −25 | 51 | 22.0 | 0.45 | 0.24 |
| PANPCL_03 | 70 | 6 | 30 | 5 | −25 | 43 | 23.6 | 0.53 | 0.25 |
| PANPCL_04 | 70 | 6 | 15 | 5 | −25 | 38 | 24.6 | 0.39 | 0.18 |
| PANPCL_05 | 90 | 6 | 30 | 5 | −20 | 36 | 24.9 | 0.44 | 0.15 |
| PANPCL_06 | 90 | 6 | 15 | 5 | −20 | 35 | 25.7 | 0.42 | 0.16 |
| PAN_001 | 100 | 4 | 30 | 5 | −25 | 28 | 21.0 | 0.38 | 0.13 |
| PAN_ 002 | 100 | 4 | 30 | 5 | −25 | 27 | 23.4 | 0.42 | 0.12 |
| PAN_003 | 100 | 4 | 15 | 5 | −25 | 27 | 23.7 | 0.54 | 0.14 |
| PCLDMF_01 | 0 | 6 | 30 | 5 | −20 | 56 | 24.0 | 0.32 | 0.12 |
| PCLDMF_02 | 0 | 4 | 30 | 0 | −15 | 50 | 26.0 | 0.27 | 0.09 |
| Output Variable | Model Equation | R2 | R2adj |
|---|---|---|---|
| Y1 | Y1 = −0.354 + 0.478 X1 − 0.00573 X2 + 0.01558 X3 | 71.15% | 60.33% |
| Y2 | Y2 = −0.325 + 0.2508 X1 − 0.00338 X2 + 0.01051 X3 | 76.69% | 67.95% |
| Vars | R2 | R2adj | Cp-Mallows | S | X1 | X2 | X3 |
|---|---|---|---|---|---|---|---|
| 1 | 14.8 | 6.3 | 16.1 | 0.12231 | ✓ | ||
| 2 | 59.3 | 50.3 | 5.5 | 0.089103 | ✓ | ✓ | |
| 3 * | 71.2 | 60.3 | 4.2 | 0.079596 | ✓ | ✓ | ✓ |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Regression | 3 | 0.12501 | 71.15% | 0.12501 | 0.041669 | 6.58 | 0.015 |
| X1: PAN% | 1 | 0.01674 | 9.53% | 0.09264 | 0.092642 | 14.62 | 0.005 |
| X2: time | 1 | 0.01936 | 11.02% | 0.02077 | 0.020771 | 3.28 | 0.108 |
| X3: RH(%) | 1 | 0.08891 | 50.61% | 0.08891 | 0.088909 | 14.03 | 0.006 |
| Error | 8 | 0.05068 | 28.85% | 0.05068 | 0.006336 | ||
| Total | 11 | 0.17569 | 100.00% |
| Vars | R2 | R2 adj. | Press. | R2 Pred. | Cp-Mallows | S | X1 | X2 | X3 | X1*X2 | X1*X3 | X2*X3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 74.7 | 60.2 | 0.4 | 0.0 | 3.4 | 0.079711 | ✓ | ✓ | ✓ | ✓ | ||
| 2 * | 76.7 | 57.3 | 0.3 | 0.0 | 5.0 | 0.082627 | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 3 | 76.7 | 48.7 | 0.8 | 0.0 | 7.0 | 0.090504 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Vars | R2 | R2 adj. | Press. | R2 Pred. | Cp-Mallows | S | X1 | X2 | X3 | X1*X2 | X1*X3 | X2*X3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 * | 89.2 | 83.0 | 0.0 | 69.6 | 3.7 | 0.030835 | ✓ | ✓ | ✓ | ✓ | ||
| 2 | 90.3 | 82.2 | 0.0 | 40.5 | 5.1 | 0.031529 | ✓ | ✓ | ✓ | ✓ | ✓ | |
| 3 | 90.5 | 79.0 | 0.1 | 0.0 | 7.0 | 0.034249 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Source | DF | Seq SS | Contribution | Adj SS | Adj MS | F-Value | p-Value |
|---|---|---|---|---|---|---|---|
| Regression | 4 | 0.054811 | 89.17% | 0.054811 | 0.013703 | 14.41 | 0.002 |
| X1: PAN% | 1 | 0.000000 | 0.00% | 0.001068 | 0.001068 | 1.12 | 0.324 |
| X2: time | 1 | 0.006661 | 10.84% | 0.012288 | 0.012288 | 12.92 | 0.009 |
| X3: RH(%) | 1 | 0.040479 | 65.86% | 0.033069 | 0.033069 | 34.78 | 0.001 |
| X1*X2 | 1 | 0.007670 | 12.48% | 0.007670 | 0.007670 | 8.07 | |
| Error | 7 | 0.006656 | 10.83% | 0.006656 | 0.000951 | ||
| Total | 11 | 0.061467 | 100.00% | ||||
| Y2_augmented = −0.163 X1 − 0.01327 X2 + 0.00966 X3 + 0.01415 X1*X2 R2 = 89.17% R2adj = 82.98% | |||||||
| Sample | %PAN | Time (min) | Thickness (µm) | % | (µm) | |
|---|---|---|---|---|---|---|
| Average | std. dev. | |||||
| PAN-PCL 00 | 50 | 15 | 71 | 65% | 4.1% | 2.01 |
| PAN-PCL 01 | 50 | 15 | 82 | 73% | 10.2% | 5.56 |
| PAN-PCL 02 | 50 | 30 | 184 | 66% | 7.3% | 2.49 |
| PAN-PCL 03 | 70 | 30 | 189 | 79% | 2.7% | 5.17 |
| PAN-PCL 04 | 70 | 15 | 124 | 79% | 19.5% | 3.89 |
| PAN-PCL 05 | 90 | 30 | 337 | 87% | 8.9% | 7.31 |
| PAN-PCL 06 | 90 | 15 | 218 | 76% | 0.6% | 3.51 |
| PAN 002 | 100 | 30 | 77 | 77% | 5.7% | 3.61 |
| PAN 003 | 100 | 15 | 36 | 61% | 8.3% | 2.54 |
| PCL DMF 01 | 0 | 30 | 88 | 75% | 1.2% | 2.56 |
| PCL DMF 02 | 0 | 30 | 82 | 41% | 0.4% | 0.70 |
| Sample | PAN Percentage | Tonset | Tmax |
|---|---|---|---|
| PCL DMF 01 | 0% | 238.2 °C | 295.8 °C |
| PANPCL_02 | 50% | 239.0 °C | 313.1 °C |
| PANPCL_04 | 70% | 239.1 °C | 313.3 °C |
| PANPCL_06 | 90% | 238.7 °C | 304.6 °C |
| ID | PAN/ PCL (wt.%) | Thickness (µm) | Resistance (Ω) | Specific Conductivity (S) | Charge Transfer Resistance (Ω) |
|---|---|---|---|---|---|
| PCL DMF 01 | 0:100 | 88 | 4.85 | 1.2 × 10−3 | 450 |
| PANPCL_02 | 50:50 | 183 | 5.43 | 2.2 × 10−3 | 2430 |
| PANPCL_04 | 70:30 | 218 | 4.85 | 2.9 × 10−3 | 3570 |
| PANPCL_06 | 90:10 | 183 | 8.14 | 1.5 × 10−3 | 1510 |
| Glass fiber | - | 260 | 5.19 | 3.2 × 10−3 | 720 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Carli, M.; Aurora, A.; Rinaldi, A.; Fiaschini, N.; Prosini, P.P. Preparation of Electrospun Membranes and Their Use as Separators in Lithium Batteries. Batteries 2023, 9, 201. https://doi.org/10.3390/batteries9040201
Di Carli M, Aurora A, Rinaldi A, Fiaschini N, Prosini PP. Preparation of Electrospun Membranes and Their Use as Separators in Lithium Batteries. Batteries. 2023; 9(4):201. https://doi.org/10.3390/batteries9040201
Chicago/Turabian StyleDi Carli, Mariasole, Annalisa Aurora, Antonio Rinaldi, Noemi Fiaschini, and Pier Paolo Prosini. 2023. "Preparation of Electrospun Membranes and Their Use as Separators in Lithium Batteries" Batteries 9, no. 4: 201. https://doi.org/10.3390/batteries9040201
APA StyleDi Carli, M., Aurora, A., Rinaldi, A., Fiaschini, N., & Prosini, P. P. (2023). Preparation of Electrospun Membranes and Their Use as Separators in Lithium Batteries. Batteries, 9(4), 201. https://doi.org/10.3390/batteries9040201










