Efficient Reallocation of BESS in Monopolar DC Networks for Annual Operating Costs Minimization: A Combinatorial-Convex Approach

Abstract

This article deals with the solution of a mixed-integer nonlinear programming (MINLP) problem related to the efficient reallocation of battery energy storage systems (BESS) in monopolar direct current (DC) grids through a master–slave optimization approach. The master stage solves the integer nature of the MINLP model, which is related to the nodes where the BESS will be located. In this stage, the discrete version of the vortex search algorithm is implemented. To determine the objective function value, a recursive convex approximation is implemented to solve the nonlinear component of the MINLP model (multi-period optimal power flow problem) in the slave stage. Two objective functions are considered performance indicators regarding the efficient reallocation of BESS in monopolar DC systems. The first objective function corresponds to the expected costs of the annual energy losses, and the second is associated with the annual expected energy generation costs. Numerical results for the DC version of the IEEE 33 bus grid confirm the effectiveness and robustness of the proposed master–slave optimization approach in comparison with the solution of the exact MINLP model in the General Algebraic Modeling System (GAMS) software. The proposed master–slave optimizer was programmed in the MATLAB software. The recursive convex solution of the multi-period optimal power flow problem was implemented in the convex discipline tool (CVX) with the SDPT3 and SEDUMI solvers. The numerical reductions achieved with respect to the benchmark case in terms of energy loss costs and energy purchasing costs were $7.2091\%$ and $3.2105\%$, which surpassed the results reached by the GAMS software, with reductions of about $6.0316\%$ and $1.5736\%$.

1. Introduction

Battery energy storage systems (BESS) are efficient energy storage technologies that allow one to deal with the uncertainties introduced by renewable energy resources in electrical systems [1,2]. Currently, most BESS for grid-scale applications correspond to lithium-ion batteries that can store hundreds of kilowatt-hours (kWh) in a few hours at a high-efficiency conversion rate via power electronic converters [3,4,5]. This energy is stored in periods with high renewable generation availability and returned to the electrical network when energy consumption increases and energy production by renewables decreases [6]. The main advantage of optimally integrating BESS in electrical networks lies in the possibility of improving different performance indicators of the electrical distribution grid [7], such as minimizing energy losses [8], reducing greenhouse emissions [9,10] and energy purchasing costs [11], and maximizing the use of renewable energy [12], among others. Nevertheless, the optimal integration and operation of BESS in electrical networks constitute one of the main challenges in distribution systems analysis, as the mathematical model that expresses these problems belongs to the family of mixed-integer nonlinear programming (MINLP) models [13,14]. The binary variables are related to the nodal allocation of the BESS, and the continuous variables refer to voltages, currents, and powers, among others. In addition, the nonlinearities of the MINLP formulation are associated with the power balance constraints, which are nonlinear and non-convex. Even if the MINLP model is complex, the operation problem of BESS is a complex task since it depends on renewable energy and demand prediction, which is a time-coupling problem [15].

In the specialized literature, the problems associated with the optimal integration and operation of BESS have been widely explored. Some of these literature reports are presented below.

The authors of [11] studied the problem concerning the optimal selection and location of distributed energy resources in medium- and low-voltage distribution networks using a two-stage optimization strategy. To determine the best set of nodes to locate BESS, a sensitivity analysis is conducted in order to reduce the size of the solution space (number of candidate nodes). Then, in the first stage, the simulated annealing optimization approach obtains the final nodes where the distributed energy resources must be installed. In the second stage, the operation problem regarding the distributed energy resources is analyzed via convex programming. Numerical results in test systems composed of 11, 135, and 230 nodes demonstrated the effectiveness of the proposed optimization strategy. However, the authors did not present any comparative analysis with other solution methodologies regarding nodal selection. In [1], a methodology for the optimal participation of BESS in the Colombian electricity market is presented. A comparative analysis with different operation strategies (i.e., seasonal, statistical, and neural network-based models) was conducted in this work. The problem regarding the optimal operation of BESS was addressed by proposing a mixed-integer linear programming model. Numerical results demonstrated that, in order to obtain a better performance of BESS in the Colombian electricity market, the most important factor corresponds to the historical data available. However, in the proposed modeling, the electrical network configuration (i.e., the grid topology) was neglected. The study by [15] presented a recursive convex approximation approach to solving the problem pertaining to the optimal operation of BESS in monopolar direct current (DC) grids with high penetration of renewable energy resources. Numerical results in the DC version of the IEEE 33-node feeder demonstrated the effectiveness of the recursive convex formulation in comparison with combinatorial optimization methods regarding the final value of the energy losses within a day-ahead operation scenario. The research conducted by [16] presented a mixed-integer convex approximation to reallocate BESS in monopolar DC grids. The objective function under analysis was the minimization of the daily energy loss costs. Numerical results in the 21-node grid confirmed the effectiveness of the proposed convex approach in comparison with the exact MINLP solution of the GAMS software. A complete literature review regarding the design of efficient energy management systems for microgrids was proposed by the authors of [17]. This work is very relevant for understanding how multiple distributed energy resources can be efficiently integrated/operated in microgrids to minimize/maximize some objective function of interest (economic, technical, or environmental). The authors of [18] presented an efficient strategy for the optimal sizing of PV-BESS units that takes into account day-ahead load scheduling for demand response and self-consumption for home energy management system-equipped households. A mixed-integer linear programming model was proposed to solve the optimization model with excellent numerical results regarding the net profit for the designed system.

The main approaches presented in the literature regarding the optimal operation of BESS in electrical systems are summarized in

Table 1. Summary of the main the literature approaches regarding the integration and operation of BESS in electrical networks.

Solution Methodology	Objective Function	Grid	Year	Ref.
Mixed-integer linear and conic programming	Energy purchasing costs minimization	AC	2015	[19]
Hybrid tabu search and particle swarm optimizers	Investment and operating costs	AC	2016	[20]
Mixed-integer linear programming	Maximization of energy market profits and battery degradation rates minimization	AC	2017	[21]
Mixed-integer nonlinear programming	Energy generation costs minimization	AC	2017	[22]
Nonlinear programming	Power system regulation and peak-load shaving services	AC	2018	[23]
Mixed-integer linear programming	Cost of energy minimization and peak power demand reduction	AC	2019	[24]
Mixed-integer conic programming	Investment and operating costs	AC	2019	[25]
Mixed-integer programming	Operating costs minimization in electric vehicle charging substations	AC	2021	[26]
Simulated annealing and convex programming	Investment and operating costs	AC	2021	[11]
Mixed-integer linear programming	Net present value minimization	AC	2021	[1]
Stochastic programming	Energy costs minimization and battery use maximization	AC	2021	[27]
Mixed-integer quadratic convex modeling	Energy loss costs minimization	DC	2022	[16]
Recursive convex programming	Energy loss minimization	DC	2023	[15]

. The data in this Table are structured as follows (from left to right): solution methodology, objective function, grid type, year of publication, and reference.

These are the main characteristics of the above-presented summary of the literature review. (i) Most of the operating problems in electrical networks with AC and DC distribution system technology have been explored using mixed-integer linear programming or mixed-integer conic programming, i.e., models with convex properties. (ii) In the case of the problems regarding the optimal integration of BESS, mixed-integer nonlinear programming models have been presented with combinatorial optimization methods as solution alternatives. (iii) Most objective functions are related to minimizing energy purchasing or investment and operating costs [28]. In addition, it is essential to note that there is a clear tendency to analyze AC distribution networks instead of DC grids, which may be due to the fact that DC grids are emerging technologies that are still in development, unlike AC distribution grids, which have decades of studies and improvements.

In light of the above, this work presents the contributions detailed below:

• The formulation of the problem concerning the optimal location reallocation of BESS in monopolar DC distribution networks as a mixed-integer convex recursive programming model by linearizing the power balance constraints via Taylor’s series expansion;
• A hybrid solution methodology which combines a metaheuristic optimization method that defines the buses where the batteries must be located–reallocated in the master stage, and a recursive convex programming model to define the optimal operation of the BESS in the slave stage.

As the objective functions of the problem under study, this research considers the minimization of the expected annual costs of energy purchasing at the substation and the minimization of the expected energy loss costs in all of the network branches. However, the optimization of these objective functions is carried out using a single-objective optimization structure, applying the proposed master–slave optimization technique. In this sense, offering multi-objective optimization methodologies is an important area of research that could be covered in future research works [15]. In addition, in the scope of this study, the following is taken into consideration: (i) the initial location of the renewable generation units and the BESS have been previously defined by the distribution company in the benchmark case; (ii) the data regarding renewable power generation profiles and expected demand behaviors are considered as inputs in the optimization model, i.e., no uncertainties are taken into account; and (iii) the energy purchasing costs per kilowatt-hour at the terminals of the substation are modeled as a linear function with constant parameters, and a day-ahead operation scenario is considered for the optimal operation of renewables and batteries. Note that, in order to solve the slave component of the proposed master–slave optimization model, the convex discipline tool (CVX) of the MATLAB programming environment is used in conjunction with the SDPT3 and SEDUMI solvers. These optimization solvers for convex optimization problems can be installed at no cost, although it requires an academic or professional MATLAB license [29,30].

The remaining sections of this paper have the following structure. Section 2 explains the general mixed-integer nonlinear programming (MINLP) model that constitutes the problem regarding the optimal location reallocation of BESS in monopolar DC distribution networks. Section 3 presents the convexification associated with the product between voltage variables in the power balance constraints via a first-order Taylor’s series expansion and the generation solution methodology via a master–slave optimization method. Section 4 shows the main features of the distribution network under analysis, i.e., the monopolar version of the IEEEE 33-node grid. Section 5 presents all the main numerical validations carried out on the proposed optimization methodology, and the results are compared to the MINLP model’s solution as obtained by the GAMS software. Finally, the concluding remarks and possible future works related to this research are listed in Section 6.

2. Exact MINLP Modeling

The problem regarding the optimal reallocation of BESS in electrical monopolar DC systems can be formulated as an MINLP model, where the binary variables are related to the nodes where the BESS will be reallocated, and the continuous variables are related to the current, powers, and voltage variables, among others.

This problem can be addressed by considering two objective function formulations (technical and economic). In the case of the technical objective function, the expected costs of the annual energy losses are used to determine the best points to locate all the battery packs. However, some authors believe that the costs of energy purchasing at the terminals of the substation are the most suitable objective function, as it reflects the actual, simultaneous use of the renewables and the BESS. Here, both objective functions are presented.

2.1. Minimizing the Costs of Energy Losses

The cost of energy losses can be modeled as a quadratic function associated with the square value of the current flowing through each distribution line and its corresponding resistive effect. This objective function is defined in (1) [16].

$$\begin{array}{c}\hfill min{E}_{\mathrm{loss}}=T{C}_{kWh}^s\sum _{h\in \mathcal{H}}\sum _{j\in \mathcal{L}}{r}_j{i}_{j,h}^2{\Delta }_h,\end{array}$$

(1)

where $r_j$ is the resistive parameter related to the distribution line that connects nodes k and m; $i_{j,h}$ is the current flow on the route j in period h; T is the number of days in a year; $C_{kWh}^s$ denotes the average energy loss costs calculated at the substation terminals; and ${\Delta }_h$ corresponds to the time fraction where electrical variables take constant values, i.e., typically periods of 1 h. Note that $\mathcal{H}$ is the set containing all periods under analysis in a day-ahead operation dispatch scenario, and $\mathcal{L}$ is the set that contains all distribution branches with cardinality l.

Remark 1.

The objective function (1) is strictly convex since all the resistive parameters are positive values, which implies that it can be represented as the sum of a definite positive quadratic function with the structure shown in (2).

$$\begin{array}{c}\hfill min{E}_{\mathrm{loss}}=T{C}_{kWh}^s\sum _{h\in \mathcal{H}}{I}_h^{\top }\mathbf{R}{I}_h{\Delta }_h,\end{array}$$

(2)

where $I_h\in {\mathbb{R}}^{l\times 1}$ is a vector containing the current flows in all the distribution lines per period, and $\mathbf{R}\in {\mathbb{R}}^{l\times l}$ is a square positive definite matrix containing all of the distribution branches’ resistive parameters.

2.2. Minimization of Energy Purchasing and Operating Costs

One of the critical factors in the optimal location reallocation of BESS in electrical distribution networks is the minimization of the total energy purchasing costs at the terminals of the substation, in addition to the maintenance (operating) costs of renewable energy resources. Here, an economic objective function regarding the energy purchasing and maintenance costs of photovoltaic (PV) plants is presented, as defined in (3) [15].

$$\begin{array}{c}\hfill min{E}_{\mathrm{costs}}=T\sum _{h\in \mathcal{H}}\sum _{k\in \mathcal{N}}\left(C_{kWh}^{cg}{p}_{k,h}^{cg}+C_{kWh}^s{p}_{k,h}^s+C_{O\&M}^{pv}{p}_{k,h}^{pv}\right){\Delta }_h,\end{array}$$

(3)

where $E_{\cos \mathrm{ts}}$ denotes the expected annual energy operating costs of the monopolar DC distribution grid for an operation horizon of one year; $C_{kWh}^{cg}$ and $C_{kWh}^s$ correspond to the energy purchasing costs stemming from a thermal generation source (typically a diesel one) and those from the terminals of the equivalent electrical substation for grid-connected monopolar DC grids; and $p_{k,h}^{cg}$ and $p_{k,h}^s$ are the power generation outputs in the thermal and slack generation sources. Note that $C_{O\&M}^{pv}$ is a constant parameter regarding the expected maintenance and operating costs of generating power with PV sources ($p_{k,h}^{pv}$), and $\mathcal{N}$ is the set containing all of the network buses.

Remark 2.

The objective function (3) has a linear structure, which implies that its mathematical properties make it simultaneously concave and convex, which implies that, from a geometrical perspective, it is part of the convex space and will facilitate the solution of the studied problem if all the constraints are convex.

2.3. Model Constraints

The studied problem involves multiple technical constraints associated with the expected physical behavior of the DC network. These constraints include voltage regulation bounds, device capabilities (power generation and thermal bounds), and Kirchhoff’s laws, among others. To obtain all the set of physical constraints, the branch-to-node incidence matrix $\mathbf{A}$ was used. Each one of its elements is defined as follows:

• The component of the branch-to-node incidence matrix ${\mathbf{A}}_{jk}$ is assigned as 1 if the distribution line j is connected to node k and the current is leaving this node;
• The component of the branch-to-node incidence matrix ${\mathbf{A}}_{jk}$ is assigned as $-1$ if the distribution line j is connected to node k and the current is arriving at this node;
• The component of the branch-to-node incidence matrix ${\mathbf{A}}_{jk}$ is assigned as 0 if the distribution line j is not connected to node k.

Now, considering the structure of the branch-to-node incidence matrix $\mathbf{A}$, Tellegen’s theorem can be applied to each node of the network as a function of the product between the nodal voltage and the branch currents. The power balance constraint is thus defined in (4) [15]:

$$\begin{array}{c}\hfill p_{k,h}^{cg}+p_{k,h}^s+p_{k,h}^{pv}+\sum _{b\in \mathcal{B}}{p}_{k,h}^b-p_{k,h}^d=v_{k,h}\sum _{j\in \mathcal{L}}{\mathbf{A}}_{jk}{i}_{j,h},\left\{k\in \mathcal{N},h\in \mathcal{H}\right\}\end{array}$$

(4)

where $p_{k,h}^d$ represents the constant power load consumption at node k in period h; $p_{k,h}^b$ corresponds to the power injection/absorption in a type b BESS connected to node k in period h; and $v_{k,h}$ is the voltage variable assigned to node k per period. Note that $\mathcal{B}$ corresponds to the set containing all of the available BESS types.

To determine the current flowing through each line, it is possible to employ the difference between voltages at the terminals of each distribution line and its resistive effect ($r_j$). In other words, Ohm’s law is applied to each branch and period, as shown in (5) [16].

$$\begin{array}{c}\hfill \sum _{k\in \mathcal{N}}{\mathbf{A}}_{j,k}{v}_{k,h}=r_j{i}_{j,h},\left\{j\in \mathcal{L},h\in \mathcal{H}\right\}\end{array}$$

(5)

The operation of the BESS requires defining the battery’s state of charge ($So{C}_{k,h}^b$) for each period (note that the state of charge is a normalized measure of the energy storage capability of each BESS). This variable is defined as follows [22]:

$$\begin{array}{c}\hfill So{C}_{k,h}^b=So{C}_{k,h-1}^b-{\varphi }_k^b{p}_{k,h}^b{\Delta }_h,,\left\{k\in \mathcal{N},h\in \mathcal{H},b\in \mathcal{B}\right\}\end{array}$$

(6)

where ${\varphi }_k^b$ is the efficient charging/discharging coefficient of the type b battery assigned to node k.

To guarantee the correct operation of the BESS at the beginning and end of each day, energy storage consigns are typically assigned, i.e., $So{C}_{k,t_0}^b$ and $So{C}_{k,t_f}^b$, where $t_0$ and $t_f$ are the initial and final periods of analysis, respectively. These are stated in (7) and (8) [16].

$$\begin{array}{c}\hfill So{C}_{k,t_0}^b=x_k^{b}So{C}_{k,0}^b,\left\{k\in \mathcal{N},b\in \mathcal{B}\right\},\end{array}$$

(7)

$$\begin{array}{c}\hfill So{C}_{k,t_f}^b=x_k^{b}So{C}_{k,H}^b,\left\{k\in \mathcal{N},b\in \mathcal{B}\right\}\end{array}$$

(8)

where $So{C}_{k,0}^b$ and $So{C}_{k,H}^b$ are the initial and final operative consigns assigned to the operation of the BESS by the utility (note that H denotes the cardinality of the set $\mathcal{H}$). Note that $x_k^b$ is a binary variable associated with the possibility of assigning ($x_k^b=1$) or not assigning ($x_k^b=0$) a type b BESS to node k.

To guarantee the adequate operation of the generation sources and the BESS, their generation outputs must be contained within their lower and upper bounds, as expressed in (9)–(12) [15].

$$\begin{array}{c}\hfill p_{k,h}^{cg,min}\le p_{k,h}^{cg}\le p_{k,h}^{cg,max},\left\{k\in \mathcal{N},h\in \mathcal{H}\right\}\end{array}$$

(9)

$$\begin{array}{c}\hfill p_{k,h}^{s,min}\le p_{k,h}^s\le p_{k,h}^{s,max},\left\{k\in \mathcal{N},h\in \mathcal{H}\right\}\end{array}$$

(10)

$$\begin{array}{c}\hfill p_{k,h}^{pv,min}\le p_{k,h}^{pv}\le p_{k,h}^{pv,max},\left\{k\in \mathcal{N}.h\in \mathcal{H}\right\}\end{array}$$

(11)

$$\begin{array}{c}\hfill x_k^b{p}_{k,h}^{b,min}\le p_{k,h}^b\le x_k^b{p}_{k,h}^{b,max},\left\{k\in \mathcal{N},h\in \mathcal{H},b\in \mathcal{B}\right\}\end{array}$$

(12)

where $p_{k,h}^{cg,min}$ and $p_{k,h}^{cg,max}$ correspond to the lower and upper power generation limits for the conventional generation source; $p_{k,h}^{s,min}$ and $p_{k,h}^{s,max}$ represent the minimum and maximum generation limits at the substation node; $p_{k,h}^{pv,min}$ and $p_{k,h}^{pv,max}$ are the minimum and maximum generation bounds for the PV plants; and $p_{k,h}^{b,min}$ and $p_{k,h}^{b,max}$ correspond to the lower and upper power injection/absorption characteristics of the BESS, respectively.

To ensure the correct operation of the distribution lines when it comes to their thermal capabilities, i.e., $i_j^{max}$, it is necessary to assign the lower and upper current flow limits of each branch. This set of constraints is presented in (13) [31].

$$\begin{array}{c}\hfill -i_j^{max}\le i_{j,h}\le i_j^{max},\left\{j\in \mathcal{L},h\in \mathcal{H}\right\}\end{array}$$

(13)

Now, considering the regulatory policies regarding the behavior of the voltage profiles in the entire monopolar DC grid, the voltage regulation bounds ($v^{min}$ and $v^{max}$) are defined as presented in (14). In addition, the operating voltage of the substation bus (i.e., the slack node) is defined in (15) [15].

$$\begin{array}{c}\hfill v^{min}\le v_{k,h}\le v^{max},\left\{k\in \mathcal{N},h\in \mathcal{H}\right\}\end{array}$$

(14)

$$\begin{array}{c}\hfill v_{k,h}=v_{\mathrm{nom}},\left\{k=\mathrm{slack},h\in \mathcal{H}\right\}\end{array}$$

(15)

where $v_{\mathrm{nom}}$ represents the operating voltage of the monopolar DC network under analysis.

Finally, three constraints are added to ensure that the BESS are correctly assigned to different network nodes and that only the numbers of BESS initially installed in the studied system are reallocated. In addition, the binary nature of the decision variables is confirmed. These constraints are presented below [32].

$$\begin{array}{c}\hfill \sum _{b\in \mathcal{B}}{x}_k^b\le 1,\left\{k\in \mathcal{N}\right\},\end{array}$$

(16)

$$\begin{array}{c}\hfill \sum _{k\in \mathcal{N}}{x}_k^b\le 1,\left\{B\in \mathcal{B}\right\},\end{array}$$

(17)

$$\begin{array}{c}\hfill \sum _{k\in \mathcal{N}}\sum _{b\in \mathcal{B}}{x}_k^b=N_b^{ava},\end{array}$$

(18)

$$\begin{array}{c}\hfill x_k^b\in \left\{0,1\right\},\left\{k\in \mathcal{N},b\in \mathcal{B}\right\}.\end{array}$$

(19)

where $N_b^{ava}$ is the number of BESS available for location or reallocation.

Remark 3.

The main characteristic of the solution space defined in (4)–(19) is that it constitutes a mixed-integer nonlinear space. However, the only set of nonlinear equations corresponds to the power equilibrium at each node, as shown in Equation (4), which implies that a convexification method is applied to this set of equations. Thus, the whole solution space will take a mixed-integer convex structure.

3. Solution Methodology

To solve the MINLP model (1)–(19) that constitutes the problem regarding the location reallocation of BESS in monopolar DC networks, a hybrid optimization method is proposed, which involves a master–slave interaction. The master stage employs a combinatorial optimization method based on the vortex search algorithm to define the buses where the BESS must be placed. In the slave stage, a recursive convex programming approach is used to define the daily operating dispatch of the BESS, renewables, and conventional sources in order to minimize each one of the objective functions (i.e., the expected energy purchasing and maintenance costs or the expected costs of the energy losses). Each one of the optimization stages is described below.

3.1. Master Stage: Vortex Search Algorithm

To establish the set of nodes where the BESS must be reallocated, a vortex search algorithm (VSA) with discrete variables is proposed. The VSA approach is a physics-inspired combinatorial optimization method based on the vortex behavior experienced by starrier fluids in pipes [33]. The main feature of the VSA approach is that it explores and exploits the solution space using two concepts [34]: (i) the generation of solution individuals around the best current solution through a Gaussian distribution, and (ii) the size reduction in the solution space using an adaptive radius based on a decreasing exponential function.

To apply the VSA approach to determine the set of nodes associated with the BESS location reallocation problem, consider the following codification for the solution individual i in iteration t. The codification is a typical way to represent the decision variables with combinatorial optimizers, that in the case of the binary variables, is preferred to use a discrete codification with integer numbers to make it more compact for programming purposes [35].

$$\begin{array}{c}\hfill x_i^t=\left[\begin{array}{c}7,k,12,\cdots ,4\end{array}\right].\end{array}$$

(20)

Note that the dimension of $x_i^t$ is associated with the number of BESS available to be located and reallocated in the monopolar DC distribution grid, i.e., $1\times N_b^{ava}$. In addition, i varies from 1 to the number of individuals set for the population (i.e., $P_s$), and k represents the node where the BESS must be placed.

Next, details are provided on each one of the steps to apply the VSA approach to an optimization problem.

3.1.1. Generating the Initial Solution

At the start of the iteration process, the VSA uses the largest possible hyper-ellipse, i.e., the hyper-ellipse that contains all the possible solutions for the studied problem. It defines the initial solution alternative as the center of this hyper-ellipse by ${\mu }_t$, with $t=0$, as defined in (21) [33].

$$\begin{array}{c}\hfill {\mu }_t=\frac{x^{min}+x^{max}}{2}.\end{array}$$

(21)

Here, $x^{min}$ and $x^{max}$ are vectors with the same dimension as $x_i^t$, such that they contain the lower and upper limits of the decision variables, i.e., $x^{min}=\left[\begin{array}{c}1,1,\cdots ,1\end{array}\right]$ and $x^{min}=\left[\begin{array}{c}n,n,\cdots ,n\end{array}\right]$, where n is the number of buses in the system (cardinality of the set $\mathcal{N}$). Note that ${\mu }_t$ can contain continuous variables that need to be rounded to the feasibility of the solution space with regard to the nodes, which are integer numbers.

3.1.2. Generation of Candidate Solutions

The candidate solutions are generated using a Gaussian distribution, which allows obtaining each vector $s_i^t$ (note that this vector can contain continuous variables), as presented in [33]. These candidates are generated using (22) [33].

$$\begin{array}{c}\hfill s_i^t=p\left({\zeta }_i^t,{\mu }_t,\mathbf{V}\right)={\left({\left(2\pi \right)}^d\left|\mathbf{V}\right|\right)}^{1/2}{e}^{\left(-\frac{1}{2}{\left({\zeta }_i^t-{\mu }_t\right)}^T{\mathbf{V}}^{-1}\left({\zeta }_i^t-{\mu }_t\right)\right)}.\end{array}$$

(22)

where ${\zeta }_i^t$ is a vector with random values (note that ${\zeta }_i^t$ follows a uniform distribution), ${\mu }_t$ corresponds to the current center of the hyper-ellipse (best current solution in iteration t), and $\mathbf{V}$ is a square matrix associated with the co-variances. To simplify the structure of $\mathbf{V}$, a diagonal matrix with identical values in its diagonal (the same variance for each variable) is advised [33]. This is defined as $\mathbf{V}={\sigma }_0{\mathbf{I}}_{N_b^{ava}\times N_b^{ava}}$, where ${\sigma }_0$ is, in turn, defined as presented in (23) [36].

$$\begin{array}{c}\hfill {\sigma }_0=\frac{max\left\{x^{max}\right\}-min\left\{x^{min}\right\}}{2},\end{array}$$

(23)

Note that one of the main key factors in implementing the VSA approach is the reduction in the adaptive radius, i.e., the calculation of $r_t$ in each iteration [33]. However, at the beginning of the iterative process ($t=0$), it is recommended that the initial radius ($r_0$) be assigned as ${\sigma }_0$ [33].

Remark 4.

The variable radius of the hyper-ellipse is the parameter entrusted with controlling the dispersion of the random values of the vector ${\zeta }_i^t$, which can be defined as ${\zeta }_i^t=r_t\mathit{rand}\left(N_b^{ava}\right)$. Note that $\mathit{rand}\left(N_b^{ava}\right)$ generates a random vector with dimension $N_b^{ava}$ and values between 0 and 1 using a uniform distribution.

3.1.3. Fitting of Candidate Solutions

Because the solution space in the studied problem is defined by a set of discrete numbers between 1 and n, it is necessary to check whether the feasibility of each solution $s_i^t$ takes the structure $x_i^t$. Each candidate solution is checked through Formula (24) [33].

$$\begin{array}{c}\hfill x_i^t=\left\{\begin{array}{cc}\mathrm{round}\left(s_i^t\right)& x^{min}\le s_i^t\le x^{max}\\ \mathrm{round}\left(x^{min}+\left(x^{max}-x^{min}\right)·\mathrm{rand}\left(N_b^{ava}\right)\right)& \mathrm{otherwise}\end{array}\right.\end{array}$$

(24)

where $x·y$ is the inner product between two vectors.

3.1.4. Selection of the Hyper-Ellipse Center

The evolution of the VSA approach is determined by the location of the best current solution, which is defined as the center of the hyper-ellipse. For this reason, the next center of the hyper-ellipse (i.e., ${\mu }_{t+1}$) is set as ${\mu }_{t+1}=x_{i,\mathrm{best}}^t$ [37]. Note that $x_{i,\mathrm{best}}^t$ is determined once each candidate solution $x_i^t$ is evaluated in the slave stage problem (which will be described in the next section). However, it is worth mentioning that, due to the discrete nature of the solution space, each solution provided by the VSA approach is 100% feasible, as it only corresponds to the set of nodes where the BESS must be placed.

3.1.5. Adaptive Reduction in the Hyper-Ellipse Radius

To obtain an adaptive reduction in the hyper-ellipse radius, this research adopted an exponential function instead of an incomplete Gamma function. The exponential function is preferred because of its simple calculation [37]. The structure of the radius calculation for the next iteration is defined in (25) [37].

$$\begin{array}{c}\hfill r_{t+1}={\sigma }_0\left(1-\frac{t}{t_{max}}\right)e^{\left(-\theta \frac{t}{t_{max}}\right)},\end{array}$$

(25)

where $t_{max}$ is the maximum number of iterations assigned for the VSA approach, and $\theta$ is an adjusting parameter that allows controlling the radius reduction speed rate. As recommended by the authors of [37], this parameter is set as 6 because, with this number, the exponential function (25) behaves like an incomplete inverse Gamma function [38].

3.1.6. Stopping Criteria

To determine whether the exploration and exploitation of the solution space conducted by the VSA must finish, these two stopping criteria are tested:

✓

When the maximum number of iterations $t_{max}$ is reached, the VSA stops, and the best solution corresponds to ${\mu }_{t_{max}}$;

✓

If, during ${\tau }_{max}$ consecutive iterations, the center of the hyper-ellipse has not been improved, the VSA stops, and the best current solution ${\mu }_{t+1}$ is reported.

3.1.7. General Implementation of the VSA

Algorithm 1 illustrates the implementation of the VSA approach in solving optimization problems [37]. Note that Algorithm 1 can be applied to any optimization problem where the objective function is tested through a slave stage, as the VSA approach governs the exploration and exploitation of the solution space via an initial population that evolves based on Gaussian distribution rules and a variable radius. The slave stage is used to guide the exploration path throughout the solution space as a function of the best solution found.

Remark 5.

The solution to the problem concerning the optimal location reallocation of BESS in monopolar DC networks with the VSA approach summarized in Algorithm 1 depends on the slave stage, which, as mentioned before, controls the evolution of the VSA through the solution space.

3.2. Slave Stage: Recursive Hourly Optimal Power Flow Solution

In this study, the slave stage is entrusted with determining the objective function value (economic or technical) by ensuring the fulfillment of all the constraints associated with the expected electrical performance of the DC network under study. This research implements an iterative convex approach, as reported in [15]. As previously mentioned, in order to obtain a convex solution space, it is necessary to approximate the power balance constraints in (4) via a convexification method.

To obtain a linear approximation of the power balance constraints defined in (4), the McCormick approximation of the product between two positive variables is implemented [39]. The McCormick approximation is equivalent to linearizing two continuous variables ($wy$) using Taylor’s series expansion around the operating point ($w_0,y_0$) [40].

$$\begin{array}{c}\hfill f\left(w,y\right)=wy\approx w_{0}y+y_{0}w-w_0{y}_0.\end{array}$$

(26)

Note that if $\omega$ is set as $v_{k,h}$ and y is set as $i_{j,h}$, then (4) can be transformed as follows:

$$\begin{array}{c}\hfill p_{k,h}^{cg}+p_{k,h}^s+p_{k,h}^{pv}+\sum _{b\in \mathcal{B}}{p}_{k,h}^b-p_{k,h}^d=\sum _{j\in \mathcal{L}}{\mathbf{A}}_{jk}\left(v_{k,h}^0{i}_{j,h}+i_{j,h}^0{v}_{k,h}-v_{k,h}^0{i}_{j,h}^0\right),\left\{k\in \mathcal{N},h\in \mathcal{H}\right\}\end{array}$$

(27)

In Equation (27), it is necessary to define $v_{k,h}^0$ and $i_{j,h}^0$. In the case of $v_{k,h}^0$, these values are equal to the substation voltage. The initial current values are obtained from (5) as defined in (28).

$$\begin{array}{c}\hfill i_{j,h}^0=\frac{1}{r_j}\sum _{k\in \mathcal{N}}{{\mathbf{A}}_{j,k}{v}_{k,h}}^0,\left\{j\in \mathcal{L}.h\in \mathcal{H}\right\}\end{array}$$

(28)

Algorithm 2 presents the implementation of the slave stage for each solution $x_i^t$ provided by the master stage.

Remark 6.

The solution to the recursive convex optimization problem obtained via Algorithm 2 ensures that the optimal solution of the day-ahead operation of BESS and renewables in monopolar DC grids is found via sequential quadratic programming [41].

4. Test Feeder Characteristics

To evaluate the effectiveness of our master–slave optimization method based on the VSA approach and the recursive optimal power flow solution, this section outlines the main characteristics of the studied test feeder.

In this work, in order to demonstrate the validity of the proposed convex model used to operate BESS and PV sources in monopolar distribution networks, the IEEE 33-bus feeder configuration was employed [15]. It was adjusted for monopolar DC operation with a voltage value of 12.66 kV at the terminals of the substation. The configuration of this test feeder is shown in Figure 1.

The parametric information of this test system is reported in

Table 2. Parametric information for branches and loads in the IEEE 33-node grid.

Branch	Node i	Node j	R ($\mathbf{\Omega }$)	Pj (kW)	Imax (A)
1	1	2	0.0922	100	320
2	2	3	0.4930	90	280
3	3	4	0.3660	120	195
4	4	5	0.3811	60	195
5	5	6	0.8190	60	195
6	6	7	0.1872	200	95
7	7	8	17114	200	85
8	8	9	10300	60	70
9	9	10	10400	60	55
10	10	11	0.1966	45	55
11	11	12	0.3744	60	55
12	12	13	14.680	60	40
13	13	14	0.5416	120	40
14	14	15	0.5910	60	25
15	15	16	0.7463	60	20
16	16	17	12890	60	20
17	17	18	0.7320	90	20
18	2	19	0.1640	90	30
19	19	20	15042	90	25
20	20	21	0.4095	90	20
21	21	22	0.7089	90	20
22	3	23	0.4512	90	85
23	23	24	0.8980	420	70
24	24	25	0.8900	420	40
25	6	26	0.2030	60	85
26	26	27	0.2842	60	85
27	27	28	10590	60	70
28	28	29	0.8042	120	70
29	29	30	0.5075	200	55
30	30	31	0.9744	150	40
31	31	32	0.3105	210	25
32	32	33	0.3410	60	20

.

Figure 1 illustrates the location of the BESS and PV systems. However, its parametrization is presented below [15]:

• The BESS at bus 6 has an energy storage capability of 2 MWh, with a charging/discharging rate of 5 h (C-type BESS). The BESS at bus 14 can store 1.5 MWh with a charging/discharging rate of 4 h (B-type BESS). At node 31, there is a battery package with a capacity of 1 MWh with a charging/discharging rate of 4 h (A-type BESS);
• Regarding the PV generation units, it is assumed that each one was assigned to generate a maximum of 2.4 MWp, being located at nodes 12, 15, and 31. In addition, the expected generation curve for these units is presented in

  Table 3. Generation and demand curves.

  Hour	${\mathit{p}}_{\mathit{k},\mathit{h}}^{\mathit{pv},max}$ (%)	${\mathit{p}}_{\mathit{k},\mathit{h}}^{\mathit{d}}$ (%)	Hour	${\mathit{p}}_{\mathit{k},\mathit{h}}^{\mathit{pv},max}$ (%)	${\mathit{p}}_{\mathit{k},\mathit{h}}^{\mathit{d}}$ (%)
  1	0	65.5092	13	61.8091	94.3876
  2	0	63.0152	14	55.7162	93.1269
  3	0	61.5570	15	45.2364	92.5406
  4	0	61.5830	16	32.0524	92.2598
  5	0	64.4567	17	17.6932	90.8070
  6	0	69.8937	18	5.0658	88.8587
  7	4.5411	73.4230	19	0.0499	94.6218
  8	18.4242	79.3483	20	0	95.6175
  9	34.0999	84.3313	21	0	91.5546
  10	48.1610	87.6224	22	0	84.7794
  11	57.3749	91.7021	23	0	76.8311
  12	62.5715	94.5951	24	0	70.2960

  .

5. Computational Validation

The computational implementation of the proposed master–slave optimization approach was performed in the MATLAB software (version $2021\mathrm{b}$) on a PC with an AMD Ryzen 7 3700 @$2.3$ GHz processor and 16.0 GB RAM, on a Microsoft Windows 10 single language operating system. Note that the VSA approach (see Algorithm 1) was implemented using MATLAB scripts, and the recursive convex approach in Algorithm 2 is solved via the convex disciplined tool environment (CVX) of MATLAB via the SDPT3 and SEDUMI solvers.

The implementation of the exact MINLP model using the GAMS software follows the recommendations of [22,32]. It is worth mentioning that the processing times required by the BONMIN and the VSA-Convex approach are not comparable, since each methodology uses a different software platform, as mentioned earlier. However, in order to give an idea regarding the expected processing times, the BONMIN solver in the GAMS environment took about 25 min to solve the exact MINLP model. On the other hand, the proposed VSA-Convex approach took about 176 min to solve the studied problem. However, the CVX tool spent most of the time constructing all of the convex optimization models for each combination of batteries provided by the master stage.

5.1. Optimal Reallocation of BESS to Minimize min $E_{\mathrm{loss}}$

Table 4. BESS location reallocation when $E_{\mathrm{loss}}$ is minimized.

Scenario	${\mathit{E}}_{\mathbf{loss}}$ (USD/Year)	BESS	Reduction (%)
Benchmark case	45,246.3020	6 (C), 14 (B), 31 (A)	—
BONMIN	42,517.2110	15 (C), 18 (A), 31 (B)	6.0316
VSA-Convex	41,984.4063	13 (A), 15 (C), 31 (B)	7.2091

presents the numerical results obtained with our master–slave method and the BONMIN solver in the GAMS software when minimizing the costs of the energy losses (i.e., $E_{\mathrm{loss}}$).

The results in Table 4 allow stating the following:

• The solution provided by the BONMIM solver (i.e., the MINLP solution of GAMS) allowed for a reduction of about $6.0316\%$ with respect to the benchmark case, which corresponds to a gain of about USD/year $2729.0910$ (net profit regarding energy loss costs). To reach this solution, all the three BESS available were reallocated as follows: the C-type BESS at node 6 was transferred to node 15, the B-type BESS at node 14 was moved to node 31, and the A-type BESS at node 31 (A-type) was reallocated to node 18;
• The proposed VSA-Convex solution method found an energy loss cost reduction of about $7.2091\%$ regarding the benchmark case, i.e., a reduction of about USD/year $3261.8957$ in the annual costs of the energy losses. This solution reallocated all the BESS as follows: the C-type BESS at node 6 was transferred to node 13, the B-type BESS at node 14 was moved to node 31, and the A-type BESS at node 31 was reallocated to node 13. Note that the VSA-Convex method allowed for an additional gain of about USD/year 532.8047 when compared to the BONMIN solution, which demonstrates that the VSA-Convex finds a better solution via the proposed master–slave optimization approach than that of the exact MINLP model of the GAMS software;
• The solutions in Table 4 exhibit the following features. (a) Node 31 is the only bus that is maintained in all three options as an excellent candidate to connect a BESS. This is because a PV generation system is connected at this node, and its surplus of power can be directly stored at this generation point. (b) the BONMIN and VSA-Convex methodologies share 66.67% of the solution with the exact location and type of BESS at nodes 15 and 31.

To illustrate the positive effect of the reallocation of BESS on minimizing the expected energy loss costs in monopolar DC networks, Figure 2 presents the comparative daily energy loss curve for the benchmark case and the BONMIN and VSA-Convex approaches.

The behavior of the energy losses during a day of operation (Figure 2) allows noting the following:

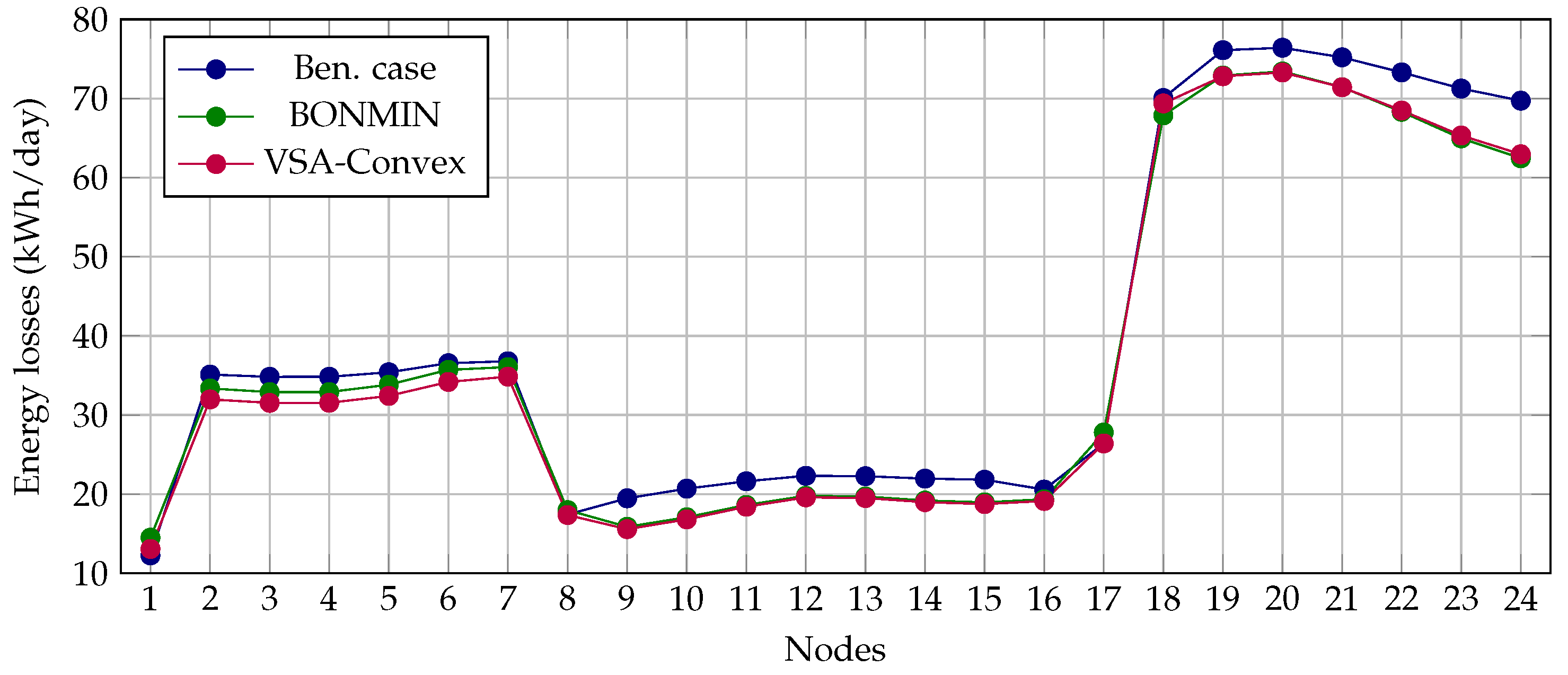
• The energy loss curve for the benchmark case is the higher curve (due to the initial location of the BESS). The current flow for some specific distribution lines is higher than the solutions obtained with the BOMIN and VSA-Convex approaches, which implies that the energy losses increase quadratically with them. Note that the daily energy losses in the benchmark case are $952.2670$ kWh/day; in the case of the exact MINLP solution, the total energy losses were $894.8310$ kWh/day; and, for the proposed VSA-Convex approach, these were $883.6200$ kWh/day;
• By comparing the BONMIN and VSA-Convex curves, it can be observed that both solutions follow a similar behavior. However, the main difference is in favor of the proposed approach during periods 1 to 7, where the BONMIN curve is higher;
• As expected, when the renewable energy generation increases considerably (periods 7 to 17), the total energy losses per hour decrease, which can be attributed to the fact that dispersed generation allows for the reduction in current flows in some distribution lines near the generators, directly impacting the reduction in the grid power losses.

5.2. Optimal Reallocation of BESS to Minimize $min{E}_{\cos \mathrm{ts}}$

Table 5. BESS location reallocation when $E_{\mathrm{costs}}$ is minimized.

Scenario	${\mathit{E}}_{\mathbf{costs}}$ (USD/Year)	BESS	Reduction (%)
Benchmark case	2,450,204.72	6 (C), 14 (B), 31 (A)	—
BONMIN	2,411,648.34	15 (A), 18 (B), 31 (C)	1.5736
VSA-Convex	2,371,542.06	14 (A), 15 (C), 31 (B)	3.2105

presents the numerical results obtained with our master–slave strategy and the BONMIN solver in the GAMS software when minimizing the energy purchasing and maintenance costs (i.e., $E_{\mathrm{costs}}$).

The numerical results in Table 5 show that

• The GAMS solution of the exact MINLP model with the BONMIN solver found an objective function value of USD/year $2,411,648.34$, which implies a reduction of USD/year $\mathrm{38,556.38}$ with respect to the benchmark case by reallocating all the batteries as follows: the C-type BESS at node 6 was transferred to node 31, the B-type BESS at node 14 was moved to node 18, and the A-type BESS in node 31 was reallocated to node 15;
• The proposed VSA-vortex approach reallocated batteries as follows: the C-type BESS at node 6 was transferred to node 15; the B-type BESS at node 14 was moved to node 31, and the A-type BESS at node 31 was reallocated to node 14. These movements allowed for a reduction of about $3.2104\%$ with respect to the benchmark case, i.e., USD/year $78,662.66$. Note that, regarding the comparison between the BONMIN solution and the VSA-Convex approach, an additional gain of about $40,106.28$ dollars per year of operation is obtained if the latter is implemented;
• As with $E_{\mathrm{loss}}$ minimization, when the annual energy purchasing and maintenance costs of the PV systems are minimized, in all the solutions, node 31 continues to be part of the set of nodes where BESS must be placed. This is also explained by the fact that there is a PV source at this node, and it is necessary to store the energy surplus during the solar hours in order to inject it when the renewable input is zero and the demand increases.

To illustrate the effect of reallocating batteries in the operation of the monopolar DC grid, Figure 3 presents the generation outputs at the terminals of the substation bus for the benchmark case and the solutions reached by the BONMIN and VSA-Convex approaches.

The generation behavior at the terminals of the substation bus depicted in Figure 3 shows that

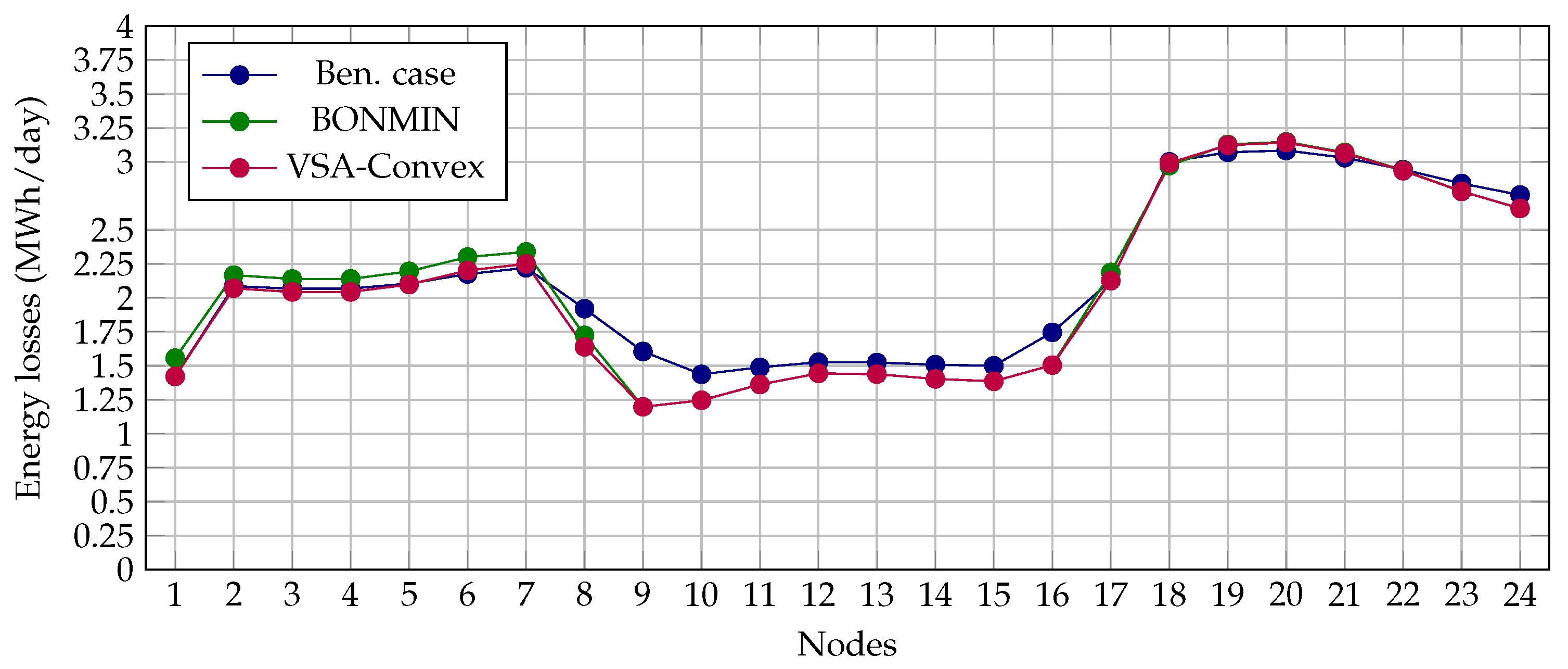
• The benchmark case (i.e., the initial location of the BESS) does not allow efficiently taking advantage of the available renewable energy, given that, when compared to the BONMIN and VSA-Convex solutions, in the period where renewable generation is significant (between hours 7 and 17), there is more generation at the substation bus, which implies that, due to the technical constraint regarding current flows in the distribution branches, less energy can be stored in contrast with that involved in BESS reallocation;
• The final objective function value is directly related to the amount of energy generated at the substation bus, which corresponds to the area of the generation curve in Figure 3. Note that the energy generation in the benchmark case was $51.2530$ MWh/day, whereas the BONMIN solver reports a daily energy generation of $50.4260$ MWh, and the VSA-Convex method generates $49.5730$ MWh/day.

6. Conclusions and Future Works

This research proposed a master–slave optimization methodology to deal with the problem regarding the optimal location reallocation of battery energy storage systems (BESS) in monopolar DC distribution grids. The master stage defined the set of nodes where the BESS must be located or reallocated, along with their corresponding types. In this stage, the discrete version of the vortex search algorithm (VSA) was implemented. To determine the optimal operation of the BESS with the aim of minimizing the costs of energy losses or energy purchasing and maintenance, a recursive convex optimization tool was proposed. The convexification approach was implemented via Taylor’s series expansion applied to the product of two continuous variables, which is equivalent to the McCormick approximation of this product. Numerical results in the monopolar version of the IEEE 33-node grid demonstrated the following:

• The proposed master–slave optimization approach (i.e., the VSA-Convex approach) achieved reductions of about USD/year $3261.8957$ when the objective function was the minimization of the annual energy loss costs. In contrast, the solution of the MINLP model with the BONMIN solver of the GAMS programming environment reached a reduction of about USD/year $3261.8957$. These results imply that the proposed VSA-Convex approach allows finding additional improvements of about USD $532.8047$ per year of operation by redistributing the nodal location of the BESS with high efficiency when compared to the BONMIN solution;
• The minimization of the energy purchasing and maintenance costs confirms that the VSA-Convex approach finds better numerical solutions in comparison with the exact MINLP solution obtained via commercial tools. In this sense, the VSA-Convex approach outperforms the benchmark case by about $3.2105\%$, i.e., USD/year $78,662.66$. In contrast, the BONMIN solver finds an improvement of about $1.5736\%$ (USD/year $\mathrm{38,556.38}$). These results show that, with the proposed master–slave optimization method, the solution of the BONMIN solver was surpassed by more than twice its value, i.e., an additional gain of USD/year $40,106.28$;
• All of the numerical results show that, with the proposed distribution of the PV generation plants, bus 31 of the IEEE 33-bus system is an efficient node to locate BESS. It was observed that, for the BONMIN and the proposed VSA-Convex approaches regarding both objective functions, node 31 was part of the optimal solution, increasing the energy storage capabilities from type A to types B and C. This change in the size of the BESS at this node can be attributed to the fact that this node contains a PV generation system, and, with a BESS on this node, better energy storage properties are provided to the monopolar DC network without causing further energy loss costs due to energy transportation between different nodes.

As future research, the following works can be carried out: (i) proposing a mixed-integer convex model to locate and size BESS in monopolar DC networks while considering different charging and discharging efficiencies and operation cycles, among other important factors; (ii) extending the proposed VSA-Convex model to the optimal location reallocation problem of BESS in AC distribution networks while including a multi-objective optimization analysis; (iii) combining the problem regarding the optimal location reallocation problem of BESS with that of the optimal sizing and operation of renewable energy resources while considering demand and generation uncertainties; and (iv) evaluating the proposed optimization model with multiple demand profiles in order to demonstrate its efficiency and robustness against exact optimization tools for different operation scenarios with uncertainties in generation sources.