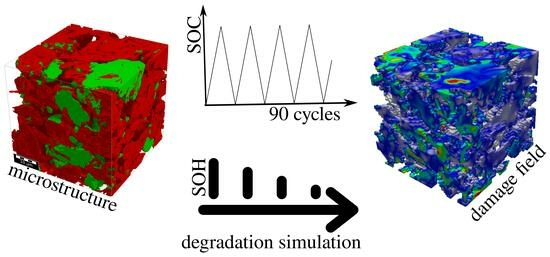
Aging and Homogenized Mechanical Character of Quasi-Statically Charged Gr-Si and NMC Based Electrodes Using Damage Material Modeling
Abstract
:1. Introduction
2. Simulation Approach
2.1. A General Approach for Mechanical Simulation at Continuum Scale
2.2. Mechanical Degradation Model
3. Results
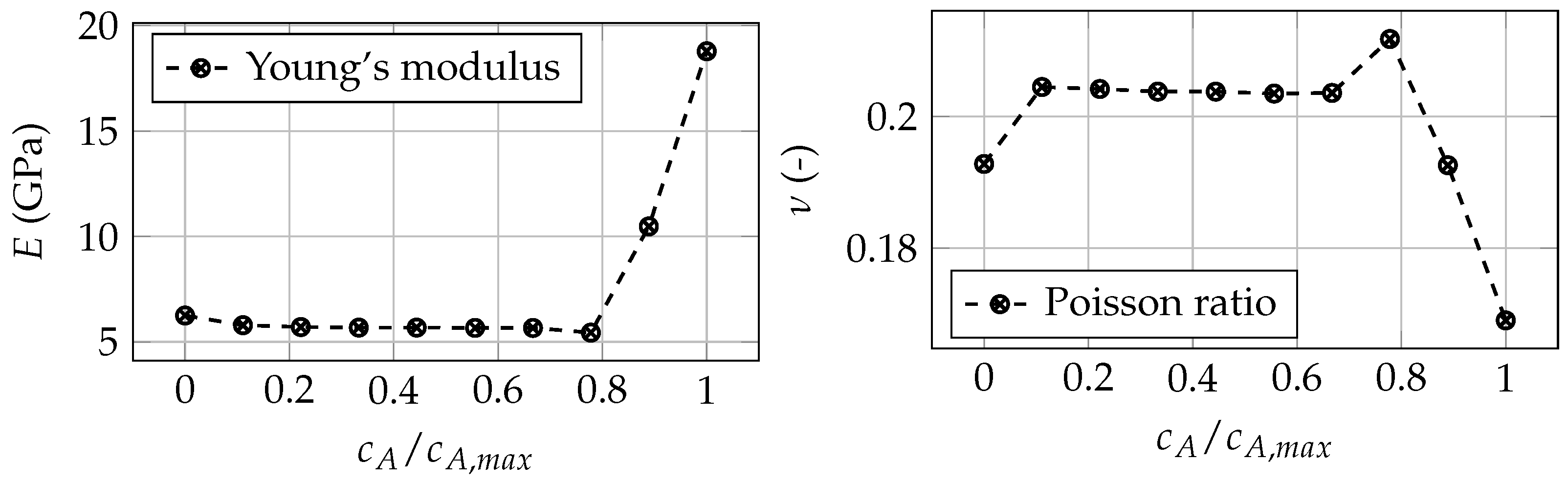
3.1. Anode Mechanical Properties
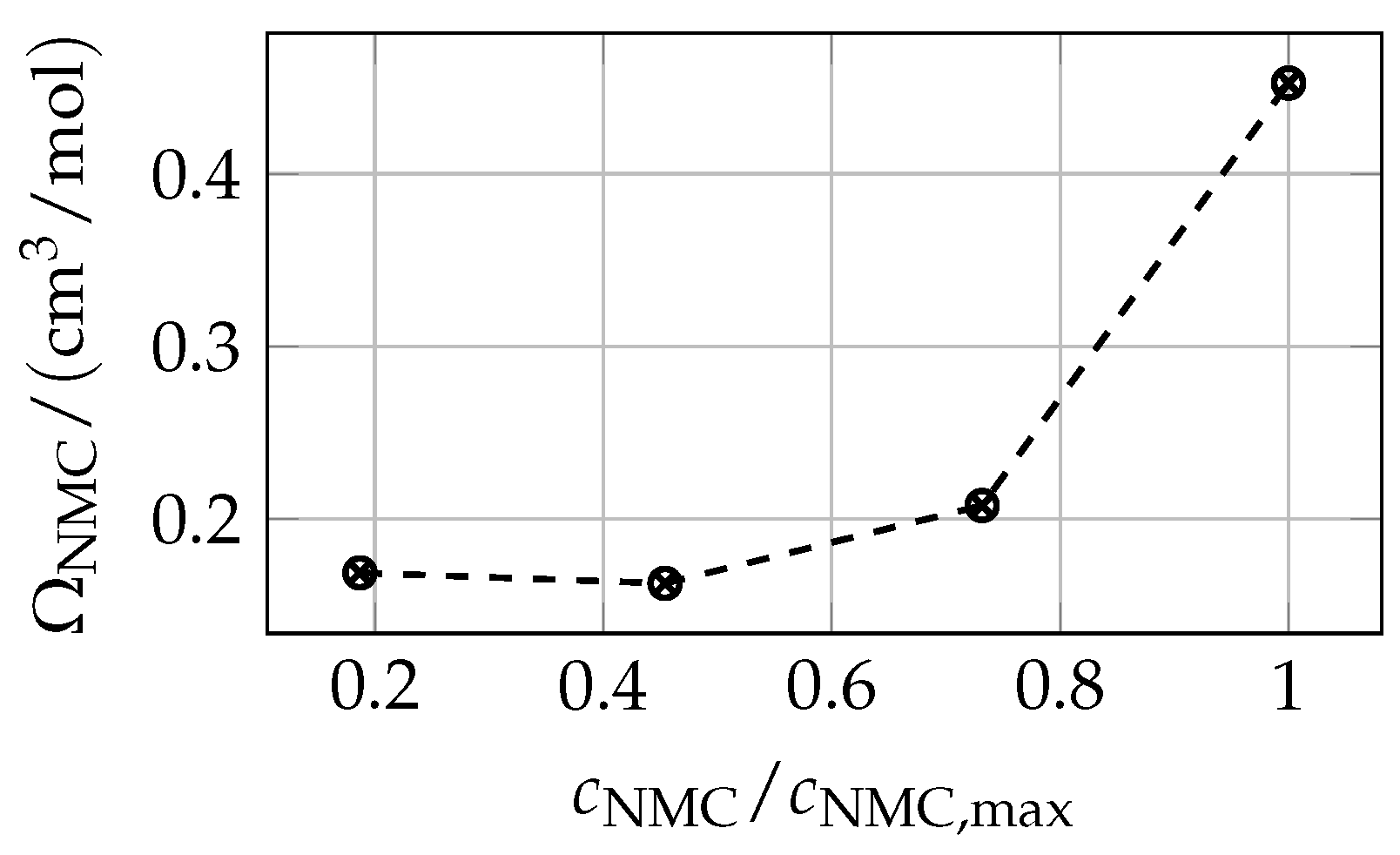
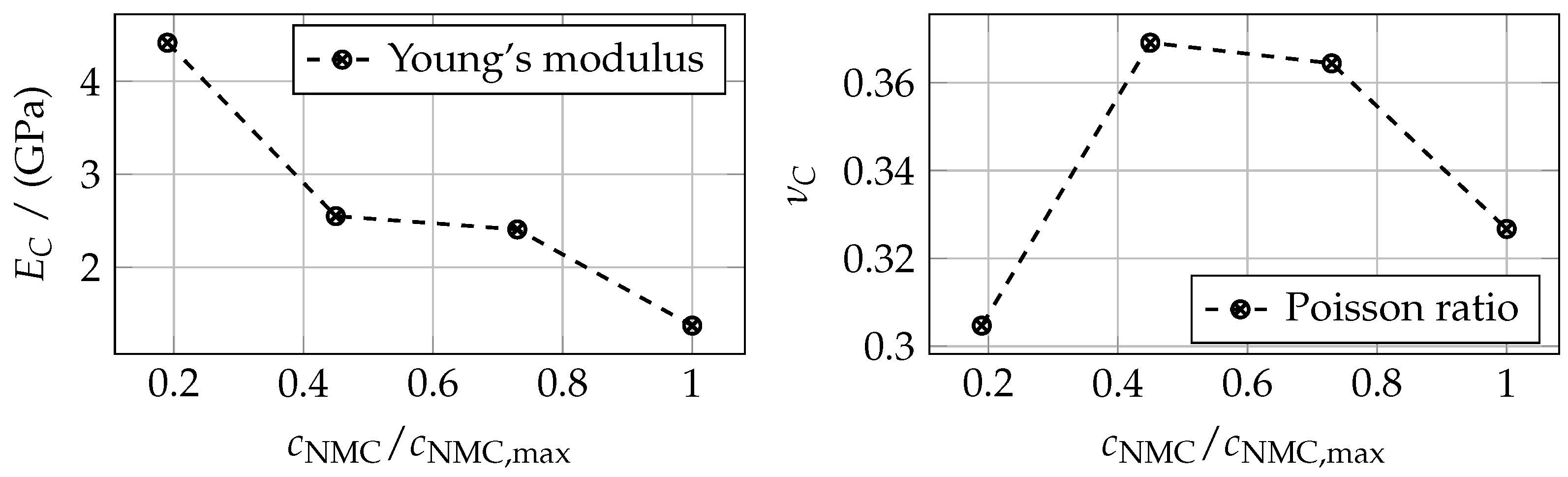
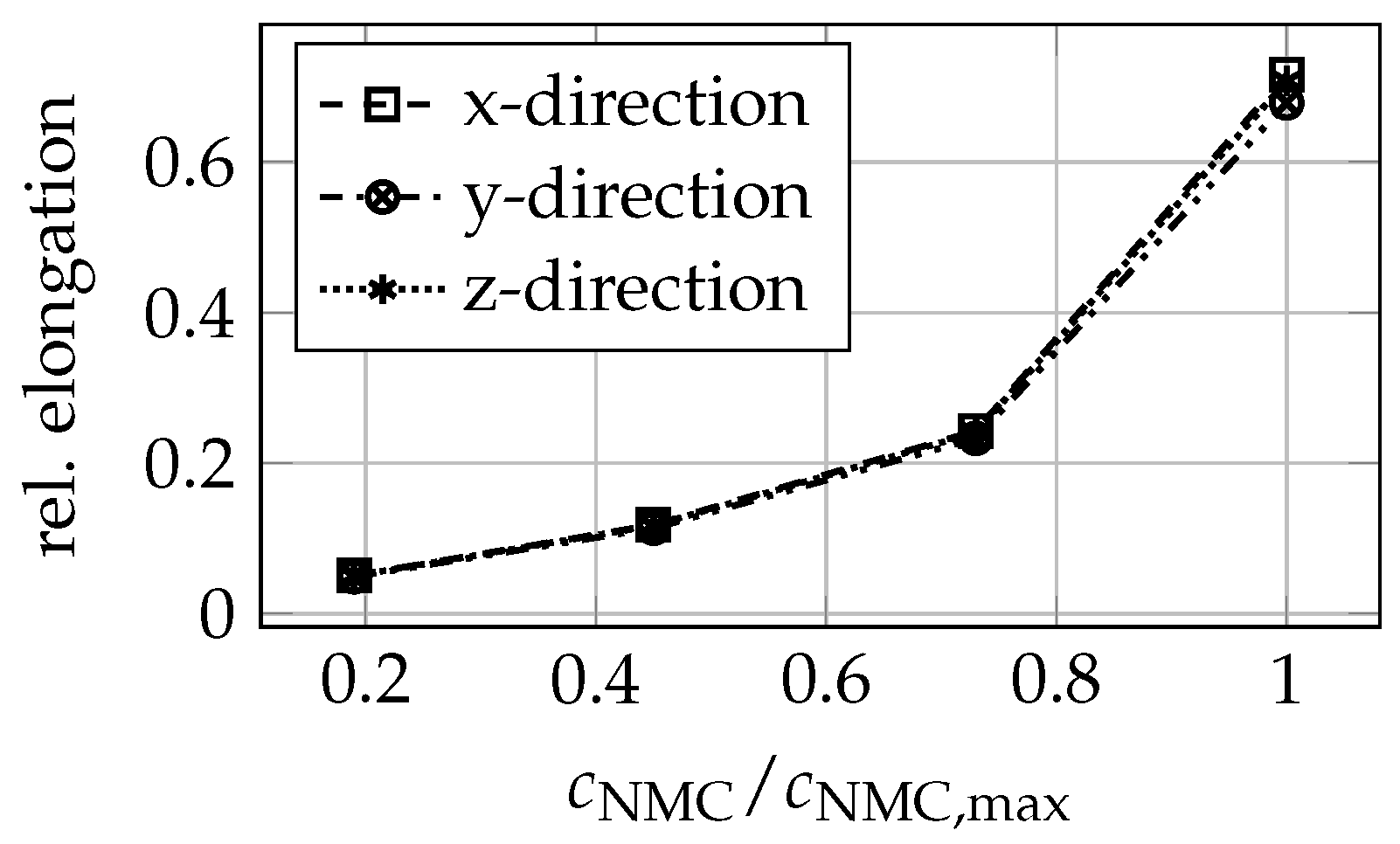
3.2. Cathode Mechanical Properties
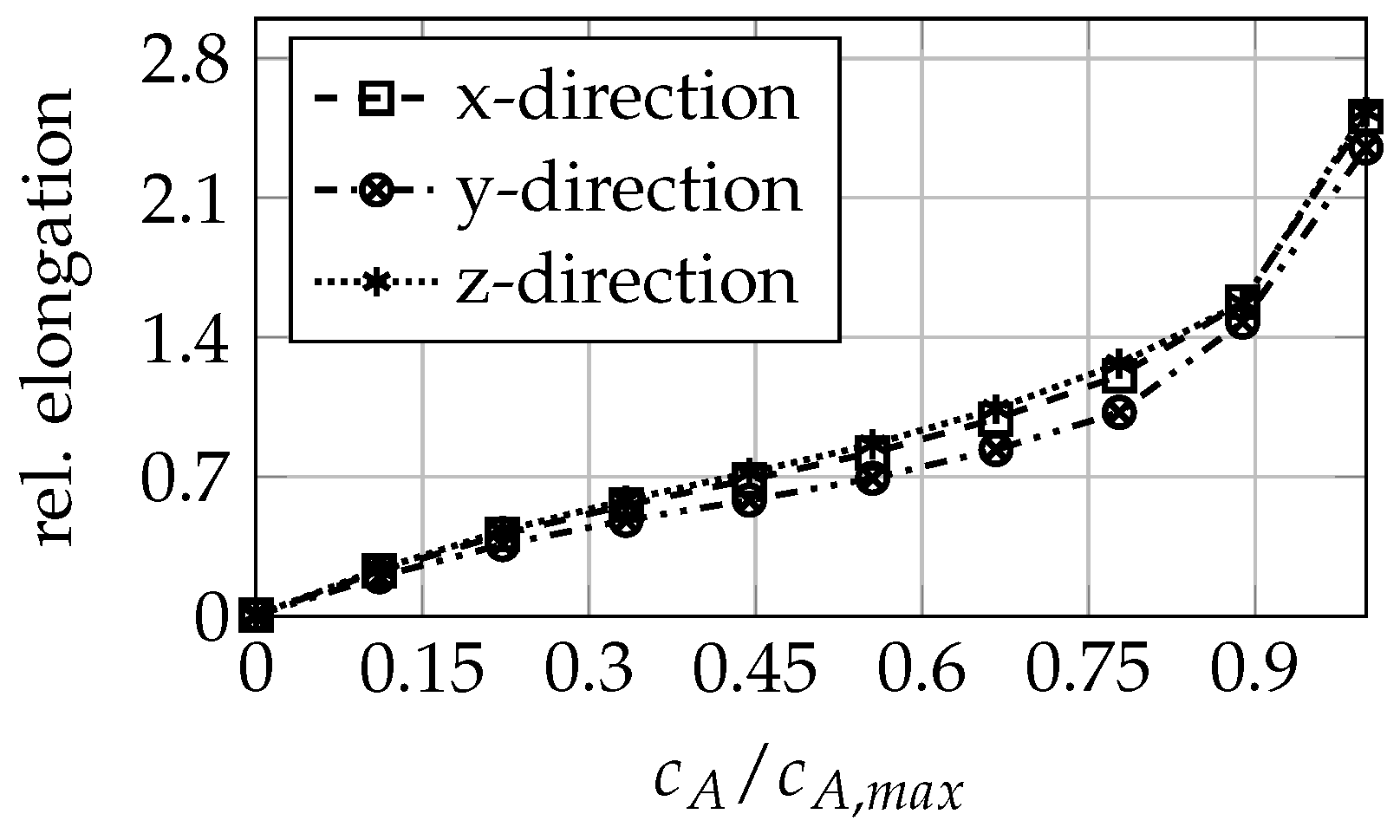
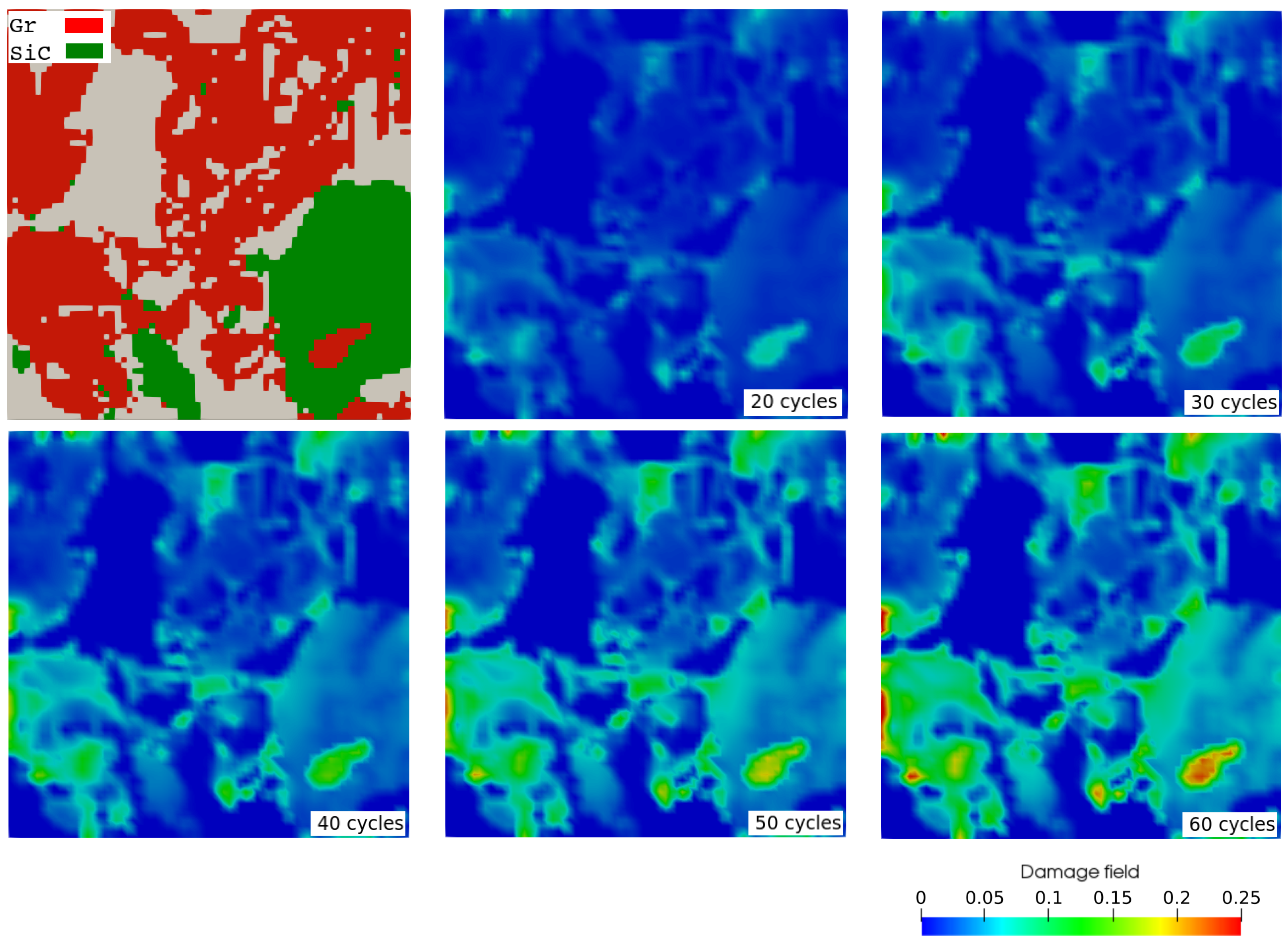
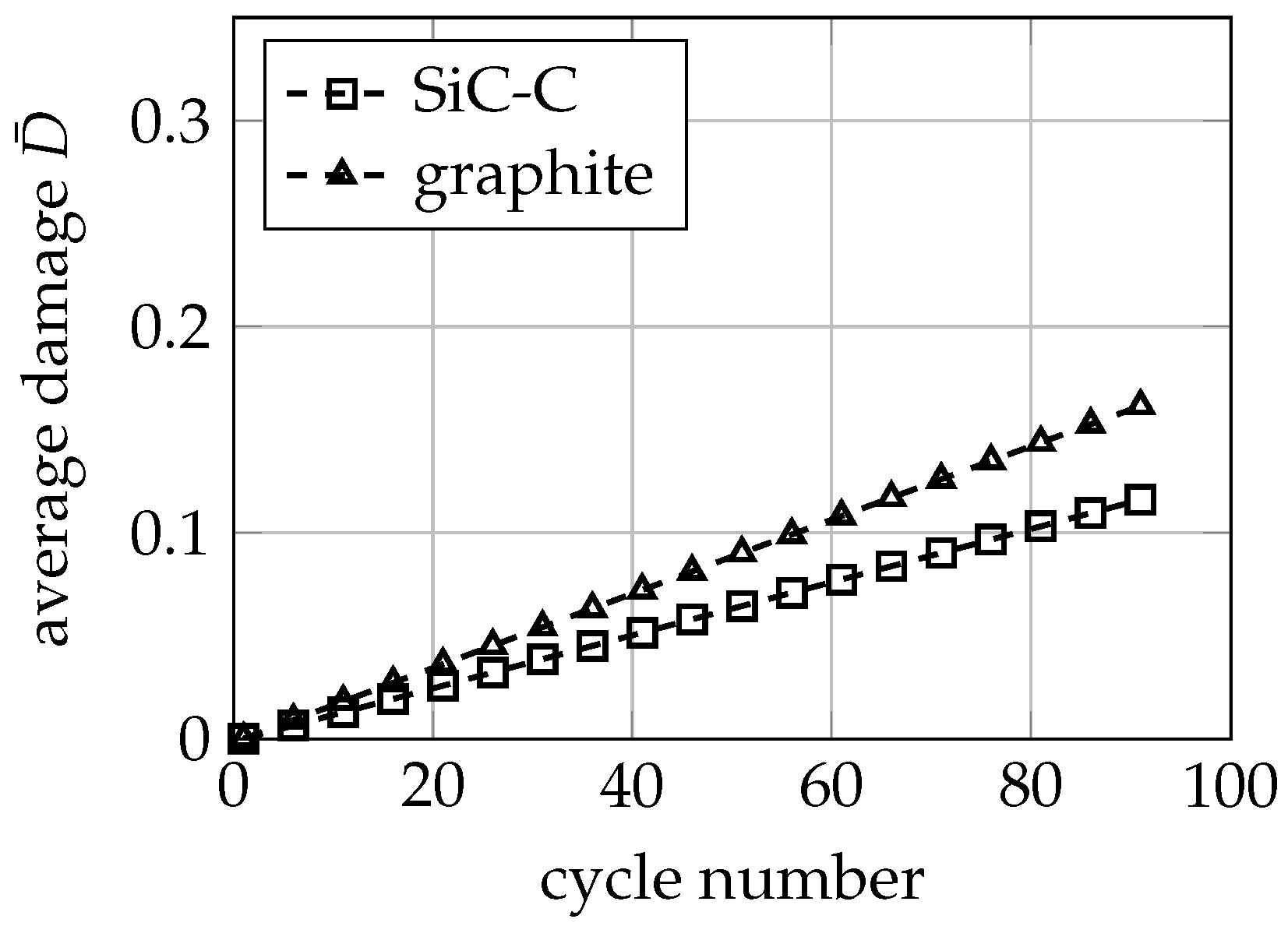
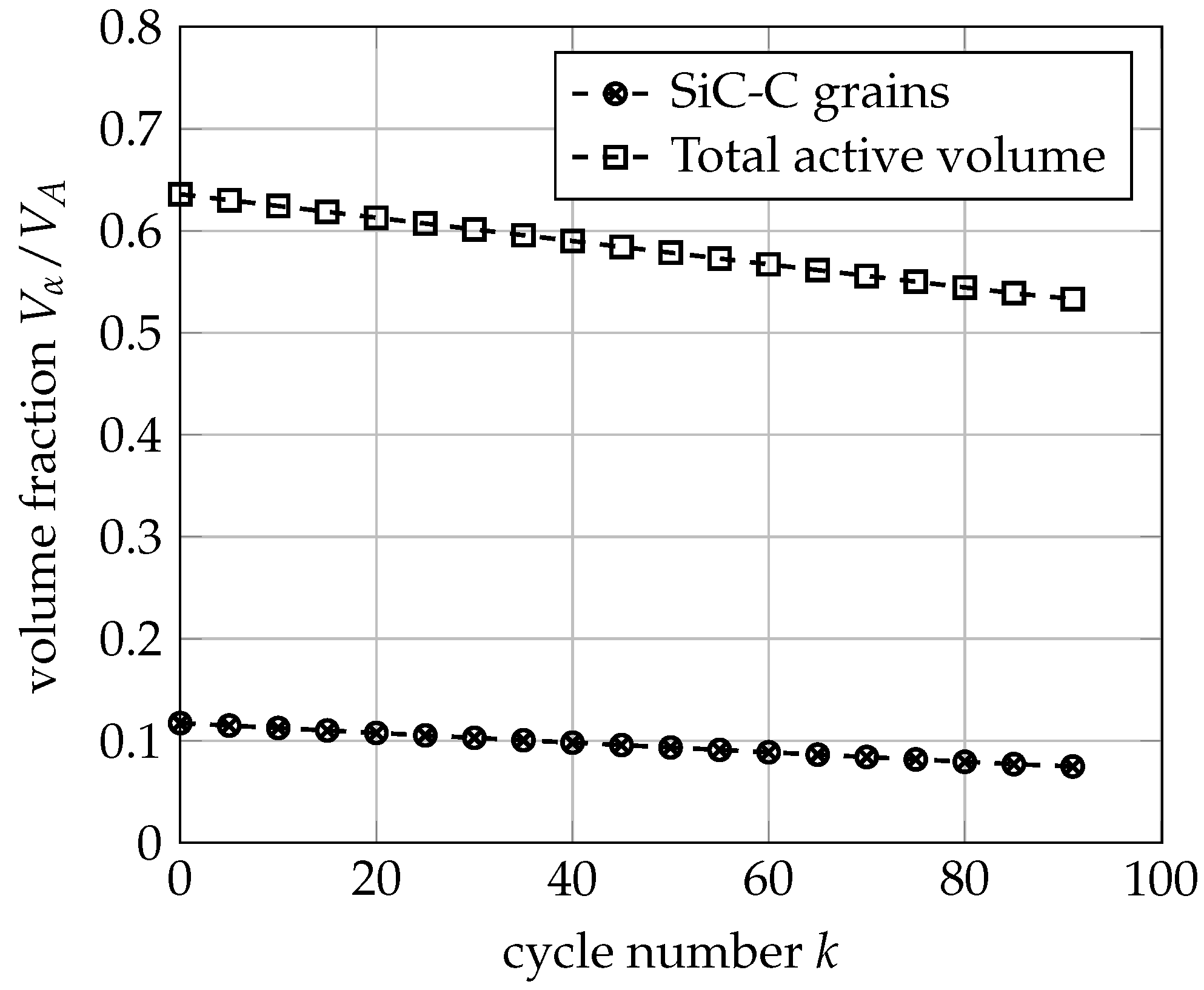
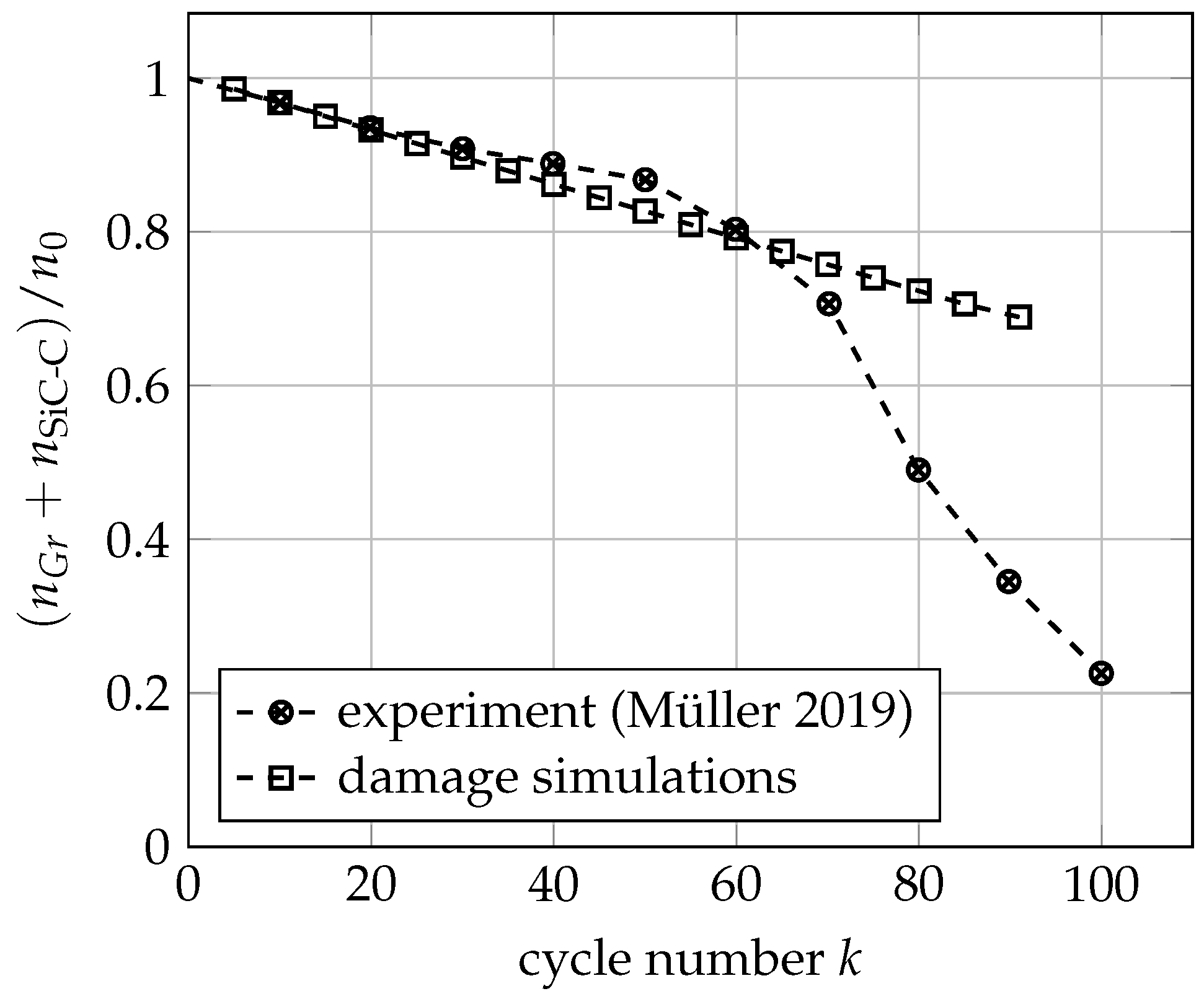
3.3. Mechanical Ageing Simulations for Gr-SiC-C Anode at Electrode Level
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BC | Boundary conditions |
| OCV | Open circuit voltage |
| SiC-C | Silicon carbon composite |
| SOC | State of Charge (of particular species) |
| FIB-SEM | Focused Ion Beam Scanning Electron Microscopy |
| DEFACTO | Battery Design and Manufacturing Optimization Project |
| p4d | Pseudo 4-Dimensional battery model |
Appendix A. Dependence of Elastic Moduli on State of Charge
| 0.01 | 0.11 | 0.22 | 0.32 | 0.43 | 0.48 | 0.58 | 0.69 | 0.79 | 1.0 | |
|---|---|---|---|---|---|---|---|---|---|---|
| K (GPa) | 81.17 | 67.58 | 54.43 | 44.16 | 35.98 | 36.10 | 36.30 | 34.10 | 31.86 | 31.11 |
| G (GPa) | 60 | 47.9 | 35.5 | 32.95 | 31.9 | 31.98 | 31.73 | 29.40 | 27.76 | 26.14 |
| 0.19 | 0.45 | 0.73 | 1 | |
|---|---|---|---|---|
| E (GPa) | 145.10 | 82.95 | 77.23 | 37.64 |
| (-) | 0.299 | 0.30 | 0.299 | 0.301 |
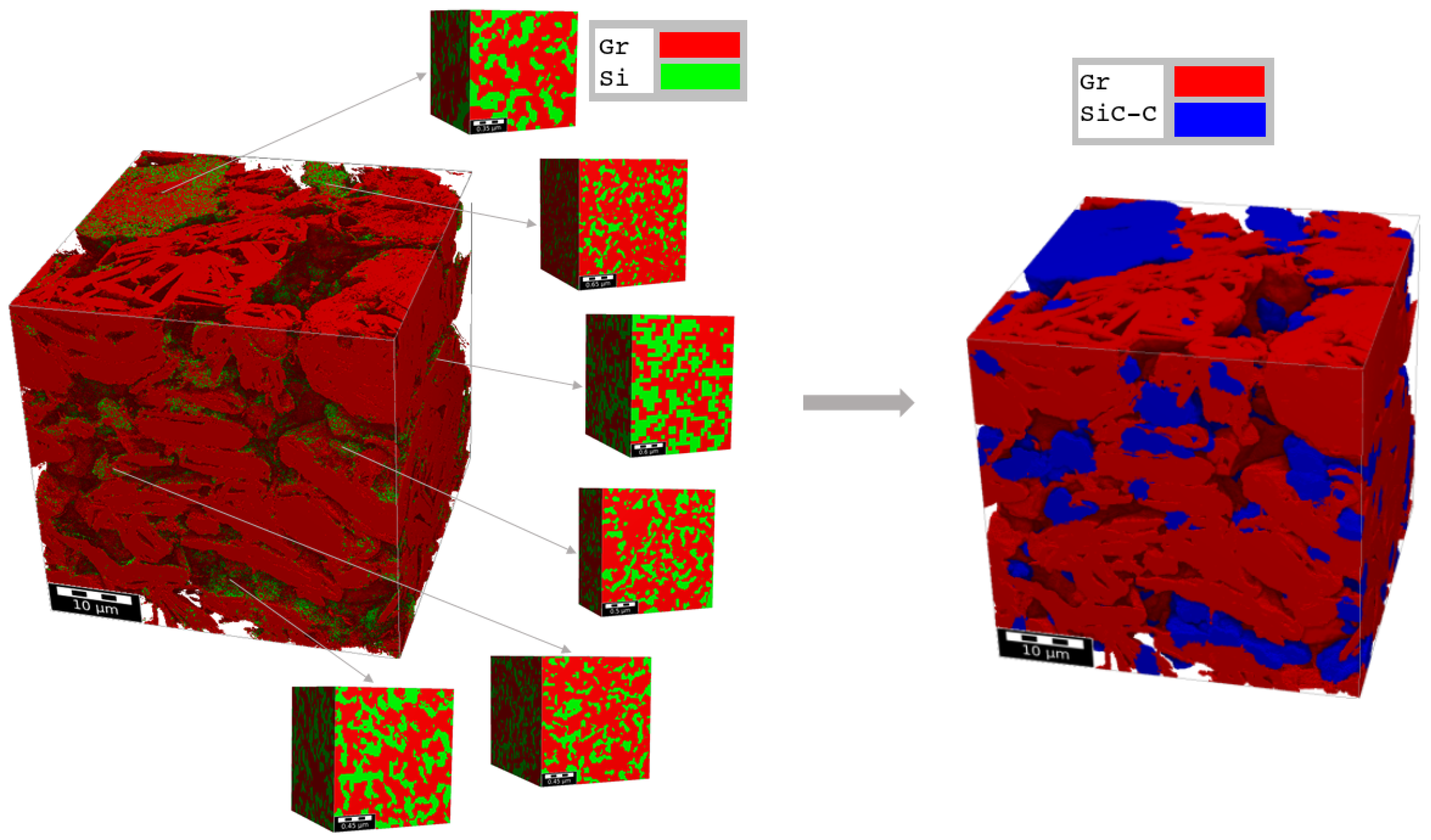
Appendix B. Selection of SiC-C Realizations

References
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Lee, Y.K.; Song, J.; Park, J. Multi-scale coupled mechanical-electrochemical modeling for study on stress generation and its impact on multi-layered electrodes in lithium-ion batteries. Electrochim. Acta 2021, 389, 138682. [Google Scholar] [CrossRef]
- Arora, P.; White, R.E.; Doyle, M. Capacity fade mechanisms and side reactions in lithium-ion batteries. J. Electrochem. Soc. 1998, 145, 3647. [Google Scholar] [CrossRef]
- Vetter, J.; Novák, P.; Wagner, M.R.; Veit, C.; Möller, K.C.; Besenhard, J.; Winter, M.; Wohlfahrt-Mehrens, M.; Vogler, C.; Hammouche, A. Ageing mechanisms in lithium-ion batteries. J. Power Sources 2005, 147, 269–281. [Google Scholar] [CrossRef]
- Zhang, W.J. Lithium insertion/extraction mechanism in alloy anodes for lithium-ion batteries. J. Power Sources 2011, 196, 877–885. [Google Scholar] [CrossRef]
- Luo, F.; Liu, B.; Zheng, J.; Chu, G.; Zhong, K.; Li, H.; Huang, X.; Chen, L. Nano-silicon/carbon composite anode materials towards practical application for next generation Li-ion batteries. J. Electrochem. Soc. 2015, 162, A2509. [Google Scholar] [CrossRef]
- McDowell, M.T.; Lee, S.W.; Nix, W.D.; Cui, Y. 25th anniversary article: Understanding the lithiation of silicon and other alloying anodes for lithium-ion batteries. Adv. Mater. 2013, 25, 4966–4985. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.Y.; Zhao, M.; Hoster, H.E. Suppressing vertical displacement of lithiated silicon particles in high volumetric capacity battery electrodes. ChemElectroChem 2015, 2, 1090–1095. [Google Scholar] [CrossRef]
- Beaulieu, L.; Hatchard, T.; Bonakdarpour, A.; Fleischauer, M.; Dahn, J. Reaction of Li with alloy thin films studied by in situ AFM. J. Electrochem. Soc. 2003, 150, A1457. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Zheng, J.; Zheng, H.; Mei, Z.; Du, X.; Li, H. Electrochemical performances and volume variation of nano-textured silicon thin films as anodes for lithium-ion batteries. Nanotechnology 2013, 24, 424011. [Google Scholar] [CrossRef]
- Louli, A.; Ellis, L.; Dahn, J. Operando pressure measurements reveal solid electrolyte interphase growth to rank Li-ion cell performance. Joule 2019, 3, 745–761. [Google Scholar] [CrossRef]
- Yoon, T.; Nguyen, C.C.; Seo, D.M.; Lucht, B.L. Capacity fading mechanisms of silicon nanoparticle negative electrodes for lithium ion batteries. J. Electrochem. Soc. 2015, 162, A2325. [Google Scholar] [CrossRef]
- Wetjen, M.; Pritzl, D.; Jung, R.; Solchenbach, S.; Ghadimi, R.; Gasteiger, H.A. Differentiating the degradation phenomena in silicon-graphite electrodes for lithium-ion batteries. J. Electrochem. Soc. 2017, 164, A2840. [Google Scholar] [CrossRef]
- Liu, W.; Oh, P.; Liu, X.; Lee, M.J.; Cho, W.; Chae, S.; Kim, Y.; Cho, J. Nickel-rich layered lithium transition-metal oxide for high-energy lithium-ion batteries. Angew. Chem. Int. Ed. 2015, 54, 4440–4457. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.K.; Myung, S.T.; Park, B.C.; Prakash, J.; Belharouak, I.; Amine, K. High-energy cathode material for long-life and safe lithium batteries. Nat. Mater. 2009, 8, 320–324. [Google Scholar] [CrossRef]
- Armand, M.; Tarascon, J.M. Building better batteries. Nature 2008, 451, 652–657. [Google Scholar] [CrossRef]
- Manthiram, A.; Knight, J.C.; Myung, S.T.; Oh, S.M.; Sun, Y.K. Nickel-rich and lithium-rich layered oxide cathodes: Progress and perspectives. Adv. Energy Mater. 2016, 6, 1501010. [Google Scholar] [CrossRef]
- Kim, H.; Kim, M.G.; Jeong, H.Y.; Nam, H.; Cho, J. A new coating method for alleviating surface degradation of LiNi0.6Co0.2Mn0.2O2 cathode material: Nanoscale surface treatment of primary particles. Nano Lett. 2015, 15, 2111–2119. [Google Scholar] [CrossRef]
- Song, B.; Sui, T.; Ying, S.; Li, L.; Lu, L.; Korsunsky, A.M. Nano-structural changes in Li-ion battery cathodes during cycling revealed by FIB-SEM serial sectioning tomography. J. Mater. Chem. 2015, 3, 18171–18179. [Google Scholar] [CrossRef]
- Du, R.; Bi, Y.; Yang, W.; Peng, Z.; Liu, M.; Liu, Y.; Wu, B.; Yang, B.; Ding, F.; Wang, D. Improved cyclic stability of LiNi0.8Co0.1Mn0.1O2 via Ti substitution with a cut-off potential of 4.5 V. Ceram. Int. 2015, 41, 7133–7139. [Google Scholar] [CrossRef]
- Lim, B.B.; Myung, S.T.; Yoon, C.S.; Sun, Y.K. Comparative study of Ni-rich layered cathodes for rechargeable lithium batteries: Li [Ni0.85Co0.11Al0.04] O2 and Li [Ni0.84Co0.06Mn0.09Al0.01] O2 with two-step full concentration gradients. ACS Energy Lett. 2016, 1, 283–289. [Google Scholar] [CrossRef]
- Miller, D.J.; Proff, C.; Wen, J.; Abraham, D.P.; Bareño, J. Observation of microstructural evolution in Li battery cathode oxide particles by in situ electron microscopy. Adv. Energy Mater. 2013, 3, 1098–1103. [Google Scholar] [CrossRef]
- Pietsch, P.; Westhoff, D.; Feinauer, J.; Eller, J.; Marone, F.; Stampanoni, M.; Schmidt, V.; Wood, V. Quantifying microstructural dynamics and electrochemical activity of graphite and silicon-graphite lithium ion battery anodes. Nat. Commun. 2016, 7, 12909. [Google Scholar] [CrossRef] [PubMed]
- Müller, S.; Pietsch, P.; Brandt, B.E.; Baade, P.; De Andrade, V.; De Carlo, F.; Wood, V. Quantification and modeling of mechanical degradation in lithium-ion batteries based on nanoscale imaging. Nat. Commun. 2018, 9, 2340. [Google Scholar] [CrossRef] [PubMed]
- Lagadec, M.F.; Zahn, R.; Wood, V. Designing polyolefin separators to minimize the impact of local compressive stresses on lithium ion battery performance. J. Electrochem. Soc. 2018, 165, A1829. [Google Scholar] [CrossRef]
- Müller, V.; Scurtu, R.G.; Richter, K.; Waldmann, T.; Memm, M.; Danzer, M.A.; Wohlfahrt-Mehrens, M. Effects of mechanical compression on the aging and the expansion behavior of Si/C-composite| NMC811 in different lithium-ion battery cell formats. J. Electrochem. Soc. 2019, 166, A3796. [Google Scholar] [CrossRef]
- Lim, J.M.; Kim, H.; Cho, K.; Cho, M. Fundamental mechanisms of fracture and its suppression in Ni-rich layered cathodes: Mechanics-based multiscale approaches. Extrem. Mech. Lett. 2018, 22, 98–105. [Google Scholar] [CrossRef]
- Wenzler, N.; Rief, S.; Linden, S.; Biebl, F.; Rütsche, S.; Glatt, I.; Streit, A.; Zahn, R.; Fingerle, M.; Wood, V. 3D Electrochemical-Mechanical Battery Simulation Tool: Implementation with Full Cell Simulations and Verification with Operando X-ray Tomography. J. Electrochem. Soc. 2023, 170, 020511. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. A mathematical model of stress generation and fracture in lithium manganese oxide. J. Electrochem. Soc. 2006, 153, A1019. [Google Scholar] [CrossRef]
- Zhang, X.; Shyy, W.; Sastry, A.M. Numerical simulation of intercalation-induced stress in Li-ion battery electrode particles. J. Electrochem. Soc. 2007, 154, A910. [Google Scholar] [CrossRef]
- Fraunhofer Institute for Industrial Mathematics ITWM. The Battery and Electrochemistry Simulation Tool BEST. Available online: https://itwm.fraunhofer.de/best (accessed on 1 November 2023).
- Latz, A.; Zausch, J. Multiscale modeling of lithium ion batteries: Thermal aspects. Beilstein J. Nanotechnol. 2015, 6, 987–1007. [Google Scholar] [CrossRef] [PubMed]
- Ciria Aylagas, R.; Ganuza, C.; Parra, R.; Yañez, M.; Ayerbe, E. cideMOD: An Open Source Tool for Battery Cell Inhomogeneous Performance Understanding. J. Electrochem. Soc. 2022, 169, 090528. [Google Scholar] [CrossRef]
- Golmon, S.; Maute, K.; Dunn, M.L. Numerical modeling of electrochemical–mechanical interactions in lithium polymer batteries. Comput. Struct. 2009, 87, 1567–1579. [Google Scholar] [CrossRef]
- Wu, B.; Lu, W. A battery model that fully couples mechanics and electrochemistry at both particle and electrode levels by incorporation of particle interaction. J. Power Sources 2017, 360, 360–372. [Google Scholar] [CrossRef]
- Wu, B.; Lu, W. A consistently coupled multiscale mechanical–electrochemical battery model with particle interaction and its validation. J. Mech. Phys. Solids 2019, 125, 89–111. [Google Scholar] [CrossRef]
- Wu, L.; Xiao, X.; Wen, Y.; Zhang, J. Three-dimensional finite element study on stress generation in synchrotron X-ray tomography reconstructed nickel-manganese-cobalt based half cell. J. Power Sources 2016, 336, 8–18. [Google Scholar] [CrossRef]
- Mendoza, H.; Roberts, S.A.; Brunini, V.E.; Grillet, A.M. Mechanical and electrochemical response of a LiCoO2 cathode using reconstructed microstructures. Electrochim. Acta 2016, 190, 1–15. [Google Scholar] [CrossRef]
- Xu, R.; Yang, Y.; Yin, F.; Liu, P.; Cloetens, P.; Liu, Y.; Lin, F.; Zhao, K. Heterogeneous damage in Li-ion batteries: Experimental analysis and theoretical modeling. J. Mech. Phys. Solids 2019, 129, 160–183. [Google Scholar] [CrossRef]
- Hofmann, T.; Westhoff, D.; Feinauer, J.; Andrä, H.; Zausch, J.; Schmidt, V.; Müller, R. Electro-chemo-mechanical simulation for lithium ion batteries across the scales. Int. J. Solids Struct. 2020, 184, 24–39. [Google Scholar] [CrossRef]
- Schneider, M.; Ospald, F.; Kabel, M. Computational homogenization of elasticity on a staggered grid. Int. J. Numer. Methods Eng. 2016, 105, 693–720. [Google Scholar] [CrossRef]
- Kabel, M.; Fliegener, S.; Schneider, M. Mixed boundary conditions for FFT-based homogenization at finite strains. Comput. Mech. 2016, 57, 193–210. [Google Scholar] [CrossRef]
- Grimm-Strele, H.; Kabel, M. FFT-based homogenization with mixed uniform boundary conditions. Int. J. Numer. Methods Eng. 2021, 122, 7241–7265. [Google Scholar] [CrossRef]
- Grimm-Strele, H.; Kabel, M. Runtime optimization of a memory efficient CG solver for FFT-based homogenization: Implementation details and scaling results for linear elasticity. Comput. Mech. 2019, 64, 1339–1345. [Google Scholar] [CrossRef]
- Lory, P.F.; Mathieu, B.; Genies, S.; Reynier, Y.; Boulineau, A.; Hong, W.; Chandesris, M. Probing Silicon Lithiation in Silicon-Carbon Blended Anodes with a Multi-Scale Porous Electrode Model. J. Electrochem. Soc. 2020, 167, 120506. [Google Scholar] [CrossRef]
- Mazars, J.; Pijaudier-Cabot, G. Continuum damage theory—Application to concrete. J. Eng. Mech. 1989, 115, 345–365. [Google Scholar] [CrossRef]
- Mazars, J.; Hamon, F.; Grange, S. A new 3D damage model for concrete under monotonic, cyclic and dynamic loadings. Mater. Struct. 2015, 48, 3779–3793. [Google Scholar] [CrossRef]
- Mathieu, B.; Gerard, M.; Daniel, L.; Boulineau, A. WP 2: Periodic Technical Report—Part B; Technical Report; The French Alternative Energies and Atomic Energy Commission (CEA): Grenoble, France, 2022. [Google Scholar]
- DEFACTO—Battery Design and Manufacturing Optimization through Multiphysics Modelling. Battery Design and Manufacturing Optimization Project. Funded by the European Union through Horizon 2020. Available online: https://defacto-project.eu (accessed on 1 November 2023).
- He, Y.L.; Hu, H.; Song, Y.C.; Guo, Z.S.; Liu, C.; Zhang, J.Q. Effects of concentration-dependent elastic modulus on the diffusion of lithium ions and diffusion induced stress in layered battery electrodes. J. Power Sources 2014, 248, 517–523. [Google Scholar] [CrossRef]
- Mutter, D.; Mayrhofer, L.; Poudel, M. Atomistic Simulations for Silicon at Different Lithiation States; Technical Report; IWM Fraunhofer: Freiburg im Breisgau, Germany, 2022. [Google Scholar]
- Mishra, A. WP 5: Periodic Technical Report—Part B; Technical Report; Avesta Battery and Energy Engineering (ABEE): Brussels, Belgium, 2023. [Google Scholar]
- Math2Market GmbH. MaterialDataBase Included in GeoDict2023. Available online: https://www.math2market.com (accessed on 1 November 2023).
- Li, J.; Downie, L.E.; Ma, L.; Qiu, W.; Dahn, J.R. Study of the Failure Mechanisms of LiNi0.8Mn0.1Co0.1O2 Cathode Material for Lithium Ion Batteries. J. Electrochem. Soc. 2015, 162, A1401. [Google Scholar] [CrossRef]
- Hwang, S.; Kim, S.M.; Bak, S.M.; Chung, K.Y.; Chang, W. Investigating the Reversibility of Structural Modifications of LixNiyMnzCo1-y-zO2 Cathode Materials during Initial Charge/Discharge, at Multiple Length Scales. Chem. Mater. 2015, 27, 6044–6052. [Google Scholar] [CrossRef]
- Ghanty, C.; Markovsky, B.; Erickson, E.M.; Talianker, M.; Haik, O.; Tal-Yossef, Y.; Mor, A.; Aurbach, D.; Lampert, J.; Volkov, A.; et al. Li-ion Extraction/Insertion of Ni-Rich Electrodes: In Situ XRD and Raman Spectroscopy Study. ChemElectroChem 2015, 2, 1406. [Google Scholar] [CrossRef]
- Rieger, B.; Erhard, S.V.; Rumpf, K.; Jossen, A. A New Method to Model the Thickness Change of a Commercial Pouch Cell during Discharge. J. Electrochem. Soc. 2016, 163, A1566–A1575. [Google Scholar] [CrossRef]
- Latz, A.; Zausch, J. Thermodynamic consistent transport theory of Li-ion batteries. J. Power Sources 2011, 196, 3296–3302. [Google Scholar] [CrossRef]


| SOC% | 0 | 11 | 19 | 29 | 38 | 47 | 57 | 66 | 82 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.1 | 0.1939 | 0.2860 | 0.3790 | 0.4720 | 0.5660 | 0.6630 | 0.8199 | 1.0 | |
| 0 | 0.071 | 0.086 | 0.094 | 0.102 | 0.110 | 0.145 | 0.2168 | 0.5108 | 0.9711 | |
| /GPa | 52.96 | 46.95 | 42.617 | 41.368 | 41.368 | 40.749 | 40.6603 | 39.882 | 38.0337 | 91.0 |
| 0.272 | 0.308 | 0.3159 | 0.3085 | 0.3085 | 0.3012 | 0.30239 | 0.3031 | 0.3299 | 0.22 |
| 62.67 | 27.58 | 27.39 | 27.38 | 62.82 | 61.12 | 18.0 | 18.01 | 18.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, S.; Zausch, J.; Grimm-Strele, H.; Kabel, M. Aging and Homogenized Mechanical Character of Quasi-Statically Charged Gr-Si and NMC Based Electrodes Using Damage Material Modeling. Batteries 2023, 9, 582. https://doi.org/10.3390/batteries9120582
Ahmed S, Zausch J, Grimm-Strele H, Kabel M. Aging and Homogenized Mechanical Character of Quasi-Statically Charged Gr-Si and NMC Based Electrodes Using Damage Material Modeling. Batteries. 2023; 9(12):582. https://doi.org/10.3390/batteries9120582
Chicago/Turabian StyleAhmed, Shahbaz, Jochen Zausch, Hannes Grimm-Strele, and Matthias Kabel. 2023. "Aging and Homogenized Mechanical Character of Quasi-Statically Charged Gr-Si and NMC Based Electrodes Using Damage Material Modeling" Batteries 9, no. 12: 582. https://doi.org/10.3390/batteries9120582
APA StyleAhmed, S., Zausch, J., Grimm-Strele, H., & Kabel, M. (2023). Aging and Homogenized Mechanical Character of Quasi-Statically Charged Gr-Si and NMC Based Electrodes Using Damage Material Modeling. Batteries, 9(12), 582. https://doi.org/10.3390/batteries9120582