Abstract
Electrolytes containing multiple redox couples are promising for improving the energy density of flow batteries. Here, two chelated chromium complexes that are structural isomers are characterized and combined to generate electrolytes containing up to 2 M of active species, corresponding to 53.6 Ah L−1. The mixed isomer approach enables a significantly higher active material content than the individual materials would allow, affording energy dense cells with Coulombic efficiencies of ≥99.6% at 100 mA cm−2 and an open circuit voltage of 1.65 V at 50% state-of-charge. This high concentration, however, comes with a caveat; at a given concentration, an equimolar mixed electrolyte leads to lower voltage efficiency compared to using the individual isomers, while Coulombic efficiency remains constant. Our work demonstrates that exploiting structural isomerism is an efficient approach to improve capacity, but active materials must be selected carefully in mixed systems as differences in operating potentials negatively affect energy efficiency.
1. Introduction
Redox flow batteries (RFBs) can competitively provide grid-scale energy storage, a key enabler of future power grids primarily relying on renewables. RFBs decouple power and energy elements by storing energy in easily scalable liquid electrolytes instead of solid electrodes like alternative battery technologies such as lithium-ion batteries [1,2]. The low energy density of RFB electrolytes, however, is often considered a major drawback of the technology and primarily depends on the solubility and number of electrons stored per active species. Since electroactive species’ solubility is often a limiting factor, recent efforts in RFB development have focused on materials that can undergo multi-electron processes to increase the number of electrons stored per mol of active species [3,4,5]. However, Neyhouse et al. posited that disparate reduction potentials of active materials in the electrolyte degrade cell performance, specifically by reducing the voltage efficiency [6]. This significantly diminishes the design space available to develop new active materials. Candidate materials not only need to fulfill the classical requirements of reversibility and high solubility, stability, and suitable operating potentials, but also concerted electron transfers, which often require a structural change, such as the addition of a proton or a bond [7]. Quinones are promising examples of such multi-redox electrolytes that undergo proton-coupled electron transfers [8]. Another approach for increasing energy density is to mix two or more active materials with similar redox potentials. Penn et al. used this approach to mix a ternary benzoquinone eutectic mixture with a binary naphthoquinone eutectic mixture to increase the energy density of flow battery electrolytes [9].
Here, we explore transition metal chelates, a tunable class of highly performant materials for near-neutral pH flow batteries [10,11,12]. Chelation can significantly shift the reduction potential of the metal cation, improve solubility across a wide pH range, and enhance redox kinetics [12]. The well-informed choice of the chelating ligand further enables the control of the chelates’ electrochemical properties, making such materials an excellent platform to study the impact of disparate reduction potentials in electrolytes that contain multiple active species. 1,3-propylenediaminetetraacetic acid (1,3-PDTA), for example, affords a highly reducing negative electrolyte (negolyte) material when chelated to chromium (−1.35 V vs. SCE) [13]. Employing a ligand with a shorter backbone such as ethylenediaminetetraacetic acid (EDTA) results in a Cr chelate with a 115 mV less reducing reduction potential [13]. Here, we focus on a structural isomer of 1,3-PDTA that contains a stereocenter in the ligand backbone, 1,2-propylenediaminetetraacetic acid (1,2-PDTA). Analogous to EDTA, the shorter backbone of 1,2-PDTA results in a less reducing redox potential than 1,3-PDTA [13]. This not only allows for studying the effect of the backbone geometry and the presence of a stereocenter on the electroactive species’ solubility and kinetics, but also how a potential difference of only approximately 100 mV in a two-component electrolyte affects cell performance, specifically voltage efficiency.
2. Materials and Methods
2.1. Materials
Potassium ferricyanide (K3Fe(CN)6), potassium ferrocyanide (K4Fe(CN)6), potassium hydroxide (KOH), 1,2-propylenediaminetetraacetic acid (1,2-PDTA), 1,3-propylenediaminetetraacetic acid (1,3-PDTA), chromium potassium sulfate (KCr(SO4)2), and potassium tetraborate (K2B4O7) were purchased from Alfa Aesar or Acros and used as received.
Preparation of KCr(1,2-PDTA): Procedure modified from literature [12]. Briefly, H41,2-PDTA (100 g, 0.33 mol) and KCr(SO4)2 (144.3 g, 0.28 mol) were added to 250 mL of DI water and then stirred at reflux for 16 h. The reaction was cooled to 70 °C and 5 M KOH was added to adjust the pH between 4 and 6. The solution was then refluxed for 16 h before cooling to 70 °C and readjusting the pH with 5 M KOH. This process was repeated until the pH was maintained between 4 and 6. The reaction was then cooled to room temperature and an equivalent volume of acetone was added to the precipitate K2SO4. The K2SO4 was removed via vacuum filtration. The purple filtrate was then concentrated on a rotary evaporator until solids formed. Crystals were grown by a volumetric equivalent of ethanol onto the saturated purple solution and then the solution was left to cool at room temperature until crystals formed.
Preparation of KCr(1,3-PDTA): Procedure modified from literature [12]. Briefly, H41,3-PDTA (100 g, 0.33 mmol) and KCr(SO4)2 (144.3 g, 0.28 mmol) were added to 250 mL of DI water and then stirred at reflux for 16 h. The reaction was cooled to 70 °C and 5 M KOH was added to adjust the pH between 4 and 6. The solution was then refluxed for 16 h before cooling to 70 °C and readjusting the pH with 5 M KOH. This process was repeated until the pH was maintained between 4 and 6. The reaction was then cooled to room temperature, an equivalent volume of acetone was added, and the K2SO4 precipitate was removed via filtration. The red filtrate was allowed to evaporate at ambient conditions until red crystals formed.
2.2. XRD
Single-crystal XRD was performed using a Bruker D8 Quest Eco three-circle goniometer platform equipped with a Bruker APEX-II CCD detector. A graphite monochromator was employed for wavelength selection of the Mo Kα radiation (λ = 0.71073 Å). APEX III software was provided by Bruker and the data were solved using the olex2.solve structure solution program in Olex2 using Charge Flipping and the data were refined using olex2.refine with the Levenberg−Marquardt minimization [14,15].
2.3. Electrolytes
Buffer solutions were prepared by adding 5 M KOH to the respective chelate solids (H41,2-PDTA or H41,3-PDTA) and adjusting the desired pH. Stock solutions of the active material were then added to stock solutions of the buffer to generate electrolytes with the desired concentration of the active material and 0.1 M of buffer. The pH of the electrolyte was confirmed using a pH meter and UV-Vis spectroscopy was used to confirm the concentration. A total of 500 mL stock potassium ferrocyanide/potassium ferricyanide (hexacyanoferrate, HCF) electrolyte solution were prepared by adding 16.462 g (0.05 mol) K3Fe(CN)6, 92.085 g (0.25 mol) K4Fe(CN)6, and 15.3 g (0.05 mol) of potassium tetraborate (KBi) to water with a final volume of 500 mL and pH of 9.4.
Viscosity was measured with a Cannon Fenske Opaque Viscometer CV004-002 that is accurate to ±0.30%. The viscometer was submerged in water at 40 °C and the electrolyte was added. Three readings were collected per test and an average was calculated.
2.4. Spectroscopy
Infrared spectroscopy was performed using an Agilent Cary 630 FTIR with ATR attachment.
Ultraviolet visible spectroscopy was performed using an Agilent Cary 60 UV-Vis Spectrophotometer with a 1 cm pathlength quartz cuvette. Spectroelectrochemistry was performed using the same instrument as well as a Gamry 1000 potentiostat to charge the electrolytes to the desired state-of-charge (SOC). The concentration of KCr(1,2-PDTA) was determined using the absorbance at 395 nm (ε = 108.13 M−1 cm−1). The concentration of KCr(1,3-PDTA) was assessed using the absorbance at 506 nm (ε = 316 M−1 cm−1) [16]. Maximum solubility was determined by performing UV-Vis of a saturated solution. The saturated solution was filtered before dilution.
2.5. Cyclic Voltammetry
Cyclic voltammograms (CV) were performed using a glassy carbon working electrode, silver/silver chloride reference electrode with 3 M KCl filling solution, and platinum counter electrode on a Gamry 1000 potentiostat. For CVs not used for kinetic analysis a bismuth-plated glassy carbon electrode was used. Bismuth plating of the electrode was performed using literature methods [17]. When the surface of the electrode is bismuth plated, the surface area is unknown, which is why kinetics experiments were performed on bare glassy carbon electrodes.
Kinetics calculations were performed using 5 mM KCr(1,2-PDTA) in 0.1 M 1,2-PDTA buffer and 0.5 M KCl supporting electrolyte at pH 7.05. The diffusion coefficient and heterogeneous reduction rate constants for KCr(1,2-PDTA) were calculated from cyclic voltammetry data, according to literature methods [18,19]. The peak current, ip, is related to the diffusion coefficient DO by:
where n is the number of electrons, F is Faraday’s constant, A is the electrode area (0.0707 cm2 for a 3 mm diameter glassy carbon disc electrode), is the bulk concentration of the electrolyte (10 mM), ν is the potential sweep rate, DO is the diffusion coefficient of the electrolyte, α is the charge transfer coefficient (0.5), and na is the number of electrons involved in the rate determining step (1). At 25 °C, this equation reduces to:
A linear fit of ip vs. ν1/2 data (R2 = 0.986) gave a slope of −0.0021 and an intercept of −9.33 × 10−5, yielding a DO of 1.7 × 10−4 cm2 s−1.
The heterogeneous reduction rate constant, k0, for the electrolytes was calculated using the following equation:
where E0 is the standard reduction potential of KCr(1,2-PDTA) (−1.2 V vs. Ag/AgCl (3 M KCl)) [13]. At different scan rates, (ip) vs. (Ep − E0′) was plotted with a linear fit (R2 = 0.992) giving a slope of −17.765 and an intercept of −16.739, yielding k0 = 1.1 × 10−4 cm s−1.
2.6. Flow Batteries
A previously described flow cell assembly was used to perform flow cell tests [11]. The electrolyte solutions were pumped through the cell at a flow rate of 60 mL min−1. Nafion 212™ was used as the membrane for these experiments.
Cycling experiments were performed on an Arbin LBT21084HC workstation galvanostat. Cycling experiments on the individual and mixed electrolytes involved charging and discharging the solutions at a constant current between 10% and 80% SOC, or cell voltage cutoffs of 0.5 V and 2.1 V. Coulombic efficiency was calculated by dividing the discharge capacity by the charge capacity of the same cycle, energy efficiency was calculated by dividing the discharge energy by the charge energy of a cycle, and the voltage efficiency was calculated by dividing the energy efficiency by the Coulombic efficiency.
Open circuit potential (OCP) experiments were conducted on a Gamry 5000 potentiostat by charging the desired electrolyte (KCr(1,2-PDTA), KCr(1,3-PDTA), or mixed) at a constant current of 0.5 A cm−2 to 0, 10, 25, 50, 75, and 90% SOC. Once the selected SOC was reached, the OCP was recorded for 30 s, which was then averaged to calculate the reported value. Cell polarization curves were then collected by performing a cyclic voltammetry experiment at a 200 mV s−1 scan rate from the OCP to 1.8 V and then to 0 V. Afterwards, the cell was discharged to 0.2 V and subsequently held at 0.2 V for 5 min to fully discharge the solution before starting the subsequent charge to a specific SOC.
3. Results and Discussion
KCr(1,2-PDTA) was synthesized analogously to KCr(1,3-PDTA) from potassium chromium sulfate and the corresponding ligand, and isolated as a crystalline solid [12]. Single-crystal X-ray diffraction showed a pseudo-octahedral coordination environment that excludes the solvent from the coordination sphere, similar to that of Cr(1,3-PDTA) (Figure S1, Table S1) [20].
Infrared spectroscopy (IR) of solid KCr(1,2-PDTA) yielded spectra analogous to the KCr(1,3-PDTA) complex (Figure S2) [20]. In the C=O stretch region, KCr(1,3-PDTA) showed three peaks around 1600, 1628, and 1662 cm−1, which shift to higher energies at 1621, 1640, and 1690 cm−1 for KCr(1,2-PDTA). The higher energy C=O vibrations in KCr(1,2-PDTA) indicate shorter C=O bonds as the carboxyl groups are pulled less strongly towards the chromium center. The lower energy, more elongated, C=O bonds in KCr(1,3-PDTA) suggest that Cr binds stronger to 1,3-PDTA than 1,2-PDTA (Table S2) [21]. The redox potential of KCr(1,2-PDTA) has been reported as −1.21 V vs. SCE, 137 mV more oxidizing than KCr(1,3-PDTA) [13]. The reduction potentials of these complexes and the ratio of binding constants of their oxidized and reduced states are related according to Equation (S1). Therefore, the more oxidizing reduction potential of KCr(1,2-PDTA) may be attributed to a weaker Cr3+ and/or stronger Cr2+ binding by the ligand than in KCr(1,3-PDTA). UV-Vis spectroscopy supports this hypothesis, showing that KCr(1,2-PDTA) has red-shifted absorption peaks compared to KCr(1,3-PDTA) (Table S3), suggesting a weaker ligand field strength [22,23].
Cyclic voltammetry (CV) for the qualitative comparison of kinetic parameters was performed with a glassy carbon electrode and demonstrated that at pH 7, KCr(1,2-PDTA) had a moderate heterogeneous electron transfer rate constant of 1.1 × 10−4 cm s−1 and a diffusion coefficient of 4.1 × 10−6 cm2 s−1, comparable to Cr(1,3-PDTA) (Figure 1a and Figure S3, Table S4) [12]. In an equimolar mixed solution of KCr(1,2-PDTA) and KCr(1,3-PDTA), the redox peaks could not be resolved via CV with a glassy carbon electrode. To isolate the peaks, Bi plating was performed on the glassy carbon electrode to generate an electrocatalytic surface [17]. A CV utilizing this Bi-plated electrode provided two distinct reduction and oxidation peaks, indicating that on the given timescale, the two complexes did not interact with one another (Figure S4) [24].
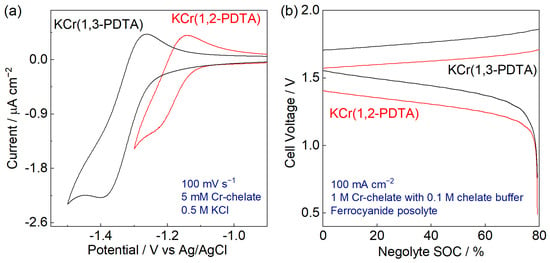
Figure 1.
Electrochemical characterization of KCr(1,2-PDTA) and KCr(1,3-PDTA). (a) Cyclic voltammetry at pH 7 on a glassy carbon electrode. (b) Cell voltage as a function of negolyte capacity for a single cycle at ±100 mA cm−2 of cells containing 1 M KCr(1,2-PDTA) or KCr(1,3-PDTA), buffered by 0.1 M of the respective ligand, as negolyte and ferro/ferricyanide as posolyte.
The maximum solubility of KCr(1,2-PDTA) is 2.2 M, almost twice as high as KCr(1,3-PDTA) at 1.3 M [12]. We hypothesize that the solubility is enhanced due to the stereocenter from the methyl group on the ligand disrupting crystal packing [23,25].
To compare KCr(1,2-PDTA) and KCr(1,3-PDTA) as RFB electrolytes, solutions of each Cr complex were cycled in an RFB setup to determine their Coulombic and voltage efficiencies. Excess positive electrolyte is used to ensure that the negolyte is always capacity limiting, so that changes in cell behavior can be attributed to the negolyte. First, a 1 M KCr(1,2-PDTA) negolyte was cycled against a mixture of 0.5 M potassium ferrocyanide, 0.1 M potassium ferricyanide, and 0.1 M potassium borate buffer, hereafter described as ferro/ferricyanide posolyte (Figure 1b). The cell was cycled to 80% state-of-charge (SOC) 50 times at a current density of ±100 mA cm−2. The equilibrium cell voltage at 50% SOC was 1.50 V and the cell demonstrated nearly quantitative Coulombic efficiency (CE) (99.7% ± 0.1%) with an average voltage efficiency (VE) of 77.8% ± 0.6% and a peak discharge power density of 418 mW cm−2 (Figures S5–S7). In comparison, an analogous RFB with a 1 M Cr(1,3-PDTA) negolyte had a CE of 99.6% ± 0.1% and VE of 78.6% ± 0.5%, comparable to KCr(1,2-PDTA) efficiencies. The peak discharge power density was higher (489 mW cm−2), resulting from the higher cell voltage (1.62 V at 50% SOC) (Figures S8 and S9, Table 1). The two RFBs were cycled three times each at ±20, 50, 100, 150, and 200 mA cm−2 and their VE decreased linearly as a function of current density in accordance with Ohm’s law, indicating that mass transport does not limit VE at the given current densities (Figure S10). Therefore, the shorter backbone and introduction of a stereocenter on 1,2-PDTA enables much higher solubility of KCr(1,2-PDTA) as compared to KCr(1,3-PDTA) without harming battery performance.

Table 1.
Comparison of average cell data using various chelate negolytes cycled against ferro/ferricyanide posolytes at 100 mA cm−2.
To examine the performance of RFBs with high concentration electrolytes, an RFB with 10 mL of a 1.5 M KCr(1,2-PDTA) negolyte, 15% more than the maximum Cr(1,3-PDTA) concentration without additives [12,26], was cycled against 40 mL ferro/ferricyanide posolyte at ±100 mA cm−2 for 50 cycles (Figure S11). The cell demonstrated an average CE of 99.9% ± 0.2%, VE of 72.8% ± 0.2%, and maximum discharge power density of 286 mW cm−2 (Table 1). The lower VE is likely caused by the higher viscosity which increased the area-specific resistance (2.1 Ω cm2 as compared to 1.6 Ω cm2 for the 1 M electrolyte) and decreased the electron transfer kinetics [26,27]. This is visualized by the increased iR drop of ca. 500 mV with the 1.5 M electrolyte (Figure S11) compared to 300 mV with the 1 M electrolytes (Figures S5 and S8). No higher concentration of pure KCr(1,2-PDTA) electrolyte was prepared for RFB cycling, because above 1.5 M, the electrolyte was too viscous to efficiently flow through the cell.
These two complexes with redox potentials approximately 100 mV apart allowed for an experimental approach to the aforementioned work performed computationally by Neyhouse et al. [6]. To compare a mixed Cr chelate negolyte to the 1 M negolytes containing individual Cr isomers, an electrolyte of 0.5 M KCr(1,2-PDTA) and 0.5 M KCr(1,3-PDTA) with 0.1 M 1,3-PDTA buffer at pH 7 (10 mL) was cycled against a ferro/ferricyanide posolyte (25 mL) (Figure 2a). The ligand was chosen as a buffer as it demonstrated no propensity towards ligand exchange with either complex (Figure S12). The cell was cycled 50 times at ±100 mA cm−2 to 80% SOC of the negolyte with a CE of 99.8% ± 0.1%, a VE of 75.8% ± 0.6%, an equilibrium cell voltage at 50% SOC of negolyte of 1.57 V, and a maximum discharge power density of 457 mW cm−2 (Table 1, Figures S13 and S14). The resultant discharge power density lies between the values achieved with the individual 1 M cells. Upon cycling, two charge and discharge plateaus corresponding to the two species present in the solution were observed. Overall, the cell maintained quantitative CE, but the VE was lower than in either of the individual 1 M cells. This is explained by the difference in the reduction potential of the two active species in the negolyte as described by Neyhouse et al., who posited that as the reduction potential difference between the species in solution increases, the VE decreases due to the increasingly imbalanced charging/discharging of the species in solution and differing mass transfer overpotentials [6].
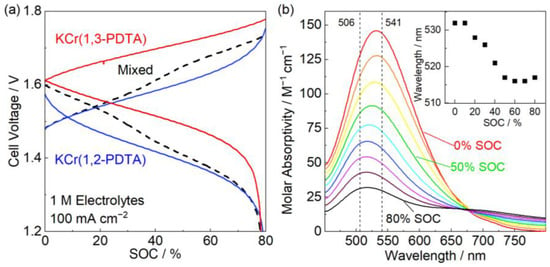
Figure 2.
Mixed electrolyte cells. (a) Voltage profiles of cells containing, in red, 1 M KCr(1,3-PDTA), in blue, 1 M KCr(1,2-PDTA), and in black, a 0.5 M KCr(1,3-PDTA) and 0.5 M KCr(1,2-PDTA) mixed electrolyte. A ferro/ferricyanide posolyte was used in all cells. The flow rate was 50 mL/min. Voltage cutoffs were set at 0.5 and 2.1 V. (b) Molar absorptivity as a function of SOC; 0.3 M KCr(1,2-PDTA) and 0.3 M KCr(1,3-PDTA) were cycled from 0% SOC to 80% SOC; 506 and 541 nm refer to the λmax of KCr(1,3-PDTA) and KCr(1,2-PDTA), respectively. The inset shows the peak wavelength of the lower energy signal as a function of SOC.
Spectroscopic analysis was performed on the mixed electrolyte with 0.3 M each of KCr(1,2-PDTA) and KCr(1,3-PDTA) charging from 0 to 80% SOC in 10% SOC increments (Figure 2b). Above 50% SOC, the Cr(1,2-PDTA) complex should be fully charged, due to its more oxidizing redox potential, and the reduction of Cr(1,3-PDTA) should begin. At approximately 40% SOC, however, we observe a red shift in the lower energy absorption band. The shift beginning before 50% SOC is reached, indicates that a fraction of KCr(1,3-PDTA) is being charged alongside KCr(1,2-PDTA) before the latter is fully reduced. This redshift further supports our interpretation that the two plateaus observed while cycling the mixed electrolyte correspond to the individual charging and discharging of the two species in the negolyte. The electrolyte was not charged beyond 80% SOC to prevent side reactions such as water reduction. The wavelength of the lower energy peak in the spectra was plotted against SOC to clarify whether the two Cr complexes are indeed being reduced sequentially during the charging step. We clearly observe the initial charging of KCr(1,2-PDTA) followed by KCr(1,3-PDTA) as indicated by the blue shift of the signal. At 0% SOC, the peak is closer to the KCr(1,2-PDTA) peak at 541 nm and gradually shifts towards the Cr(1,3-PDTA) peak at 506 nm. This spectroscopic analysis helps explain the lower VE of the mixed electrolyte; KCr(1,2-PDTA), with its more oxidizing redox potential, is generally reduced first at the electrode. Simultaneously, some KCr(1,3-PDTA) is reduced as well, and as it is reintroduced to the bulk solution, it can reduce uncharged KCr(1,2-PDTA), therefore prematurely discharging the KCr(1,3-PDTA) in a homogeneous redox reaction. The energy wasted in charging of the lower potential (higher energy) species Cr(1,3-PDTA) and discharging of the higher potential (lower energy) species Cr(1,2-PDTA) effectively reduces the VE of the cell, but the available capacity and CE should not be affected [28]. At a smaller potential separation between the two species, this loss in VE would be less pronounced.
To demonstrate cell cycling with the highest concentration of active species that can be achieved in the mixed electrolyte system, a cell was assembled using a negolyte containing 1 M each of the Cr(1,2- and 1,3-PDTA) species with 0.1 M borate buffer for a total 2 M Cr concentration at pH 7.4 (10 mL). 50 mL ferro/ferricyanide posolyte was used. The cell was cycled 40 times at ±100 mA cm−2 to an upper cell voltage cutoff of 2.1 V (Figures S15 and S16). During the initial cycles, two voltage plateaus are visible during charging and discharging. However, as the cycling continues, the two plateaus become more difficult to distinguish (Figure S15). The cell exhibited an average voltage of 1.65 V at 50% SOC (Figure S16). Spectroscopic analysis of the solution after cycling showed no change in electrolyte composition besides the significant dilution from water crossover across the membrane due to differences in osmotic strength of the 2 M negolyte and 0.5 M posolyte (Figure S17) [29]. The cell had an average CE of 99.6% ± 0.8% and VE of 67.0 ± 1% (Table 1). We point out that the contribution of disparate redox potentials to decreased VE is clearly overshadowed by the high viscosity of the 2 M solution, at 5.5 cP compared to 1.4 cP for the 1 M KCr(1,2-PDTA) solution (Table S5). Although the 2 M cell had a CE comparable to the 1 M cells, the maximum discharge power density for the RFB was only 232 mW cm−2, as would be expected with the more viscous electrolyte. Our results highlight the trade-off between higher energy density (high concentration) and reduced energy efficiency (high viscosity) [29,30].
4. Conclusions
We evaluated two structurally isomeric and electrochemically similar Cr chelates and showed that solubility is significantly enhanced by the presence of the stereocenter in the ligand backbone. The mixed isomer electrolyte takes advantage of molecular geometry to achieve a total active material concentration of 2 M, corresponding to a negolyte capacity of 53.6 Ah L−1, while also having a high equilibrium cell voltage of 1.65 V when paired with a ferro/ferricyanide posolyte. We further demonstrate that in mixed-species electrolytes, a difference of 100–150 mV in reduction potentials causes losses in voltage efficiency. The effect, however, is less significant than viscosity-induced efficiency losses at high concentrations. This work demonstrates the tunability of chelates and highlights the need to select electroactive materials with carefully tuned redox potentials in mixed-species electrolytes.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/batteries9120573/s1. Figures S1–S4: material characterization; Figures S5–S17: flow cell data; Tables S1–S5: crystallographic data and physicochemical properties; Equation S1 relating redox potential and binding constants. CCDC 2294324 contains the supplementary crystallographic data for this paper. The data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/structures. Reference [31] is cited in the supplementary materials.
Author Contributions
Investigation, formal analysis, visualization, writing—original draft, C.M.D.; methodology, writing—original draft, S.E.W.; methodology, B.H.R.; investigation, J.R.T.; methodology, supervision, visualization, writing—review and editing, D.R.; conceptualization, resources, funding acquisition, M.P.M. All authors have read and agreed to the published version of the manuscript.
Funding
The research presented was funded by the National Science Foundation under Grant No. 2155227. The views and opinions of the authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. C.M.D was funded by the Graduate Assistance in Areas of National Need fellowship and S.E.W and J.R.T were funded by the King fellowship. B.H.R. was supported by the National Science Foundation Graduate Research Fellowship Program under Grant No. DGE 1650115. D.R. acknowledges funding from the Swiss National Science Foundation (SNSF) Ambizione Fellowship Z00P2_209078.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Conflicts of Interest
The University of Colorado has filed a PCT patent on some of the flow battery chemistry disclosed in this manuscript [32]. M.P.M. is the founder of a startup company, Otoro Energy, which is commercializing flow battery electrolyte materials.
References
- Chalamala, B.R.; Soundappan, T.; Fisher, G.R.; Anstey, M.R.; Viswanathan, V.V.; Perry, M.L. Redox Flow Batteries: An Engineering Perspective. Proc. IEEE 2014, 102, 976–999. [Google Scholar] [CrossRef]
- Bae, C.; Roberts, E.P.L.; Chakrabarti, M.H.; Saleem, M. All-Chromium Redox Flow Battery for Renewable Energy Storage. Int. J. Green Energy 2011, 8, 248–264. [Google Scholar] [CrossRef]
- Kowalski, J.A.; Casselman, M.D.; Kaur, A.P.; Milshtein, J.D.; Elliott, C.F.; Modekrutti, S.; Attanayake, N.H.; Zhang, N.; Parkin, S.R.; Risko, C.; et al. A stable two-electron-donating phenothiazine for application in nonaqueous redox flow batteries. J. Mater. Chem. A 2017, 5, 24371–24379. [Google Scholar] [CrossRef]
- VanGelder, L.E.; Kosswattaarachchi, A.M.; Forrestel, P.L.; Cook, T.R.; Matson, E.M. Polyoxovanadate-alkoxide clusters as multi-electron charge carriers for symmetric non-aqueous redox flow batteries. Chem. Sci. 2018, 9, 1692–1699. [Google Scholar] [CrossRef] [PubMed]
- Kwon, G.; Lee, K.; Lee, M.H.; Lee, B.; Lee, S.; Jung, S.K.; Kyojin, K.; Jihyeon, K.; Young, P.S.; Eon, K.J.; et al. Bio-inspired Molecular Redesign of a Multi-redox Catholyte for High-Energy Non-aqueous Organic Redox Flow Batteries. Chem 2019, 5, 2642–2656. [Google Scholar] [CrossRef]
- Neyhouse, B.J.; Fenton, A.M.; Brushett, F.R. Too Much of a Good Thing? Assessing Performance Tradeoffs of Two-Electron Compounds for Redox Flow Batteries. J. Electrochem. Soc. 2021, 168, 050501. [Google Scholar] [CrossRef]
- Quan, M.; Sanchez, D.; Wasylkiw, M.F.; Smith, D.K. Voltammetry of Quinones in Unbuffered Aqueous Solution: Reassessing the Roles of Proton Transfer and Hydrogen Bonding in the Aqueous Electrochemistry of Quinones. J. Am. Chem. Soc. 2007, 129, 12847–12856. [Google Scholar] [CrossRef]
- Pahlevaninezhad, M.; Leung, P.; Velasco, P.Q.; Pahlevani, M.; Walsh, F.C.; Roberts, E.P.; de Leon, C.P. A nonaqueous organic redox flow battery using multi-electron quinone molecules. J. Power Sources 2021, 500, 229942. [Google Scholar] [CrossRef]
- Penn, E.; Baclig, A.; Ganapathi, D.; Chueh, W. Exploring Eutectic Mixing of Quinones for Engineering High Energy-Density Electrolytes. ChemRxiv 2023. [Google Scholar] [CrossRef]
- Ruan, W.; Mao, J.; Yang, S.; Shi, C.; Jia, G.; Chen, Q. Designing Cr complexes for a neutral Fe–Cr redox flow battery. Chem. Commun. 2020, 56, 3171–3174. [Google Scholar] [CrossRef]
- Waters, S.E.; Thurston, J.R.; Armstrong, R.W.; Robb, B.H.; Marshak, M.P.; Reber, D. Holistic design principles for flow batteries: Cation dependent membrane resistance and active species solubility. J. Power Sources 2022, 520, 230877. [Google Scholar] [CrossRef]
- Robb, B.H.; Farrell, J.M.; Marshak, M.P. Chelated Chromium Electrolyte Enabling High-Voltage Aqueous Flow Batteries. Joule 2019, 3, 2503–2512. [Google Scholar] [CrossRef]
- Ogino, H.; Nagata, T.; Ogino, K. Redox potentials and related thermodynamic parameters of (diaminopolycarboxylato)metal(III/II) redox couples. Inorg. Chem. 1989, 28, 3656–3659. [Google Scholar] [CrossRef]
- Bourhis, L.J.; Dolomanov, O.V.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. The anatomy of a comprehensive constrained, restrained refinement program for the modern computing environment—Olex2 dissected. Acta Cryst. A 2015, 71, 59–75. [Google Scholar] [CrossRef] [PubMed]
- Dolomanov, O.V.; Bourhis, L.J.; Gildea, R.J.; Howard, J.A.K.; Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 2009, 42, 339–341. [Google Scholar] [CrossRef]
- Douglas, B.E.; Radanović, D.J. Coordination chemistry of hexadentate EDTA-type ligands with M(III) ions. Coord. Chem. Rev. 1993, 128, 139–165. [Google Scholar] [CrossRef]
- Proctor, A.D.; Robb, B.H.; Saraidaridis, J.D.; Marshak, M.P. Bismuth Electrocatalyst Enabling Reversible Redox Kinetics of a Chelated Chromium Flow Battery Anolyte. J. Electrochem. Soc. 2022, 169, 030506. [Google Scholar] [CrossRef]
- Sum, E.; Skyllas-Kazacos, M. A study of the V(II)/V(III) redox couple for redox flow cell applications. J. Power Sources 1985, 15, 179–190. [Google Scholar] [CrossRef]
- Bard, A.J.; Faulkner, L.R. Electrochemical Methods: Fundamentals and Applications, 2nd ed.; Wiley: New York, USA, 2000. [Google Scholar]
- Waters, S.E.; Robb, B.H.; Scappaticci, S.J.; Saraidaridis, J.D.; Marshak, M.P. Isolation and Characterization of a Highly Reducing Aqueous Chromium(II) Complex. Inorg. Chem. 2022, 61, 8752–8759. [Google Scholar] [CrossRef]
- Schmidt, M.H.; Miskelly, G.M.; Lewis, N.S. Effects of redox potential, steric configuration, solvent, and alkali metal cations on the binding of carbon dioxide to cobalt(I) and nickel(I) macrocycles. J. Am. Chem. Soc. 1990, 112, 3420–3426. [Google Scholar] [CrossRef]
- Wheeler, W.D.; Legg, J.I. Solution structure of the chromium(III) complex with EDTA by deuteron NMR spectroscopy. Inorg. Chem. 1984, 23, 3798–3802. [Google Scholar] [CrossRef]
- Feng, K.; Wang, S.; Ma, H.; Chen, Y. Chirality plays critical roles in enhancing the aqueous solubility of nocathiacin I by block copolymer micelles. J. Pharm. Pharmacol. 2013, 65, 64–71. [Google Scholar] [CrossRef] [PubMed]
- Miessler, G.L.; Tarr, D.A. Chemistry of the Main Group Elements. In Inorganic Chemistry; Prentice Hall, Inc.: Englewood Cliffs, NJ, USA, 1991; pp. 227–230. [Google Scholar]
- Kerr, E.F.; Tang, Z.; George, T.Y.; Jin, S.; Fell, E.M.; Amini, K.; Jing, Y.; Wu, M.; Gordon, R.G.; Aziz, M.J. High Energy Density Aqueous Flow Battery Utilizing Extremely Stable, Branching-Induced High-Solubility Anthraquinone near Neutral pH. ACS Energy Lett. 2023, 8, 600–607. [Google Scholar] [CrossRef]
- Reber, D.; Thurston, J.R.; Becker, M.; Pach, G.F.; Wagoner, M.E.; Robb, B.H.; Waters, S.E.; Marshak, M.P. Mediating anion-cation interactions to improve aqueous flow battery electrolytes. Appl. Mater. Today 2022, 28, 101512. [Google Scholar] [CrossRef]
- Miao, W.; Ding, Z.; Bard, A.J. Solution Viscosity Effects on the Heterogeneous Electron Transfer Kinetics of Ferrocenemethanol in Dimethyl Sulfoxide−Water Mixtures. J. Phys. Chem. B 2002, 106, 1392–1398. [Google Scholar] [CrossRef]
- Amini, K.; Jing, Y.; Gao, J.; Sosa, J.; Gordon, R.; Aziz, M. Electrochemical Performance of Mixed Redox-Active Organic Molecules in Redox Flow Batteries. ChemRxiv 2023. [Google Scholar] [CrossRef]
- Reber, D.; Thurston, J.R.; Becker, M.; Marshak, M.P. Stability of highly soluble ferrocyanides at neutral pH for energy-dense flow batteries. Cell Rep. Phys. Sci. 2023, 4, 101215. [Google Scholar] [CrossRef]
- Reber, D.; Jarvis, S.R.; Marshak, M.P. Beyond energy density: Flow battery design driven by safety and location. Energy Adv. 2023, 2, 1357–1365. [Google Scholar] [CrossRef]
- Robb, B.H.; Waters, S.E.; Marshak, M.P. Evaluating Aqueous Flow Battery Electrolytes: A Coordinated Approach. Dalton Trans. 2020, 49, 16047–16053. [Google Scholar] [CrossRef]
- Water, S.; Marshak, M.P.; Robb, B. Electrochemical Storage Devices Comprising Chelated Metals. U.S. Patent Application No. 17/440,596, 20 March 2020. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).