The Influence of Testing Conditions on State of Health Estimations of Electric Vehicle Lithium-Ion Batteries Using an Incremental Capacity Analysis
Abstract
1. Introduction
2. Materials and Methods
2.1. Battery Used
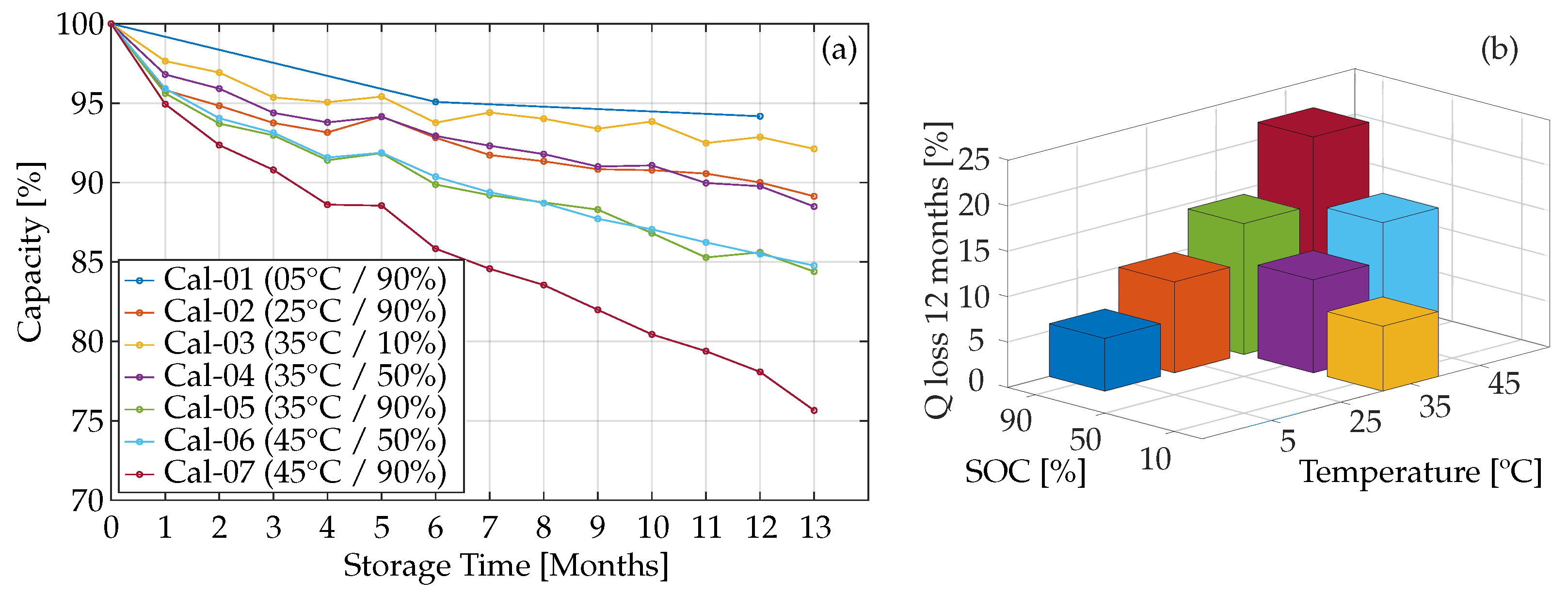
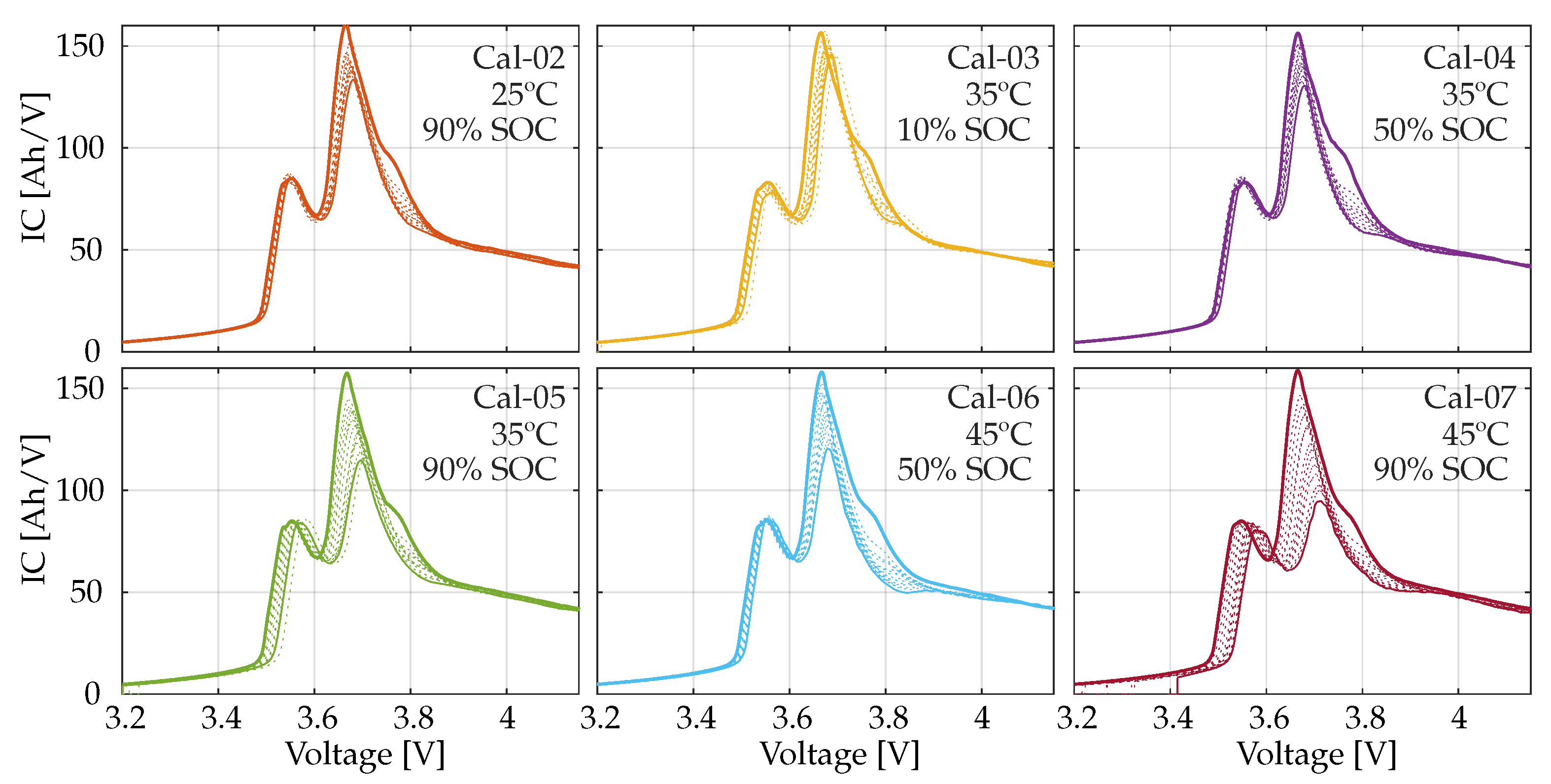
2.2. Calendar Aging Test
3. Results
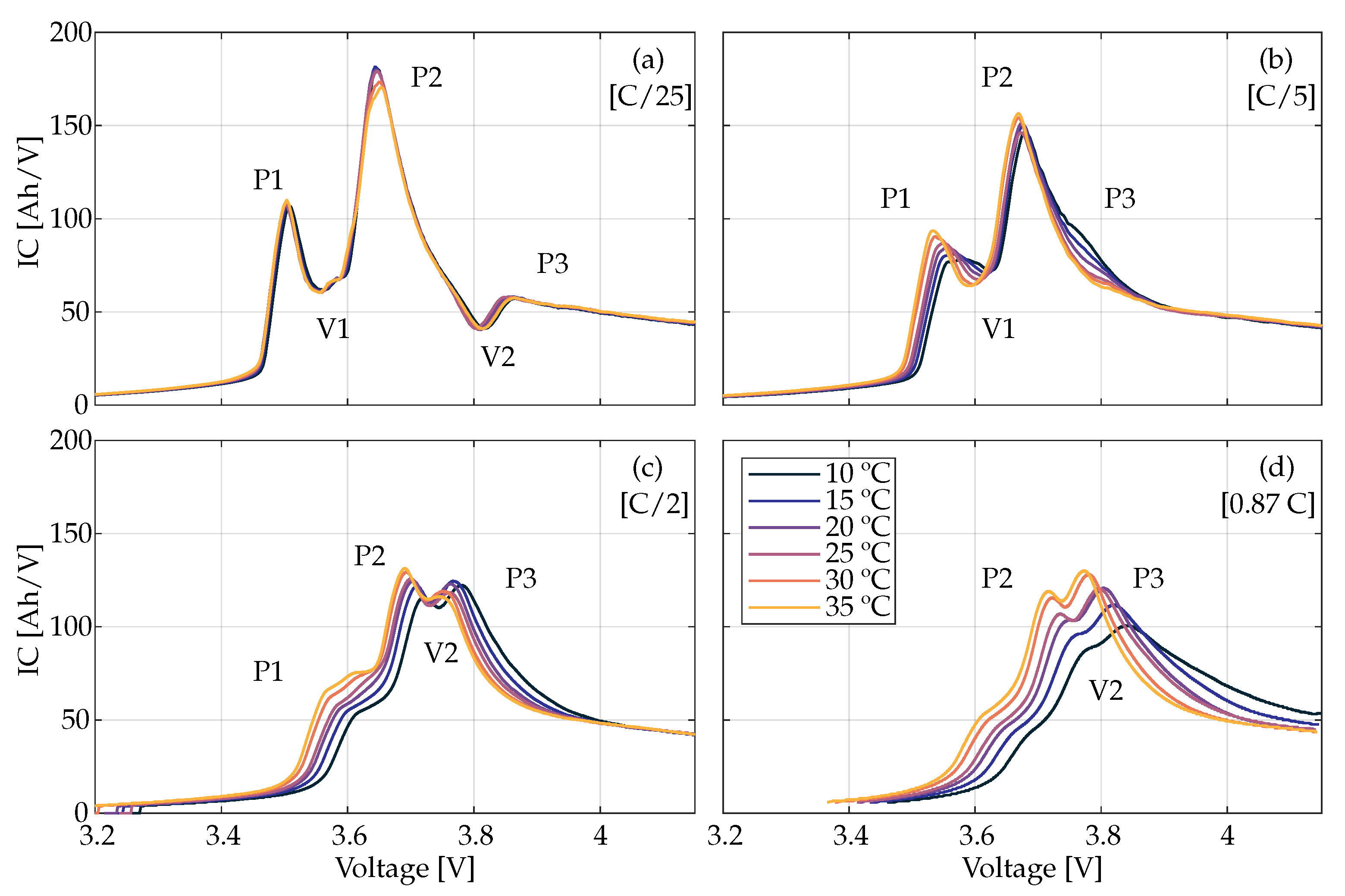
3.1. Cell Characterization
3.1.1. Full Cell Characterization
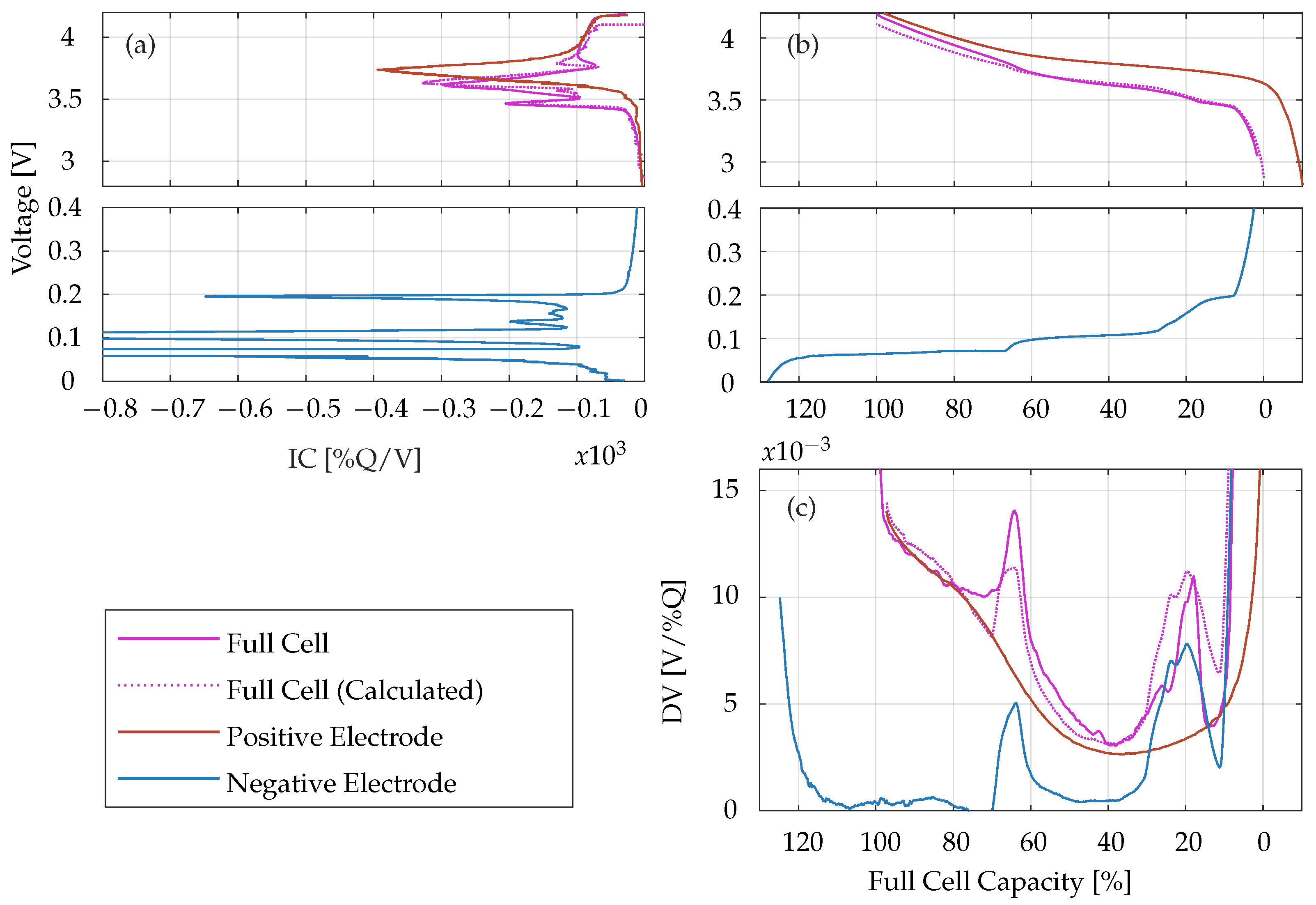
3.1.2. From Half Cell to Full Cell
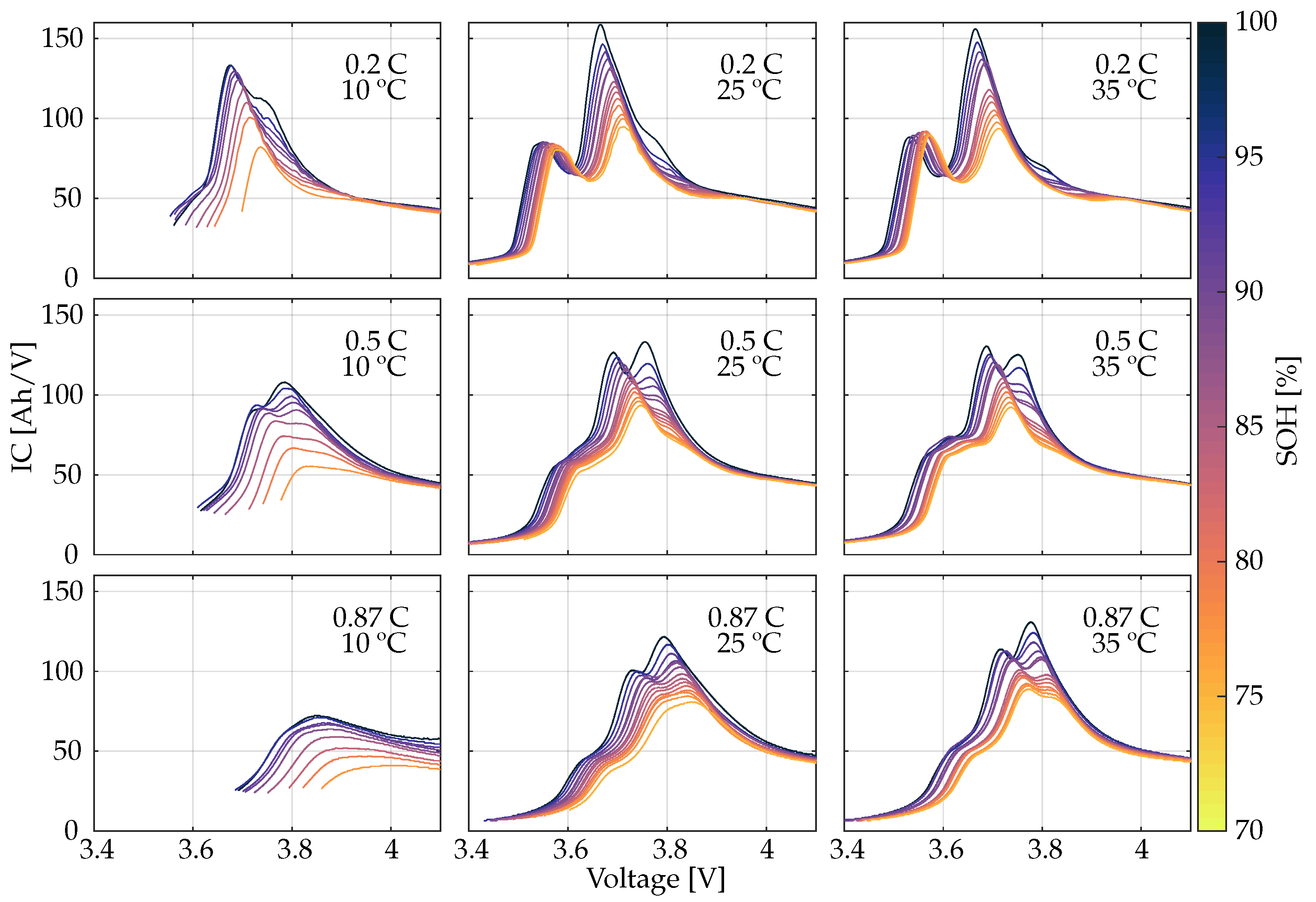
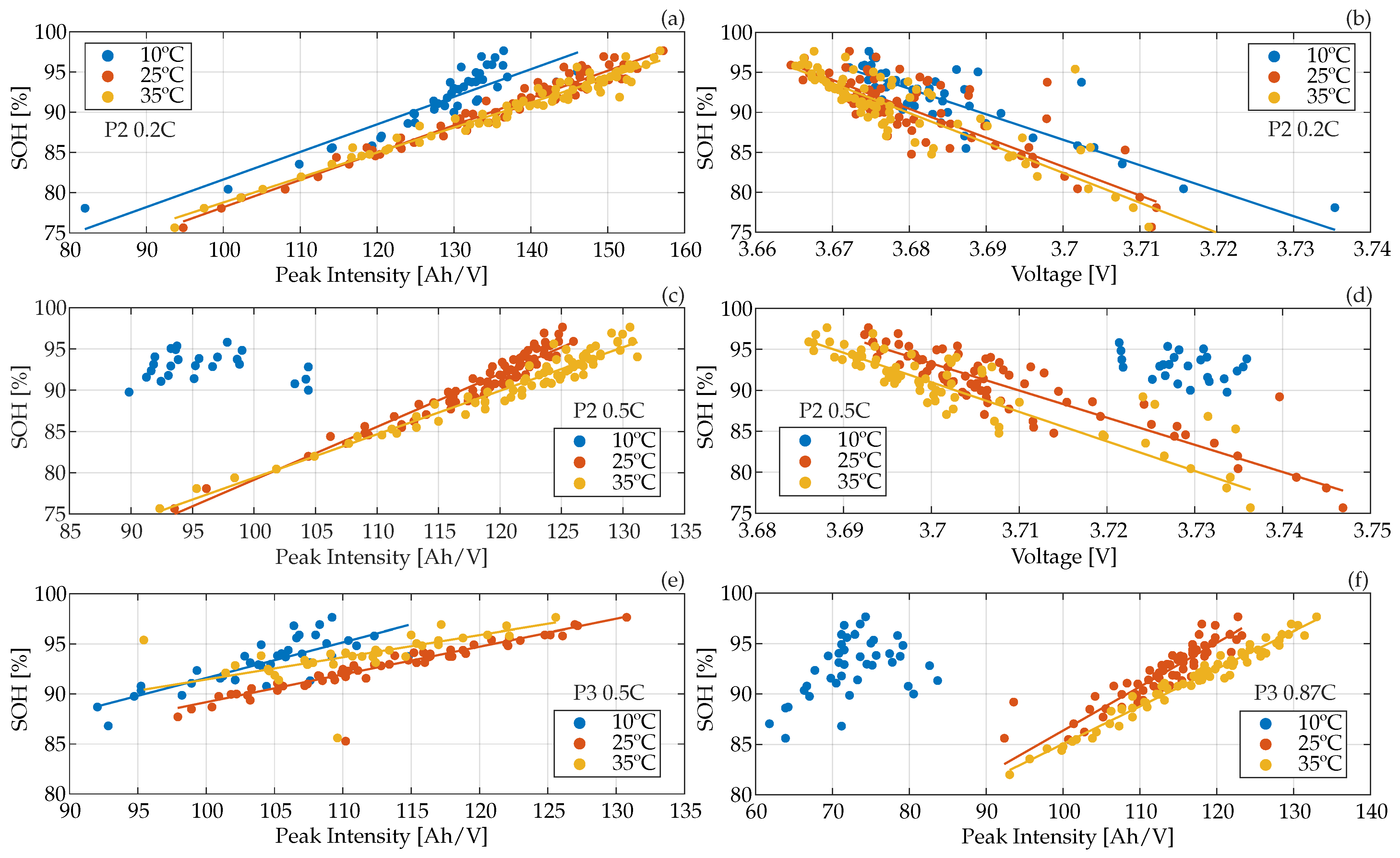
3.2. Peak Tracking and SOH Estimation
3.2.1. Calendar Aging Results
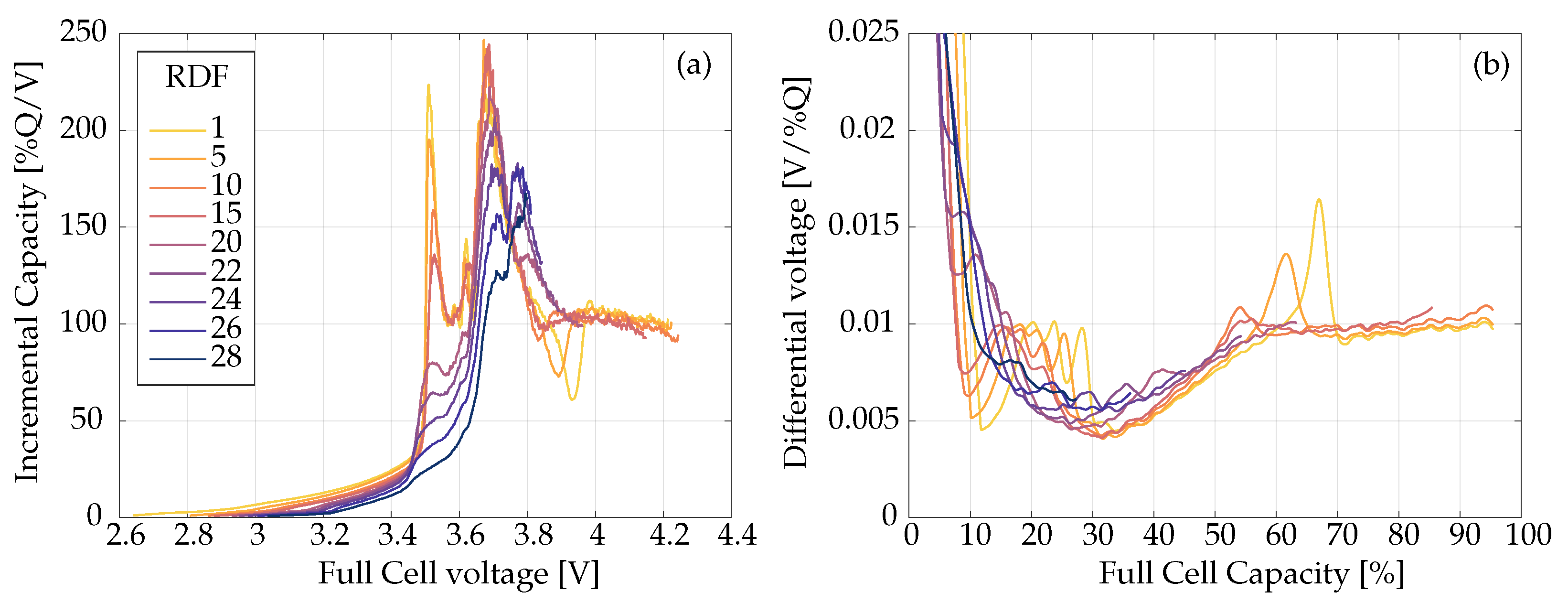
3.2.2. Incremental Capacity Signature Evolution
3.2.3. SOH Estimation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lockheed Idaho Technologies Co. USABC Electric Vehicle Battery Test Procedures Manual. Revision 2; USDOE: Washington, DC, USA, 1996. [CrossRef][Green Version]
- Dubarry, M.; Baure, G.; Devie, A. Durability and Reliability of EV Batteries under Electric Utility Grid Operations: Path Dependence of Battery Degradation. J. Electrochem. Soc. 2018, 165, A773–A783. [Google Scholar] [CrossRef]
- Gering, K.L.; Sazhin, S.V.; Jamison, D.K.; Michelbacher, C.J.; Liaw, B.Y.; Dubarry, M.; Cugnet, M. Investigation of path dependence in commercial lithium-ion cells chosen for plug-in hybrid vehicle duty cycle protocols. J. Power Sources 2011, 196, 3395–3403. [Google Scholar] [CrossRef]
- Raj, T.; Wang, A.; Monroe, C.; Howey, D. Investigation of Path Dependent Degradation in Lithium-Ion Batteries. Batter. Supercaps 2020, 3, 1377–1385. [Google Scholar] [CrossRef]
- Knap, V.; Stroe, D.I.; Purkayastha, R.; Walus, S.; Auger, D.J.; Fotouhi, A.; Propp, K. Reference Performance Test Methodology for Degradation Assessment of Lithium-Sulfur Batteries. J. Electrochem. Soc. 2018, 165, 1601–1609. [Google Scholar] [CrossRef]
- Chen, L.; Lü, Z.; Lin, W.; Li, J.; Pan, H. A new state-of-health estimation method for lithium-ion batteries through the intrinsic relationship between ohmic internal resistance and capacity. Meas. J. Int. Meas. Confed. 2018, 116, 586–595. [Google Scholar] [CrossRef]
- Dubarry, M.; Berecibar, M.; Devie, A.; Anseán, D.; Omar, N.; Villarreal, I. State of health battery estimator enabling degradation diagnosis: Model and algorithm description. J. Power Sources 2017, 360, 59–69. [Google Scholar] [CrossRef]
- Schaltz, E.; Stroe, D.I.; Norregaard, K.; Ingvardsen, L.S.; Christensen, A. Incremental Capacity Analysis Applied on Electric Vehicles for Battery State-of-Health Estimation. IEEE Trans. Ind. Appl. 2021, 57, 1810–1817. [Google Scholar] [CrossRef]
- Berecibar, M.; Devriendt, F.; Dubarry, M.; Villarreal, I.; Omar, N.; Verbeke, W.; Mierlo, J.V. Online state of health estimation on NMC cells based on predictive analytics. J. Power Sources 2016, 320, 239–250. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Y.; Wang, J.; Zhang, T. State-of-health estimation for lithium-ion batteries by combining model-based incremental capacity analysis with support vector regression. Energy 2022, 239, 121986. [Google Scholar] [CrossRef]
- Li, Y.; Abdel-Monem, M.; Gopalakrishnan, R.; Berecibar, M.; Nanini-Maury, E.; Omar, N.; van den Bossche, P.; Mierlo, J.V. A quick on-line state of health estimation method for Li-ion battery with incremental capacity curves processed by Gaussian filter. J. Power Sources 2018, 373, 40–53. [Google Scholar] [CrossRef]
- Jiang, B.; Dai, H.; Wei, X. Incremental capacity analysis based adaptive capacity estimation for lithium-ion battery considering charging condition. Appl. Energy 2020, 269, 115074. [Google Scholar] [CrossRef]
- Li, X.; Yuan, C.; Wang, Z. State of health estimation for Li-ion battery via partial incremental capacity analysis based on support vector regression. Energy 2020, 203, 117852. [Google Scholar] [CrossRef]
- Dubarry, M.; Beck, D. Analysis of Synthetic Voltage vs. Capacity Datasets for Big Data Li-ion Diagnosis and Prognosis. Energies 2021, 14, 2371. [Google Scholar] [CrossRef]
- Lin, Y.; Jiang, B.; Dai, H. Battery Capacity Estimation Based on Incremental Capacity Analysis Considering Charging Current Rate. World Electr. Veh. J. 2021, 12, 224. [Google Scholar] [CrossRef]
- Chen, Y.; Torres-Castro, L.; Chen, K.H.; Penley, D.; Lamb, J.; Karulkar, M.; Dasgupta, N.P. Operando detection of Li plating during fast charging of Li-ion batteries using incremental capacity analysis. J. Power Sources 2022, 539, 231601. [Google Scholar] [CrossRef]
- Maures, M.; Mathieu, R.; Capitaine, A.; Delétage, J.Y.; Vinassa, J.M.; Briat, O. An Incremental Capacity Parametric Model Based on Logistic Equations for Battery State Estimation and Monitoring. Batteries 2022, 8, 39. [Google Scholar] [CrossRef]
- Schindler, S.; Baure, G.; Danzer, M.A.; Dubarry, M. Kinetics accommodation in Li-ion mechanistic modeling. J. Power Sources 2019, 440, 227117. [Google Scholar] [CrossRef]
- MarkLines Co., Ltd. Nissan LEAF Teardown: Lithium-Ion Battery Pack Structure. 2018. Available online: https://www.marklines.com/en/report_all/rep1786_201811 (accessed on 17 June 2022).
- Dubarry, M.; Qin, N.; Brooker, P. Calendar aging of commercial Li-ion cells of different chemistries—A review. Curr. Opin. Electrochem. 2018, 9, 106–113. [Google Scholar] [CrossRef]
- Gismero, A. Electric Vehicle Batteries State Estimation under a Wide Range of Test and Aging Conditions. Ph.D. Thesis, Aalborg Universitetsforlag, Aalborg, Denmark, 2022. [Google Scholar] [CrossRef]
- Dubarry, M.; Truchot, C.; Liaw, B.Y. Synthesize battery degradation modes via a diagnostic and prognostic model. J. Power Sources 2012, 219, 204–216. [Google Scholar] [CrossRef]
- Dubarry, M. ‘Alawa: A Unique Mechanistic Model for Battery Diagnosis and Prognosis. Available online: https://www.soest.hawaii.edu/HNEI/alawa (accessed on 3 October 2022).
- Jung, R.; Metzger, M.; Maglia, F.; Stinner, C.; Gasteiger, H. Oxygen Release and Its Effect on the Cycling Stability of LiNixMnyCozO2 (NMC) Cathode Materials for Li-Ion Batteries. J. Electrochem. Soc. 2017, 164, A1361–A1377. [Google Scholar] [CrossRef]
- Dubarry, M.; Anseán, D. Best practices for incremental capacity analysis. Front. Energy Res. 2022, 10, 1023555. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Dubarry, M.; Somerville, L.; McGordon, A.; Jennings, P.; Bloom, I. A comparison of methodologies for the non-invasive characterisation of commercial Li-ion cells. Prog. Energy Combust. Sci. 2019, 72, 1–31. [Google Scholar] [CrossRef]
- Hudson, B.G.; Mason, S.E. Metal Release Mechanism and Electrochemical Properties of Lix (Ni1/3Mn1/3Co1/3)O2. Appl. Sci. 2022, 12, 4065. [Google Scholar] [CrossRef]
- Xu, C.; Reeves, P.J.; Jacquet, Q.; Grey, C.P. Phase Behavior during Electrochemical Cycling of Ni-Rich Cathode Materials for Li-Ion Batteries. Adv. Energy Mater. 2021, 11, 2003404. [Google Scholar] [CrossRef]
- Anseán, D.; Baure, G.; González, M.; Cameán, I.; García, A.B.; Dubarry, M. Mechanistic investigation of silicon-graphite/LiNi0.8Mn0.1CO0.1O2 commercial cells for non-intrusive diagnosis and prognosis. J. Power Sources 2020, 459, 227882. [Google Scholar] [CrossRef]
- Dahn, J.R. Phase diagram of LixC6. Phys. Rev. B 1991, 44, 9170–9177. [Google Scholar] [CrossRef]
| Cell ID | Test Conditions | |
|---|---|---|
| T (°C) | SOC (%) | |
| Cal-01 | 5 | 90 |
| Cal-02 | 25 | 90 |
| Cal-03 | 35 | 10 |
| Cal-04 | 35 | 50 |
| Cal-05 | 35 | 90 |
| Cal-06 | 45 | 90 |
| Cal-07 | 45 | 50 |
| 10 °C | 25 °C | 35 °C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MAE | RMSE | MAE | RMSE | ||||||
| Intensity | P2 | C/5 | 0.79 | 1.56 | 2.01 | 0.95 | 0.71 | 0.98 | 0.97 | 0.65 | 0.84 |
| C/2 | 0.02 | - | - | 0.94 | 0.86 | 1.12 | 0.94 | 0.83 | 1.08 | ||
| 0.87C | X | X | X | 0.43 | - | - | 0.9 | 1.13 | 1.49 | ||
| P3 | C/5 | X | X | X | X | X | X | X | X | X | |
| C/2 | 0.6 | - | - | 0.95 | 0.44 | 0.49 | 0.76 | 0.81 | 0.83 | ||
| 0.87C | 0.18 | - | - | 0.86 | 0.95 | 1.17 | 0.97 | 0.49 | 0.64 | ||
| V2 | C/5 | X | X | X | X | X | X | X | X | X | |
| C/2 | 0.25 | - | - | 0.79 | 0.83 | 1.06 | 0.76 | 0.95 | 1.03 | ||
| 0.87C | 0.73 | 0.8 | 1.09 | 0.69 | - | - | 0.85 | 1.37 | 1.54 | ||
| Voltage | P2 | C/5 | 0.79 | 1.61 | 2.03 | 0.73 | 1.93 | 2.48 | 0.8 | 2.09 | 2.41 |
| C/2 | 0.1 | - | - | 0.84 | 1.53 | 1.92 | 0.86 | 1.68 | 1.95 | ||
| 0.87C | X | X | X | 0.54 | - | - | 0.78 | 1.7 | 2.23 | ||
| P3 | C/5 | X | X | X | X | X | X | X | X | X | |
| C/2 | 0.7 | 1.66 | 1.82 | 0.03 | - | - | 0.02 | - | - | ||
| 0.87C | 0.62 | - | - | 0.35 | - | - | 0.58 | - | - | ||
| V2 | C/5 | X | X | X | X | X | X | X | X | X | |
| C/2 | 0.78 | 1.24 | 1.38 | 0.73 | 1.26 | 1.45 | 0.83 | 1.43 | 1.24 | ||
| 0.87C | 0.47 | - | - | 0.77 | 2.36 | 2.5 | 0.64 | - | - | ||
| Model | ||||||||
|---|---|---|---|---|---|---|---|---|
| 10 °C | 25 °C | 35 °C | ||||||
| C/5 | C/2 | C/5 | C/2 | C/5 | C/2 | |||
| Actual conditions | 10 °C | C/5 | 2.01 | - | 3.99 | 7.31 | 4.23 | 4.21 |
| C/2 | 12.71 | - | 16.24 | 16.77 | 15.48 | 15.99 | ||
| 25 °C | C/5 | 3.66 | - | 0.98 | 12.71 | 1.09 | 8.54 | |
| C/2 | 3.53 | - | 6.75 | 1.12 | 6.73 | 2.21 | ||
| 35 °C | C/5 | 4.18 | - | 1.11 | 14.01 | 0.84 | 9.59 | |
| C/2 | 2.53 | - | 5.54 | 2.6 | 5.63 | 1.08 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gismero, A.; Dubarry, M.; Guo, J.; Stroe, D.-I.; Schaltz, E. The Influence of Testing Conditions on State of Health Estimations of Electric Vehicle Lithium-Ion Batteries Using an Incremental Capacity Analysis. Batteries 2023, 9, 568. https://doi.org/10.3390/batteries9120568
Gismero A, Dubarry M, Guo J, Stroe D-I, Schaltz E. The Influence of Testing Conditions on State of Health Estimations of Electric Vehicle Lithium-Ion Batteries Using an Incremental Capacity Analysis. Batteries. 2023; 9(12):568. https://doi.org/10.3390/batteries9120568
Chicago/Turabian StyleGismero, Alejandro, Matthieu Dubarry, Jia Guo, Daniel-Ioan Stroe, and Erik Schaltz. 2023. "The Influence of Testing Conditions on State of Health Estimations of Electric Vehicle Lithium-Ion Batteries Using an Incremental Capacity Analysis" Batteries 9, no. 12: 568. https://doi.org/10.3390/batteries9120568
APA StyleGismero, A., Dubarry, M., Guo, J., Stroe, D.-I., & Schaltz, E. (2023). The Influence of Testing Conditions on State of Health Estimations of Electric Vehicle Lithium-Ion Batteries Using an Incremental Capacity Analysis. Batteries, 9(12), 568. https://doi.org/10.3390/batteries9120568









