A Switch-Reduced Multicell-to-Multicell Battery Equalizer Based on Full-Bridge Bipolar-Resonant LC Converter

Abstract

Many battery equalizers have been proposed to achieve voltage consistency between series connected battery cells. Among them, the multicell-to-multicell (MC2MC) equalizers, which can directly transfer energy from consecutive more-charged cells to less-charged cells, can enable fast balancing and a high efficiency. However, due to the limitations of the equalizers, it is not possible to achieve fast equalization and reduce the size of the circuit at the same time. Therefore, a MC2MC equalizer based on a full-bridge bipolar-resonant LC Converter (FBBRLCC) is proposed in this paper, which not only implements MC2MC equalization, but also greatly reduces the circuit size by reducing the number of switches by nearly half. A mathematical model and simulation comparison with conventional equalizers are used to illustrate the high-speed equalization performance of the proposed equalizer and excellent balancing efficiency. An experimental prototype for eight cells is built to verify the performance of the proposed FBBRLCC equalizer and the balancing efficiencies in different operating modes are from 85.19% to 88.77% with the average power from 1.888 W to 14.227 W.

1. Introduction

With the global climate warming and the exhaustion of fossil fuels, the electrification of the powertrain in vehicles has gradually become a core concern of countries, automobile manufacturers and consumers [1,2,3]. As a core component of electric vehicles, the energy storage systems (ESSs) largely determine the performance, safety, and manufacturing cost of electric vehicles (EVs) [4,5,6]. At present, there are mainly two types of renewable energy storage components in electric vehicles: lithium batteries and ultracapacitors (UCs). Lithium batteries have the advantages of high energy density, low self-discharge rate, and no memory effect, and are widely used in electric vehicles (EVs), hybrid electric vehicles (HEVs), and other energy storage systems (ESSs) [7,8,9]. However, the application of lithium batteries in electric vehicles and new energy power generation is facing challenges because the voltage and capacity of a single lithium battery cannot meet the requirements of high voltage and capacity of these applications, so it must be connected in series and in parallel to improve the voltage and capacity, and finally form a battery pack [10,11,12].

However, due to the limitation of the battery manufacturing process and different environments, the battery voltage in the battery string will be imbalanced [13,14,15]. This inconsistency will become more and more serious with increasing cycle charge and discharge times, which will significantly reduce the available capacity and life of the battery pack, and even cause serious safety problems [16]. As a key technology of battery management systems (BMS), voltage equalization techniques can effectively improve the voltage inconsistency between cells [17]. Hence, it is very important to study voltage equalization techniques.

Various voltage equalization techniques have been proposed and developed. These techniques can be divided into dissipative types and non-dissipative types [18,19]. Dissipative voltage equalizers have a simple structure and are easy to implement [20]. However, they consume a lot of energy in the balancing process, which is their fatal disadvantage [21]. Compared with dissipative voltage equalizers, non-dissipative voltage equalizers transfer the energy from the strong cells to the weak cells by using energy storage elements, so the imbalanced energy will not be wasted, and the capacity of the pack can be improved [21,22,23]. According to equalization paths, non-dissipative voltage equalizers can be divided into adjacent cell-to-cell (AC2C) equalizers [24,25,26], direct cell-to-cell (DC2C) equalizers [27,28,29], cell-to-pack (C2P) equalizers [30], pack-to-cell (P2C) equalizers [31], and multicell-to-multicell (MC2MC) equalizers [21,32].

The AC2C equalizers can achieve equalization between adjacent two cells, but energy can only be transferred between two adjacent cells, which will lead to a slow balancing speed and low balancing efficiency when the number of batteries increases, for example, in equalizers based on quasi-resonant switched-capacitor converters (QRSSC) [24] and automatic buck-boost converters based on coupled inductors (CI) [26].

Compared to the AC2C equalizers, the DC2C equalizers achieve direct equalization of the more-charged battery and the less-charged battery by using common energy storage units such as LC resonators [27], inductors [28], or capacitors [29], which reduces the path of energy transmission. However, only one pair of batteries can be balanced at a time and the other batteries have to wait, which results in a slow balancing speed when the number of unbalanced batteries is very large, such as in equalizers based on full-bridge LC converters (FBLCC) [27].

The C2P equalizers deliver the excess energy of a single more-charged cell to the whole pack and can realize fast equalization when a few cells are more charged than other cells [30]. However, when only a few batteries in the battery pack are less charged than the other cells, this will lead to slow equalization and low efficiency. Contrary to the C2P equalizers, the P2C equalizers deliver the excess energy of the whole pack to a single less-charged cell and can realize fast equalization when a few cells are less charged than other cells [31]. However, in an opposite case when only a few batteries in the battery pack are more charged than the other cells, the P2C equalizers will be like the C2P equalizers, having slow equalization and low efficiency.

Considering the advantages and limitations of the above equalizers, a multicell-to-multicell (MC2MC) equalizer was proposed in [32] that can transfer energy from consecutive more-charged cells to less-charged cells. However, the half-bridge LC converter (HBLCC) in [32] cannot realize step-up conversion, which will slow down the balancing speed. Based on HBLCC, a novel bipolar-resonant LC converter (BRLCC) was proposed in [21] that can realize resonant tank-to-resonant LC in a bipolar way and thus improve balancing speeding and power. However, due to its symmetric switch matrix structure, the number of switches increases dramatically as the number of batteries increases, which results in large circuit size with low reliability.

Consequently, to improve the balancing speed and reduce the circuit size, this paper proposes a full-bridge bipolar-resonant LC converter (FBBRLCC) equalizer, as shown in Figure 1. Compared to HBLCC and BRLCC, the proposed FBBRLCC equalizer can realize fast balancing by transferring energy from consecutive odd number of more-charged cells to consecutive odd number of less-charged cells and reduce the number of switches by nearly half, which greatly reduces circuit cost and size and improves reliability. In Section 2, the circuit structure, operation principle, mathematical model, and mathematical analysis of the proposed FBBRLCC equalizer are provided. Section 3 shows a simulation comparison between the proposed FBBRLCC equalizer and several typical equalizers. Section 4 introduces the experimental prototype for eight cells, verifies its fast-balancing performance and presents a comprehensive evaluation. Section 5 shows a comprehensive discussion, and Section 6 provides a conclusion.

2. Proposed Equalizer

2.1. Circuit Structure

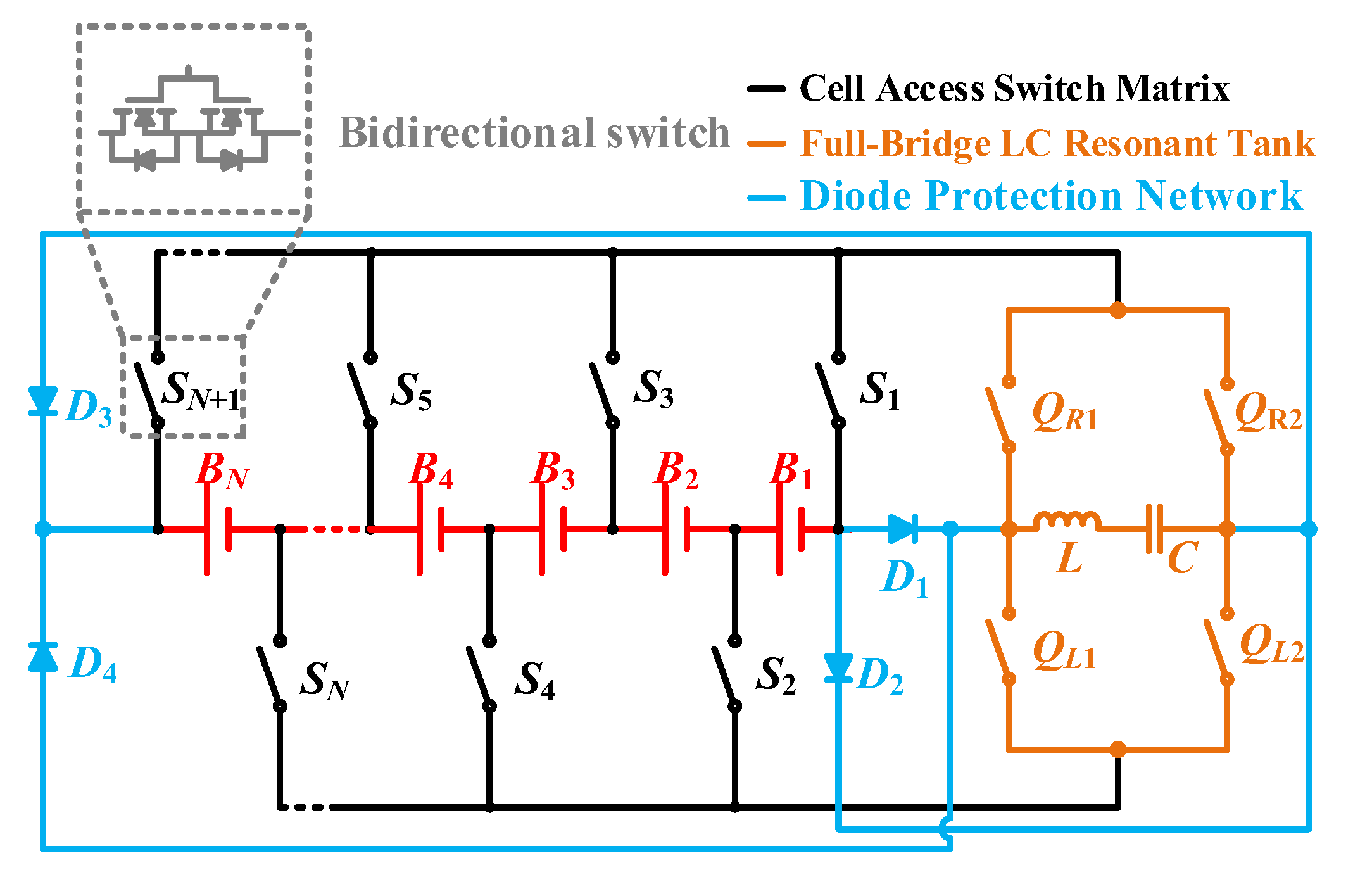
As shown in Figure 1, the proposed FBBRLCC equalizer has a cell access switch matrix, a full-bridge LC resonant tank, and a diode protection network. The cell access switch matrix consists of N + 1 bidirectional switches (S₁ − S_N+1). The full-bridge LC resonant tank consists of a resonant tank and a full-bridge switch structure (Q_R1, Q_R2, Q_L1, Q_L2). The diode protection network consists of four free-wheeling diodes (D₁–D₄).

The resonant tank collects energy from the consecutive odd number of more-charged cells (release group) through the cell access switch matrix and the full-bridge switches (Q_R1, Q_R2, Q_L1, Q_L2), and then releases the energy to the consecutive odd number of less-charged cells (collect group).

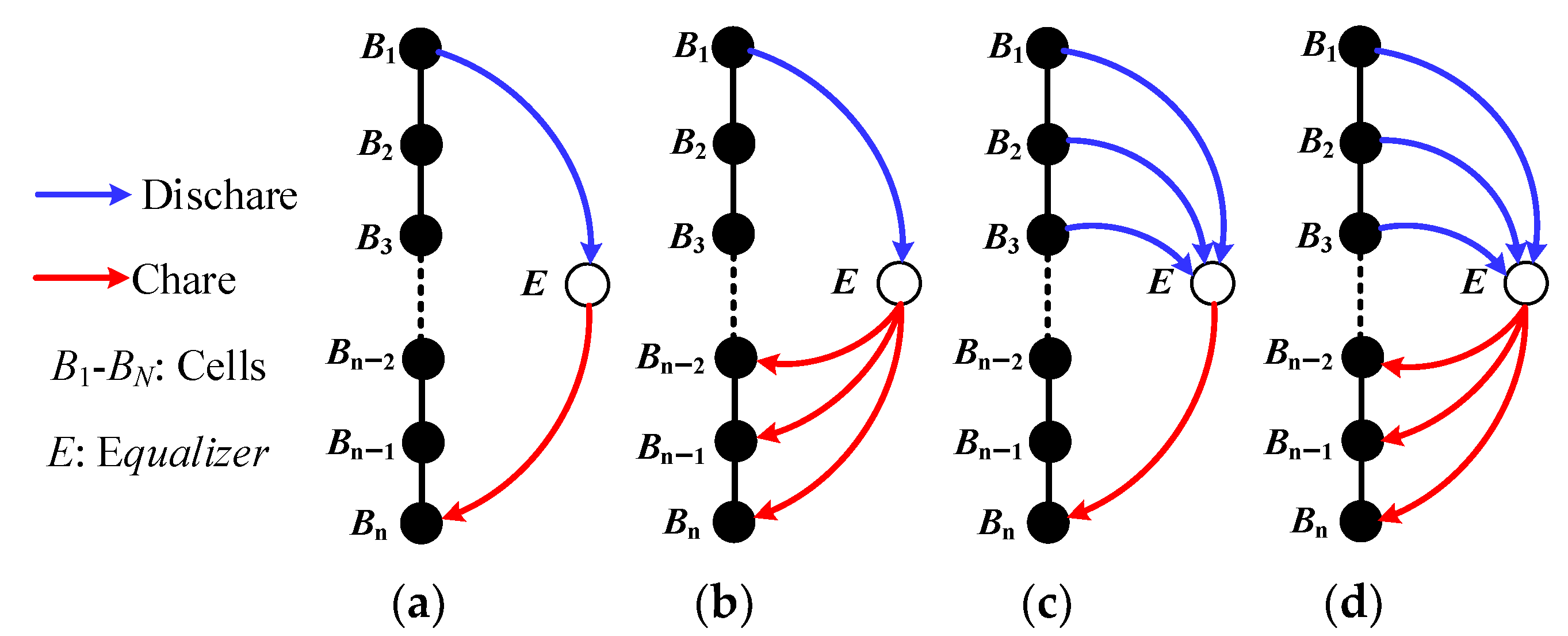
Figure 2 presents four potential operation modes including one-cell-to-one-cell mode (1-1 mode), one-cell-to-three-cell mode (1-3 mode), three-cell-to-one-cell mode (3-1 mode), and three-cell-to-three-cell mode (3-3 mode). Due to the circuit’s resonant nature, the driving signals’ switching frequency and duty cycle are fixed. As a result, it is possible to make a simple control. Meanwhile, all switches are controlled to work with zero-current switching (ZCS), which can reduce the switching loss and the electromagnetic interference (EMI) and help reduce circuit size by increasing switching frequency.

2.2. Operation Principle

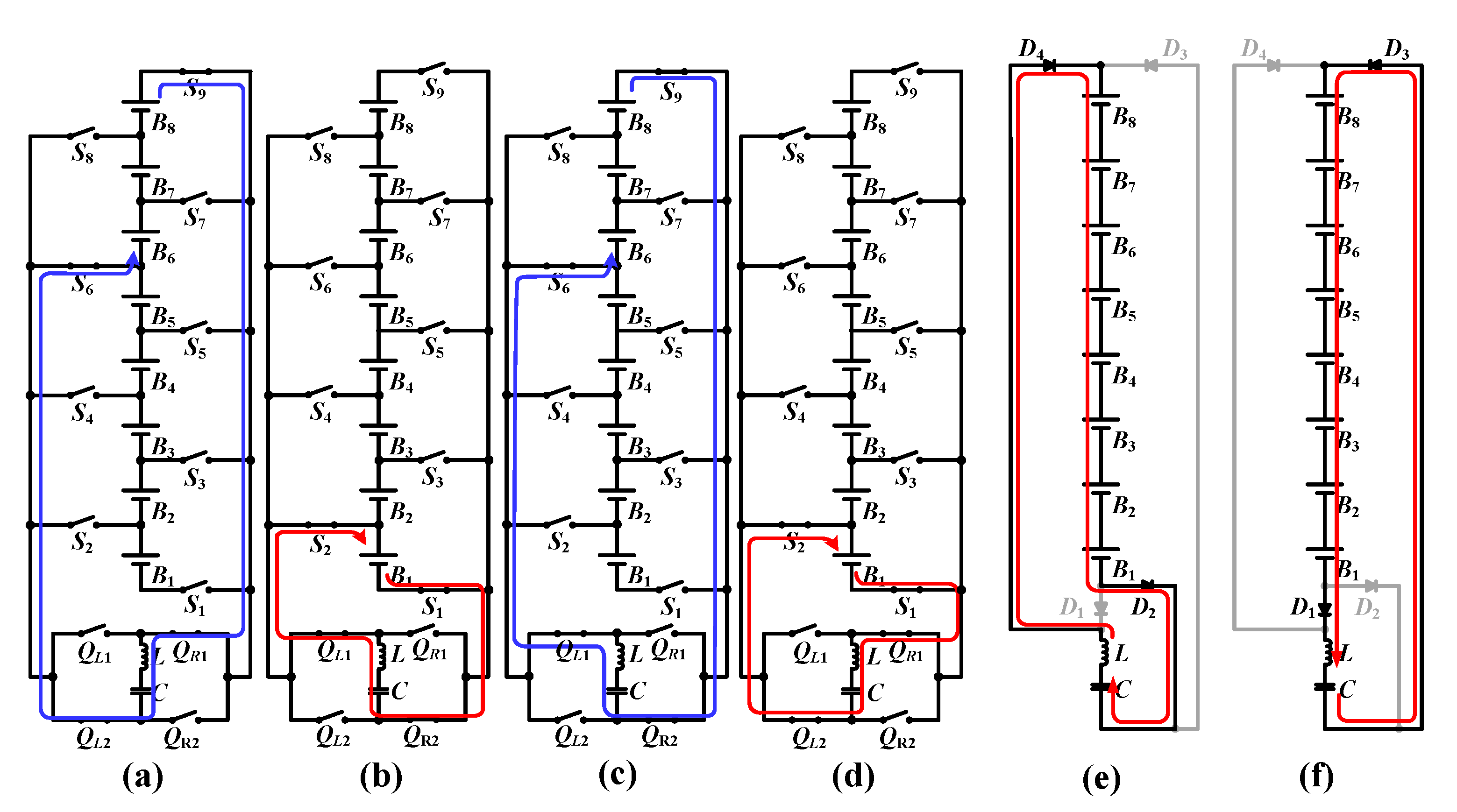
Figure 3 presents the operating states along with the current flow of the proposed equalizer. To facilitate the analysis, the balancing loop and the protection loop are analyzed separately, and it is assumed that the battery pack has eight cells with V_B8 = V_B7 = V_B6 > V_B5 > V_B4 > V_B3 > V_B2 > V_B1, which is arranged to illustrate the 3-1 mode equalization. The voltage of release group and collect group are V_BR = V_B8 + V_B7 + V_B6 and V_BC = V_B1, respectively.

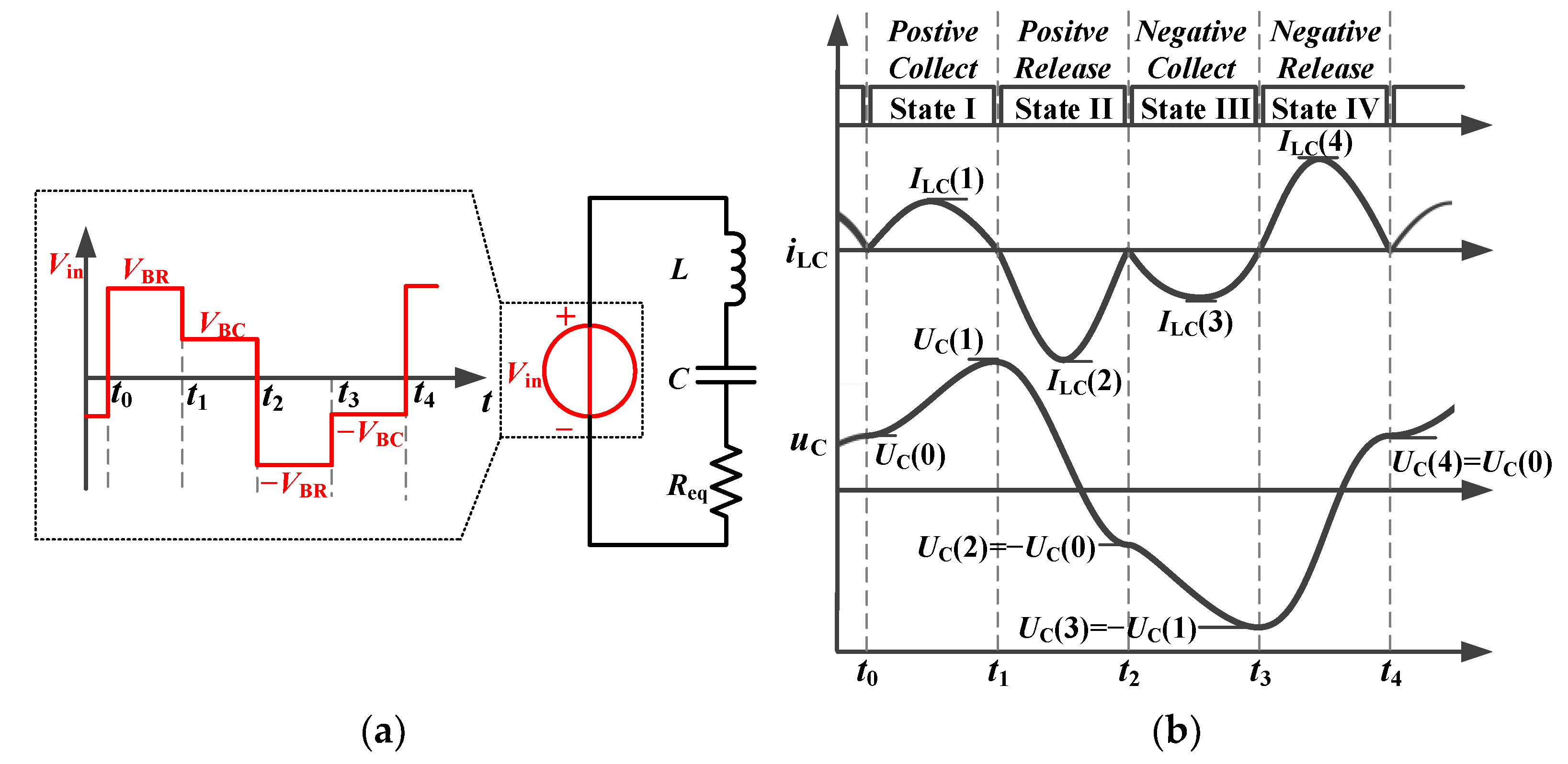
In Figure 4a, an equivalent input of the full-bridge LC resonant converter is given. Figure 4b shows the theoretical waveforms of the proposed equalizer at V_BR ≈ 3V_BC. In Figure 4a, the R_eq represents the total parasitic resistance and can be expressed as R_eq = R_LC + 8R_ON, where R_LC is the total resistance of the LC resonant tank and R_ON is the ON-resistance of a MOSFET.

The proposed equalizer has a similar equivalent input to the bipolar-resonant LC converter (BRLCC) equalizer presented in [21]. However, compared with the symmetrical switch matrix in [21], the proposed equalizer achieves a change in the polarity of the input terminal through a full-bridge switch structure, which can reduce the number of switches by nearly half. As a result, the proposed equalizer not only achieves MC2MC equalization, but also greatly reduces the size of the circuit and improves the reliability of the circuit.

Figure 4b shows the waveforms including driving signals, inductor current i_LC, and capacitor voltage u_C of the equalizer, which shows the inductor current i_LC achieves ZCS by resonance, and the capacitor voltage u_C is charged/discharged to different voltage values at the end of each switching state. More details are described in Section 2.3.

2.3. Mathematical Model

Based on the equivalent input of the full-bridge LC resonant converter and according to Kirchhoff’s voltage law, u_C and i_LC meet:

$$\left\{\begin{array}{l}L\frac{\mathrm{d}{i}_{\mathrm{LC}}\left(t\right)}{\mathrm{d}t}+i_{\mathrm{L}}\left(t\right)R_{\mathrm{eq}}+u_{\mathrm{C}}\left(t\right)=V_{\mathrm{in}}\\ i_{\mathrm{LC}}\left(t\right)=C\frac{\mathrm{d}{u}_{\mathrm{C}}\left(t\right)}{\mathrm{d}t}\end{array}\right.$$

(1)

where L is the inductance, C is the capacitance, R_eq is the total parasitic resistance.

In positive collect state I [t₀–t₁]: during this state, switches S₆ and S₉ connect the release group (V_BR = V_B8 + V_B7 + V_B6) to the full-bridge LC resonant tank. The LC resonant tank is charged positively using Q_L2 and Q_R1. Since U_C(0) is a remnant u_C from the previous period and is lower than V_BR, u_C increases from U_C(0) to U_C(1), and the peak value of i_LC is I_LC(1). According to (1), u_C and i_LC can be given by:

$$u_{\mathrm{C}}\left(t\right)=V_{\mathrm{BR}}+\left(U_{\mathrm{C}}(0)-V_{\mathrm{BR}}\right)\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_0\right)} \cdot \left(\cos \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_0\right)\right)+\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_0\right)\right)\right)$$

(2)

$$i_{\mathrm{LC}}\left(t\right)=\frac{\left(V_{\mathrm{BR}}-U_{\mathrm{C}}\left(0\right)\right)}{Z_{\mathrm{r}}\cdot \sqrt{1-{\zeta }^2}}\cdot {\mathrm{e}}^{-\zeta {\omega }_{\mathrm{n}}\left(t-t_0\right)}\cdot \sin \left({\omega }_{\mathrm{n}}\cdot \sqrt{1-{\zeta }^2}\cdot \left(t-t_0\right)\right)$$

(3)

where ${\omega }_{\mathrm{n}}=1/\sqrt{LC}$, $Z_{\mathrm{r}}=\sqrt{L/C}$, and $\xi =R_{\mathrm{eq}}/2Z_{\mathrm{r}}$. The positive collect state ends when i_LC reaches zero at t = t₁, and the duration of this state is:

$$\Delta t=t_1-t_0=\frac{\mathsf{\pi }}{{\omega }_{\mathrm{n}}\times \sqrt{1-{\xi }^2}}$$

(4)

At the end of this state, u_C is positively charged to U_C(1):

$$U_C(1)=V_{\mathrm{BR}}+(V_{\mathrm{BR}}-U_C(0)){\mathrm{e}}^{-\frac{\xi \pi }{\sqrt{1-{\xi }^2}}}$$

(5)

In positive release state Ⅱ [t₁–t₂]: during this state, switches S₁ and S₂ connect the collect group (V_BC = V_B1) to the full-bridge LC resonant tank. The LC resonant tank positively releases charges to V_BC using Q_L1 and Q_R2. Since U_C(1) is higher than V_BC, u_C discharges from U_C(1) to U_C(2), and the peak value of i_LC is I_LC(2). In this state, u_C and i_LC can be given by:

$$u_{\mathrm{C}}\left(t\right)=V_{\mathrm{BC}}+\left(U_{\mathrm{C}}(1)-V_{\mathrm{BC}}\right)\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_1\right)}\cdot \left(\cos \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_1\right)\right)+\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_1\right)\right)\right)$$

(6)

$$i_{\mathrm{LC}}\left(t\right)=\frac{\left(V_{\mathrm{BC}}-U_{\mathrm{C}}\left(1\right)\right)}{Z_{\mathrm{r}}\cdot \sqrt{1-{\xi }^2}}\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_1\right)}\cdot \sin \left({\omega }_{\mathrm{n}}\cdot \sqrt{1-{\xi }^2}\cdot \left(t-t_1\right)\right)$$

(7)

At the end of this state, i_LC reaches zero at t = t₂ = t₁ + Δt, u_C is positively charged to U_C(2):

$$U_C(2)=V_{\mathrm{BC}}+(V_{\mathrm{BC}}-U_C(1)){\mathrm{e}}^{-\frac{\xi \pi }{\sqrt{1-{\xi }^2}}}$$

(8)

In negative collect state Ⅲ [t₂–t₃]: during this state, switches S₆ and S₉ connect the release group (V_BR = V_B8 + V_B7 + V_B6) to the full-bridge LC resonant tank. The LC resonant tank is charged negatively using Q_L1 and Q_R2. Since U_C(2) is negatively lower than −V_BR, u_C is negatively charged from U_C(2) to U_C(3), and the peak value of i_LC is I_LC(3). In this state, u_C and i_LC can be given by:

$$u_{\mathrm{C}}\left(t\right)=V_{\mathrm{BC}}+\left(U_{\mathrm{C}}(1)-V_{\mathrm{BC}}\right)\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_2\right)}\cdot \left(\cos \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_2\right)\right)+\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_2\right)\right)\right)$$

(9)

$$i_{\mathrm{LC}}\left(t\right)=\frac{\left(-V_{\mathrm{BR}}-U_{\mathrm{C}}\left(2\right)\right)}{Z_{\mathrm{r}}\cdot \sqrt{1-{\xi }^2}}\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_2\right)}\cdot \sin \left({\omega }_{\mathrm{n}}\cdot \sqrt{1-{\xi }^2}\cdot \left(t-t_2\right)\right)$$

(10)

At the end of this state, i_LC reaches zero at t = t₃ = t₁ + 2Δt, u_C is negatively charged to U_C(3):

$$U_C(3)=-V_{\mathrm{BR}}+(-U_C(2)-V_{\mathrm{BR}}){\mathrm{e}}^{-\frac{\xi \pi }{\sqrt{1-{\xi }^2}}}$$

(11)

By substituting t into Equations (9) and (10), it can be found that the waveforms in Equations (9) and (10) are identical to those in Equations (2) and (3) except for the polarity.

In negative release state Ⅳ [t₃–t₄]: during this state, switches S₁ and S₂ connect the collect group (V_BC = V_B1) to the full-bridge LC resonant tank. The LC resonant tank negatively releases charges to V_BC using Q_L2 and Q_R1. Since U_C(3) is negatively higher than −V_BC, u_C negatively discharges from U_C(3) to U_C(4), and the peak value of i_LC is I_LC(4). In this state, u_C and i_LC can be given by:

$$u_{\mathrm{C}}\left(t\right)=-V_{\mathrm{BC}}+\left(U_{\mathrm{C}}(3)+V_{\mathrm{BC}}\right)\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_3\right)}\cdot \left(\cos \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_3\right)\right)+\frac{\xi }{\sqrt{1-{\xi }^2}}\sin \left({\omega }_{\mathrm{n}}\sqrt{1-{\xi }^2}\left(t-t_3\right)\right)\right)$$

(12)

$$i_{\mathrm{LC}}\left(t\right)=\frac{\left(-V_{\mathrm{BR}}-U_{\mathrm{C}}\left(3\right)\right)}{Z_{\mathrm{r}}\cdot \sqrt{1-{\xi }^2}}\cdot {\mathrm{e}}^{-\xi {\omega }_{\mathrm{n}}\left(t-t_3\right)}\cdot \sin \left({\omega }_{\mathrm{n}}\cdot \sqrt{1-{\xi }^2}\cdot \left(t-t_3\right)\right)$$

(13)

At the end of this state, i_LC reaches zero at t = t₄ = t₂ + 2Δt, u_C negatively discharges to U_C(4):

$$U_C(4)=-V_{\mathrm{BC}}+(-U_C(3)-V_{\mathrm{BC}}){\mathrm{e}}^{-\frac{\xi \pi }{\sqrt{1-{\xi }^2}}}$$

(14)

By substituting t into Equations (12) and (13), it can be found that the waveforms in Equations (12) and (13) are identical to those in Equations (6) and (7) except for the polarity.

Based on Equations (5), (8), (11) and (14), the capacitor voltage u_C and peak inductor current i_L in each state can be calculated by combining U_C(0) = U_C(4):

$$\left[\begin{array}{c}{U}_{\mathrm{C}}\left(0\right)\\ U_{\mathrm{C}}\left(1\right)\end{array}\right]=-\left[\begin{array}{c}{U}_{\mathrm{C}}\left(2\right)\\ U_{\mathrm{C}}\left(3\right)\end{array}\right]=\left[\begin{array}{c}k{V}_{\mathrm{BR}}-V_{\mathrm{BC}}\\ V_{\mathrm{BR}}+k{V}_{\mathrm{BC}}\end{array}\right]\times \frac{1+k}{1+k^2}$$

(15)

$$\left[\begin{array}{c}{I}_{\mathrm{LC}}\left(1\right)\\ I_{\mathrm{LC}}\left(2\right)\end{array}\right]=-\left[\begin{array}{c}{I}_{\mathrm{LC}}\left(3\right)\\ I_{\mathrm{LC}}\left(4\right)\end{array}\right]=\left[\begin{array}{c}{V}_{\mathrm{BR}}-U_{\mathrm{C}}\left(0\right)\\ V_{\mathrm{BC}}-U_{\mathrm{C}}\left(1\right)\end{array}\right]\times \frac{\sqrt{k}}{Z_{\mathrm{r}}\sqrt{1-{\xi }^2}}$$

(16)

where

$$k={\mathrm{e}}^{-\frac{\xi \pi }{\sqrt{1-{\xi }^2}}}$$

(17)

According to the analysis above, the release group will charge the capacitor in positive collect state I and in negative collect state Ⅲ. As a result, u_C rises from U_C(0) to U_C(1) positively and rises negatively from U_C(2) to U_C(3). According to (15), it also should be noticed that U_C(0)–U_C(1) and U_C(2)–U_C(3) are equal. As the total duration of one switching period is 4Δt, the average power released by the release group can be expressed as:

$$P_{\mathrm{R}}=\frac{V_{\mathrm{BR}}\sqrt{1-{\xi }^2}}{2\mathsf{\pi }{Z}_{\mathrm{r}}}\cdot \frac{\left(1-k^2\right)V_{\mathrm{BR}}+{\left(1+k\right)}^2{V}_{\mathrm{BC}}}{1+k^2}$$

(18)

Similarly, the capacitor will charge the collect group in positive release state II and in negative release state IV. As a result, u_C falls from U_C(1) to U_C(2) positively and falls negatively from U_C(3) to U_C(4). Therefore, the average power received by the collect group can be expressed as:

$$P_{\mathrm{C}}=\frac{V_{\mathrm{BR}}\sqrt{1-{\xi }^2}}{2\mathsf{\pi }{Z}_{\mathrm{r}}}\cdot \frac{\left(1-k^2\right)V_{\mathrm{BR}}+{\left(1+k\right)}^2{V}_{\mathrm{BC}}}{1+k^2}$$

(19)

Based on (18) and (19), the balancing efficiency η_FBBRLCC can be calculated as:

$${\eta }_{\mathrm{FBBRLCC}}=\frac{P_{\mathrm{C}}}{P_{\mathrm{R}}}=\frac{V_{\mathrm{BC}}}{V_{\mathrm{BR}}}\times \left(\frac{\left(1+k\right)V_{\mathrm{BR}}-\left(1-k\right)V_{\mathrm{BC}}}{\left(1-k\right)V_{\mathrm{BR}}+\left(1+k\right)V_{\mathrm{BC}}}\right)$$

(20)

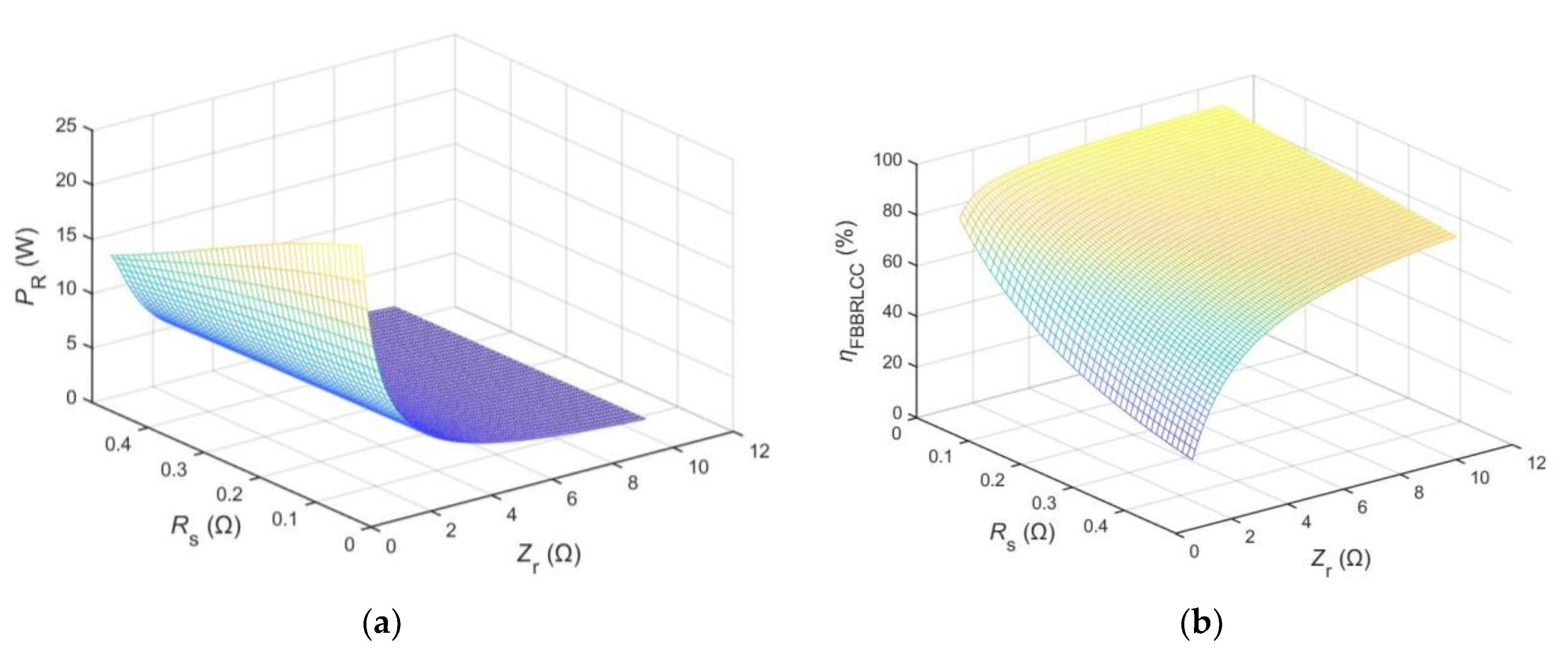
Based on Equations (18) and (20), Figure 5a presents the average power P_R versus Z_r and R_eq and Figure 5b presents the balancing efficiency η_FBBRLCC versus Z_r and R_eq when V_BR = 12 V and V_BC = 3.9 V. From Figure 5, we can observe that, as the total parasitic resistance R_eq decreases, both the balancing efficiency η_FBBRLCC and the average power P_R increase. As a result, the total parasitic resistance R_eq should be minimized to achieve a maximum average power P_R and a maximum balancing efficiency η_FBBRLCC. It can also be observed that, when the total parasitic resistance R_eq is determined, a larger Z_r will result in a higher η_FBBRLCC, while a smaller Z_r will result in a higher P_R, which can be used to adjust the average power and the balancing efficiency by changing Z_r.

3. Simulation Comparison with Conventional Equalizers

In this section, we use the PSIM9.1.3 simulation software to simulate the proposed equalizer and several classic equalizers. The objects of the simulation are the proposed full-bridge bipolar-resonant LC converter (FBBRLCC) equalizer, quasi-resonant switched-capacitor converter (QRSSC) equalizer [24], the half-bridge LC converter (HBLCC) equalizer [32], and the bipolar-resonant LC converter (BRLCC) equalizer [21]. To reduce the simulation time, we used eight 0.01 F capacitors instead of the batteries for the simulation [21]. All simulation models have the same parameters of L = 10 µH, C = 1 µF.

At the same time, due to the different structures of different equalizers, the values of the total parasitic resistance R_eq in different equalizers are different. Suppose the total resistance R_LC of the LC resonant is 0.16 Ω and the ON-resistance of a MOSFET is 0.01 Ω. As a result, the total parasitic resistance R_eq of the equalizers above are 0.24 Ω, 0.18 Ω, 0.2 Ω, and 0.2 Ω, respectively.

Figure 6 shows the flowchart for the control strategy of the proposed FBBRLCC equalizer. The balancing process will start when the maximum voltage difference V_Bmax–V_Bmin is more than 10 mV.

To compare the four equalizers above, two voltage distributions are set, namely initial voltage #1 and initial voltage #2. The initial voltage #1 of V_B1 = 3.75 V, V_B2 = 4.20 V, V_B3 = 4.10 V, V_B4 = 4.00 V, V_B5 = 3.85 V, V_B6 = 3.74 V, V_B7 = 3.72 V, and V_B8 = 3.70 V is used to simulate the emergency discharge of B₂, B₃ and B₄, which are close to full-charged. The initial voltage #2 of V_B1 = 3.50 V, V_B2 = 3.48 V, V_B3 = 3.46 V, V_B4 = 3.44 V, V_B5 = 3.42 V, V_B6 = 3.10 V, V_B7 = 3.05 V, and V_B8 = 3.00 V is used to simulate the emergency charge of B₆, B₇ and B₈, which are close to full-discharged. The simulation results are shown in Figure 7 and are summarized in

Table 1. Simulation comparison of different equalizers with initial voltages #1 and #2.

Equalizer	Initial Voltage #1		Initial Voltage #2
	Time	Efficiency	Time	Efficiency
QRSCC [24]	0.20640 s	94.21%	0.23240 s	93.55%
HBLCC [32]	0.06448 s	95.76%	0.06877 s	93.46%
BRLCC [21]	0.00835 s	86.86%	0.01064 s	89.15%
Proposed FBBRLCC	0.00826 s	86.23%	0.01006 s	88.68%

.

Based on the results in Table 1, it can be seen that, for both the initial voltages #1 and the initial voltages #2, the proposed FBBRLCC equalizer takes the shortest time to achieve equalization. Meanwhile, at the initial voltages #1, the balancing speed of the FBBRLCC equalizer is 23 times that of the QRSCC equalizer, 6.8 times that of the HBLCC equalizer, 1.1 times that of the BRLCC equalizer, and at the initial voltages #2, the balancing speed of the FBBRLCC equalizer is 25 times that of the QRSCC equalizer, 7.8 times that of the HBLCC equalizer, 1.01 times that of the BRLCC equalizer. The energy transfer efficiencies of the proposed FBBRLCC equalizer are 86.23% and 88.68%, at the initial voltages #1 and the initial voltages #2, respectively. It is worth mentioning that, in the two voltage distributions, the balancing speed of the proposed equalizer is slightly faster than that of the BRLCC equalizer, and the efficiencies of the two equalizers are very close, and are slightly lower than the other two equalizers. It is reasonable that faster balancing speed means higher balancing current, which will incur more losses and lead to a slight decrease in efficiency. Compared with the decrease in balancing efficiency, the increase in balancing speed is significant. In addition, compared to the BRLCC equalizer, the proposed FBBRLCC equalizer reduces the number of switches by nearly half, which means fewer MOSFET drivers and higher reliability. As a result, it is worthwhile taking such a trade-off.

To figure out how the balancing time scales with cell capacity,

Table 2. Simulation comparison of the influence of different cell capacities on balancing time under the initial voltages #1.

Equalizer	Cell Capacity of Simulation
	0.001 F	0.005 F	0.01 F	0.02 F	0.05 F
QRSCC [24]	0.02282 s	0.11544 s	0.20640 s	0.46157 s	1.15661 s
HBLCC [32]	0.00634 s	0.03321 s	0.06448 s	0.13291 s	0.33239 s
BRLCC [21]	0.00089 s	0.00430 s	0.00835 s	0.01690 s	0.04258 s
Proposed FBBRLCC	0.00088 s	0.00419 s	0.00826 s	0.01568 s	0.03934 s

and

Table 3. Simulation comparison of the influence of different cell capacities on balancing time under the initial voltages #2.

Equalizer	Cell Capacity of Simulation
	0.001 F	0.005 F	0.01 F	0.02 F	0.05 F
QRSCC [24]	0.02323 s	0.11571 s	0.23240 s	0.46367 s	1.15756 s
HBLCC [32]	0.00681 s	0.03360 s	0.06877 s	0.15016 s	0.37573 s
BRLCC [21]	0.00108 s	0.00531 s	0.01064 s	0.02051 s	0.05334 s
Proposed FBBRLCC	0.00102 s	0.00504 s	0.01006 s	0.01994 s	0.05315 s

respectively show the influence of different cell capacities on balancing time under the initial voltages #1 and the initial voltages #2. According to the results in Table 2 and Table 3, under the two voltage distributions, the increase of cell capacity of simulation makes the time for all equalizers to achieve equalization longer, but the order of equalizers’ balancing speed does not change.

4. Experiment

In this section, an experimental prototype for eight cells is built to verify the performance of the proposed FBBRLCC equalizer, as shown in Figure 8. An STM32 (STM32F103VET6) is used as the controller for the FBBRLCC equalizer and gives the driving signals to the FBBRLCC equalizer through the gate driver board. The parameters of the prototype are present in

Table 4. The parameters of the prototype.

Components		Parameters
Inductor L	Ferrite inductance	10 µH
Capacitor C	CBB	1 µF
Switches	nMOSFET	IRF3205PBF
Gate Drivers	MOSFET driver	1EDI20N12AFXUMA1
Free-wheeling Diodes	Schottky diode	MBRS360BT3G
Battery Pack	Lithium-ion battery	ICR18650-22F (2200 mAh)

.

Figure 9 shows the experimental waveforms of the proposed FBBRLCC equalizer in different operating modes. The inductor current i_LC waveforms indicates that, at the end of each state, the inductor current i_LC will drop to zero and ZCS is realized.

To verify the accuracy of the mathematical model analysis in Section 2.3, the measured data and the theoretical values are compared in

Table 5. Experimentally measured data of the proposed FBBRLCC equalizer in different operating modes.

Mode	VBR/V	VBC/V	ILC (1) /A	ILC (2) /A	PR/W	PC/W		ηFBBRLCC/%
						Exp.	Model	Exp.	Model	Error
1-1	3.903	3.871	1.52	1.36	1.888	1.676	1.437	88.77	90.54	−1.80
1-3	3.995	11.583	4.05	1.19	5.150	4.388	4.642	85.19	83.14	−2.05
3-1	11.487	3.929	1.38	3.50	5.046	4.377	4.447	86.75	85.22	1.52
3-3	11.287	11.750	3.96	3.32	14.227	12.417	12.584	87.28	90.06	−3.32

. The voltages are measured using a BQ76PL455 16-cell battery monitor, and the currents I_LC (1) and I_LC (2) are measured by a CYBERTEK CP8030H current probe. In the 1-1 mode, when V_BR and V_BC are set to 3.903 V and 3.871 V, respectively, the average power P_C is about 1.888 W and the balancing efficiency is 88.77%. In the 1-3 mode, when V_BR and V_BC are set to 3.995 V and 11.583 V, respectively, the average power P_C is about 5.150 W and the balancing efficiency is 85.19%. In the 3-1 mode, when V_BR and V_BC are set to 11.487 V and 3.929 V, respectively, the average power P_C is about 5.049 W and the balancing efficiency is 86.75%. In the 3-3 mode, when V_BR and V_BC are set to 11.287 V and 11.750 V, respectively, the average power P_C is about 14.227 W and the balancing efficiency is 87.28%. The above experimental results prove that the average power of the proposed FBBRLCC equalizer in the four operating modes are from 1.888 W to 14.227 W with the balancing efficiencies from 85.19% to 88.77%.

Figure 10 shows the balancing experiments for eight cells with initial voltages #1 and #2. Since we let the equalizer equalize for 20 s and then rest for 10 s, the voltage curve is cyclical [21,32]. With the initial voltage #1, the balancing voltage waveform of the proposed FBBRLCC equalizer is shown in Figure 10a, and the proposed FBBRLCC equalizer takes about 149 min to realize equalization. With the initial voltage #2, the balancing voltage waveform of the proposed FBBRLCC equalizer is shown in Figure 10b, and the proposed FBBRLCC equalizer takes about 46 min to realize equalization. These two experiments with initial voltages #1 and #2 prove that the proposed FBBRLCC equalizer has the ability to equalize quickly.

It can be seen from the above experimental results, compared with the experimental results of the equalizer in [21], both of them have excellent balancing speed and efficiency, and the proposed equalizer has a great advantage in terms of size.

5. Discussion

For a comprehensive evaluation of the proposed FBBRLCC equalizer,

Table 6. Comparison of equalizers for n cells in terms of size, efficiency, balancing speed, and type.

Equalizer	Component Number					Size	Efficiency	Speed	Type
	MOSFET	MOSFET Driver	Inductor	Capacitor	Diode
QRSCC [24]	2n	2n	n − 1	n − 1	0	Large	High	Slow	AC2C
CI [26]	4(n − 1)	4(n − 1)	2(n − 1)	0	0	Large	Medium	Slow	AC2C
FBLCC [27]	2n + 10	n + 5	1	1	4	Small	High	Medium	DC2C
HBLCC [32]	4n	2n	1	1	4	Medium	High	Medium	MC2MC
BRLCC [21]	4(n + 1)	2(n + 1)	1	1	4	Medium	High	Fast	MC2MC
Proposed FBBRLCC	2n + 10	n + 5	1	1	4	Small	High	Fast	MC2MC

compares it with several traditional equalizers in terms of size, efficiency, balancing speed, and type in the case of n cells.

Table 7. Costs of different experimental prototypes.

Equalizer	Component Number					Costs ($)	Type
	MOSFET	MOSFET Driver	Inductor	Capacitor	Diode
QRSCC [24]	216	216	95	95	0	292.0	AC2C
CI [26]	380	380	190	0	0	494.0	AC2C
FBLCC [27]	346	173	13	13	4	225.8	DC2C
HBLCC [32]	432	216	13	13	52	277.4	MC2MC
BRLCC [21]	484	242	13	13	52	308.6	MC2MC
Proposed FBBRLCC	346	173	13	13	52	225.8	MC2MC

gives the costs of different experimental prototypes under the assumption that the battery pack has 96 series-connected cells and is divided into 12 battery modules [21]. Each module manages eight cells, and the pack manages twelve modules. Taking the proposed FBBRLCC equalizer as an example: each module needs 2 × (9 + 4) = 26 MOSFETs, and the pack needs 2 × (13 + 4) = 34 MOSFETs, so the total number of MOSFETs is 26 × 12 + 52 = 346. The component prices per unit are approximated as: MOSFET ($0.2), MOSFET Driver ($0.8), Inductor ($0.6), Capacitor ($0.2), Diode ($0.15) [21].

The AC2C equalizers based on quasi-resonant switched-capacitor converters (QRSSC) in [24] and based on coupled inductors (CI) in [26] can only transfer energy between adjacent batteries, which results in large size and slow balancing speed. Compared with the CI, the QRSSC realizes ZCS; as a result, it has higher balancing efficiency.

The DC2C equalizer based on a full-bridge LC converter (FBLCC) in [27] achieves direct equalization of the more-charged battery and the less-charged battery by using a common energy storage unit, so it has small size. However, only one pair of batteries can be balanced at a time, and the other batteries have to wait, which reduces the balancing speed. Meanwhile, the QRSSC realizes ZCS, so its balancing efficiency is high.

The MC2MC equalizer based on half-bridge LC converter (HBLCC) in [32] and bipolar-resonant LC converter (BRLCC) in [21] can transfer the energy from consecutive more-charged cells to consecutive less-charged cells. As a result, both have a high balancing speed, but the HBLCC cannot realize step-up conversion, which will slow down the balancing speed. At the same time, both realize ZCS, so they have a high balancing efficiency. Thus, the BRLCC has a better performance. However, due to its symmetric switch matrix structure, the number of switches will increase dramatically as the number of batteries increases, which makes circuit size large with low reliability. The proposed FBBRLCC equalizer not only achieves faster balancing speed by transferring energy from consecutive odd numbers of more-charged cells to consecutive odd numbers of less-charged cells, but also greatly reduces the size of the circuit by reducing the number of switches. Due to the structure of the proposed FBBRLCC equalizer, it could only achieve an equalization between consecutive odd number of cells and consecutive odd number of cells, as a result, it has fewer operation modes than the BRLCC equalizer. Compared with the increase in balancing speed and the reduction in circuit size, the decrease in balancing efficiency is insignificant and can still be maintained at a high level.

6. Conclusions

In this paper, a full-bridge bipolar-resonant LC converter (FBBRLCC) equalizer is proposed and an experimental prototype for eight cells is built to verify the performance of the proposed FBBRLCC equalizer. The circuit structure, operation principle, and mathematical model are presented. Simulation comparison with the traditional equalizer is done to prove that the proposed equalizer can achieve fast equalization while maintaining high equalization efficiency and small size. The final experimental results present that the proposed FBBRLCC equalizer can transfer energy from consecutive odd more-charged cells to consecutive odd less-charged cells, which increases the balancing speed but requires a small sacrifice in balancing efficiency. While the balancing efficiencies of the proposed FBBRLCC equalizer in the different operating modes still could keep from 85.19% to 88.77% with the average power from 1.888 W to 14.227 W. Meanwhile, compared with the two MC2MC equalizers HBLCC and BRLCC, the proposed FBBRCC not only implements MC2MC equalization, but also greatly reduces the circuit size by reducing the number of switches by nearly half, as well as the circuit reliability.