Quantitative Design for the Battery Equalizing Charge/Discharge Controller of the Photovoltaic Energy Storage System
Abstract
:1. Introduction
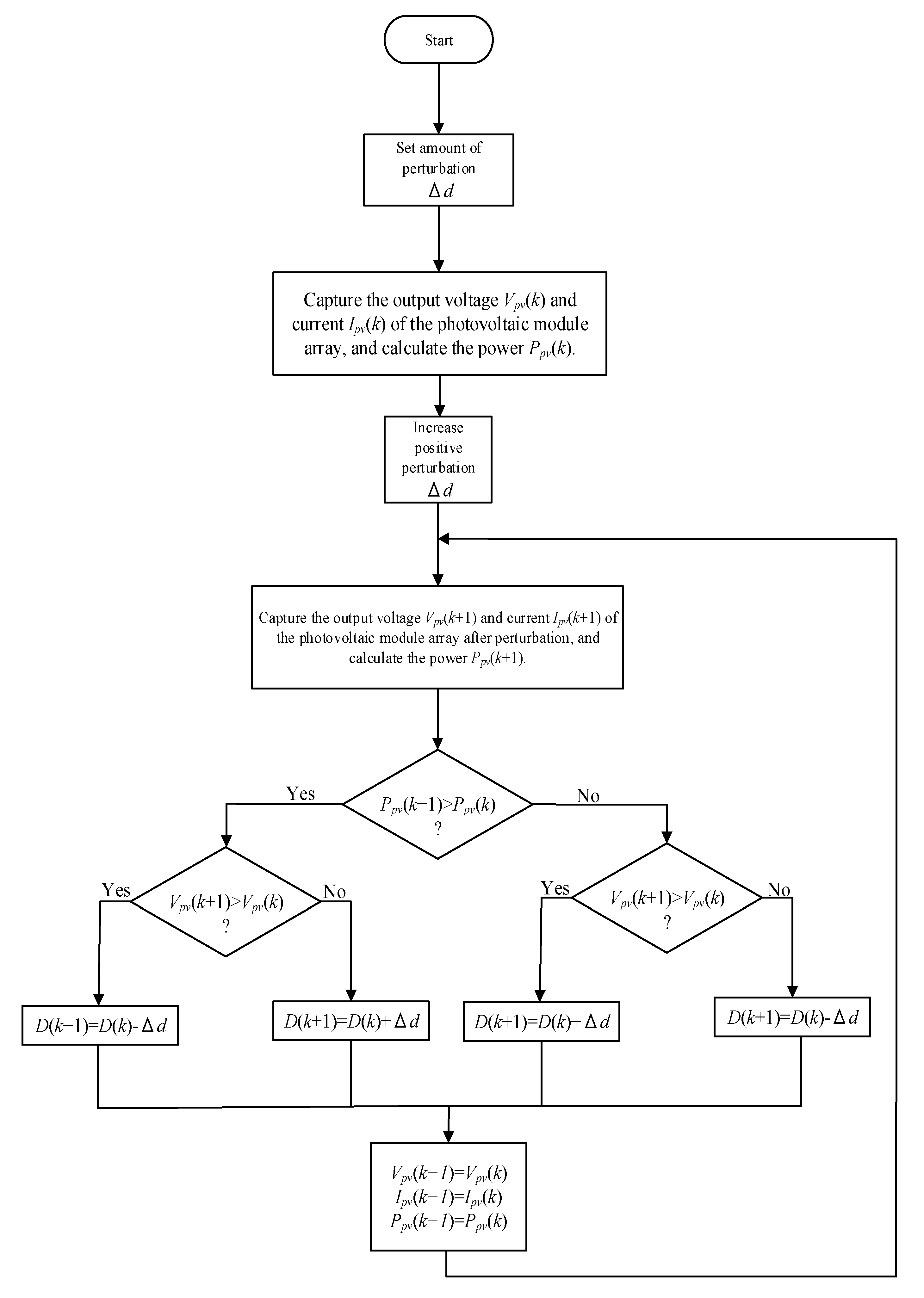
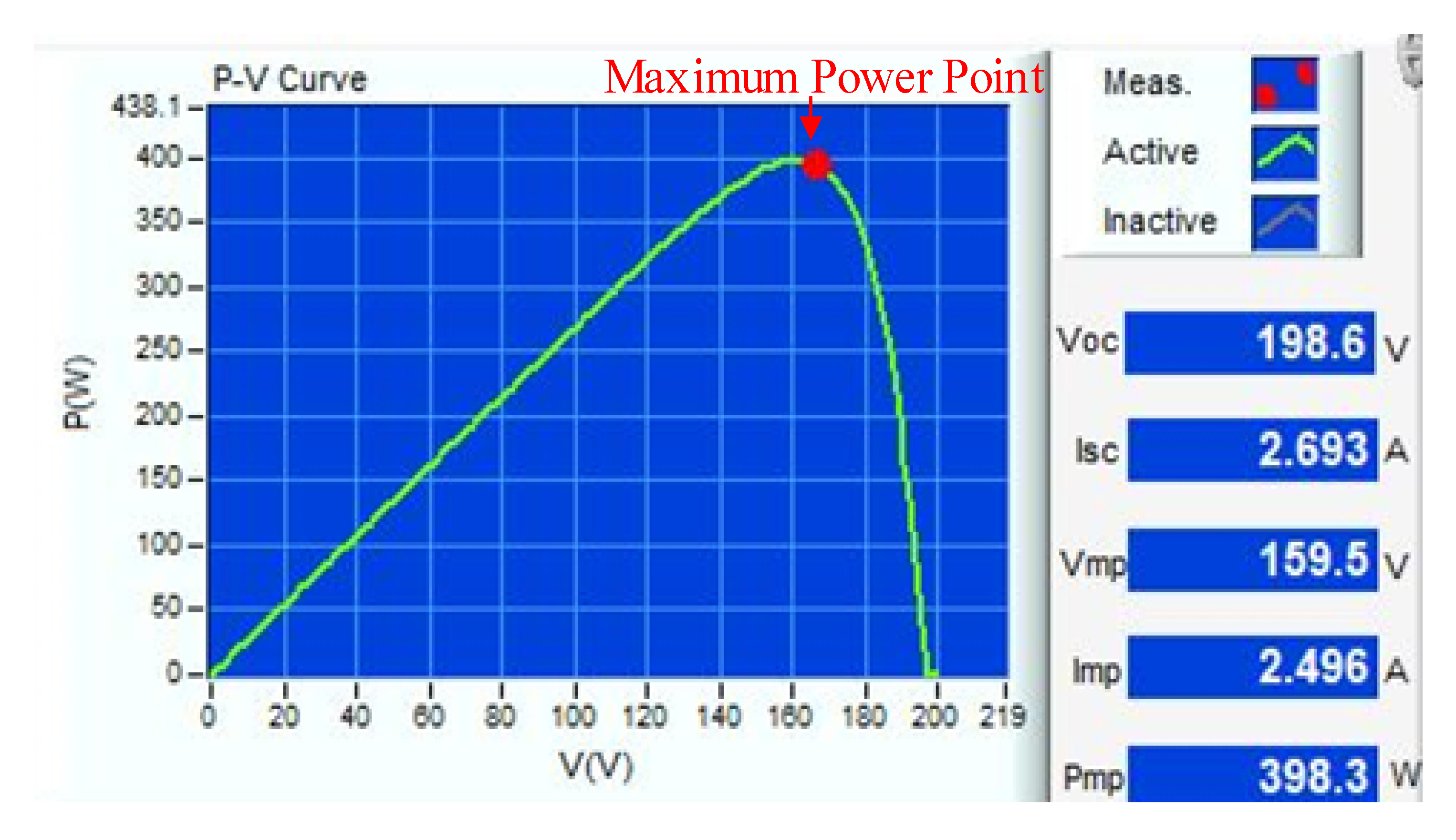
2. The Adopted MPPT Method
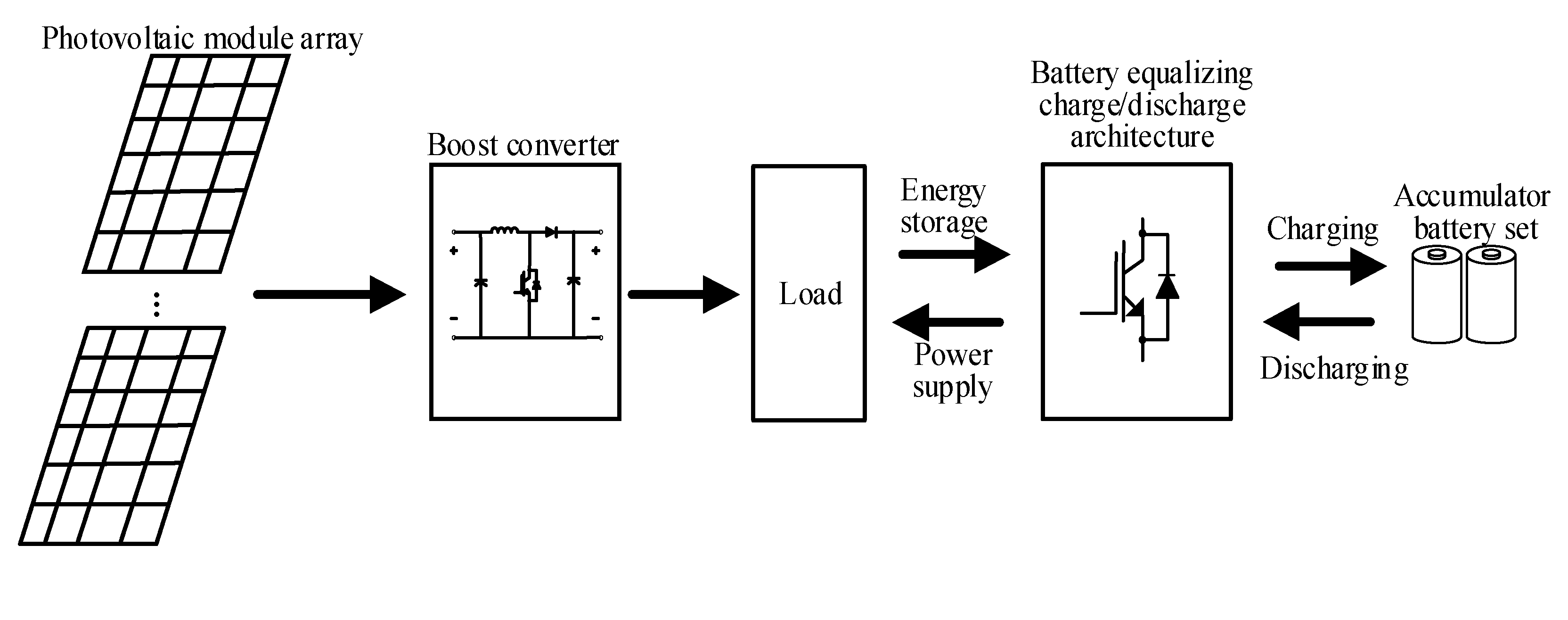
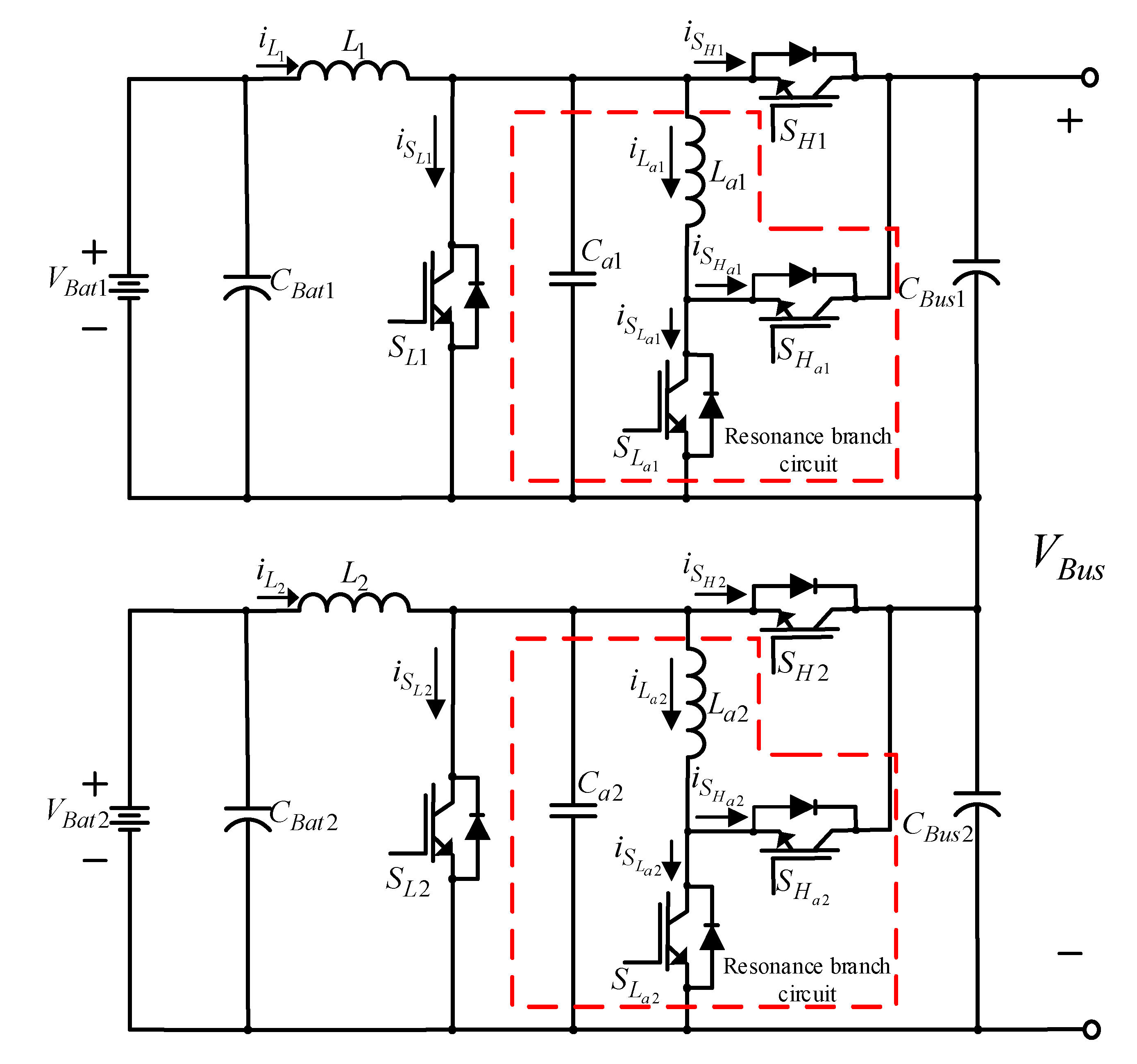
3. The Adopted Equalizing Charge/Discharge Architecture
4. Quantitative Design of the Bidirectional Buck–Boost Soft-Switching Converter Controller
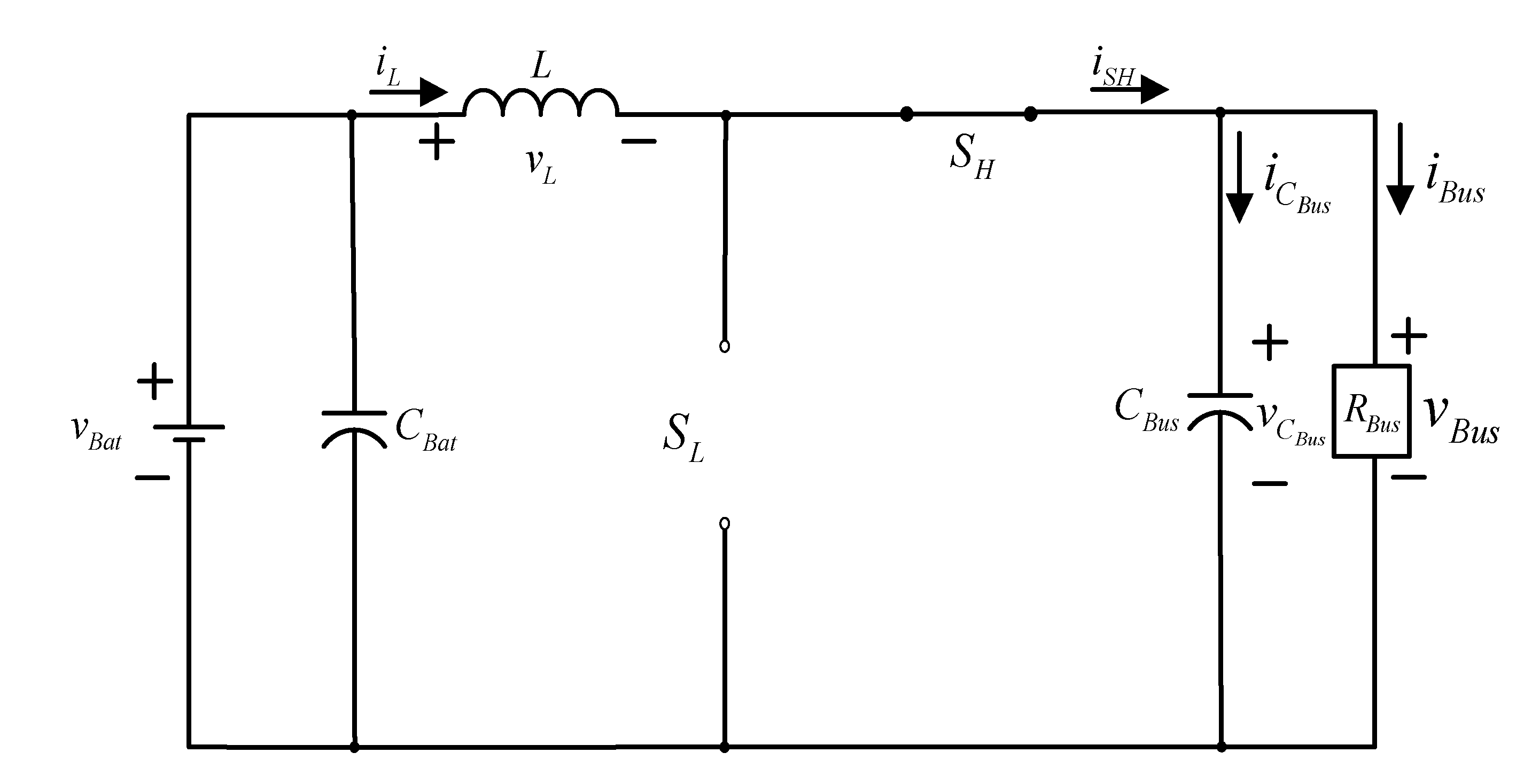
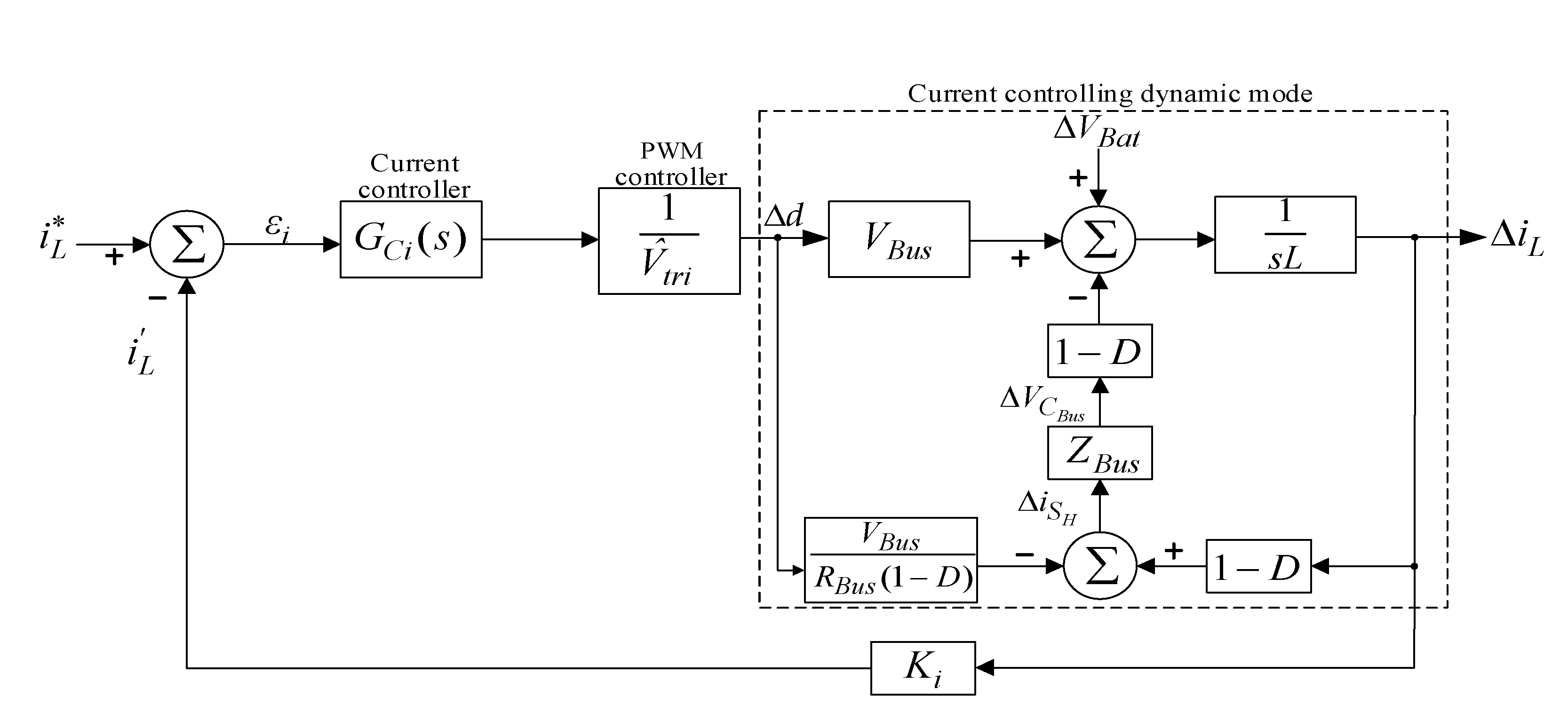
4.1. Quantitative Design of the Current Controller
4.1.1. Conducting State of Low-Voltage Side Switch SL ()
4.1.2. Cut-Off State of Low-Voltage Side Switch SL ()
4.1.3. Steady State
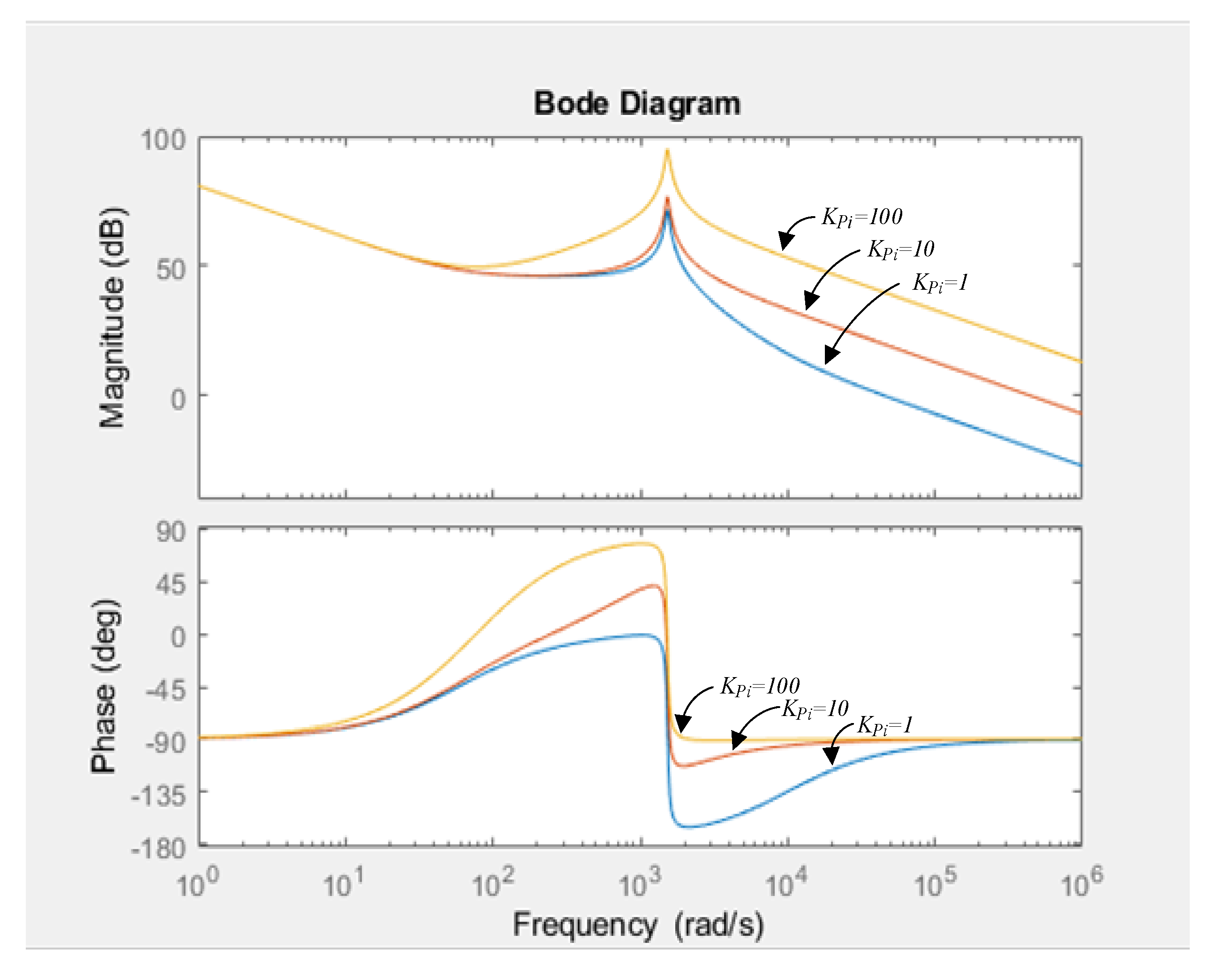
4.1.4. Dynamic State
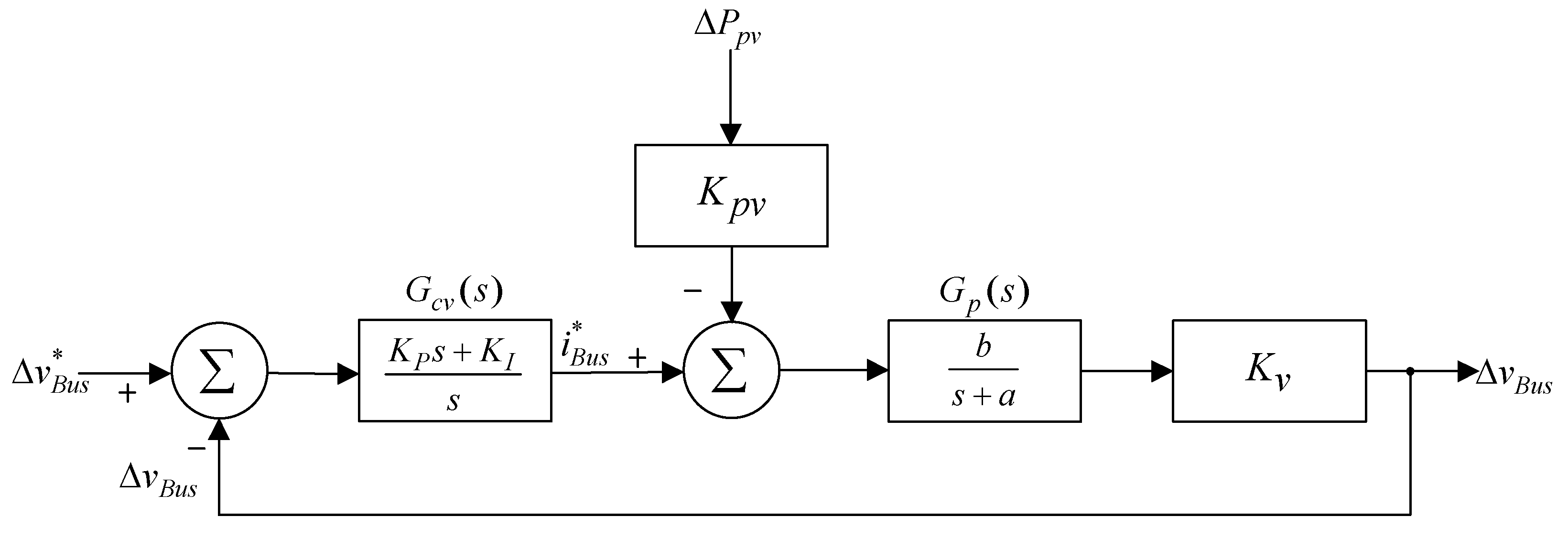
4.2. Dynamic Mode Estimation
- (a)
- When carrying out estimation mode, the proportional controller is adopted as the voltage controller, making Gcv(s) = KP = 10, then selecting an operating point (VBus = 180 V, P = 300 W), setting this system operation as closed-loop control. This paper hypothesizes that the dynamic model of the bidirectional buck–boost converter can be derived using the step response estimation method. Therefore, the parameter KP of the proportional controller is given at will as long as the step response is without overshoot.
- (b)
- Given a step command (, Kv = 0.01, voltage VBus at high-voltage side increases from 180 V→240 V), then the measured variable waveform for the DC-link VBus voltage is shown in Figure 9; its steady-state voltage is at 220 V. The step command change Δv*Bus is also given arbitrarily, and Kv is the conversion factor of the voltage sensor.
- (c)
- Under the same operating conditions, given a set sunlight variation, so the output power variation is , which is Ppv from 1000 W→900 W, the measured DC-link voltage VBus variable waveform is shown in Figure 10, and the steady-state voltage is at 173 V.
- (d)
- The transfer functions for to and to can be derived from Figure 8 as shown in Equations (17) and (18), respectively.
- (e)
- From the DC-link voltage step response shown in Figure 9, the steady-state value and the time to reach times the steady-state value can be observed and the parameters can be calculated as = 53.77 and r = 80.65.
- (f)
- The steady-state response of power step change can be obtained against DC-link voltage from Figure 10 and calculate = 0.056 and Kpv = 0.00967 from Equation (18).
- (g)
- a = 26.88 and b = 537.7 can be estimated from Equation (17); therefore, the transfer function Gp(s) of the bidirectional soft-switching converter can be written as:
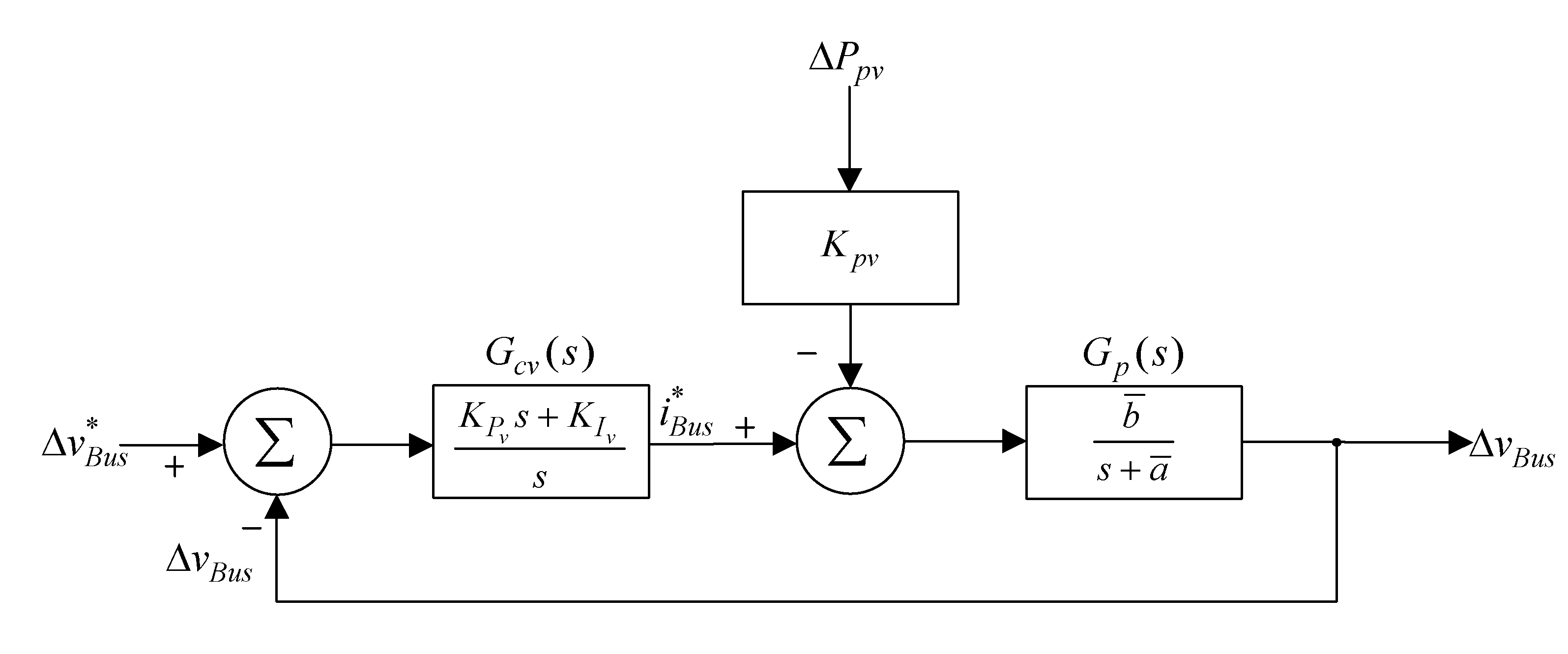
4.3. Quantitative Design of the Voltage Controller
5. Test Results
5.1. Response Performance Comparison between Quantitative Design and Traditional P-I Controller
- (1)
- Non-overshoot.
- (2)
- No steady-state error.
- (3)
- From the maximum voltage drop induced by the step sunlight variation (that is, photovoltaic module array output power variation) (meaning ).
- (4)
- From the voltage recovery time induced by the step sunlight variation .
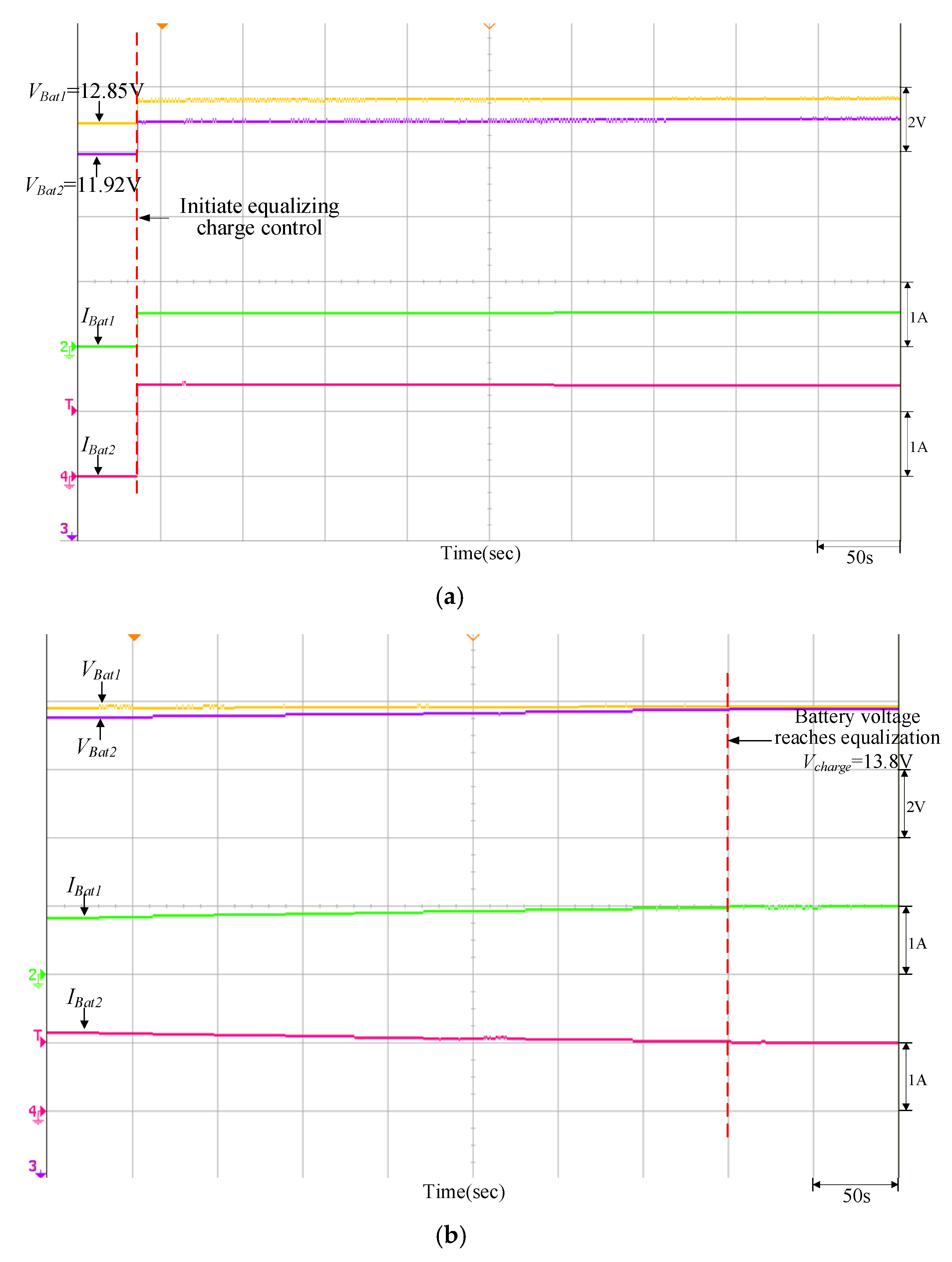
5.2. Response Test for the Photovoltaic Array Combined with the Equalizing Charge/Discharge Controller
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Botelho, A.; Pinto, L.M.C.; Louren-Gomes, L.; Valente, M.; Social, S. Sustainability of Renewable Energy Sources in Electricity Production: An Application of the Contingent Valuation Method. Sustain. Cities Societ. 2016, 26, 429–437. [Google Scholar] [CrossRef]
- Okonkwo, P.C.; Mansir, I.B.; Barhoumi, E.M.; Emori, W.; Radwan, A.B.; Shakoor, R.A.; Uzoma, P.C.; Pugalenthi, M.R. Utilization of Renewable Hybrid Energy for Refueling Station in Al-Kharj, Saudi Arabia. Int. J. Hhydr. Energy 2022, 47, 22273–22284. [Google Scholar] [CrossRef]
- Alhousni1, F.K.; Ismail1, F.B.; Okonkwo, P.C.; Mohamed, H.; Okonkwo, B.O.; Al-ShahriA, O.A. Review of PV Solar Energy System Operations and Applications in Dhofar Oman. AIMS Energy 2022, 10, 858–884. [Google Scholar] [CrossRef]
- Pérez-Deniciaa, E.; Fernández-Luqueñob, F.; Vilariño-Ayalac, D.; Montaño-Zetinad, L.M.; Maldonado-López, L.A. Renewable Energy Sources for Electricity Generation in Mexico: A Review. Renew. Sust. Energy Rev. 2017, 78, 597–613. [Google Scholar] [CrossRef]
- Beitelmal, W.H.; Okonkwo, P.C.; Housni, F.A.; Grami, S.; Emori, W.; Uzoma, P.C.; Das, B.K. Renewable Energy as a Source of Electricity for Murzuq Health Clinic during COVID-19. MRS Energy Sustain. 2022, 9, 79–93. [Google Scholar] [CrossRef]
- Chao, K.H.; Huang, B.Z.; Jian, J.J. An Energy Storage System Composed of Photovoltaic Arrays and Batteries with Uniform Charge/Discharge. Energies 2022, 15, 2883. [Google Scholar] [CrossRef]
- Ramireddy, K.; Hirpara, Y.; Kumar, Y.V.P. Transient performance analysis of buck boost converter using various PID gain tuning methods. In Proceedings of the 12th International Conference on Computational Intelligence and Communication Networks (CICN), Bhimtal, India, 25–26 September 2020; pp. 321–326. [Google Scholar]
- Lei, W.; Li, C.; Chen, M.Z.Q. Robust Adaptive Tracking Control for Quadrotors by Combining PI and Self-tuning Regulator. IEEE Trans. Control Syst. Technol. 2019, 27, 2663–2671. [Google Scholar] [CrossRef]
- Kaicheng, D.; Yan, Z.; Jinjun, L.; Pengxiang, Z.; Jinshui, Z. Dynamic performance improvement of bidirectional switched-capacitor DC/DC converter by right-half-plane zero elimination. In Proceedings of the International Power Electronics Conference (IPEC-Niigata 2018-ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 4181–4185. [Google Scholar]
- Kesarkar, A.A.; Narayanasamy, S. Asymptotic Magnitude Bode Plots of Fractional-order Transfer Functions. IEEE/CAA J. Autom. Sin. 2019, 6, 1019–1026. [Google Scholar] [CrossRef]
- Tufenkci, S.; Senol, B.; Alagoz, B.B. Disturbance rejection fractional order PID controller design in V-domain by particle swarm optimization. In Proceedings of the International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, 21–22 September 2019; pp. 1–6. [Google Scholar]
- Nicola, M.; Nicola, C.I. Improved performance of grid-connected photovoltaic system based on fractional-order PI controller and particle swarm optimization. In Proceedings of the 9th International Conference on Modern Power Systems (MPS), Cluj-Napoca, Romania, 16–17 June 2021; pp. 1–5. [Google Scholar]
- Tufenkci, S.; Senol, B.; Alagoz, B.B. Stabilization of fractional order PID controllers for time-delay fractional order plants by using genetic algorithm. In Proceedings of the International Conference on Artificial Intelligence and Data Processing (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–6. [Google Scholar]
- Peng, C.C.; Lee, C.L. Performance demands based servo motor speed control: A genetic algorithm proportional-integral control parameters design. In Proceedings of the International Symposium on Computer, Consumer and Control (IS3C), Taichung City, Taiwan, 13–16 November 2020; pp. 469–472. [Google Scholar]
- Wang, Y.; Ying, Z.; Zhang, W. Unified sliding mode control of boost converters with quantitative dynamic and static performances. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society (IECON 2020), Singapore, 18–21 October 2020; pp. 3271–3276. [Google Scholar]
- Mohanty, S.; Choudhury, A.; Pati, S.; Kar, S.K.; Khatua, S. A comparative analysis between a single loop PI, double loop PI and sliding mode control structure for a buck converter. In Proceedings of the 1st Odisha International Conference on Electrical Power Engineering, Communication and Computing Technology (ODICON), Bhubaneswar, India, 8–9 January 2021; pp. 1–6. [Google Scholar]
- Li, Z.; Yuan, Y.; Wang, H.N. Fuzzy adaptive time-delay feedback controlling chaos in buck converter. In Proceedings of the Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4732–4737. [Google Scholar]
- Aarti, D.S.; Arun, N.K. Liquid level control of quadruple conical tank system using linear PI and fuzzy PI controllers. In Proceedings of the 2nd International Conference for Emerging Technology (INCET), Belagavi, India, 21–23 May 2021; pp. 1–5. [Google Scholar]
- Liu, Z.H.; Nie, J.; Wei, H.L.; Chen, L.; Li, X.H.; Lv, M.Y. Switched PI Control Based MRAS for Sensorless Control of PMSM Drives Using Fuzzy-logic-controller. IEEE J. Power Electron. 2022, 3, 368–381. [Google Scholar] [CrossRef]
- Naung, Y.; Anatolii, S.; Lin, Y.H. Speed control of DC motor by using neural network parameter tuner for PI-controller. In Proceedings of the IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (EIConRus), Saint Petersburg and Moscow, Russia, 28–31 January 2019; pp. 2152–2156. [Google Scholar]
- Chao, K.H.; Huang, C.H. Bidirectional DC-DC Soft-switching Converter for Stand-alone Photovoltaic Power Generation Systems. IET Power Electron. 2014, 7, 1557–1565. [Google Scholar] [CrossRef]
- Jian, J.J. Energy Storage System with Uniform Battery Charging and Discharging Control. Master’s Thesis, National Chin-Yi University of Technology, Taichung City, Taiwan, 23 July 2020. [Google Scholar]
- Ram, J.P.; Pillai, D.S.; Rajasekar, N.; Strachan, S.M. Detection and Identification of Global Maximum Power Point Operation in Solar PV Applications Using a Hybrid ELPSO-P&O Tracking Technique. IEEE Trans. Emerg. Sel. Topics Power Electron. 2020, 8, 1361–1374. [Google Scholar]
- Tang, C.Y.; Wu, H.J.; Liao, C.Y.; Wu, H.H. An Optimal Frequency-modulated Hybrid MPPT Algorithm for the LLC Resonant Converter in PV Power Applications. IEEE Trans. Power Electron. 2022, 37, 944–954. [Google Scholar] [CrossRef]
- TMS320F2809 Data Manual, Texas Instruments. October 2003. Available online: https://www.ti.com/lit/ds/symlink/tms320f2809.pdf?ts=1594465026502&ref_url=https%253A%252F%252Fwww.ti.com%252Fprodu107ct%252FTMS320F2809.pdf (accessed on 23 August 2022).
- Gao, Z.H.; Xie, H.C.; Yang, X.B.; Niu, W.F.; Li, S.; Chen, S.Y. The Dilemma of C-Rate and Cycle Life for Lithium-Ion Batteries under Low Temperature Fast Charging. Batteries 2022, 8, 234. [Google Scholar] [CrossRef]
- Chen, P.Y.; Chao, K.H.; Chen, H.J. Modeling and Quantitative Design of a Controller for a Bidirectional Converter with High Voltage Conversion Ratio. Int. J. Innov. Comput. Inf. Control 2018, 14, 2203–2219. [Google Scholar]
- R&S®NGL200/NGM200 Power Supply Series User Manual. Available online: https://scdn.rohde-schwarz.com/ur/pws/dl_downloads/pdm/cl_manuals/user_manual/1178_8736_01/NGL200_NGM200_UserManual_en_10.pdf. (accessed on 23 August 2022).








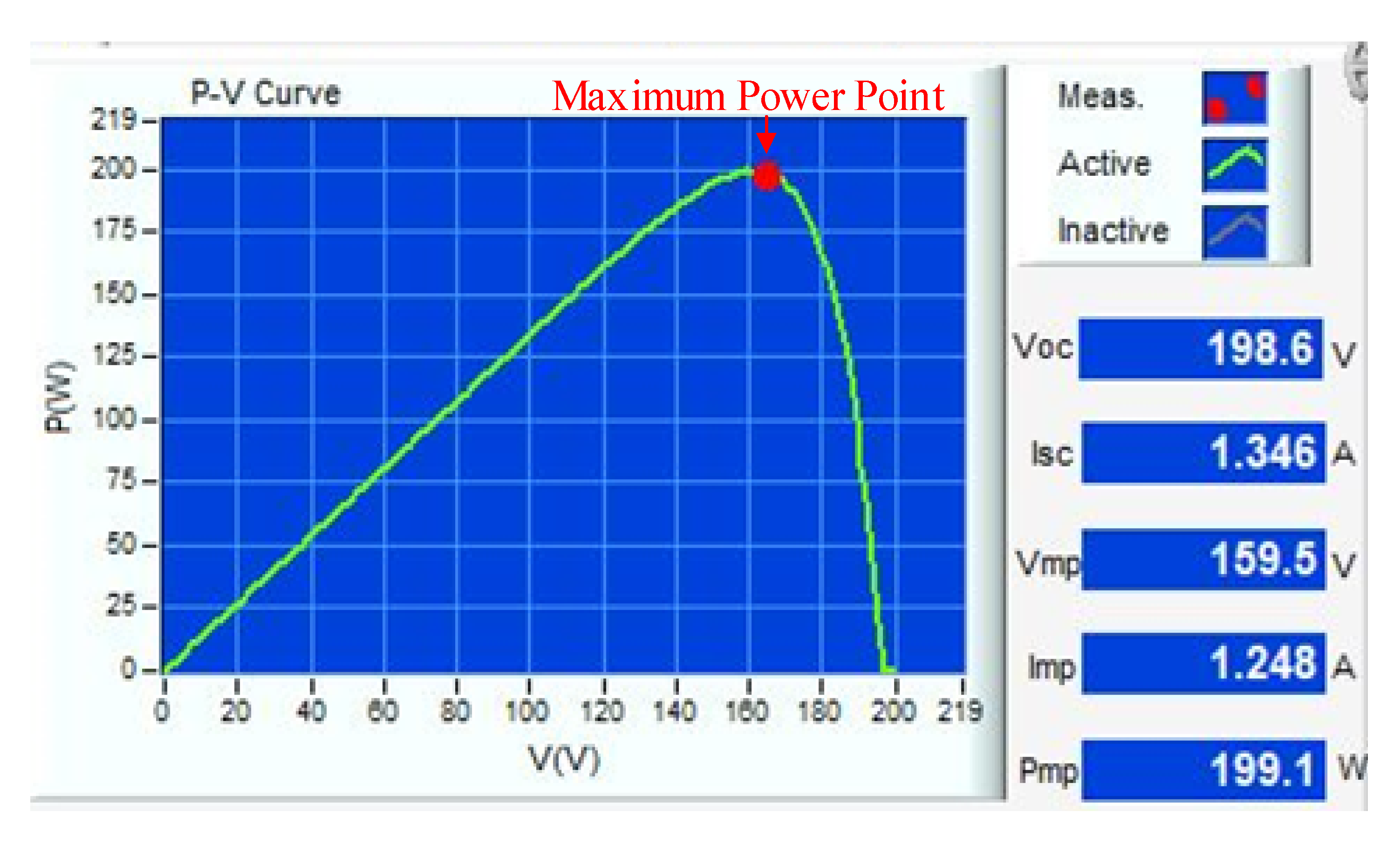
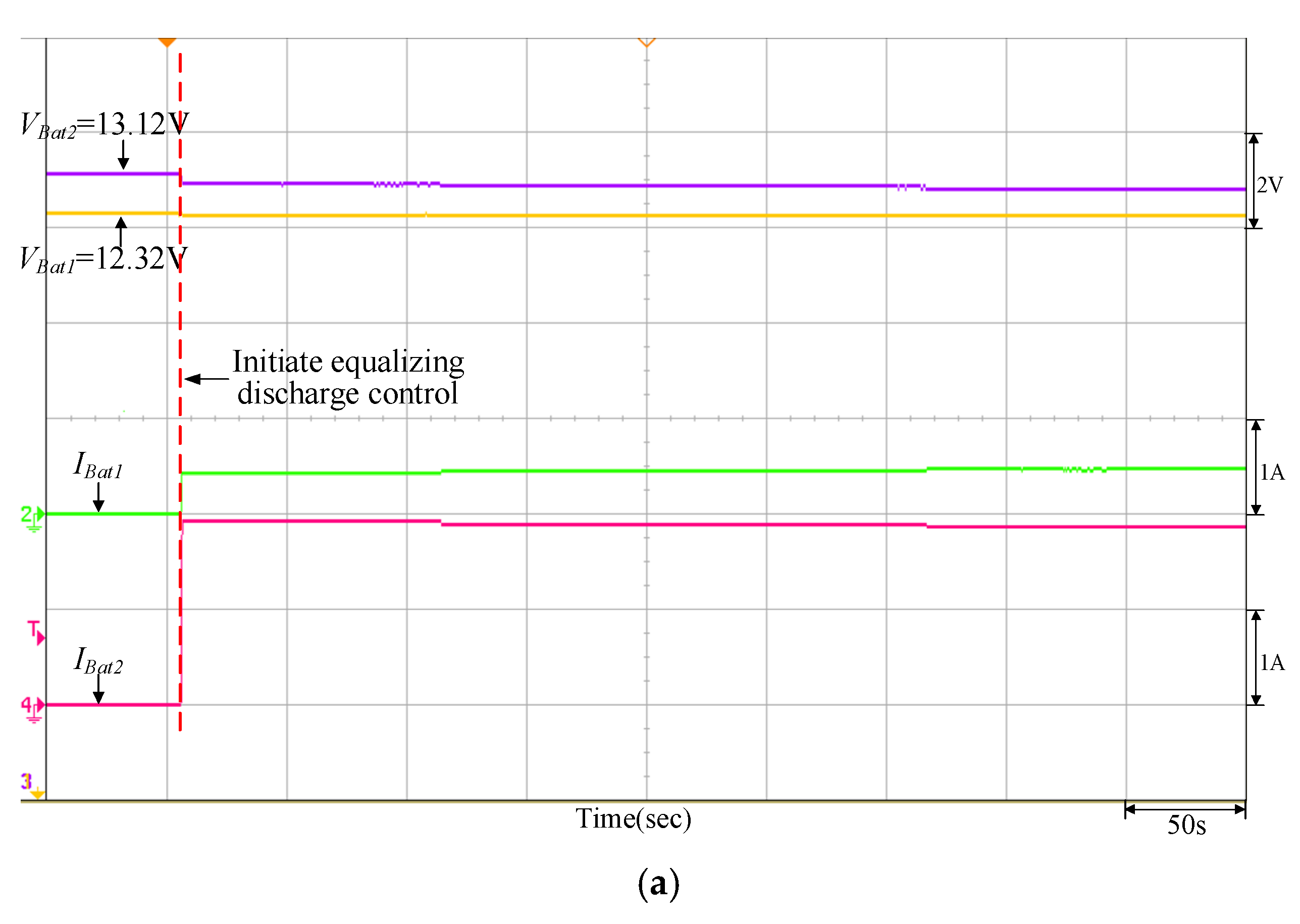
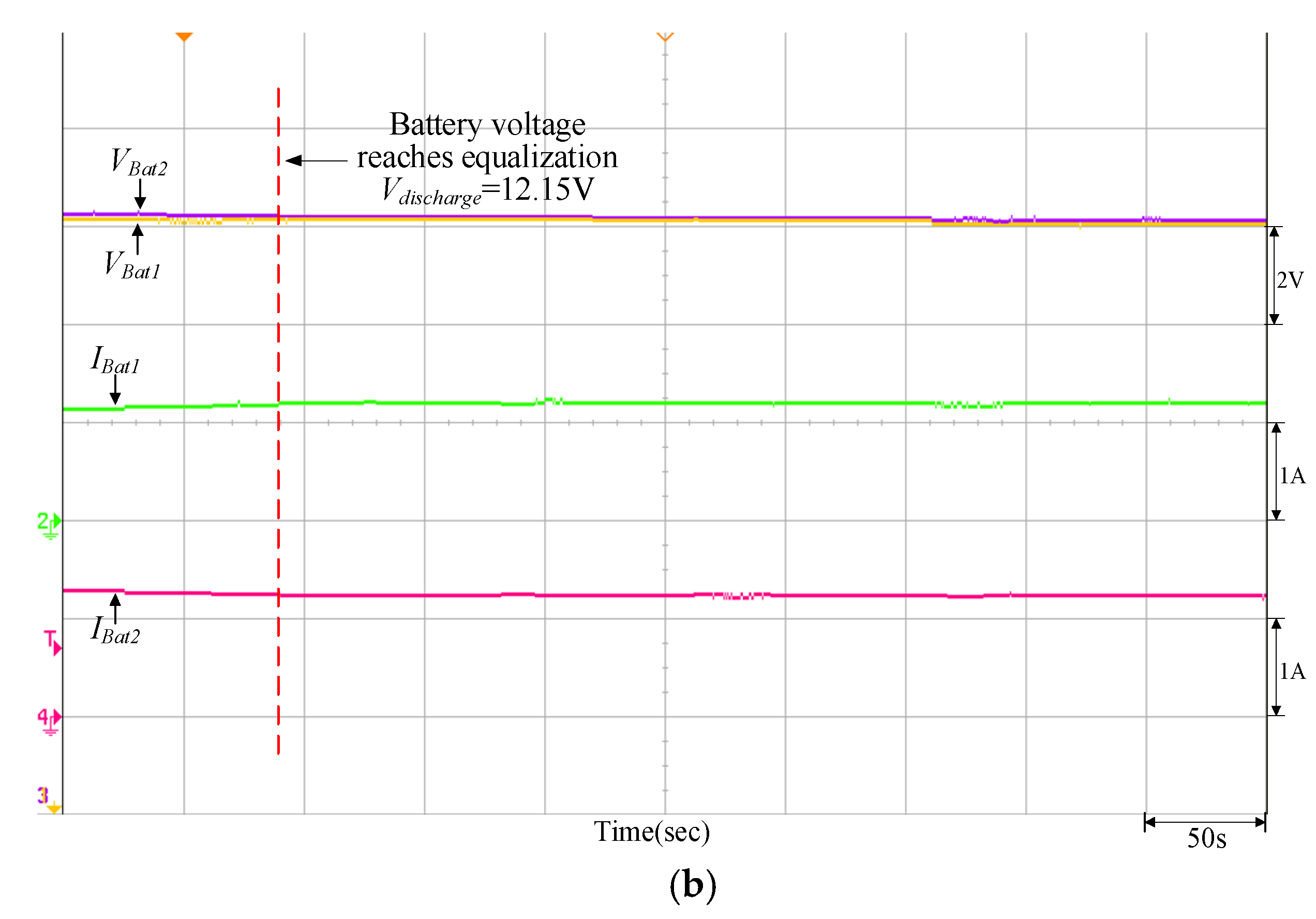
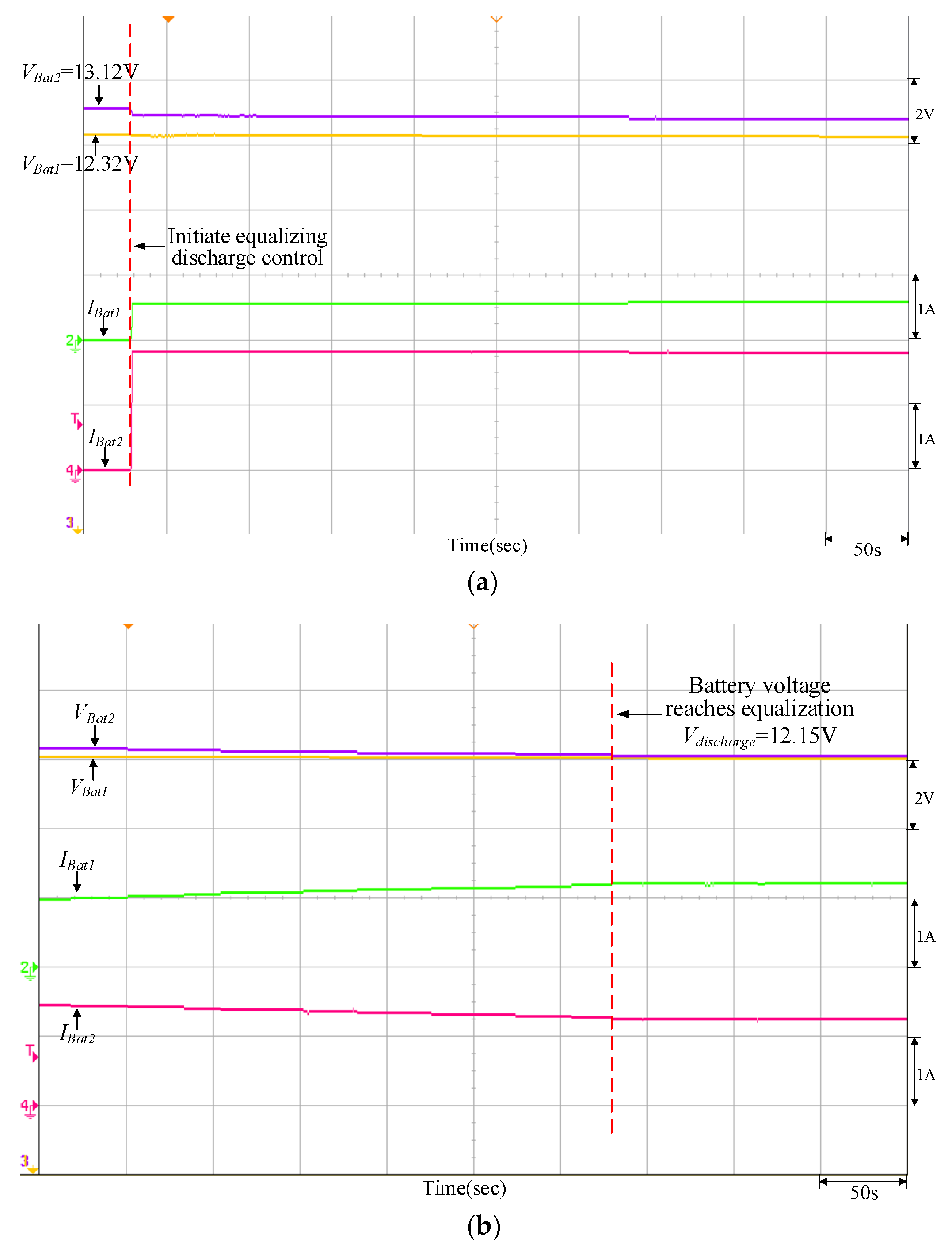
| Parameters | Specifications |
|---|---|
| Voltage at high-voltage side(VBus) | 240 V |
| Voltage of first battery set at low-voltage side (VBat1) | 12 V |
| Voltage of second battery set at low-voltage side (VBat2) | 12 V |
| Switching frequency (f) | 25 kHz |
| Maximum operating power (Pmax) | 300 W |
| Voltage ripple at high-voltage side (ΔVBus,ripple) | 0.5% |
| Voltage ripple at low-voltage side (ΔVBat,ripple) | 0.5% |
| Component Name | Specifications |
|---|---|
| Main inductor (L1, L2) | 1.425 mH |
| Resonance inductor (La1, La2) | 18 μH |
| Capacitor at high-/low-voltage side (CBat1, CBat2, CBus1, CBus2) | 270 μF/450 V |
| Main switch and auxiliary switch | IGBT-IXGH48N60C3D1 (600 V/48 A) |
| Operating Mode | Voltage Status | |||
|---|---|---|---|---|
| Initial Voltage of First Set | Final Equalizing Charge/Discharge Voltage | Initial Voltage of Second Set | Final Equalizing Charge/Discharge Voltage | |
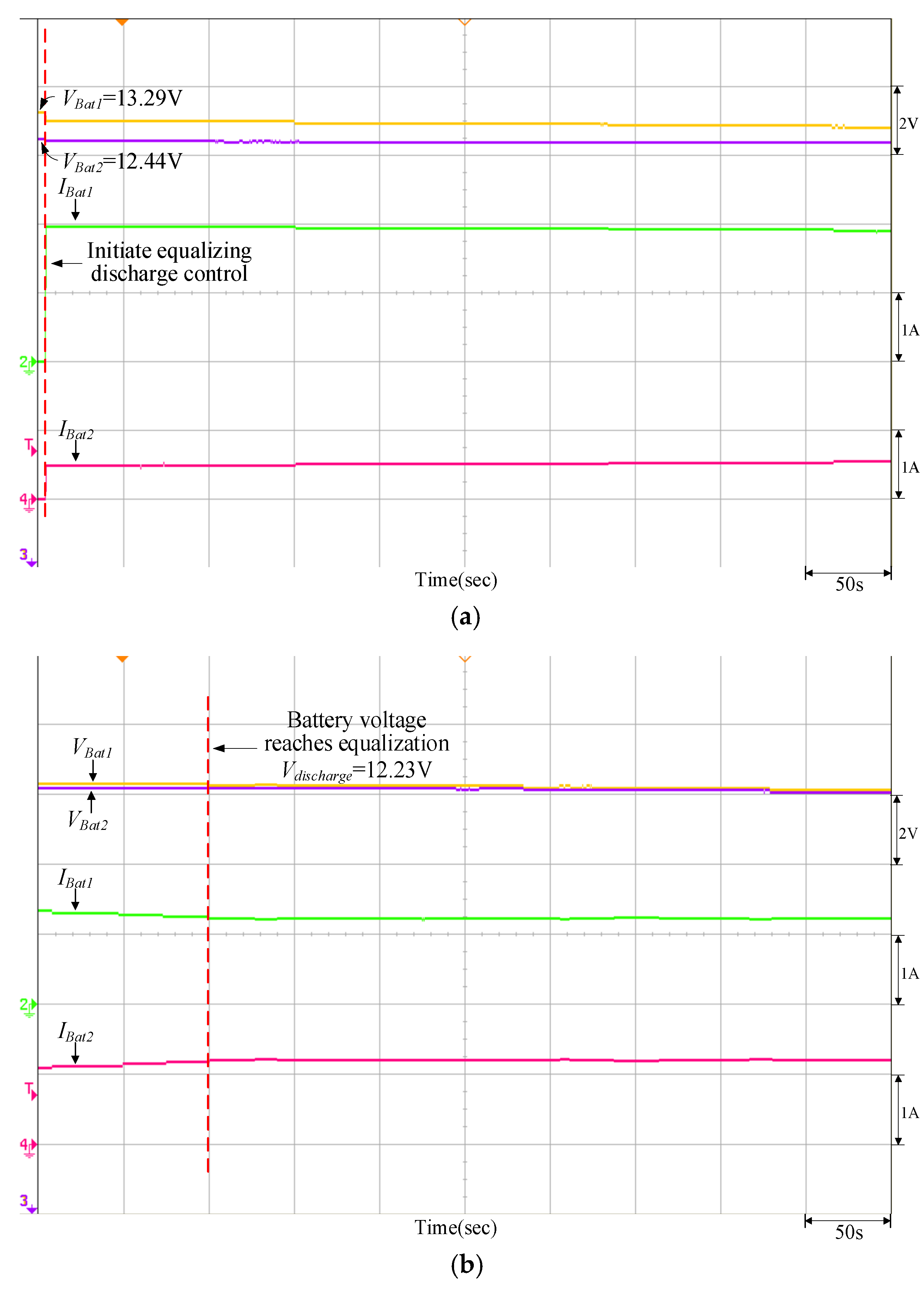
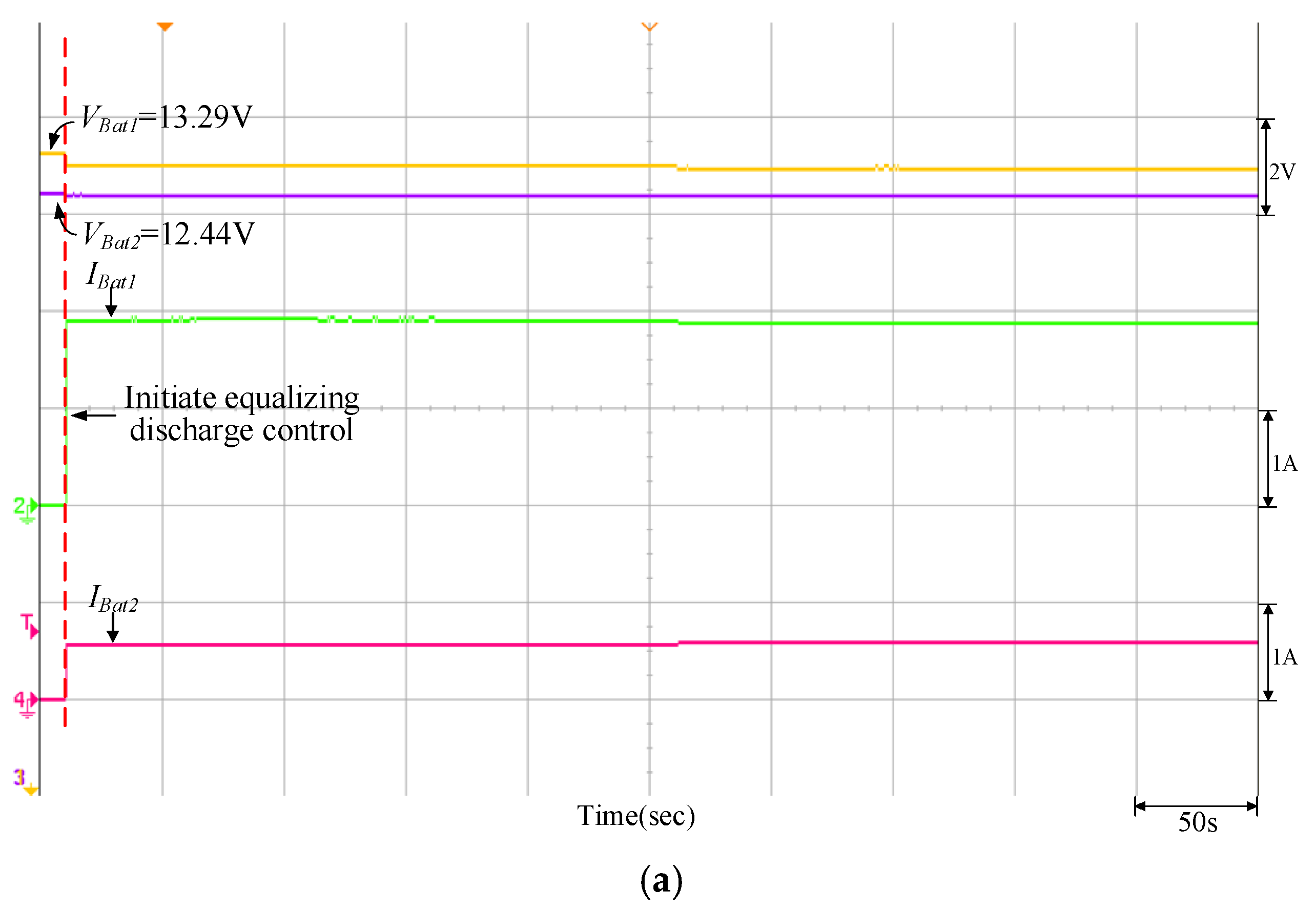
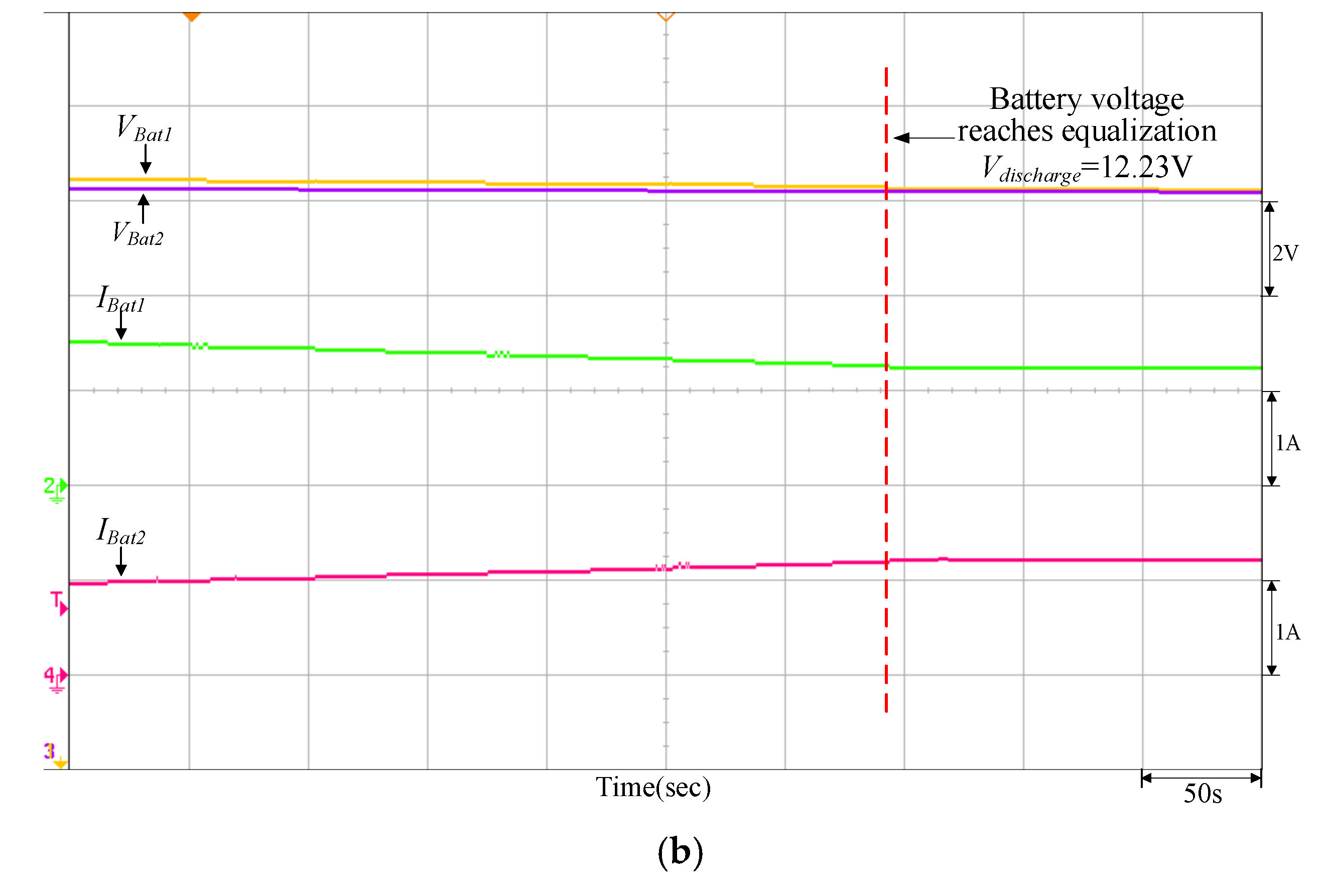
| Discharging | VBat1 = 12.32 V | Vdischarge = 12.15 V (PV power = 200 W) | VBat1 = 13.29 V | Vdischarge = 12.23 V (PV power = 200 W) |
| VBat2 = 13.12 V | VBat2 = 12.44 V | |||
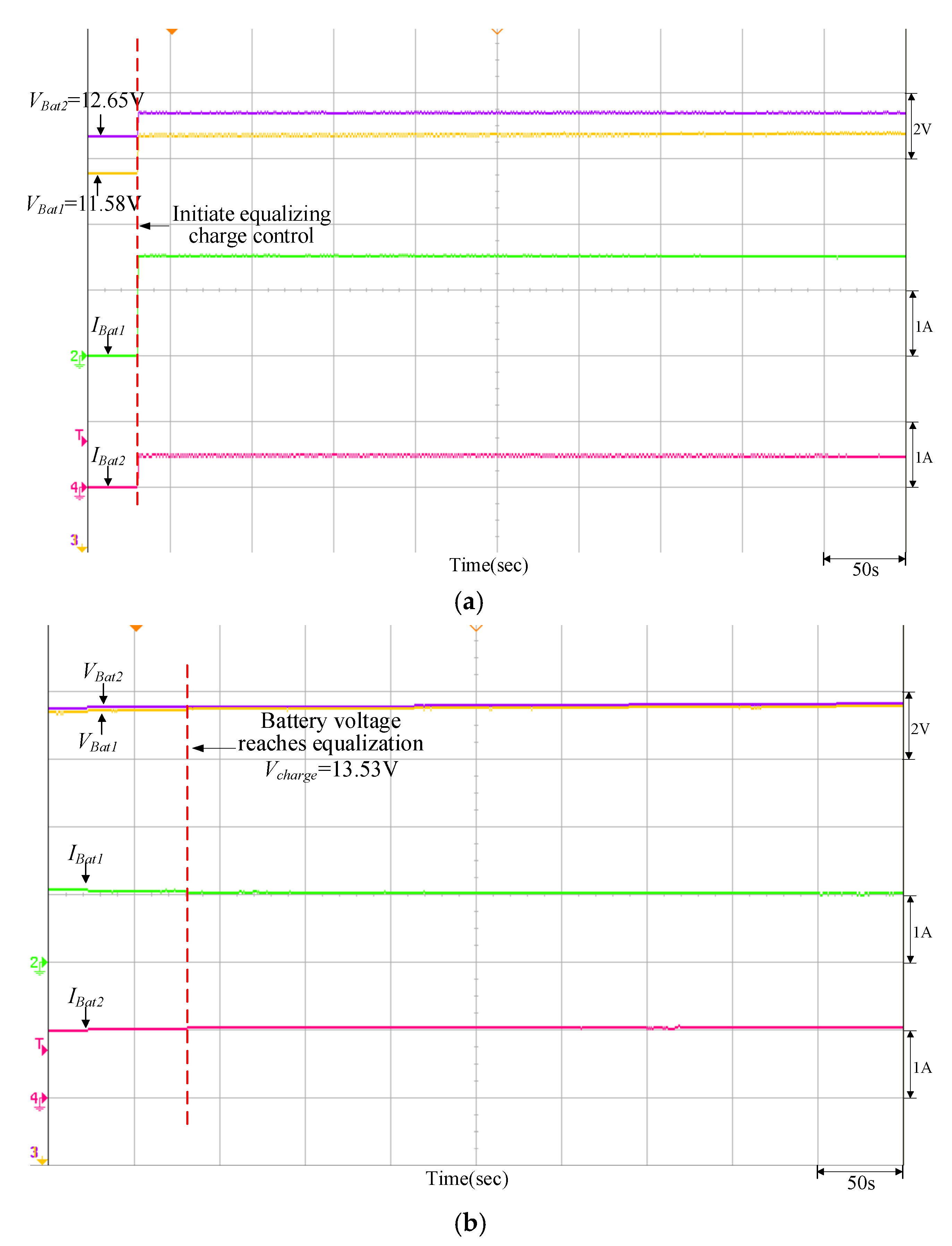
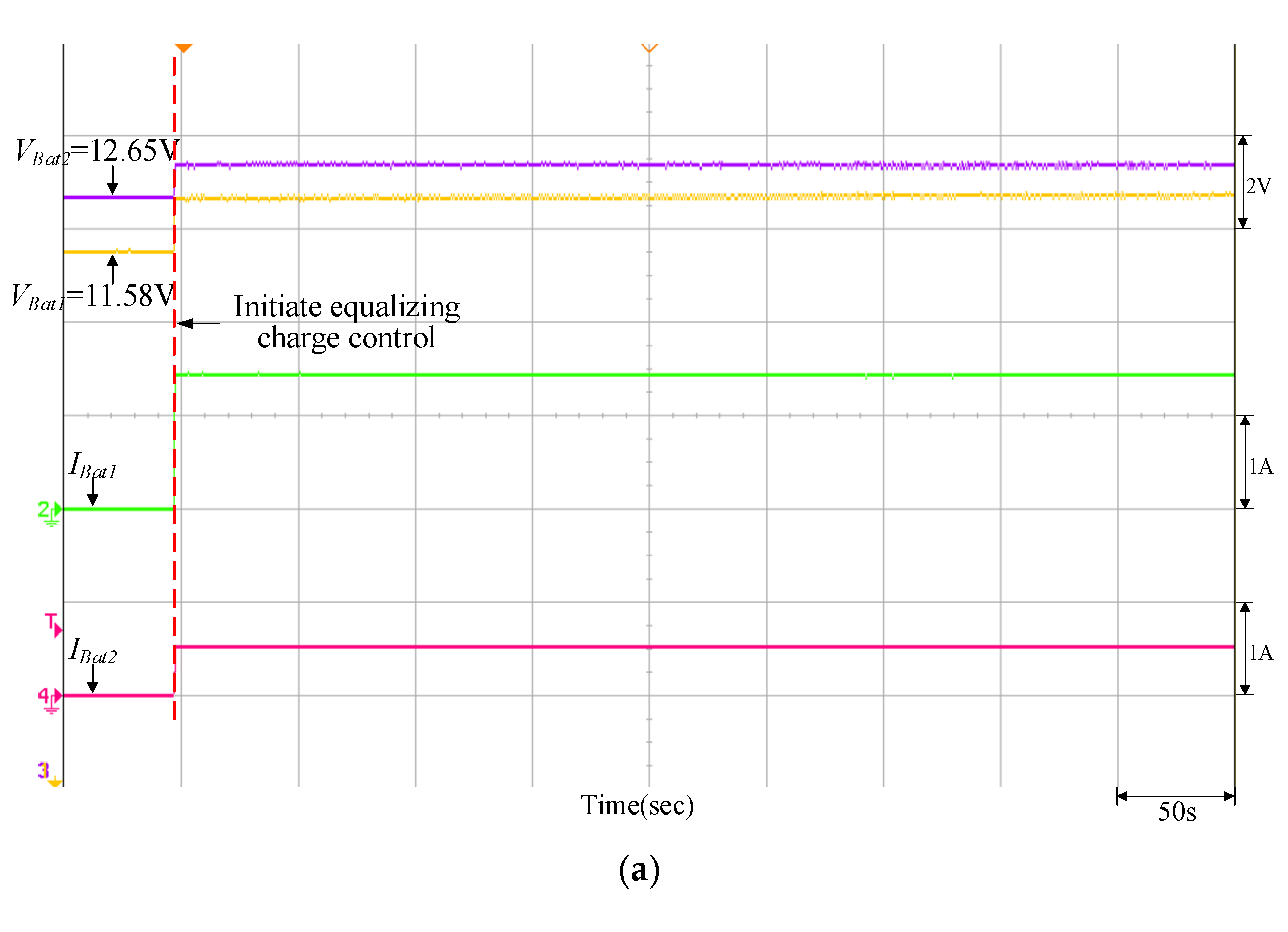
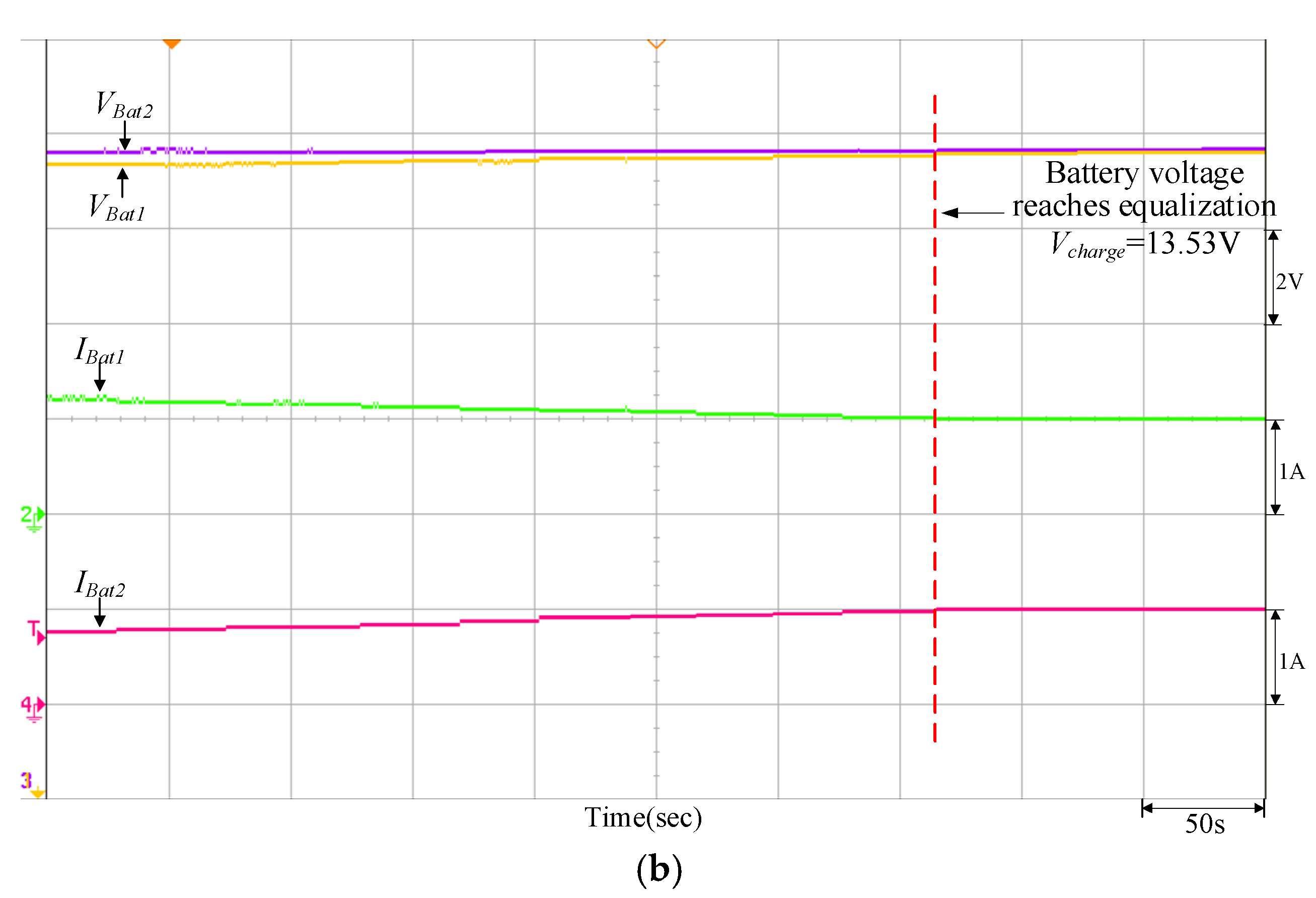
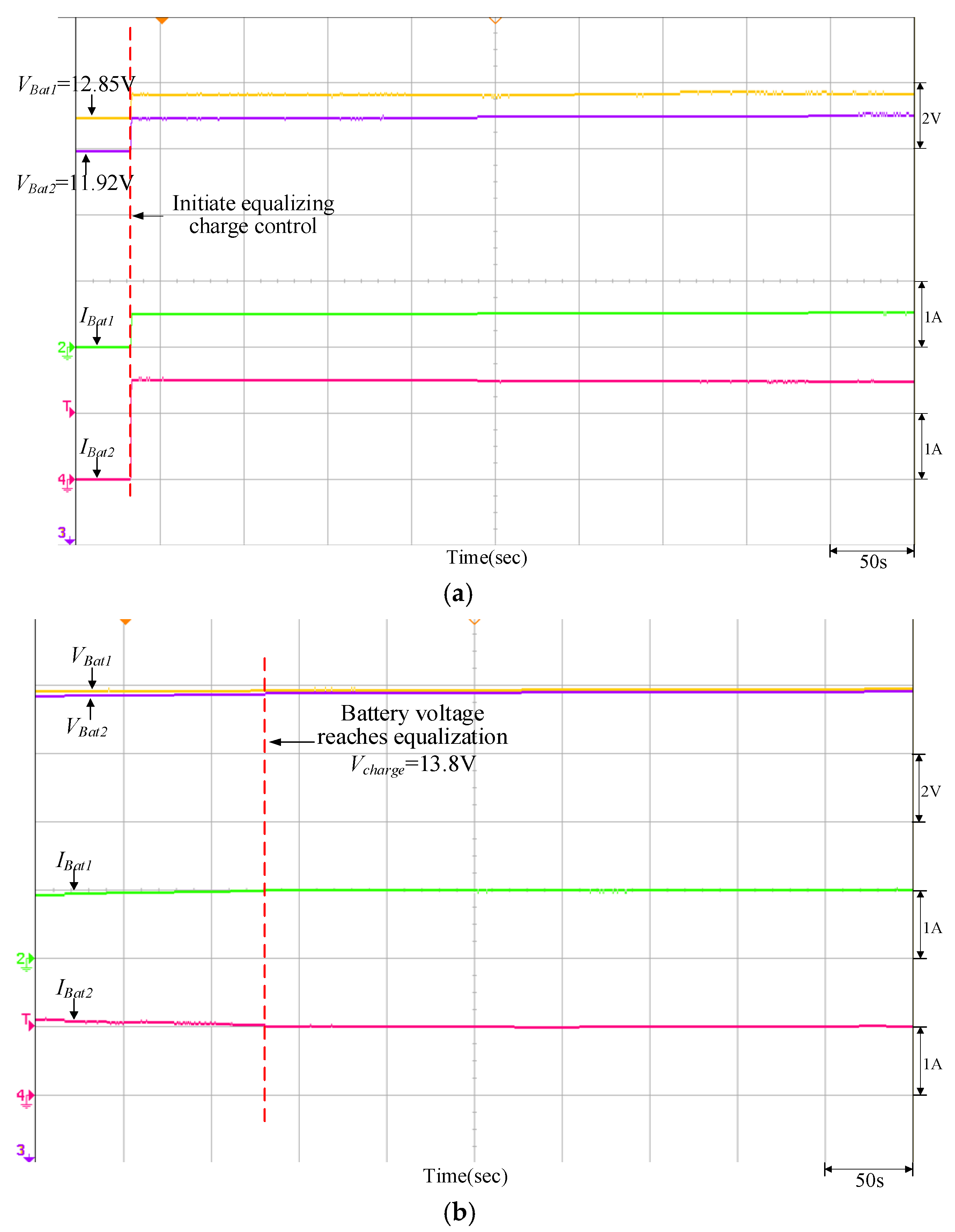
| Charging | VBat1 = 11.58 V | Vcharge = 13.53 V (PV power = 400 W) | VBat1 = 12.85 V | Vcharge = 13.8 V (PV power = 400 W) |
| VBat2 = 12.65 V | VBat2 = 11.92 V | |||
| Controller Used | Battery Status | |
|---|---|---|
| VBat1 = 12.32 V VBat2 = 13.12 V | VBat1 = 13.29 V VBat2 = 12.44 V | |
| Quantitatively designed controller | 33 m 54 s | 34 m 55 s |
| Traditional P-I controller | 38 m 28 s | 39 m 05 s |
| Controller Used | Battery Status | |
|---|---|---|
| VBat1 = 11.58 V VBat2 = 12.65 V | VBat1 = 12.85 V VBat2 = 11.92 V | |
| Quantitatively designed controller | 42 m 31 s | 41 m 40 s |
| Traditional P-I controller | 46 m 40 s | 46 m 04 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chao, K.-H.; Huang, B.-Z. Quantitative Design for the Battery Equalizing Charge/Discharge Controller of the Photovoltaic Energy Storage System. Batteries 2022, 8, 278. https://doi.org/10.3390/batteries8120278
Chao K-H, Huang B-Z. Quantitative Design for the Battery Equalizing Charge/Discharge Controller of the Photovoltaic Energy Storage System. Batteries. 2022; 8(12):278. https://doi.org/10.3390/batteries8120278
Chicago/Turabian StyleChao, Kuei-Hsiang, and Bing-Ze Huang. 2022. "Quantitative Design for the Battery Equalizing Charge/Discharge Controller of the Photovoltaic Energy Storage System" Batteries 8, no. 12: 278. https://doi.org/10.3390/batteries8120278
APA StyleChao, K.-H., & Huang, B.-Z. (2022). Quantitative Design for the Battery Equalizing Charge/Discharge Controller of the Photovoltaic Energy Storage System. Batteries, 8(12), 278. https://doi.org/10.3390/batteries8120278








