The Dilemma of C-Rate and Cycle Life for Lithium-Ion Batteries under Low Temperature Fast Charging
Abstract
1. Introduction
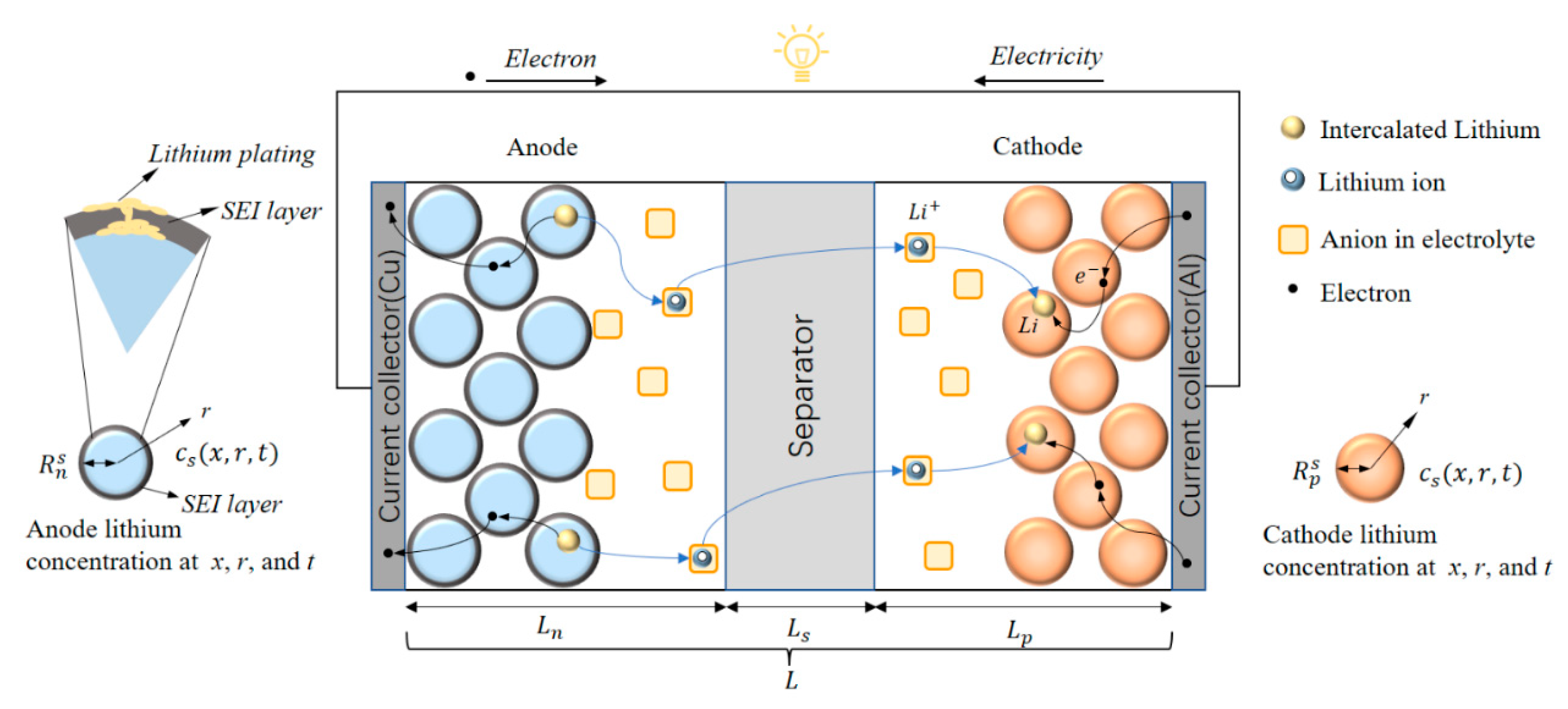
2. Battery Model
2.1. Electrochemical Model
2.2. Thermal Model
3. Results and Discussion
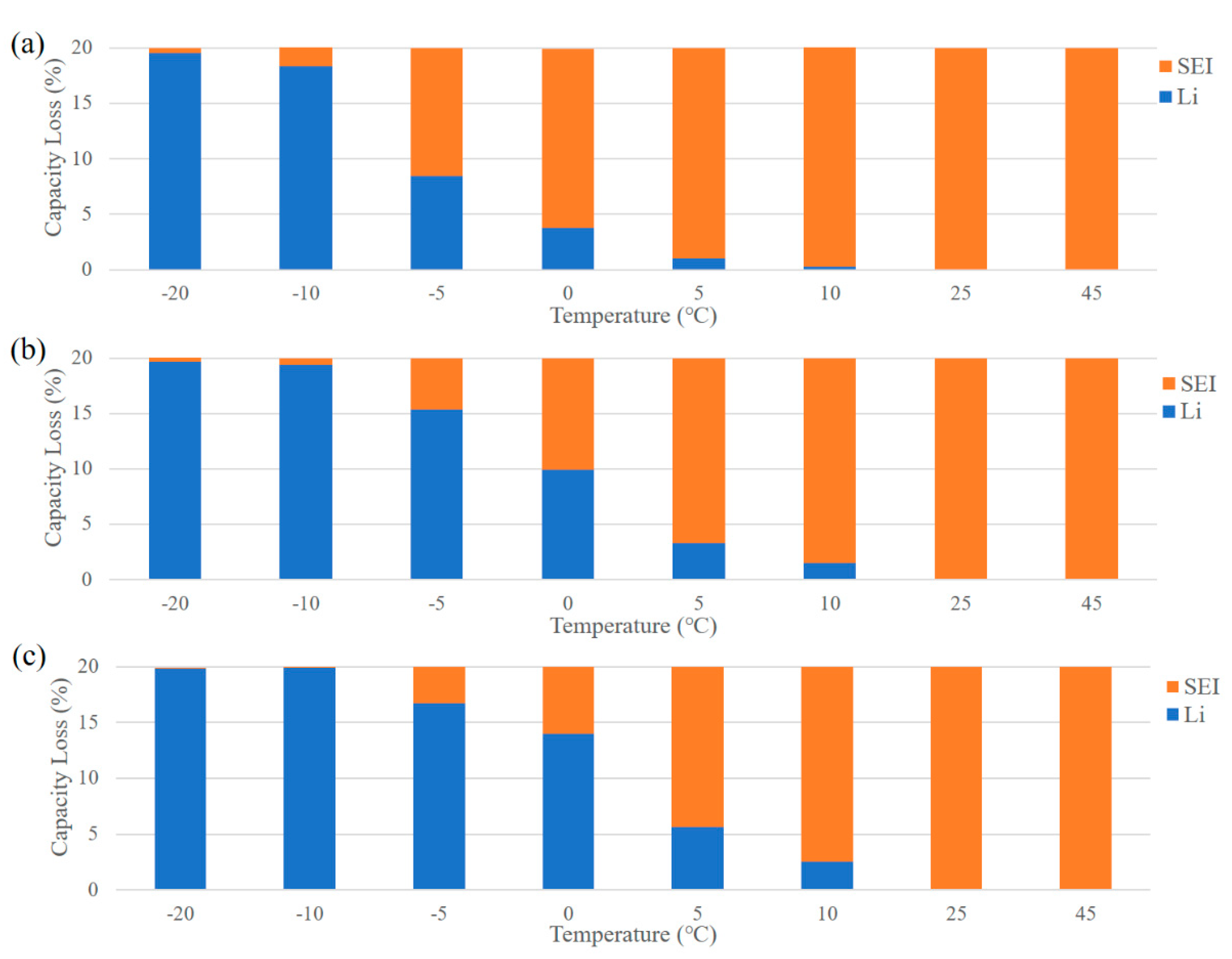
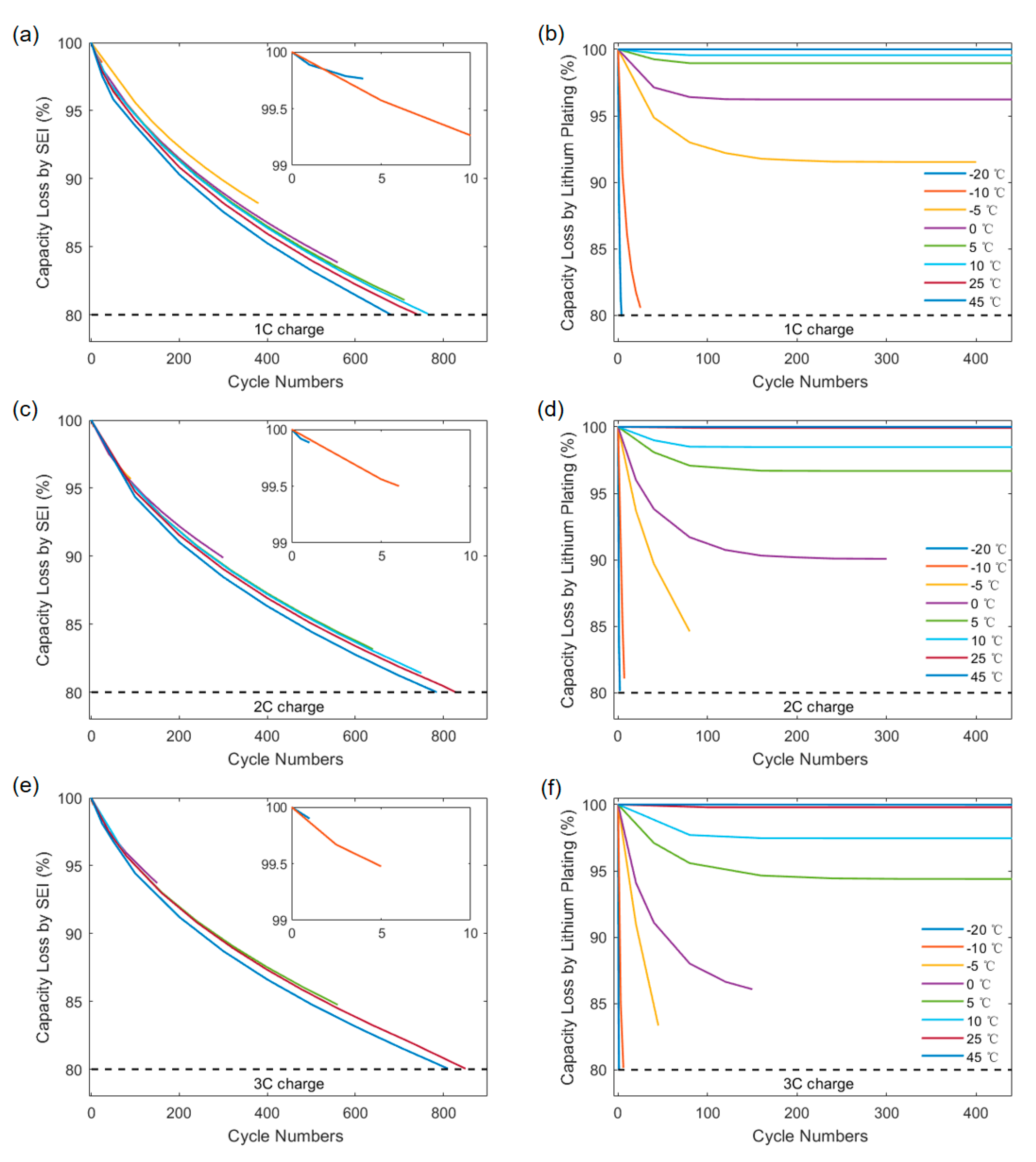
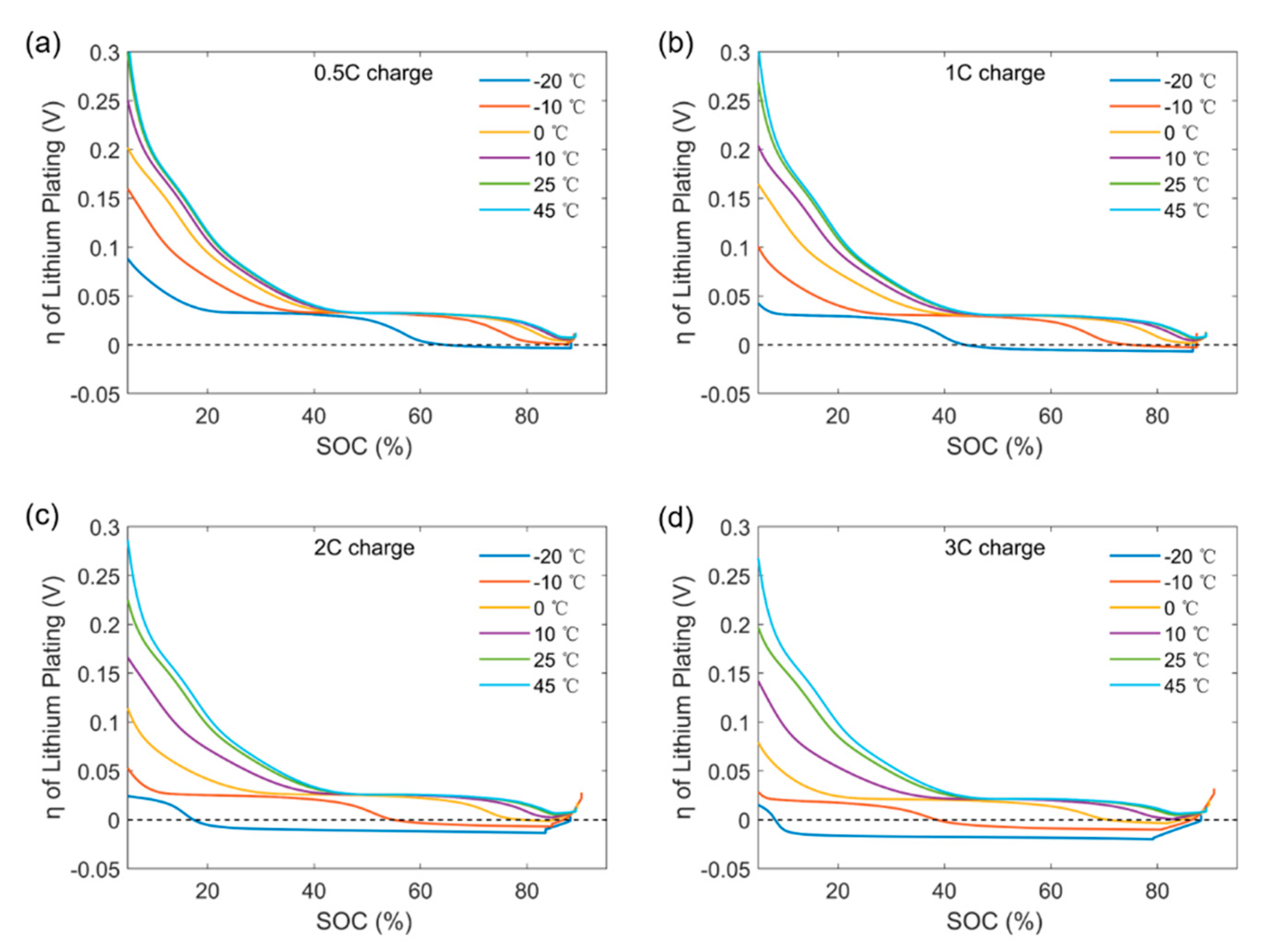
3.1. The Change for Contribution of SEI and Lithium Plating to Capacity Degradation under Different Charging Strategies
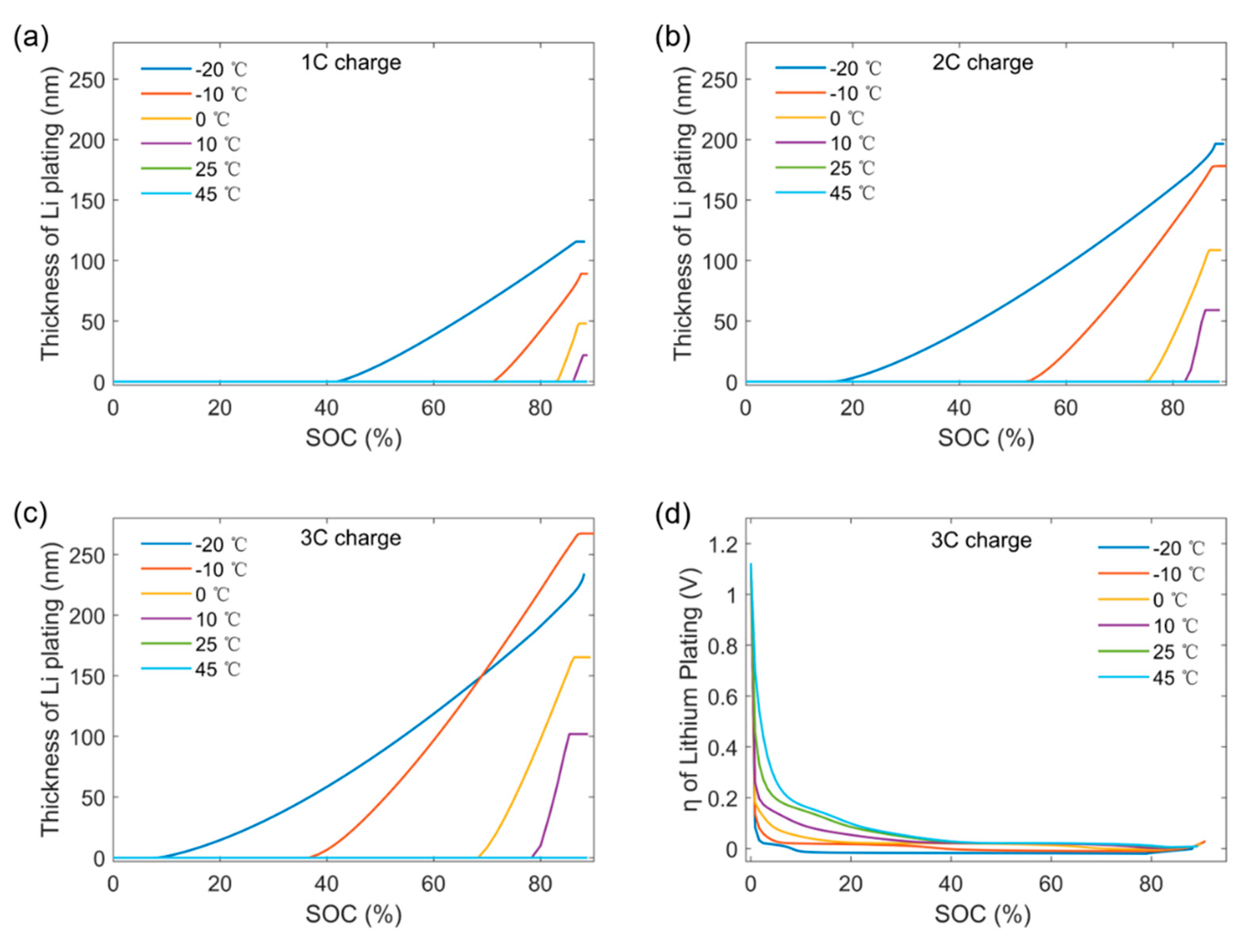
3.2. The Cause for Large Amounts of Capacity Degradation Caused by Lithium Plating under Low Temperatures
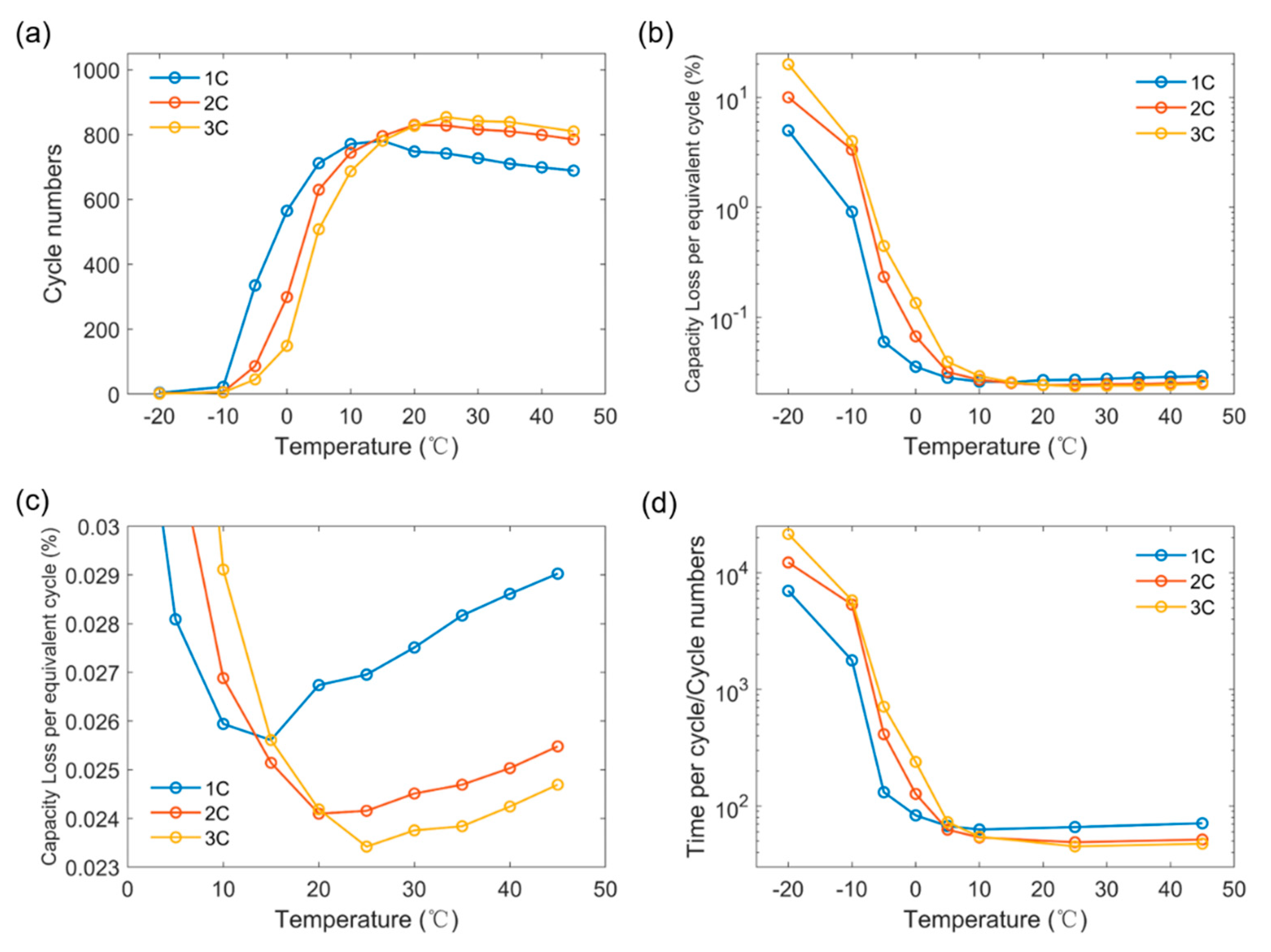
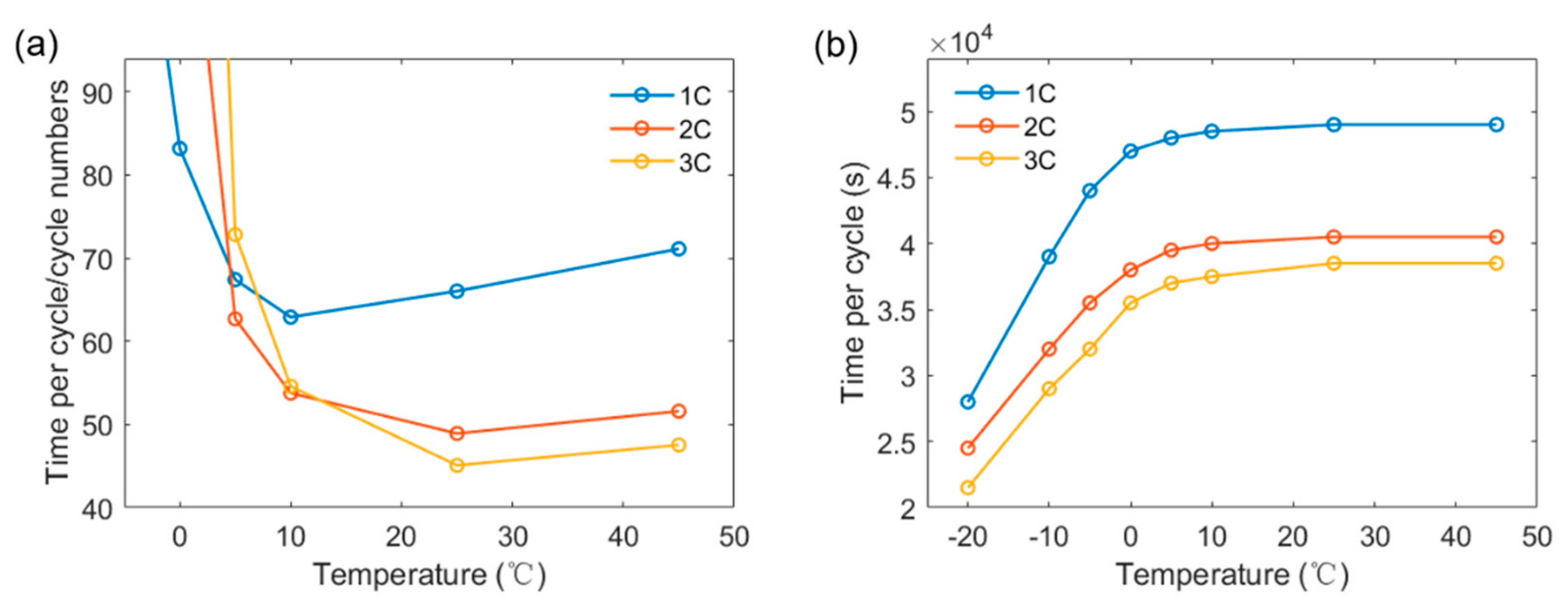
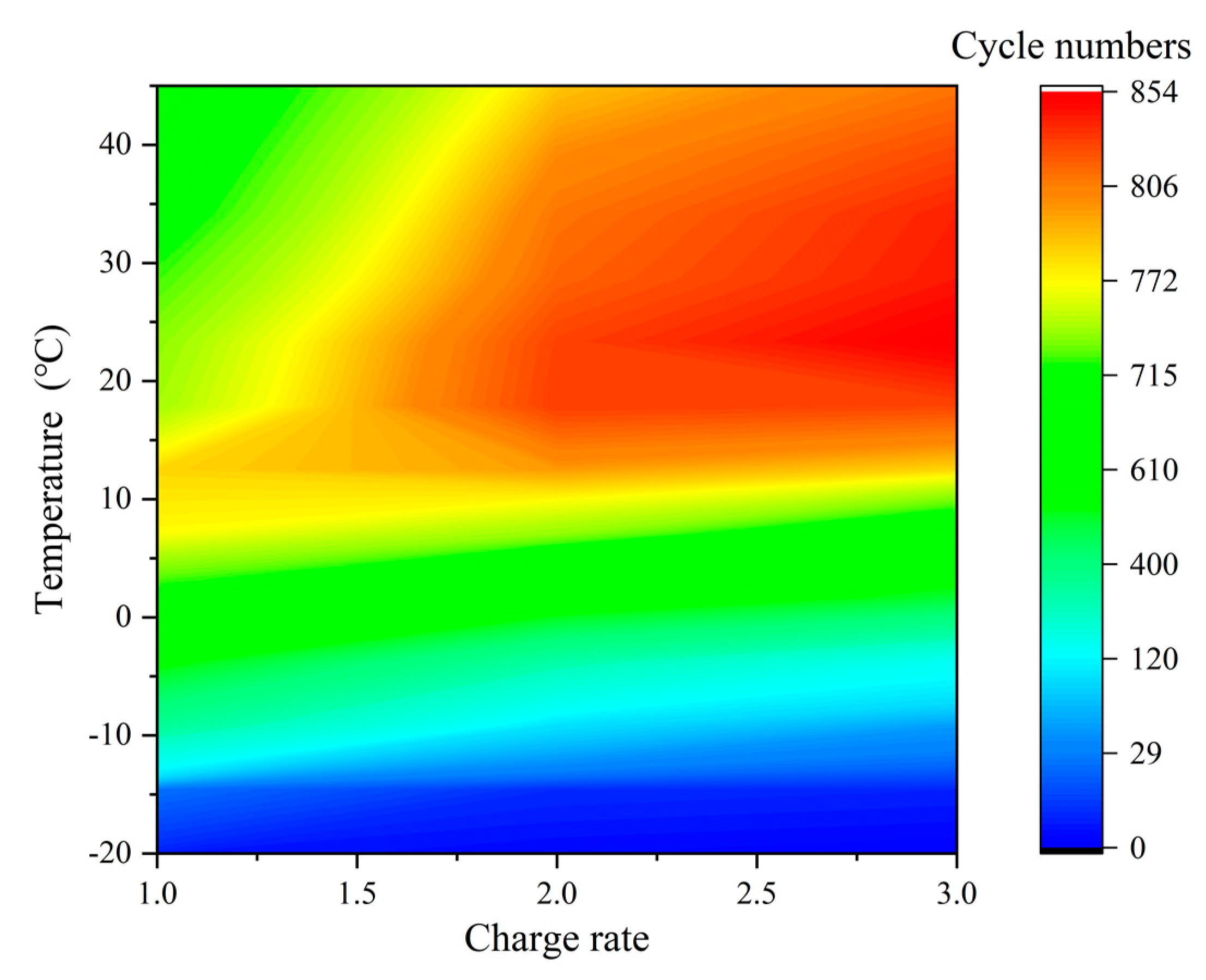
3.3. Determination of Optimal Charging Strategy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lin, C.; Kong, W.; Tian, Y.; Wang, W.; Zhao, M. Heating Lithium-Ion Batteries at Low Temperatures for Onboard Applications: Recent Progress, Challenges and Prospects. Automot. Innov. 2022, 5, 3–17. [Google Scholar] [CrossRef]
- Chandrasekaran, R. Quantification of Bottlenecks to Fast Charging of Lithium-Ion-Insertion Cells for Electric Vehicles. J. Power Sources 2014, 271, 622–632. [Google Scholar] [CrossRef]
- Somerville, L.; Bareño, J.; Trask, S.; Jennings, P.; McGordon, A.; Lyness, C.; Bloom, I. The Effect of Charging Rate on the Graphite Electrode of Commercial Lithium-Ion Cells: A Post-Mortem Study. J. Power Sources 2016, 335, 189–196. [Google Scholar] [CrossRef]
- Tomaszewska, A.; Chu, Z.; Feng, X.; O’Kane, S.; Liu, X.; Chen, J.; Ji, C.; Endler, E.; Li, R.; Liu, L.; et al. Lithium-Ion Battery Fast Charging: A Review. eTransportation 2019, 1, 100011. [Google Scholar] [CrossRef]
- Chen, K.; Li, G.; Wang, Y.; Chen, W.; Mi, L. High Loading FeS2 Nanoparticles Anchored on Biomass-Derived Carbon Tube as Low Cost and Long Cycle Anode for Sodium-Ion Batteries. Green Energy Environ. 2020, 5, 50–58. [Google Scholar] [CrossRef]
- Cao, R.; Cheng, H.; Jia, X.; Gao, X.; Zhang, Z.; Wang, M.; Li, S.; Zhang, C.; Ma, B.; Liu, X.; et al. Non-Invasive Characteristic Curve Analysis of Lithium-Ion Batteries Enabling Degradation Analysis and Data-Driven Model Construction: A Review. Automot. Innov. 2022, 5, 146–163. [Google Scholar] [CrossRef]
- Petzl, M.; Kasper, M.; Danzer, M.A. Lithium Plating in a Commercial Lithium-Ion Battery—A Low-Temperature Aging Study. J. Power Sources 2015, 275, 799–807. [Google Scholar] [CrossRef]
- Liu, Q.; Du, C.; Shen, B.; Zuo, P.; Cheng, X.; Ma, Y.; Yin, G.; Gao, Y. Understanding Undesirable Anode Lithium Plating Issues in Lithium-Ion Batteries. RSC Adv. 2016, 6, 88683–88700. [Google Scholar] [CrossRef]
- Han, X.; Feng, X.; Ouyang, M.; Lu, L.; Li, J.; Zheng, Y.; Li, Z. A Comparative Study of Charging Voltage Curve Analysis and State of Health Estimation of Lithium-Ion Batteries in Electric Vehicle. Automot. Innov. 2019, 2, 263–275. [Google Scholar] [CrossRef]
- Lu, Q.; Jie, Y.; Meng, X.; Omar, A.; Mikhailova, D.; Cao, R.; Jiao, S.; Lu, Y.; Xu, Y. Carbon Materials for Stable Li Metal Anodes: Challenges, Solutions, and Outlook. Carbon Energy 2021, 3, 957–975. [Google Scholar] [CrossRef]
- Meng, X.; Xu, Y.; Cao, H.; Lin, X.; Ning, P.; Zhang, Y.; Garcia, Y.G.; Sun, Z. Internal Failure of Anode Materials for Lithium Batteries—A Critical Review. Green Energy Environ. 2020, 5, 22–36. [Google Scholar] [CrossRef]
- Legrand, N.; Knosp, B.; Desprez, P.; Lapicque, F.; Raël, S. Physical Characterization of the Charging Process of a Li-Ion Battery and Prediction of Li Plating by Electrochemical Modelling. J. Power Sources 2014, 245, 208–216. [Google Scholar] [CrossRef]
- Waldmann, T.; Hogg, B.-I.; Wohlfahrt-Mehrens, M. Li Plating as Unwanted Side Reaction in Commercial Li-Ion Cells—A Review. J. Power Sources 2018, 384, 107–135. [Google Scholar] [CrossRef]
- Gao, X.; Liu, X.; Xie, W.; Zhang, L.; Yang, S. Multiscale Observation of Li Plating for Lithium-Ion Batteries. Rare Met. 2021, 40, 3038–3048. [Google Scholar] [CrossRef]
- Hein, S.; Latz, A. Influence of Local Lithium Metal Deposition in 3D Microstructures on Local and Global Behavior of Lithium-Ion Batteries. Electrochim. Acta 2016, 201, 354–365. [Google Scholar] [CrossRef]
- Bugga, R.V.; Smart, M.C. Lithium Plating Behavior in Lithium-Ion Cells. ECS Trans. 2010, 25, 241–252. [Google Scholar] [CrossRef]
- Li, Y.; Feng, X.; Ren, D.; Ouyang, M.; Lu, L.; Han, X. Thermal Runaway Triggered by Plated Lithium on the Anode after Fast Charging. ACS Appl. Mater. Interfaces 2019, 11, 46839–46850. [Google Scholar] [CrossRef]
- Tan, X.; Qiu, J.; Li, J.; Fan, Y.; Liu, J. Lithium Plating as Limiting Phenomena for Estimating Safety during Lithium-Ion Battery Charging. Int. J. Electrochem. Sci. 2020, 15, 9233–9244. [Google Scholar] [CrossRef]
- Cai, W.; Yan, C.; Yao, Y.X.; Xu, L.; Chen, X.R.; Huang, J.Q.; Zhang, Q. The Boundary of Lithium Plating in Graphite Electrode for Safe Lithium-Ion Batteries. Angew. Chem. Int. Ed. 2021, 60, 13007–13012. [Google Scholar] [CrossRef]
- Fan, J.; Tan, S. Studies on Charging Lithium-Ion Cells at Low Temperatures. J. Electrochem. Soc. 2006, 153, A1081. [Google Scholar] [CrossRef]
- Ouyang, M.; Chu, Z.; Lu, L.; Li, J.; Han, X.; Feng, X.; Liu, G. Low Temperature Aging Mechanism Identification and Lithium Deposition in a Large Format Lithium Iron Phosphate Battery for Different Charge Profiles. J. Power Sources 2015, 286, 309–320. [Google Scholar] [CrossRef]
- An, S.J.; Li, J.; Daniel, C.; Mohanty, D.; Nagpure, S.; Wood, D.L. The State of Understanding of the Lithium-Ion-Battery Graphite Solid Electrolyte Interphase (SEI) and Its Relationship to Formation Cycling. Carbon 2016, 105, 52–76. [Google Scholar] [CrossRef]
- Zhang, S.; Xu, K.; Jow, T. Low-Temperature Performance of Li-Ion Cells with a LiBF4-Based Electrolyte. J. Solid State Electrochem. 2003, 7, 147–151. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. The Low Temperature Performance of Li-Ion Batteries. J. Power Sources 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Tao, H.; Lian, C.; Liu, H. Multiscale Modeling of Electrolytes in Porous Electrode: From Equilibrium Structure to Non-Equilibrium Transport. Green Energy Environ. 2020, 5, 303–321. [Google Scholar] [CrossRef]
- Gao, F.; Tang, Z. Kinetic Behavior of LiFePO4/C Cathode Material for Lithium-Ion Batteries. Electrochim. Acta 2008, 53, 5071–5075. [Google Scholar] [CrossRef]
- Schimpe, M.; von Kuepach, M.E.; Naumann, M.; Hesse, H.C.; Smith, K.; Jossen, A. Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries. J. Electrochem. Soc. 2018, 165, A181–A193. [Google Scholar] [CrossRef]
- Ecker, M.; Shafiei Sabet, P.; Sauer, D.U. Influence of Operational Condition on Lithium Plating for Commercial Lithium-Ion Batteries—Electrochemical Experiments and Post-Mortem-Analysis. Appl. Energy 2017, 206, 934–946. [Google Scholar] [CrossRef]
- Matadi, B.P.; Geniès, S.; Delaille, A.; Chabrol, C.; de Vito, E.; Bardet, M.; Martin, J.-F.; Daniel, L.; Bultel, Y. Irreversible Capacity Loss of Li-Ion Batteries Cycled at Low Temperature Due to an Untypical Layer Hindering Li Diffusion into Graphite Electrode. J. Electrochem. Soc. 2017, 164, A2374–A2389. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The Use of Mathematical Modeling in the Design of Lithium/Polymer Battery Systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Momeni Boroujeni, S.; Birke, K.P. Study of a Li-Ion Cell Kinetics in Five Regions to Predict Li Plating Using a Pseudo Two-Dimensional Model. Sustainability 2019, 11, 6392. [Google Scholar] [CrossRef]
- Sturm, J.; Rheinfeld, A.; Zilberman, I.; Spingler, F.B.; Kosch, S.; Frie, F.; Jossen, A. Modeling and Simulation of Inhomogeneities in a 18650 Nickel-Rich, Silicon-Graphite Lithium-Ion Cell during Fast Charging. J. Power Sources 2019, 412, 204–223. [Google Scholar] [CrossRef]
- Müller, D.; Dufaux, T.; Birke, K.P. Model-Based Investigation of Porosity Profiles in Graphite Anodes Regarding Sudden-Death and Second-Life of Lithium Ion Cells. Batteries 2019, 5, 49. [Google Scholar] [CrossRef]
- Burns, J.C.; Stevens, D.A.; Dahn, J.R. In-Situ Detection of Lithium Plating Using High Precision Coulometry. J. Electrochem. Soc. 2015, 162, A959–A964. [Google Scholar] [CrossRef]
- Sieg, J.; Schmid, A.U.; Rau, L.; Gesterkamp, A.; Storch, M.; Spier, B.; Birke, K.P.; Sauer, D.U. Fast-Charging Capability of Lithium-Ion Cells: Influence of Electrode Aging and Electrolyte Consumption. Appl. Energy 2022, 305, 117747. [Google Scholar] [CrossRef]
- Kim, S.-P.; van Duin, A.C.T.; Shenoy, V.B. Effect of Electrolytes on the Structure and Evolution of the Solid Electrolyte Interphase (SEI) in Li-Ion Batteries: A Molecular Dynamics Study. J. Power Sources 2011, 196, 8590–8597. [Google Scholar] [CrossRef]
- Tippmann, S.; Walper, D.; Balboa, L.; Spier, B.; Bessler, W.G. Low-Temperature Charging of Lithium-Ion Cells Part I: Electrochemical Modeling and Experimental Investigation of Degradation Behavior. J. Power Sources 2014, 252, 305–316. [Google Scholar] [CrossRef]
- Yang, X.-G.; Wang, C.-Y. Understanding the Trilemma of Fast Charging, Energy Density and Cycle Life of Lithium-Ion Batteries. J. Power Sources 2018, 402, 489–498. [Google Scholar] [CrossRef]
- Rangarajan, S.P.; Barsukov, Y.; Mukherjee, P.P. In Operando Signature and Quantification of Lithium Plating. J. Mater. Chem. A Mater. 2019, 7, 20683–20695. [Google Scholar] [CrossRef]
- Peled, E.; Menkin, S. Review-SEI: Past, Present and Future. J. Electrochem. Soc. 2017, 164, A1703–A1719. [Google Scholar] [CrossRef]
- Wang, A.; Kadam, S.; Li, H.; Shi, S.; Qi, Y. Review on Modeling of the Anode Solid Electrolyte Interphase (SEI) for Lithium-Ion Batteries. NPJ Comput. Mater. 2018, 4, 15. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| Solid particle potential [] | |
| Electrolyte potential [] | |
| Open-circuit potential [] | |
| Lithium concentration in solid phase [] | |
| Lithium concentration in electrolyte phase [] | |
| Maximum lithium concentration in solid phase [] | |
| Lithium concentration at surface in solid phase [] | |
| Effective solid particle conductivity [] | |
| Effective electrolyte conductivity [] | |
| Effective electrolyte diffusional conductivity [] | |
| Effective solid particle diffusivity [] | |
| Effective electrolyte diffusivity [] | |
| Porosity [%] | |
| Reaction rate constant of intercalating, plating, and SEI [] | |
| Specific surface area [1/m] | |
| Transference number [-] | |
| Ionic flux of intercalating, plating, and SEI [] | |
| Local current density [] | |
| Transfer coefficient [-] | |
| Faraday constant [] | |
| Universal gas constant [] | |
| Overpotential of intercalating, plating, and SEI [] | |
| Battery temperature [] | |
| Ambient temperature [] | |
| Cell surface area [] | |
| Mass of the battery [] | |
| Specific heat capacity of the battery [] | |
| Thickness [] | |
| Convective heat transfer coefficient [] | |
| Activity coefficient |
| Temperature (°C) | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| −20 | −10 | −5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | ||
| C-rate | 1C | 4 | 22 | 335 | 565 | 712 | 771 | 781 | 748 | 742 | 727 | 710 | 699 | 689 | 680 |
| 2C | 2 | 6 | 86 | 299 | 630 | 744 | 796 | 830 | 828 | 816 | 810 | 799 | 785 | 776 | |
| 3C | 1 | 5 | 45 | 149 | 508 | 687 | 781 | 827 | 854 | 842 | 839 | 825 | 810 | 804 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Z.; Xie, H.; Yang, X.; Niu, W.; Li, S.; Chen, S. The Dilemma of C-Rate and Cycle Life for Lithium-Ion Batteries under Low Temperature Fast Charging. Batteries 2022, 8, 234. https://doi.org/10.3390/batteries8110234
Gao Z, Xie H, Yang X, Niu W, Li S, Chen S. The Dilemma of C-Rate and Cycle Life for Lithium-Ion Batteries under Low Temperature Fast Charging. Batteries. 2022; 8(11):234. https://doi.org/10.3390/batteries8110234
Chicago/Turabian StyleGao, Zhenhai, Haicheng Xie, Xianbin Yang, Wanfa Niu, Shen Li, and Siyan Chen. 2022. "The Dilemma of C-Rate and Cycle Life for Lithium-Ion Batteries under Low Temperature Fast Charging" Batteries 8, no. 11: 234. https://doi.org/10.3390/batteries8110234
APA StyleGao, Z., Xie, H., Yang, X., Niu, W., Li, S., & Chen, S. (2022). The Dilemma of C-Rate and Cycle Life for Lithium-Ion Batteries under Low Temperature Fast Charging. Batteries, 8(11), 234. https://doi.org/10.3390/batteries8110234








