Abstract
The development of a supercapacitor management system (SMS) for clean energy applications is crucial to addressing carbon emissions problems. Consequently, state of charge (SOC), state of health (SOH), and remaining useful life (RUL) for SMS must be developed to evaluate supercapacitor robustness and reliability for mitigating supercapacitor issues related to safety and economic loss. State estimation of SMS results in safe operation and eliminates undesirable event occurrences and malfunctions. However, state estimations of SMS are challenging and tedious, as SMS is subject to various internal and external factors such as internal degradation mechanism and environmental factors. This review presents a comprehensive discussion and analysis of model-based and data-driven-based techniques for SOC, SOH, and RUL estimations of SMS concerning outcomes, advantages, disadvantages, and research gaps. The work also investigates various key implementation factors such as a supercapacitor test bench platform, experiments, a supercapacitor cell, data pre-processing, data size, model operation, functions, hyperparameter adjustments, and computational capability. Several key limitations, challenges, and issues regarding SOC, SOH, and RUL estimations are outlined. Lastly, effective suggestions are outlined for future research improvements towards delivering accurate and effective SOC, SOH, and RUL estimations of SMS. Critical analysis and discussion would be useful for developing accurate SMS technology for state estimation of a supercapacitor with clean energy and high reliability, and will provide significant contributions towards reducing greenhouse gas (GHG) to achieve global collaboration and sustainable development goals (SDGs).
1. Introduction
The need for clean energy has emerged as a pressing issue in today’s scenario, due to increased consumption of fossil-based energy resources [1,2,3]. To comply with the increasing needs worldwide, various applications, particularly electric vehicles (EV), smart grids, etc., are moving towards Energy Storage System (ESS) technology [4]. Primarily, the ESS consists of a battery, a supercapacitor or hybrid-based technology such as lithium-ion, capacitor, etc. [5]. Lithium-ion battery technology has been widely employed in EV applications, due to various advantages such as high capacity, high power density, low cost, and low self-discharge rate [6]. Nonetheless, the lithium-ion battery suffers from high internal resistance and drop in power density ratio limits, resulting in reduced power delivery capacity under a heavy loading current. Moreover, the battery life is exposed to high current profile and transient loading [7]. In contrast to to the lithium-ion battery, a supercapacitor delivers high output in short cycles due to high power density, high safety, wide operating temperature range, and capacity [8]. Due to this, supercapacitor technology is gaining interest in various fields such as EVs, electrical power systems, and hybrid-based vehicle systems [9,10,11,12].
The supercapacitor technology, also termed an electrode double layer capacitor (EDLC) ultra-capacitor, is considered an energy storage technology that differs from the conventional capacitor and battery system. The supercapacitor structure comprises electrode, diaphragm, electrolyte and fluid collector [13,14]. The effectiveness and performance accuracy of a supercapacitor is demonstrated in several applications, due to various factors mentioned earlier. However, the advancements in supercapacitor technology can be enhanced with the development of a supercapacitor management system (SMS). The SMS technology conducts various tasks such as current, voltage measurement, and signal processing from acceleration and regenerative braking, and monitors states such as state of charge (SOC), state of health (SOH) and remaining useful life (RUL) [8]. The schematic framework of an SMS is presented in Figure 1.
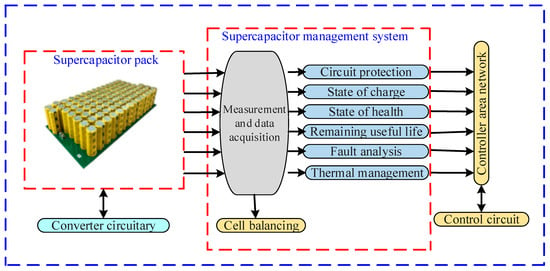
Figure 1.
Schematic diagram of SOC, SOH, and RUL estimation in SMS.
The SMS in EV technology consists of a data acquisition system, measurement system, control system, mechanical system, data processing system and other software/hardware technologies [15]. The implementation of an SMS in a supercapacitor for state estimation and RUL prediction is essential. Considerable research has been conducted to implement an appropriate framework for SMS [16]. Model-based and data-driven based techniques have been introduced in SMS for achieving SOC, SOH estimation, and RUL prediction [17]. The model-based method requires a mathematical model and extensive knowledge related to experimentation and empirical data to capture the algorithm performance [18]. Additionally, model-based methods utilize a smaller amount of data and require large functional relationships and complex mathematical equations to depict various internal material characteristics for SOC, SOH estimation, and RUL prediction. However, the execution of data-driven methods requires a large volume of data without the inclusion of a mathematical model (physics-based) for its operation [19]. In recent times, the application of the data-driven model has increased, due to the availability of large volumes of data, increased processing power and advanced graphics processors unit (GPU). Furthermore, supercapacitor-based SOC, SOH estimation, and RUL prediction by deep learning (DL) methods are also gaining popularity, due to their strong computation capability, better generalization performance, convergence speed and high accuracy [20].
To date, very few notable review articles have been published for SOC, SOH estimation and RUL predictions of supercapacitor technology. For instance, Zhang et al. [21] conducted a review of supercapacitor modeling and SOC and SOH estimation techniques and their industrial applications. However, the review based on SOC and SOH estimations was not comprehensive, and lacked the delivery of associated critical issues and challenges. Laadjal and Cardoso [22] reviewed supercapacitor modeling and state estimation, such as state of energy (SOE) and SOH models. Nevertheless, the reviews based on the implementation factor for state estimation techniques and issues and challenges were not discussed. Liu et al. [17] presented a review of various SOC estimations and RUL prediction techniques for a supercapacitor. However, the review conducted did not include intelligent-based models. In summary, the abovementioned reviews were carried out to deliver an insight into modeling and state estimations. However, reviews based on state estimations and RUL prediction, along with the inclusion of implementation factors, limitations, issues, and challenges, were not conducted comprehensively.
To bridge the current research gaps, this review presents new contributions with a comprehensive explanation of recent SOC, SOH estimation, and RUL prediction techniques for SMS. The list of the contributions is as follows:
- Numerous SOC, SOH, and RUL estimation techniques are comprehensively reviewed regarding their implementation, execution, strength, weakness, and research gaps.
- Important implementation factors such as test bench experiments, battery data sources, data features, data size, computational capability, and model training are explained.
- Existing limitations, research gaps, and issues, and challenges regarding supercapacitor SOC, SOH, and RUL estimation are discussed.
- Some important suggestions for future research development of state estimation techniques are delivered.
The rest of the paper is divided into eight sections. Section 2 covers the survey methodology used to conduct the presented review. Failure mode and aging in supercapacitors are presented in Section 3. In Section 4, the SOC, SOH, and RUL estimation techniques are discussed. Critical implementation factors to conduct supercapacitor states estimation are highlighted in Section 5. Issues and challenges are examined in Section 6. Future prospects and suggestions are discussed in Section 7. Lastly, the conclusion is presented in Section 8.
2. Survey Methodology
The review articles aim to deliver important discussion and analyses by gathering recent information regarding various techniques for SOC, SOH estimation, and RUL prediction in SMS. To conduct this review, the process of screening and analysis was conducted in three phases, to select the appropriate number of research articles. In the first phase of screening and analysis, some important databases such as Scopus and Web of Science (WoS) were utilized to perform a detailed survey of SOC, SOH, and RUL methods for supercapacitor technology. Several web platforms, such as IEEE Xplore, ScienceDirect, MDPI, Google Scholar, etc., were applied, to explore the suitable manuscripts. Furthermore, several keywords were employed to search for suitable research works within the scope and target, consisting of supercapacitor, state of charge, state of health, remaining useful life, supercapacitor management system, and electric vehicle, in the second phase of screening. Additionally, suitable research articles were searched for with respect to title, abstract, novelty, contributions and research gaps. A total of 290 papers were selected and analyzed. In the final phase of screening, the analysis was conducted based on the journal’s quartile, citation, impact factor and review process. In this way, 85 research articles were selected to draft the presented review paper.
The outcomes of the discussion and analyses can be classified into four sections. Firstly, SOC, SOH and RUL estimation based on several techniques are reviewed. Secondly, the implementation factors of various approaches are discussed. Thirdly, key issues and challenges are presented. Lastly, future prospects and suggestions for future advancement and improvements are delivered. The screening methodology to conduct the review is presented in Figure 2.
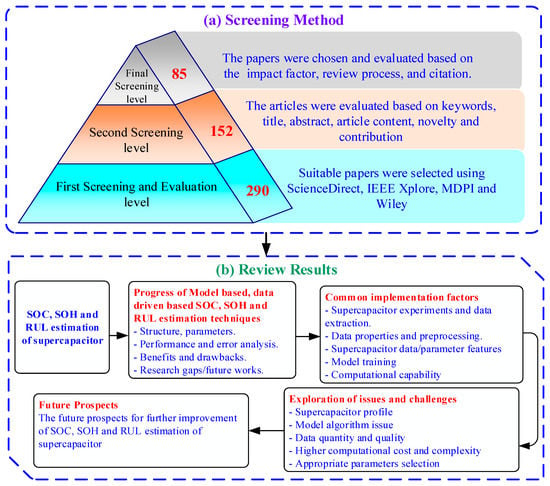
Figure 2.
Schematic process of the (a) screening method, (b) review results for the presented review.
3. Failure Modes and Aging in Supercapacitor Technology
The energy storage system (ESS) represents an important component in many applications such as communication, electrical power systems, medical applications, and EV. Primarily, the ESS consists of a battery, supercapacitor, or hybrid-based technology such as lithium-ion, capacitor, etc. The application of ESS technology is based on longevity, which dictates ownership cost, lifetime and feasibility. Hence, the estimation of ESS degradation is important for improving its framework and applicability. Supercapacitor lifetime is calculated as the average time before degradation, also referred to as the incapability of the part to perform its proper function. Primarily, the failure mechanism in the supercapacitor can be classified into two categories, i.e., early failure curve, wear-out failure curve acquired from bathtub curve, and cylindrical deformation caused by internal atmospheric pressure [23].
Based on the material classification, two operational modes can be observed for storing charges in a supercapacitor [24,25]. Firstly, a non-faradaic process is involved, in which double electrode layer (EDL) capacitance originates from EDL and results in electron accumulation at the electrode, as shown in Figure 3 [26]. Secondly, there is a faradaic process in which pseudo capacitance (PC) is observed, due to the occurrence of a redox reaction between an electrode and an electrolyte. The electrons generated during the redox reaction can be transported across the electrolyte-electrode interface. Even though the operational modes, i.e., EDL capacitance and PC, differ from each other, the pseudo capacitance mode is not dissimilar to a battery, due to the occurrence of a faradaic process on the pseudocapacitive material surface for a supercapacitor, as opposed to the same mode occurring in bulk for battery-type materials. The capacitive features of PC material are depicted in the cyclic voltammogram curve [27]. The operational modes discussed above could explain the internal process with EDL capacitance and PC-based electrodes. However, the functional operation with regard to the hybrid-based supercapacitor is more complex [28].
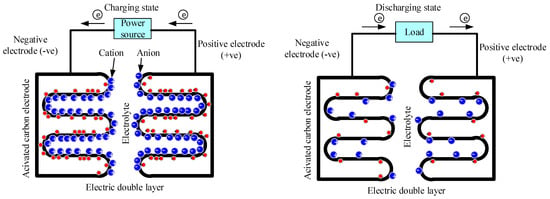
Figure 3.
Charging and discharging process in EDL supercapacitor. The Blue colour refers to cation and anion whereas red colour refers to activated carbon electrode ions.
The failure modes in the EDLC can usually be attributed to many factors, as discussed in the literature. Several failure modes occurring in the EDLC are electrolyte leakage and evaporation, capacitance loss, structure deformation, and equivalent series resistance increase [29,30,31]. It is observed that supercapacitor aging occurs in the zone of double-layer formation [32]. The magnitude of the electric field gradient is maximum in the double-layer zone, resulting in an aging reaction between electrolyte and electrode. Due to this, the formation of solid and gaseous products occurs inside the supercapacitor chamber [33]. Due to the formation of solid products, the electrode porosity is blocked, and hence the size of the contact surface is minimized between the electrolyte and electrode. The formation of gaseous products results in an internal pressure increase, reduces the contact surface between electrolyte and electrode, and stops ionic charge circulation. Furthermore, the increase in internal pressure inside the supercapacitor chamber leads to electrode cracking and elongation, resulting in collector structure damage.
4. Progress of SOC, SOH, and RUL Estimation Techniques in SMS
The current progress of the various SOC, SOH, and RUL estimation techniques have been reviewed based on mode-based and data-driven techniques. The various crucial factors such as outcomes, methods, operation features, advantages, disadvantages, and research gaps are examined.
4.1. Progress of SOC Estimation Techniques in SMS
In general terms, the SOC is defined as the proportion of the current capacity in relation to the maximum capacity. An accurate SOC estimation for EV application is crucial, as it ensures system safety, prolongs life, lowers the cost of energy consumption, and improves EV driving mileage [34]. The SOC estimation is not conducted directly from the supercapacitor terminals and therefore an appropriate SOC estimation framework should be developed. An accurate SOC estimation is required for energy management and to protect the energy storage system from uneven degradation [35]. In recent times, significant progress in estimating the SOC of supercapacitors based on model-based and data-driven based methods has been conducted [8]. A comprehensive review of the model-based and data-driven based techniques has been discussed, based on modeling, benefits, drawbacks, and research gaps.
4.1.1. Model-Based Methods for SOC Estimation of Supercapacitor
The model-based techniques for an SOC estimation of a supercapacitor consists of Kalman filter (KF) based models [36,37,38,39,40] and fractional order models [41,42,43], which are discussed in the following subsections.
Based on Kalman Filter (KF) Technique
Chiang et al. [39] proposed an extended KF (EKF) technique to determine temperature and SOC for an ultra-capacitor. The implementation of the framework was conducted by considering terminal voltage and current. The expression of the implemented equivalent circuit model (ECM) for the ultra-capacitor was expressed as [39]
where, is referred to as impedance of capacitor , , denotes the impedance of the first and second RC circuit and represents the operating frequency. The EKF-based method delivered satisfactory results by considering model uncertainties and measurement noises during the estimation of different states and model parameters. Furthermore, the strength of the EKF estimation model over the open-loop prediction was more significant during dynamic charging/discharging cycles. Nonetheless, the current-based leakage state estimation using other ECM integrated with KF techniques in real-time implementation was not considered. Nadeau et al. [44] presented a three-branch ECM (TBECM) with a KF model to provide highly accurate energy awareness and efficient SOC tracking, by considering the model leakage effect, as presented in Figure 4:
Figure 4.
Three-branch ECM (TBECM) model for SOC estimation of supercapacitor.
The charging current in the proposed TBECM can be expressed as:
where denotes fixed capacitance, represents voltage-dependent capacitance and and denote the resistance and voltage in the second branch. and express the resistance and voltage in the third branch, and denotes the terminal voltage of the TBECM of the supercapacitor. A novel method based on the parameter estimation technique (PET) was introduced so that parameter fitting for TBECM could be performed accurately. The experimental validation was conducted based on different ratings of the supercapacitor in farad (F). The delivered outcomes suggested the superiority of TBECM over one branch ECM (OBECM) due to appropriate charge redistribution phenomena. However, the robustness and efficiency of the TBECM can be validated with online estimation in a real-time environment. Saha et al. [45] developed an ECM model for supercapacitor modeling to address the leakage effect due to faradaic reactions and short circuits (SC) between the electrodes. The proposed ECM for modeling supercapacitor dynamics is shown in Figure 5.
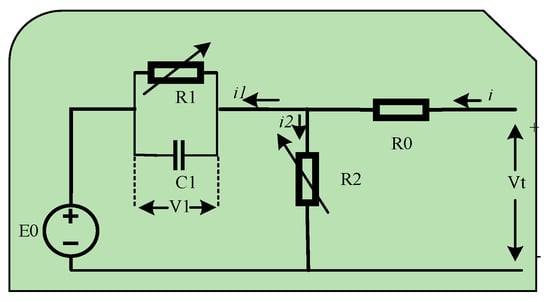
Figure 5.
One branch ECM model for SOC estimation of supercapacitor.
The following expressions were acquired by applying Kirchhoff’s law in the proposed supercapacitor model [45]:
where refers to the summation of and . is the current across the - and is the current across , denotes the voltage drop across -, and and represent variable resistance and value of charge distribution, respectively. is open-circuit voltage, is equivalent to series resistance, and is referred to as terminal voltage. Additionally, the execution of the unscented KF (UKF) based SOC estimation framework was performed, based on the UKF ability to preserve model non-linearities compared with conventional KF or EKF. The study showed that consideration of the leakage effect was important for conducting online monitoring in low-duty-cycle applications such as WSN [46]. However, further improvement in ECM can be executed by considering temperature and degradation of model parameters. Similarly, Saha et al. [37] introduced a co-estimation framework for SOC estimation, leakage current and open-circuit voltage (OCV)-SOC mapping for supercapacitors in real-time applications. The proposed technique was developed using UKF with ECM. Work in [45] estimated supercapacitor SOC in real-time by offline leakage current, whereas the work in [37] delivered a co-estimation platform towards estimating SOC, leakage current, and an OCV-SOC map. Satisfactory performance accuracy for SOC estimation was achieved in the simulation and experimental process. Nonetheless, the model complexity and cost-effectiveness can be improved with the real-time calculation of OCV-SOC parameters,
where, and represent the polarization voltage, battery OCV, and terminal voltage, respectively. and denote the polarization resistance and capacitance, respectively. signifies the battery current and is the ohmic resistance of the battery circuit. For supercapacitors, and represent the voltage across capacitance and terminal voltage, respectively. and are the equivalent series capacitance and resistance, respectively. denotes the current flowing through the supercapacitor. The prediction accuracy for the proposed UKF model was significant in terms of mean absolute error (MAE), and root mean absolute error (RMSE). However, further investigation could be carried out for energy optimization management and energy efficiency of hybrid storage technologies. Jarraya et al. [47] developed a real-time technique and EKF-based SOC estimation model for lithium-ion and supercapacitor storage technologies. Furthermore, the inclusion of the Recursive Least Square (RLS) and OCV method with a forgetting factor was performed, to obtain high estimation accuracy in a real-time environment. The estimation outcomes were validated based on different scenarios, and it was concluded that OCV and two online algorithms (RLS and EKF) achieved significant results (MAE) compared with other researches [48,49,50]. In addition, Jarraya et al. [47] discussed extending the presented work with more sophisticated algorithms with control and security features. Wang et al. [51] proposed different SOC estimation techniques for supercapacitor and lithium-ion batteries by applying KF and UKF models, respectively, as shown in Figure 6. The results demonstrated high accuracy for supercapacitor and lithium-ion SOC estimation, indicating [−0.94%, 0.34%] and [−1.16%, 0.85%], respectively.
Figure 6.
Improved KF based technique for SOC estimation of supercapacitor.
Based on Fractional-Order Model Technique
It is essential to develop an effective, accurate, and robust equivalent physical model for characterizing the electrical behavior of a supercapacitor. Firstly, the design requires accurate modeling, considering complicated conditions. Secondly, a highly accurate SOC estimation can be achieved with an appropriate model parameters definition. To track the electrical behavior of the supercapacitor, Zhang et al. [41] developed an SOC estimation framework based on fractional-order modeling consisting of a series resistor, a constant-phase-element (CPE) and a Warburg-like element for replicating the supercapacitor characteristics. The deduced impedance of the proposed fractional model for SOC estimation of supercapacitor can be stated as [41],
where, denotes the impedance of the proposed fractional model and and represent the series resistance and charge transfer resistance, respectively. C denotes the constant, denotes the total capacitance coefficient and and denote the fractional-order coefficient and capacitance dispersion, respectively. The fractional model parameters are determined by a genetic algorithm (GA) under various operating temperatures such as −40 °C, −20 °C, 0 °C, 20 °C, and 40 °C. The outcomes depicted stability and accuracy in characterizing electrical behavior. Wang et al. [42] proposed fractional-order modeling integrated with GA for parameter identification, as shown in Figure 7. The SOC estimation was achieved with a combined particle filter (PF) and fractional KF (FKF). The fractional-order model was analyzed with Kirchhoff’s equations, as presented in the following expressions [42],
where denotes supercapacitor current and , and are the capacitances in different phase elements, respectively. The value of and is between 0 to 1. are the source voltage and output voltage, respectively. are the voltage across the different phase elements.
Figure 7.
Fractional model and GA-based flowchart for SOC estimation.
Krishnan et al. [43] developed an online identification framework for parameter estimation of a fractional order model for SOC estimation of a supercapacitor. The proposed method delivered a precise characterization of the SC dynamics in terms of accurate SOC estimation. However, the method is complex, as it involves numerical evaluation of the fractional order differentiation (FOD) in real-time, which can be computationally intensive and challenging.
4.1.2. Data-Driven-Based Methods for SOC Estimation of Supercapacitor
Weigert et al. [52] developed an SOC estimation technique for supercapacitors and batteries, by employing the ANN model. A 3-layer feedforward neural network (FFNN) was considered for SOC estimation, which was trained with the Levenberg–Marquardt backpropagation algorithm. The selection of the suitable model hyperparameters was conducted with a trial and error method. The proposed method demonstrated satisfactory performance with a short initial segment (less than 4% of the average lifetime) of the discharge curve. Although the technique did not employ data representing the internal battery characteristics, the accuracy of the proposed data-driven model could be enhanced by utilizing a suitable meta-heuristic optimization technique for hyperparameter selection. Houlian et al. [53] introduced a hybrid data-driven technique consisting of a backpropagation neural network (BPNN) and KF model for an SOC estimation of a supercapacitor. Firstly, the battery temperature was considered as input data for the KF model to deliver the SOC estimation. Subsequently, the SOC estimation results obtained from the KF technique were utilized as training data to train the BPNN model for estimating the future SOC. The following equations demonstrate the proposed Thevenin’s model for the supercapacitor [53]:
where denotes time, represents temperature, is the polarization voltage and signifies the supercapacitor capacity. The model structure of the proposed BPNN model consists of three layers, i.e., input layer, hidden layer and output layer. Similarly to [52], a trial and error technique was implemented to select the suitable model hyperparameters, while the LM algorithm was used as a model training function. The maximum prediction error estimated was <6%, which was related to the poor estimation ability of the BPNN model. The poor estimation ability could be improved with the execution of the DL technique, which depicts high estimation ability with the time input sequence. A tabulated summary consisting of various SOC estimation methods with their strengths, weaknesses, and research gaps is presented in Table 1.

Table 1.
Comparative analysis of model-based and data-driven methods for SOC estimation of supercapacitor.
4.2. Progress of SOH Estimation Techniques in SMS
During the continuous charging and discharging of the supercapacitor, the health of the supercapacitor degrades. In this regard, the SOH estimation in the supercapacitor is considered an important index for estimating the health of the supercapacitor. The SOH estimation describes the degradation profile of the supercapacitor and acts as an important reference for evaluating the health parameter of the supercapacitor. It is defined as the ratio of available maximum capacity to the rated capacity [54]. The SOH estimation of supercapacitor utilizing model-based and data-driven based methods is explored concerning methods, contributions, advantages, disadvantages, and research gaps.
4.2.1. Model-Based Methods for SOH Estimation of Supercapacitor
The model-based SOH estimation of the supercapacitor can be classified into empirical model based [55,56,57], filter-based [58,59,60], and other methods [61,62,63]. The SOH estimation techniques have been reviewed under the guidelines of methodological aspect, strength, weakness, and research gap.
Based on the Empirical Model
The Empirical model (EM)-based SOH estimation framework for supercapacitors is based on the evaluation of large volumes of data. Kötz et al. [55] developed an EM-based mechanism for analyzing the aging and failure mode of supercapacitors under constant load conditions at different voltages and temperatures. Several parameters, such as internal capacitance and resistance, and leakage current were studied, to estimate supercapacitor aging. The investigation showed that the aging phenomenon is severe during high temperature and voltage, where the supercapacitor internal mechanism breaks apart at the voltage of 3.5 V or temperatures above 70 °C. However, a conclusion was not reached regarding the occurrence of a semi-circle in Electrochemical impedance spectra (EIS), leading to incomplete outcomes. Kreczanik et al. [57] examined the supercapacitor aging and lifetime estimation based on accelerated cycling tests. The supercapacitor aging was monitored based on various parameters such as voltage, current and temperature. The experimentation was performed on five packs, each consisting of four supercapacitors. The expression of supercapacitor lifetime estimation for the presented aging model was stated as [57],
where represents the dynamic lifetime (in seconds) and , and are the dynamic voltage value across the supercapacitor, dynamic temperature in °C and RMS current, respectively. and refer to the start time and end time, respectively. The value of is s, , and . Examination showed that capacity degradation occurs at a faster rate in cycling compared with calendar aging during low voltage and temperature. Nonetheless, the regeneration phenomena occurring during the rest time between the charging and discharging cycle was not investigated. Torregrossa and Paolone [56] presented an SOH estimation model based on the supercapacitor capacity regeneration and accelerated aging phenomena. The SOH estimation was conducted with various conditions such as life endurance and power cycling stress. The study showed that that the maximum error estimated was 4.6%, which could increase significantly if the recovering phases and accelerated aging phases were not accounted for during the SOH estimation.
Based on Filter Techniques
Mejdoubi et al. [60] designed an online SOH estimation by employing EKF. The EKF was utilized due to its recursion ability, making it suitable for real-time applications. The application of different sensors for parameter estimation was reduced due to the utilization of voltage and current measurements only. The voltage-current dynamics characteristics for the presented supercapacitor model can be denoted with the following expression,
where, represents the supercapacitor voltage, and denote the equivalent series resistance and capacitance, respectively, and signifies the charge/discharge current. The performance of the EFK-based SOH estimation was satisfactory under various current conditions and noise. Nevertheless, the proposed method could be further improved with the extraction of suitable supercapacitor parameters during charging/discharging. Naseri et al. [58] developed an online multi-state estimation technique for SOH and SOE based on UKF. The UKF-based estimation technique employed the non-linear supercapacitor dynamics, resulting in higher accuracy. The predicted results delivered 99.58% accuracy with a computational power usage of 9.1% for SOH estimation. Additionally, the presented model showed a remarkably low computational burden, making it suitable for real-time applications. Bououchma and Sabor [59] conducted a comparative analysis with the RLS method, and KF was employed for the SOH estimation of the supercapacitor.
4.2.2. Data-Driven-Based Methods for SOH Estimation of Supercapacitor
Several state-of-the-art data-driven techniques such as recursive least square (RLS) [58,59,64] and the ANN model [65] have been implemented for the SOH estimation of supercapacitor in SMS. The determination of SOH estimation in a supercapacitor is carried out with two critical parameters, which are capacitance and internal resistance.
Oukaour et al. [66] introduced an RLS technique to diagnose the aging effect in the supercapacitor. The supercapacitor parameters such as equivalent series resistance (ESR) and equivalent capacitance were measured and analyzed. It was detected that supercapacitor aging resulted in an increase in ESR and a decrease in equivalent capacitance. The observed ESR curve with aging depicted acceptable outcomes. However, the developed technique only considered some parts of the component behavior. Naseri et al. [67] proposed a recursive extended least-square algorithm (RELS) technique for determining the ESR and equivalent capacitance towards an SOH estimation, as presented in Figure 8. The presented model obtained satisfactory outcomes considering ESR and noise dynamics.
Figure 8.
RELS model-based for SOH estimation of supercapacitor.
With regard to ANN models, Soualhi et al. [65] developed a neuro-fuzzy neural network (NFNN) consisting of four inputs and two membership functions for estimating the capacity degradation profile of the supercapacitor. The design of a neuro-fuzzy neural network was proposed by combining ANN and fuzzy logic to minimize the overfitting issue and depict a clear explanation of input and output parameters. The proposed model showed an accurate approach toward SOH estimation, depicting a normalized root mean square error (NRMSE) of 0.772 × 10−6. Although the technique depicted robustness and accuracy, further research to enhance the model accuracy and robustness by selecting suitable hyperparameters could be conducted. A tabulated summary consisting of various SOH estimation methods with their strengths, weaknesses, and research gaps is presented in Table 2.

Table 2.
Comparative analysis of model-based and data-driven methods for SOH estimation of supercapacitor.
4.3. Progress of RUL Estimation Techniques in SMS
The accurate, effective and robust EV operation depends on the supercapacitor’s RUL. The RUL estimation assists in timely predictive maintenance by providing important information regarding fault occurrences. In general terms, the RUL is defined as the useful operative life of the supercapacitor before it attains the threshold level (70% or 80% of the initial capacity). Therefore, it is suggested that the supercapacitor is replaced when the threshold level is achieved [68]. The estimation of the RUL of a supercapacitor is important, as it provides crucial information by determining the occurrence of failure and eliminating issues [6,69]. Supercapacitor health is represented by RUL, which has attracted enormous attention, due to its application in various ESSs. The RUL estimation of a supercapacitor is conducted using model-based and data-driven techniques.
4.3.1. Model-Based Methods for RUL Estimation of Supercapacitor
Xu et al. [70] developed a RUL estimation model for supercapacitors by considering various parameters such as temperature, current intensity, and cycle times, based on the classical Arrhenius model. The attenuation function for the capacity of the supercapacitor regarding temperature is represented by the Arrhenius model, as represented by the following equations [70],
where, represents the capacity attenuation, denotes the pre-exponential factor, is defined as activation energy, signifies the temperature, expresses the constant number, and and represent the cycle number and power index, respectively. Considering the log function on both sides of the equation, the modified equation can be written as
The above equation is employed to determine the model parameters at different temperatures, and a modified capacity attenuation model () is achieved as
Additionally, the capacity attenuation model is utilized to establish the supercapacitor at different charging and discharging currents. Examination showed that activation energy is associated linearly with electric current (), given by the following expression:
Hence, the capacity attenuation model at different temperatures and currents can be expressed as
It was estimated that the predicted curve depicted error within the range of 3%, and fits well with the experimental data. However, the proposed model-based RUL estimation is applicable within the temperature range of 25–55 °C. Liu et al. [71] proposed an exploration technique for RUL estimation of supercapacitor. The capacity attenuation model for the proposed model can be expressed as
where denotes the capacitance retention rate, signifies the number of samples, expresses the number of cycles, denotes the ratio of the initial capacity to the rated capacitance, and are the constants associated with capacity attenuation rate. The above expression is used to identify the model parameters and determine the average extrapolation operating limit. Examination showed that the proposed model estimated the supercapacitor life accurately under the different number of cycles.
4.3.2. Data-Driven-Based Methods for RUL Estimation of Supercapacitor
Weigert et al. [72] previously developed a three-layer ANN model for estimating the cycle life of the battery-supercapacitor system. The RUL estimation of the supercapacitor was conducted based on short charge-discharge curve data. A three-layer backpropagation neural network (BPNN) was employed, where the model hyperparameters were selected using the trial and error method. The input to the BPNN model was ESR, duty ratio and battery type. However, the estimated outcomes were unsatisfactory. Hence, new input in the form of voltage from the discharge curve was considered, which resulted in satisfactory outcomes with an estimation error under 4%. Even though the estimation accuracy increased with a suitable selection of input data the optimal values of model hyperparameters were nonetheless crucial factors. Additionally, the memory space was not provided for previous weights, resulting in ineffectiveness in finding a global optimal. In recent times, the application of RNN has effectively solved the limitations of the above-mentioned work. Several research studies for RUL estimation based on RNN models such as the long short term memory (LSTM) model, have been accomplished. Zhou et al. [73] developed an LSTM-based method for an RUL estimation of supercapacitors. The RUL estimation was carried out considering a number of charging and discharging cycles as an input to the LSTM model. The model hyperparameters such as learning rate, hidden layer and dropout ratio were selected, based on the trial and error method. The outcomes of the LSTM model in RUL prediction were compared to other RNN models, such as simple RNN and gated recurrent unit (GRU). The proposed model achieved satisfactory outcomes, but the application of suitable functions such as the call-back function could be implemented to optimize the model with the best hyperparameters. Furthermore, Zhou et al. [74] extended earlier work and proposed a hybrid GA and LSTM-based technique for a RUL estimation of a supercapacitor, as shown in Figure 9.
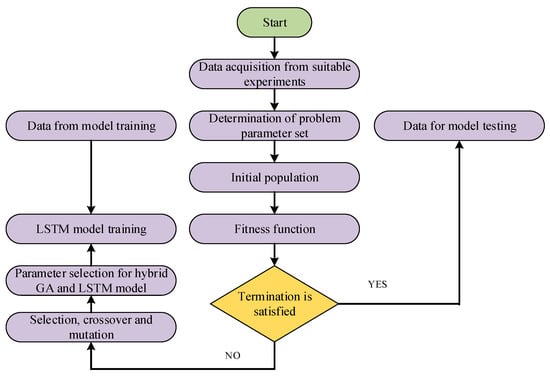
Figure 9.
Hybrid GA and LSTM model for RUL prediction of supercapacitor.
The application of a GA optimization technique was considered, to enhance global search ability, thereby allowing a quick search for the optimal local solution. The hybrid GA-LSTM model was employed to evaluate the RUL of supercapacitor under steady-state and hybrid pulse power characterization mode, and achieved a negligible deviation of 1.61%. However, the proposed model showed computational complexity with high training time.
To avoid long training time and cost-consuming lifecycle testing, Haris et al. [75] developed a hybrid DL-based deep belief network (DBN) and Bayesian Optimization and HyperBand (BOHB) for a RUL estimation of the supercapacitor. The model training time required a 6% lower amount of data compared with other research activities using 70% data. The performance of the hybrid DBN-BOHB model was compared with the Bayesian Optimization and HyperBand technique, and results suggested that the BOHB algorithm was 77% faster than other two algorithms for our prediction network. Although the proposed method depicted high computational training ability, a suitable sampling technique could be employed for extracting the supercapacitor data samples, to improve its training. Additionally, a hybrid model based on a convolutional neural network (CNN) and LSTM was developed for the RUL estimation of lithium-ion capacitors, due to its high reliability and prediction accuracy, and which can be applied to battery monitoring and prognostics [76]. The proposed hybrid technique demonstrated an ability to resist environmental interference, thus delivering accurate and stable RUL estimation outcomes. Although minimal error with RUL estimation was achieved with the hybrid CNN-LSTM model, the model estimation uncertainty should be carefully considered for further research works. A comparative summary of the various model-based and data-driven-based RUL prediction techniques for supercapacitors is tabulated in Table 3.

Table 3.
Comparative analysis of model-based and data-driven-based RUL estimation technique for supercapacitor.
5. Implementation Factors for SOC, SOH and RUL Estimation Methods in SMS
The execution of various SOC, SOH and RUL estimation techniques requires implementation factors that have substantial effects on state estimation outcomes. Therefore, it is crucial to investigate the significance of the implementation factors on various supercapacitor state estimations.
5.1. Supercapacitor Test Bench Platform and Experiments
A supercapacitor test bench model is important for extracting suitable data for SOC, SOH and RUL estimation. The supercapacitor test bench model consists of various components, such as a battery test system (BTS), a host computer, a thermal chamber and a test supercapacitor. Test bench equipment such as Arbin BT-5HC, Neware BTS-5V200A and Land CT2001A battery test systems are primarily utilized for data acquisition of the supercapacitor for SOC, SOH, and RUL estimation [53,73,77]. The operational performance, estimation accuracy, data acquisition time, processing speed and robustness differ for each BTS [77]. Wang et al. [78] studied different ECM models of supercapacitors by using the Digatron Battery Test System (BTS-600). Wang et al. [79] developed an estimation technique based on the ECM model by employing the ARBIN BT-5HC test system, where data samples from current, terminal voltage, charging-discharging capacity and energy, record step-index and cycle index were extracted. Saha et al. [45] employed a Bitrode FTV supercapacitor testing module for SOC estimation of the supercapacitor. The Bitrode testing platform depicts the capacity to supply current up to 6 A and 100 A in its low current and high current operating modes, respectively. Additionally, the modeling and SOC estimation of the supercapacitor was performed with Neware BTS800 to capture the suitable battery and supercapacitor data [40]. An Arbin instrument test platform was considered in the health estimation of the supercapacitor by Kreczanik et al. [57]. Liu et al. [71] developed the RUL estimation technique considering the Neware BTS800 test platform with a series of Maxwell BCAP3000 supercapacitors.
5.2. Supercapacitor Cell
The estimation of various supercapacitor states such as SOC, SOH and RUL can be conducted with the application of suitable supercapacitor cells. Several supercapacitor cells with different ratings, such as the Maxwell 350F2.5V, Maxwell BCAP3000 P270 K04, Maxwell BCAP0005, and WiMa SuperCapType R, have been employed for SOC, SOH and RUL estimations of the supercapacitor [41]. Houlian and Gongbo [53] developed an SOC estimation technique considering the Maxwell series supercapacitor BCAP3000P270, specified as C = 3000 °F. The operating voltage of the supercapacitor is 2.7 V with an operational temperature range of −40 °C to +65 °C. Nadeau et al. [44] employed KF to examine SOC estimation using Maxwell BoostCap supercapacitor and Illinois Capacitor. A fractional-order ECM for SOC estimation for the supercapacitor was constructed considering the Maxwell 350F operating at 2.5 V [42]. The supercapacitor has a small size with a 33 mm diameter and a long lifetime, with up to 500,000 duty cycles. Soulahi et al. [65] developed a health prognostic technique for supercapacitor technology, comprising a metalized polymer film (MPF) capacitor, with a rating of 15 µF and an operational voltage of 400 V. Mejdoubi et al. [80] presented a PF-based RUL estimation, utilizing the series of BCAP0350 Maxwell technology supercapacitors with a capacity of 350 F.
5.3. Supercapacitor Data Features
The suitable extraction of supercapacitor data features is crucial for the acquisition of appropriate and effective estimation outcomes. Primarily, SOC, SOH and RUL estimations of the supercapacitor take place by considering several input parameters such as voltage, current, temperature and capacity [81]. For instance, Lei et al. [81] proposed an ANN network to conduct an SOC estimation of supercapacitors. Several critical parameters such as terminal voltage, charge/discharge current and temperature were considered to conduct the experimentation. The residual charge was considered as the output of the ANN model. A KF-based technique was utilized, and circuit resistance was considered as an input factor for determining the SOC of the supercapacitor [44]. Additionally, Zhang et al. [41] employed the supercapacitor voltage and current as an input parameter to estimate the SOC based on the fractional order model. Regarding the SOH estimation, a hybrid neo-fuzzy neural network was utilized, and a series of impedances calculated at different frequencies were employed as model inputs to calculate the ESR. The estimated ESR and capacitance were employed to analyze the health diagnosis of the supercapacitor. Mejdoubi et al. [82] proposed an SOH estimation technique and utilized current and voltage as potential input parameters for an SOH estimation of the supercapacitor. Capacity cycle data were considered for the RUL estimation, which was processed by using the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) [76].
5.4. Supercapacitor Data Pre-Processing
Data pre-processing is an important step in evaluating the SOC, SOH and RUL of the supercapacitor accurately. Various data processing methods such as data transformation, data cleaning, data filtering, data normalization and data reduction are considered before the data is utilized. Data cleansing is employed to remove unwanted noise and incomplete data from the dataset. Additionally, suitable transformation of data can be observed with data normalization and the data averaging method [77]. For instance, Yang et al. [76] employed empirical mode decomposition (EMD) and the CEEMDAN technique to process the supercapacitor dataset for conducting the RUL estimation. Data obtained after the pre-processing stage effectively eliminates outliers and high-frequency oscillations, while retaining the main information of the original signal.
5.5. EV Supercapacitor Data Size
The appropriate selection of the data size results in accurate outcomes with less calculation complexity and high accuracy. Houlian and Gongbo [53] estimated the SOC of supercapacitor considering two different working conditions, the United States New York Bus Cycles (New York Bus) and New York City Driving Cycles (NYCC). The data size varied from 100 to 300 with an interval of 50 s to estimate the SOC of the supercapacitor. Zhou et al. [73] developed a RUL estimation technique for supercapacitors using the LSTM model, where the first 70% of the supercapacitor data set was used for model training. Furthermore, the model testing was conducted with random data which was obtained from the experimental data. On the other hand, Soualhi et al. [83] developed an aging prediction model of supercapacitor considering the initial 50% capacitance data for prediction. A RUL estimation of supercapacitor by PF technique was proposed where different training samples such as 30%, 50%, and 70% were employed [80]. In recent times, a DL method consisting of the DBN and BOHB technique was introduced for the RUL estimation of supercapacitors, where only 6% of the dataset was used as a training dataset and demonstrated high accuracy as compared to previous studies [75].
5.6. Model Operations, Functions and Hyperparameter Adjustments
The suitable selection of models, their functions and hyperparameters results in high accuracy with low computational cost. For instance, Zhang et al. [78] developed a GA-based SOC estimation algorithm where several parameters of GA, such as population size, number of generations, tournament selection, crossover probability and mutation probability, were determined, using the trial and error method. A BPNN model comprising three layers, i.e., input layer, hidden layer and output layer, with 16 hidden neurons, was constructed for an SOC estimation of the supercapacitor. The Transig and Purelin function were considered as the activation function of the hidden layer and the output layer, respectively. The Levenberg-Marquardt algorithm was applied as a learning algorithm of the BPNN model. Hammou and Gualous [84] compared the EKF and high gain observer (HGO) technique for SOH estimation of the supercapacitor. The EKF-based parameters such as noise variance and covariance matrices noise were selected, indicating R = 0.01 and Q = diag {[0.01 × 10−8 0.01 × 10−8]}, respectively, and the tuning parameter for HGO was chosen as 1.5. Zhou et al. [74] developed a hybrid model with LSTM and GA for the RUL estimation of supercapacitor. The dropout probability and the number of hidden neurons of the LSTM model were optimized using the GA algorithm, where the optimized dropout was 0.58, and the hidden layer consisted of 156 units. Other model hyperparameters such as epoch number, initial learning rate and reduction factor of the learning rate were selected using the trial and error method.
5.7. Computational Capability
The computational capability in supercapacitor SOC, SOH and RUL estimation is a vital factor in delivering appropriate outcomes with low calculation complexity, power requirement and limited storage capacity. Currently, some notable research developments have been undertaken regarding fast computational processors and a high volume of storage space. The upgradation of computational capabilities SOC, SOH and RUL estimation have created a pathway for the growth of advanced and hybrid models for state estimation. For instance, Zhou et al. [74] utilized an Intel core i7-based host computer to develop a hybrid GA and LSTM model for the RUL estimation of the supercapacitor.
6. Limitations, Issues, and Challenges in SOC, SOH, and RUL Estimation of SMS
The estimation of SOC, SOH and RUL for SMS has delivered significant outcomes. However, there remain some concerns and issues that need to be addressed. The limitations, issues and challenges for SOC, SOH, and RUL estimation of supercapacitor are discussed below.
- The estimation accuracy of various SOC, SOH, and RUL models varies with different supercapacitor chemistries. As discussed earlier, many supercapacitor chemistries such as Maxwell 350F2.5V, Maxwell BCAP3000 P270 K04, Maxwell BCAP0005, and WiMa SuperCapType R are currently employed. For instance, the commonly used Maxwell BCAP3000 P270 K04 supercapacitor technology depicts contrasting outcomes compared with WiMa SuperCapType R supercapacitor technology with the same model and hyperparameters. Therefore, further investigation is suggested to estimate SOC, SOH and RUL with different supercapacitor technology.
- Supercapacitor aging is a critical factor that lowers the estimation accuracy of models. Various aspects, such as electrolyte leakage, evaporation, capacitance loss, etc., are some of the causes related to the supercapacitor aging mechanism. The state-of-the-art DL techniques have proven to be incapable of depicting accurate outcomes associated with supercapacitor aging. The identification of the supercapacitor degradation curve can be integrated into online supercapacitor estimation methods. The application of the differential analysis (DA) method is promising as a way of addressing supercapacitor aging, and could be combined with data-driven models. Nonetheless, further studies of supercapacitor aging are required, and accordingly, exploration of critical supercapacitor aging indicators should be carried out.
- The SOC, SOH, and RUL estimation demonstrates satisfactory estimation accuracy based on the model framework. Various models/techniques illustrate shortcomings due to some limitations. For instance, the PF technique delivers satisfactory outcomes with high dimensional systems. Nevertheless, it requires high computational power. KF models are light and deliver reasonable results with low training time, but the outcomes suffer from low accuracy. Data-driven models rely on historical data and demonstrate fast training responses. However, human intervention is required to select suitable model hyperparameters for achieving accurate outcomes. The DL techniques deliver excellent estimation outcomes but require a large volume of training datasets. Henceforth, the appropriate selection of a model framework requires further study to develop estimation algorithms.
- Several critical factors such as data size, computational complexity and model hyperparameters determine the performance accuracy of the models. For instance, suitable data sizes should be extracted and used for assessing SOC, SOH and RUL estimation. Low volume of data size may lead to improper outcomes, while a high volume of data size may result in computational complexity and overfitting issues. The computational complexity depends on data size, model structure and hyperparameters. The computational complexity remains low when a suitable data size with an appropriate model with its hyperparameters is selected. On the contrary, a high volume of data size with an inappropriate model and hyperparameter selection may lead to computational complexity. Lastly, the selection of model hyperparameters such as hidden layers, hidden neurons, activation function, number of epochs, batch size, number of iterations, weights, bias, and training function should be chosen quantity, computational complexity and hyperparameter selection.
- Currently, the acquisition of a supercapacitor dataset may be extracted from suitable sources under various conditions, such as Constant-current constant-voltage (CCCV). In contrast to this, the operational principles for real-world supercapacitor applications vary significantly. Additionally, the operational profile of the supercapacitor switches dynamically. Therefore, further analysis should be conducted to study the behavior of real-world supercapacitor data.
7. Future Research Improvements and Suggestions for SOC, SOH, and RUL Estimation of Supercapacitor
Based on the proposed review of various model-based and data-driven based methods for SOC, SOH, and RUL estimation of the supercapacitor, some critical future suggestions are delivered.
- Primarily, the SOC, SOH and RUL estimation is based on a single supercapacitor cell. However, the utilization of supercapacitor packs, i.e., supercapacitors connected in series and in parallel, could also be employed for the state estimation. In the case of the supercapacitor pack, performance inconsistency may occur due to different material composition and manufacturing guidelines. Furthermore, uneven aging may occur in supercapacitor cells, due to the presence of a temperature gradient in the pack. Therefore, the application of different controller and converter topologies can be undertaken to remove unbalancing issue. Additionally, extensive investigation is required to study issues related to cell inconsistencies towards SOC, SOH and RUL estimation.
- In recent times, several supercapacitor testing setups have been utilized for SOC, SOH and RUL estimation. Nonetheless, data acquired from the experimental setup may not be desirable, due to various factors such as electromagnetic interference (EMI), unwanted noise, and equipment precision. Furthermore, the outcomes of the various SOC, SOH, and RUL estimation techniques may not deliver satisfactory outcomes due to faulty sensors and EMI. Therefore, a highly sophisticated experimental testing platform should be constructed to access supercapacitor data without the inclusion of noise and EMI. To overcome these issues, techniques such as wavelength transformation and the recursive total least squares method can be employed.
- At the present time, the development of DL techniques for conducting state estimation has seen a drastic increase among researchers worldwide. Therefore, a requirement of host computers with high configuration computational processors for conducting the model training becomes an evident necessity. The application of DL techniques on high configuration computers would result in achieving high estimation accuracy for supercapacitors.
- The application of hybrid techniques in the SOC, SOH and RUL estimation of the supercapacitor compared to the single model technique has become increasingly important among researchers. The development of a hybrid model takes place by integrating two or more models to develop a single technique. The application of various hybrid PF and KF techniques for SOC, SOH and RUL estimation has been conducted in recent times, as discussed in Section 4. Nevertheless, the hybridization of models may lead to inaccurate outcomes, overfitting, and computational complexity. Henceforth, the assessment of hybrid models to estimate various states should be carefully analyzed regarding their practicality and feasibility.
- The estimation accuracy of data-driven models such as ANN depends on the suitable selection of model hyperparameters. The appropriate value of hyperparameters would result in satisfactory results and a low computational burden, but inappropriate selection of model hyperparameters would lead to inaccurate results and a high computational burden [85]. As a common practice, the model utilizes the ‘trial and error’ technique to select suitable hyperparameters. However, the technique is time-consuming and requires human expertise.
8. Conclusions
The estimation of various supercapacitor states such as SOC, SOH and RUL is crucial to achieving high robustness and accuracy with supercapacitor-operated applications. The SOC, SOH and RUL estimation is affected by various internal and external factors, such as electrochemical reactions, supercapacitor material, temperature, methods, and supercapacitor aging. To address these issues, significant research has been performed to develop suitable SOC, SOH and RUL estimation methods. In this review, state-of-the-art SOC, SOH and RUL estimation methods which are both model-based and data-driven-based are reviewed comprehensively with respect to implementations, methods, advantages, disadvantages, contributions and research limitations. The outcomes indicate that each SOC, SOH and RUL estimation technique demonstrates significant contributions. Model-based techniques are best suited to study the supercapacitor internal degradation mechanism, whereas data-driven methods are best suited to parameter data, to achieve various state estimations.
Secondly, the review paper discusses various implementation factors such as the supercapacitor test bench platform and experiments, supercapacitor cell, data pre-processing, data size, model operation, functions, hyperparameter adjustments and computational capability. The outcomes reveal that a suitable selection of various implementation factors is critical to achieve the satisfactory estimation accuracy.
Thirdly, various issues are discussed, which comprise supercapacitor technology, supercapacitor aging, model structure, and real-world supercapacitor data issues. The study shows that outlined issues should be considered, to develop an accurate supercapacitor estimation model. Lastly, some key future suggestions and prospects for the development of SOC, SOH and RUL estimation methods are delivered, highlighting the importance of implementing DL techniques, hybrid models, appropriate hyperparameter selection, etc.
All in all, the in-depth review of various SOC, SOH, and RUL estimation techniques along with implementation factors, issues, and future suggestions would prove beneficial for researchers, policymakers, and industrialists globally in formulating and conducting further research on SOC, SOH and RUL estimation of the supercapacitor. Additionally, the information delivered would be beneficial for improving supercapacitor performance, guaranteeing clean energy, high reliability and efficiency, increasing energy efficiency, and reducing GHG emissions, towards achieving global collaboration and SDGs.
Author Contributions
Conceptualization, S.A., A.A. and M.S.H.L.; methodology, S.A. and M.S.H.L.; validation, S.A., A.A. and M.S.H.L.; formal analysis, S.A. and A.A.; investigation, S.A. and M.S.H.L.; resources, S.A. and M.S.H.L.; data curation, S.A., A.A. and M.S.H.L.; writing—original draft preparation, S.A. and M.S.H.L.; writing—review and editing, S.A., A.A. and M.S.H.L.; visualization, S.A. and M.S.H.L.; supervision, A.A., A.H., M.S.H.L. and M.H.M.S.; project administration, A.A. and A.H.; funding acquisition, A.A. and A.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by Universiti Kebangsaan Malaysia under Grant Number DIP 2021-003.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the financial support provided by Universiti Kebangsaan Malaysia.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| ANN | Artificial neural network |
| BOHB | Bayesian optimization and hyperband |
| BPNN | Backpropagation neural network |
| BTS | Battery testing system |
| CCCV | Constant current constant voltage |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CPE | Constant phase element |
| CNN | Convolutional neural network |
| DBN | Deep belief network |
| DL | Deep learning |
| ECM | Equivalent circuit model |
| EDL | Electrode double layer |
| EDLC | Electrode double layer capacitor |
| EIS | Electrochemical impedance spectra |
| EKF | Elman Kalman filter |
| EMD | Empirical mode decomposition |
| EM | Electrochemical model |
| EMI | Electromagnetic interference |
| ESR | Equivalent series resistance |
| ESS | Energy storage system |
| EV | Electric vehicle |
| FFNN | Feedforward neural network |
| FKF | Factional Kalman filter |
| FOD | Fractional order differentiation |
| GA | Genetic Algorithm |
| GHG | Greenhouse gas |
| GPU | Graphical processing unit |
| GRU | Gated recurrent unit |
| KF | Kalman filter |
| LM | Levenberg marquardt |
| LSTM | Long short term memory |
| MAE | Mean absolute error |
| MPF | Metalized polymer film |
| NFNN | Neuro-fuzzy neural network |
| NRMSE | Normalized root mean square error |
| NYCC | New York City driving cycle |
| OBECM | One-branch equivalent circuit model |
| OCV | Open circuit voltage |
| PC | Pseudo capacitance |
| PET | Parameter estimation technique |
| PF | Particle filter |
| PMP | Pontryagin’s minimum principle |
| RELS | Recursive extended least square algorithm |
| RLS | Recursive least square |
| RMS | Root mean square |
| RUL | Remaining useful life |
| SDG | Sustainable development goal |
| SMS | Supercapacitor management system |
| SOC | State of charge |
| SOH | State of health |
| TBECM | Three-branch equivalent circuit model |
| UKF | Unscented Kalman filter |
References
- Tarhan, C.; Çil, M.A. A study on hydrogen, the clean energy of the future: Hydrogen storage methods. J. Energy Storage 2021, 40, 102676. [Google Scholar] [CrossRef]
- Nosratabadi, S.M.; Hemmati, R.; Bornapour, M.; Abdollahpour, M. Economic evaluation and energy/exergy analysis of PV/Wind/PEMFC energy resources employment based on capacity, type of source and government incentive policies: Case study in Iran. Sustain. Energy Technol. Assessments 2021, 43, 100963. [Google Scholar] [CrossRef]
- Pao, H.T.; Chen, C.C. Decoupling strategies: CO2 emissions, energy resources, and economic growth in the Group of Twenty. J. Clean. Prod. 2019, 206, 907–919. [Google Scholar] [CrossRef]
- Khalid, M.R.; Khan, I.A.; Hameed, S.; Asghar, M.S.J.; Ro, J.S. A Comprehensive Review on Structural Topologies, Power Levels, Energy Storage Systems, and Standards for Electric Vehicle Charging Stations and Their Impacts on Grid. IEEE Access 2021, 9, 128069–128094. [Google Scholar] [CrossRef]
- Song, Z.; Li, J.; Hou, J.; Hofmann, H.; Ouyang, M.; Du, J. The battery-supercapacitor hybrid energy storage system in electric vehicle applications: A case study. Energy 2018, 154, 433–441. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.M. Data-Driven Remaining Useful Life Prediction for Lithium-Ion Batteries Using Multi-Charging Profile Framework: A Recurrent Neural Network Approach. Sustainability 2021, 13, 13333. [Google Scholar] [CrossRef]
- Kachhwaha, A.; Rashed, G.I.; Garg, A.R.; Mahela, O.P.; Khan, B.; Shafik, M.B.; Hussien, M.G. Design and Performance Analysis of Hybrid Battery and Ultracapacitor Energy Storage System for Electrical Vehicle Active Power Management. Sustainability 2022, 14, 776. [Google Scholar] [CrossRef]
- Naseri, F.; Karimi, S.; Farjah, E.; Schaltz, E. Supercapacitor management system: A comprehensive review of modeling, estimation, balancing, and protection techniques. Renew. Sustain. Energy Rev. 2022, 155, 111913. [Google Scholar] [CrossRef]
- Kouchachvili, L.; Yaïci, W.; Entchev, E. Hybrid battery/supercapacitor energy storage system for the electric vehicles. J. Power Source 2018, 374, 237–248. [Google Scholar] [CrossRef]
- Shi, X.; Chen, S.; Zhang, H.; Jiang, J.; Ma, Z.; Gong, S. Portable Self-Charging Power System via Integration of a Flexible Paper-Based Triboelectric Nanogenerator and Supercapacitor. ACS Sustain. Chem. Eng. 2019, 7, 18657–18666. [Google Scholar] [CrossRef]
- Rahman, A.U.; Ahmad, I.; Malik, A.S. Variable structure-based control of fuel cell-supercapacitor-battery based hybrid electric vehicle. J. Energy Storage 2020, 29, 101365. [Google Scholar] [CrossRef]
- Yang, Y.; Han, Y.; Jiang, W.; Zhang, Y.; Xu, Y.; Ahmed, A.M. Application of the supercapacitor for energy storage in China: Role and strategy. Appl. Sci. 2022, 12, 354. [Google Scholar] [CrossRef]
- Gu, P.; Liu, W.; Hou, Q.; Ni, Y. Lignocellulose-derived hydrogel/aerogel-based flexible quasi-solid-state supercapacitors with high-performance: A review. J. Mater. Chem. A 2021, 9, 14233–14264. [Google Scholar] [CrossRef]
- Guan, M.; Wang, Q.; Zhang, X.; Bao, J.; Gong, X.; Liu, Y. Two-Dimensional Transition Metal Oxide and Hydroxide-Based Hierarchical Architectures for Advanced Supercapacitor Materials. Front. Chem. 2020, 8, 390. [Google Scholar] [CrossRef]
- Xue, X.D.; Fan, Y.L.; Fong, Y.C.; Raghu Raman, S.; Mei, J.; Wang, X.L.; Cheng, K.W.E. Development of battery-supercapacitor management system for battery-supercapacitor hybrid energy storage system. In Proceedings of the 11th IET International Conference on Advances in Power System Control, Operation and Management (APSCOM 2018), Hongkong, China, 11–15 November 2018; pp. 1–5. [Google Scholar]
- Tahri, A.; El Fadil, H.; Belhaj, F.Z.; Gaouzi, K.; Rachid, A.; Giri, F.; Chaoui, F.Z. Management of fuel cell power and supercapacitor state-of-charge for electric vehicles. Electr. Power Syst. Res. 2018, 160, 89–98. [Google Scholar] [CrossRef]
- Liu, C.; Li, Q.; Wang, K. State-of-charge estimation and remaining useful life prediction of supercapacitors. Renew. Sustain. Energy Rev. 2021, 150, 111408. [Google Scholar] [CrossRef]
- Yu, J. State-of-Health Monitoring and Prediction of Lithium-Ion Battery Using Probabilistic Indication and State-Space Model. IEEE Trans. Instrum. Meas. 2015, 64, 2937–2949. [Google Scholar] [CrossRef]
- Liao, L.; Köttig, F. Review of hybrid prognostics approaches for remaining useful life prediction of engineered systems, and an application to battery life prediction. IEEE Trans. Reliab. 2014, 63, 191–207. [Google Scholar] [CrossRef]
- Tong, Z.; Miao, J.; Tong, S.; Lu, Y. Early prediction of remaining useful life for Lithium-ion batteries based on a hybrid machine learning method. J. Clean. Prod. 2021, 317, 128265. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. A review of supercapacitor modeling, estimation, and applications: A control/management perspective. Renew. Sustain. Energy Rev. 2018, 81, 1868–1878. [Google Scholar] [CrossRef]
- Laadjal, K.; Cardoso, A.J.M. A review of supercapacitors modeling, SoH, and SoE estimation methods: Issues and challenges. Int. J. Energy Res. 2021, 45, 18424–18440. [Google Scholar] [CrossRef]
- Kurzweil, P.; Schottenbauer, J.; Schell, C. Past, Present and Future of Electrochemical Capacitors: Pseudocapacitance, Aging Mechanisms and Service Life Estimation. J. Energy Storage 2021, 35, 102311. [Google Scholar] [CrossRef]
- Zhi, M.; Xiang, C.; Li, J.; Li, M.; Wu, N. Nanostructured carbon-metal oxide composite electrodes for supercapacitors: A review. Nanoscale 2013, 5, 72–88. [Google Scholar] [CrossRef] [PubMed]
- Shao, Y.; El-Kady, M.F.; Sun, J.; Li, Y.; Zhang, Q.; Zhu, M.; Wang, H.; Dunn, B.; Kaner, R.B. Design and Mechanisms of Asymmetric Supercapacitors. Chem. Rev. 2018, 118, 9233–9280. [Google Scholar] [CrossRef]
- Shiraishi, S. Electric Double Layer Capacitor. In Carbon Alloys; Elsevier: Amsterdam, The Netherlands, 2003; pp. 447–457. [Google Scholar]
- Liu, S.; Wei, L.; Wang, H. Review on reliability of supercapacitors in energy storage applications. Appl. Energy 2020, 278, 115436. [Google Scholar] [CrossRef]
- Augustyn, V.; Simon, P.; Dunn, B. Pseudocapacitive oxide materials for high-rate electrochemical energy storage. Energy Environ. Sci. 2014, 7, 1597–1614. [Google Scholar] [CrossRef]
- Temsamani, A.B.; Kauffmann, S.; Helsen, S.; Gaens, T.; Driesen, V. Physics-of-Failure (PoF) methodology for qualification and lifetime assessment of supercapacitors for industrial applications. Microelectron. Reliab. 2018, 88–90, 54–60. [Google Scholar] [CrossRef]
- Gualous, H.; Gallay, R.; Alcicek, G.; Tala-Ighil, B.; Oukaour, A.; Boudart, B.; Makany, P. Supercapacitor ageing at constant temperature and constant voltage and thermal shock. Microelectron. Reliab. 2010, 50, 1783–1788. [Google Scholar] [CrossRef]
- Gualous, H.; Gallay, R.; Al Sakka, M.; Oukaour, A.; Tala-Ighil, B.; Boudart, B. Calendar and cycling ageing of activated carbon supercapacitor for automotive application. Microelectron. Reliab. 2012, 52, 2477–2481. [Google Scholar] [CrossRef]
- German, R.; Sari, A.; Briat, O.; Vinassa, J.M.; Venet, P. Impact of Voltage Resets on Supercapacitors Aging. IEEE Trans. Ind. Electron. 2016, 63, 7703–7711. [Google Scholar] [CrossRef]
- Azaïs, P.; Duclaux, L.; Florian, P.; Massiot, D.; Lillo-Rodenas, M.A.; Linares-Solano, A.; Peres, J.P.; Jehoulet, C.; Béguin, F. Causes of supercapacitors ageing in organic electrolyte. J. Power Source 2007, 171, 1046–1053. [Google Scholar] [CrossRef]
- Tudoroiu, R.E.; Zaheeruddin, M.; Tudoroiu, N.; Radu, S.M. Soc estimation of a rechargeable li-ion battery used in fuel cell hybrid electric vehicles—Comparative study of accuracy and robustness performance based on statistical criteria. Part ii: Soc estimators. Batteries 2020, 6, 41. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Mamun, A.A.; Ansari, S.; Miah, S.; Hasan, K.; Meraj, S.T.; Abdolrasol, M.G.M.; Rahman, T.; Maruf, H.; Sarker, M.R.; et al. Battery Management, Key Technologies, Methods, Issues, and Future Trends of Electric Vehicles: A Pathway toward Achieving Sustainable Development Goals. Batteries 2022, 8, 119. [Google Scholar] [CrossRef]
- Parvini, Y.; Siegel, J.B.; Stefanopoulou, A.G.; Vahidi, A. Supercapacitor Electrical and Thermal Modeling, Identification, and Validation for a Wide Range of Temperature and Power Applications. IEEE Trans. Ind. Electron. 2015, 63, 1574–1585. [Google Scholar] [CrossRef]
- Saha, P.; Dey, S.; Khanra, M. Accurate estimation of state-of-charge of supercapacitor under uncertain leakage and open circuit voltage map. J. Power Source 2019, 434, 226696. [Google Scholar] [CrossRef]
- Chiang, C.J.; Yang, J.L.; Cheng, W.C. EKF-based estimation of SOC and temperature in ultracapacitors. In Proceedings of the 2013 10th IEEE International Conference on Control and Automation (ICCA), Hangzhou, China, 12–14 June 2013; pp. 274–279. [Google Scholar]
- Chiang, C.J.; Yang, J.L.; Cheng, W.C. Temperature and state-of-charge estimation in ultracapacitors based on extended Kalman filter. J. Power Source 2013, 234, 234–243. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Pan, R.; Chen, Z. Modeling and state-of-charge prediction of lithium-ion battery and ultracapacitor hybrids with a co-estimator. Energy 2017, 121, 739–750. [Google Scholar] [CrossRef]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. Fractional-order modeling and State-of-Charge estimation for ultracapacitors. J. Power Source 2016, 314, 28–34. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, L.; Mao, J.; Zhou, J.; Xu, D. Fractional order equivalent circuit model and SOC estimation of supercapacitors for use in HESS. IEEE Access 2019, 7, 52565–52572. [Google Scholar] [CrossRef]
- Krishnan, G.; Das, S.; Agarwal, V. An Online Identification Algorithm to Determine the Parameters of the Fractional-Order Model of a Supercapacitor. IEEE Trans. Ind. Appl. 2019, 56, 763–770. [Google Scholar] [CrossRef]
- Nadeau, A.; Hassanalieragh, M.; Sharma, G.; Soyata, T. Energy awareness for supercapacitors using Kalman filter state-of-charge tracking. J. Power Source 2015, 296, 383–391. [Google Scholar] [CrossRef]
- Saha, P.; Dey, S.; Khanra, M. Modeling and state-of-charge estimation of supercapacitor considering leakage effect. IEEE Trans. Ind. Electron. 2019, 67, 350–357. [Google Scholar] [CrossRef]
- Diab, Y.; Venet, P.; Gualous, H.; Rojat, G. Self-discharge characterization and modeling of electrochemical capacitor used for power electronics applications. IEEE Trans. Power Electron. 2008, 24, 510–517. [Google Scholar] [CrossRef]
- Jarraya, I.; Masmoudi, F.; Chabchoub, M.H.; Trabelsi, H. An online state of charge estimation for Lithium-ion and supercapacitor in hybrid electric drive vehicle. J. Energy Storage 2019, 26, 100946. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Dang, X.; Yan, L.; Xu, K.; Wu, X.; Jiang, H.; Sun, H. Open-Circuit Voltage-Based State of Charge Estimation of Lithium-ion Battery Using Dual Neural Network Fusion Battery Model. Electrochim. Acta 2016, 188, 356–366. [Google Scholar] [CrossRef]
- Cui, D.; Xia, B.; Zhang, R.; Sun, Z.; Lao, Z.; Wang, W.; Sun, W.; Lai, Y.; Wang, M. A novel intelligent method for the state of charge estimation of lithium-ion batteries using a discrete wavelet transform-based wavelet neural network. Energies 2018, 11, 995. [Google Scholar] [CrossRef]
- Wang, K.; Liu, C.; Sun, J.; Zhao, K.; Wang, L.; Song, J.; Duan, C.; Li, L. State of Charge Estimation of Composite Energy Storage Systems with Supercapacitors and Lithium Batteries. Complexity 2021, 2021, 8816250. [Google Scholar] [CrossRef]
- Weigert, T.; Tian, Q.; Lian, K. State-of-charge prediction of batteries and battery-supercapacitor hybrids using artificial neural networks. J. Power Source 2011, 196, 4061–4066. [Google Scholar] [CrossRef]
- Houlian, W.; Gongbo, Z. State of charge prediction of supercapacitors via combination of Kalman filtering and backpropagation neural network. IET Electr. Power Appl. 2018, 12, 588–594. [Google Scholar] [CrossRef]
- Ezemobi, E.; Silvagni, M.; Mozaffari, A.; Tonoli, A.; Khajepour, A. State of Health Estimation of Lithium-Ion Batteries in Electric Vehicles under Dynamic Load Conditions. Energies 2022, 15, 1234. [Google Scholar] [CrossRef]
- Kötz, R.; Ruch, P.W.; Cericola, D. Aging and failure mode of electrochemical double layer capacitors during accelerated constant load tests. J. Power Source 2010, 195, 923–928. [Google Scholar] [CrossRef]
- Torregrossa, D.; Paolone, M. Modelling of current and temperature effects on supercapacitors ageing. Part II: State-of-Health assessment. J. Energy Storage 2016, 5, 95–101. [Google Scholar] [CrossRef]
- Kreczanik, P.; Venet, P.; Hijazi, A.; Clerc, G. Study of supercapacitor aging and lifetime estimation according to voltage, temperature, and RMS current. IEEE Trans. Ind. Electron. 2013, 61, 4895–4902. [Google Scholar] [CrossRef]
- Naseri, F.; Farjah, E.; Ghanbari, T.; Kazemi, Z.; Schaltz, E.; Schanen, J.L. Online Parameter Estimation for Supercapacitor State-of-Energy and State-of-Health Determination in Vehicular Applications. IEEE Trans. Ind. Electron. 2019, 67, 7963–7972. [Google Scholar] [CrossRef]
- Bououchma, Z.; Jalal, S. Comparison Between Recursive Least Squares Method and Kalman Filter for Online Identification of Supercapacitor State of Health. Stat. Optim. Inf. Comput. 2022, 10, 119–134. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Oukaour, A.; Chaoui, H.; Slamani, Y.; Sabor, J.; Gualous, H. Online supercapacitor diagnosis for electric vehicle applications. IEEE Trans. Veh. Technol. 2015, 65, 4241–4252. [Google Scholar] [CrossRef]
- Shili, S.; Hijazi, A.; Sari, A.; Bevilacqua, P.; Venet, P. Online supercapacitor health monitoring using a balancing circuit. J. Energy Storage 2016, 7, 159–166. [Google Scholar] [CrossRef]
- German, R.; Hammar, A.; Lallemand, R.; Sari, A.; Venet, P. Novel experimental identification method for a supercapacitor multipore model in order to monitor the state of health. IEEE Trans. Power Electron. 2015, 31, 548–559. [Google Scholar] [CrossRef]
- Chaoui, H.; Gualous, H. Online Lifetime Estimation of Supercapacitors. IEEE Trans. Power Electron. 2016, 32, 7199–7206. [Google Scholar] [CrossRef]
- Reichbach, N.; Kuperman, A. Recursive-Least-Squares-Based Real-Time Estimation of Supercapacitor Parameters. IEEE Trans. Energy Convers. 2016, 31, 810–812. [Google Scholar] [CrossRef]
- Soualhi, A.; Makdessi, M.; German, R.; Echeverria, F.R.; Razik, H.; Sari, A.; Venet, P.; Clerc, G. Heath Monitoring of Capacitors and Supercapacitors Using the Neo-Fuzzy Neural Approach. IEEE Trans. Ind. Inform. 2017, 14, 24–34. [Google Scholar] [CrossRef]
- Oukaour, A.; Pouliquen, M.; Tala-Ighil, B.; Gualous, H.; Pigeon, E.; Gehan, O.; Boudart, B. Supercapacitors aging diagnosis using least square algorithm. Microelectron. Reliab. 2013, 53, 1638–1642. [Google Scholar] [CrossRef]
- Naseri, F.; Farjah, E.; Allahbakhshi, M.; Kazemi, Z. Online condition monitoring and fault detection of large supercapacitor banks in electric vehicle applications. IET Electr. Syst. Transp. 2017, 7, 318–326. [Google Scholar] [CrossRef]
- Ossai, C.I. Prognosis and remaining useful life estimation of lithium-ion battery with optimal multi-level particle filter and genetic algorithm. Batteries 2018, 4, 15. [Google Scholar] [CrossRef]
- Ansari, S.; Ayob, A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.M. Multi-Channel Profile Based Artificial Neural Network Approach for Remaining Useful Life Prediction of Electric Vehicle Lithium-Ion Batteries. Energies 2021, 14, 7521. [Google Scholar] [CrossRef]
- Xu, X.; Liu, H.; Lu, X.; Zhao, Y. Research on capacity life prediction model of supercapacitors. Chin. J. Power Source 2019, 49, 270–282. [Google Scholar]
- Liu, C.; Wang, Y.; Chen, Z.; Ling, Q. A variable capacitance based modeling and power capability predicting method for ultracapacitor. J. Power Source 2018, 374, 121–133. [Google Scholar] [CrossRef]
- Tian, Q.; Lian, K.K. Cycle Life Prediction of Battery-Supercapacitor Hybrids Using Artificial Neural Network. ECS Meet. Abstr. 2010, MA2010-01, 388. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Y.; Pang, J.; Wang, K. Remaining useful life prediction for supercapacitor based on long short-term memory neural network. J. Power Source 2019, 440, 227149. [Google Scholar] [CrossRef]
- Zhou, Y.; Wang, Y.; Wang, K.; Kang, L.; Peng, F.; Wang, L.; Pang, J. Hybrid genetic algorithm method for efficient and robust evaluation of remaining useful life of supercapacitors. Appl. Energy 2020, 260, 114169. [Google Scholar] [CrossRef]
- Haris, M.; Hasan, M.N.; Qin, S. Early and robust remaining useful life prediction of supercapacitors using BOHB optimized Deep Belief Network. Appl. Energy 2021, 286, 116541. [Google Scholar] [CrossRef]
- Yang, H.; Wang, P.; An, Y.; Shi, C.; Sun, X.; Wang, K.; Zhang, X.; Wei, T.; Ma, Y. Remaining useful life prediction based on denoising technique and deep neural network for lithium-ion capacitors. eTransportation 2020, 5, 100078. [Google Scholar] [CrossRef]
- Wang, C.; He, H.; Zhang, Y.; Mu, H. A comparative study on the applicability of ultracapacitor models for electric vehicles under different temperatures. Appl. Energy 2017, 196, 268–278. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Hannan, M.A.; Hussain, A.; Ayob, A.; Saad, M.H.M.; Karim, T.F.; How, D.N.T. Data-driven state of charge estimation of lithium-ion batteries: Algorithms, implementation factors, limitations and future trends. J. Clean. Prod. 2020, 277, 124110. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Hu, X.; Sun, F.; Dorrell, D.G. A comparative study of equivalent circuit models of ultracapacitors for electric vehicles. J. Power Source 2015, 274, 899–906. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Chaoui, H.; Sabor, J.; Gualous, H. Remaining Useful Life Prognosis of Supercapacitors under Temperature and Voltage Aging Conditions. IEEE Trans. Ind. Electron. 2017, 65, 4357–4367. [Google Scholar] [CrossRef]
- Lei, Z.; Wang, Z.; Hu, X.; Dorrell, D.G. Residual capacity estimation for ultracapacitors in electric vehicles using artificial neural network. IFAC Proc. Vol. 2014, 19, 3899–3904. [Google Scholar] [CrossRef]
- El Mejdoubi, A.; Chaoui, H.; Gualous, H.; Sabor, J. Online parameter identification for supercapacitor state-of-health diagnosis for vehicular applications. IEEE Trans. Power Electron. 2017, 32, 9355–9363. [Google Scholar] [CrossRef]
- Soualhi, A.; Sari, A.; Razik, H.; Venet, P.; Clerc, G.; German, R.; Briat, O.; Vinassa, J.M. Supercapacitors ageing prediction by neural networks. In Proceedings of the IECON Proceedings (Industrial Electronics Conference), Vienna, Austria, 10–13 November 2013; pp. 6812–6818. [Google Scholar]
- Hammou, A.; Gualous, H. Comparative study between High gain observer and Extended Kalman filter for supercapacitor state of health estimation. In Proceedings of the 2021 9th International Conference on Systems and Control, ICSC 2021, Caen, France, 24–26 November 2021; pp. 332–337. [Google Scholar]
- Miah, M.S.; Lipu, M.S.H.; Ansari, S.; Meraj, S.T.; Hasan, K.; Masaoud, A.; Hussain, A.; Mahmud, M.S.; Bashar, S.S. Energy Storage Controllers and Optimization Schemes Integration to Microgrid: An Analytical Assessment Towards Future Perspectives. IEEE Access 2022, 10, 52982–53014. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).