Implementation of Battery Digital Twin: Approach, Functionalities and Benefits
Abstract
:1. Introduction
- Limited use cases and implementation results available to learn from others;
- No clear guidance on how much to budget;
- Difficult to know where to start to get value quickly;
- Initiatives that are misleadingly branded as “Digital Twin”;
- Limited know-how.
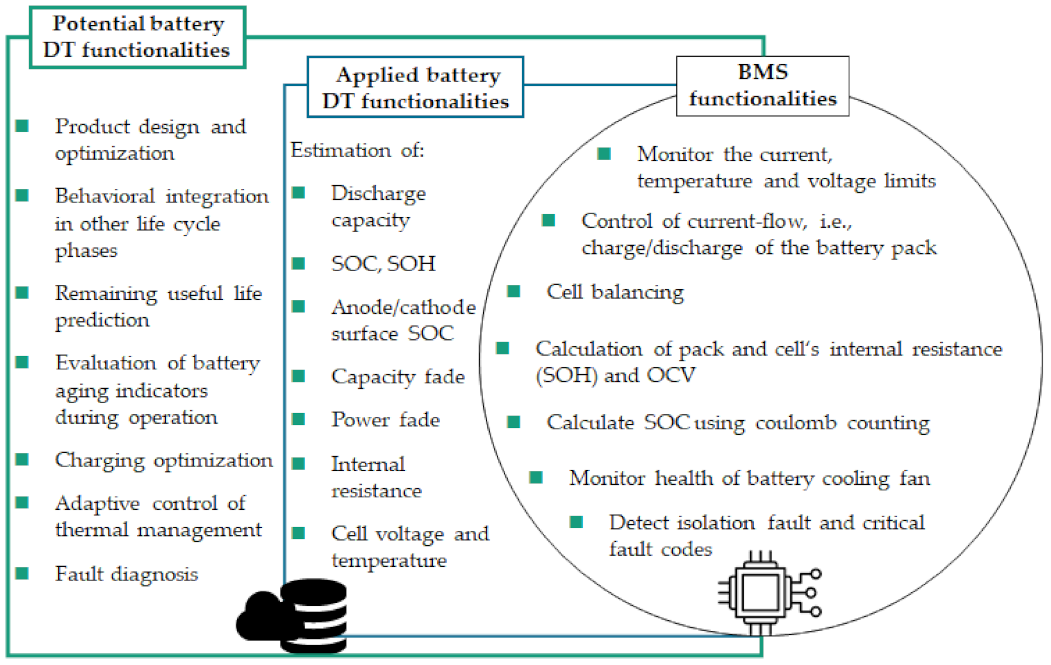
2. Battery DT Functionalities during Operation and End-of-Life
- Some articles only mentioned battery DTs as a possible application
- Some of them did not explain the architecture to support battery DTs
- Others were only theoretical articles.
- Battery DT influence on life cycle phases;
- Current BMS functionalities.
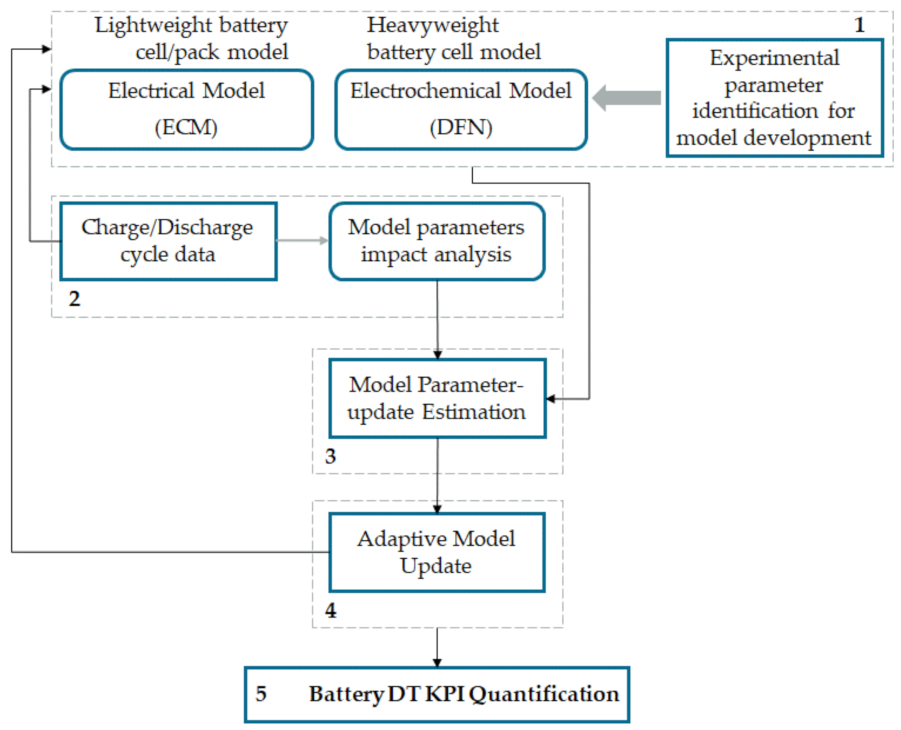
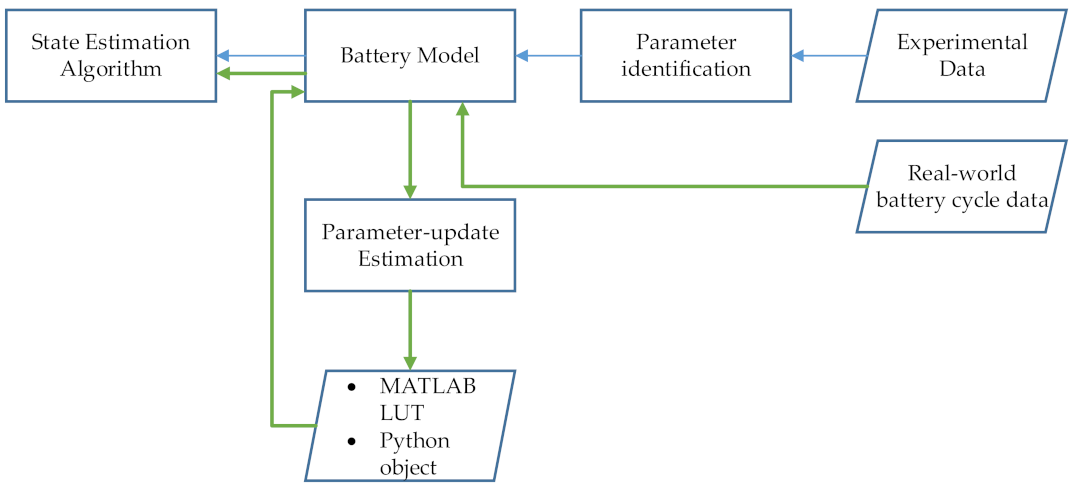
3. Approach
3.1. Step 1: Lightweight or Heavyweight Battery Model Development
- Electrical model (ECM);
- Electrochemical model (P2D);
- Thermal model;
- Mechanical model;
- Interdisciplinary combined model.
- Battery dynamics represented by the model
- Number of parameters
- Computation time
- Accuracy
- Ease of understanding and complexity for implementation.
Experimental Parameter Identification Techniques
3.2. Step 2: Impact Analysis of Real-World Charge/Discharge Cycles on Battery Model Parameter
3.3. Step 3: Model Parameter-Update Estimation
- Calculate the model parameters at the end of N cycles, and repeat the update process iteratively. Identify the reduced set of parameters (such as in Table 1) directly influenced by the number of cycles and operating conditions. The initial conditions (from the governing equations) of the model are certainly updated. Thus, new parameters set and initial conditions are available to the model for its next simulation (N cycles). For DFN, the mathematical estimations of parameters mainly involves revaluating the governing equations which employs Fick’s law of diffusion, charge and mass conservation, concentrated solution theory and Butler-Volmer electrochemical kinetic expression.
- Calculate the rate of degradation physics caused by lithium plating and SEI growth through the reaction equations and rate expressions [62]. Lithium-plating passive film layers formed by consuming of cyclable Li-ions is influenced by the charge transfer mechanism. The rate of SEI formation reaction is affected by mass transport within the anode and by surface kinetics. Effects of degradation physics are integrated in the model after every N cycles.
- Utilize the fast minimization algorithms such as Gauss-Newton method, prediction error minimization by estimating the parameter-update through synthetic experimental data [63]. Synthetic experimental data can be obtained using simulated battery output with computer-generated randomness. However, this method has an unjustified validation scheme because the input would also be simulated; hence this approach is mainly beneficial for initial testing purposes of the battery DT.
- Apply data-driven parameter identification methods estimation which employs the terminal voltage and load current for parameter update (partially applied in [64]). A comprehensive literature survey of the data-driven parameter identification methods is not conducted. Therefore, this paper does not attempt to review the data-driven parameter identification methods thoroughly. Instead, we choose to review if data-driven approaches can support the parameter-update step. There is no doubt that a large amount of training data (collected at the beginning of life) is a requirement for data-driven parameter-update during usage. Nonetheless, the cost and computation time of the data-driven algorithms [65,66] for application in battery DT need to be compared.
3.4. Step 4: Adaptive Model Update
3.5. Step 5: Battery DT KPI Quantification
- Investment
- ◦
- Effect on optimization cost due to battery DT functionalities.
- ◦
- Cost to establish data acquisition from BMS to the battery model. Here, we assume the preexisting cost of sensors installed on the BMS and the cells.
- ◦
- Cost of data storage method, i.e., cloud server, memory drive, etc.
- ◦
- Computational cost of simulating the algorithms of the battery DT.
- Time
- ◦
- Time needed for the state estimation algorithms, optimization algorithms and other battery DT functionalities
- ◦
- Time to retrieve battery data from its application and assign it to the DT
- ◦
- Speed of battery DT alignment with actual battery, i.e., total time for executing the parameter-update step.
- Accuracy
- ◦
- Accuracy of parameter identification.
- ◦
- Accuracy of parameter-update estimation parameter identification.
- ◦
- Accuracy of state estimation
- Functionalities
- ◦
- DT functionalities that support the battery designers (battery design optimization)
- ◦
- DT functionalities that support the battery users
- ◦
- DT functionalities that support the battery EoL handler (RUL assessment)
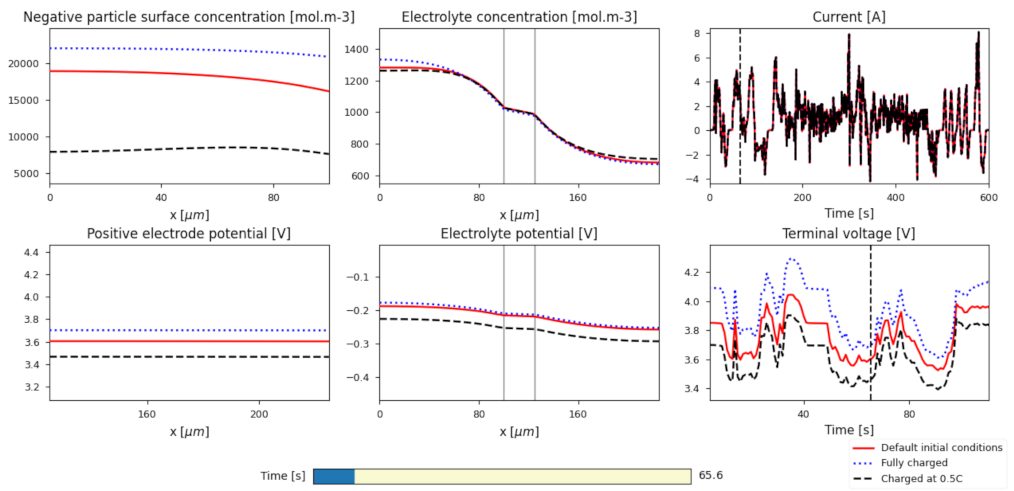
4. Results
5. Discussion
- Level of fidelity expected from a battery DT—A model that captures the electrical, thermal, electrochemical, mechanical and aging aspects of a battery is deemed a high fidelity model. The reality and practicality of such a model are not clear. The cost and time needed for an exhaustive high-fidelity battery DT are high, and the estimate of accuracy improvement is also missing;
- Number of DTs across the battery lifecycle—The idea of a DT across the lifecycle of a product is not entirely understood. This is due to the uncertainty of the number of DTs needed in such cases. Either there is one DT with a large capacity, or there are many small-sized DTs coupled together. For battery DT, the coupling of process and product DT is a possible use case during manufacturing;
- Scaling the battery DT to module and pack-level DT—Achieving battery DTs at scale will require a reduction in technical barriers for their adoption. This implies that for a pack-level battery DT, the number of sensors and the amount of data retrieved will drastically increase. Hence, the data acquisition and storage needs to be seamless;
- Accuracy of behavioral prediction using battery DT—For commercial utilization of battery DTs, it is necessary to compare and quantify the accuracy of existing BMS predictions vs. the prediction of battery DT. Quantification and comparison of percentage error in DT estimations should be the primary focus in future works.
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| DFN Model | Derived through | Governing Equations 1 |
|---|---|---|
| Solid phase mass transport equation—Li+ concentration in electrodes and separator | Fick’s law of diffusion | |
| Liquid phase mass transport equation—Li+ concentration in electrolyte | Conservation of Li+ ions (Conservation of mass) | |
| Solid phase charge transport equation—Potential in electrode | Ohm’s law (Conservation of charge) | |
| Liquid phase charge transport equation—Potential in electrolyte | Ohm’s law and Kirchhoff’s law (Concentrated solution theory, conservation of charge) | |
| Flux density between solid and liquid phase | Butler-Volmer Equation |
| ECM Model Equations | Variables |
|---|---|
| pi = fi(SOC, SOH, T, I) p1 = {VOCV, R1, C1, RS} | i is the i-th parameter of the model. R1 and C1 are the polarization resistance and capacitance and RS is the ohmic resistance. VOCV is the open circuit voltage |
| Vt = VOCV − V1 − VRs; VRs = I * RS | where VRs refers to the voltage reduction from Rs and Vt is the terminal voltage |
| SOC = SOC0 − | SOC calculation using CC, where C is capacity, Ib is current, and SOC0 is the initial SOC |
References
- Singh, S.; Weeber, M.; Birke, K.-P. Advancing digital twin implementation: A toolbox for modelling and simulation. Procedia CIRP 2021, 99, 567–572. [Google Scholar] [CrossRef]
- Shafto, M.; Conroy, M.; Doyle, R.; Glaessgen, E.; Kemp, C.; LeMoigne, J.; Wang, L. Modeling, simulation, information technology & processing roadmap. Natl. Aeronaut. Space Adm. 2012, 32, 1–38. [Google Scholar]
- Boschert, S.; Rosen, R. Digital twin—The simulation aspect. In Mechatronic Futures; Springer: Cham, Switzerland, 2016; pp. 59–74. [Google Scholar]
- Kunath, M.; Winkler, H. Integrating the Digital Twin of the manufacturing system into a decision support system for improving the order management process. Procedia CIRP 2018, 72, 225–231. [Google Scholar] [CrossRef]
- Batty, M. Digital twins. Environ. Plan. B Urban. Anal. City Sci. 2018, 45, 817–820. [Google Scholar] [CrossRef]
- Wright, L.; Davidson, S. How to tell the difference between a model and a digital twin. Adv. Model. Simul. Eng. Sci. 2020, 7, 13. [Google Scholar] [CrossRef]
- Arup Research. Digital Twin—Towards a Meaningful Framework. Available online: https://research.arup.com/publications/digital-twin-towards-a-meaningful-framework/ (accessed on 26 July 2021).
- Singh, M.; Fuenmayor, E.; Hinchy, E.P.; Qiao, Y.; Murray, N.; Devine, D. Digital Twin: Origin to Future. ASI 2021, 4, 36. [Google Scholar] [CrossRef]
- Saracco, R. Digital Twins: Bridging Physical Space and Cyberspace. Computer 2019, 52, 58–64. [Google Scholar] [CrossRef]
- Al-Ali, A.R.; Gupta, R.; Zaman Batool, T.; Landolsi, T.; Aloul, F.; Al Nabulsi, A. Digital twin conceptual model within the context of internet of things. Future Internet 2020, 12, 163. [Google Scholar] [CrossRef]
- Lin, W.D.; Low, M.Y.H. Concept design of a system architecture for a manufacturing cyber-physical Digital Twin system. In Proceedings of the 2020 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 14–17 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1320–1324, ISBN 978-1-5386-7220-4. [Google Scholar]
- Wagg, D.J.; Worden, K.; Barthorpe, R.J.; Gardner, P. Digital Twins: State-of-the-Art and Future Directions for Modeling and Simulation in Engineering Dynamics Applications. ASCE-ASME J. Risk. Uncert. Eng. Syst. Part. B Mech. Eng. 2020, 6, 101001. [Google Scholar] [CrossRef]
- Lim, K.Y.H.; Zheng, P.; Chen, C.-H. A state-of-the-art survey of Digital Twin: Techniques, engineering product lifecycle management and business innovation perspectives. J. Intell. Manuf. 2020, 31, 1313–1337. [Google Scholar] [CrossRef]
- Jones, D.; Snider, C.; Nassehi, A.; Yon, J.; Hicks, B. Characterising the Digital Twin: A systematic literature review. CIRP J. Manuf. Sci. Technol. 2020, 29, 36–52. [Google Scholar] [CrossRef]
- Merkle, L.; Segura, A.S.; Grummel, J.T.; Lienkamp, M. Architecture of a digital twin for enabling digital services for battery systems. In Proceedings of the 2019 IEEE International Conference on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, 6–9 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 155–160. [Google Scholar]
- Schluse, M.; Atorf, L.; Rossmann, J. Experimentable digital twins for model-based systems engineering and simulation-based development. In Proceedings of the 2017 Annual IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 24–27 April 2017; IEEE: Piscataway, NJ, USA, 2017. ISBN 9781509046232. [Google Scholar]
- Josifovska, K.; Yigitbas, E.; Engels, G. Reference Framework for Digital Twins within cyber-physical systems. In Proceedings of the 2019 IEEE/ACM 5th International Workshop on Software Engineering for Smart Cyber-Physical Systems (SEsCPS), Montreal, QC, Canada, 28 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 25–31, ISBN 978-1-7281-2282-3. [Google Scholar]
- Kritzinger, W.; Karner, M.; Traar, G.; Henjes, J.; Sihn, W. Digital Twin in manufacturing: A categorical literature review and classification. IFAC-Pap. 2018, 51, 1016–1022. [Google Scholar] [CrossRef]
- Sitterly, M.; Le Wang, Y.; Yin, G.G.; Wang, C. Enhanced identification of battery models for real-time battery management. IEEE Trans. Sustain. Energy 2011, 2, 300–308. [Google Scholar] [CrossRef]
- Niederer, S.A.; Sacks, M.S.; Girolami, M.; Willcox, K. Scaling digital twins from the artisanal to the industrial. Nat. Comput. Sci. 2021, 1, 313–320. [Google Scholar] [CrossRef]
- Qu, X.; Song, Y.; Liu, D.; Cui, X.; Peng, Y. Lithium-ion battery performance degradation evaluation in dynamic operating conditions based on a digital twin model. Microelectron. Reliab. 2020, 114, 113857. [Google Scholar] [CrossRef]
- Li, W.; Rentemeister, M.; Badeda, J.; Jöst, D.; Schulte, D.; Sauer, D.U. Digital twin for battery systems: Cloud battery management system with online state-of-charge and state-of-health estimation. J. Energy Storage 2020, 30, 101557. [Google Scholar] [CrossRef]
- Merkle, L.; Pöthig, M.; Schmid, F. Estimate e-Golf Battery State Using Diagnostic Data and a Digital Twin. Batteries 2021, 7, 15. [Google Scholar] [CrossRef]
- Peng, Y.; Zhang, X.; Song, Y.; Liu, D. A low cost flexible digital twin platform for spacecraft lithium-ion battery pack degradation assessment. In Proceedings of the 2019 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Auckland, New Zealand, 20–23 May 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6, ISBN 978-1-5386-3460-8. [Google Scholar]
- Baumann, M.; Rohr, S.; Lienkamp, M. Cloud-connected battery management for decision making on second-life of electric vehicle batteries. In Proceedings of the 2018 Thirteenth International Conference on Ecological Vehicles and Renewable Energies (EVER), Monte-Carlo, Monaco, 10–12 April 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1–6, ISBN 978-1-5386-5966-3. [Google Scholar]
- Ramachandran, R.; Ganeshaperumal, D.; Subathra, B. Parameter estimation of battery pack in EV using extended kalman filters. In Proceedings of the 2019 IEEE International Conference on Clean Energy and Energy Efficient Electronics Circuit for Sustainable Development (INCCES), Krishnankoil, India, 18–20 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–5, ISBN 978-1-7281-4407-8. [Google Scholar]
- Wu, B.; Widanage, W.D.; Yang, S.; Liu, X. Battery digital twins: Perspectives on the fusion of models, data and artificial intelligence for smart battery management systems. Energy AI 2020, 1, 100016. [Google Scholar] [CrossRef]
- Sancarlos, A.; Cameron, M.; Abel, A.; Cueto, E.; Duval, J.-L.; Chinesta, F. From ROM of electrochemistry to ai-based battery digital and hybrid twin. Arch. Comput. Methods Eng. 2021, 28, 979–1015. [Google Scholar] [CrossRef]
- Soleymani, A.; Maltz, W. Real time prediction of Li-Ion battery pack temperatures in EV vehicles. In Proceedings of the ASME 2020 International Technical Conference and Exhibition on Packaging and Integration of Electronic and Photonic Microsystems, Virtual, 27–29 October 2020; American Society of Mechanical Engineers: New York, NY, USA, 2020; p. 10272020, ISBN 978-0-7918-8404-1. [Google Scholar]
- Ahmed, R.; Gazzarri, J.; Onori, S.; Habibi, S.; Jackey, R.; Rzemien, K.; Tjong, J.; LeSage, J. Model-Based Parameter Identification of Healthy and Aged Li-ion Batteries for Electric Vehicle Applications. SAE Int. J. Alt. Power. 2015, 4, 233–247. [Google Scholar] [CrossRef] [Green Version]
- Dühnen, S.; Betz, J.; Kolek, M.; Schmuch, R.; Winter, M.; Placke, T. Toward green battery cells: Perspective on materials and technologies. Small Methods 2020, 4, 2000039. [Google Scholar] [CrossRef]
- Wang, W.; Wang, J.; Tian, J.; Lu, J.; Xiong, R. Application of Digital Twin in Smart Battery Management Systems. Chin. J. Mech. Eng. 2021, 34, 1–19. [Google Scholar] [CrossRef]
- Balasingam, B.; Ahmed, M.; Pattipati, K. Battery Management Systems—Challenges and Some Solutions. Energies 2020, 13, 2825. [Google Scholar] [CrossRef]
- Gabbar, H.A.; Othman, A.M.; Abdussami, M.R. Review of Battery Management Systems (BMS) Development and Industrial Standards. Technologies 2021, 9, 28. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Xiong, R.; Shen, W.; He, H. Towards a smarter battery management system: A critical review on optimal charging methods of lithium ion batteries. Energy 2019, 183, 220–234. [Google Scholar] [CrossRef]
- Orion BMS 2. Orion Li-Ion Battery Management System. Available online: https://www.orionbms.com/products/orion-bms-standard/ (accessed on 27 July 2021).
- LION Smart. LION Smart—Battery Management System (BMS). Available online: https://lionsmart.com/en/battery-management-system/ (accessed on 27 July 2021).
- van Dao, Q.; Dinh, M.-C.; Kim, C.S.; Park, M.; Doh, C.-H.; Bae, J.H.; Lee, M.-K.; Liu, J.; Bai, Z. Design of an effective State of Charge estimation method for a lithium-ion battery pack using extended kalman filter and artificial neural network. Energies 2021, 14, 2634. [Google Scholar] [CrossRef]
- Danko, M.; Adamec, J.; Taraba, M.; Drgona, P. Overview of batteries State of Charge estimation methods. Transp. Res. Procedia 2019, 40, 186–192. [Google Scholar] [CrossRef]
- Rivera-Barrera, J.; Muñoz-Galeano, N.; Sarmiento-Maldonado, H. SoC Estimation for Lithium-ion Batteries: Review and Future Challenges. Electronics 2017, 6, 102. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Tian, J.; Sun, Z.; Wang, L.; Xu, R.; Li, M.; Chen, Z. A comprehensive review of battery modeling and state estimation approaches for advanced battery management systems. Renew. Sustain. Energy Rev. 2020, 131, 110015. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of lithium-ion battery modeling methods for State-of-Charge estimation in electrical vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef] [Green Version]
- Schellenberg, S.; Berndt, R.; Eckhoff, D.; German, R. A Computationally inexpensive battery model for the microscopic simulation of electric vehicles. In Proceedings of the 2014 IEEE 80th Vehicular Technology Conference (VTC Fall), Vancouver, BC, Canada, 14–17 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 1–6, ISBN 978-1-4799-4449-1. [Google Scholar]
- Li, Y.; Vilathgamuwa, D.M.; Farrell, T.W.; Choi, S.S.; Tran, N.T. An equivalent circuit model of li-ion battery based on electrochemical principles used in grid-connected energy storage applications. In Proceedings of the 2017 IEEE 3rd International Future Energy Electronics Conference and ECCE Asia (IFEEC 2017—ECCE Asia), Kaohsiung, Taiwan, 3–7 June 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 959–964, ISBN 978-1-5090-5157-1. [Google Scholar]
- Kim, H.-K.; Lee, K.-J. Scale-Up of Physics-Based Models for Predicting Degradation of Large Lithium Ion Batteries. Sustainability 2020, 12, 8544. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Barcellona, S.; Piegari, L. Lithium Ion Battery Models and Parameter Identification Techniques. Energies 2017, 10, 2007. [Google Scholar] [CrossRef] [Green Version]
- Uddin, K.; Perera, S.; Widanage, W.; Somerville, L.; Marco, J. Characterising Lithium-Ion Battery Degradation through the Identification and Tracking of Electrochemical Battery Model Parameters. Batteries 2016, 2, 13. [Google Scholar] [CrossRef]
- Forman, J.C.; Moura, S.J.; Stein, J.L.; Fathy, H.K. Genetic parameter identification of the Doyle-Fuller-Newman model from experimental cycling of a LFP battery. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 362–369, ISBN 978-1-4577-0081-1. [Google Scholar]
- Rahman, M.A.; Anwar, S.; Izadian, A. Electrochemical model parameter identification of a lithium-ion battery using particle swarm optimization method. J. Power Sources 2016, 307, 86–97. [Google Scholar] [CrossRef]
- Yang, G. Battery parameterisation based on differential evolution via a boundary evolution strategy. J. Power Sources 2014, 245, 583–593. [Google Scholar] [CrossRef]
- Yang, K.; Tang, Y.; Zhang, Z. Parameter Identification and State-of-Charge Estimation for Lithium-Ion Batteries Using Separated Time Scales and Extended Kalman Filter. Energies 2021, 14, 1054. [Google Scholar] [CrossRef]
- Harlow, J.E.; Ma, X.; Li, J.; Logan, E.; Liu, Y.; Zhang, N.; Ma, L.; Glazier, S.L.; Cormier, M.M.E.; Genovese, M.; et al. A Wide Range of Testing Results on an Excellent Lithium-Ion Cell Chemistry to be used as Benchmarks for New Battery Technologies. J. Electrochem. Soc. 2019, 166, A3031–A3044. [Google Scholar] [CrossRef]
- Jin, N.; Danilov, D.L.; van den Hof, P.M.; Donkers, M. Parameter estimation of an electrochemistry-based lithium-ion battery model using a two-step procedure and a parameter sensitivity analysis. Int. J. Energy Res. 2018, 42, 2417–2430. [Google Scholar] [CrossRef]
- Li, W.; Cao, D.; Jöst, D.; Ringbeck, F.; Kuipers, M.; Frie, F.; Sauer, D.U. Parameter sensitivity analysis of electrochemical model-based battery management systems for lithium-ion batteries. Appl. Energy 2020, 269, 115104. [Google Scholar] [CrossRef]
- Miniguano, H.; Barrado, A.; Lazaro, A.; Zumel, P.; Fernandez, C. General Parameter Identification Procedure and Comparative Study of Li-Ion Battery Models. IEEE Trans. Veh. Technol. 2020, 69, 235–245. [Google Scholar] [CrossRef]
- Madani, S.; Schaltz, E.; Knudsen Kær, S. Effect of Current Rate and Prior Cycling on the Coulombic Efficiency of a Lithium-Ion Battery. Batteries 2019, 5, 57. [Google Scholar] [CrossRef] [Green Version]
- Tran, M.-K.; Mevawala, A.; Panchal, S.; Raahemifar, K.; Fowler, M.; Fraser, R. Effect of integrating the hysteresis component to the equivalent circuit model of Lithium-ion battery for dynamic and non-dynamic applications. J. Energy Storage 2020, 32, 101785. [Google Scholar] [CrossRef]
- Ovejas, V.J.; Cuadras, A. Effects of cycling on lithium-ion battery hysteresis and overvoltage. Sci. Rep. 2019, 9, 14875. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Stroe, A.-I.; Knap, V.; Stroe, D.-I. Comparison of lithium-ion battery performance at beginning-of-life and end-of-life. Microelectron. Reliab. 2018, 88–90, 1251–1255. [Google Scholar] [CrossRef]
- Atalay, S.; Sheikh, M.; Mariani, A.; Merla, Y.; Bower, E.; Widanage, W.D. Theory of battery ageing in a lithium-ion battery: Capacity fade, nonlinear ageing and lifetime prediction. J. Power Sources 2020, 478, 229026. [Google Scholar] [CrossRef]
- Boovaragavan, V.; Harinipriya, S.; Subramanian, V.R. Towards real-time (milliseconds) parameter estimation of lithium-ion batteries using reformulated physics-based models. J. Power Sources 2008, 183, 361–365. [Google Scholar] [CrossRef]
- Ali, M.; Kamran, M.A.; Kumar, P.S.; Himanshu; Nengroo, S.H.; Khan, M.A.; Hussain, A.; Kim, H.-J. An Online Data-Driven Model Identification and Adaptive State of Charge Estimation Approach for Lithium-ion-Batteries Using the Lagrange Multiplier Method. Energies 2018, 11, 2940. [Google Scholar] [CrossRef] [Green Version]
- Hou, Y.; Zhang, Z.; Liu, P.; Song, C.; Wang, Z. Research on a novel data-driven aging estimation method for battery systems in real-world electric vehicles. Adv. Mech. Eng. 2021, 13, 168781402110277. [Google Scholar] [CrossRef]
- Hashemi, S.R. An Intelligent Battery Managment System for Electric and Hybrid Electric Aircraft. Ph.D. Thesis, University of Akron, Akron, OH, USA, 2021. [Google Scholar]
- Sulzer, V.; Marquis, S.G.; Timms, R.; Robinson, M.; Chapman, S.J. Python Battery Mathematical Modelling (PyBaMM). J. Open Res. Softw. 2020, 9, 14. [Google Scholar] [CrossRef]
- Welcome to PyBaMM’s Documentation!—PyBaMM 0.4.0 Documentation. Available online: https://pybamm.readthedocs.io/en/latest/ (accessed on 28 July 2021).
- GitHub. PyBaMM/pybamm/input/parameters/lithium_ion/cells at developpybamm-team/PyBaMM. Available online: https://github.com/pybamm-team/PyBaMM/tree/develop/pybamm/input/parameters/lithium_ion/cells (accessed on 27 July 2021).
- Chen, C.-H.; Brosa Planella, F.; O’Regan, K.; Gastol, D.; Widanage, W.D.; Kendrick, E. Development of Experimental Techniques for Parameterization of Multi-scale Lithium-ion Battery Models. J. Electrochem. Soc. 2020, 167, 80534. [Google Scholar] [CrossRef]
- Luder, D.; Caliandro, P.; Vezzini, A. Enhanced physics-based models for state estimation of Li-Ion batteries. In Proceedings of the Comsol Conference 2020 Europe, Virtual, 14–15 October 2020. [Google Scholar]
- Madani, S.; Schaltz, E.; Knudsen Kær, S. An Electrical Equivalent Circuit Model of a Lithium Titanate Oxide Battery. Batteries 2019, 5, 31. [Google Scholar] [CrossRef] [Green Version]
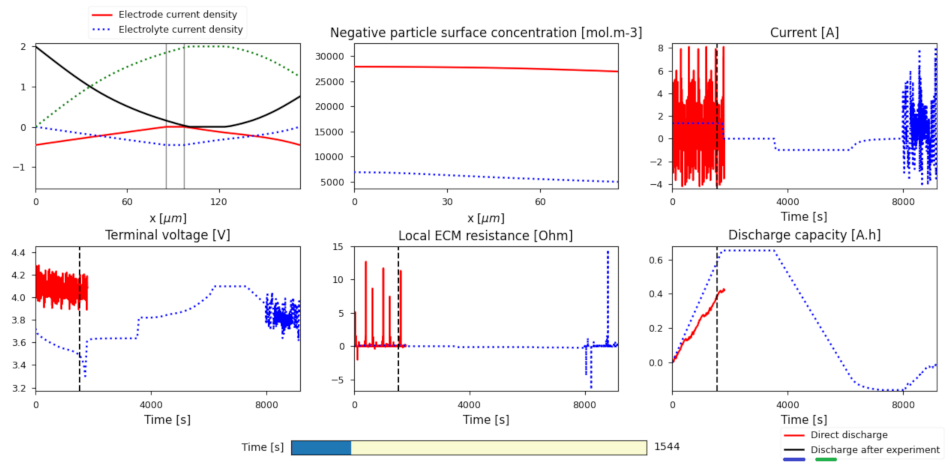
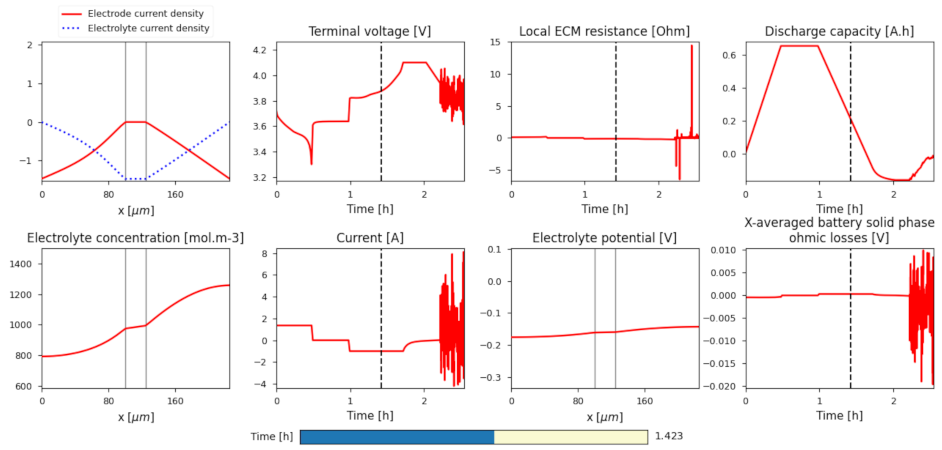
| Reference | Implementation Method 1 | DT Functionality |
|---|---|---|
| [21] | HI and LSTM algorithm | Estimation of battery’s actual discharge capacity |
| [22] | Cloud BMS with AEHF-based SOC estimation algorithm and PSO-based SOH estimation algorithm | Estimation of SOC, SOH, capacity fade, power fade |
| [23] | On-board diagnosis to cloud environment; ECM model parameter fitting, curve fitting and SOC-OCV curve | SOC, capacity, internal resistance, SOH-R, SOH-C |
| [24] | Visual software in LabVIEW; ECM with SVM and filter algorithms | DT platform for spacecraft lithium-ion battery pack degradation assessment; SOC estimation |
| [25] | Cloud connected BMS; electric-thermal model and empirical ageing model | Cell voltage and temperature |
| [26] | ECM and EFK algorithm | SOC estimation |
| [27] | Review paper on battery DT | Battery DT framework and its cyber-physical elements |
| [28] | Offline—Regression model using sparse-Proper Generalized Decomposition (s-PGD); Online—Dynamic Mode Decomposition technique | Cell voltage, anode/cathode bulk SOC, anode/cathode surface SOC |
| [29] | Linking reduced order model with ECM in Ansys Twin Builder | Real-time temperature of the battery pack at different locations; What-if scenarios for root cause analysis |
| Parameters | Symbol (Unit) 1 | High Cycle Number | High C-Rate |
|---|---|---|---|
| DFN | |||
| Thickness | Lp, Ln, Ls (µm) | x [55] | Moderate [55] |
| Surface area | Ap, An, As, (m2) | x [48] | Moderate [55] |
| Particle radius | Rp+, Rp− (µm) | x [54] | x [54] |
| Active/Inactive material volume fraction | εsp, εsn | x [55] | Moderate [55] |
| Electrolyte phase volume fraction | εep; εen | - | - |
| Maximum Li+ concentration | csp,n,se (mol cm−3) | x [48] | Moderate [55] |
| Average electrolyte concentration | ce (mol cm−3) | - | x [48] |
| Stoichiometry of n, p at 0% and 100% SOC | xp,n0,100 | - | - |
| Diffusion coefficient in solid and liquid phase | Dsp, Dsn, De (m2 s−1) | x [54] | - |
| Solid phase conductivity | σsp, σsn (µm) | x [48] | x [48] |
| Li transference number | t+0 | Not sensitive [54] | Not sensitive [54] |
| Resistivity of film layers (including SEI) | Rf (Ω) | Not significant [54] | x [48] |
| Negative electrode potential, U− coefficients | - | x [48] | - |
| Positive electrode potential, U+, coefficients | - | x [48] | - |
| Open circuit potential | V | x [48] | - |
| Overpotential | η | Not significant [55] | - |
| Reaction flux at the solid particle surface | j (mol cm−1 s−1) | - | - |
| Exchange (electrolyte and solid) current density | ie (A cm−2) | - | - |
| Electrolyte activity coefficient | ±f | C | C |
| Bruggeman porosity exponent | p | C | C |
| Anodic/Cathodic charge transfer coefficient | αa, αc | C | C |
| Intercalation/deintercalation reaction-rate coefficient | kn,p (A cm2.5 mol−1.5) | C | C |
| Universal gas constant | R | C | C |
| Absolute temperature | T | C | C |
| Faraday’s constant | F | C | C |
| ECM | |||
| Internal ohmic resistance | RO (Ω) | Sensitive [56] | Sensitive [56] |
| OCV | VOCV (V) | ||
| Polarization Resistances | R1, R2… (Ω) | ||
| Polarization Capacitances | C1, C2… (F) | ||
| Coulomb efficiency | η | Almost constant [57] | Sensitive [57] |
| Hysteresis voltage, hysteresis decaying factor | H (V), k | Not significant [58] | Impact of overvoltage [59] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, S.; Weeber, M.; Birke, K.P. Implementation of Battery Digital Twin: Approach, Functionalities and Benefits. Batteries 2021, 7, 78. https://doi.org/10.3390/batteries7040078
Singh S, Weeber M, Birke KP. Implementation of Battery Digital Twin: Approach, Functionalities and Benefits. Batteries. 2021; 7(4):78. https://doi.org/10.3390/batteries7040078
Chicago/Turabian StyleSingh, Soumya, Max Weeber, and Kai Peter Birke. 2021. "Implementation of Battery Digital Twin: Approach, Functionalities and Benefits" Batteries 7, no. 4: 78. https://doi.org/10.3390/batteries7040078
APA StyleSingh, S., Weeber, M., & Birke, K. P. (2021). Implementation of Battery Digital Twin: Approach, Functionalities and Benefits. Batteries, 7(4), 78. https://doi.org/10.3390/batteries7040078







