Abstract
The lithium ion battery, with its high energy density and low reduction potential, continues to enchant researchers and dominate the landscape of energy storage systems development. However, the demands of technology in modern society have begun to reveal limitations of the lithium energy revolution. A combination of safety concerns, strained natural resources and geopolitics have inspired the search for alternative energy storage and delivery platforms. Traditional liquid electrolytes prove precarious in large scale schemes due to the propensity for leakage, the potential for side reactions and their corrosive nature. Alternative electrolytic materials in the form of solid inorganic ion conductors and solid polymer matrices offer new possibilities for all solid state batteries. In addition to the engineering of novel electrolyte materials, there is the opportunity to employ post-lithium chemistries. Utility of multivalent cation (Ca, Mg, Zn and Al) transport promises a reduction in cost and increase in safety. In this review, we examine the current research focused on developing solid electrolytes using multivalent metal cation charge carriers and the outlook for their application in all solid state batteries.
1. Introduction
Within the next decade the energy needs of society are set to out pace the current availability of low cost renewable energy sources. The lithium ion battery has been hailed as the future of energy storage and is indeed an integral component of the technology sustaining our daily lives. In recent years it has become apparent that there are limits to our reliance on using lithium in energy storage. Traditional organic liquid electrolytes commonly used for Li transport were found to pose significant safety and environmental risks due to leakage and flammability. The development of solid electrolytes in the form of solid inorganic ion conductors and solid polymer matrices is on track to improve thermal and mechanical stability in realization of all solid state batteries [1,2,3]. Unfortunately, the development of improved electrolytes does not solve the problem of strained natural resources [4]. Aside from possibly “running out” of mined lithium, we do not have the technology nor availability of sufficient recyclable material to keep up with projected lithium demand over the next 20 years [4,5,6].
One way to meet the energy demands of the world in a safe, effective and environmentally sustainable way is to develop batteries using alternative charge carriers with higher theoretical energy volume. The multivalent metal cations Ca, Mg, Zn and Al have been considered to be alternatives to univalent ions since the first lithium batteries were under development. The challenges to using higher valence cations in solid electrolytes are generally related to mobility loss due to high charge per volume and slow diffusion under ambient conditions. However, the energy payoff to employing these cations promises significant increases in energy storage capacity and their availability in the Earth’s crust offer an improvement over lithium from an environmental perspective. Calcium, for example, has a theoretical energy volume of 2073 mA h cm, and is the fifth most abundant naturally occuring metal [7]. Magnesium has long been considered a strong candidate for beyond lithium batteries because it is the lightest of the multivalent metals, has a high volumetric charge capacity (3833 mA h cm) and is the eighth most abundant metal in the Earth’s crust (third most abundant element in seawater) [8]. Zinc represents an increase in volumetric charge capacity to 5851 mA h cm, is the 24th most abundant metal and can easily be handled under atmospheric conditions with little reactivity [9]. Aluminum, with its trivalent charge, boasts the highest volumetric charge capacity (8040 mA h cm) and is the most abundant metal in the Earth’s crust as well as the most recycled [10].
While we have chosen to focus on the aforementioned multivalent metal charge carriers and their transport properties in solid electrolytes, it is important to mention that there continues to be significant research in post lithium univalent cations as well. In particular, sodium and potassium technologies have emerged as promising platforms for the development of non-lithium batteries. Review of Na and K charge transport and the state of research regarding development of suitable electrolytes for them is beyond the scope of this review. However, we direct the interested reader to recent reviews covering the topics of Na [11,12,13,14,15,16,17,18] and K [19,20,21,22,23,24] technologies and the references provided therein.
In this review, we explore the current knowledge of ion transport mechanisms in solid inorganic and “dry” solid polymer electrolytes that feature Ca, Mg, Zn and Al as their charge carriers. First, we briefly describe some of the most widely used techniques for examining ion dynamics in electrolytic systems and discuss the relevant theory behind application of these methods. This is followed by a survey of the ion transport models proposed for the respective ion conductor types. We then present findings from our review of the literature regarding what is known to date about the transport of the noted multivalent cations in all solid electrolytes. Finally, we conclude with some considerations regarding the applicability of these multivalent metal electrolytes in all solid state batteries.
2. Methods for Evaluating Ion Transport
The definition of bulk conductivity in any material is described by the equation:
where is the conductivity, is the ion mobility, is the charge carrier ion concentration and is the ionic charge of the ith species. Electrical properties of a bulk material, including ionic conductivity, are often evaluated using electrochemical impedance spectroscopy (EIS), also referred to as ac impedance or dielectric spectroscopy [25]. Temperature, ion mobility and the type and volume of charge carriers all contribute to the conductive properties of the electrolyte. The general method of EIS involves application of a frequency dependent voltage signal through the sample of interest and subsequent measurement of the impedance which typically ranges from to [26]. Conductivity measurements made as a function of temperature allow for computation of the activation energy, , by least squares fitting of the conductivity to the Arrhenius equation:
where A is the pre-exponential factor, is the activation energy for conduction and is Boltzmann’s constant. Linear variation of ionic conductivity with the inverse of absolute temperature indicates that a material obeys Arrhenius type behavior.
Information regarding the type of charged species contributing to the total conductivity in an electrolyte is given by measuring the transference number. Several methods have been applied to estimate transference numbers [27], though the most widely used are based on potentiostatic polarization [28,29,30,31]. In combined ac/dc polarization the sample is placed between a set of non-blocking electrodes which selectively limit transfer to the ion of interest. A constant voltage is applied to drive the cation of interest toward the anode where the cation accumulates. This creates a concentration gradient as indicated by a continuous decrease in current density until a steady state is reached [30]. The transference number can then be calculated according to:
where is the initial current (), is the steady state current, is the initial resistance of the passivation layer on the electrodes before polarization, is the resistance of the passivation layer after polarization and is the applied voltage bias [30]. While transference numbers retain their status as important contributing players in characterizing conductivity in electrolytic materials, there are several considerations that must be made when applying polarization techniques and analyzing their results. For inorganic ion conductors, the role of grain boundaries on impedance measurements becomes an important factor. It is generally accepted that the grain boundaries within a sample can be considered uniform and that they possess conductivities that are separate from the bulk conductivity [32,33]. In polymers, ion aggregation changes the conductive landscape of the material and is especially influential when considering multivalent cation conduction [31].
Traditional lithium batteries are known to be limited by their low cation transference numbers due to the formation of a solvation shell around Li combined with highly mobile counteranions [34,35,36]. Tuning transport pathways in a way that facilitates cation diffusion while immobilizing anions has proven a useful approach for inorganic ion conductors [37,38,39]. In solid polymers, cation transference is influenced by ion pairing interactions and segmental mobility. Solid polymer matrices that limit conduction to single ions have been one method proposed to improve transference numbers for Li [40]. Another method suggests that tethering anions to the polymeric backbone would improve cation mobility without significantly impairing transport via segmental dynamics [36,41]. The strong interactions between higher valence cations and counter anions suggests that these effects would be intensified for multivalent species as compared to lithium.
Nuclear magnetic resonance techniques, especially pulsed field gradient (PFG) experiments, have long been an important tool for studying lithium ion transport, primarily in liquid electrolytes but also in solid polymer electrolytes [42,43,44,45,46]. Magnetic resonance has been used far less to examine ion dynamics of multivalent species. The low natural abundance and gyromagnetic ratios of Ca, Mg and Zn make dynamics information difficult to extract. The nucleus of Al has a gyromagnetic ratio similar to that of carbon with 100% natural abundance which makes it more sensitive to NMR [47]. Despite this information, PFG diffusion studies on Al remain limited, with the first report appearing in 2018 by Graham et al. who used the technique to measure diffusion coefficients for Al in concentrated liquid electrolyte solutions [48]. The relatively large electric quadrupole moment of the Al nucleus results in significant line broadening which makes diffusion studies in solids essentially impossible. In a PFG NMR experiment, a spin echo pulse sequence is applied along with a set of spatially encoded gradient pulses. The gradient pulses are applied for some duration, , at some interval, known as the diffusion time, . A series of experiments are made by varying a set of parameters in the Stejskal-Tanner equation. In practice this is done by measuring an array of experiments in which the gradient strength is increased incrementally. The resultant signal is attenuated as a function of molecular translocation when the strength of the spatially encoded PFG is of sufficient magnitude [49]. The diffusion coefficient is then calculated according to the Stejskal-Tanner equation:
where I and are the signal intensity at and (where is the echo time), is the gyromagnetic ratio, g is the strength of the PFG, is the gradient duration and is the diffusion time. The value of the diffusion coefficient is found by plotting the logarithm of vs. and finding the slope from the linear fit. This diffusion coefficient is related to conductivity throught the Nernst-Einstein equation:
where F is Faraday’s constant, R is the ideal gas constant, T is the temperature (in Kelvin), and the term term is the product of the valency, molar concentration and diffusion coefficient of the charge carriers.
In addition to PFG diffusion, experiments using variable temperature relaxometry [50] and exchange spectroscopy [51] can be used to derive information regarding transport phenomena. While the vast majority of these studies pertain to lithium dynamics, the repertoire of experiments applied to multivalent ion transport is growing [52]. An example of this can be seen in recent work by Jadhav et al. in which quantitative magic angle spinning and Al–Al EXSY was used to study intercalation events of Al into a Chevrel type electrode [47]. In 2D exchange spectroscopy two nuclei are excited by an RF pulse and allowed to interact during some mixing time. After mixing, the resonant frequency of one ion becomes correlated with the resonant frequency of the other ion. If one of the ions jumps to another site during the mixing time, the 2D spectra reveal an off diagonal signal directly related to the jump. The off diagonal signal intensity is analyzed according to mixing time by the equation [53]:
where is the off diagonal signal intensity after mixing, is the diagonal signal intensity before mixing, is jump time from position i to j, and is the mixing time. If the jump distance, a, can be assumed, the parameter can be inserted into the Einstein-Smoluchowski equation:
to determine the self diffusion coefficient, D, of an ion transport event from site i to j [53].
Atomic scale dynamics can be probed using Quasi-Elastic Neutron Scattering (QENS) whereby neutrons serve to measure density variations within a sample. Neutron scattering is both temporal and spatial and defined according to the neutron scattering law [54]:
where is the distribution of neutrons after sample scattering. The scattering function, , is defined by the change in momentum of scattered neutrons, , and the magnitude of exchanged energy, . The intensity of the scattered neutrons depends upon whether the scattering is coherent or incoherent. In the case of coherent scattering, the population of nuclei is distinct and varied. The intensity is related to the collective dynamics of the different atoms. Incoherent scattering refers to the intensity contribution from a population of nuclei that is all the same. In this case, observation is made on individual dynamics of the atoms [54,55]. The scattering intensity is measured by plotting the scattering function, against the exchange energy, . Figure 1a shows a diagram depicting the contributions to a QENS spectrum [55]. The sharp central peak is the elastic contribution caused by slow moving atoms incapable of being resolved at the instrument’s resolution. The inelastic peaks to either side of the central peaks represent atoms that vibrate at fixed frequency with periodicity. Stokes scattering is the result of neutrons losing energy while anti-Stokes scattering refers to neutrons that gained energy. The quasi elastic peak, the QENS peak, is the central broad signal. The broadening results from stochastic movement of atoms [55]. Using QENS, dynamic processes on a timescale from – seconds are accessible. This makes the technique applicable to ion transport studies in both solid inorganic ion conductors [55,56,57,58] and polymers [59,60,61,62]. In solid polymer studies, QENS is an important probe of segmental dynamics [61,62]. Mongcopa et al. used QENS to evaluate the effect of salt concentration on segmental dynamics in PEO. Figure 1b displays the QENS spectra overlayed for each concentration of lithium bis(trifluoromethane)sulfonamide salt [61]. The black line shows the purely elastic signal representing the resolution of the instrument. The resolution function is determined by measuring the sample at low temperature, in the case of the authors’ work, 20 K [55,61]. The overlayed spectra represent the elastic signal at increasing salt concentration. As the concentration increased, the width of the structure factor narrowed, indicating association between polymer segments and salt slowing the segmental dynamics. The diagram below, Figure 1c, is a representation of the data in the time domain after Fourier transform where the ratio / is plotted as a function of time [61]. The data are fit according to the Kohlrausch-Williams-Watts (KWW) function in order to evaluate relaxation processes:
where is the stretched exponential and is an adjustable parameter [61,63].
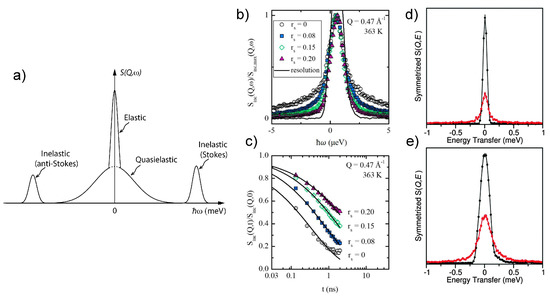
Figure 1.
(a) Components of the QENS spectrum. Adapted with permission from reference [55]. Copywrite 1999. Royal Society of Chemistry. (b) Elastic component of QENS spectrum demonstrating slowing of semental dynamics in PEO upon addition of LiTFSI salt. Adapted with permission from reference [61]. Copywrite 2018. American Chemical Society. (c) Fourier transformed data in the time domain fit to the KWW function. Adapted with permission from reference [61]. Copywrite 2018. American Chemical Society. (d) QENS spectrum for LiCBH. Adapted with permission from reference [56]. Copywrite 2015. Royal Society of Chemsitry. (e) QENS spectrum for NaCBH. Adapted with permission from reference [56]. Copywrite 2015. Royal Society of Chemsitry.
Tang et al. used QENS to show that anion reorientional jumps occur at elevated temperature in LiCBH and NaCBH [56]. Figure 1d,e, compare the (black) elastic resolution spectrum at 200 K versus the red overlayed spectra representing quasi-elastic broadening due to anionic jump reorientations at 433 K in Figure 1d LiCBH and 375 K in Figure 1e NaCBH, respectively [56].
3. Overview of Ion Transport Models
3.1. Solid Inorganic Ion Conductors
Solid inorganic electrolytes are characterized by the presence of a wide band gap, excellent thermal stability and high conductivities. In general, the structure of the solid inorganic ion conductor is composed of a framework of polyhedral forming metal and non-metallic atoms with an external skeleton of functionalized ligands. Ionic mobility in these materials require a high volume of charge carriers, a suitable ratio of ions to vacant sites, a low enough activation energy to encourage site to site hopping, a structural landscape conducive to ion transport, the potential to induce polarity between lattice and mobile species and generally low coordination numbers for mobile ions [64]. Defects in the crystal such as Schottky disorder or Frenkel disorder are a requirement for ion migration. A Schottky site refers to a vacancy in a crystalline sublattice [65]. A Frenkel site indicates the appearance of a vacancy that results from a lattice atom moving into an interstitial site in a single sublattice [66,67]. The concentration of these defects is thermally dependent, requiring elevated temperatures in order to activate ions and increase defect concentration. For multivalent cations the hurdle to be overcome is that of strong Coulombic interactions with the anionic framework, as charge increases so does the migration energy [64].
The classical model for ion transport in crystalline solids involves the hopping of individual ions between interstitial sites or vacancies within a lattice. The structure of the crystal is defined by an energy landscape of planes and channels or tunnels through which ion migration proceeds. During a transport event, the mobile species navigate the energy landscape along which the highest energy encountered determines the barrier to diffusion and defines the activation energy, , of the migration path. A low activation energy and high concentration of ion carriers induce high conductivity [64,68]. The random walk model can be applied to describe uncorrelated hopping for individual ions [67]:
The classical concept of ion transport assumes no correlation between the occurrence of hopping phenomena and interaction between ions, or interaction of an ion with its environment. While the overall physical foundation lays the groundwork and identifies the variables necessary to describe more complex transport events, the classical model is generally lacking in the complexity suitable for describing transport in super conducting solids. Several models, and their variations, have been proposed to describe correlated ion transport events in crystalline solid conductors.
One of the earliest ion transport models proposed for solid crystalline electrolytes was the interstitial vacancy model used to describe ion transport in - and -alumina compounds by Whittingham and Huggins and computationally supported by Wang et al. in the 1970s [69,70]. In this description, the metal ion positioned in an interstitial displaces a lattice ion which in turn moves into an adjacent interstitial site [70]. It was noted that this mechanism drives conductivity as a result of an excess in mobile ion concentration as opposed to the mobility of the ions themselves [69]. A mechanism similar to the interstitial model is that of concerted ion migration. In this model, two or more ions hop simultaneously along neighboring occupied sites triggering continuous jumps in a series of ions [68,71]. The Coulombic interaction between mobile ions lowers the activation energy to migration [68,72].This mechanism is thought to be responsible for the superionic conductivity induced within certain classes of materials possessing sublattice motifs capable of activation under high temperatures and high ion concentration [68]. Ion diffusion in borohydrides, oxides and intercalation within Chevrel type conductors have been found consistent with this mechanism [71,72,73]. In batteries research, studies concerned with concerted migration have focused primarily on Li and Na transport [72,74,75,76]; however, there is evidence that this mechanism can work with higher valence cations and in duel ion systems [71,77]. A recent report by Li et al. using a MOS cathode with a duel lithium and magnesium ion electrolyte indicated a concerted Mg/Li solid phase diffusion in which the Mg activation energy was significantly reduced as a result of introducing Li [71]. In 2020 Hu et al. reported concerted migration of Na/Zn in a ZnNaV(PO) cathode, noting that the intercalation of Zn improved the stability and bulk conductivity of the structure [77].
The jump relaxation model has been explored extensively by Funke and co-workers starting in the 1980s and was the topic of a comprehensive review in 1993 (citation [78] and references therein). In this model, mobile ions are positioned at some distance from eachother due to the repulsive Coulombic interaction between them. This distribution of ions is called the “Coulomb cage effect” whereby each mobile ion is at an energy minimum position in relation to neighboring mobile ions. The potential actually experienced by a moving ion is the result of a superposition of the periodic lattice potential due to the non-moving ions responsible for the cage [78]. Shifts in the energy potential of the cage perturb the system away from equilibrium and induce compensatory relaxation processes. After an ion overcomes an activation barrier and hops to an adjacent vacant site from the start point, two subsequent relaxation processes are possible; either the ion reverse hops to the starting point in a correlated forward-backward sequence, or, the ion remains in the new site and the neighboring ion cloud relaxes into a new potential minimum. In general, the migrating ion favors the backward hop because the energy barrier returning to its’ original position is lower than that required to continue to move forward. The net effect results in a reduced contribution to long range ion diffusion in the macroscopic sense [78].
The paddle-wheel mechanism was first introduced by Kvist et al. to describe transport in lithium sulfates at high temperature [79,80]. This mechanism and the associated mechanisms of polyanion reorientation have since been attributed to transport function in materials based upon a variety of anionic frameworks containing phosphorus [81,82,83,84,85], sulfur [84,85,86,87,88,89,90,91], boron [58,92,93,94,95], nitrogen [96,97] and oxide [98] building blocks. The basic principle of this mechanism argues that materials having complex anions that are fixed with respect to translational motion are still capable of rotational degrees of motion. If the diffusion processes of the cation and polyanion are coupled, the rotational diffusion of the polyanionic complex propels translational diffusion of the cation [87]. This mechanism is not entirely straight forward [99,100], and is thought to have some overlap with, or work in addition to, other models [90]. Although, recently, Zhang and colleagues provided direct evidence in support of the paddle wheel mechanism using a combination of neutron diffraction and AIMD simulations [101]. The authors propose that cation conductivity can be enhanced by tuning anions in such a way as to promote fast cation transport via this mechanism.
3.2. Solid Polymer Electrolytes
Solid polymer electrolytes are regarded as mechanically stable, leak proof and provide interfacial connectivity between electrode and electrolyte due to their ability to conform in shape. From a safety perspective, polymers are non-volatile, non-toxic and have low vapor pressures. Electrostatic interactions between cations and negatively charged groups along the polymer backbone drive the enthalpy of solvation, resulting in salt dissolution within the polymeric solvent [102]. Lone pairs on oxygen and nitrogen over the polymer chain can form coordinate bonds with salt cations which drives complex formation. The complete and spontaneous dissociation of a salt within a polymer matrix requires that the Gibbs free energy of the system is decreased in favor of the polymer over the lattice energy of the salt, resulting in a high concentration of mobile charge carriers [102]. Transport of dissolved ions is thought to occur via uncorrelated hopping between occupied solvation sites to local open sites [102,103,104,105]. However, ion mobility is also coupled to the segmental dynamics of the polymer chain. Facile movement of ions occurs above the glass transition temperature, , of the polymer when the system has significant amorphous character [30,106]. Thus, a decrease in increases segmental mobility and conductivity under ambient conditions [103,107]. The relationship between conductivity, ion concentration and glass transition temperature is given by the Vogel-Tamman-Fulcher (VTF) equation [108,109],
where a factor that accounts for the volume of charge carriers and temperature variation [110,111], B is referred to as “pseudo activation energy” and accounts for the segmental motion of the polymer chain [109,112], is the glass transition temperature at infinite polymer relaxation [113] and is Boltzmann’s constant. Increasing salt concentration introduces a greater volume of available charge carriers; however, the subsequent improvement in conductivity is limited by the formation of ion aggregates [114]. This re-association of ions causes a drop in conductivity as the polymer system also displays enhanced crystallinity with further addition of salt [30,106,115]. Multivalent cations are expected to be less mobile and form aggregates more readily than single valent cations on account of their increased charge densities [115]. There is some evidence to suggest that the crystalline phase of solid polymer electrolytes is itself highly conductive in certain cases [116]. To explore the influence that polarity of the polymer backbone has on cation transport, Schauser et al. evaluated the properties of Zn, Cu and Li TFSI salts in three polymers with different dielectric constants and s [117]. The authors found that while was similar in all of the polymers, the degree of ion aggregation depended on the backbone polarity of the polymer and, surprisingly, the aggregation did not notably effect the ionic conductivity.
4. Ion Transport of Multivalent Cations in Solid Electrolytes
Solid Inorganic Electrolytes
Solid state electrolytes based on -alumina compounds were found, in some reports, to conduct divalent cations [118,119,120]. Those that have demonstrated appreciable conductivities, required high temperatures [119,120]. In 1982 Farrington and Dunn reported a series of sodium -alumina derivatives with Ca and Zn conductivities around S/cm at 40 °C and S/cm in a range of 300 to 400 °C [121]. NASICON (Na Super Ionic Conductor) was first introduced by Goodenough, Hong and Kafalas in 1976 as a fast Na conductor with a unique skeletal structure possessing transport capabilities on par with the -alumina compounds [122]. Structurally, -alumina and MZr(PO) type crystalline compounds are composed of layers or distorted 3D networks that restrict ion conduction by skewing the geometry of the conduction pathways [120,123,124]. The [Zr(PO))] component of the NASICON skeleton inspired several phosphate-based solid inorganic electrolytes, the development of which continues to be motivated by the high natural abundance, low toxicity and electrochemical stability of oxide and phosphate compounds [125]. Multivalent materials of the type MZr(PO) where M = Mg, Ca, Zn, have demonstrated conductivities from S/cm to S/cm at temperatures above 400 °C [123,124,126,127]. In 2014 Anuar et al. synthesized MgZr(PO) with a room temperature conductivity on the order of S/cm and S/cm at 500 °C. The authors determined that Mg was the conducting species based on the magnesium transference number of 0.69 [128]. In 2016 Tamura and colleagues introduced a NASICON-type Mg conductor based on the representative material HfNb(PO). The authors chose HfNb(PO) as the “mother solid” for a series of (MgHf)Nb(PO) compounds due the reported conductivity of the Hf cation [129,130]. The highest Mg conductivity ( S/cm at 600 °C) belonged to (MgHf)Nb(PO) measured at the solid solubility limit. The authors credit this conductivity to be the result of both high cation concentration and expansion of the conduction pathway. Estimation of the transference number (0.99) combined with DC and Tubant electrolysis experiments led the authors to conclude that Mg was the only migrating species in the solid [129]. Lee et al. expanded on the work of Tamura with NASICON-type electrolytes and evaluated divalent cations in (MHf)Nb(PO) where M = Ni, Mg, Ca, Sr Ba [131]. In this study, the authors found direct correlations between the treatment of the sample and the ion conducting capability of the material. Comparison between cations in (MHf)Nb(PO) revealed that the structures with smaller radii tended to have the largest conducting pathways with higher conductivities and lower activation energies. To this end, Ni had the highest conductivity ( S/cm) and lowest activation energy (49.99 kJ/mol) at 600 °C while Ba was too large for substitution into the Hf site. In order to more accurately compare properties between cation species the authors introduced a correction based on the ratio of cation to lattice volume that reflected the size of conducting species relative to conduction pathway [131]. Based on this correction (called the A ratio), Ca was expected to demonstrate lower conductivity than that of Mg, but instead their conductivities were found to be similar. The authors attributed this phenomena to the weaker covalent bonding character in Ca-O versus that of Mg-O which results from the smaller electronegativity of calcium versus magnesium. This finding indicated that, in addition to cationic radius, the electronegativity of ions affect their migration in solids [131].
While solid state electrolyte development for multivalent cation transport has focused primarily on divalent species, chemistries with higher charge volumes have been developed in oxides and NASICON type conductors. Conductivity of Al was reported in Al(WO) [132]. However, the extremely low conductivity combined with high temperature ( S/cm at 600 °C) indicated that the material had no practical use as an electrolyte [132,133]. In 2002 Imanaka et al. designed a NASICON type conductor capable of Al transport having the general formula (AlZr)Nb(PO) and reported the highest conductivity of S/cm at 600 °C for (AlZr)Nb(PO) [133]. In a 2004 followup to this work, improved conductivity ( S/cm at 600 °C) as well as mechanical stability was demonstrated in (AlZr)Nb(PO) with the addition of up to 6 wt% BO [134]. In 2018 the diffusion pathway of Al in (AlZr)Nb(PO) was identified using temperature-dependent neutron powder diffraction and aberration-corrected scanning transmission electron microscopy [135]. Characterization of the crystal structure revealed a random distribution of Al sites and vacancies. The crystal structure itself was verified to be symmetrically rhombohedral by neutron powder diffraction with anisotropic aluminum diffusion capable along the c-axis of the crystal. Weak chemical bonds between Al and O in which aluminum ions are loosely housed in cages allows for high Al conductivity due to bond flexibility from thermal expansion about the c-axis [135].
Oxide based ion conductors developed using bismuth vanadate (BiVO) began to attract attention in the 1990s for use as solid state electrolytes [136]. Sinclair et al. became the first to synthesize an example of an M-Bi-O-VO material (in this case NaBiVO) in 1998 [137]. Porob and Row later developed the calcium conducting bismuth vanadate (CaBiVO) in 2004 but found that the ion conducting capacity of this material was lower than that of previously reported compounds within the M-Bi-O-VO family [138]. This finding led the authors to conclude that disorder was necessary within the vanadium and oxygen sites in order for high ionic conductivity [138].
In addition to oxides, metal hydrides have garnered interest due to their fast ion conducting performance and hydrogen storage capabilities [139,140,141,142]. In this class of compounds the anionic structure becomes a superionic conductor at elevated temperatures through rotation of anions in the lattice leading to a disordered framework [143]. Cation mobility is most facile when the bond between cation and lattice anion is weakest [144]. For this reason cations with smaller radii like Li and Na remain popular in the development of solid hydride electrolytes [141,145,146,147,148]. Structures using chemistries for multivalent ion transport have been gaining popularity [149]. Magnesium borohydrides, in particular, have been well characterized [150]. Some simulations have supported the possibility of magnesium ion conduction in pristine Mg(BH) at high temperatures [145], but conductivity at 30 °C remained less than S/cm presumably because the Mg ions are trapped inside a cage of hydrogen coordinated BH groups, rendering Mg immobile [151]. First principles studies on a variety of MBH, and BH metal borohydrides conducted by Lu and Ciucci demonstrated no hopping type transport mechanism for either Ca or Mg cations in the time frame of the simulations [143]. Additional DFT calculations to examine the stability and mechanical properties of Li, Na, Ca and Mg in these MBH and BH metal borohydrides supported mobile character in the monovalent examples while vacancy formation energy calculations and molecular dynamics calculations indicated slow ion transport for the divalent species [143].
Enhanced ion transport has been reported in lithium conducting borohydrides by tuning the crystal structure of the material either through atomic or molecular substitution within the structure [146], incorporating groups through complex formation [152], or stabilizing the material using nano particle dopants [148,153,154]. In 2017 Roerdern et al. reported high near room temperature Mg conductivity in Mg(BH) based material coordinated to the ethylenediamine ligand (NHCHCHNH = “en”) [155]. In this case Mg becomes mobile upon chelation with a single bidentate ligand resulting in mixed coordination between both [BH] and [en]. The authors synthesized Mg(en)(BH) according to Chen et al. [156] and verified the structure using FTIR. The reported conductivity for Mg(en)(BH) was S/cm at 30 °C with an Arrhenius type temperature dependence for conductivity between 30 and 70 °C measured by EIS [155]. The promising results of Roedern et al. inspired Yan and colleagues to evaluate a series of ammine magnesium borohydrides, Mg(BH)• xNH [157]. Through these investigations, the authors discovered that Mg(BH) NH demonstrated the highest Mg conductivity of S/cm at 80 °C. DFT calculations revealed that flexible di-hydrogen bonds throughout the structure facilitated fast ion conduction in this material through the exchange of neutral NH ligands between the lattice and interstitial magnesium ions [157]. The ability for this class of materials, Mg(BH)• xNH, to conduct magnesium relies heavily on the amount of NH which alters the coordination environment of Mg and the overall structure of the crystal [157,158]. In a following report, Yan et al. increased the conductivities of Mg(BH)• xNH compounds by generating composites with non integer x values [158]. When (1 < x < 2) for Mg(BH)• xNH, an amorphous phase eutectic melt is generated at 55 °C that can be stabilized with the addition of MgO nanoparticles [158]. This nano-composite was found to have an Mg conductivity on the order of S/cm at room temperature [158].
Higashi et al. had reported in 2014 that Mg(BH)(NH) has an ionic conductivity of S/cm at 150 °C [159]. The authors noted that the Mg(BH)(NH) framework was structurally unique, with both an Mg “zigzag chain” and tunneling features which indicated the possibility of a favorable environment for hopping diffusion [159]. This work inspired further exploration by Le Ruyet et al. who synthesized Mg(BH)(NH) under highly controlled conditions in order to rule out contributions to conductivity enhancement resulting from impurities in the material. The authors discovered that improved purity increased total ionic conductivity to as high as S/cm at 100 °C [160]. This enhancement was credited to the formation of an amorphous phase in the Mg(BH)-Mg(NH) system and revealed through B NMR spectroscopy. The suspected glass-ceramic-like composite was projected to arise under similar phenomena as that characterized in LiBH-LiNH [153,160,161]. After analyzing the phase diagram for Mg(BH)-Mg(NH), Le Ruyet and colleagues selectively synthesized Mg(BH)(NH) and reported a conductivity of S/cm at 100 °C at an activation energy of 0.84 eV. Figure 2 displays (a) the temperature dependent conductivities and (b) structure drawn in VESTA software [162] for Mg(BH)(NH) [161].
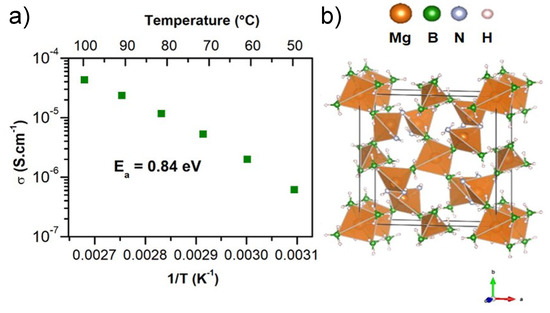
Figure 2.
Adapted with permission from reference [161]. Copywrite 2020. American Chemical Society. (a) Temperature dependent conductivity for Mg(BH)(NH). (b) Crystal structure of Mg(BH)(NH).
Recently, Kisu et al. reported a near room temperature (30 °C) Mg conductivity of S/cm for the complex (BH)(NHBH) [163]. The authors had expected Mg-(BH)(NHBH) to act as a molten salt ionic conductor at temperatures above its melting point (<45 °C ); however, high cell impedance measurements indicated that this was not the case for this compound. Structurally, the Mg are predicted to be surrounded by a large tetrahedron of asymmetrically coordinated boron species. The NHBH groups are thought to behave as ligands capable of being distorted away from migrating magnesium ions, thus allowing for Mg diffusion through the crystal structure [163].
In 2020 Heere and colleagues used synchotron radiation powder X-ray diffraction and total scattering analysis (SR-PDX) along with pair distribution function (PDF) analysis to structurally characterize -Mg(BH) and ball milled amorphous Mg(BH) [95]. The goal of the authors was to elucidate the correlation between conductivity in magnesium borohydrides and the development of an amorphous phase suspected to enhance conductivity seen by other researchers [95,155,160]. The SR-PDX revealed a highly symmetric cubic structure for -Mg(BH) in which individual Mg atoms were coordinated to four tetrahedral BH groups where the whole of the crystalline structure formed a 3D network of channels having an outer diameter of approximately 12.3 Å. Upon ball milling, the amorphous Mg(BH) retained the general structure of the crystalline Mg(BH) but in a state of increased disorder with less coordination to the tetrahedra. The amorphous sample was analyzed using quasi-elastic neutron scattering (QENS) and found to possess a greater number of rotating BH units [95]. The authors suspect that the increase in rotating BH within the amorphous material resulted in super conductive behavior through the paddle wheel conduction mechanism [95,164].
The search for ion conducting polycrystalline electrolytes has been significantly facilitated by the use of computational methods and high throughput screening of crystal structures available in the inorganic crystal structure database (ICSD) [165]. In the search for solid state electrolyte candidates, Morkhova et al. applied a “geometrical-topological approach” based on Voronoi-Dirichlet partitioning (VDP) implemented in the ToposPro software suite [166]. This method identifies ion conductive crystallographic structures and maps the cation migration from zero to three dimensions. The higher the map dimension, the greater probability that a cation will be capable of transport through a polycrystalline structure [167]. The authors tailored their study to identify compounds containing oxygen and one of the divalent cations, Mg, Ca or Sr. The structures returned with non-zero dimensional migration maps were evaluated and compounds already known in the literature or projected to require exceedingly difficult synthesis conditions were eliminated from the sample set. Structures with repeat entries in the ICSD, such as compounds having the same structural information (chemical composition, space group and unit cell parameters) were also eliminated. Screened candidates were then analyzed using DFT to determine cation migration energy. The lowest migration energy observed was the Mg conductor, MgNbO at 0.4 eV/ion. After considering the migration energies from several candidates the authors also noted that materials incorporating niobium, vanadium, titanium and chromium into the crystalline structure had higher theoretical conduction capacities [167].
Nestler and coworkers employed similar techniques to Morkhova et al. in the search for Al conducting solids [168]. The authors used a combination of VDP implemented in ToposPro [166], bond-valence site energy (BVSE) and DFT calculations in order to screen for and predict promising aluminum oxides [168]. The oxide class of materials was chosen for data mining purposes owing to the large variety of oxygen containing compounds statistically possible as well as the accepted stability of oxide materials. The results of the VDP search returned 17 structures of the garnet family, all with cubic structure possessing 3D migration networks consisting of two main sites having four and six fold coordination with Al. The most promising structure returned in the screening was the spinel AlVO, which had an estimated energy barrier of 0.52 eV. BVSE was capable of identifying more complex migration pathways and provided an estimate of migration energy. DFT generally estimated higher migration energies for Al by accounting for the repulsive Coulombic interactions between aluminum atoms. This interaction is not considered in VDP or BVSE. The Al migration pathway was predicted to adhere to previously reported hopping mechanisms for spinels with high valent ions where by the Al would need to hop between tetrahedral sites by passing an octahedral site representing an energy minima [168]. AlVO has already been characterized according to DFT and predicted to be potential cathode material with metallic character. Figure 3a,b illustrate the migration pathway for Al (shown in light blue) in AlVO predicted using BVSE. The energy pathway is highlighted in orange. For comparison in Figure 3c, depicts the pathways available to aluminum determined using DFT with Nudged Elastic Band (NEB) analysis.
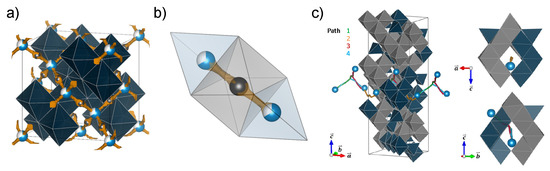
Figure 3.
Adapted with permission from reference [168]. Copywrite 2019. American Chemical Society. (a) Dark blue polyhedra correspond to a 16d site occupied by V and Al coordinated by 8 oxygens. Gray denotes hopping positions for Al calculated by VDP. (b) Gray octahedral sites must be passed by aluminum during migration (c) Pathways available to Al determined by DFT-NEB. Blue octahedra represent VO, gray octahedra are AlO, occupied Al sites are shown as dark blue octahedra and blue balls indicate the start and stop positions of the pathways.
In general, Nestler and colleagues found that the VDP and BVSE combination worked to identify ion transport pathways available for Al while DFT served to determine how Al migration and insertion would affect crystal structure of the compound of interest [168].
Recently, Takeda and colleagues used a high-throughput search for Mg-O containing compounds recorded in the ICSD [165,169]. The authors selected -cordierite (MgAl SiO) as a potential Mg conducting electrolyte due to its low migration energy ( 0.4 eV) and synthesized the compound. The experimental conductivity at 500 °C for MgAlSiO was S/cm measured by AC impedance spectroscopy, a conductivity similar to that of previously reported MgZr(PO) [124,169]. The conductivity calculated using first principles molecular dynamics (FPMD), however, was significantly higher ( S/cm), indicating that the simulations overestimated the migration energy [169]. The migration pathway of Mg was also evaluated using FPMD. Simulations revealed Mg migration followed a 3-dimensional diffusion pathway over a spiral-like network along the c-axis of the lattice for a material belonging to space group [169].
High throughput methods have been successful in the identification of potential spinel and intercalation structures for application in cathode materials [167,170,171]. The use of spinel structures as solid electrolytes was introduced recently by Canepa et al. who first demonstrated high Mg mobility can be achieved at room temperature in the crystalline solid spinels MgScSe and MgYSe [172]. Statistical analysis showed that Mg favors octahedral coordination environment in oxides and sulfides. The authors sought spinel structures based on previous work demonstrating that fast ion motion can be achieved when there is a decrease in activation state energy occurring when the stable site for an ion has unfavorable coordination over the activated site [170,173]. This quickens diffusion by reducing the overall energy profile along the path of ion migration [172]. The findings inspired the development of spinel structures for conducting Mg, the argument being that the stable site is tetrahedral, the undesired arrangement for magnesium cations. Solid state Mg NMR and relaxometry were used to probe local structure and dynamics. A single resonance at 53.3 p.p.m. (Figure 4a) indicated that there was a single tetrahedral Mg site in the spinel lattice of scandium selenide. Variable temperature NMR experiments did not demonstrate a change in chemical shift; however, there was line width narrowing noted upon increasing temperature. The authors attributed this effect to motional contributions from a less rigid lattice at higher temperatures. The mobility of Mg was further supported by static spin lattice relaxometric measurements made at varying temperature. This technique was used to derive the Mg migration barrier by fitting the relaxation data to an Arrhenius fit (Figure 4b). The measured migration barrier for the spinel MgScSe was determined via the Arrhenius fit to be around 370 meV. This was confirmed using impedance spectroscopy and supported through AIMD calculations. Further ab initio calculations identified other structures, including MgYS and MgYSe, as materials with similarly high Mg mobility. However, the authors noted that in order for these materials to be developed into a practical solid state electrolytes, their high electronic conductivity would require suppression measures. Aside from magnesium based ion conductors, Canepa et al. also evaluated barriers to Zn migration. Similarly to Mg, they found that high Zn mobility is favored when the coordination environment is unfavorable. For zinc, the preferred coordination site is of tetrahedral geometry [172].
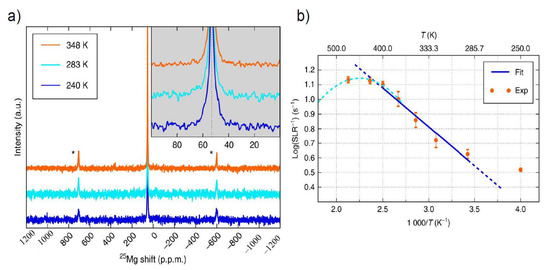
Figure 4.
Adapted with permission from reference [172]. Copywrite 2017. Nature Communications. (a) Variable temperature stack plot of Mg magic angle spinning (MAS) variable temperature NMR of MgScSe at 11.7 Tesla and 20 kHz spinning speed. * denotes a spinning sideband. (b) Mg static variable temperature spin lattice relaxation data collected at 7.02 Tesla plotted as function of temperature. The blue line indicates the data fit to the Arrhenius equation.
5. Solid Polymer Electrolytes
The first solid polymer electrolytes reported with divalent cations were mixtures of poly(ethylene oxide) with MgCl and PEO:PbCl synthesized by Yang and colleagues in 1986 [174].The authors reported ion conductivity comparable to PEO:LiCFSO, however, this level of conductivity required elevated temperatures [174]. Additional work by Yang et al. in which a series of PEO:MgCl ratios were analyzed led the authors to conclude that the PEO:MgCl complexes were primarily anion conductors [175]. Higher room temperature conductivies ranging from to S/cm were reported slightly later when formulations containing Mg(ClO) were introduced [176]. Work by Reddy and colleagues to characterize the charge transport mechanisms of Mg in PEO indicated that the cation dissociated from coordinated oxygen sites on PEO to an adjacent site on the polymer and that high conductivity resulted from an increase in concentration of the charge carrier. The authors found the salt concentration upper limit occurred at 15 wt%, after which additional salt led to decreased conductivity due to ion aggregation [177]. Studies that looked at other salts such as Mg(NO) and magnesium TFSI, Mg[N(CFSO)], demonstrated decent room temperature conductivity at S/cm [178] and S/cm [179], respectively. Bakker et al. compared Ca complexes with Mg complexes and noted that the two cations formed different coordination structures depending on salt concentration. When the volume of PEO is increased with respect to salt the conductivity of Ca increases due to its larger ionic radius whereas for lower volumes of PEO, Mg is the more conducting species. In comparing the two different conducting species, the influence of salt choice and concentration dependence becomes more apparent. The cations of smaller radii form fewer but stronger bonds to ether oxygens on the PEO backbone. On one hand, stronger cation interaction with the polymer backbone decreases ion mobility, on the other hand, segmental motions will be faster if fewer ether oxygens are coordinated [179]. Similar conclusions regarding the effects of ion pairing were found for PEO:Zn[N(CFSO)] complexes [180].
PEO blended with poly(vinyl pyrrolidone), PVP, was used as a matrix for Mg(NO) [181]. The pyrrolidone groups in PVP contribute to its high glass transition temperature (), a characteristic for which it was chosen as copolymer [181,182]. Rathika and colleagues have described a series of PEO fluoropolymer blends with both magnesium and zinc TFSI salt [183,184]. Both the PEO-PVdF:Mg(CFSO) complex and PEO-PVdF:Zn(CFSO) complex demonstrated the highest conductivity values for salt concentrations of 15 wt%. The conductivity values were also comparable, S/cm for Mg(CFSO) and S/cm for PEO-PVdF:Zn(CFSO) at room temperature, respectively. For this particular blended polymer, the authors suspect that enhanced ion transport results both from coordination between the cations in both PEO groups as will as fluorine in PVdF. The additional electronegativity of fluorine is thought to induce ion dissociation of the salt in greater volume while segmental motion is increased in the system due to the nature of the polymer blend [183,184].
In addition mixing polymers, doping with ceramic particles, nanoparticles and plasticizers has improved ion conductivity in systems with PEO matrices. Yang et al. combined PEO with the plasticizer poly(ethylene) glycol dimethyl ether (PEGM), which has the benefit of introducing more electrochemically stable ether end groups from PEGM versus the hydroxyl end groups of PEO. Salts of various concentrations of ZnCl and ZnBr were added to the PEO-PEGM matrix and found to be multiphase at room temperature despite SEM and EDX mapping that indicated homogeneous salt distribution throught the electrolyte. The conductivity and transference numbers improved significantly with addition of PEGM versus pure PEO as a matrix for ZnX [185].
Poly(vinyl alcohol) gained some interest as a potential polymer matrix for Mg conducting electrolytes, but the rigid structure of the PVA deters conduction through segmental motion of the polymer, the dominant ion transport mechanism in this case is ion hopping between aggregate ion sites [186]. Jeong et al. were able to directly observe the arrangement and size variations of the ion aggregates using atomic force microscopy [186]. Blends of PVA and PVP are known to be highly miscible due to hydrogen bonding between their respective hydroxyl and carbonyl groups [187]. Polu et al. evaluated systems of PVA-PVP with Mg(NO) and observed the highest room temperature ionic conductivity at S/cm for the complex of 50PVA:50PVP to 30 wt% (Mg(NO) [188]. This conductivity value was an improvement over previously reported conductivity for a pure PVA matrix complexed with Mg(NO) indicating enhanced Mg mobility as a direct result of adding PVP [188,189]. Ramaswamy et al. studied PVA-PVP:Mg(ClO) complexes of varying salt content. The authors attributed the high conductivity found for Mg(ClO) ( S/cm) in 50PVA:50PVP matrix to the creation of a conduction pathway directly resulting from the inter-/intra-molecular interactions between the two polymers [190]. Manjuladevi et al. synthesized and analyzed a series of blended polymer electrolytes using Mg(ClO) dissolved in a mixture of PVA-PAN in various ratios. The highest room temperature conductivity was S/cm for (92.5)PVA:(7.5)PAN:(0.25 m.m.%)Mg(ClO) [191]. In calculating transference number, the authors used a technique proposed by Evans et al. which correlated with the conclusion that Mg was the predominant conductive species in the sample [29].
In 2020 Viviani and colleagues synthesized a series of poly(allyl glycidyl ether), PAGE, based electrolytes complexed with Mg(TFSI) and MgCl and compared to the equivalent complexes synthesized with lithium. The goal of the work, in part, was to develop a synthetic procedure in order to design polymers with functional side chains projected to aid conductivity [192]. PAGE was chosen due to its low , ease of modification and reports of ion transport capability superior to that of PEO at relatively low temperature [192,193]. Figure 5 provides the authors’ graphical data comparing conductivities measured using EIS at 90 °C of lithium and magnesium salt complexes in three polymer matrices. The authors noted that Mg(TFSI) complexes, in particular, demonstrated improved ion conductivity as compared to the comparable PEO-based complexes.
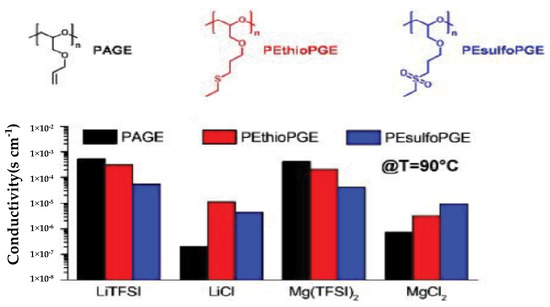
Figure 5.
Adapted with permission from reference [192]. Copywrite 2020. Royal Society of Chemistry. Bar graph comparing the conductivities at 90 °C of lithium and magnesium salt complexes in the three polymer matrices shown above the graph.
In the search for suitable replacements for PEO, poly(ethylene glycol) diacrylate (PEGDA) has gained popularity owing to its high tensile strength and thermal stability [194,195,196]. In 2019 Genier and colleagues synthesized a unique PEGDA-based solid electrolyte for calcium ion conduction. The PEGDA was complexed with Ca(NO) using UV photopolymerization at room temperature [196]. Samples were prepared at increasing concentrations of calcium to ethylene oxide (EO) monomer and measured by AC impedance spectroscopy from room temperature to 110 °C. The highest reported room temperature ion conductivity was S/cm for a ratio of 5 EO/Ca. Thermal degradation was recorded at temperatures greater than 136 °C. The ionic conductivities at different ratios of ethylene oxide to calcium concentration are displayed Figure 6. Conductivity demonstrated almost linear fit to the Arrhenius model (Equation (2)) as noted by the blue line on the graphs. These findings lead the authors to conclude that Ca in this system demonstrates hopping type ion transport upon thermal activation. In addition to hopping, the authors suspect conduction is influenced by segmental motion of the polymer as well due to the fit to the VTF equation (Equation (11)) shown as the red lines in Figure 6 [196].
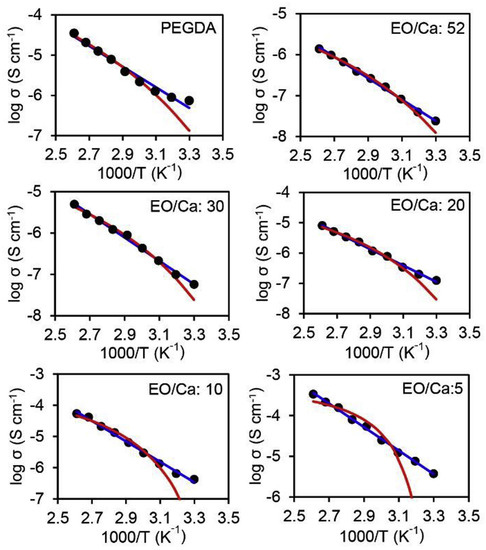
Figure 6.
Adapted with permission from reference [196]. Copywrite 2019. Elsevier B.V. Arrhenius plots of PEGDA/Ca(NO) electrolytes at different ratios of the monomeric unit, ethylene oxide (EO), to calcium concentration.
Synthesis of novel solid polymer electrolytes offers a variety of potential new matrices for multivalent cations. Recently, Liu et al. reported a film electrolyte capable of Zn conduction, PVdF-HFP:Zn(Tf) [197]. The authors found that optimal characteristics were reached at a mass ratio of 0.4(Zn(Tf):PVdF-HFP based on a high ion transference number (0.983) and high room temperature conductivity ( S/cm). Beyond this ratio there was a decrease in conductivity attributed to ion agglomeration. The authors propose a transport mechanism through the polymer matrix in which Zn is complexed then decomplexed driving migration of the cation along the segments of the polymer, as depicted in Figure 7 [197]. In addition to ion flow through the matrix, enhanced diffusion is expected at the film surface due to the presence of nanopores.
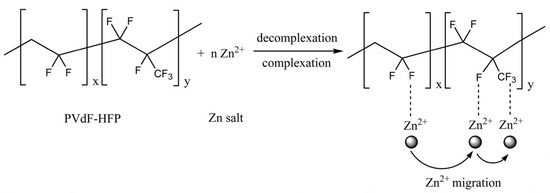
Figure 7.
Reproduced with permission from reference [197]. Copywrite 2020. Springer Nature. Proposed transport mechanism through the polymer matrix in which Zn is complexed then decomplexed driving migration of the cation.
An interesting aluminum conducting electrolyte was developed by Yao et al. in 2018. The system uses polytetrahydrofuran (PTHF) crosslinked with epoxy as the host for aluminum nitrate [198]. Conductivity was measured over a range of salt concentrations and temperatures. The highest reported conductivity was at over 100 °C, while the conductivities at ambient temperature varied between 10 to slightly less than . Even at the highest concentrations Raman spectroscopy supported total dissolution of the salt, indicating availability of free Al ions contributing to the conductivity increase.
6. Applications in Batteries
Integration of all solid electrolytes into a fully functional battery requires compatible, stable and efficient operation with electrode designs as well as current collectors and containment architecture. For inorganic solid ion conductors, the general caveat to electrolyte performance is the barrier to ion diffusion inherent in solids and exacerbated by increased charge volumes of multivalent species. Raising operating temperatures of solid inorganic ion conductors improves transport performance, but is not practical in full-cell constructions for nominal operation at ambient conditions. Solid polymers tend to operate at lower temperatures than solid inorganic ion conductors and make excellent contact with electrodes due to their shape-ability. However, challenged long term thermal stability against cathode materials has raised concerns regarding the use of polymeric electrolytes for large scale extended lifetimes [199]. While solid inorganic ion conductors are more thermally stable compared to solid polymer electrolytes, the formation of grain boundaries reduces ion migration at the cathode-electrolyte interface [200]. Failure modes due to cathode-electrolyte interactions in solid state batteries has been explored in lithium ion technology but is far less researched in multivalent chemistries. Many theoretical multivalent batteries are straighforward in the choice of metal anodes due to the availability and low cost of construction materials in addition to providing high charge capacity and the likely uniform deposition of intercalation ions upon cycling [201,202]. The choice of cathode, however, is less obvious [202]. Implementation of multivalent batteries will first require exploration into cycling longevity, compatibility and lifetime stability of the cation matrices in addition to the interaction and transport of individual cationic species within electrolytes and cathode materials.
Looking at cation species of interest, electrolyte chemistries employing Mg as the charge carrier are functionally popular in both polymeric designs and inorganic structures. One of the noted drawbacks to large scale design of magnesium batteries is stability of the full-cells over time. Inorganic magnesium conductors, in particular, tend to suffer from low voltage stability. In polymers, accounts of ion transfer have been on par with lithium, however, deposition and stripping of Mg requires sustained over-potentials due to increased interfacial resistance.
Research on solid Ca electrolytes is extremely limited and focused primarily on liquid electrolytes. In fact, there is a lack of research on calcium battery design in general [203]. One reason for this could be that calcium has been shown to diffuse poorly through the solid electrolyte interfaces formed on the metal anode surface, which significantly inhibits ion migration [204]. Some improvement to conductivity has been noted using alloyed anode materials or operating the cell at higher temperatures. However, the mobility of Ca is generally considered limited, especially in solid electrolytes, due to both ion aggregation and dissolution difficulties at the electrode/electrolyte interface [205,206]. Cathode materials have demonstrated similarly disappointing results. Chevrel phases, which are known Mg intercalation cathodes, are predicted to have much lower diffusion rates for Ca [207]. The unique chemistry of metal organic frameworks (MOFs) or Prussian blue derivatives are known to work as a cathode materials for calcium, but still exhibit cycling rates too low to be practical in scaled up applications [203,208].
Like calcium, most research on zinc electrolytes have investigated variations on liquid or aqueous solutions and it is well known that zinc reactions with anodes are strongly correlated with the type of liquid zinc electrolyte used [9]. The application of zinc charge carriers has been hindered by slow Zn intercalation rates, anodic dendrite formation and reduced long term cyclability [209]. The formation of nonuniform zinc deposits at anodes and incomplete dissolution upon cycling have caused reduced performance and shortened lifetimes in zinc batteries of all constructions. While approaches to controlling this problem are under research, there are limited examples of all solid state designs, even as proof of concept [210,211,212]. One positive development came in 2013 when Banik and coworkers found that PEG suppressed dendrite growth without reducing conductivity, possibly indicating that solid polymer electrolytes would be capable of cycling with metallic zinc anodes [212]. Diffusion of Zn tends to be slow in all solid electrolytes, especially within solid inorganic frameworks. Several methods using nearly solid designs have been proposed for both zinc and aluminum batteries. For instance, Chao and colleagues developed a “quasi-solid-state” zinc ion battery comprised on an arrayed zinc vanadate cathode supported by graphene foam, zinc nanoflake array anode and fumed silica/ZnSO electrolyte [209].
The idea of aluminum conducting solid electrolytes and fully solid aluminum batteries are concepts that have garnered some scrutiny and are generally thought implausible. One reason is that a bulk of computational research has demonstrated that solid electrolytes with higher valence cations are actually better anion conductors than cation conductors [168,213,214]. This is due to the high Coulomb potential between Al and the anionic framework. Imanaka and Tamura noted that their group had been working toward trivalent ion conduction in rigid lattices since the 1990s, including Al [215]. However, these conductors often required temperatures around 600 °C. More recent evidence has shown that Al reversibly intercalates with Chevrel phases, indicating that Al conducting electrolytes and cathodes based on solid inorganic matrices is still possible [47,216,217].
7. Summary and Conclusions
The objective of this review was to evaluate current understanding of transport properties in solid inorganic and dry solid polymer electrolytes where the cation charge carriers were Ca, Mg, Zn and Al. To the best of our knowledge, a complete and fully operational all solid state battery using multivalent metal cation charge transport has yet to be realized outside of laboratory and conceptual frameworks. One of the limiting conditions for many practical battery applications is operating temperature. When the current literature is screened for materials functioning at or near room temperature, magnesium appeared as the most commonly employed charge carrier. In solid inorganic ion conductors, phosphate based MgZr(PO) demonstrated room temperature conductivity on the order of S/cm [128]. Magnesium conductivity in the borohydride Mg(en)(BH) was measured S/cm at 30 °C [155] and, most recently, a Mg conductivity of S/cm at 30 °C was noted for the complex (BH)(NHBH) [163]. The spinel ion conductors MgScSe and MgYSe also demonstrated appreciable Mg conductivity near S/cm at 25 °C and are predicted to be conductive of Zn under similar conditions [172]. For high temperature applications, there exists the possibility to employ inorganic ion conductors of Ca and Al as well as increased options using Mg and Zn [123,124,126,127,129,132,133]. Solid polymer electrolytes offer more diversity with regard to choice of cation, however, factors of ionic radius size, polymer backbone polarity and ion aggregation complicate practical applications in fully functional batteries. Conductivity values ranging from S/cm to S/cm have been reported for several Ca, Mg and Zn salts in polymer matrices over the years [176,178,179,183,184,188,191,196,197] and more recently, Al [198]. Long term thermal and cycling stability of the polymer matrix as well as extended interface compatibility between the electrode surfaces and electrolyte appear to be the limiting factors for this class of battery construction. Inasmuch, ongoing polymer development and studies into the robustness of polymers against cathode candidates is an area where attention should be directed.
Development of multivalent cation conducting electrolytes for all solid state batteries relies on a future in which design schema account for transport pathways capable of accommodating large charge volumes at high concentration with mobility at ambient temperature. Synthetic design strategies informed by computational methods and large scale structural databases continue to identify frameworks capable of facile cation mobility. Powerful analytic techniques beyond evaluating transference numbers are significant in understanding diffusion phenomena. Local dynamics have proven of importance when analyzing mechanisms of transport in higher valence cations. Techniques such as QENS, variable temperature NMR and EXSY NMR combined with computational methods offer the opportunity to probe materials for both local and bulk dynamics. Current considerations indicate that all solid state batteries based on multivalent metal cation chemistries face significant obstacles. However, advanced techniques for discovery and application of new electrolytic materials is quickly evolving and encourages ongoing pursuit of solid high valence cation conductors. The payoff for discovery and implementation of high capacity, safe, large scale energy storage is vital to environmental and socioeconomic sustainability. Despite the caveats seen to date, the progress made in ongoing research warrants continued investigation into these materials.
Author Contributions
The manuscript was written by L.F.O., who also conducted most of the literature search. S.G.G. assisted in the literature search and provided the conceptual framework for this review. All authors have read and agreed to the published version of the manuscript.
Funding
SG acknowledges support from the U.S. Office of Naval Research, grant #N00014-20-1-2186.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, H.; Sheng, L.; Yasin, G.; Wang, L.; Xu, H.; He, X. Reviewing the current status and development of polymer electrolytes for solid-state lithium batteries. Energy Storage Mater. 2020, 33, 188–215. [Google Scholar] [CrossRef]
- Jia, M.; Zhao, N.; Huo, H.; Guo, X. Comprehensive Investigation into Garnet Electrolytes Toward Application-Oriented Solid Lithium Batteries. Electrochem. Energy Rev. 2020, 3, 656–689. [Google Scholar] [CrossRef]
- Randau, S.; Weber, D.A.; Kötz, O.; Koerver, R.; Braun, P.; Weber, A.; Ivers-Tiffée, E.; Adermann, T.; Kulisch, J.; Zeier, W.G.; et al. Benchmarking the performance of all-solid-state lithium batteries. Nat. Energy 2020, 5, 259–270. [Google Scholar] [CrossRef]
- Wanger, T.C. The Lithium future—Resources, recycling, and the environment. Conserv. Lett. 2011, 4, 202–206. [Google Scholar] [CrossRef]
- Watari, T.; Nansai, K.; Nakajima, K. Review of critical metal dynamics to 2050 for 48 elements. Resour. Conserv. Recycl. 2020, 155, 104669. [Google Scholar] [CrossRef]
- Agusdinata, D.B.; Liu, W.; Eakin, H.; Romero, H. Socio-environmental impacts of lithium mineral extraction: Towards a research agenda. Environ. Res. Lett. 2018, 13, 123001. [Google Scholar] [CrossRef]
- Li, Z.; Fuhr, O.; Fichtner, M.; Zhao-Karger, Z. Towards stable and efficient electrolytes for room-temperature rechargeable calcium batteries. Energy Environ. Sci. 2019, 12, 3496–3501. [Google Scholar] [CrossRef]
- Park, B.; Schaefer, J.L. Review—Polymer Electrolytes for Magnesium Batteries: Forging Away from Analogs of Lithium Polymer Electrolytes and Towards the Rechargeable Magnesium Metal Polymer Battery. J. Electrochem. Soc. 2020, 167, 070545. [Google Scholar] [CrossRef]
- Mainar, A.R.; Iruin, E.; Colmenares, L.C.; Kvasha, A.; de Meatza, I.; Bengoechea, M.; Leonet, O.; Boyano, I.; Zhang, Z.; Blazquez, J.A. An overview of progress in electrolytes for secondary zinc-air batteries and other storage systems based on zinc. J. Energy Storage 2018, 15, 304–328. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, H.; Wang, H.; Zhang, F.; Li, Q.; Li, H. Nonaqueous Aluminum Ion Batteries: Recent Progress and Prospects. ACS Mater. Lett. 2020, 2, 887–904. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Myung, S.T.; Sun, Y.K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef] [PubMed]
- Delmas, C. Sodium and Sodium-Ion Batteries: 50 Years of Research. Adv. Energy Mater. 2018, 8, 1703137. [Google Scholar] [CrossRef]
- Chayambuka, K.; Mulder, G.; Danilov, D.L.; Notten, P.H.L. Sodium-Ion Battery Materials and Electrochemical Properties Reviewed. Adv. Energy Mater. 2018, 8, 1800079. [Google Scholar] [CrossRef]
- Chen, L.; Fiore, M.; Wang, J.E.; Ruffo, R.; Kim, D.K.; Longoni, G. Readiness Level of Sodium-Ion Battery Technology: A Materials Review. Adv. Sustain. Syst. 2018, 2, 1700153. [Google Scholar] [CrossRef]
- Skundin, A.M.; Kulova, T.L.; Yaroslavtsev, A.B. Sodium-Ion Batteries (a Review). Russ. J. Electrochem. 2018, 54, 113–152. [Google Scholar] [CrossRef]
- Li, L.; Zheng, Y.; Zhang, S.; Yang, J.; Shao, Z.; Guo, Z. Recent progress on sodium ion batteries: Potential high-performance anodes. Energy Environ. Sci. 2018, 11, 2310–2340. [Google Scholar] [CrossRef]
- Vaalma, C.; Buchholz, D.; Weil, M.; Passerini, S. A cost and resource analysis of sodium-ion batteries. Nat. Rev. Mater. 2018, 3, 18013. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, Y.; Xing, G.; Tang, Y. Building High Power Density of Sodium-Ion Batteries: Importance of Multidimensional Diffusion Pathways in Cathode Materials. Front. Chem. 2020, 8, 152. [Google Scholar] [CrossRef]
- Xu, J.; Dou, S.; Cui, X.; Liu, W.; Zhang, Z.; Deng, Y.; Hu, W.; Chen, Y. Potassium-based electrochemical energy storage devices: Development status and future prospect. Energy Storage Mater. 2021, 34, 85–106. [Google Scholar] [CrossRef]
- Komaba, S. Sodium-driven Rechargeable Batteries: An Effort towards Future Energy Storage. Chem. Lett. 2020, 49, 1507–1516. [Google Scholar] [CrossRef]
- Yao, Q.; Zhu, C. Advanced Post-Potassium-Ion Batteries as Emerging Potassium-Based Alternatives for Energy Storage. Adv. Funct. Mater. 2020, 30, 2005209. [Google Scholar] [CrossRef]
- Yi, Y.; Zhao, Y.; Sun, J. Promise and reality of practical potassium-based energy storage systems. Eng. Rep. 2020, 2, e12328. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, C.; Dai, L.; Deng, Q.; Wang, L.; Luo, J.; Liu, S.; Hu, N. The Features and Progress of Electrolyte for Potassium Ion Batteries. Small 2020, 16, 2004096. [Google Scholar] [CrossRef] [PubMed]
- Desai, A.V.; Morris, R.E.; Armstrong, A.R. Advances in Organic Anode Materials for Na-/K-Ion Rechargeable Batteries. ChemSusChem 2020, 13, 4866–4884. [Google Scholar] [CrossRef] [PubMed]
- Qian, X.; Gu, N.; Cheng, Z.; Yang, X.; Wang, E.; Dong, S. Methods to study the ionic conductivity of polymeric electrolytes using ac impedance spectroscopy. J. Solid State Electrochem. 2001, 6, 8–15. [Google Scholar] [CrossRef]
- Irvine, J.T.S.; Sinclair, D.C.; West, A.R. Electroceramics: Characterization by Impedance Spectroscopy. Adv. Mater. 1990, 2, 132–138. [Google Scholar] [CrossRef]
- Zugmann, S.; Fleischmann, M.; Amereller, M.; Gschwind, R.M.; Wiemhöfer, H.D.; Gores, H.J. Measurement of transference numbers for lithium ion electrolytes via four different methods, a comparative study. Electrochim. Acta 2011, 56, 3926–3933. [Google Scholar] [CrossRef]
- Vest, R.W.; Tallan, N.M. High–Temperature Transference Number Determinations by Polarization Measurements. J. Appl. Phys. 1965, 36, 543–547. [Google Scholar] [CrossRef]
- Evans, J.; Vincent, C.A.; Bruce, P.G. Electrochemical measurement of transference numbers in polymer electrolytes. Polymer 1987, 28, 2324–2328. [Google Scholar] [CrossRef]
- Bruce, P.G.; Vincent, C.A. Polymer electrolytes. J. Chem. Soc. Faraday Trans. 1993, 89, 3187–3203. [Google Scholar] [CrossRef]
- Balsara, N.P.; Newman, J. Relationship between Steady-State Current in Symmetric Cells and Transference Number of Electrolytes Comprising Univalent and Multivalent Ions. J. Electrochem. Soc. 2015, 162, A2720–A2722. [Google Scholar] [CrossRef]
- Haile, S.M.; Staneff, G.; Ryu, K.H. Non-stoichiometry, grain boundary transport and chemical stability of proton conducting perovskites. J. Mater. Sci. 2001, 36, 1149–1160. [Google Scholar] [CrossRef]
- Fleig, J.; Maier, J. Finite-Element Calculations on the Impedance of Electroceramics with Highly Resistive Grain Boundaries: I, Laterally Inhomogeneous Grain Boundaries. J. Am. Ceram. Soc. 1999, 82, 3485–3493. [Google Scholar] [CrossRef]
- Valoen, L.O.; Reimers, J.N. Transport Properties of LiPF6–Based Li-Ion Battery Electrolytes. J. Electrochem. Soc. 2005, 152, A882. [Google Scholar] [CrossRef]
- Gering, K.L. Prediction of Electrolyte Conductivity: Results from a Generalized Molecular Model Based on Ion Solvation and a Chemical Physics Framework. Electrochim. Acta 2017, 225, 175–189. [Google Scholar] [CrossRef]
- Fong, K.D.; Self, J.; Diederichsen, K.M.; Wood, B.M.; McCloskey, B.D.; Persson, K.A. Ion Transport and the True Transference Number in Nonaqueous Polyelectrolyte Solutions for Lithium Ion Batteries. ACS Cent. Sci. 2019, 5, 1250–1260. [Google Scholar] [CrossRef]
- Aono, H.; Sugimoto, E.; Sadaoka, Y.; Imanaka, N.; ya Adachi, G. Ionic Conductivity of Solid Electrolytes Based on Lithium Titanium Phosphate. J. Electrochem. Soc. 1990, 137, 1023–1027. [Google Scholar] [CrossRef]
- Murugan, R.; Thangadurai, V.; Weppner, W. Fast Lithium Ion Conduction in Garnet-Type Li7La3Zr2O12. Angew. Chem. Int. Ed. 2007, 46, 7778–7781. [Google Scholar] [CrossRef]
- Kato, Y.; Hori, S.; Saito, T.; Suzuki, K.; Hirayama, M.; Mitsui, A.; Yonemura, M.; Iba, H.; Kanno, R. High-power all-solid-state batteries using sulfide superionic conductors. Nat. Energy 2016, 1, 16030. [Google Scholar] [CrossRef]
- Zhang, H.; Li, C.; Piszcz, M.; Coya, E.; Rojo, T.; Rodriguez-Martinez, L.M.; Armand, M.; Zhou, Z. Single lithium-ion conducting solid polymer electrolytes: Advances and perspectives. Chem. Soc. Rev. 2017, 46, 797–815. [Google Scholar] [CrossRef]
- Klein, R.J.; Welna, D.T.; Weikel, A.L.; Allcock, H.R.; Runt, J. Counterion Effects on Ion Mobility and Mobile Ion Concentration of Doped Polyphosphazene and Polyphosphazene Ionomers. Macromolecules 2007, 40, 3990–3995. [Google Scholar] [CrossRef]
- Muñoz, S.; Greenbaum, S. Review of Recent Nuclear Magnetic Resonance Studies of Ion Transport in Polymer Electrolytes. Membranes 2018, 8, 120. [Google Scholar] [CrossRef] [PubMed]
- Berman, M.; Greenbaum, S. NMR Studies of Solvent-Free Ceramic Composite Polymer Electrolytes—A Brief Review. Membranes 2015, 5, 915–923. [Google Scholar] [CrossRef] [PubMed]
- Gainaru, C.; Stacy, E.W.; Bocharova, V.; Gobet, M.; Holt, A.P.; Saito, T.; Greenbaum, S.; Sokolov, A.P. Mechanism of Conductivity Relaxation in Liquid and Polymeric Electrolytes: Direct Link between Conductivity and Diffusivity. J. Phys. Chem. B 2016, 120, 11074–11083. [Google Scholar] [CrossRef]
- Krachkovskiy, S.; Trudeau, M.L.; Zaghib, K. Application of Magnetic Resonance Techniques to the In Situ Characterization of Li-Ion Batteries: A Review. Materials 2020, 13, 1694. [Google Scholar] [CrossRef]
- Morales, D.J.; Greenbaum, S. NMR Investigations of Crystalline and Glassy Solid Electrolytes for Lithium Batteries: A Brief Review. Int. J. Mol. Sci. 2020, 21, 3402. [Google Scholar] [CrossRef]
- Jadhav, A.L.; Xu, J.H.; Messinger, R.J. Quantitative Molecular-Level Understanding of Electrochemical Aluminum-Ion Intercalation into a Crystalline Battery Electrode. ACS Energy Lett. 2020, 5, 2842–2848. [Google Scholar] [CrossRef]
- Graham, T.R.; Han, K.S.; Dembowski, M.; Krzysko, A.J.; Zhang, X.; Hu, J.; Clark, S.B.; Clark, A.E.; Schenter, G.K.; Pearce, C.I.; et al. 27Al Pulsed Field Gradient, Diffusion—NMR Spectroscopy of Solvation Dynamics and Ion Pairing in Alkaline Aluminate Solutions. J. Phys. Chem. B 2018, 122, 10907–10912. [Google Scholar] [CrossRef]
- Sinnaeve, D. The Stejskal–Tanner equation generalized for any gradient shape—An overview of most pulse sequences measuring free diffusion. Concepts Magn. Reson. Part A 2012, 40, 39–65. [Google Scholar] [CrossRef]
- Volgmann, K.; Epp, V.; Langer, J.; Stanje, B.; Heine, J.; Nakhal, S.; Lerch, M.; Wilkening, M.; Heitjans, P. Solid-State NMR to Study Translational Li Ion Dynamics in Solids with Low-Dimensional Diffusion Pathways. Z. Phys. Chem. 2017, 231, 1215–1241. [Google Scholar] [CrossRef]
- Smiley, D.L.; Goward, G.R. Solid-state NMR studies of chemical exchange in ion conductors for alternative energy applications. Concepts Magn. Reson. Part A 2016, 45, e21419. [Google Scholar] [CrossRef]
- Messinger, R.J. (Invited) Molecular-Level Understanding of Ion Intercalation Mechanisms in Aluminum and Zinc Battery Electrodes Revealed By Solid-State NMR Spectroscopy. In Proceedings of the 235th ECS Meeting Abstracts, Dallas, TX, USA, 26–30 May 2019. [Google Scholar] [CrossRef]
- Bottke, P.; Freude, D.; Wilkening, M. Ultra slow Li Exchange Processes in Diamagnetic Li2ZrO3 As Monitored by EXSY NMR. J. Phys. Chem. C 2013, 117, 8114–8119. [Google Scholar] [CrossRef]
- Bée, M. Localized and long-range diffusion in condensed matter: State of the art of QENS studies and future prospects. Chem. Phys. 2003, 292, 121–141. [Google Scholar] [CrossRef]
- Karlsson, M. Proton dynamics in oxides: Insight into the mechanics of proton conduction from quasielastic neutron scattering. Phys. Chem. Chem. Phys. 2015, 17, 26–38. [Google Scholar] [CrossRef]
- Tang, W.S.; Unemoto, A.; Zhou, W.; Stavila, V.; Matsuo, M.; Wu, H.; Orimo, S.i.; Udovic, T.J. Unparalleled lithium and sodium superionic conduction in solid electrolytes with large monovalent cage-like anions. Energy Environ. Sci. 2015, 8, 3637–3645. [Google Scholar] [CrossRef]
- Dimitrievska, M.; Shea, P.; Kweon, K.E.; Bercx, M.; Varley, J.B.; Tang, W.S.; Skripov, A.V.; Stavila, V.; Udovic, T.J.; Wood, B.C. Carbon Incorporation and Anion Dynamics as Synergistic Drivers for Ultrafast Diffusion in Superionic LiCB11H12 and NaCB11H12. Adv. Energy Mater. 2018, 8, 1703422. [Google Scholar] [CrossRef]
- Duchêne, L.; Lunghammer, S.; Burankova, T.; Liao, W.C.; Embs, J.P.; Copéret, C.; Wilkening, H.M.R.; Remhof, A.; Hagemann, H.; Battaglia, C. Ionic Conduction Mechanism in the Na2(B12H12)0.5(B10H10)0.5 closo-Borate Solid-State Electrolyte: Interplay of Disorder and Ion–Ion Interactions. Chem. Mater. 2019, 31, 3449–3460. [Google Scholar] [CrossRef]
- Mao, G.; Perea, R.F.; Howells, W.S.; Price, D.L.; Saboungi, M.L. Relaxation in polymer electrolytes on the nanosecond timescale. Nature 2000, 405, 163–165. [Google Scholar] [CrossRef]
- Senses, E.; Tyagi, M.; Natarajan, B.; Narayanan, S.; Faraone, A. Chain dynamics and nanoparticle motion in attractive polymer nanocomposites subjected to large deformations. Soft Matter 2017, 13, 7922–7929. [Google Scholar] [CrossRef]
- Mongcopa, K.I.S.; Tyagi, M.; Mailoa, J.P.; Samsonidze, G.; Kozinsky, B.; Mullin, S.A.; Gribble, D.A.; Watanabe, H.; Balsara, N.P. Relationship between Segmental Dynamics Measured by Quasi-Elastic Neutron Scattering and Conductivity in Polymer Electrolytes. ACS Macro Lett. 2018, 7, 504–508. [Google Scholar] [CrossRef]
- Mongcopa, K.I.S.; Gribble, D.A.; Loo, W.S.; Tyagi, M.; Mullin, S.A.; Balsara, N.P. Segmental Dynamics Measured by Quasi-Elastic Neutron Scattering and Ion Transport in Chemically Distinct Polymer Electrolytes. Macromolecules 2020, 53, 2406–2411. [Google Scholar] [CrossRef]
- Lukichev, A. Physical meaning of the stretched exponential Kohlrausch function. Phys. Lett. A 2019, 383, 2983–2987. [Google Scholar] [CrossRef]
- Köhler, J.; Imanaka, N.; Adachi, G.Y. Multivalent Cationic Conduction in Crystalline Solids. Chem. Mater. 1998, 10, 3790–3812. [Google Scholar] [CrossRef]
- Schottky, W.; Wagner, C. Theory of ordered mixed phases, I. Z. Phys. Chem. B 1931, 11, 163–210. [Google Scholar]
- Frenkel, J. Über die Wärmebewegung in festen und flüssigen Körpern. Z. Phys. 1926, 35, 652–669. [Google Scholar] [CrossRef]
- Mehrer, H. Diffusion In Solids: Fundementals, Methods, Materials, Diffusion-Controlled Processes; Springer: Berlin/Heidelberg, Germany, 2007; Volume 1. [Google Scholar]
- He, X.; Zhu, Y.; Mo, Y. Origin of fast ion diffusion in super-ionic conductors. Nat. Commun. 2017, 8, 15893. [Google Scholar] [CrossRef]
- Whittingham, M.S.; Huggins, R.A. Transport Properties of Silver Beta Alumina. J. Electrochem. Soc. 1971, 118, 1. [Google Scholar] [CrossRef]
- Wang, J.C.; Gaffari, M.; Choi, S. On the ionic conduction in β-alumina: Potential energy curves and conduction mechanism. J. Chem. Phys. 1975, 63, 772–778. [Google Scholar] [CrossRef]
- Li, H.; Okamoto, N.L.; Hatakeyama, T.; Kumagai, Y.; Oba, F.; Ichitsubo, T. Fast Diffusion of Multivalent Ions Facilitated by Concerted Interactions in Dual-Ion Battery Systems. Adv. Energy Mater. 2018, 8, 1801475. [Google Scholar] [CrossRef]
- Jalem, R.; Yamamoto, Y.; Shiiba, H.; Nakayama, M.; Munakata, H.; Kasuga, T.; Kanamura, K. Concerted Migration Mechanism in the Li Ion Dynamics of Garnet-Type Li7La3Zr2O12. Chem. Mater. 2013, 25, 425–430. [Google Scholar] [CrossRef]
- Cuan, J.; Zhou, Y.; Zhou, T.; Ling, S.; Rui, K.; Guo, Z.; Liu, H.; Yu, X. Borohydride-Scaffolded Li/Na/Mg Fast Ionic Conductors for Promising Solid-State Electrolytes. Adv. Mater. 2019, 31, 1803533. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.; Yi, J.; He, P.; Zhou, H. Solid-State Electrolytes for Lithium-Ion Batteries: Fundamentals, Challenges and Perspectives. Electrochem. Energy Rev. 2019, 2, 574–605. [Google Scholar] [CrossRef]
- Chen, F.; Cheng, S.; Liu, J.B.; Li, S.; Ouyang, W.; Yuan, K.; Liu, B. Lithium superionic conduction in α-Li10P4N10: A promising inorganic solid electrolyte candidate. J. Power Sources 2020, 477, 228744. [Google Scholar] [CrossRef]
- Zou, Z.; Ma, N.; Wang, A.; Ran, Y.; Song, T.; Jiao, Y.; Liu, J.; Zhou, H.; Shi, W.; He, B.; et al. Relationships Between Na+ Distribution, Concerted Migration, and Diffusion Properties in Rhombohedral NASICON. Adv. Energy Mater. 2020, 10, 2001486. [Google Scholar] [CrossRef]
- Hu, P.; Zou, Z.; Sun, X.; Wang, D.; Ma, J.; Kong, Q.; Xiao, D.; Gu, L.; Zhou, X.; Zhao, J.; et al. Uncovering the Potential of M1-Site-Activated NASICON Cathodes for Zn-Ion Batteries. Adv. Mater. 2020, 32, 1907526. [Google Scholar] [CrossRef]
- Funke, K. Jump relaxation in solid electrolytes. Prog. Solid State Chem. 1993, 22, 111–195. [Google Scholar] [CrossRef]
- Kvist, A. Notizen: The Electrical Conductivity of Solid and Molten 6Li2SO4 and 7Li2SO4. Z. Naturforsch. A 1966, 21, 487. [Google Scholar] [CrossRef]
- Van Gool, W. Fast ion transport in solids, solid state batteries and devices. In Proceedings of the NATO-Sponsored Advanced Study Institute of Fast Ion Transport in Solids, Solid State Batteries and Devices, Belgirate, Italy, 5–15 September 1972. [Google Scholar]
- Wilmer, D.; Feldmann, H.; Lechner, R.E.; Combet, J. Correlated motion of anions and cations in fast cation conducting rotor phases. Solid State Ion. 2004, 175, 463–466. [Google Scholar] [CrossRef]
- Wilmer, D.; Meyer, H.W. Crystalline Cation Conductors with Rotational Anion Disorder: Results of Quasielastic Neutron Scattering Experiments on Orthophosphates. Z. Phys. Chem. 2009, 223, 1341–1357. [Google Scholar] [CrossRef]
- Burmakin, E.I.; Shekhtman, G.S. On ion transport mechanism in K+-conducting solid electrolytes based on K3PO4. Solid State Ion. 2014, 265, 46–48. [Google Scholar] [CrossRef]
- Smith, J.G.; Siegel, D.J. Low–temperature paddlewheel effect in glassy solid electrolytes. Nat. Commun. 2020, 11, 1483. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Assoud, A.; Shyamsunder, A.; Huq, A.; Zhang, Q.; Hartmann, P.; Kulisch, J.; Nazar, L.F. An Entropically Stabilized Fast-Ion Conductor: Li3.25[Si0.25P0.75]S4. Chem. Mater. 2019, 31, 7801–7811. [Google Scholar] [CrossRef]
- Secco, E.A. Electrical conductivity measurements to test for rotating sulfate ions in fast ion conductors. Phys. Status Solidi (A) 1985, 88, K75–K77. [Google Scholar] [CrossRef]
- Lundén, A. Evidence for and against the paddle-wheel mechanism of ion transport in superionic sulphate phases. Solid State Commun. 1988, 65, 1237–1240. [Google Scholar] [CrossRef]
- Lundén, A. Enhancement of cation mobility in some sulphate phases due to a paddle-wheel mechanism. Solid State Ion. 1988, 28–30, 163–167. [Google Scholar] [CrossRef]
- Lunde’n, A. Paddle-wheel versus percolation model, revisited. Solid State Ion. 1994, 68, 77–80. [Google Scholar] [CrossRef]
- Karlsson, L.; McGreevy, R.L. Mechanisms of ionic conduction in Li2SO4 and LiNaSO4: Paddle wheel or percolation? Solid State Ion. 1995, 76, 301–308. [Google Scholar] [CrossRef]
- Wilmer, D.; Funke, K.; Witschas, M.; Banhatti, R.D.; Jansen, M.; Korus, G.; Fitter, J.; Lechner, R.E. Anion reorientation in an ion conducting plastic crystal –coherent quasielastic neutron scattering from sodium ortho-phosphate. Phys. B Condens. Matter 1999, 266, 60–68. [Google Scholar] [CrossRef]
- Skripov, A.V.; Babanova, O.A.; Soloninin, A.V.; Stavila, V.; Verdal, N.; Udovic, T.J.; Rush, J.J. Nuclear Magnetic Resonance Study of Atomic Motion in A2B12H12 (A = Na, K, Rb, Cs): Anion Reorientations and Na+ Mobility. J. Phys. Chem. C 2013, 117, 25961–25968. [Google Scholar] [CrossRef]
- Verdal, N.; Udovic, T.J.; Stavila, V.; Tang, W.S.; Rush, J.J.; Skripov, A.V. Anion Reorientations in the Superionic Conducting Phase of Na2B12H12. J. Phys. Chem. C 2014, 118, 17483–17489. [Google Scholar] [CrossRef]
- Kweon, K.E.; Varley, J.B.; Shea, P.; Adelstein, N.; Mehta, P.; Heo, T.W.; Udovic, T.J.; Stavila, V.; Wood, B.C. Structural, Chemical, and Dynamical Frustration: Origins of Superionic Conductivity in closo-Borate Solid Electrolytes. Chem. Mater. 2017, 29, 9142–9153. [Google Scholar] [CrossRef]
- Heere, M.; Hansen, A.L.; Payandeh, S.; Aslan, N.; Gizer, G.; Sørby, M.H.; Hauback, B.C.; Pistidda, C.; Dornheim, M.; Lohstroh, W. Dynamics of porous and amorphous magnesium borohydride to understand solid state Mg-ion-conductors. Sci. Rep. 2020, 10, 9080. [Google Scholar] [CrossRef] [PubMed]
- Müller, W.; Jansen, M. (CN)ONa3, Kristallstruktur und Natriumionenleitfähigkeit. Z. Anorg. Und Allg. Chem. 1990, 591, 41–46. [Google Scholar] [CrossRef]
- Jansen, M.; Feldmann, C.; Müller, W. Über die quasi-binären Systeme NaNO2/Na2O und NaCN/Na2O. Phasendiagramme und Natrium-Ionenleitung in Na3O(NO2) und Na3O(CN). Z. Anorg. Und Allg. Chem. 1992, 611, 7–10. [Google Scholar] [CrossRef]
- Tripathi, S.; Mishra, K.M.; Tiwari, S.N. Electrical conduction of superionic conductors: Na2ZrO3. Emerg. Mater. Res. 2012, 1, 205–211. [Google Scholar] [CrossRef]
- Secco, E.A. Paddle wheel mechanism in lithium sulfates: Arguments in defense and evidence against. J. Solid State Chem. 1992, 96, 366–375. [Google Scholar] [CrossRef]
- Lundén, A. On the Paddle–Wheel Mechanism for Cation Conduction in Lithium Sulphate. Z. Naturforsch. A 1995, 50, 1067–1076. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Kaup, K.; Zhou, L.; Roy, P.N.; Nazar, L.F. Targeting Superionic Conductivity by Turning on Anion Rotation at Room Temperature in Fast Ion Conductors. Matter 2020, 2, 1667–1684. [Google Scholar] [CrossRef]
- Ratner, M.A.; Shriver, D.F. Ion transport in solvent-free polymers. Chem. Rev. 1988, 88, 109–124. [Google Scholar] [CrossRef]
- Angell, C. Perspective on the glass transition. J. Phys. Chem. Solids 1988, 49, 863–871. [Google Scholar] [CrossRef]
- Dyre, J.C. The random free-energy barrier model for ac conduction in disordered solids. J. Appl. Phys. 1988, 64, 2456–2468. [Google Scholar] [CrossRef]
- Maitra, A.; Heuer, A. Cation Transport in Polymer Electrolytes: A Microscopic Approach. Phys. Rev. Lett. 2007, 98, 227802. [Google Scholar] [CrossRef] [PubMed]
- Mao, G.; Saboungi, M.L.; Price, D.L.; Armand, M.; Mezei, F.; Pouget, S. α-Relaxation in PEO—LiTFSI Polymer Electrolytes. Macromolecules 2002, 35, 415–419. [Google Scholar] [CrossRef]
- Stacy, E.W.; Gainaru, C.P.; Gobet, M.; Wojnarowska, Z.; Bocharova, V.; Greenbaum, S.G.; Sokolov, A.P. Fundamental Limitations of Ionic Conductivity in Polymerized Ionic Liquids. Macromolecules 2018, 51, 8637–8645. [Google Scholar] [CrossRef]
- Tamman, G.; Hesse, W. Die Abhängigkeit der Viscosität von der Temperatur bie unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 1926, 156, 245–247. [Google Scholar] [CrossRef]
- Ferry, A. Ionic Interactions and Transport Properties in Methyl Terminated Poly(propylene glycol)(4000) Complexed with LiCF3SO3. J. Phys. Chem. B 1997, 101, 150–157. [Google Scholar] [CrossRef]
- Larsson, R.; Andersson, O. Properties of electrolytes under pressure: PPG400 and PPG4000 complexed with LiCF3SO3. Electrochim. Acta 2003, 48, 3481–3489. [Google Scholar] [CrossRef]
- Furtado, C.A.; Silva, G.G.; Machado, J.C.; Pimenta, M.A.; Silva, R.A. Study of Correlations between Microstructure and Conductivity in a Thermoplastic Polyurethane Electrolyte. J. Phys. Chem. B 1999, 103, 7102–7110. [Google Scholar] [CrossRef]
- Hou, W.H.; Chen, C.Y. Studies on comb-like polymer electrolyte with a nitrile group. Electrochim. Acta 2004, 49, 2105–2112. [Google Scholar] [CrossRef]
- Garcia-Colin, L.S.; del Castillo, L.F.; Goldstein, P. Theoretical basis for the Vogel-Fulcher-Tammann equation. Phys. Rev. B 1989, 40, 7040–7044. [Google Scholar] [CrossRef]
- Wheatle, B.K.; Lynd, N.A.; Ganesan, V. Effect of Polymer Polarity on Ion Transport: A Competition between Ion Aggregation and Polymer Segmental Dynamics. ACS Macro Lett. 2018, 7, 1149–1154. [Google Scholar] [CrossRef]
- Vincent, C.A. Ion transport in polymer electrolytes. Electrochim. Acta 1995, 40, 2035–2040. [Google Scholar] [CrossRef]
- Gadjourova, Z.; Andreev, Y.G.; Tunstall, D.P.; Bruce, P.G. Ionic conductivity in crystalline polymer electrolytes. Nature 2001, 412, 520–523. [Google Scholar] [CrossRef] [PubMed]
- Schauser, N.S.; Grzetic, D.J.; Tabassum, T.; Kliegle, G.A.; Le, M.L.; Susca, E.M.; Antoine, S.; Keller, T.J.; Delaney, K.T.; Han, S.; et al. The Role of Backbone Polarity on Aggregation and Conduction of Ions in Polymer Electrolytes. J. Am. Chem. Soc. 2020, 142, 7055–7065. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.F.Y.; Kummer, J.T. Ion exchange properties of and rates of ionic diffusion in beta-alumina. J. Inorg. Nucl. Chem. 1967, 29, 2453–2475. [Google Scholar] [CrossRef]
- Semkow, K.W.; Sammells, A.F. Ionic and Electronic Conductivity Measurements on Polycrystalline Calcium Conducting β″-Alumina. J. Electrochem. Soc. 1988, 135, 244–247. [Google Scholar] [CrossRef]
- Dorner, G.; Durakpasa, H.; Fafilek, G.; Breiter, M. Production and characterization of polycrystalline (Na, Ca)β″-alumina. Solid State Ion. 1992, 53-56, 553–558. [Google Scholar] [CrossRef]
- Farrington, G.; Dunn, B. Divalent β″-aluminas: High conductivity solid electrolytes for divalent cations. Solid State Ion. 1982, 7, 267–281. [Google Scholar] [CrossRef]
- Goodenough, J.; Hong, H.P.; Kafalas, J. Fast Na+–ion transport in skeleton structures. Mater. Res. Bull. 1976, 11, 203–220. [Google Scholar] [CrossRef]
- Ikeda, S.; Takahashi, M.; Ishikawa, J.; Ito, K. Solid electrolytes with multivalent cation conduction. 1. Conducting species in MgZrPO4 system. Solid State Ion. 1987, 23, 125–129. [Google Scholar] [CrossRef]
- Nomura, K.; Ikeda, S.; Ito, K.; Einaga, H. Framework Structure, Phase Transition, and Transport Properties in MIIZr4(PO4)6 Compounds (MII = Mg, Ca, Sr, Ba, Mn, Co, Ni, Zn, Cd, and Pb). Bull. Chem. Soc. Jpn. 1992, 65, 3221–3227. [Google Scholar] [CrossRef]
- Hosono, H.; Hayashi, K.; Kamiya, T.; Atou, T.; Susaki, T. New functionalities in abundant element oxides: Ubiquitous element strategy. Sci. Technol. Adv. Mater. 2011, 12, 034303. [Google Scholar] [CrossRef] [PubMed]
- Imanaka, N. Divalent Magnesium Ionic Conduction in Mg(1−2x)(Zr(1−x)Nbx)4P6O24(x = 0–0.4) Solid Solutions. Electrochem. Solid-State Lett. 1999, 3, 327. [Google Scholar] [CrossRef]
- Imanaka, N.; Okazaki, Y.; Adachi, G. Optimization of divalent magnesium ion conduction in phosphate based polycrystalline solid electrolytes. Ionics 2001, 7, 440–446. [Google Scholar] [CrossRef]
- Anuar, N.; Adnan, S.; Mohamed, N. Characterization of Mg00.5Zr2(PO4)3 for potential use as electrolyte in solid state magnesium batteries. Ceram. Int. 2014, 40, 13719–13727. [Google Scholar] [CrossRef]
- Tamura, S.; Yamane, M.; Hoshino, Y.; Imanaka, N. Highly conducting divalent Mg2+ cation solid electrolytes with well-ordered three-dimensional network structure. J. Solid State Chem. 2016, 235, 7–11. [Google Scholar] [CrossRef]
- Imanaka, N.; Itaya, M.; Adachi, G. First identification of tetravalent Hf4+ ion-conducting solid. Mater. Lett. 2002, 53, 1–5. [Google Scholar] [CrossRef]
- Lee, W.; Tamura, S.; Imanaka, N. Synthesis and characterization of divalent ion conductors with NASICON-type structures. J. Asian Ceram. Soc. 2019, 7, 221–227. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Egawa, T.; Tamura, S.; Imanaka, N.; Adachi, G.Y. Trivalent Al3+ Ion Conduction in Aluminum Tungstate Solid. Chem. Mater. 1997, 9, 1649–1654. [Google Scholar] [CrossRef]
- Imanaka, N.; Hasegawa, Y.; Yamaguchi, M.; Itaya, M.; Tamura, S.; Adachi, G.Y. Extraordinary High Trivalent Al3+ Ion Conduction in Solids. Chem. Mater. 2002, 14, 4481–4483. [Google Scholar] [CrossRef]
- Imanaka, N.; Hasegawa, Y.; Hasegawa, I. Novel trivalent cation conducting solids and their application. Ionics 2004, 10, 385–390. [Google Scholar] [CrossRef]
- Wang, J.; Sun, C.W.; Gong, Y.D.; Zhang, H.R.; Alonso, J.A.; Fernández-Díaz, M.T.; Wang, Z.L.; Goodenough, J.B. Imaging the diffusion pathway of Al3+ ion in NASICON-type (Al0.2Zr0.8)20/19 Nb(PO4)3as electrolyte for rechargeable solid-state Al batteries. Chin. Phys. B 2018, 27, 128201. [Google Scholar] [CrossRef]
- Kendall, K.R.; Navas, C.; Thomas, J.K.; zur Loye, H.C. Recent Developments in Oxide Ion Conductors: Aurivillius Phases. Chem. Mater. 1996, 8, 642–649. [Google Scholar] [CrossRef]
- Sinclair, D.C.; Watson, C.J.; Howie, R.A.; Skakle, J.M.; Coats, A.M.; Kirk, C.A.; Lachowski, E.E.; Marr, J. NaBi3V2O10: A new oxide ion conductor. J. Mater. Chem. 1998, 8, 281–282. [Google Scholar] [CrossRef]
- Porob, D.G.; Guru Row, T. Synthesis crystal structure and ionic conductivity of Ca0.5Bi3V2O10 and Sr0.5Bi3V2O10. J. Solid State Chem. 2004, 177, 4535–4541. [Google Scholar] [CrossRef]
- El Kharbachi, A.; Dematteis, E.M.; Shinzato, K.; Stevenson, S.C.; Bannenberg, L.J.; Heere, M.; Zlotea, C.; Szilágyi, P.Á.; Bonnet, J.P.; Grochala, W.; et al. Metal Hydrides and Related Materials. Energy Carriers for Novel Hydrogen and Electrochemical Storage. J. Phys. Chem. C 2020, 124, 7599–7607. [Google Scholar] [CrossRef]
- Rowberg, A.J.E.; Weston, L.; Van de Walle, C.G. Ion-Transport Engineering of Alkaline-Earth Hydrides for Hydride Electrolyte Applications. Chem. Mater. 2018, 30, 5878–5885. [Google Scholar] [CrossRef]
- Luo, X.; Aguey-Zinsou, K.F. Correlations between the ionic conductivity and cation size in complex borohydrides. Ionics 2020, 26, 5287–5291. [Google Scholar] [CrossRef]
- Unemoto, A.; Matsuo, M.; Orimo, S.I. Complex Hydrides for Electrochemical Energy Storage. Adv. Funct. Mater. 2014, 24, 2267–2279. [Google Scholar] [CrossRef]
- Lu, Z.; Ciucci, F. Metal Borohydrides as Electrolytes for Solid-State Li, Na, Mg, and Ca Batteries: A First-Principles Study. Chem. Mater. 2017, 29, 9308–9319. [Google Scholar] [CrossRef]
- Portier, J.M.R.J.; Levasseur, A.; Villeneuve, G.; Pouchard, M. Characteristic properties of new solid electrolytes. Mater. Res. Bull. 1978, 13, 1415–1423. [Google Scholar] [CrossRef]
- Matsuo, M.; Remhof, A.; Martelli, P.; Caputo, R.; Ernst, M.; Miura, Y.; Sato, T.; Oguchi, H.; Maekawa, H.; Takamura, H.; et al. Complex Hydrides with (BH4)– and (NH2)– Anions as New Lithium Fast–Ion Conductors. J. Am. Chem. Soc. 2009, 131, 16389–16391. [Google Scholar] [CrossRef] [PubMed]
- Mezaki, T.; Kuronuma, Y.; Oikawa, I.; Kamegawa, A.; Takamura, H. Li-Ion Conductivity and Phase Stability of Ca-Doped LiBH4 under High Pressure. Inorg. Chem. 2016, 55, 10484–10489. [Google Scholar] [CrossRef]
- Kim, S.; Kisu, K.; Takagi, S.; Oguchi, H.; Orimo, S.I. Complex Hydride Solid Electrolytes of the Li(CB9H10)–Li(CB11H12) Quasi-Binary System: Relationship between the Solid Solution and Phase Transition, and the Electrochemical Properties. ACS Appl. Energy Mater. 2020, 3, 4831–4839. [Google Scholar] [CrossRef]
- Zettl, R.; Gombotz, M.; Clarkson, D.; Greenbaum, S.G.; Ngene, P.; de Jongh, P.E.; Wilkening, H.M.R. Li-Ion Diffusion in Nanoconfined LiBH4-LiI/Al2O3: From 2D Bulk Transport to 3D Long-Range Interfacial Dynamics. ACS Appl. Mater. Interfaces 2020, 12, 38570–38583. [Google Scholar] [CrossRef] [PubMed]
- Schuth, F.; Bogdanović, B.; Felderhoff, M. Light metal hydrides and complex hydrides for hydrogen storage. Chem. Commun. 2004, 20, 2249–2258. [Google Scholar] [CrossRef]
- Cerny, R.; Filinchuk, Y.; Hagemann, H.; Yvon, K. Magnesium Borohydride: Synthesis and Crystal Structure. Angew. Chem. Int. Ed. 2007, 46, 5765–5767. [Google Scholar] [CrossRef]
- Ikeshoji, T.; Tsuchida, E.; Takagi, S.; Matsuo, M.; Orimo, S.I. Magnesium ion dynamics in Mg(BH4)2(1−x)X2x (X = Cl or AlH4) from first-principles molecular dynamics simulations. RSC Adv. 2014, 4, 1366–1370. [Google Scholar] [CrossRef]
- Liu, H.; Ren, Z.; Zhang, X.; Hu, J.; Gao, M.; Pan, H.; Liu, Y. Incorporation of Ammonia Borane Groups in the Lithium Borohydride Structure Enables Ultrafast Lithium Ion Conductivity at Room Temperature for Solid-State Batteries. Chem. Mater. 2020, 32, 671–678. [Google Scholar] [CrossRef]
- Yan, Y.; Grinderslev, J.B.; Lee, Y.S.; JÞrgensen, M.; Cho, Y.W.; Černý, R.; Jensen, T.R. Ammonia-assisted fast Li-ion conductivity in a new hemiammine lithium borohydride, LiBH4·1/2NH3. Chem. Commun. 2020, 56, 3971–3974. [Google Scholar] [CrossRef]
- Ngene, P.; Lambregts, S.F.H.; Blanchard, D.; Vegge, T.; Sharma, M.; Hagemann, H.; de Jongh, P.E. The influence of silica surface groups on the Li–ion conductivity of LiBH4/SiO2 nanocomposites. Phys. Chem. Chem. Phys. 2019, 21, 22456–22466. [Google Scholar] [CrossRef] [PubMed]
- Roedern, E.; Kühnel, R.S.; Remhof, A.; Battaglia, C. Magnesium Ethylenediamine Borohydride as Solid-State Electrolyte for Magnesium Batteries. Sci. Rep. 2017, 7, 46189. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.; Chua, Y.S.; Wu, H.; Xiong, Z.; He, T.; Zhou, W.; Ju, X.; Yang, M.; Wu, G.; Chen, P. Synthesis, structures and dehydrogenation of magnesium borohydride–ethylenediamine composites. Int. J. Hydrog. Energy 2015, 40, 412–419. [Google Scholar] [CrossRef]
- Yan, Y.; Dononelli, W.; JÞrgensen, M.; Grinderslev, J.B.; Lee, Y.S.; Cho, Y.W.; Černý, R.; Hammer, B.; Jensen, T.R. The mechanism of Mg2+ conduction in ammine magnesium borohydride promoted by a neutral molecule. Phys. Chem. Chem. Phys. 2020, 22, 9204–9209. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Grinderslev, J.B.; Jorgensen, M.; Skov, L.N.; Skibsted, J.; Jensen, T.R. Ammine Magnesium Borohydride Nanocomposites for All-Solid-State Magnesium Batteries. ACS Appl. Energy Mater. 2020, 3, 9264–9270. [Google Scholar] [CrossRef]
- Higashi, S.; Miwa, K.; Aoki, M.; Takechi, K. A novel inorganic solid state ion conductor for rechargeable Mg batteries. Chem. Commun. 2014, 50, 1320–1322. [Google Scholar] [CrossRef] [PubMed]
- Le Ruyet, R.; Berthelot, R.; Salager, E.; Florian, P.; Fleutot, B.; Janot, R. Investigation of Mg(BH4)(NH2)-Based Composite Materials with Enhanced Mg2+ Ionic Conductivity. J. Phys. Chem. C 2019, 123, 10756–10763. [Google Scholar] [CrossRef]
- Le Ruyet, R.; Fleutot, B.; Berthelot, R.; Benabed, Y.; Hautier, G.; Filinchuk, Y.; Janot, R. Mg3(BH4)4(NH2)2 as Inorganic Solid Electrolyte with High Mg2+ Ionic Conductivity. ACS Appl. Energy Mater. 2020, 3, 6093–6097. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data JAC. Available online: https://scripts.iucr.org/cgi-bin/paper?db5098 (accessed on 12 July 2020).
- Kisu, K.; Kim, S.; Inukai, M.; Oguchi, H.; Takagi, S.; Orimo, S.I. Magnesium Borohydride Ammonia Borane as a Magnesium Ionic Conductor. ACS Appl. Energy Mater. 2020, 3, 3174–3179. [Google Scholar] [CrossRef]
- Fang, H.; Jena, P. Li-rich antiperovskite superionic conductors based on cluster ions. Proc. Natl. Acad. Sci. USA 2017, 114, 11046–11051. [Google Scholar] [CrossRef]
- For Information Infrastructure, F.K.L.I. Available online: https://www.sciencedirect.com/topics/computer-science/information-infrastructure (accessed on 12 June 2020).
- ToposPro. Available online: https://topospro.com/ (accessed on 16 June 2020).
- Morkhova, E.A.; Kabanov, A.A.; Blatov, V.A. Modeling of Ionic Conductivity in Inorganic Compounds with Multivalent Cations. Russ. J. Electrochem. 2019, 55, 762–777. [Google Scholar] [CrossRef]
- Nestler, T.; Meutzner, F.; Kabanov, A.A.; Zschornak, M.; Leisegang, T.; Meyer, D.C. Combined Theoretical Approach for Identifying Battery Materials: Al3+ Mobility in Oxides. Chem. Mater. 2019, 31, 737–747. [Google Scholar] [CrossRef]
- Takeda, H.; Nakano, K.; Tanibata, N.; Nakayama, M. Novel Mg-ion conductive oxide of μ-cordierite Mg0.6Al1.2Si1.8O6. Sci. Technol. Adv. Mater. 2020, 21, 131–138. [Google Scholar] [CrossRef] [PubMed]
- Sai Gautam, G.; Canepa, P.; Urban, A.; Bo, S.H.; Ceder, G. Influence of Inversion on Mg Mobility and Electrochemistry in Spinels. Chem. Mater. 2017, 29, 7918–7930. [Google Scholar] [CrossRef]
- Liu, M.; Rong, Z.; Malik, R.; Canepa, P.; Jain, A.; Ceder, G.; Persson, K.A. Spinel compounds as multivalent battery cathodes: A systematic evaluation based on ab initio calculations. Energy Environ. Sci. 2015, 8, 964–974. [Google Scholar] [CrossRef]
- Canepa, P.; Bo, S.H.; Sai Gautam, G.; Key, B.; Richards, W.D.; Shi, T.; Tian, Y.; Wang, Y.; Li, J.; Ceder, G. High magnesium mobility in ternary spinel chalcogenides. Nat. Commun. 2017, 8, 1759. [Google Scholar] [CrossRef]
- Rong, Z.; Malik, R.; Canepa, P.; Sai Gautam, G.; Liu, M.; Jain, A.; Persson, K.; Ceder, G. Materials Design Rules for Multivalent Ion Mobility in Intercalation Structures. Chem. Mater. 2015, 27, 6016–6021. [Google Scholar] [CrossRef]
- Yang, L.L.; Huq, R.; Farrington, G.; Chiodelli, G. Preparation and properties of PEO complexes of divalent cation salts. Solid State Ion. 1986, 18–19, 291–294. [Google Scholar] [CrossRef]
- Yang, L.L.; McGhie, A.R.; Farrington, G.C. Ionic Conductivity in Complexes of Poly(ethylene oxide) and MgCl2. J. Electrochem. Soc. 1986, 133, 1380–1385. [Google Scholar] [CrossRef]
- Patrick, A.; Glasse, M.; Latham, R.; Linford, R. Novel solid state polymeric batteries. Solid State Ion. 1986, 18–19, 1063–1067. [Google Scholar] [CrossRef]
- Jaipal Reddy, M.; Chu, P.P. Ion pair formation and its effect in PEO:Mg solid polymer electrolyte system. J. Power Sources 2002, 109, 340–346. [Google Scholar] [CrossRef]
- Ramalingaiah, S.; SrinivasReddy, D.; Reddy, M.J.; Laxminarsaiah, E.; SubbaRao, U.V. Conductivity and discharge characteristic studies of novel polymer electrolyte based on PEO complexed with Mg(NO3)2 salt. Mater. Lett. 1996, 29. [Google Scholar] [CrossRef]
- Bakker, A.; Gejji, S.; Lindgren, J.; Hermansson, K.; Probst, M.M. Contact ion pair formation and ether oxygen coordination in the polymer electrolytes M[N(CF3SO2)2]2PEOn for M = Mg, Ca, Sr and Ba. Polymer 1995, 36, 4371–4378. [Google Scholar] [CrossRef]
- Wendsjo, Å.; Lindgren, J.; Thomas, J.; Farrington, G. The effect of temperature and concentration on the local environment in the system M(CF3SO3)2PEOn for M = Ni, Zn and Pb. Solid State Ion. 1992, 53–56, 1077–1082. [Google Scholar] [CrossRef]
- Anilkumar, K.; Jinisha, B.; Manoj, M.; Jayalekshmi, S. Poly(ethylene oxide) (PEO)–Poly(vinyl pyrrolidone) (PVP) blend polymer based solid electrolyte membranes for developing solid state magnesium ion cells. Eur. Polym. J. 2017, 89, 249–262. [Google Scholar] [CrossRef]
- Feng, H.; Feng, Z.; Shen, L. A High Resolution Solid-State n.m.r. and d.s.c. Study of Miscibility and Crystallization Behaviour of Poly(vinyl alcohol)poly(N–vinyl–2–pyrrolidone) Blends. Polymer 1993, 34, 2516–2519. [Google Scholar] [CrossRef]
- Rathika, R.; Suthanthiraraj, S.A. Ionic Interactions and Dielectric Relaxation of PEO/PVDF-Mg(CF3SO2)2N2) Blend Electrolytes for Magnesium Ion Rechargeable Batteries. Macromol. Res. 2016, 24, 422–428. [Google Scholar] [CrossRef]
- Rathika, R.; Padmaraj, O.; Suthanthiraraj, S.A. Electrical conductivity and dielectric relaxation behaviour of PEO/PVdF-based solid polymer blend electrolytes for zinc battery applications. Ionics 2018, 24, 243–255. [Google Scholar] [CrossRef]
- Yang, H.; Huq, R.; Farrington, G. Conductivity in PEO-based Zn(II) polymer electrolytes. Solid State Ion. 1990, 40–41, 663–665. [Google Scholar] [CrossRef]
- Jeong, S.K.; Jo, Y.K.; Jo, N.J. Decoupled ion conduction mechanism of poly(vinyl alcohol) based Mg-conducting solid polymer electrolyte. Electrochim. Acta 2006, 52, 1549–1555. [Google Scholar] [CrossRef]
- Nishio, Y.; Haratani, T.; Takahashi, T. Miscibility and orientation behavior of poly(vinyl alcohol)/poly(vinyl pyrrolidone) blends. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 355–376. [Google Scholar] [CrossRef]
- Polu, A.R.; Kumar, R.; Rhee, H.W. Magnesium ion conducting solid polymer blend electrolyte based on biodegradable polymers and application in solid-state batteries. Ionics 2015, 21, 125–132. [Google Scholar] [CrossRef]
- Polu, A.R.; Kumar, R. Preparation and characterization of pva based solid polymer electrolytes for electrochemical cell applications. Chin. J. Polym. Sci. 2013, 31, 641–648. [Google Scholar] [CrossRef]
- Ramaswamy, M.; Malayandi, T.; Subramanian, S.; Srinivasalu, J.; Rangaswamy, M. Magnesium ion conducting polyvinyl alcohol–polyvinyl pyrrolidone-based blend polymer electrolyte. Ionics 2017, 23, 1771–1781. [Google Scholar] [CrossRef]
- Manjuladevi, R.; Thamilselvan, M.; Selvasekarapandian, S.; Mangalam, R.; Premalatha, M.; Monisha, S. Mg-ion conducting blend polymer electrolyte based on poly(vinyl alcohol)-poly (acrylonitrile) with magnesium perchlorate. Solid State Ion. 2017, 308, 90–100. [Google Scholar] [CrossRef]
- Viviani, M.; Meereboer, N.L.; Saraswati, N.L.P.A.; Loos, K.; Portale, G. Lithium and magnesium polymeric electrolytes prepared using poly(glycidyl ether)-based polymers with short grafted chains. Polym. Chem. 2020, 11, 2070–2079. [Google Scholar] [CrossRef]
- Barteau, K.P.; Wolffs, M.; Lynd, N.A.; Fredrickson, G.H.; Kramer, E.J.; Hawker, C.J. Allyl Glycidyl Ether-Based Polymer Electrolytes for Room Temperature Lithium Batteries. Macromolecules 2013, 46, 8988–8994. [Google Scholar] [CrossRef]
- Wei, Z.; Chen, S.; Wang, J.; Wang, Z.; Zhang, Z.; Yao, X.; Deng, Y.; Xu, X. A large-size, bipolar-stacked and high-safety solid-state lithium battery with integrated electrolyte and cathode. J. Power Sources 2018, 394, 57–66. [Google Scholar] [CrossRef]
- Fu, G.; Dempsey, J.; Izaki, K.; Adachi, K.; Tsukahara, Y.; Kyu, T. Highly conductive solid polymer electrolyte membranes based on polyethylene glycol-bis-carbamate dimethacrylate networks. J. Power Sources 2017, 359, 441–449. [Google Scholar] [CrossRef]
- Genier, F.S.; Burdin, C.V.; Biria, S.; Hosein, I.D. A novel calcium-ion solid polymer electrolyte based on crosslinked poly(ethylene glycol) diacrylate. J. Power Sources 2019, 414, 302–307. [Google Scholar] [CrossRef]
- Liu, J.; Khanam, Z.; Muchakayala, R.; Song, S. Fabrication and characterization of Zn-ion-conducting solid polymer electrolyte films based on PVdF-HFP/Zn(Tf)2 complex system. J. Mater. Sci. Mater. Electron. 2020, 31, 6160–6173. [Google Scholar] [CrossRef]
- Yao, T.; Genier, F.S.; Biria, S.; Hosein, I.D. A solid polymer electrolyte for aluminum ion conduction. Results Phys. 2018, 10, 529–531. [Google Scholar] [CrossRef]
- Xia, Y.; Fujieda, T.; Tatsumi, K.; Prosini, P.P.; Sakai, T. Thermal and electrochemical stability of cathode materials in solid polymer electrolyte. J. Power Sources 2001, 92, 234–243. [Google Scholar] [CrossRef]
- Tippens, J.; Miers, J.C.; Afshar, A.; Lewis, J.A.; Cortes, F.J.Q.; Qiao, H.; Marchese, T.S.; Di Leo, C.V.; Saldana, C.; McDowell, M.T. Visualizing Chemomechanical Degradation of a Solid-State Battery Electrolyte. ACS Energy Lett. 2019, 4, 1475–1483. [Google Scholar] [CrossRef]
- Kim, H.; Jeong, G.; Kim, Y.U.; Kim, J.H.; Park, C.M.; Sohn, H.J. Metallic anodes for next generation secondary batteries. Chem. Soc. Rev. 2013, 42, 9011–9034. [Google Scholar] [CrossRef]
- Canepa, P.; Sai Gautam, G.; Hannah, D.C.; Malik, R.; Liu, M.; Gallagher, K.G.; Persson, K.A.; Ceder, G. Odyssey of Multivalent Cathode Materials: Open Questions and Future Challenges. Chem. Rev. 2017, 117, 4287–4341. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, F.; Tang, Y. A Novel Calcium-Ion Battery Based on Dual-Carbon Configuration with High Working Voltage and Long Cycling Life. Adv. Sci. 2018, 5, 1701082. [Google Scholar] [CrossRef]
- Aurbach, D.; Skaletsky, R.; Gofer, Y. The Electrochemical Behavior of Calcium Electrodes in a Few Organic Electrolytes. J. Electrochem. Soc. 1991, 138, 3536–3545. [Google Scholar] [CrossRef]
- Tchitchekova, D.S.; Monti, D.; Johansson, P.; Bardé, F.; Randon-Vitanova, A.; Palacín, M.R.; Ponrouch, A. On the Reliability of Half-Cell Tests for Monovalent (Li+, Na+) and Divalent (Mg2+, Ca2+) Cation Based Batteries. J. Electrochem. Soc. 2017, 164, A1384–A1392. [Google Scholar] [CrossRef]
- Gummow, R.J.; Vamvounis, G.; Kannan, M.B.; He, Y. Calcium-Ion Batteries: Current State-of-the-Art and Future Perspectives. Adv. Mater. 2018, 30, 1801702. [Google Scholar] [CrossRef]
- Juran, T.R.; Smeu, M. Hybrid density functional theory modeling of Ca, Zn, and Al ion batteries using the Chevrel phase Mo6S8 cathode. Phys. Chem. Chem. Phys. 2017, 19, 20684–20690. [Google Scholar] [CrossRef]
- Padigi, P.; Goncher, G.; Evans, D.; Solanki, R. Potassium barium hexacyanoferrate—A potential cathode material for rechargeable calcium ion batteries. J. Power Sources 2015, 273, 460–464. [Google Scholar] [CrossRef]
- Chao, D.; Zhu, C.R.; Song, M.; Liang, P.; Zhang, X.; Tiep, N.H.; Zhao, H.; Wang, J.; Wang, R.; Zhang, H.; et al. A High-Rate and Stable Quasi-Solid-State Zinc-Ion Battery with Novel 2D Layered Zinc Orthovanadate Array. Adv. Mater. 2018, 30, 1803181. [Google Scholar] [CrossRef]
- Lee, B.S.; Cui, S.; Xing, X.; Liu, H.; Yue, X.; Petrova, V.; Lim, H.D.; Chen, R.; Liu, P. Dendrite Suppression Membranes for Rechargeable Zinc Batteries. ACS Appl. Mater. Interfaces 2018, 10, 38928–38935. [Google Scholar] [CrossRef]
- Trudgeon, D.P.; Qiu, K.; Li, X.; Mallick, T.; Taiwo, O.O.; Chakrabarti, B.; Yufit, V.; Brandon, N.P.; Crevillen-Garcia, D.; Shah, A. Screening of effective electrolyte additives for zinc-based redox flow battery systems. J. Power Sources 2019, 412, 44–54. [Google Scholar] [CrossRef]
- Banik, S.J.; Akolkar, R. Suppressing Dendrite Growth during Zinc Electrodeposition by PEG-200 Additive. J. Electrochem. Soc. 2013, 160, D519–D523. [Google Scholar] [CrossRef]
- Adams, S. From bond valence maps to energy landscapes for mobile ions in ion-conducting solids. Solid State Ion. 2006, 177, 1625–1630. [Google Scholar] [CrossRef]
- Neiman, A.Y.; Pestereva, N.N.; Zhou, Y.; Nechaev, D.O.; Koteneva, E.A.; Vanec, K.; Higgins, B.; Volkova, N.; Korchuganova, I.G. The nature and the mechanism of ion transfer in tungstates Me2+{WO4} (Ca, Sr, Ba) and {WO4}3 (Al, Sc, In) according to the data acquired by the tubandt method. Russ. J. Electrochem. 2013, 49, 895–907. [Google Scholar] [CrossRef]
- Imanaka, N.; Tamura, S. Development of Multivalent Ion Conducting Solid Electrolytes. Bull. Chem. Soc. Jpn. 2011, 84, 353–362. [Google Scholar] [CrossRef]
- Lee, B.; Lee, H.; Yim, T.; Kim, J.; Lee, J.; Chung, K.; Cho, B.; Oh, S. Investigation on the structural evolutions during the insertion of aluminum ions into Mo6S8 Chevrel phase. J. Electrochem. Soc. 2016, 163, A1070–A1076. [Google Scholar] [CrossRef]
- Geng, L.; Lv, G.; Xing, X.; Guo, J. Reversible Electrochemical Intercalation of Aluminum in Mo6S8. Chem. Mater. 2015, 27, 4926–4929. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).