The Impact of Environmental Factors on the Thermal Characteristic of a Lithium–ion Battery
Abstract
1. Introduction
2. Methods
2.1. Experimental Techniques
2.1.1. Battery Description
2.1.2. Thermal Parameter Assessment
2.1.3. Thermal Validation Assessment
2.2. Simulation Techniques
2.2.1. Heat Transfer in Solids
2.2.2. Heat Transfer in Fluids
2.2.3. Convection
2.2.4. Radiation
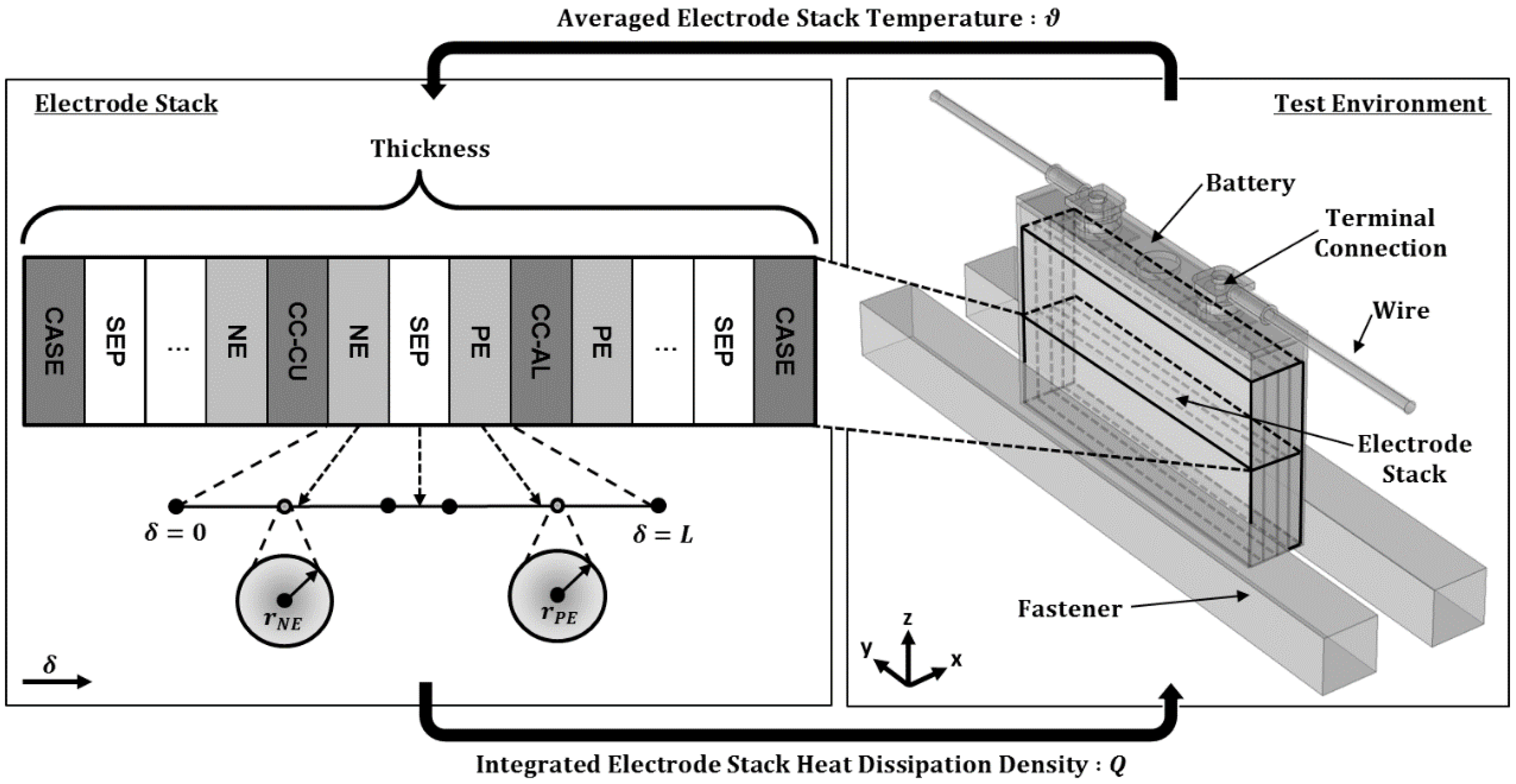
2.2.5. Electrode Stack Thermal Behavior
2.2.6. Coupling of Physics
3. Results and Discussion
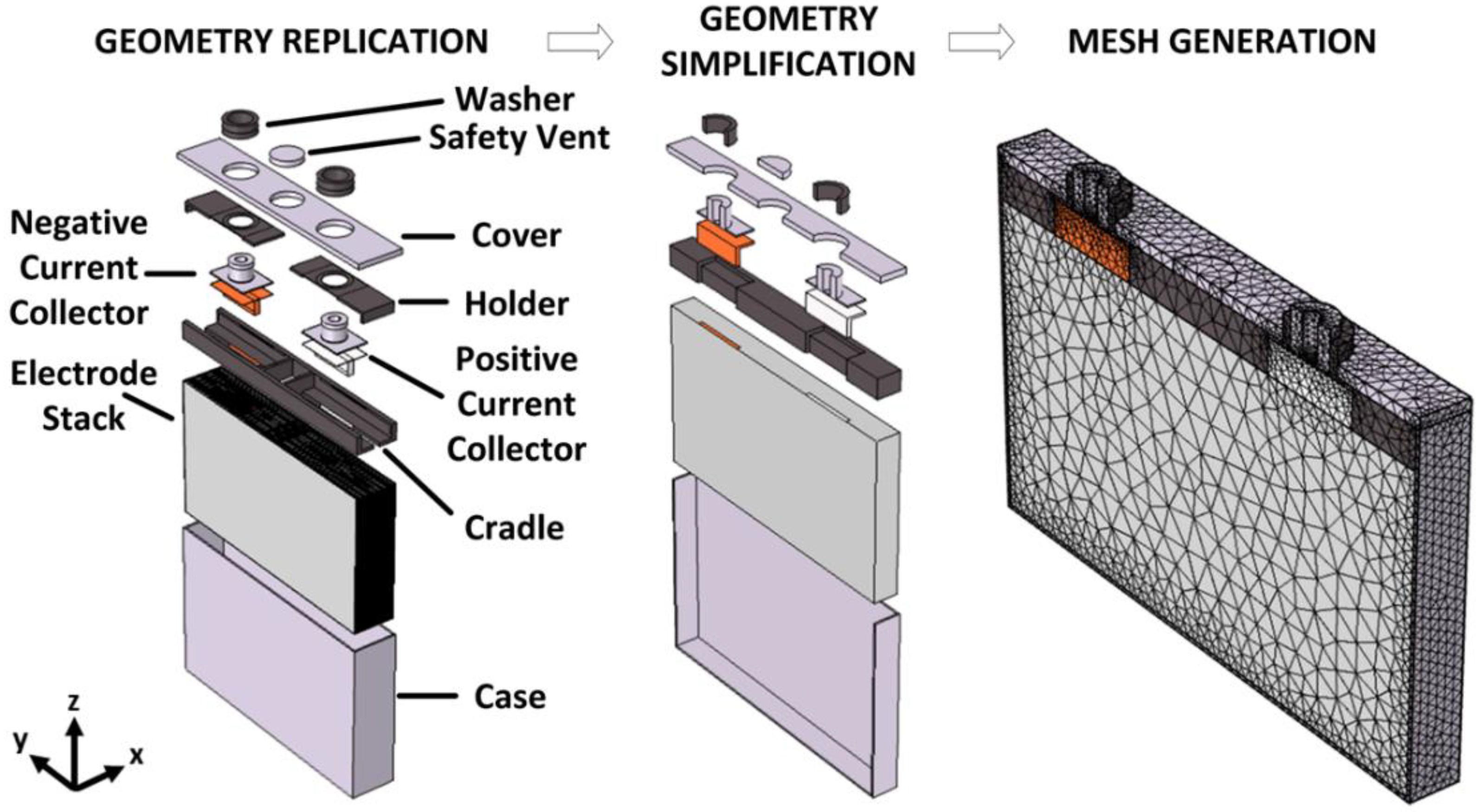
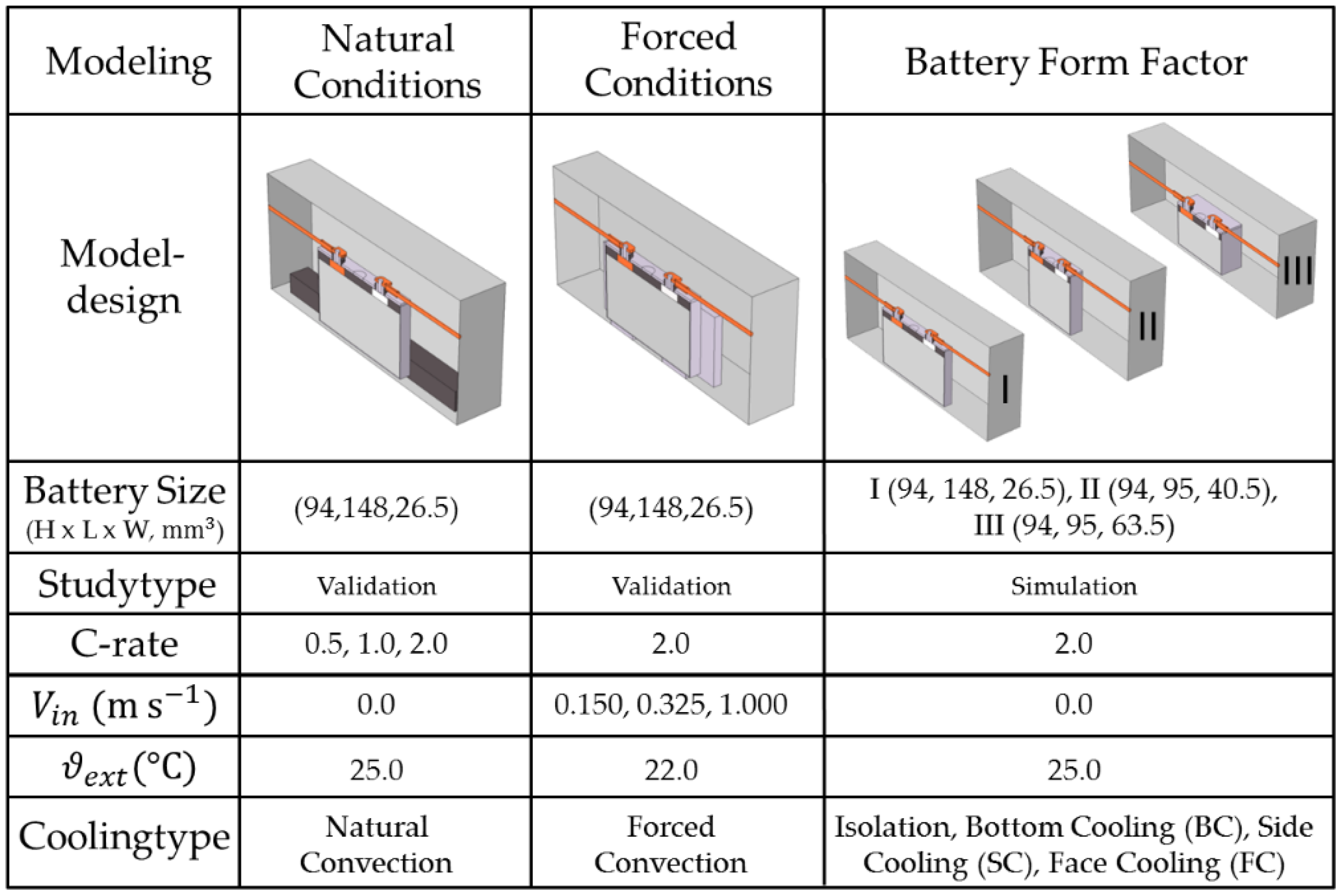
3.1. Geometrical Battery Characterization
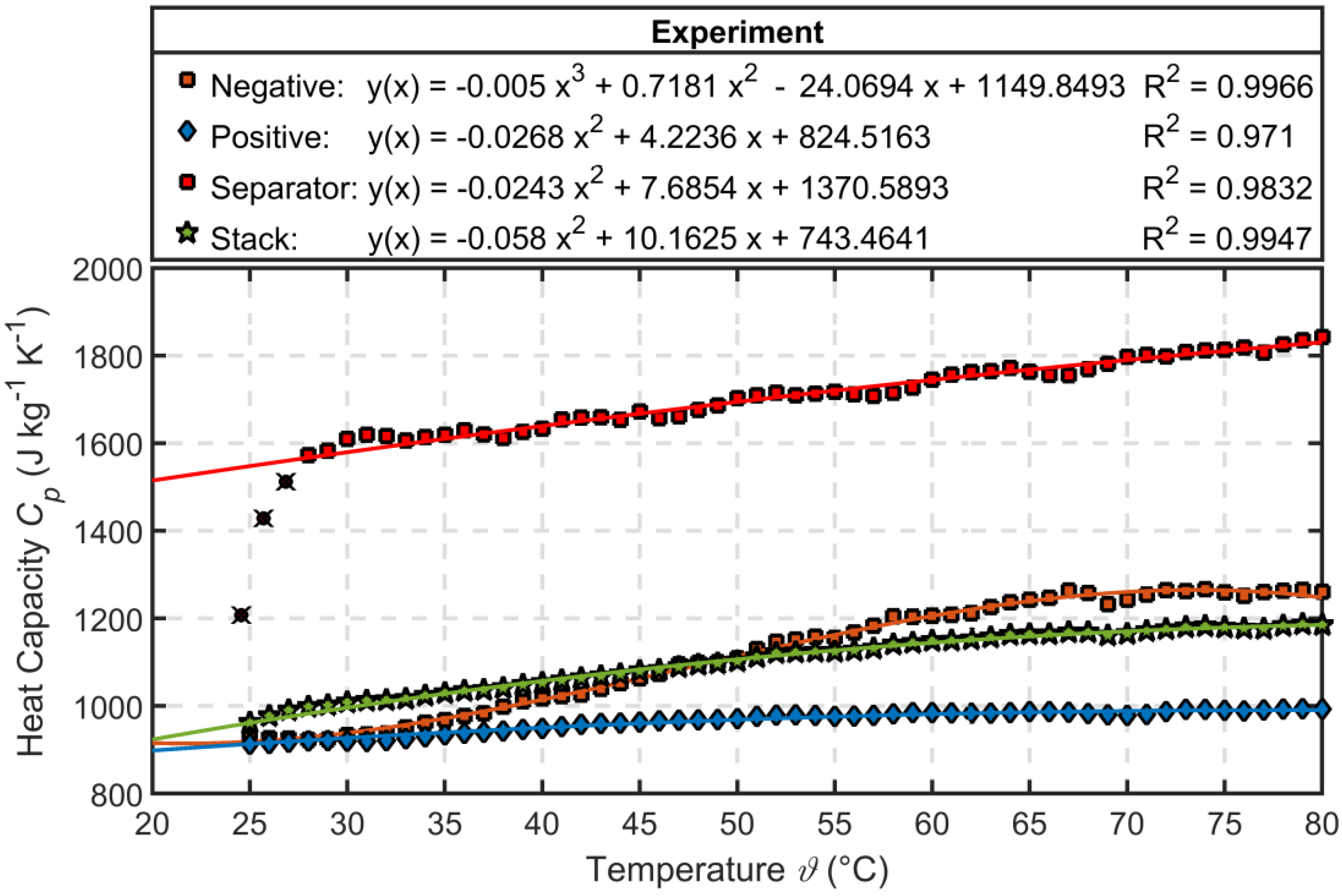
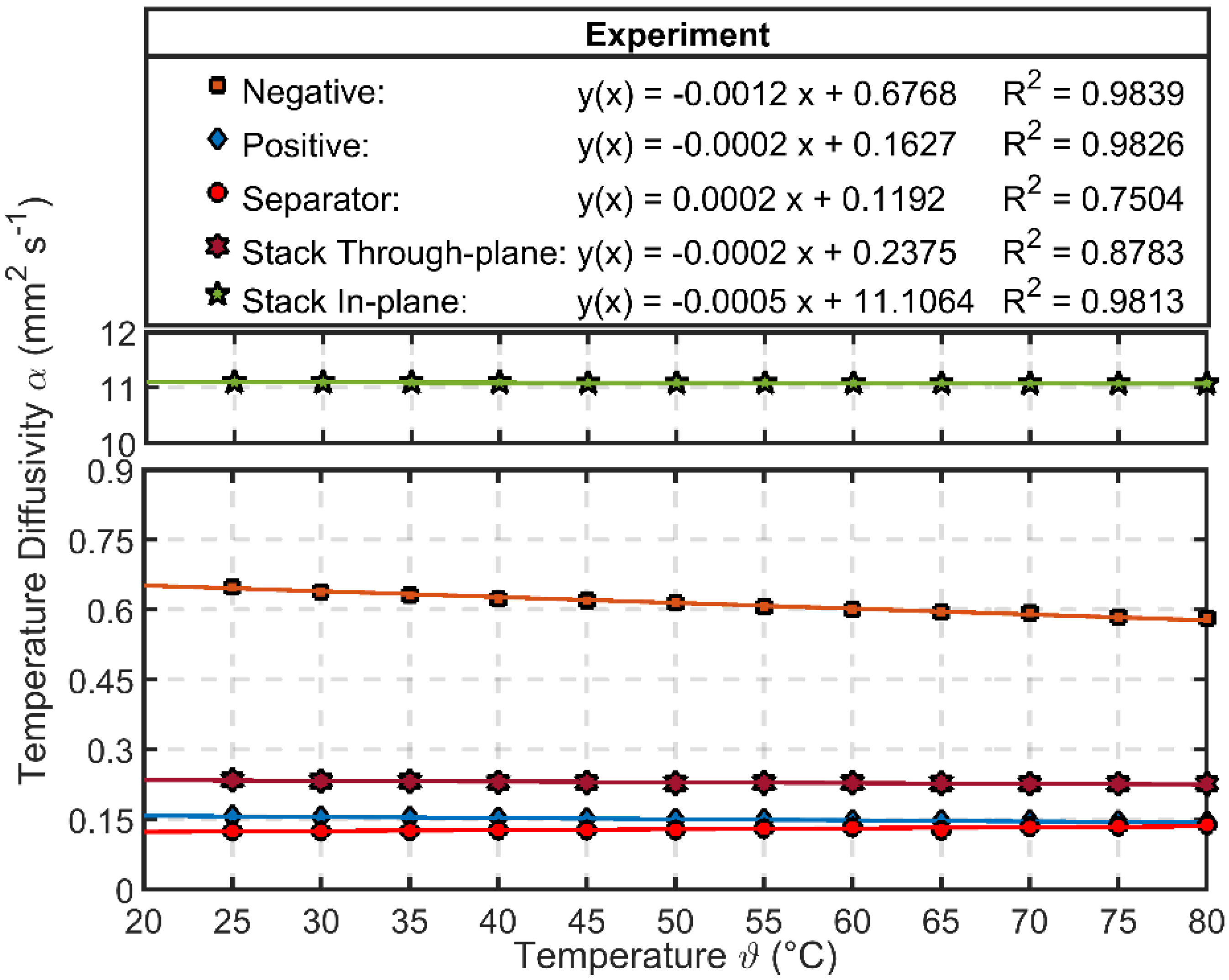
3.2. Characterization Results of Thermal Parameters
3.3. Thermal Model Study
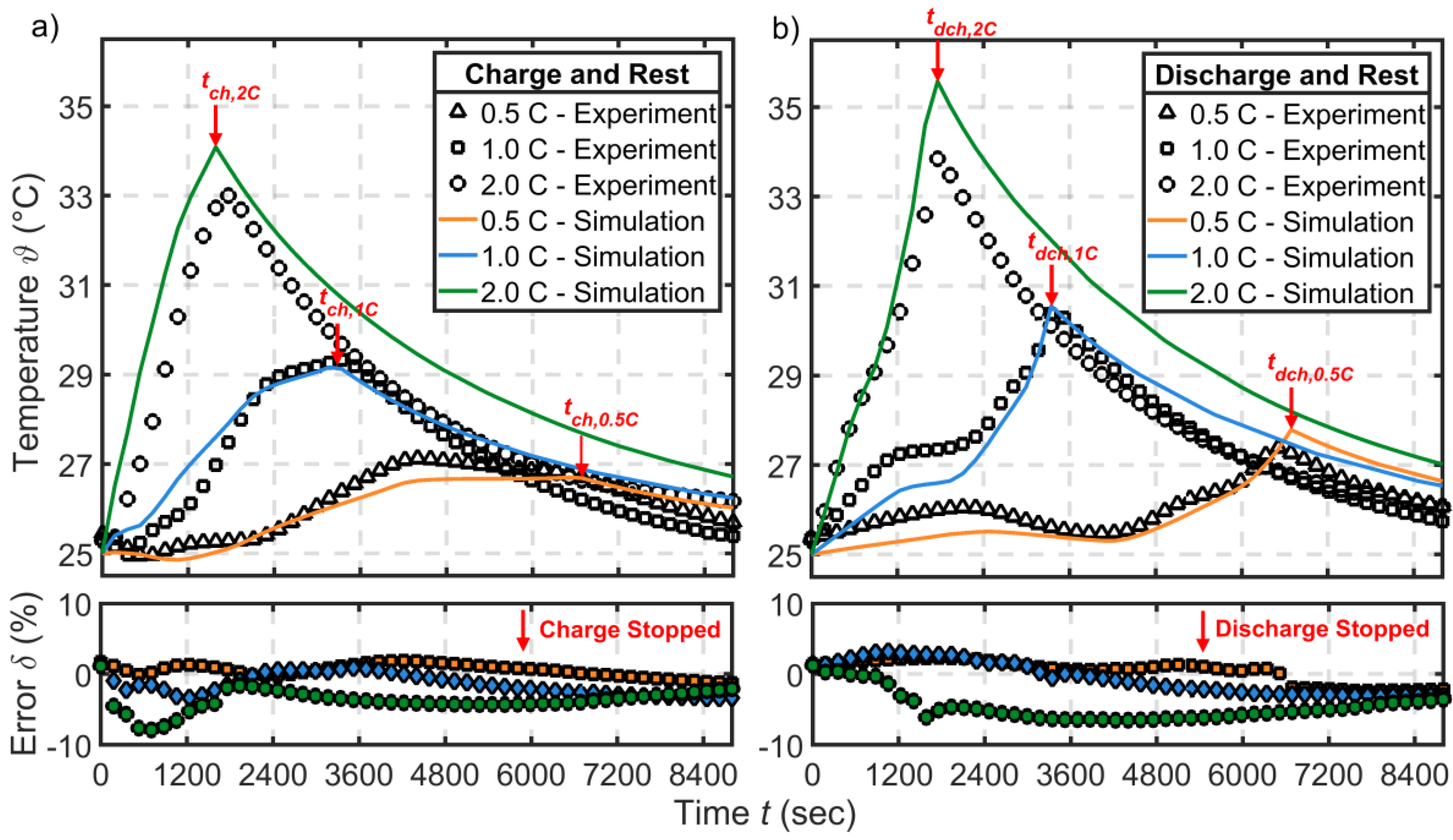
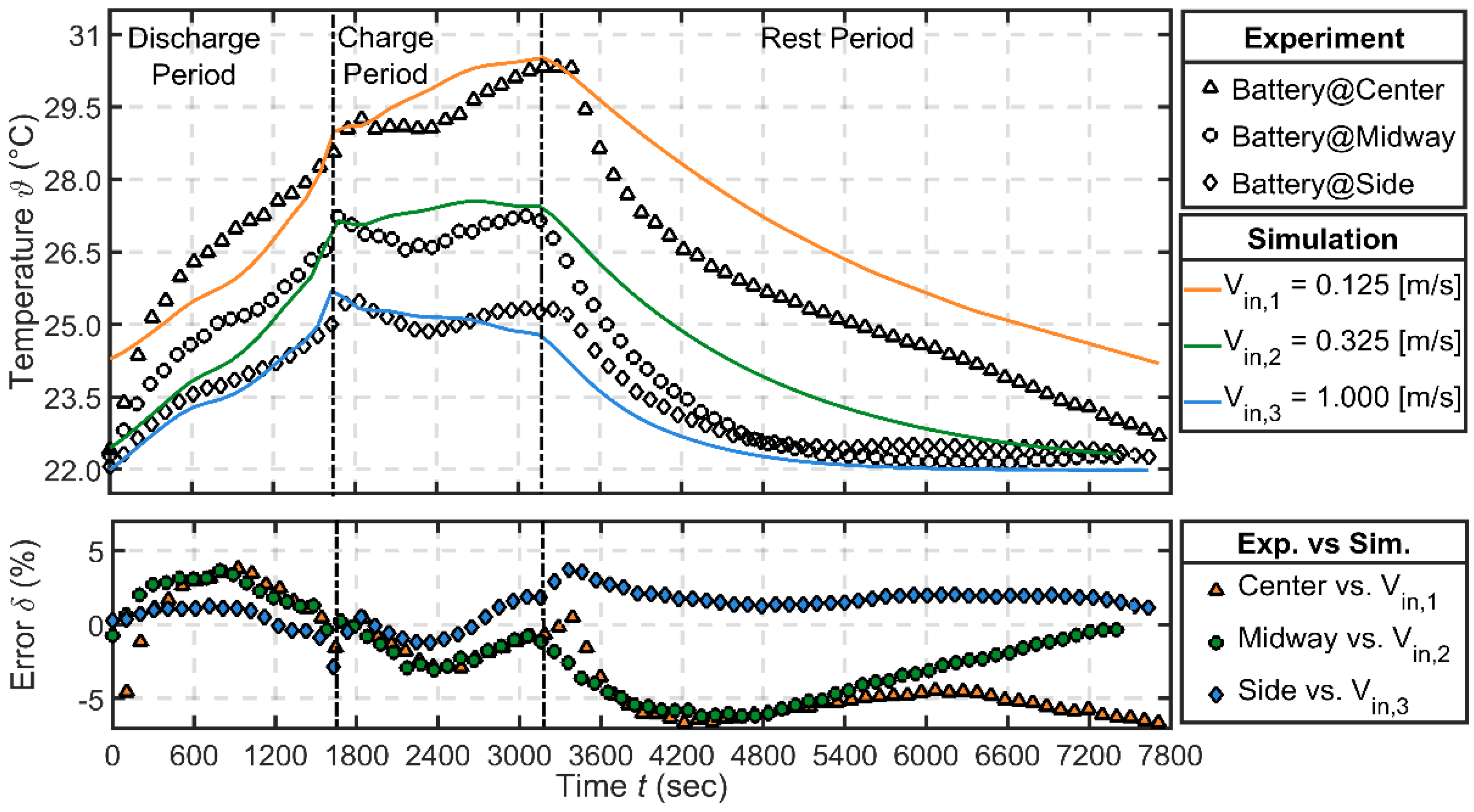
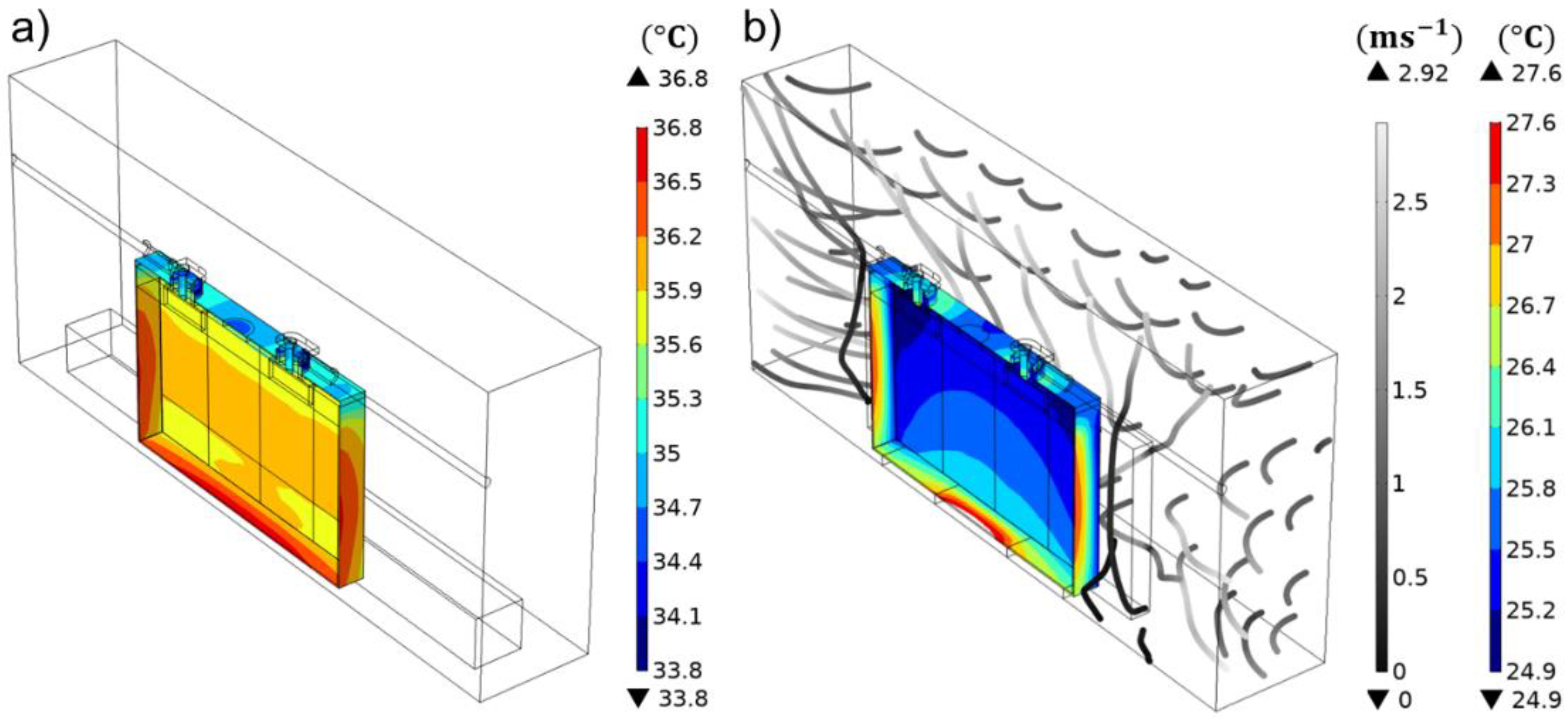
3.3.1. Thermal Validation—Natural and Forced Conditions
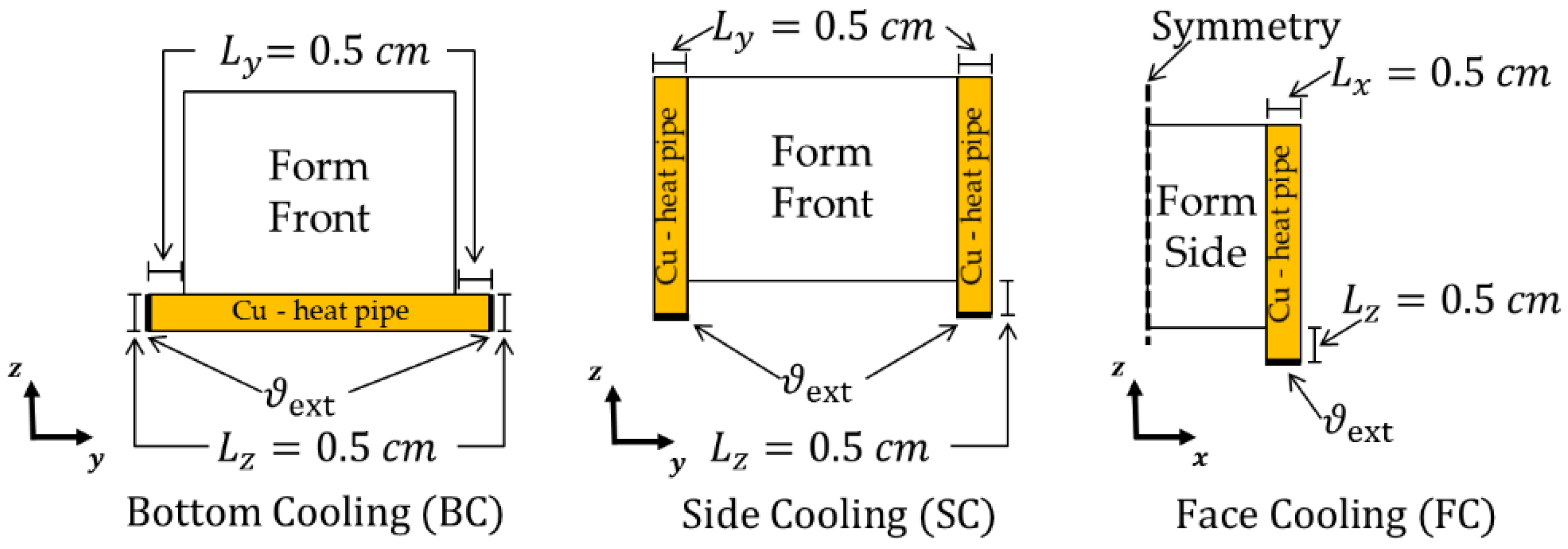
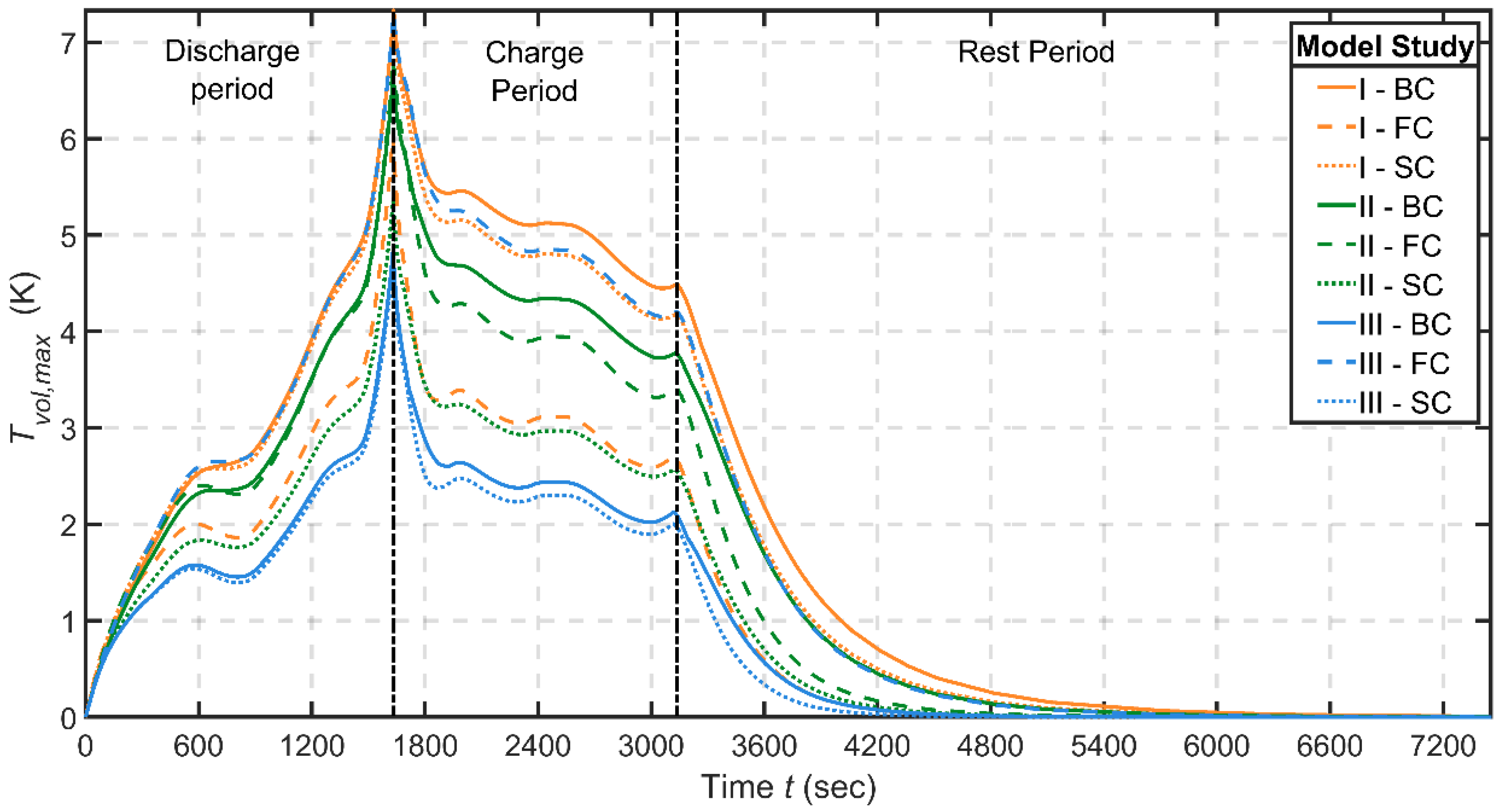
3.3.2. Model Study—BTMS Compatibility under Battery form Factor Variation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Domain/Meaning | Governing Equation | Boundary Condition |
|---|---|---|
| Solid Phase/Electrodes | ||
| Mass Conservation | ||
| Charge Conservation | ||
| Liquid-Phase/Electrolyte | ||
| Mass Conservation | ||
| Charge Conservation | ||
| Reaction Kinetics | ||
| Reaction Rate Pore Wall Flux | ||
| Over-Potential | ||
| Electrode Stack | ||
| Terminal Voltage | ||
| Domain/Meaning | Equation |
|---|---|
| Electrode | |
| Reversible Heat | |
| Irreversible Polarization Heat | |
| Irreversible Ohmic Heat | |
| Separator | |
| Irreversible Ohmic Heat | |
| Terminal/Current Collector | |
| Irreversible Ohmic Heat | |
| Electrode Stack | |
| Total Heat Dissipation | |
- The inactive fraction of the electrodes’ SoC windows is calculated by:
- The actual electrode capacities and are calculated based on the fact that the usable capacity represents the active material loading, while the counterparts in each electrode remain inactive:
- The theoretical electrode capacities are calculated as follows:
- The electrodes’ active material fraction is received by calculating the ratio of the actual electrode capacity of the theoretical electrode capacity:
- The specific surface area is calculated as follows:
- Similarly the actual surface area is calculated as follows:
- The temperature dependence of model variables is considered by applying the Arrhenius relation:where is the variable, is the variables value at the reference temperature , is the activation energy, is the universal gas constant and is the temperature variable.
- Each electrode’s exchange current density is defined as temperature-dependent with respect to [56]:
- Each electrode’s diffusion coefficient is dependent upon the electrodes SoC and temperature. Therefore, the following equations are defined with respect to [56]:whereand
- The electrolyte diffusion coefficient is defined as follows, as is taken from Nyman et al. [81]:where
- The transference number is defined as follows, as taken from Nyman et al. [81]:
- The effective thermodynamic activity coefficient is defined as follows, as taken from [81]:
- The effective electrode conductivity is defined as follows:
- The effective diffusional electrolyte conductivity is defined as follows:
| Meaning | Symbol | Unit | Negative Electrode | Separator | Positive Electrode | Reference |
|---|---|---|---|---|---|---|
| Design Specifications | ||||||
| Domain Thickness | L | 47.5 | 24.7 | 54.5 | [47] | |
| Electrode Plate Area | A | 2.1024 | [47] | |||
| Particle Radius | 9.89 | 1.72 | [47] | |||
| Actual Capacity | 48.17 | 69.20 | (A2) | |||
| Active Electrode Volume | 99.86 | 114.58 | [47] | |||
| Molar Mass | ( | 72.0 | 96.5 | [56] | ||
| Density | 2260 [83] | 4670 [84] | [56] | |||
| Theoretical Capacity | 84.01 | 148.61 | (A3) | |||
| Lower Electrode SoC | 0.01 | 0.415 | [47] | |||
| Upper Electrode SoC | 0.785 | 0.955 | [47] | |||
| Active Material Fraction | 0.548 | 0.457 | (A4) | |||
| Specific Surface Area | 172,730 | 825880 | (A5) | |||
| Surface Area | 17.25 | 94.63 | (A6) | |||
| Electrolyte Volume Fraction | 0.308 | 0.395 [56] | 0.191 | [47,56] | ||
| Inactive Volume Fraction | 0.189 | 0.45 | (A1) | |||
| Kinetic and Transport Properties | ||||||
| Open-Circuit Potential | U | Taken from [47] | Taken from [56] | [47,56] | ||
| Temperature derivative of Open-Circuit Potential | Taken from [27] | [26] | [26,27] | |||
| Charge Transfer Symmetry Factor | 0.5 | 0.5 | [53] | |||
| Maximum Lithium Intercalation Concentration | 31389 | 48396 | [56] | |||
| Equilibrium Electrolyte Concentration | 1000 | [56] | ||||
| Effective Electrode Diffusion Coefficient | (A9) | (A9) | [56] | |||
| Reference Electrode Diffusion Coefficient | (A10) | (A11) | [56] | |||
| Effective Electrode Electronic Conductivity | (A18) | (A18) | [56] | |||
| Reference Electrode Electronic Conductivity | 100 | 10 | [56] | |||
| Effective Electrolyte Conductivity | (A16) | [81] | ||||
| Reference Electrolyte Conductivity | (A17) | [81] | ||||
| Bruggeman Exponent | 1.5 | 1.5 | 1.5 | [85] | ||
| Effective Diffusional Electrolyte conductivity | (A19) | [60] | ||||
| Effective Electrolyte Diffusion Coefficient | (A12) | [81,82] | ||||
| Reference Electrolyte Diffusion Coefficient | (A13) | [81] | ||||
| Li-transference Number | (A14) | [81] | ||||
| Effective Electrolyte Activity coefficient | (A15) | [81,82] | ||||
| Reaction Rate Coefficient | [47] | |||||
| Double Layer Capacitance | 5.18 | 0.96 | [47] | |||
| Ohmic Resistance | 1.24 | [47] | ||||
| Exchange Current Density Activation Energy | 48.9 | 78.1 | [56] | |||
| Electrode Diffusion Activation Energy | 28.8 | 49.6 | [56] | |||
| Electrolyte Diffusion Activation Energy | 16.5 | [82] | ||||
| Electrolyte Conductivity Activation Energy | 4.0 | [82] | ||||
| Electrolyte Activity Coefficient | −1.0 | [82] | ||||
References
- Arora, S. Selection of thermal management system for modular battery packs of electric vehicles: A review of existing and emerging technologies. J. Power Sources 2018, 400, 621–640. [Google Scholar] [CrossRef]
- Khan, M.; Swierczynski, M.; Kær, S. Towards an ultimate battery thermal management system: A review. Batteries 2017, 3, 9. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, S.; Liu, J.; Gu, J. A review of thermal performance improving methods of lithium ion battery: Electrode modification and thermal management system. J. Power Sources 2015, 299, 557–577. [Google Scholar] [CrossRef]
- Waldmann, T.; Wilka, M.; Kasper, M.; Fleischhammer, M.; Wohlfahrt-Mehrens, M. Temperature dependent ageing mechanisms in Lithium-ion batteries—A Post-Mortem study. J. Power Sources 2014, 262, 129–135. [Google Scholar] [CrossRef]
- Barré, A.; Deguilhem, B.; Grolleau, S.; Gérard, M.; Suard, F.; Riu, D. A review on lithium-ion battery ageing mechanisms and estimations for automotive applications. J. Power Sources 2013, 241, 680–689. [Google Scholar] [CrossRef]
- Ma, S.; Jiang, M.; Tao, P.; Song, C.; Wu, J.; Wang, J.; Deng, T.; Shang, W. Temperature effect and thermal impact in lithium-ion batteries: A review. Prog. Nat. Sci. Mater. Int. 2018, 28, 653–666. [Google Scholar] [CrossRef]
- Smith, K.; Shi, Y.; Wood, E.; Pesaran, A. Advanced automotive battery conference, Detroit, Michigan. In Presentation: Optimizing Battery Usage and Management for Long Life; National Renewable Energy Laboratory: Golden, CO, USA, 2016. [Google Scholar]
- Ye, B.; Rubel, M.; Li, H. Design and optimization of cooling plate for battery module of an electric vehicle. Appl. Sci. 2019, 9, 754. [Google Scholar] [CrossRef]
- Liu, L.; Park, J.; Lin, X.; Sastry, A.M.; Lu, W. A thermal-electrochemical model that gives spatial-dependent growth of solid electrolyte interphase in a Li-ion battery. J. Power Sources 2014, 268, 482–490. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, M. Modeling of SEI layer growth and electrochemical impedance spectroscopy response using a thermal-electrochemical model of Li-ion batteries. ECS Trans. 2014, 61, 43–61. [Google Scholar] [CrossRef]
- Bizeray, A.M.; Zhao, S.; Duncan, S.R.; Howey, D.A. Lithium-ion battery thermal-electrochemical model-based state estimation using orthogonal collocation and a modified extended Kalman filter. J. Power Sources 2015, 296, 400–412. [Google Scholar] [CrossRef]
- Behrou, R.; Maute, K. Numerical modeling of damage evolution phenomenon in solid-state lithium-ion batteries. J. Electrochem. Soc. 2017, 164, 2573–2589. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Mathematical modeling of a lithium ion battery with thermal effects in COMSOL Inc. Multiphysics (MP) software. J. Power Sources 2011, 196, 5985–5989. [Google Scholar] [CrossRef]
- Jalkanen, K.; Aho, T.; Vuorilehto, K. Entropy change effects on the thermal behavior of a LiFePO 4/graphite lithium-ion cell at different states of charge. J. Power Sources 2013, 243, 354–360. [Google Scholar] [CrossRef]
- Capron, O.; Jaguemont, J.; Gopalakrishnan, R.; Van Den Bossche, P.; Omar, N.; Van Mierlo, J. Impact of the temperature in the evaluation of battery performances during long-term cycling—Characterisation and modelling. Appl. Sci. 2018, 8, 1364. [Google Scholar] [CrossRef]
- Liu, C.; Liu, L. Optimal design of Li-ion batteries through multi-physics modeling and multi-objective optimization. J. Electrochem. Soc. 2017, 164, 3254–3264. [Google Scholar] [CrossRef]
- Mei, W.; Chen, H.; Sun, J.; Wang, Q. The effect of electrode design parameters on battery performance and optimization of electrode thickness based on the electrochemical–thermal coupling model. Sustain. Energy Fuels 2019, 3, 148–165. [Google Scholar] [CrossRef]
- Vega-Garita, V.; Ramirez-Elizondo, L.; Bauer, P. Physical integration of a photovoltaic-battery system: A thermal analysis. Appl. Energy 2017, 208, 446–455. [Google Scholar] [CrossRef]
- Keyser, M.; Pesaran, A.; Li, Q.; Santhanagopalan, S.; Smith, K.; Wood, E.; Ahmed, S.; Bloom, I.; Dufek, E.; Shirk, M.; et al. Enabling fast charging—Battery thermal considerations. J. Power Sources 2017, 367, 228–236. [Google Scholar] [CrossRef]
- Rahn, C.D.; Wang, C.Y. Battery Systems Engineering; John Wiley & Sons Ltd.: Chichester, UK, 2013. [Google Scholar]
- Bohn, P.; Liebig, G.; Komsiyska, L.; Wittstock, G. Temperature propagation in prismatic lithium-ion-cells after short term thermal stress. J. Power Sources 2016, 313, 30–36. [Google Scholar] [CrossRef]
- Becker, J.; Nemeth, T.; Wegmann, R.; Sauer, D. Dimensioning and optimization of hybrid Li-ion battery systems for EVs. World Electr. Veh. J. 2018, 9, 19. [Google Scholar] [CrossRef]
- Liu, H.; Wei, Z.; He, W.; Zhao, J. Thermal issues about Li-ion batteries and recent progress in battery thermal management systems: A review. Energy Convers. Manag. 2017, 150, 304–330. [Google Scholar] [CrossRef]
- Schweiger, H.G.; Obeidi, O.; Komesker, O.; Raschke, A.; Schiemann, M.; Zehner, C.; Gehnen, M.; Keller, M.; Birke, P. Comparison of several methods for determining the internal resistance of lithium ion cells. Sensors 2010, 10, 5604–5625. [Google Scholar] [CrossRef] [PubMed]
- Park, M.; Zhang, X.; Chung, M.; Less, G.B.; Sastry, A.M. A review of conduction phenomena in Li-ion batteries. J. Power Sources 2010, 195, 7904–7929. [Google Scholar] [CrossRef]
- Viswanathan, V.V.; Choi, D.; Wang, D.; Xu, W.; Towne, S.; Williford, R.E.; Zhang, J.G.; Liu, J.; Yang, Z. Effect of entropy change of lithium intercalation in cathodes and anodes on Li-ion battery thermal management. J. Power Sources 2010, 195, 3720–3729. [Google Scholar] [CrossRef]
- Thomas, K.E.; Newman, J. Heats of mixing and of entropy in porous insertion electrodes. J. Power Sources 2003, 119, 844–849. [Google Scholar] [CrossRef]
- Bernardi, D.; Newman, J.; Pawlikowski, E. A general energy balance for battery systems. J. Electrochem. Soc. 1985, 132. [Google Scholar] [CrossRef]
- Loges, A.; Herberger, S.; Seegert, P.; Wetzel, T. A study on specific heat capacities of Li-ion cell components and their influence on thermal management. J. Power Sources 2016, 336, 341–350. [Google Scholar] [CrossRef]
- Maleki, H.; Al Hallaj, S.A.H.; Selman, R.; Dinwiddie, R.B.; Wang, H. Thermal properties of lithium-ion battery and components. J. Electrochem. Soc. 1999, 146, 947. [Google Scholar] [CrossRef]
- Maleki, H.; Wang, H.; Porter, W.; Hallmark, J. Li-Ion polymer cells thermal property changes as a function of cycle-life. J. Power Sources 2014, 263, 223–230. [Google Scholar] [CrossRef]
- Werner, D.; Loges, A.; Becker, D.J.; Wetzel, T. Thermal conductivity of Li-ion batteries and their electrode configurations—A novel combination of modelling and experimental approach. J. Power Sources 2017, 364, 72–83. [Google Scholar] [CrossRef]
- Koo, B.; Goli, P.; Sumant, A.V.; Dos Santos Claro, P.C.; Rajh, T.; Johnson, C.S.; Balandin, A.A.; Shevchenko, E.V. Toward lithium ion batteries with enhanced thermal conductivity. ACS Nano 2014, 8, 7202–7207. [Google Scholar] [CrossRef] [PubMed]
- Reimers, J.N. Accurate and efficient treatment of foil currents in a spiral wound Li-ion cell. J. Electrochem. Soc. 2013, 161, 118–127. [Google Scholar] [CrossRef]
- Erhard, S.V.; Osswald, P.J.; Keil, P.; Höffer, E.; Haug, M.; Noel, A.; Wilhelm, J.; Rieger, B.; Schmidt, K.; Kosch, S.; et al. Simulation and measurement of the current density distribution in lithium-ion batteries by a multi-tab cell approach. J. Electrochem. Soc. 2017, 164, 6324–6333. [Google Scholar] [CrossRef]
- Yi, J.; Kim, U.S.; Shin, C.B.; Han, T.; Park, S. Three-dimensional thermal modeling of a lithium-ion battery considering the combined effects of the electrical and thermal contact resistances between current collecting tab and lead wire. J. Electrochem. Soc. 2013, 160, 437–443. [Google Scholar] [CrossRef]
- Hales, A.; Diaz, L.B.; Marzook, M.W.; Zhao, Y.; Patel, Y.; Offer, G. The cell cooling coefficient: A standard to define heat rejection from lithium-ion batteries. J. Electrochem. Soc. 2019, 166, 2383–2395. [Google Scholar] [CrossRef]
- Yu, K.; Yang, X.; Cheng, Y.; Li, C. Thermal analysis and two-directional air flow thermal management for lithium-ion battery pack. J. Power Sources 2014, 270, 193–200. [Google Scholar] [CrossRef]
- Park, H. A design of air flow configuration for cooling lithium ion battery in hybrid electric vehicles. J. Power Sources 2013, 239, 30–36. [Google Scholar] [CrossRef]
- Wang, T.; Tseng, K.J.; Zhao, J. Development of efficient air-cooling strategies for lithium-ion battery module based on empirical heat source model. Appl. Therm. Eng. 2015, 90, 521–529. [Google Scholar] [CrossRef]
- Sun, H.; Dixon, R. Development of a liquid cooled battery module. J. Electrochem. Soc. 2016, 163, 313–321. [Google Scholar] [CrossRef]
- Zhao, C.; Cao, W.; Dong, T.; Jiang, F. Thermal behavior study of discharging/charging cylindrical lithium-ion battery module cooled by channeled liquid flow. Int. J. Heat Mass Transf. 2018, 120, 751–762. [Google Scholar] [CrossRef]
- Tran, T.-H.; Harmand, S.; Desmet, B.; Filangi, S. Experimental investigation on the feasibility of heat pipe cooling for HEV/EV lithium-ion battery. Appl. Therm. Eng. 2014, 63, 551–558. [Google Scholar] [CrossRef]
- Khateeb, S.A.; Amiruddin, S.; Farid, M.; Selman, J.R.; Al-Hallaj, S. Thermal management of Li-ion battery with phase change material for electric scooters: Experimental validation. J. Power Sources 2005, 142, 345–353. [Google Scholar] [CrossRef]
- Somasundaram, K.; Birgersson, E.; Mujumdar, A.S. Thermal–electrochemical model for passive thermal management of a spiral-wound lithium-ion battery. J. Power Sources 2012, 203, 84–96. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, J.; Li, Y.; Liu, Q.; Li, W. Experimental investigation of a lithium battery cooling system. Sustainability 2019, 11, 5020. [Google Scholar] [CrossRef]
- Liebig, G.; Gupta, G.; Kirstein, U.; Schuldt, F.; Agert, C. Parameterization and validation of an electrochemical thermal model of a lithium-ion battery. Batteries 2019, 5, 62. [Google Scholar] [CrossRef]
- Ecker, M.; Tran, T.K.D.; Dechent, P.; Kabitz, S.; Warnecke, A.; Sauer, D.U. Parameterization of a physico-chemical model of a lithium-ion battery: I. Determination of parameters. J. Electrochem. Soc. 2015, 162, A1836–A1848. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Rahe, C.; Ecker, M.; Sauer, D.U. Full cell parameterization of a high-power lithium-ion battery for a physico-chemical model: Part I. Physical and electrochemical parameters. J. Electrochem. Soc. 2018, 165, 3799–3810. [Google Scholar] [CrossRef]
- Dai, H.; Jiang, B.; Wei, X. Impedance characterization and modeling of lithium-ion batteries considering the internal temperature gradient. Energies 2018, 11, 220. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Sauer, D.U. Full cell parameterization of a high-power lithium-ion battery for a physico-chemical model: Part II. Thermal parameters and validation. J. Electrochem. Soc. 2018, 165, 3811–3819. [Google Scholar] [CrossRef]
- Ecker, M.; Kabitz, S.; Laresgoiti, I.; Sauer, D.U. Parameterization of a Physico-chemical model of a lithium-ion battery: II. Model validation. J. Electrochem. Soc. 2015, 162, 1849–1857. [Google Scholar] [CrossRef]
- Erhard, S. Mehrdimensionale Elektrochemisch-Thermische Modellierung Von Lithium-Ionen-Batterien. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2017. [Google Scholar]
- Christen, R.; Rizzo, G.; Gadola, A.; Stöck, M. Test method for thermal characterization of Li-ion cells and verification of cooling concepts. Batteries 2017, 3, 3. [Google Scholar] [CrossRef]
- Wu, B.; Li, Z.; Zhang, J. Thermal design for the pouch-type large-format lithium-ion batteries: I. Thermo-electrical modeling and origins of temperature non-uniformity. J. Electrochem. Soc. 2014, 162, 181–191. [Google Scholar] [CrossRef]
- Schmalstieg, J. Physikalisch-Elektrochemische Simulation Von Lithium-Ionen-Batterien: Implementierung, Parametrierung und Anwendung. Ph.D. Thesis, RWTH Aachen University, Aachener Beiträge des ISEA, Aachen, Germany, 2017. [Google Scholar]
- Ecker, M. Lithium Plating in Lithium-Ion Batteries: An Experimental and Simulation Approach. Ph.D. Thesis, RWTH Aachen University, Aachener Beiträge des ISEA, Aachen, Germany, 2016. [Google Scholar]
- Höhne, G.W.H.; Hemminger, W.F.; Flammersheim, H.J. Theoretical fundamentals of differential scanning calorimeters. In Differential Scanning Calorimetry; Springer: Berlin, Heidelberg, 2003; pp. 31–63. [Google Scholar]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash method of determining thermal diffusivity, heat capacity, and thermal conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Kim, S.U.; Albertus, P.; Cook, D.; Monroe, C.W.; Christensen, J. Thermoelectrochemical simulations of performance and abuse in 50-Ah automotive cells. J. Power Sources 2014, 268, 625–633. [Google Scholar] [CrossRef]
- Pals, C.R.; Newman, J. Thermal modeling of the lithium/polymer battery, I. Discharge behavior of a single cell. J. Electrochem. Soc. 1995, 10, 3274–3281. [Google Scholar] [CrossRef]
- Zhang, G.; Cao, L.; Ge, S.; Wang, C.Y.; Shaffer, C.E.; Rahn, C.D. In situ measurement of radial temperature distributions in cylindrical Li-ion cells. J. Electrochem. Soc. 2014, 161, 1499–1507. [Google Scholar] [CrossRef]
- Pop, I.; Ingham, D.B. Chapter 2—Mixed convection boundary-layer flow along a vertical flat plate. In Convective Heat Transfer; Pop, I., Ingham, D.B., Eds.; Pergamon: Oxford, UK, 2001; pp. 45–85. [Google Scholar]
- Kim, G.H.; Smith, K.; Lee, K.J.; Santhanagopalan, S.; Pesaran, A. Multi-domain modeling of lithium-ion batteries encompassing multi-physics in varied length scales. J. Electrochem. Soc. 2011, 158, 955. [Google Scholar] [CrossRef]
- Lundgren, H.; Svens, P.; Ekström, H.; Tengstedt, C.; Lindström, J.; Behm, M.; Lindbergh, G. Thermal management of large-format prismatic lithium-ion battery in PHEV application. J. Electrochem. Soc. 2015, 163, 309–317. [Google Scholar] [CrossRef]
- Optris GmbH. Basic Principles of Non-Contact Temperature Measurement. Available online: https://www.optris.de/lexikon?file=tl_files/pdf/Downloads/Zubehoer/IR-Grundlagen.pdf (accessed on 3 July 2019).
- Zhang, J.; Wu, B.; Li, Z.; Huang, J. Simultaneous estimation of thermal parameters for large-format laminated lithium-ion batteries. J. Power Sources 2014, 259, 106–116. [Google Scholar] [CrossRef]
- Touloukian, Y.S.; Liley, P.E.; Saxena, S.C. Thermophysical Properties of Matter—The TPRC Data Series. Volume 3. Thermal Conductivity—Nonmetallic Liquids and Gases. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a951937.pdf (accessed on 30 December 2019).
- Brainard, A.J.; Keenan, J.H.; Chao, J.; Kaye, J. Gas tables: International version second edition (SI units). AIChE J. 1984, 30, 172. [Google Scholar] [CrossRef]
- Klein, S.A.; Alvarado, F.L. Table Properties of Air at 1 Atm Pressure. Available online: https://www.me.psu.edu/cimbala/me433/Links/Table_A_9_CC_Properties_of_Air.pdf (accessed on 16 October 2019).
- Lee, K.J.; Smith, K.; Pesaran, A.; Kim, G.H. Three dimensional thermal-, electrical-, and electrochemical-coupled model for cylindrical wound large format lithium-ion batteries. J. Power Sources 2013, 241, 20–32. [Google Scholar] [CrossRef]
- Bazinski, S.J.; Wang, X. Experimental study on the influence of temperature and state-of-charge on the thermophysical properties of an LFP pouch cell. J. Power Sources 2015, 293, 283–291. [Google Scholar] [CrossRef]
- Sarge, S.M.; Poeßnecker, W. The influence of heat resistances and heat transfers on the uncertainty of heat-capacity measurements by means of differential scanning calorimetry (DSC). Thermochim. Acta 1999, 329, 17–21. [Google Scholar] [CrossRef]
- Vertiz, G.; Oyarbide, M.; Macicior, H.; Miguel, O.; Cantero, I.; Fernandez De Arroiabe, P.; Ulacia, I. Thermal characterization of large size lithium-ion pouch cell based on 1d electro-thermal model. J. Power Sources 2014, 272, 476–484. [Google Scholar] [CrossRef]
- Loges, A.; Herberger, S.; Werner, D.; Wetzel, T. Thermal characterization of Li-ion cell electrodes by photothermal deflection spectroscopy. J. Power Sources 2016, 325, 104–115. [Google Scholar] [CrossRef]
- Jarrett, A.; Kim, I.Y. Influence of operating conditions on the optimum design of electric vehicle battery cooling plates. J. Power Sources 2014, 245, 644–655. [Google Scholar] [CrossRef]
- Uddin, K.; Perera, S.; Widanage, W.; Somerville, L.; Marco, J. Characterising lithium-ion battery degradation through the identification and tracking of electrochemical battery model parameters. Batteries 2016, 2, 13. [Google Scholar] [CrossRef]
- Dao, T.S.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- Hadigol, M.; Maute, K.; Doostan, A. On uncertainty quantification of lithium-ion batteries: Application to an LiC6/LiCoO2 cell. J. Power Sources 2015, 300, 507–524. [Google Scholar] [CrossRef]
- Liu, G.; Ouyang, M.; Lu, L.; Li, J.; Han, X. Analysis of the heat generation of lithium-ion battery during charging and discharging considering different influencing factors. J. Therm. Anal. Calorim. 2014, 116, 1001–1010. [Google Scholar] [CrossRef]
- Nyman, A.; Behm, M.; Lindbergh, G. Electrochemical characterisation and modelling of the mass transport phenomena in LiPF6–EC–EMC electrolyte. Electrochim. Acta 2008, 53, 6356–6365. [Google Scholar] [CrossRef]
- Zavalis, T.G.; Behm, M.; Lindbergh, G. Investigation of short-circuit scenarios in a lithium-ion battery cell. J. Electrochem. Soc. 2012, 159, 848–859. [Google Scholar] [CrossRef]
- Pierson, H.O. Handbook of Carbon, Graphite, Diamonds and Fullerenes—Processing, Properties and Applications; Noyes Publications: Park Ridge, NJ, USA, 1993. [Google Scholar]
- Villars, P.; Cenzual, K. Li[Ni1/3Co1/3Mn1/3]O2 Crystal Structure: Datasheet from “PAULING FILE Multinaries Edition—2012”. Available online: https://materials.springer.com/isp/crystallographic/docs/sd_1125611 (accessed on 5 September 2019).
- Von Srbik, M.T.; Marinescu, M.; Martinez-Botas, R.F.; Offer, G.J. A physically meaningful equivalent circuit network model of a lithium-ion battery accounting for local electrochemical and thermal behaviour, variable double layer capacitance and degradation. J. Power Sources 2016, 325, 171–184. [Google Scholar] [CrossRef]
| Material/Meaning | |||||
|---|---|---|---|---|---|
| Electrode Stack | |||||
| Positive Electrode Coating | 29.29 | 4670 [56] | 940.00 | 0.150 | 0.66 |
| Negative Electrode Coating | 25.53 | 2260 [56] | 1040.00 | 0.615 | 1.45 |
| Separator | 12.90 | 1009.00 | 1907.00 | 0.352 | 0.68 |
| Aluminum [21] | 4.03 *1 | 2700.0. | 900.00 | 84.00 | 238 |
| 0.26 *2 | |||||
| Copper [21] | 5.37 *1 | 8700.00 | 385.00 | 111.00 | 400 |
| 0.26*2 | |||||
| Battery | |||||
| Electrode Stack | 77.12 | 2650.98 | 987.55 | 11.095 *3 | 29.50 *3 |
| 0.234 *4 | 0.62 *4 | ||||
| Steel [60] | 13.00 | 8030.00 | 502.48 | 4.03 | 16.27 |
| Synthetic [65] (Acrylic Plastic) | 9.36 | 1190.00 | 1470.00 | 0.10 | 0.18 |
| Environment | |||||
| Air [68,69,70] | - | 1.184 | 1007 | 21.14 | 0.026 |
| Significantly Better *2 | Better | Reference | Worse | Significantly Worse *3 |
|---|---|---|---|---|
| Study Type | Model Parameter | |||||
|---|---|---|---|---|---|---|
| Natural Convection | 1.8 | 0.9 | 0.1 | 0.2 | >60:00 | |
| 3.0 | 0.7 | 0.3 | 0.3 | >60:00 | ||
| 4.5 | 2.5 | 0.3 | 0.7 | >60:00 | ||
| 6.2 | 1.9 | 0.8 | 0.8 | >60:00 | ||
| 9.8 | 5.4 | 0.8 | 2.2 | >60:00 | ||
| 12.2 | 4.4 | 1.7 | 2.0 | >60:00 | ||
| Forced Convection | 10.0 | 6.3 | 3.4 | 4.7 | >60:00 | |
| 8.3 | 4.2 | 3.7 | 5.9 | >60:00 | ||
| 7.2 | 2.9 | 4.2 | 7.2 | 26:44 | ||
| Conduction– Face – | 6.1 | 1.8 | 5.4 | 8.8 | 16:20 | |
| 6.8 | 2.4 | 6.1 | 10.7 | 21:00 | ||
| 7.3 | 3.0 | 6.6 | 12.6 | 30:20 | ||
| Conduction– Side – | 7.3 | 3.1 | 6.4 | 11.9 | 31:17 | |
| 5.4 | 2.1 | 4.4 | 7.8 | 18:12 | ||
| 4.7 | 1.6 | 3.8 | 6.1 | 12:45 | ||
| Conduction– Bottom – | 7.3 | 3.1 | 6.4 | 12.4 | 39:09 | |
| 6.7 | 2.6 | 5.8 | 11.1 | 31:09 | ||
| 4.8 | 1.7 | 3.9 | 6.6 | 16:29 | ||
| Isolation | 14.7 | 5.7 | 1.5 | 1.7 | / | |
| 15.0 | 5.8 | 1.6 | 1.9 | / | ||
| 14.4 | 5.5 | 1.4 | 1.7 | / |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liebig, G.; Kirstein, U.; Geißendörfer, S.; Zahid, O.; Schuldt, F.; Agert, C. The Impact of Environmental Factors on the Thermal Characteristic of a Lithium–ion Battery. Batteries 2020, 6, 3. https://doi.org/10.3390/batteries6010003
Liebig G, Kirstein U, Geißendörfer S, Zahid O, Schuldt F, Agert C. The Impact of Environmental Factors on the Thermal Characteristic of a Lithium–ion Battery. Batteries. 2020; 6(1):3. https://doi.org/10.3390/batteries6010003
Chicago/Turabian StyleLiebig, Gerd, Ulf Kirstein, Stefan Geißendörfer, Omio Zahid, Frank Schuldt, and Carsten Agert. 2020. "The Impact of Environmental Factors on the Thermal Characteristic of a Lithium–ion Battery" Batteries 6, no. 1: 3. https://doi.org/10.3390/batteries6010003
APA StyleLiebig, G., Kirstein, U., Geißendörfer, S., Zahid, O., Schuldt, F., & Agert, C. (2020). The Impact of Environmental Factors on the Thermal Characteristic of a Lithium–ion Battery. Batteries, 6(1), 3. https://doi.org/10.3390/batteries6010003






