Properties of Ion Complexes and Their Impact on Charge Transport in Organic Solvent-Based Electrolyte Solutions for Lithium Batteries: Insights from a Theoretical Perspective
Abstract
1. Introduction
- Which factors determine ion–ion interactions, and how do the corresponding effects modify charge transport?
- Which properties of solvents are appropriate discriminators in order to distinguish between good and poor solvents, and which solvents are well-suited to increase the performance of electrochemical cells in terms of high salt solubility and beneficial charge transport behavior?
- How does the presence of co-solvents or additives affect the solvation of ions, and which conclusions can be drawn for the solubility of salts?
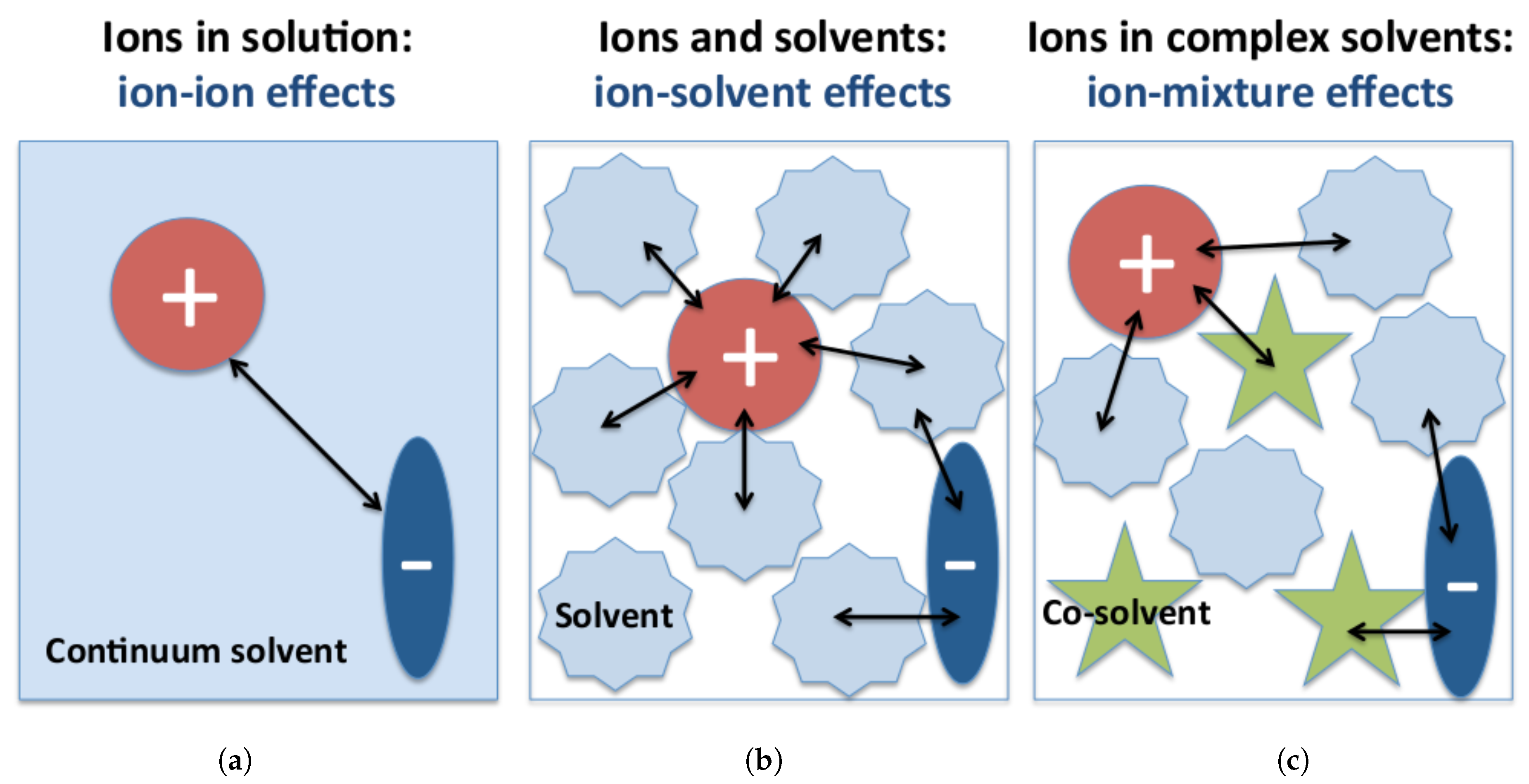
2. Ions in Solution: Correlation Effects and Their Influence on Charge Transport
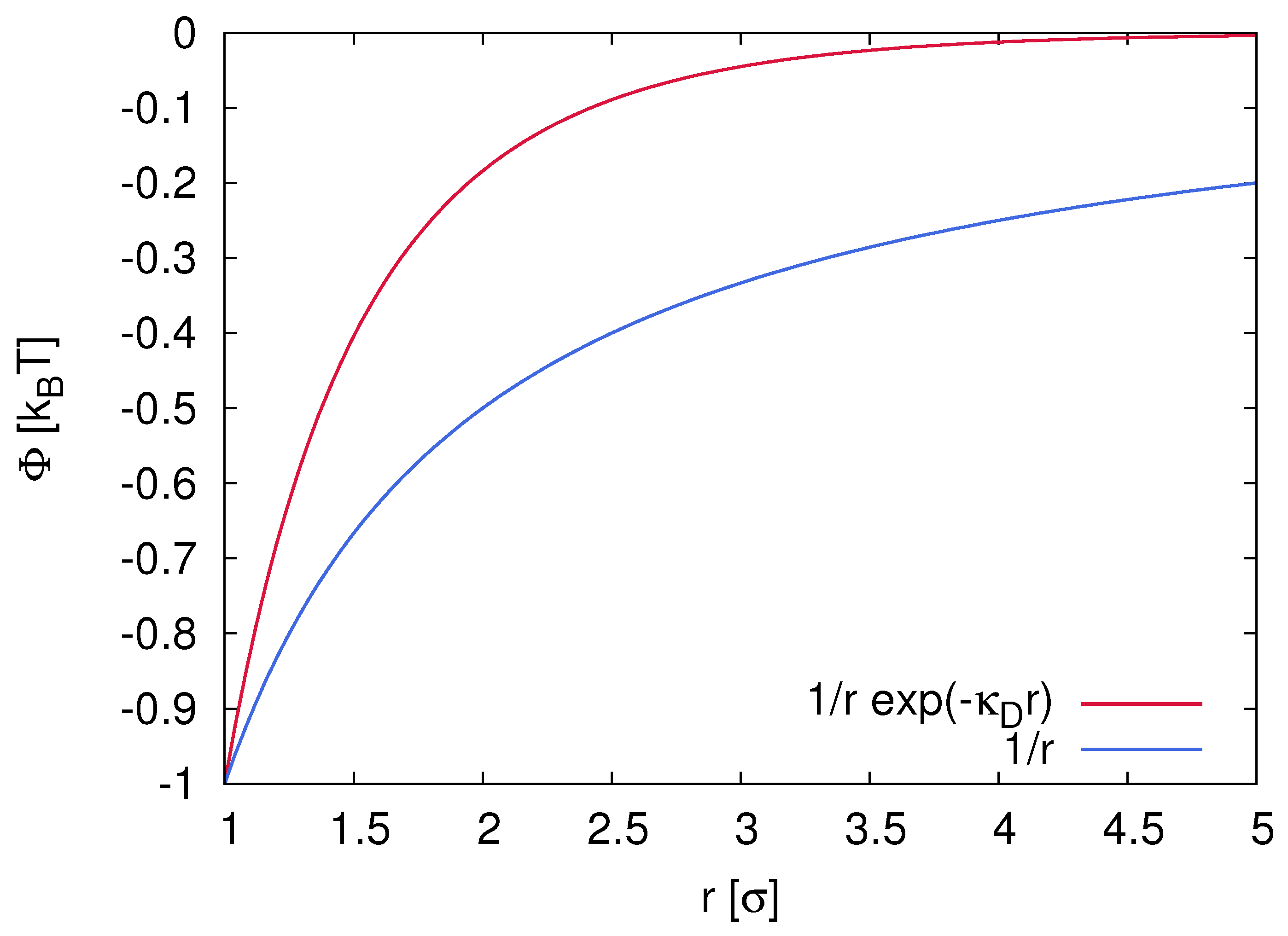
2.1. Electrostatic Interactions and Properties of Ion Complexes
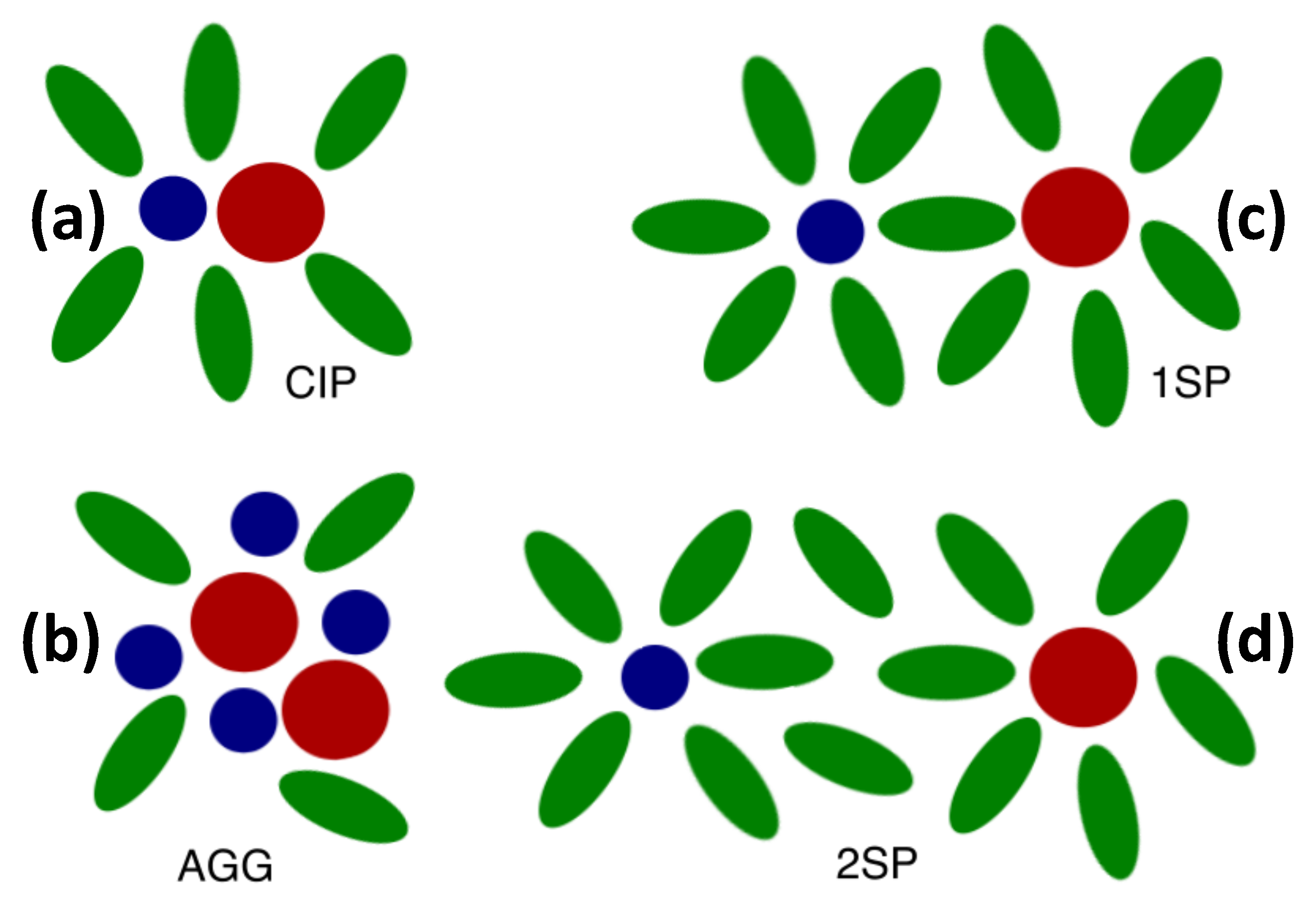
2.2. Distinct States of Ion Complexes
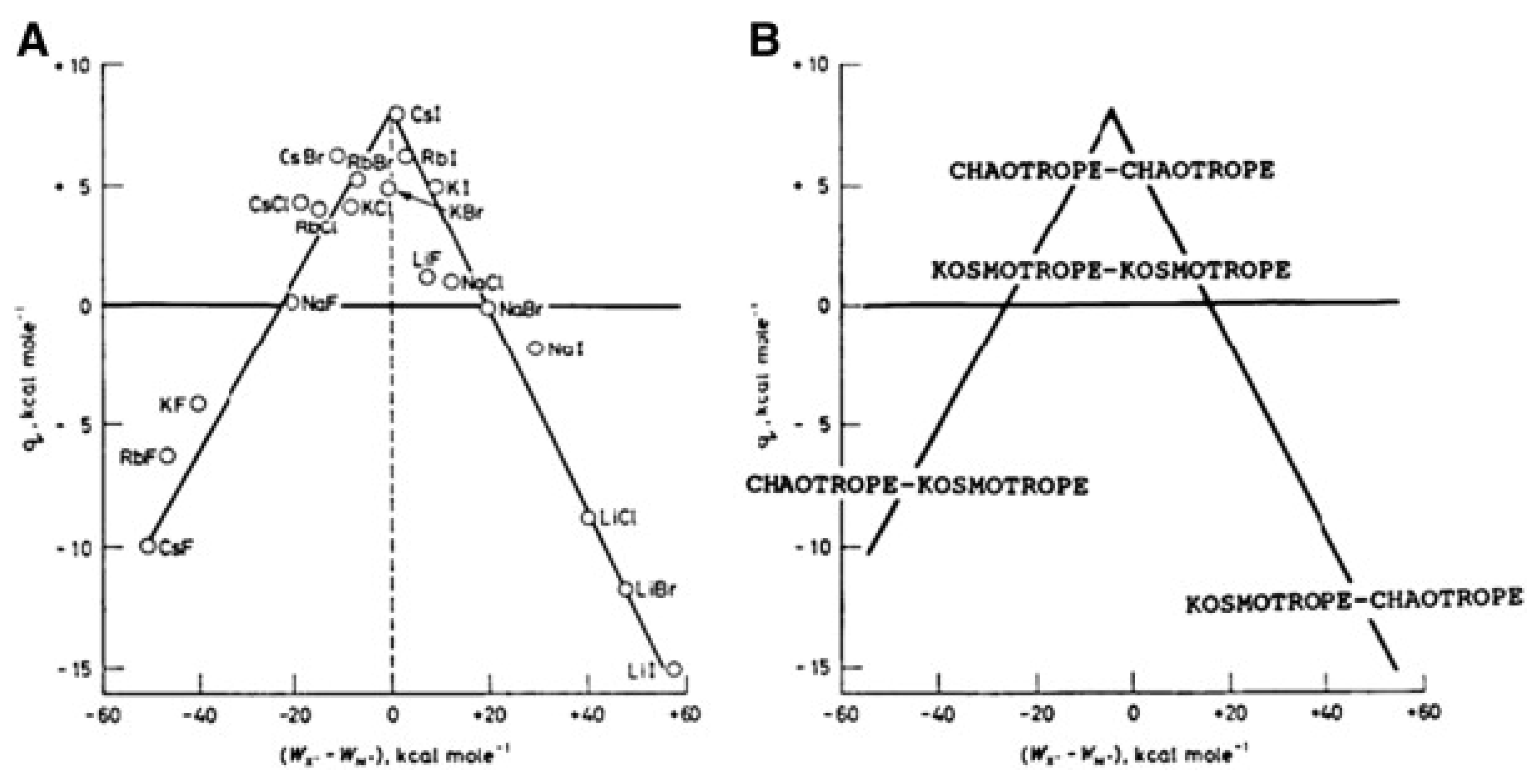
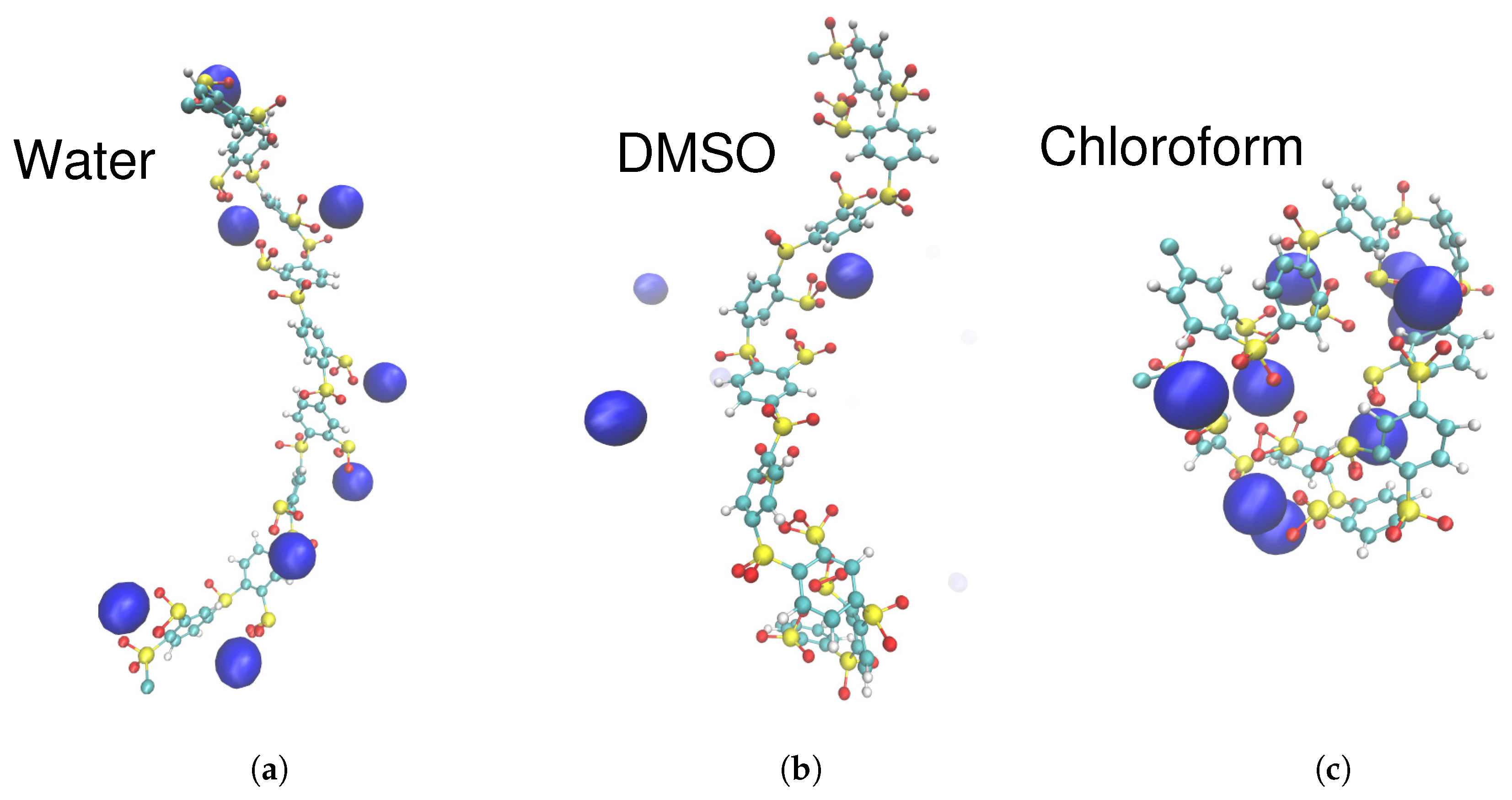
2.3. Specific Ion Effects
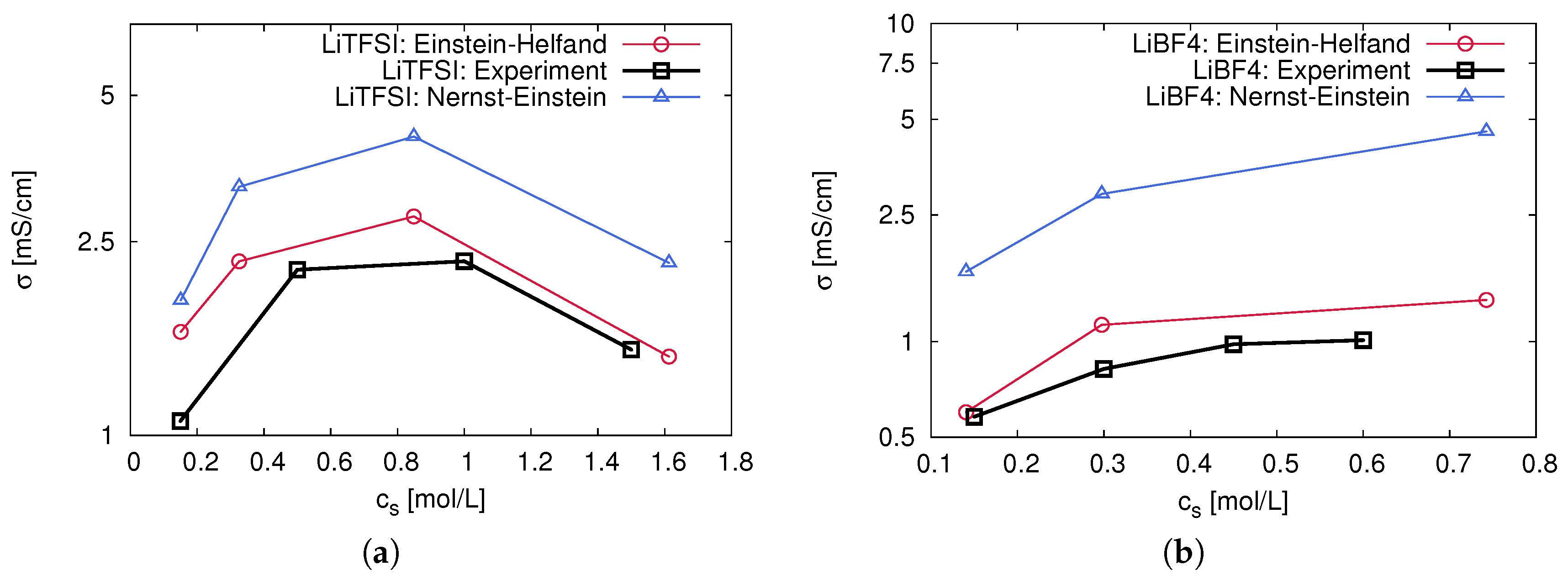
2.4. Ion Correlation Effects and Transport Behavior
3. Solvent–Ion Interactions at the Molecular Scale
3.1. Dielectric Decrement Effects
3.2. Molecular Properties of the Solvent: Donor/Acceptor Numbers and Chemical Hardnesses
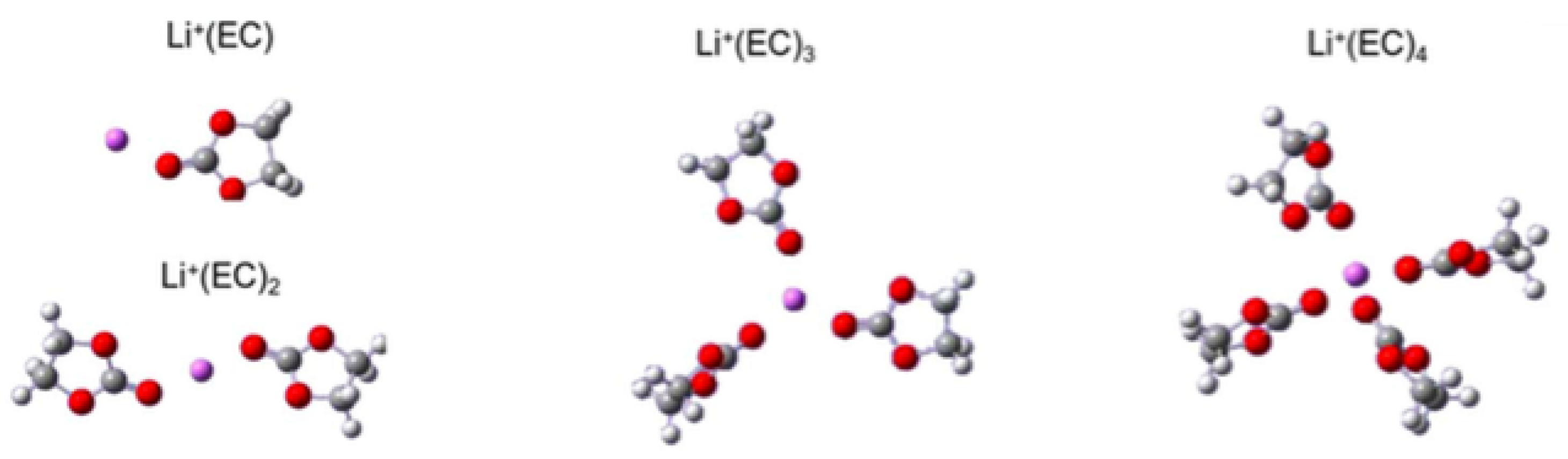
3.3. Solvation of Ions: Benefits of Computational Approaches
4. Ions in Multicomponent Solutions: Influence of Co-Solvent and Additive Molecules on the Properties of Ion Complexes
4.1. Molecular Theories of Solution: Co-Solvent–Ion Interactions
4.2. Ion Complexes in Presence of Co-Solvent Molecules: Influence on the Ion Dissociation Equilibrium
4.3. Chemical Equilibrium Constant and Binding Behavior of Co-Solvent Molecules
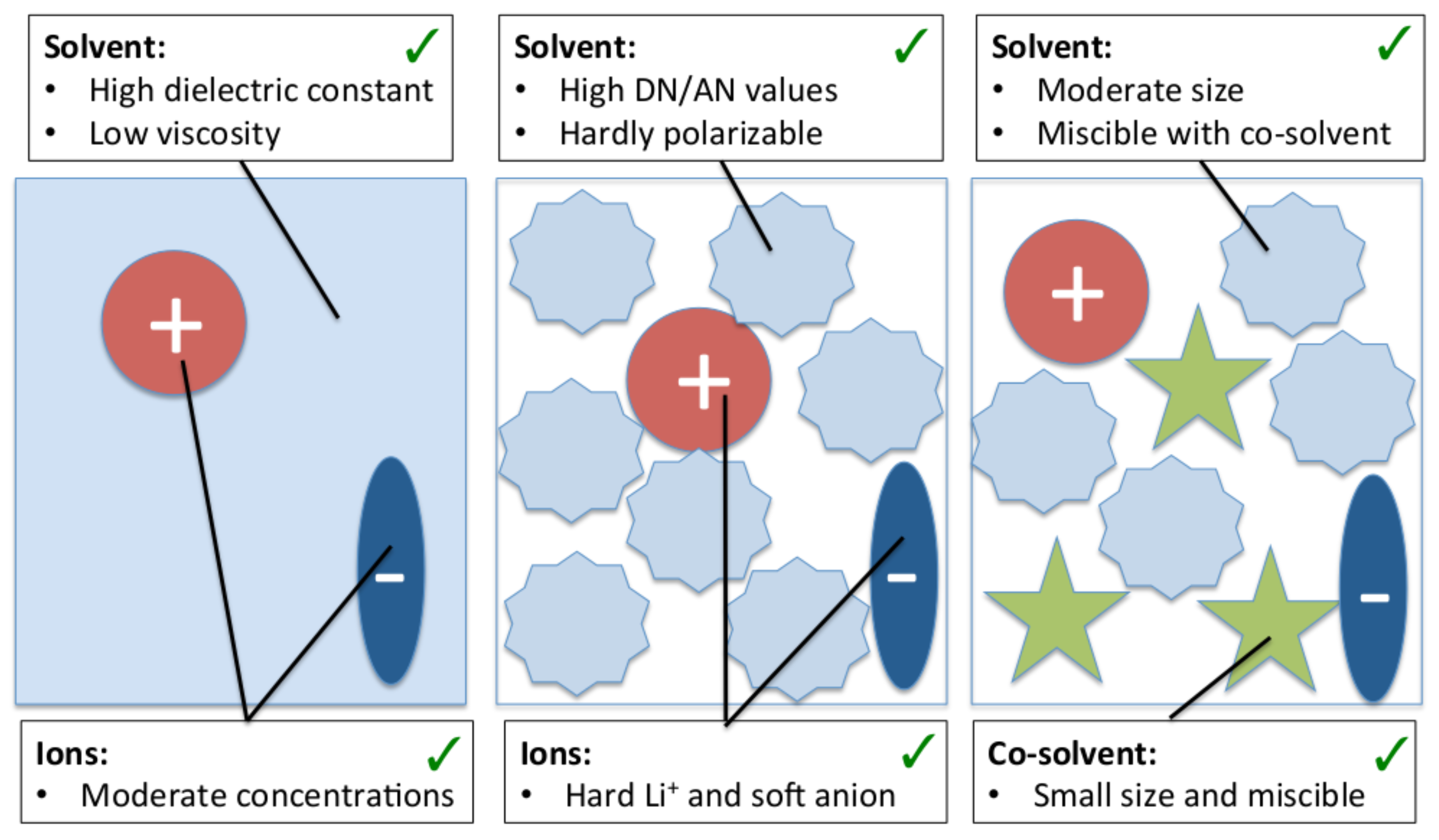
4.4. Beneficial Properties of Co-Solvent Molecules
4.5. Solubility of Salts in Presence of Co-Solvent Molecules
5. Remarks and Future Perspectives
6. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbol | Meaning |
| Dielectric constant | |
| Vacuum permittivity | |
| Electrostatic Coulomb potential | |
| Salt concentration | |
| T | Temperature |
| r | Distance |
| Valency of ionic species j | |
| e | electron charge |
| Boltzmann constant | |
| Hydrodynamic boundary position | |
| Maximum electrostatic potential at | |
| Ion number density of species j in bulk phase | |
| total ion number density in bulk phase | |
| Debye–Hückel length | |
| Radius of solute | |
| Bjerrum length | |
| CIP | Contact ion pair |
| 1SP | Solvent-shared ion pair |
| 2SP | Solvent-separated ion pair |
| AGG | Ion aggregate |
| B | Jones–Dole viscosity coefficient |
| Cation hydration enthalpy | |
| Anion hydration enthalpy | |
| Difference between cation and anion hydration enthalpy | |
| Standard heat of solution of a crystalline salt in infinite dilution | |
| Ideal (Nernst–Einstein) ionic conductivity | |
| Effective (Einstein–Helfand) ionic conductivity | |
| Self-diffusion coefficient for cations | |
| Self-diffusion coefficient for anions | |
| Mutual diffusion coefficient for cations | |
| Mutual diffusion coefficient for anions | |
| Cross-correlated diffusion coefficient between cations | |
| Cross-correlated diffusion coefficient between anions | |
| Symmetric cross-correlated diffusion coefficient between cations and anions | |
| Dynamic correlation factor | |
| Cation transference number | |
| Cation transport number | |
| Shear viscosity | |
| Onsager prefactor | |
| V | Volume |
| Excess volume | |
| Partial molar volume | |
| Total translational dipole moment | |
| Modified dielectric constant as influenced by dielectric decrement effect | |
| Electrostatic field | |
| Dielectric coupling constant | |
| DN | Donor number |
| AN | Acceptor number |
| Experimental softness parameter | |
| NMR chemical shift value | |
| Diamagnetic susceptibility | |
| Kamlet–Taft number | |
| Electronegativity | |
| E | Energy |
| Energy of highest occupied molecular orbital (HOMO) | |
| Energy of lowest unoccupied molecular orbital (LUMO) | |
| Solvation enthalpy (binding energy) | |
| Desolvation enthalpy | |
| n | Number of electrons |
| Chemical hardness | |
| S | Chemical softness |
| G | Free energy |
| Transfer free energy | |
| Solvation free energy | |
| ZPE | Zero point energy |
| p | Pressure |
| R | Universal gas constant |
| Molecular partition function with zero ground state energy | |
| K | Chemical equilibrium constant |
| Chemical potential | |
| Standard chemical potential | |
| Pseudo-chemical potential | |
| Stoichiometric coefficient | |
| Chemical activity | |
| Chemical activity coefficient | |
| m | m-value |
| Apparent chemical equilibrium constant | |
| Modified chemical equilibrium constant in presence of co-solvent | |
| Preferential binding coefficient | |
| Excess coordination number | |
| Radial distribution function | |
| Kirkwood–Buff integral | |
| Derivative of the chemical activity | |
| Thermal de-Broglie wavelength | |
| Maximum saturation density | |
| Maximum salt solubility |
References
- Xu, K. Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries. Chem. Rev. 2004, 104, 4303–4417. [Google Scholar] [CrossRef] [PubMed]
- Winter, M.; Brodd, R.J. What are batteries, fuel cells, and supercapacitors? Chem. Rev. 2004, 104, 4245–4269. [Google Scholar] [CrossRef] [PubMed]
- Xu, K. Electrolytes and Interphases in Li-Ion Batteries and Beyond. Chem. Rev. 2014, 114, 11503–11618. [Google Scholar] [CrossRef] [PubMed]
- Balducci, A. Ionic Liquids in Lithium-Ion Batteries. Top. Curr. Chem. 2017, 375, 20. [Google Scholar] [CrossRef] [PubMed]
- Goodeneough, J.B.; Park, K.S. The Li-Ion Rechargeable Battery: A Perspective. J. Am. Chem. Soc. 2013, 135, 1167–1176. [Google Scholar] [CrossRef] [PubMed]
- Cekic-Laskovic, I.; von Aspern, N.; Imholt, L.; Kaymaksiz, S.; Oldiges, K.; Rad, B.R.; Winter, M. Synergistic Effect of Blended Components in Nonaqueous Electrolytes for Lithium Ion Batteries. Top. Curr. Chem. 2017, 375, 37. [Google Scholar] [CrossRef] [PubMed]
- Deng, D. Li-ion batteries: Basics, progress, and challenges. Energy Sci. Eng. 2015, 3, 385–418. [Google Scholar] [CrossRef]
- Yamada, Y.; Yamada, A. Superconcentrated electrolytes for lithium batteries. J. Electrochem. Soc. 2015, 162, A2406–A2423. [Google Scholar] [CrossRef]
- Diederichsen, K.M.; McShane, E.J.; McCloskey, B.D. The Most Promising Routes to a High Li+ Transference Number Electrolyte for Lithium Ion Batteries. ACS Energy Lett. 2017, 2, 2563–2575. [Google Scholar] [CrossRef]
- Ponrouch, A.; Monti, D.; Boschin, A.; Steen, B.; Johansson, P.; Palacin, M. Non-aqueous electrolytes for sodium-ion batteries. J. Mater. Chem. A 2015, 3, 22–42. [Google Scholar] [CrossRef]
- Schmuch, R.; Wagner, R.; Hörpel, G.; Placke, T.; Winter, M. Performance and cost of materials for lithium-based rechargeable automotive batteries. Nat. Energy 2018, 3, 267. [Google Scholar] [CrossRef]
- Placke, T.; Kloepsch, R.; Dühnen, S.; Winter, M. Lithium ion, lithium metal, and alternative rechargeable battery technologies: The odyssey for high energy density. J. Solid State Electrochem. 2017, 21, 1939–1964. [Google Scholar] [CrossRef]
- Meister, P.; Jia, H.; Li, J.; Kloepsch, R.; Winter, M.; Placke, T. Best practice: Performance and cost evaluation of lithium ion battery active materials with special emphasis on energy efficiency. Chem. Mater. 2016, 28, 7203–7217. [Google Scholar] [CrossRef]
- Wagner, R.; Preschitschek, N.; Passerini, S.; Leker, J.; Winter, M. Current research trends and prospects among the various materials and designs used in lithium-based batteries. J. Appl. Electrochem. 2013, 43, 481–496. [Google Scholar] [CrossRef]
- Zhang, S.S. A review on electrolyte additives for lithium-ion batteries. J. Power Sources 2006, 162, 1379–1394. [Google Scholar] [CrossRef]
- Winter, M. The solid electrolyte interphase—The most important and the least understood solid electrolyte in rechargeable Li batteries. Z. Phys. Chem. 2009, 223, 1395–1406. [Google Scholar] [CrossRef]
- Wang, J.; Wang, W.; Kollman, P.A.; Case, D.A. Automatic atom type and bond type perception in molecular mechanical calculations. J. Mol. Graph. Model. 2006, 25, 247–260. [Google Scholar] [CrossRef]
- Schmitz, R.W.; Murmann, P.; Schmitz, R.; Müller, R.; Krämer, L.; Kasnatscheew, J.; Isken, P.; Niehoff, P.; Nowak, S.; Röschenthaler, G.V.; et al. Investigations on novel electrolytes, solvents and SEI additives for use in lithium-ion batteries: Systematic electrochemical characterization and detailed analysis by spectroscopic methods. Prog. Solid State Chem. 2014, 42, 65–84. [Google Scholar] [CrossRef]
- Wrodnigg, G.H.; Besenhard, J.O.; Winter, M. Cyclic and acyclic sulfites: New solvents and electrolyte additives for lithium ion batteries with graphitic anodes? J. Power Sources 2001, 97, 592–594. [Google Scholar] [CrossRef]
- Besenhard, J.O.; Von Werner, K.; Winter, M. Fluorine-Containing Solvents for Lithium Batteries Having Increased Safety. U.S. Patent 5,916,708, 29 June 1999. [Google Scholar]
- Isken, P.; Dippel, C.; Schmitz, R.; Schmitz, R.; Kunze, M.; Passerini, S.; Winter, M.; Lex-Balducci, A. High flash point electrolyte for use in lithium-ion batteries. Electrochim. Acta 2011, 56, 7530–7535. [Google Scholar] [CrossRef]
- Placke, T.; Fromm, O.; Lux, S.F.; Bieker, P.; Rothermel, S.; Meyer, H.W.; Passerini, S.; Winter, M. Reversible intercalation of bis (trifluoromethanesulfonyl) imide anions from an ionic liquid electrolyte into graphite for high performance dual-ion cells. J. Electrochem. Soc. 2012, 159, A1755–A1765. [Google Scholar] [CrossRef]
- Placke, T.; Bieker, P.; Lux, S.F.; Fromm, O.; Meyer, H.W.; Passerini, S.; Winter, M. Dual-ion cells based on anion intercalation into graphite from ionic liquid-based electrolytes. Z. Phys. Chem. 2012, 226, 391–407. [Google Scholar] [CrossRef]
- Schmuelling, G.; Placke, T.; Kloepsch, R.; Fromm, O.; Meyer, H.W.; Passerini, S.; Winter, M. X-ray diffraction studies of the electrochemical intercalation of bis (trifluoromethanesulfonyl) imide anions into graphite forádual-ion cells. J. Power Sources 2013, 239, 563–571. [Google Scholar] [CrossRef]
- Rothermel, S.; Meister, P.; Schmuelling, G.; Fromm, O.; Meyer, H.W.; Nowak, S.; Winter, M.; Placke, T. Dual-graphite cells based on the reversible intercalation of bis (trifluoromethanesulfonyl) imide anions from an ionic liquid electrolyte. Energy Environ. Sci. 2014, 7, 3412–3423. [Google Scholar] [CrossRef]
- Suo, L.; Borodin, O.; Gao, T.; Olguin, M.; Ho, J.; Fan, X.; Luo, C.; Wang, C.; Xu, K. “Water-in-salt” electrolyte enables high-voltage aqueous lithium-ion chemistries. Science 2015, 350, 938–943. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhao, D.; Wang, P.; Cui, X.; Tang, F. Electrochemical effect and mechanism of adiponitrile additive for high-voltage electrolyte. Electrochim. Acta 2016, 222, 668–677. [Google Scholar] [CrossRef]
- Ehteshami, N.; Paillard, E. Ethylene Carbonate-Free, Adiponitrile-Based Electrolytes Compatible with Graphite Anodes. ECS Trans. 2017, 77, 11–20. [Google Scholar] [CrossRef]
- Farhat, D.; Ghamouss, F.; Maibach, J.; Edström, K.; Lemordant, D. Adiponitrile–Lithium Bis (trimethylsulfonyl) imide Solutions as Alkyl Carbonate-free Electrolytes for Li4Ti4O12 (LTO)/LiNi1/3Co1/3Mn1/3O2 (NMC) Li-Ion Batteries. ChemPhysChem 2017, 18, 1333–1344. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.N.; Oldiges, K.; Heuer, A.; Winter, M.; Cekic-Laskovic, I.; Holm, C.; Smiatek, J. Electrolyte solvents for high voltage lithium ion batteries: Ion pairing mechanisms, ionic conductivity, and specific anion effects in adiponitrile. Phys. Chem. Chem. Phys. 2018, 20, 25861–25874. [Google Scholar]
- Beltrop, K.; Meister, P.; Klein, S.; Heckmann, A.; Gruenebaum, M.; Wiemhöfer, H.D.; Winter, M.; Placke, T. Does size really matter? New insights into the intercalation behavior of anions into a graphite-based positive electrode for dual-ion batteries. Electrochim. Acta 2016, 209, 44–55. [Google Scholar] [CrossRef]
- Suo, L.; Borodin, O.; Wang, Y.; Rong, X.; Sun, W.; Fan, X.; Xu, S.; Schroeder, M.A.; Cresce, A.V.; Wang, F.; et al. “Water-in-Salt” Electrolyte Makes Aqueous Sodium-Ion Battery Safe, Green, and Long-Lasting. Adv. Energy Mater. 2017, 7, 1701189. [Google Scholar] [CrossRef]
- Pierotti, R.A. A scaled particle theory of aqueous and nonaqueous solutions. Chem. Rev. 1976, 76, 717–726. [Google Scholar] [CrossRef]
- Ben-Naim, A. Statistical Thermodynamics for Chemists and Biochemists; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Seo, D.M.; Borodin, O.; Han, S.D.; Ly, Q.; Boyle, P.D.; Henderson, W.A. Electrolyte Solvation and Ionic Association. J. Electrochem. Soc. 2012, 159, A553–A565. [Google Scholar] [CrossRef]
- Seo, D.M.; Borodin, O.; Han, S.D.; Boyle, P.D.; Henderson, W.A. Electrolyte solvation and ionic association II. Acetonitrile-lithium salt mixtures: Highly dissociated salts. J. Electrochem. Soc. 2012, 159, A1489–A1500. [Google Scholar] [CrossRef]
- Seo, D.M.; Borodin, O.; Balogh, D.; O’Connell, M.; Ly, Q.; Han, S.D.; Passerini, S.; Henderson, W.A. Electrolyte solvation and ionic association III. Acetonitrile-lithium salt mixtures–transport properties. J. Electrochem. Soc. 2013, 160, A1061–A1070. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.N.; Holm, C.; Smiatek, J. Specific ion effects for polyelectrolytes in aqueous and non-aqueous media: The importance of the ion solvation behavior. Soft Matter 2018, 14, 6243–6255. [Google Scholar] [CrossRef] [PubMed]
- Ehteshami, N.; Egula-Barrio, A.; de Meatza, I.; Porcher, W.; Paillard, E. Adiponitrile-based electrolytes for high voltage, graphite-based Li-ion battery. J. Power Sources 2018, 397, 52–58. [Google Scholar] [CrossRef]
- Yamada, Y.; Furukawa, K.; Sodeyama, K.; Kikuchi, K.; Yaegashi, M.; Tateyama, Y.; Yamada, A. Unusual stability of acetonitrile-based superconcentrated electrolytes for fast-charging lithium-ion batteries. J. Am. Chem. Soc. 2014, 136, 5039–5046. [Google Scholar] [CrossRef]
- Kirkwood, J.G.; Buff, F.P. The statistical mechanical theory of solutions. I. J. Chem. Phys. 1951, 19, 774–777. [Google Scholar] [CrossRef]
- Pierce, V.; Kang, M.; Aburi, M.; Weerasinghe, S.; Smith, P.E. Recent Applications of Kirkwood–Buff Theory to Biological Systems. Cell Biochem. Biophys. 2008, 50, 1–22. [Google Scholar] [CrossRef]
- Smith, P.E. Computer simulation of cosolvent effects on hydrophobic hydration. J. Phys. Chem. B 1999, 103, 525–534. [Google Scholar] [CrossRef]
- Newman, K.E. Kirkwood–Buff solution theory: Derivation and applications. Chem. Soc. Rev. 1994, 23, 31–40. [Google Scholar] [CrossRef]
- Smiatek, J. Aqueous ionic liquids and their influence on protein conformations: An overview on recent theoretical and experimental insights. J. Phys. Condens. Matter 2017, 29, 233001. [Google Scholar] [CrossRef]
- Kusalik, P.G.; Patey, G. The thermodynamic properties of electrolyte solutions: Some formal results. J. Chem. Phys. 1987, 86, 5110–5116. [Google Scholar] [CrossRef]
- Liu, X.; Vlugt, T.J.; Bardow, A. Maxwell–Stefan diffusivities in binary mixtures of ionic liquids with dimethyl sulfoxide (DMSO) and H2O. J. Phys. Chem. B 2011, 115, 8506–8517. [Google Scholar] [CrossRef]
- Fyta, M.; Netz, R.R. Ionic force field optimization based on single-ion and ion-pair solvation properties: Going beyond standard mixing rules. J. Chem. Phys. 2012, 136, 124103. [Google Scholar] [CrossRef]
- Gee, M.B.; Cox, N.R.; Jiao, Y.; Bentenitis, N.; Weerasinghe, S.; Smith, P.E. A Kirkwood–Buff derived force field for aqueous alkali halides. J. Chem. Theory Comput. 2011, 7, 1369–1380. [Google Scholar] [CrossRef]
- Peters, C.; Wolff, L.; Vlugt, T.J.H.; Bardow, A. Diffusion in Liquids: Experiments, Molecular Dynamics, and Engineering Models. Experimental Thermodynamics Volume X: Non-equilibrium Thermodynamics with Applications; Royal Society of Chemistry: Cambridge, UK, 2015; Volume 10, p. 78. [Google Scholar]
- Krishnamoorthy, A.N.; Holm, C.; Smiatek, J. The influence of co-solutes on the chemical equilibrium—A Kirkwood–Buff theory for ion pair association-dissociation processes in ternary electrolyte solutions. J. Phys. Chem. C 2018, 122, 10293–10392. [Google Scholar] [CrossRef]
- Oprzeska-Zingrebe, E.A.; Smiatek, J. Preferential binding of urea to single-stranded DNA structures:a molecular dynamics study. Biophys. J. 2018, 10, 809. [Google Scholar]
- Marcus, Y.; Hefter, G. Ion pairing. Chem. Rev. 2006, 106, 4585–4621. [Google Scholar] [CrossRef]
- Marcus, Y. Effect of ions on the structure of water: Structure making and breaking. Chem. Rev. 2009, 109, 1346–1370. [Google Scholar] [CrossRef]
- Borodin, O. Molecular Modeling of Electrolytes. In Electrolytes for Lithium and Lithium-Ion Batteries; Springer: Berlin/Heidelberg, Germany, 2014; pp. 371–401. [Google Scholar]
- Urban, A.; Seo, D.H.; Ceder, G. Computational understanding of Li-ion batteries. NPJ Comput. Mater. 2016, 2, 16002. [Google Scholar] [CrossRef]
- Borodin, O.; Ren, X.; Vatamanu, J.; von Wald Cresce, A.; Knap, J.; Xu, K. Modeling insight into battery electrolyte electrochemical stability and interfacial structure. Acc. Chem. Res. 2017, 50, 2886–2894. [Google Scholar] [CrossRef]
- Etacheri, V.; Marom, R.; Elazari, R.; Salitra, G.; Aurbach, D. Challenges in the development of advanced Li-ion batteries: A review. Energy Environ. Sci. 2011, 4, 3243–3262. [Google Scholar] [CrossRef]
- Zheng, J.; Lochala, J.A.; Kwok, A.; Deng, Z.D.; Xiao, J. Research progress towards understanding the unique interfaces between concentrated electrolytes and electrodes for energy storage applications. Adv. Sci. 2017, 4, 1700032. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces; Acdemic Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Andelman, D. Electrostatic properties of membranes: The Poisson-Boltzmann theory. In Handbook of Biological Physics; Elsevier: Amsterdam, The Netherlands, 1995; Volume 1, pp. 603–642. [Google Scholar]
- Grochowski, P.; Trylska, J. Continuum molecular electrostatics, salt effects, and counterion binding—A review of the Poisson—Boltzmann theory and its modifications. Biopolymers 2008, 89, 93–113. [Google Scholar] [CrossRef]
- Marcus, Y. Ions in Solution and Their Solvation; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Vögele, M.; Holm, C.; Smiatek, J. Coarse-grained simulations of polyelectrolyte complexes: MARTINI models for poly (styrene sulfonate) and poly (diallyldimethylammonium). J. Chem. Phys. 2015, 143, 243151. [Google Scholar] [CrossRef]
- Krishnamoorthy, A.N.; Zeman, J.; Holm, C.; Smiatek, J. Preferential solvation and ion association properties in aqueous dimethyl sulfoxide solutions. Phys. Chem. Chem. Phys. 2016, 18, 31312–31322. [Google Scholar] [CrossRef]
- Michalowsky, J.; Schäfer, L.V.; Holm, C.; Smiatek, J. A refined polarizable water model for the coarse-grained MARTINI force field with long-range electrostatic interactions. J. Chem. Phys. 2017, 146, 054501. [Google Scholar] [CrossRef]
- Zhang, Y.; Cremer, P.S. Interactions between macromolecules and ions: The Hofmeister series. Curr. Opin. Chem. Biol. 2006, 10, 658–663. [Google Scholar] [CrossRef]
- Lo Nostro, P.; Ninham, B.W. Hofmeister Phenomena: An Update on Ion Specificity in Biology. Chem. Rev. 2012, 112, 2286–2322. [Google Scholar] [CrossRef]
- Van Der Vegt, N.F.; Haldrup, K.; Roke, S.; Zheng, J.; Lund, M.; Bakker, H.J. Water-mediated ion pairing: Occurrence and relevance. Chem. Rev. 2016, 116, 7626–7641. [Google Scholar] [CrossRef]
- Collins, K.D. Ions from the Hofmeister series and osmolytes: Effects on proteins in solution and in the crystallization process. Methods 2004, 34, 300–311. [Google Scholar] [CrossRef]
- Ball, P. Water as an active constituent in cell biology. Chem. Rev. 2008, 108, 74–108. [Google Scholar] [CrossRef]
- Yang, Z. Hofmeister effects: An explanation for the impact of ionic liquids on biocatalysis. J. Biotechnol. 2009, 144, 12–22. [Google Scholar] [CrossRef]
- Schröder, C. Proteins in Ionic Liquids: Current Status of Experiments and Simulations. Top. Curr. Chem. 2017, 375, 25. [Google Scholar] [CrossRef]
- Zhao, H. Protein stabilization and enzyme activation in ionic liquids: Specific ion effects. J. Chem. Technol. Biotechnol. 2015, 91, 25–50. [Google Scholar] [CrossRef]
- Kunz, W. Specific Ion Effects; World Scientific: Singapore, 2010. [Google Scholar]
- Mazzini, V.; Craig, V.S. Specific-ion effects in non-aqueous systems. Curr. Opin. Colloid Int. Sci. 2016, 23, 82–93. [Google Scholar] [CrossRef]
- Mazzini, V.; Craig, V.S. What is the fundamental ion-specific series for anions and cations? Ion specificity in standard partial molar volumes of electrolytes and electrostriction in water and non-aqueous solvents. Chem. Sci. 2017, 8, 7052–7065. [Google Scholar] [CrossRef]
- Mazzini, V.; Liu, G.; Craig, V.S. Probing the Hofmeister series beyond water: Specific-ion effects in non-aqueous solvents. J. Chem. Phys. 2018, 148, 222805. [Google Scholar] [CrossRef]
- Ciccotti, G.; Ferrario, M.; Hynes, J.T.; Kapral, R. Constrained molecular dynamics and the mean potential for an ion pair in a polar solvent. Chem. Phys. 1989, 129, 241–251. [Google Scholar] [CrossRef]
- Ganguly, P.; Schravendijk, P.; Hess, B.; van der Vegt, N.F. Ion pairing in aqueous electrolyte solutions with biologically relevant anions. J. Phys. Chem. B 2011, 115, 3734–3739. [Google Scholar] [CrossRef]
- Hess, B.; van der Vegt, N.F. Cation specific binding with protein surface charges. Proc. Natl. Acad. Sci. USA 2009, 106, 13296–13300. [Google Scholar] [CrossRef]
- Borodin, O.; Suo, L.; Gobet, M.; Ren, X.; Wang, F.; Faraone, A.; Peng, J.; Olguin, M.; Schroeder, M.; Ding, M.S.; et al. Liquid Structure with Nano-Heterogeneity Promotes Cationic Transport in Concentrated Electrolytes. ACS Nano 2017, 11, 10462–10471. [Google Scholar] [CrossRef]
- Mazzini, V.; Craig, V.S. Volcano Plots Emerge from a Sea of Nonaqueous Solvents: The Law of Matching Water Affinities Extends to All Solvents. ACS Cent. Sci. 2018, 4, 1056–1084. [Google Scholar] [CrossRef]
- Batys, P.; Luukkonen, S.; Sammalkorpi, M. Ability of Poisson–Boltzmann Equation to Capture Molecular Dynamics Predicted Ion Distribution around Polyelectrolytes. Phys. Chem. Chem. Phys. 2017, 19, 24583–24593. [Google Scholar] [CrossRef]
- Heyda, J.; Dzubiella, J. Ion-specific counterion condensation on charged peptides: Poisson–Boltzmann vs. atomistic simulations. Soft Matter 2012, 8, 9338–9344. [Google Scholar] [CrossRef]
- Salis, A.; Ninham, B.W. Models and mechanisms of Hofmeister effects in electrolyte solutions, and colloid and protein systems revisited. Chem. Soc. Rev. 2014, 43, 7358–7377. [Google Scholar] [CrossRef]
- Smiatek, J.; Wohlfarth, A.; Holm, C. The solvation and ion condensation properties for sulfonated polyelectrolytes in different solvents—A computational study. New J. Phys. 2014, 16, 025001. [Google Scholar] [CrossRef]
- Hahn, M.B.; Uhlig, F.; Solomun, T.; Smiatek, J.; Sturm, H. Combined influence of ectoine and salt: Spectroscopic and numerical evidence for compensating effects on aqueous solutions. Phys. Chem. Chem. Phys. 2016, 18, 28398–28402. [Google Scholar] [CrossRef]
- Collins, K.D. Charge density-dependent strength of hydration and biological structure. Biophys. J. 1997, 72, 65. [Google Scholar] [CrossRef]
- Collins, K.D. Why continuum electrostatics theories cannot explain biological structure, polyelectrolytes or ionic strength effects in ion–protein interactions. Biophys. Chem. 2012, 167, 43–59. [Google Scholar] [CrossRef]
- Pearson, R.G. Hard and soft acids and bases. J. Am. Chem. Soc. 1963, 85, 3533–3539. [Google Scholar] [CrossRef]
- Hwang, J.Y.; Myung, S.T.; Sun, Y.K. Sodium-ion batteries: Present and future. Chem. Soc. Rev. 2017, 46, 3529–3614. [Google Scholar] [CrossRef]
- Marcus, Y. Transfer of ions between solvents: Some new results concerning volumes, heat capacities and other quantities. Pure Appl. Chem. 1996, 68, 1495–1500. [Google Scholar] [CrossRef]
- García-Giménez, E.; Alcaraz, A.; Aguilella, V.M. Overcharging below the nanoscale: Multivalent cations reverse the ion selectivity of a biological channel. Phys. Rev. E 2010, 81, 021912. [Google Scholar] [CrossRef]
- Besteman, K.; Zevenbergen, M.; Lemay, S. Charge inversion by multivalent ions: Dependence on dielectric constant and surface-charge density. Phys. Rev. E 2005, 72, 061501. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Annapureddy, H.V.; Raineri, F.O.; Margulis, C.J. How is charge transport different in ionic liquids and electrolyte solutions? J. Phys. Chem. B 2011, 115, 13212–13221. [Google Scholar] [CrossRef]
- Weyman, A.; Bier, M.; Holm, C.; Smiatek, J. Microphase separation and the formation of ion conductivity channels in poly(ionic liquid)s: A coarse-grained molecular dynamics study. J. Chem. Phys. 2018, 148, 193824. [Google Scholar] [CrossRef]
- Schröder, C.; Haberler, M.; Steinhauser, O. On the computation and contribution of conductivity in molecular ionic liquids. J. Chem. Phys. 2008, 128, 134501. [Google Scholar] [CrossRef]
- Wohde, F.; Balabajew, M.; Roling, B. Li+ Transference Numbers in Liquid Electrolytes Obtained by Very-Low-Frequency Impedance Spectroscopy at Variable Electrode Distances. J. Electrochem. Soc. 2016, 163, A714–A721. [Google Scholar] [CrossRef]
- Gouverneur, M.; Kopp, J.; van Wüllen, L.; Schönhoff, M. Direct determination of ionic transference numbers in ionic liquids by electrophoretic NMR. Phys. Chem. Chem. Phys. 2015, 17, 30680–30686. [Google Scholar] [CrossRef]
- Wohde, F.; Bhandary, R.; Moldrickx, J.M.; Sundermeyer, J.; Schönhoff, M.; Roling, B. Li+ ion transport in ionic liquid-based electrolytes and the influence of sulfonate-based zwitterion additives. Solid State Ionics 2015, 284, 37–44. [Google Scholar] [CrossRef]
- Debye, P.; Hückel, E. The theory of electrolytes. I. Z. Phys. 1923, 24, 305–324. [Google Scholar]
- Onsager, L.; Fuoss, R. Irreversible processes in electrolytes. Diffusion, conductance and viscous flow in arbitrary mixtures of strong electrolytes. J. Phys. Chem. 1932, 36, 2689–2778. [Google Scholar] [CrossRef]
- Gering, K.L. Prediction of electrolyte conductivity: Results from a generalized molecular model based on ion solvation and a chemical physics framework. Electrochim. Acta 2017, 225, 175–189. [Google Scholar] [CrossRef]
- Logan, E.; Tonita, E.M.; Gering, K.; Dahn, J. A Critical Evaluation of the Advanced Electrolyte Model. J. Electrochem. Soc. 2018, 165, A3350–A3359. [Google Scholar] [CrossRef]
- Maitra, A.; Heuer, A. Understanding correlation effects for ion conduction in polymer electrolytes. J. Phys. Chem. B 2008, 112, 9641–9651. [Google Scholar] [CrossRef]
- Neumann, M. Dipole moment fluctuation formulas in computer simulations of polar systems. Mol. Phys. 1983, 50, 841–858. [Google Scholar] [CrossRef]
- Caillol, J.; Levesque, D.; Weis, J. Theoretical calculation of ionic solution properties. J. Chem. Phys. 1986, 85, 6645–6657. [Google Scholar] [CrossRef]
- Caillol, J.M.; Levesque, D.; Weis, J.J. Electrical properties of polarizable ionic solutions. I. Theoretical aspects. J. Chem. Phys. 1989, 91, 5544–5554. [Google Scholar] [CrossRef]
- Bonthuis, D.J.; Gekle, S.; Netz, R.R. Dielectric profile of interfacial water and its effect on double-layer capacitance. Phys. Rev. Lett. 2011, 107, 166102. [Google Scholar] [CrossRef]
- Gekle, S.; Netz, R.R. Anisotropy in the dielectric spectrum of hydration water and its relation to water dynamics. J. Chem. Phys. 2012, 137, 104704. [Google Scholar] [CrossRef] [PubMed]
- Fahrenberger, F.; Hickey, O.A.; Smiatek, J.; Holm, C. The influence of charged-induced variations in the local permittivity on the static and dynamic properties of polyelectrolyte solutions. J. Chem. Phys. 2015, 143, 243140. [Google Scholar] [CrossRef] [PubMed]
- Fahrenberger, F.; Hickey, O.A.; Smiatek, J.; Holm, C. Importance of varying permittivity on the conductivity of polyelectrolyte solutions. Phys. Rev. Lett. 2015, 115, 118301. [Google Scholar] [CrossRef]
- Hahn, M.B.; Solomun, T.; Wellhausen, R.; Hermann, S.; Seitz, H.; Meyer, S.; Kunte, H.J.; Zeman, J.; Uhlig, F.; Smiatek, J.; et al. Influence of the Compatible Solute Ectoine on the Local Water Structure: Implications for the Binding of the Protein G5P to DNA. J. Phys. Chem. B 2015, 119, 15212–15220. [Google Scholar] [CrossRef] [PubMed]
- Manning, G. Limiting Laws and Counterion Condensation in Polyelectrolyte Solutions I. Colligative Properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar] [CrossRef]
- Manning, G.S.; Ray, J. Counterion condensation revisited. J. Biomol. Struct. Dyn. 1998, 16, 461–476. [Google Scholar] [CrossRef]
- Deserno, M.; Holm, C.; May, S. Fraction of condensed counterions around a charged rod: Comparison of Poisson-Boltzmann theory and computer simulations. Macromolecules 2000, 33, 199–206. [Google Scholar] [CrossRef]
- Borodin, O.; Smith, G.D. LiTFSI structure and transport in ethylene carbonate from molecular dynamics simulations. J. Phys. Chem. B 2006, 110, 4971–4977. [Google Scholar] [CrossRef]
- Lesch, V.; Heuer, A.; Holm, C.; Smiatek, J. Properties of Apolar Solutes in Alkyl Imidazolium-Based Ionic Liquids: The Importance of Local Interactions. ChemPhysChem 2016, 17, 387–394. [Google Scholar] [CrossRef] [PubMed]
- Gutmann, V. Empirical parameters for donor and acceptor properties of solvents. Electrochim. Acta 1976, 21, 661–670. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Younesi, R.; Veith, G.M.; Johansson, P.; Edström, K.; Vegge, T. Lithium salts for advanced lithium batteries: Li–metal, Li–O2, and Li–S. Energy Environ. Sci. 2015, 8, 1905. [Google Scholar] [CrossRef]
- Cataldo, F. A revision of the Gutmann donor numbers of a series of phosphoramides including TEPA. Eur. Chem. Bull. 2015, 4, 92–97. [Google Scholar]
- Laoire, C.O.; Mukerjee, S.; Abraham, K.; Plichta, E.J.; Hendrickson, M.A. Influence of nonaqueous solvents on the electrochemistry of oxygen in the rechargeable lithium- air battery. J. Phys. Chem. C 2010, 114, 9178–9186. [Google Scholar] [CrossRef]
- Barthel, J.; Gores, H.; Mamantov, G.; Papov, A. Chemistry of Nonaqueous Solutions: Current Progress; VCH: New York, NY, USA, 1994; pp. 6–11. [Google Scholar]
- Pistoia, G. Lithium Batteries: New Materials, Developments And Perspectives; Elsevier: Amsterdam, The Netherlands, 1994; Volume 5. [Google Scholar]
- Salomon, M. Electrolyte solvation in aprotic solvents. J. Power Sources 1989, 26, 9–21. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Geerlings, P.; De Proft, F.; Langenaeker, W. Conceptual density functional theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef]
- Liu, S.B. Conceptual density functional theory and some recent developments. Acta Phys. Chim. Sin. 2009, 25, 590–600. [Google Scholar]
- Chattaraj, P.K.; Giri, S. Electrophilicity index within a conceptual DFT framework. Ann. Rep. Phys. Chem. C 2009, 105, 13–39. [Google Scholar] [CrossRef]
- Korth, M. Large-scale virtual high-throughput screening for the identification of new battery electrolyte solvents: Evaluation of electronic structure theory methods. Phys. Chem. Chem. Phys. 2014, 16, 7919–7926. [Google Scholar] [CrossRef]
- Borodin, O.; Olguin, M.; Spear, C.E.; Leitner, K.W.; Knap, J. Towards high throughput screening of electrochemical stability of battery electrolytes. Nanotechnology 2015, 26, 354004. [Google Scholar] [CrossRef]
- Bhatt, M.D.; O’Dwyer, C. The Role of Carbonate and Sulfite Additives in Propylene Carbonate-Based Electrolytes on the Formation of SEI Layers at Graphitic Li-Ion Battery Anodes. J. Electrochem. Soc. 2014, 161, A1415–A1421. [Google Scholar] [CrossRef]
- Wang, R.L.; Buhrmester, C.; Dahn, J.R. Calculations of Oxidation Potentials of Redox Shuttle Additives for Li-Ion Cells. J. Electrochem. Soc. 2006, 153, A445–A449. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
- Ho, J.; Coote, M.L.; Cramer, C.J.; Truhlar, D.G. Theoretical calculation of reduction potentials. In Organic Electrochemistry; CRC Press: Boca Raton, FL, USA, 2012; pp. 229–259. [Google Scholar]
- Shimizu, S.; Matubayasi, N. A unified perspective on preferential solvation and adsorption based on inhomogeneous solvation theory. Physica A 2018, 492, 1988–1996. [Google Scholar] [CrossRef]
- Galiński, M.; Lewandowski, A.; Stepniak, I. Ionic liquids as electrolytes. Electrochim. Acta 2006, 51, 5567–5580. [Google Scholar] [CrossRef]
- Atkins, P.W.; de Paula, J. Physical Chemistry; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Schnell, S.K.; Englebienne, P.; Simon, J.M.; Krüger, P.; Balaji, S.P.; Kjelstrup, S.; Bedeaux, D.; Bardow, A.; Vlugt, T.J. How to apply the Kirkwood–Buff theory to individual species in salt solutions. Chem. Phys. Lett. 2013, 582, 154–157. [Google Scholar] [CrossRef]
- Canchi, D.R.; García, A.E. Cosolvent effects on protein stability. Ann. Rev. Phys. Chem. 2013, 64, 273–293. [Google Scholar] [CrossRef] [PubMed]
- Hall, D. Kirkwood–Buff theory of solutions. An alternative derivation of part of it and some applications. Trans. Faraday Soc. 1971, 67, 2516–2524. [Google Scholar] [CrossRef]
- Chitra, R.; Smith, P.E. Preferential interactions of cosolvents with hydrophobic solutes. J. Phys. Chem. B 2001, 105, 11513–11522. [Google Scholar] [CrossRef]
- Smith, P.E. Cosolvent interactions with biomolecules: Relating computer simulation data to experimental thermodynamic data. J. Phys. Chem. B 2004, 108, 18716–18724. [Google Scholar] [CrossRef]
- Shimizu, S.; Smith, D.J. Preferential hydration and the exclusion of cosolvents from protein surfaces. J. Chem. Phys. 2004, 121, 1148–1154. [Google Scholar] [CrossRef] [PubMed]
- Schurr, J.M.; Rangel, D.P.; Aragon, S.R. A contribution to the theory of preferential interaction coefficients. Biophys. J. 2005, 89, 2258–2276. [Google Scholar] [CrossRef] [PubMed]
- Shulgin, I.L.; Ruckenstein, E. A protein molecule in an aqueous mixed solvent: Fluctuation theory outlook. J. Chem. Phys. 2005, 123, 054909. [Google Scholar] [CrossRef] [PubMed]
- Shulgin, I.L.; Ruckenstein, E. The Kirkwood–Buff theory of solutions and the local composition of liquid mixtures. J. Phys. Chem. B 2006, 110, 12707–12713. [Google Scholar] [CrossRef] [PubMed]
- Rösgen, J.; Pettitt, B.M.; Bolen, D.W. Uncovering the basis for nonideal behavior of biological molecules. Biochemistry 2004, 43, 14472–14484. [Google Scholar] [CrossRef]
- Rösgen, J.; Pettitt, B.M.; Bolen, D.W. Protein folding, stability, and solvation structure in osmolyte solutions. Biophys. J. 2005, 89, 2988–2997. [Google Scholar] [CrossRef]
- Smith, P.E. Chemical potential derivatives and preferential interaction parameters in biological systems from Kirkwood–Buff theory. Biophys. J. 2006, 91, 849–856. [Google Scholar] [CrossRef] [PubMed]
- Rösgen, J.; Pettitt, B.M.; Bolen, D.W. An analysis of the molecular origin of osmolyte-dependent protein stability. Protein Sci. 2007, 16, 733–743. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.E.; Matteoli, E.; O’Connell, J.P. Fluctuation Theory of Solutions: Applications in Chemistry, Chemical Engineering, and Biophysics; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Smiatek, J. Osmolyte effects: Impact on the aqueous solution around charged and neutral spheres. J. Phys. Chem. B 2014, 118, 771–782. [Google Scholar] [CrossRef] [PubMed]
- Shimizu, S.; Boon, C.L. The Kirkwood–Buff theory and the effect of cosolvents on biochemical reactions. J. Chem. Phys. 2004, 121, 9147–9155. [Google Scholar] [CrossRef] [PubMed]
- Smith, P.E.; Mazo, R.M. On the Theory of Solute Solubility in Mixed Solvents. J. Phys. Chem. B 2008, 112, 7875–7884. [Google Scholar] [CrossRef] [PubMed]
- Fredenslund, A.; Jones, R.L.; Prausnitz, J.M. Group-contribution estimation of activity coefficients in nonideal liquid mixtures. AIChE J. 1975, 21, 1086–1099. [Google Scholar] [CrossRef]
- Ben-Naim, A. Inversion of the Kirkwood–Buff theory of solutions: Application to the water–ethanol system. J. Chem. Phys. 1977, 67, 4884–4890. [Google Scholar] [CrossRef]
- Smith, P.E. On the Kirkwood–Buff inversion procedure. J. Chen. Phys. 2008, 129, 124509. [Google Scholar] [CrossRef]
- Kobayashi, T.; Reid, J.E.; Shimizu, S.; Fyta, M.; Smiatek, J. The properties of residual water molecules in ionic liquids: A comparison between direct and inverse Kirkwood–Buff approaches. Phys. Chem. Chem. Phys. 2017, 19, 18924–18937. [Google Scholar] [CrossRef]
- Von Wald Cresce, A.; Gobet, M.; Borodin, O.; Peng, J.; Russell, S.M.; Wikner, E.; Fu, A.; Hu, L.; Lee, H.S.; Zhang, Z.; et al. Anion solvation in carbonate-based electrolytes. J. Phys. Chem. C 2015, 119, 27255–27264. [Google Scholar] [CrossRef]
- Chaban, V. Solvation of the fluorine containing anions and their lithium salts in propylene carbonate and dimethoxyethane. J. Mol. Model. 2015, 21, 172. [Google Scholar] [CrossRef] [PubMed]
- Yabuuchi, N.; Kubota, K.; Dahbi, M.; Komaba, S. Research development on sodium-ion batteries. Chem. Rev. 2014, 114, 11636–11682. [Google Scholar] [CrossRef] [PubMed]
- Von Aspern, N.; Roeser, S.; Rad, B.R.; Murmann, P.; Streipert, B.; Moennighoff, X.; Tillmann, S.; Shevchuk, M.; Stubbmann-Kazakova, O.; Roeschenthaler, G.V.; et al. Phosphorus additives for improving high voltage stability and safety of lithium ion batteries. J. Fluor. Chem. 2017, 198, 24–33. [Google Scholar] [CrossRef]
- Ploetz, E.A.; Smith, P.E. Local fluctuations in solution mixtures. J. Chem. Phys. 2011, 135, 044506. [Google Scholar] [CrossRef]
- Ploetz, E.A.; Smith, P.E. Local fluctuations in solution: Theory and applications. Adv. Chem. Phys. 2013, 153, 311. [Google Scholar] [PubMed]
- Kuehnel, R.S.; Boeckenfeld, N.; Passerini, S.; Winter, M.; Balducci, A. Mixtures of ionic liquid and organic carbonate as electrolyte with improved safety and performance for rechargeable lithium batteries. Electrochim. Acta 2011, 56, 4092–4099. [Google Scholar] [CrossRef]
- Friesen, A.; Horsthemke, F.; Moennighoff, X.; Brunklaus, G.; Krafft, R.; Boerner, M.; Risthaus, T.; Winter, M.; Schappacher, F. Impact of cycling at low temperatures on the safety behavior of 18650-type lithium ion cells: Combined study of mechanical and thermal abuse testing accompanied by post-mortem analysis. J. Power Sources 2016, 334, 1–11. [Google Scholar] [CrossRef]
- Gallus, R.; Wagner, R.; Wiemers-Meyer, S.; Winter, M.; Cekic-Laskovic, I. New insights into the structure-property relationship of high-voltage electrolyte components for lithium-ion batteries using the pKa value. Electrochim. Acta 2015, 184, 410–416. [Google Scholar] [CrossRef]
- Wagner, R.; Streipert, B.; Kraft, V.; Reyes Jimenez, A.; Roeser, S.; Kasnatscheew, J.; Gallus, D.; Boerner, M.; Mayer, C.; Arlinghaus, H.F.; et al. Counterintuitive role of magnesium salts as effective electrolyte additives for high voltage lithium-ion batteries. Adv. Mater. Interfaces 2016, 3, 1600096. [Google Scholar] [CrossRef]
- Wagner, M.R.; Albering, J.H.; Moeller, K.C.; Besenhard, J.O.; Winter, M. XRD evidence for the electrochemical formation of Li(PC)yCn in PC-based electrolytes. Electrochem. Commun. 2005, 7, 947–952. [Google Scholar] [CrossRef]
- Tasaki, K.; Goldberg, A.; Winter, M. On the difference in cycling behaviors of lithium-ion battery cell between the ethylene carbonate- and propylene carbonate-based electrolytes. Electrochim. Acta 2011, 56, 10424–10435. [Google Scholar] [CrossRef]
- Wagner, M.R.; Raimann, P.; Moeller, K.C.; Besenhard, J.O.; Winter, M. The electrolyte decomposition reactions on tin and graphite based anodes are different. Electrochem. Solid State Lett. 2004, 7, A201–A205. [Google Scholar] [CrossRef]
- Gallus, D.; Schmitz, R.; Wagner, R.; Hoffmann, B.; Nowak, S.; Cekic-Laskovic, I.; Schmitz, R.W.; Winter, M. The influence of different conducting salts on the metal dissolution and capacity fading of NCM cathode material. Electrochim. Acta 2014, 134, 393–398. [Google Scholar] [CrossRef]
- Jia, H.; Kloepsch, R.; He, X.; Evertz, M.; Nowak, S.; Li, J.; Winter, M.; Placke, T. Nanostructured ZnFe2O4 as anode material for lithium ion batteries: Ionic liquid-assisted synthesis and performance evaluation with special emphasis on comparative metal dissolution. Acta Chim. Slov. 2016, 63, 470–483. [Google Scholar] [CrossRef] [PubMed]
- Evertz, M.; Horsthemke, F.; Kasnatscheew, J.; Boerner, M.; Winter, M.; Nowak, S. Unraveling transition metal dissolution of Li1.04Ni1/3Co1/3Mn1/3O2 (NCM 111) in lithium ion full cells by using the total reflection X-ray fluorescence technique. J. Power Sources 2016, 329, 364–371. [Google Scholar] [CrossRef]
- Nowak, S.; Winter, M. Chemical analysis for a better understanding of aging and degradation mechanisms of non-aqueous electrolytes for lithium ion batteries: Method development, application and lessons learned. J. Electrochem. Soc. 2015, 162, A2500–A2508. [Google Scholar] [CrossRef]
| Solvent | DN | AN | |
|---|---|---|---|
| Water | 18.0 | 54.8 | 0.0 |
| Propylene carbonate | 15.1 | 18.3 | −0.09 |
| Ethylene carbonate | 16.4 | ||
| Dimethyl carbonate | 17.2 | ||
| Diethyl carbonate | 16.0 | ||
| 1,2–dimethoxyethane | 20.0 | ||
| 1,3–dioxolane | 21.3 | ||
| Tetraethylene glycol dimethyl ether | 16.6 | ||
| N,N–Dimethylformamide | 26.6 | 16.0 | 0.11 |
| N,N–Dimethylacetamide | 27.8 | 13.6 | 0.17 |
| Dimethyl sulfoxide | 29.8 | 19.3 | 0.22 |
| Chloroform | 4.0 | 23.1 | |
| Tetramethylene sulfone | 14.8 | 19.2 | 0.00 |
| Methanol | 30.0 | 41.5 | 0.02 |
| Ethylene glycol | 20.0 | 43.4 | −0.03 |
| Acetonitrile | 32.0 | 18.9 | 0.34 |
| N–Propanol | 30.0 | 33.7 | 0.16 |
| 1,4–Dioxane | 14.8 | 10.8 | 0.07 |
| –Butyrolactone | 18.0 | 17.3 | 0.02 |
| N–Methylformamide | 27.0 | 32.1 | 0.17 |
| N,N–Dimethylformamide | 26.6 | 16.0 | 0.11 |
| N,N–Dimethylacetamide | 27.8 | 13.6 | 0.17 |
| Pyridine | 33.1 | 14.2 | 0.64 |
| Benzonitrile | 11.9 | 15.5 | 0.34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smiatek, J.; Heuer, A.; Winter, M. Properties of Ion Complexes and Their Impact on Charge Transport in Organic Solvent-Based Electrolyte Solutions for Lithium Batteries: Insights from a Theoretical Perspective. Batteries 2018, 4, 62. https://doi.org/10.3390/batteries4040062
Smiatek J, Heuer A, Winter M. Properties of Ion Complexes and Their Impact on Charge Transport in Organic Solvent-Based Electrolyte Solutions for Lithium Batteries: Insights from a Theoretical Perspective. Batteries. 2018; 4(4):62. https://doi.org/10.3390/batteries4040062
Chicago/Turabian StyleSmiatek, Jens, Andreas Heuer, and Martin Winter. 2018. "Properties of Ion Complexes and Their Impact on Charge Transport in Organic Solvent-Based Electrolyte Solutions for Lithium Batteries: Insights from a Theoretical Perspective" Batteries 4, no. 4: 62. https://doi.org/10.3390/batteries4040062
APA StyleSmiatek, J., Heuer, A., & Winter, M. (2018). Properties of Ion Complexes and Their Impact on Charge Transport in Organic Solvent-Based Electrolyte Solutions for Lithium Batteries: Insights from a Theoretical Perspective. Batteries, 4(4), 62. https://doi.org/10.3390/batteries4040062






