Prognosis and Remaining Useful Life Estimation of Lithium-Ion Battery with Optimal Multi-Level Particle Filter and Genetic Algorithm

Abstract

Prognosis and remaining useful life (RUL) estimation of components and systems (C&S) are vital for intelligent asset-integrity management. The implementation of the traditional multi-level particle filter (TRMPF) has improved prognosis when compared with the one-step traditional particle filter that depended on the first-order state equation. However, despite this improvement, the need to enhance the accuracy of fault prognosis, diagnosis and detection cannot be overemphasized. To this end, an optimal multi-level particle filter (OPMPF) algorithm that combines genetic algorithm (GA) optimization and multi-level particle filter (MPF) techniques is used to predict the RUL of the C&S in order to enhance the accuracy of the estimation at different forms of deterioration in operation. A 9-fold cross-validation ensemble MPF that utilized lithium-ion (Li⁺) batteries’ charge capacity decay to test the developed OPMPF algorithm showed an improvement of over 200% in the estimated RUL when compared with the TRMPF estimation.

1. Introduction

Since the components and systems (C&S) of microelectronics and other complex electromechanical systems degrade over the period of operation, it is important that the trend of the deterioration is understood to enhance maintenance management, forestall downtime and optimize operating cost. Different techniques that include data-driven prognosis, physics-of-failure modeling and hybrid prognosis that combines both data-driven and physics-of-failure methodologies have been used for the integrity management of C&S of devices [1,2,3,4,5].

The abundance of condition-monitored data from numerous complex systems have unfortunately not translated into enhanced fault diagnosis, detection and identification, as poor prognosis, resulting from unoptimized performance characteristics of the C&S, have culminated in increased costs due to unwarranted failures. To this end, it is important to develop prognostics architecture that will ensure an increased level of accuracy for the remaining useful life (RUL) prediction of C&S to improve fault detection and identification.

Li+ batteries capacity fade occurs during cycling due to factors that include the unwarranted reactions that occur in the system resulting in volume change [6]. The overcharging and over discharging of the battery results in electrolyte decomposition, passive film formation, active material dissolution, mechanical degradation, lithium metal plating and corrosion [7,8]. Changes in electrode and electrolyte interfaces, which is the result of the depletion of the active compositions of the active materials used for their manufacture, cause a solid electrolyte interface that forms on the surface of the graphite materials [8]. This interface contributes to the capacity fade of the Li⁺ battery due to impedance rise at the anode, corrosion of the lithium in the active carbon, loss of mobile Li⁺ and contact loss.

Although many researchers [1,2,3,4,5,9] have used numerous techniques such as limit and trend checking, reconstructed phase planes and regression curves for fault detection, diagnosis and prognosis, the need to reduce error margins [10] in prognosis have made it imperative to keep searching for new techniques. Hence, other researchers have implemented probabilistic estimation techniques [10,11,12], physics-of-failure model-infused statistical techniques [13] and electrical signature analysis [14]. Similarly, the implementation of a hidden Markov model and semi-Markov model for prognostics and diagnostics has also been popularized, due to the ease of applying the time-series analysis, which gives information about the RUL of the C&S [15,16,17,18]. Again, there has also been increased application of artificial intelligence procedures with machine learning in prognostics [19,20,21], due to the convenience of developing algorithms for learning non-linear multivariate relationships of C&S parameters. This area has been one of the core focus of researchers who have incorporated different forms of particle filter (PF) and genetic algorithm (GA) techniques into the various optimization frameworks to enhance prognosis.

Jiang et al. [22] implemented a multi-level particle filter (MPF) using least square support vector regression (LSSVR) and GA to optimize fault prognosis of electronic devices. The study incorporated multi-level state equations into a PF and used GA to determine the optimal values of the MPF. The results of the study showed that the LSSVR-optimized MPF produced more accurate RUL estimations when compared with the traditional on-step-before state PF technique. Despite the improved RUL estimation in the procedure used by these authors, the implementation of the MPF with the same parametric values in the optimization of the MPF raises a question about the practical applications of the results, since the decay pattern of C&S will be distinctive in practice. The work of Sbarufatti et al. [23] used online adaptively trained particle filter with a radial basis function (RBF) neural network for the prognostics of Li⁺ batteries’ charge capacity decay. Although the results of the study indicated that the end-of-life discharge of the batteries was more accurately predicted with the algorithm than the traditional PF, the fact that MPF has shown improved estimations accuracy than the traditional PF [22,24] makes it pertinent to use the technique for enhancing battery charge capacity estimation. Similarly, Li et al. [25] showed that an adaptive order PF made a better prediction of the RUL of an aviation piston pump compared with the physics-of-failure modeling technique. This data-driven procedure showed the dynamic attribute of real-time updating of the status of the aviation piston pump by fusing new observations to the current model and using Monte Carlo simulation for estimating the posterior distributions. On the other hand, Orchard et al. [26] used PF for the state-of-charge prognosis and risk of failure measurement of Li⁺ batteries and computed the confidence interval of the prediction algorithm by using the time of failure and the standard deviation of the RUL. Due to the enhanced time of estimation of the RUL and the confidence intervals, the algorithm can be integrated into a real-time prognostic and risk-management monitoring system. Again, Hu et al. [27] showed that Li⁺ batteries state-of-charge, and the RUL can be determined with Gauss–Hermite PF because of the computational advantage of not requiring a Jacobian matrix, which makes the extended Kalman filter require much computational time.

In this study, the advantages of the MPF over the traditional PF will be explored in a prognostic and RUL estimation of C&S by implementing a GA optimization framework that will enhance the MPF estimations for different GA generations. A multiphase sigmoidal model (MPSM) will be used to describe the decay pattern of the Li⁺ batteries’ charge capacities that will be used to exemplify the working of the developed algorithm. Using MPSM to extract the decay pattern of the Li⁺ batteries’ charge capacities will help to show the uniqueness in the GA estimated charge capacities at each generation. Hence, this gives more credence to the optimal multi-level particle filter (OPMPF) estimation results given that the MPF will be implemented with distinct charge decay information that depicts the original experimental results. This procedure will be in sharp contrast to the technique of using similar parametric values to determine the OPMPF by other researchers [22] who embarked on a similar study. The study will also compare the traditional multi-level particle filter (TRMPF) with the OPMPF that implements optimization of the charge capacities at the GA generations, prior to the establishment of the optimal generation that will give the best estimation of the charge capacities. The RUL will be estimated with the optimal MPF charge capacities in consideration of the different training/testing dataset partitions (TTDP) in a 9-fold cross-validation ensemble MPF architecture.

To further enhance the estimation of the retained life of C&S, and improve the prognostics, diagnostics and fault estimation, an algorithm that implements MPF with GA optimization is developed in this study. The use of MPF and GA is warranted by the effectiveness of the techniques in solving numerous computational modelling problems and the ease of implementation in complex systems analysis due to the robustness in the management of unknown data. The objective of this study is to develop a technique for prognostics health monitoring and estimation of the RUL of C&S, and test the developed algorithm with Li⁺ batteries’ charge capacity fade over the cycle time. This paper discusses the PF concept and the procedures for using MPF for future estimation of C&S states in Section 2. Section 3 describes the framework for OPMPF whereas Section 4 explains the working of the developed algorithm based on lithium-ion battery capacity fade. The new algorithm for OPMPF was also compared with the TRMPF in Section 4 while results and discussion are discussed in Section 5 and Section 6 was used for concluding the findings of the study.

2. Particle Filter Concept

The particle filter, which was introduced for optimal solutions of non-linear and non-Gaussian problems, has a great advantage of non-reliance on the local linearization technique for the computation process, which can be time-consuming with an increasing number of particles [28]. As a special form of generic sequential Monte Carlo simulation algorithm, it involves a state-space discretization that changes with time, due to the influence of measurement noises at the time steps [29]. Therefore, for a discrete state model, the state of the system will change according to Equation (1):

$$\{\begin{array}{c}{x}_k=f_k\left(x_{k-1},{\nu }_{k-1}\right)\\ z_k=h_k\left(x_k,{\Upsilon }_{k-1}\right) \end{array}$$

(1)

where, x_k, ν_k−1, f_k, z_k, h_k, and ϒ_k represent the vector of the system state at time k, the state noise vector at time k − 1, a non-linear, and time-dependent function of the state vector, noisy measurement of x_k, a nonlinear, and time-dependent function that describes the noise measurement process, and noise measurement vector, respectively.

The optimal solution of a particle filter problem involves the estimation of the system state (z_1:k) at time 1, 2, 3, …, k − 1, k using a Bayesian approach that has predicting steps requiring the probability distribution function p(x_0:k|z_1:k−1) to be computed recursively at the time k − 1 as per Equation (2):

$$p\left(x_{0:k}|z_{1:k-1}\right)={{\displaystyle \int }}^{\text{}}p\left(x_{0:k}|x_{k-1}\right)p\left(x_{k-1}|z_{1:k-1}\right)d{x}_{k-1}$$

(2)

Generally, a system with probability distribution p (x_0:k−1|z_1:k−1), will form the prior distribution for a future state p(x_0:k|z_1:k−1) if the future state depends on the discrete state function shown in Equation (1) [29]. In the same vein, p(x_0:k|z_1:k−1) will be the prior distribution for a future state p(x_0:k|z_1:k) if the system follows the condition of the system state vector x_k. Hereafter, the updating step of the Bayesian concept depends on the prior probability distribution, and the probability density function of the observed new measurements obtained from the system at the time k, to determine the posterior distribution as per Equation (3) [29,30]:

$$\{\begin{array}{l}p\left(x_{0:k}|z_{1:k}\right)\propto p\left(z_k|x_{0:k}\right)p\left(x_{0:k}|z_{1:k-1}\right)\\ p\left(x_{0:k}|z_{1:k}\right)=\frac{p\left(z_k|x_{0:k}\right)p\left(x_{0:k}|z_{1:k-1}\right)}{p\left(x_{0:k}|z_{1:k-1}\right)}\end{array}$$

(3)

The complex nature of Equation (3) results in the use of Monte Carlo estimation for the solution.

2.1. Sequential Important Sampling (SIS)

This basic Monte Carlo estimation technique has found a useful application in the optimal solution of PF problems because of the challenges of obtaining analytical solutions of the posterior distributions of the system state vector [29,31]. Sequential important sampling (SIS) uses weighted sets of samples for the recursive approximation of the values of the posterior distribution p(x_k|z_1:k) at a time k from the prior distribution p(x_k−1|z_1:k−1) at a time k − 1, by using the target distribution [p(x)] samples drawn from a proposed distribution [q(x)]. This is done in such a way that the future sample µ is a representative of the non-linear function of the original sample f(x) and can be represented with Equation (4) [31]:

$$\mu =E\left(f\left(x\right)\right)={{\displaystyle \int }}^{\text{}}f\left(x\right)p\left(x\right)dx$$

(4)

For f(x)p(x) ≠ 0, q(x) ≥ 0 and E|.| represents the expectation of q(x), Equation (4) can be rewritten as per Equation (5) [28]:

$$\{\begin{array}{l}\mu =E\left|w\left(x\right)f\left(x\right)\right|\\ w\left(x\right)=\frac{p\left(x\right)}{q\left(x\right)}\end{array}$$

(5)

If the sample is identically and independently drawn from a distribution of q(x), it can be used to estimate p(x) once the weighted element (important weight) w(x) in Equation (5) is properly sorted out [29,31]. Henceforward, for some random samples drawn from q(x), the future sample µ^(ns) can be estimated with Equation (6):

$${\mu }^{\left(n_s\right)}={\displaystyle \sum _{i=1}^{n_s}}\frac{w\left(x^i\right)f\left(x^i\right)}{w\left(x^i\right)}$$

(6)

The value of the future distribution µ^(ns) obtained with n_s samples tends to µ at infinity [32] and solving Monte Carlo simulation problems requires an enormous generation of many variables over a given time k. However, the target distribution p(x) induces a chain-looking decomposition of x = (x₁, …, x_d) in a state-space model, and that can be represented by Equation (7) [33]:

$$\{\begin{array}{l}p\left(x\right)=p\left(x_1\right){\displaystyle \prod _{k=2}^d}p\left(x_{0:k}|z_{1:k}\right)\\ for \left[x_1,x_2, \dots ,x_d\right],1\le k\le d\end{array}$$

(7)

The proposed distribution q(x) unto the time (1 ≤ k ≤ d) can equally be written in the form of Equation (7) as per Equation (8), and the important weight w(x) shown in Equation (5) can be represented by Equation (9) [31]:

$$\{\begin{array}{l}q\left(x\right)=q\left(x_1\right){\displaystyle \prod _{k=2}^d}q\left(x_{0:k}|z_{1:k}\right)\\ for \left[x_1,x_2, \dots ,x_d\right],1\le k\le d\end{array}$$

(8)

$$w_k^i=w_{k-1}^i\frac{p\left(x_{0:k}^i|z_{1:k}^i\right)}{q\left(x_{0:k}^i|z_{1:k}^i\right)}$$

(9)

2.2. Resampling Technique

Sequential important sampling has a few issues such as degeneracy, which is a situation where few particles have significant weights whereas others have smaller weights, and sample impoverishment, which occurs due to the redrawing of particles with large important weights many times in a simulation experiment [29]. Minimization of the variance of the important weight via resampling has been adopted to solve the problem of degeneracy whereas the introduction of an auxiliary random variable to the sample has acted as marginal distribution to the target distribution and helped to increase the variability of the important weight [28,34].

2.3. Multi-Level Particle Filter (MPF)

For a state-space model that has multiple levels, the system state of the PF can be represented using the original PF formulation in Equation (1) as per Equation (10) with τ representing the higher levels [23,24]:

$$x_k=f_k\left(x_{k-1},x_{k-2}, \dots , x_{k-\tau }, {\nu }_{k-1}\right)$$

(10)

By applying the SIS theory that requires the particles to be drawn from the important density q(x_0:k|z_1:k) and using the conditional independency property, the relationship between particle filter and MPF can be obtained by substituting the vector of the system state shown in Equation (1) with that shown in Equation (10), and updating the important weight shown in Equation (9) will result in the new MPF important weight as per Equation (11) [22,24]:

$$\{\begin{array}{l}{w}_k^i\propto \frac{p\left(z_k|x_k^i\right)p\left(x_k^i|x_{k-\tau :k-1}^i\right)p\left(x_{0:k-1}^i|z_{1:k-1}\right)}{q\left(x_k^i|x_{1:k-\tau :k-1}^i\right)q\left(x_{0:k-1}^i|z_{1:k-1}\right)}\\ w_k^i=w_{k-1}^i\frac{p\left(z_k|x_k^i\right)p\left(x_k^i|x_{k-\tau :k-1}^i\right)}{q\left(x_k^i|x_{1:k-\tau :k-1}^i,z_k\right)}\end{array}$$

(11)

In this study, the implementation of the MPF involves following the procedures shown below:

-

for i = 1, 2, 3, …, n_s samples;

-

$x_k^{\left(i\right)}~q\left(x_k^i|x_{k-\tau :k-1,}^i{z}_k\right)$;

-

then set $x_k^{\left(i\right)}\triangleq \left(x_k^{\left(i\right)},x_{k-\tau :k-1}^{\left(i\right)}\right)$;

-

estimate the importance weights using Equation (11) and normalize them;

-

the normalized important weights $w_k^{\left(i\right)}=w_k^{\left(i\right)}{\left[{{\displaystyle \sum }}_{i=1}^{n_s}{w}_k^{\left(i\right)}\right]}^{-1}$;

-

randomly select a variable θ with values between 0 and 1;

-

find particles from $x_k^{\left(i\right)}$ such that $\theta \ge w_k^{\left(i\right)}$; NB: normalized weight is used;

-

the estimated particle: $x_k^{\left(est\right)}=x_{k-\tau :k-1}^{\left(1\right)}$;

-

end.

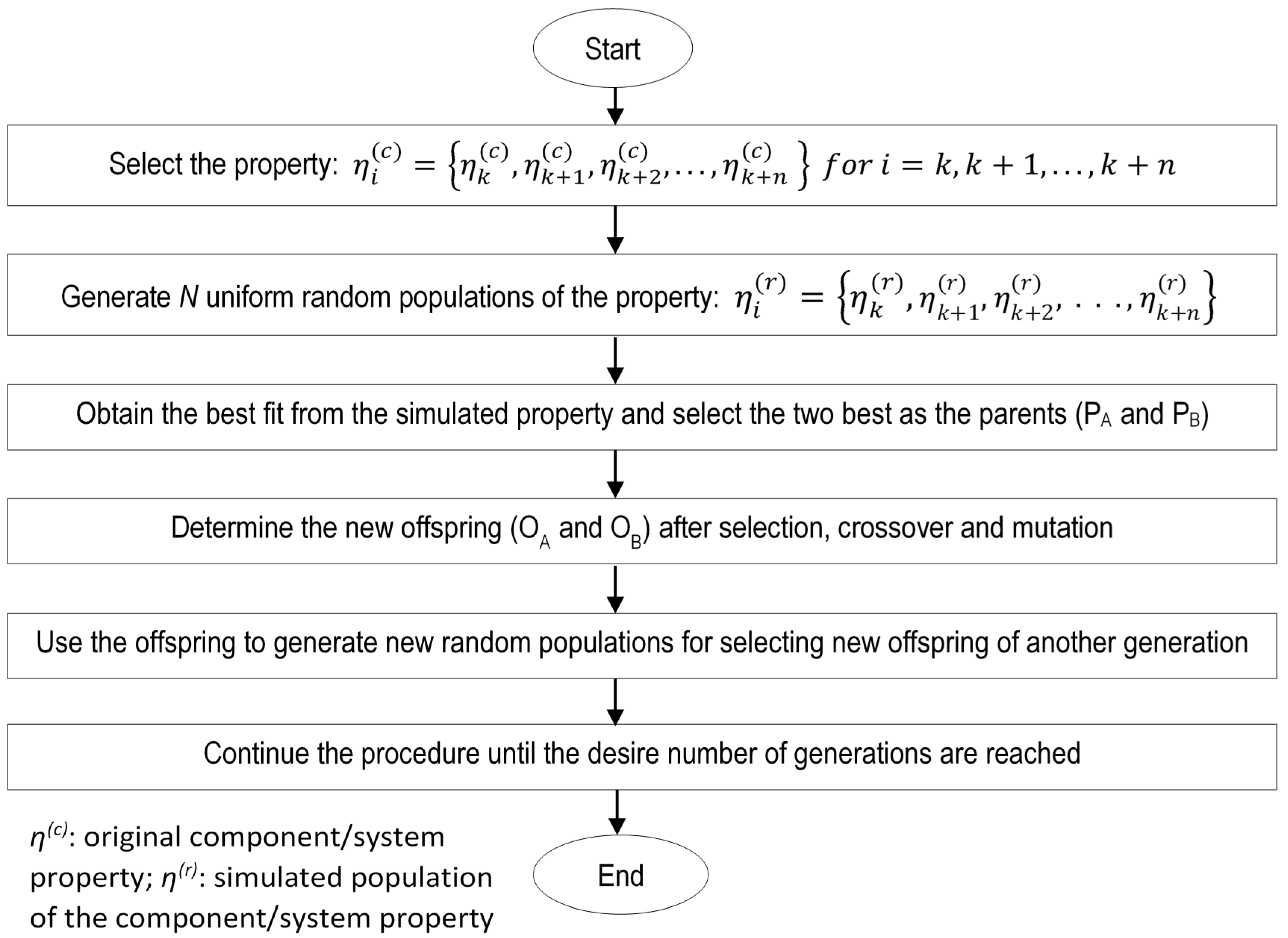
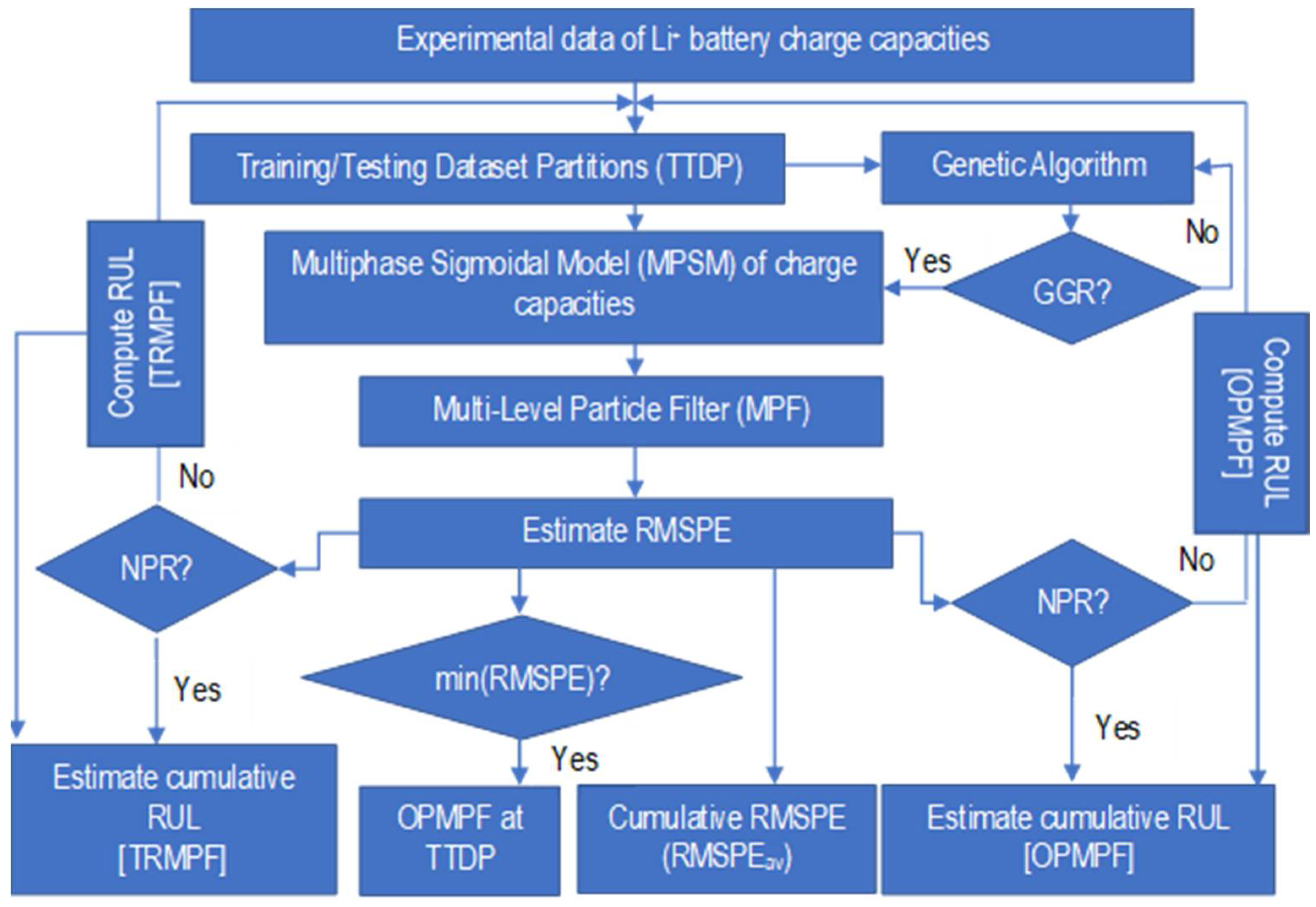
3. Framework for Optimal Multi-Level Particle Filter (OPMPF) Estimation

Despite the ease of implementing a PF and the possibilities of obtaining improved results with MPF as exemplified with the works of different authors [22,24,35], there is also room for improvement. This is the reason why it is important to improve the results that are obtained from the MPF via an optimization framework, which can be provided by the GA via evolutionary theory-based new estimations.

Genetic Algorithm (GA) for OPMPF Estimation

GA is an evolutionary theory technique that employs natural evolution principles to find solutions to natural problems using chromosomes, which represent individual solutions to problems [36,37]. GA has found useful applications in many industrial problems and has been used by numerous authors [38,39,40,41,42,43] in literature for numerous optimization problems; hence, interested readers could consult the references for more insight on the topic. In GA, the arrangement of the discrete constituents of the chromosomes known as genes, give them their unique characteristics; hence, the need for selection, crossover, and mutation in GA to develop new traits of emerging individuals in the solutions of real-world problems. A binary (“1” & “0”) encoding of the chromosomes was used in this work given the successful implementation of the technique by many researchers [36,37]. The process of natural selection in GA requires the picking of the best genes of the chromosomes involved in the evolutionary process and combining them according to a certain proportion (crossover rate). These genes can also be flipped in some special instances (mutation) due to modifications caused by their specific adaptations and environmental constraints. The processes of chromosome selection, gene crossover and mutation are shown in Figure 1.

For the GA to be used for solving optimization problems, many chromosomes are randomly generated from the known parametric values that represent the original or known characteristics of the variable(s) of interest, and two parents (P_A and P_B), which are the best fit amongst the populations, are selected. The combination of the genes of these parents through a process known as crossover requires the swapping of the genes to form new offspring (O_A and O_B). The crossover normally occurs at a rate that is sufficient to allow for evolution to occur and can range from 50% to 85% [37]. Since genetic traits can be influenced by environmental conditions, and the passage of time in the evolutionary process, the genes in the chromosomes sometimes develop some new adaptive features via the process of mutation. This procedure (mutation) results in the flipping of the genes from “1” to “0” or vice versa, as shown in O_AM and O_BM. Considering the influence of time on evolutionary changes, it is possible that the near-ideal characteristics of the chromosomes could be achieved after many generations, hence, helping in the optimization of a given real-life problem. The procedure for using GA to estimate the evolution of C&S characteristics over time is shown in Figure 2. To determine the generation of the GA that will give the OPMPF solution, the estimated values at the generations are subjected to MPF and the best fit result determined by comparison with the original experimental results, using error estimation standards.

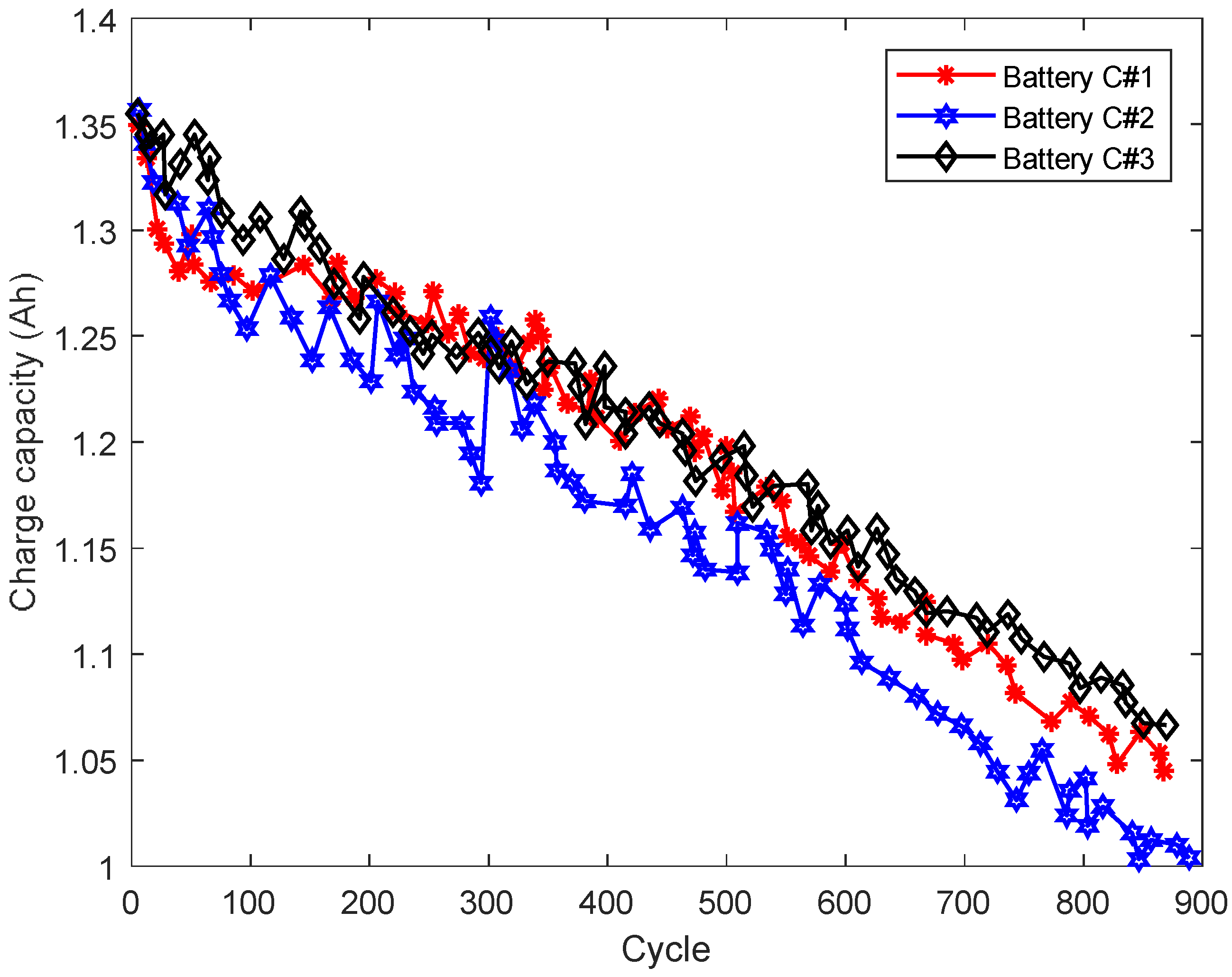
4. Illustrative Case Study of Lithium-Ion Battery Charge Capacity Decay

To illustrate the application of GA in OPMPF estimation, and the determination of the RUL of C&S, the charge capacity fade of lithium-ion batteries was used. Three lithium ion (Li⁺) batteries designated as C#1, C#2 and C#3 were obtained from the database of the Centre for Advanced Lifecycle Engineering (CALCE) of Maryland University [44,45]. The batteries were tested at room temperature using an Airbin BT 2000 battery-testing system with the initial manufacturer-rated capacity of 1.35 Ah. This lithium cobalt oxide (LiCoO₂) cathode battery underwent constant charging at the rate of 0.5 C to a voltage of 4.2 V, which was constantly maintained until the current got to 0.05 A. The discharge of the battery also followed the same procedure with a constant discharge current of 0.5 C from 4.2 V to a cutoff voltage of 2.7 V. The estimated charge capacities of the batteries from the experimental results is shown in Figure 3.

4.1. Lithium-Ion Battery Remaining Useful Life (RUL) Estimation

It is very important to note that the TRMPF implemented the MPF procedure for the Li⁺ batteries’ charge capacities with the original experimental data, whereas GA optimization of the charge capacities at different generations was done prior to MPF in OPMPF estimation. For effective prognosis and RUL estimation with MPF, GA was introduced to determine the optimal generation of the battery charge capacity that will produce the best fit result when compared with the experimental data. To this end, to determine the OPMPF of the Li⁺ battery charge capacity, GA was used to estimate the evolutionary charge capacities of the batteries at the charging cycles for different generations, and the charge capacities at the generations were subjected to MPF following the procedures described in Section 2.3. The framework used for TRMPF and OPMPF is shown in Figure 4.

In this study, 2000 random uniform values of the charge capacities of the Li⁺ batteries were generated using the minimum and maximum values of the experimental data of the charge capacities, for each of the charging cycles. This count of the random numbers was used after several trials because it provided the adequate randomization for selecting the values that best fit the charge capacities of the batteries for each of the charging cycles.

For an experimental Li⁺ battery dataset given by Q^(exp)(k) = {Q^(exp)(k_i), Q^(exp)(k₂), …, Q^(exp)(k_ns)} obtained at a given experimental charging cycle time k_i = {k₁, k₂, …, k_ns}, the objective functions {f₁, f₂, …, f_ns} of the GA is to obtain the optimal values of the charge capacities for each charging cycle. This was determined using the expression shown in Equation (12):

$$Obj\left(function\right)=min\{\begin{array}{c}{f}_1={\displaystyle \sum _{i=1}^M}\left|Q^{\left(exp\right)}(k_1)-Q_i^{\left(sim\right)}\left(k_1\right)\right|\\ f_2={\displaystyle \sum _{i=1}^M}\left|Q^{\left(exp\right)}(k_2)-Q_i^{\left(sim\right)}\left(k_2\right)\right|\\ ⋮\\ f_{ns}={\displaystyle \sum _{i=1}^M}\left|Q^{\left(exp\right)}(k_n)-Q_i^{\left(sim\right)}\left(k_{n_s}\right)\right|\end{array}$$

(12)

Here, M represents the number of the randomly generated initial population of the charge capacities of the battery, Q^(exp)(k₁), Q^(exp)(k₂), …, Q^(exp)(k_ns) represents the experimental charge capacities of the battery at the different charging cycle, Q^(sim)(k₁), Q^(sim)(k₂), …, Q^(sim)(k_ns) represents the simulated value of the charge capacities at the charging cycles, and n_s represents the number of charging cycles from which the charge capacities were measured in the charging/discharging experiment.

The optimal solutions obtained at each of the charge capacities helps to select the two parents for crossing. Although several crossover rates could be used as stated previously, 0.70 was adopted because it gave reasonable estimations, and the mutation rate of 0.01 was applied to the evolutionary process. Some researchers have used mutation rates that were as high as 0.2 because of the need to give significant room for evolution, and to prevent chromosomes from being similar [37]. Unfortunately, high values of the mutation rate could result in the introduction of new genetic characteristics that may significantly alter the original traits of the chromosomes, and then result in an excessive evolutionary variation [36]. The crossed chromosomes from the parents result in two offspring with one of them most fitted to the original chromosomes of the experimental battery charge capacity. This offspring is taken as the expected evolutionary generated battery charge capacity at that generation and the charging cycle. To preserve the genetic traits of original chromosomes, the two offspring are used for randomly generating the new population that is used for selecting the next fitted offspring for the succeeding generation. This procedure continues until the expected number of generations of interest is reached.

The optimization for obtaining the OPMPF solution was formulated according to the objective function shown in Equation (13):

$$obj \left(function\right)=\{\begin{array}{l}\min f_R\left(Q_i^{\left(exp\right)},Q_{ij}^{\left(g\right)}\right)\\ f_R={\displaystyle \sum _{j=1}^{n_g}}{\displaystyle \sum _{i=1}^{n_s}}{\left[\frac{Q_i^{\left(exp\right)}-Q_{ij}^{\left(g\right)}}{Q_i^{\left(exp\right)}}\right]}^2*100\\ Q_{ij}^{\left(g\right)}={\left[\begin{array}{ccc}{Q}_{\left(1,1\right)}^{\left(g\right)}& \cdots & Q_{\left(1,i\right)}^{\left(g\right)}\\ ⋮& \ddots & ⋮\\ Q_{\left(j,1\right)}^{\left(g\right)}& \dots & Q_{\left(j,i\right)}^{\left(g\right)}\end{array}\right]}_{\begin{array}{c}i=1,2,\dots ,n_s\\ j=1,2,\dots ,n_g\end{array}}\end{array}$$

(13)

Here, Q^(exp) is the experimental data of the charge capacities that is expressed as Q^(exp) = {Q^(exp)(k₁), Q^(exp) (k₂), …, Q^(exp)(k_ns)}and k₁, k₂, …, k_ns are the charge cycles at which the charge capacities were obtained, Q^(g) represents the charge capacity obtained at the GA generations, n_s represents the number of samples of the experimental data, and n_g represents the number of generations of the GA under consideration. For this study, the algorithm has been used to obtain 20 generations of the battery charge capacities, which were further used to get the OPMPF by determining the generation with the least root mean square percentage error (RMSPE) after MPF at the various TTDP.

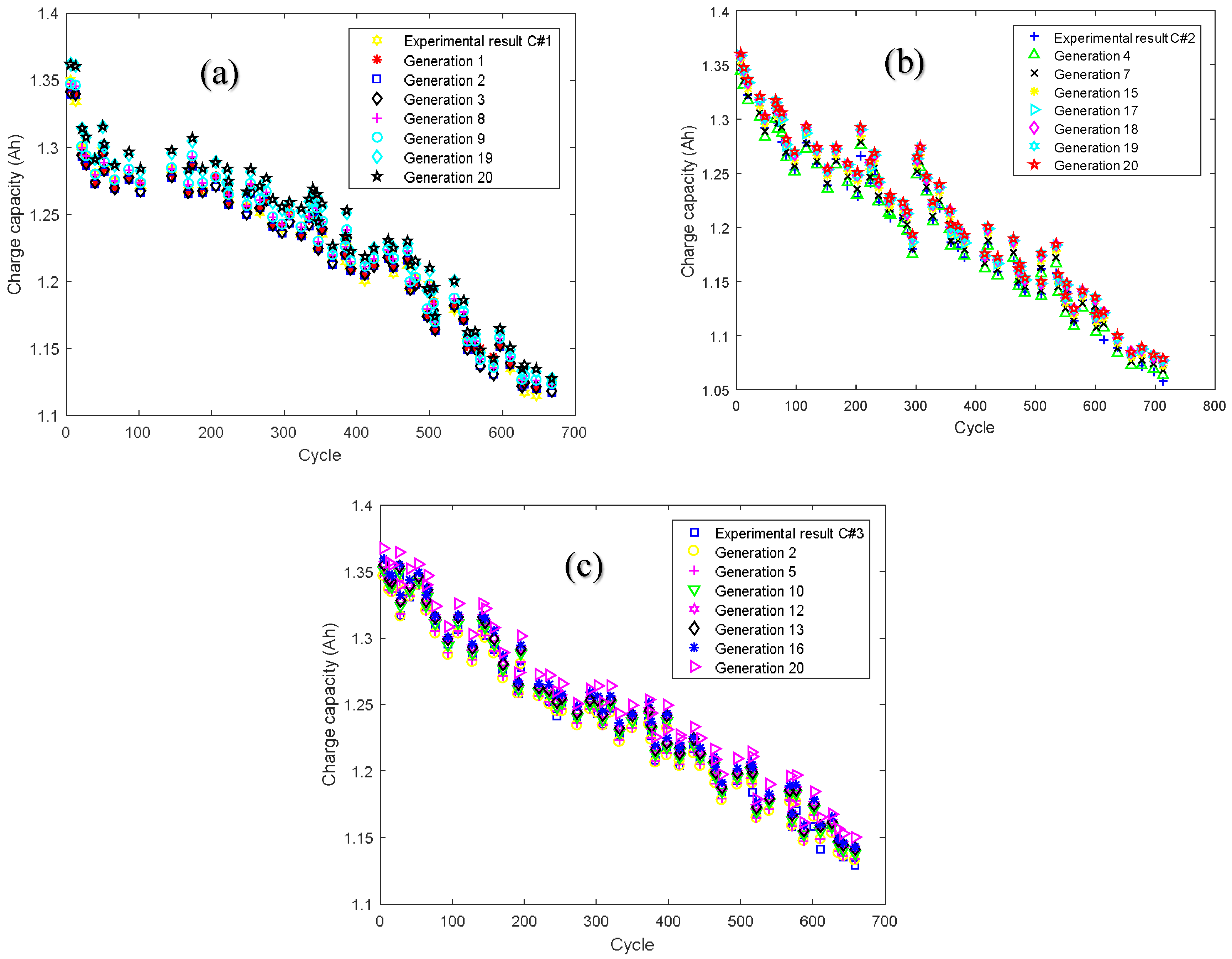
4.2. Decay Trend of GA-Estimated Lithium-Ion Battery Charge Capacity

Before the implementation of MPF, the decay pattern of the GA-estimated battery charge capacities at the generations was determined. This was done with a MPSM that represents a confined exponential decay model shown in Equation (14) because the battery charge capacities decay follows a sigmoidal pattern [27,45,46]:

$$Q\left(k\right)=P_1{e}^{\left(-r_{1}k\right)}+P_2{e}^{\left(-r_{2}k\right)}$$

(14)

Here, P₁, r₁, P₂, r₂ are model parameters that will be estimated with the battery charge capacities (Q) and k represent the charging cycle.

The model equation is vital for determining the system state equation of the GA obtained charge capacities and gives an initial working guide for estimating the measurement noise in the MPF. The prediction errors of the MPSM, which were determined as the difference between the MPSM and GA-estimated charge capacities at the generations, were used to compute the measurement noises in the MPF. After different trials of various values of the mean absolute errors (MAEs) in the MPF, the best estimates for the measurement noises were obtained as 35% of the MAE for batteries C#1, and C#2, and 50% for battery C#3. This variation in the estimated measurement noises of the batteries could be attributed to the process of the genes’ recombination in the evolution processes at the GA generations.

4.3. Lithium-Ion Battery RUL Estimation

The RUL of the batteries were determined at 80% end-of-life (EOL) threshold by estimating the time it takes to have the initial charge capacity of the batteries depleted to 80% for the various TTDP, using a 9-fold cross-validation ensemble (Figure 5) of the TRMPF and OPMPF. The average of the RUL estimation at the TTDP formed the expected cumulative RUL (RUL_av) of the batteries as per Equation (15). The fitness of the cross-validation ensemble of the TRMPF and OPMPF were also determined using RMSPE as per Equation (16), and the average RMSPE (RMSPE_av) was computed with Equation (17):

$$RU{L}_{av}\left(k\right)=\frac{RU{L}_1\left(k\right)+RU{L}_2\left(k\right)+ \dots +RU{L}_{n_{cv}}\left(k\right)}{n_{cv}}=\frac{1}{n_{cv}}{\displaystyle \sum _{i=1}^{n_{cv}}}RU{L}_i\left(k\right)$$

(15)

$$RMSPE=\sqrt{\frac{1}{n_s}{\displaystyle \sum _{i=1}^{n_s}}{\left[\frac{Q_i^{\left(exp\right)}-Q_i^{\left(mpf\right)}}{Q_i^{\left(exp\right)}}\right]}^2}$$

(16)

$$RMSP{E}_{av}=\frac{RMSP{E}_1+RMSP{E}_2+ \dots +RMSP{E}_{n_{cv}}}{n_{cv}}=\frac{1}{n_{cv}}{\displaystyle \sum _{i=1}^{n_{cv}}}RMSP{E}_i$$

(17)

Here, Q^(mpf), Q^(exp), n_cv and n_s represent TRMPF or OPMPF estimated charge capacities, experimentally determined charge capacity, number of the TTDP and the number of tested samples in the computation, respectively.

5. Results and Discussion

The results obtained from the GA of the three Li⁺ battery charge capacities for some of the GA generations for the 80% training and 20% testing dataset partition (80:20 TTDP) is shown in Figure 6. The difference between the GA estimations of the charge capacities at the various generations and the experimental results of the datasets were determined with mean absolute error (MAE) and mean absolute percentage error (MAPE), and are shown in

Table 1. Summary of the difference between the GA estimated charge capacities and the experimental results as determined with the mean absolute error (MAE) and mean absolute percentage error (MAPE) at the 80:20 TTDP.

Genetic Algorithm Generations	Battery C#1		Battery C#2		Battery C#3
	MAE	MAPE (%)	MAE	MAPE (%)	MAE	MAPE (%)
1	0.012542	1.0262	0.014126	1.1692	0.009827	0.7885
2	0.012780	1.0494	0.013663	1.1326	0.009964	0.8084
3	0.012692	1.0426	0.013521	1.1211	0.010006	0.8123
4	0.012692	1.0426	0.013590	1.1267	0.009875	0.8022
5	0.012693	1.0427	0.013614	1.1290	0.009932	0.8066
6	0.012472	1.0240	0.013190	1.0919	0.010561	0.8568
7	0.012583	1.0327	0.013432	1.1102	0.010215	0.8281
8	0.012591	1.0334	0.013410	1.1083	0.010224	0.8287
9	0.012512	1.0268	0.013429	1.1091	0.010210	0.8275
10	0.012539	1.0287	0.013446	1.1114	0.010172	0.8243
11	0.012437	1.0201	0.013350	1.1032	0.010081	0.8158
12	0.012690	1.0398	0.013484	1.1112	0.009742	0.7879
13	0.012690	1.0398	0.013478	1.1107	0.009742	0.7879
14	0.012648	1.0357	0.013847	1.1398	0.009795	0.7907
15	0.012585	1.0306	0.013723	1.1292	0.009771	0.7888
16	0.012454	1.0194	0.013779	1.1333	0.009680	0.7812
17	0.012967	1.0583	0.013960	1.1443	0.010447	0.8396
18	0.013049	1.0647	0.013625	1.1170	0.010437	0.8389
19	0.013126	1.0714	0.013863	1.1355	0.010392	0.8352
20	0.013250	1.0810	0.013605	1.1133	0.010576	0.8499

. The small difference between the GA values of the charge capacities and the original experimental results (<1.2%) is a good indication of the high precision of the study technique. Lithium-ion battery C#3 charge capacities were determined with the highest accuracy level with MAPE of between 0.79% and 0.85% followed by battery C#1 with MAPE of 1.02% to 1.08%, whereas battery C#2 has a MAPE of between 1.09% to 1.17%.

The MPF estimations of some of the GA generations shown in Figure 7 give an indication of the correlation of the original experimental dataset with the MPF of the GA generations at 80:20 TTDP. The figures also show that battery C#3 has a higher prediction accuracy with a smaller difference between the MPF and the experimental dataset compared to batteries C#1 and C#2. This is further substantiated by the difference between the MPF-estimated charge capacities and the experimental results per

Table 2. Summary of the difference between the MPF-estimated charge capacities at the GA generations with the experimental data, as measured with the root mean square percentage error (RMSPE) at the 80:20 TTDP.

Generations	Battery C#1		Battery C#2		Battery C#3
	Training	Testing	Training	Testing	Training	Testing
	RMPSE (%)	RMPSE (%)	RMPSE (%)	RMPSE (%)	RMPSE (%)	RMPSE (%)
1	1.0119	1.4345	1.6339	2.0210	1.2979	0.9196
2	2.2817	1.7134	1.7442	1.1866	0.9316	0.8407
3	2.1552	1.0190 *	1.6275	2.9504	1.0506	2.5433
4	2.9195	3.0299	1.8242	0.9584 *	0.9463	0.7707
5	2.3627	2.4592	1.6717	1.3328	1.0331	0.9112
6	2.4744	2.4617	1.6797	3.4521	1.0659	1.8295
7	2.7419	1.1883	1.6813	3.7837	0.8799	2.8126
8	2.4283	2.0409	1.5439	2.6058	1.0385	1.8660
9	2.3687	1.5284	1.5756	3.5130	1.0959	2.7003
10	4.8160	5.3376	2.7919	1.1718	1.7588	1.0078
11	1.8373	1.5030	1.7296	3.3415	1.1747	2.1394
12	3.9640	4.7354	2.0801	1.1794	1.2603	0.6644
13	2.6407	1.8496	1.7156	2.8668	1.1547	2.1764
14	1.6035	1.6166	1.8933	2.7728	1.7223	2.2987
15	2.7887	2.0031	1.6621	2.1270	1.0690	1.6782
16	2.9095	4.0364	1.6345	1.2570	1.1555	0.4609
17	2.2468	2.4977	1.6312	1.2087	1.4299	1.1629
18	2.1851	1.3490	1.6992	3.3097	1.1238	2.0182
19	2.4045	2.6096	1.7789	1.5067	1.3861	0.7031 *
20	3.5188	3.9359	1.8373	0.9990	1.3124	1.2113

Bold *: represents the optimal GA generation, which was considered with respect to the RMSPE of the testing dataset.

.

The GA generation, which gave the best fit value of the charge capacities for the testing dataset at the TTDP, was used as the optimal value for estimating the RUL at the OPMPF (see Table 2). The testing dataset was used for determining the optimal solution because it was not used in the initial training of the model, and will give an unbiased judgement of the trained model’s behavior. Considering the 9-fold cross-validation ensemble in Figure 5, and using Equation (16), the average RMSPE of the OPMPF was obtained for the batteries. The average RMSPE for the TRMPF was also determined at the TTDP after using the experimental data for the RMSPE estimation. The summary of the results of the RMSPE estimated with TRMPF and OPMPF are shown in

Table 3. Comparison of the RMSPE of the OPMPF and traditional multi-level particle filter (TRMPF) of the batteries.

Training/Testing Dataset Partitions (TTDP)	Battery C#1		Battery C#2		Battery C#3
	OPMPF	TRMPF	OPMPF	TRMPF	OPMPF	TRMPF
90:10	0.4798	9.028	1.0752	2.3793	0.5422	9.4759
80:20	1.0191	7.4073	0.9756	2.1281	0.4413	8.2846
70:30	1.159	11.0494	1.0518	5.7559	0.7156	11.8412
60:40	1.0437	11.8767	1.1141	9.3161	0.652	12.6843
50:50	1.2067	13.2404	1.219	8.7671	0.8023	12.1215
40:60	0.9692	13.4266	0.9435	10.8667	1.0859	15.5847
30:70	0.8164	12.7947	1.6497	11.3206	1.5076	17.0099
20:80	7.5976	27.6519	7.3983	12.0204	11.8386	31.4732
10:90	7.855	33.1341	9.6566	14.6807	1.4086	20.922
RMSPEav (%)	2.4607	15.5121	2.7871	8.5817	2.1105	15.4886
Standard deviation	2.8224	8.2709	3.1203	4.0882	3.4572	6.7322

. It is important to note that the difference between the battery charge capacities obtained at the various TTDP was consistently lower for the OPMPF than the TRMPF. This is an indication of the immense importance of the GA in the optimization of the Li⁺ battery charge capacities. From Table 3, the RMSPE of battery C#1 obtained by TRMPF is 6.3 times more than that obtained by OPMPF while batteries C#2 and C#3 have the RMSPE obtained by the TRMPF as 3.08 times and 7.33 times, respectively, higher than those obtained by the OPMPF.

The variation of the RUL of the batteries determined with the OPMPF and TRMPF for some of the TTDP is shown in Figure 8. The figures show that the greater the training dataset, the closer the determined RUL of the batteries to the ideal values because of the enhanced fitting. To avoid an overfitting problem, the cross-validation ensemble that considered training and testing partitions from lower values to higher ones was necessary; hence the estimation of the RUL as the average values of the individual RUL results at the TTDP, as per

Table 4. End-of-life (EOL) failure cycle for the optimal and traditional particle filters for the batteries.

Experimental Result
Battery	C#1		C#2		C#3
80% EOL failure cycle	746		660		830
OPMPF and TRMPF predictions RUL at different Training (TR) and Testing (TS) datasets partitions
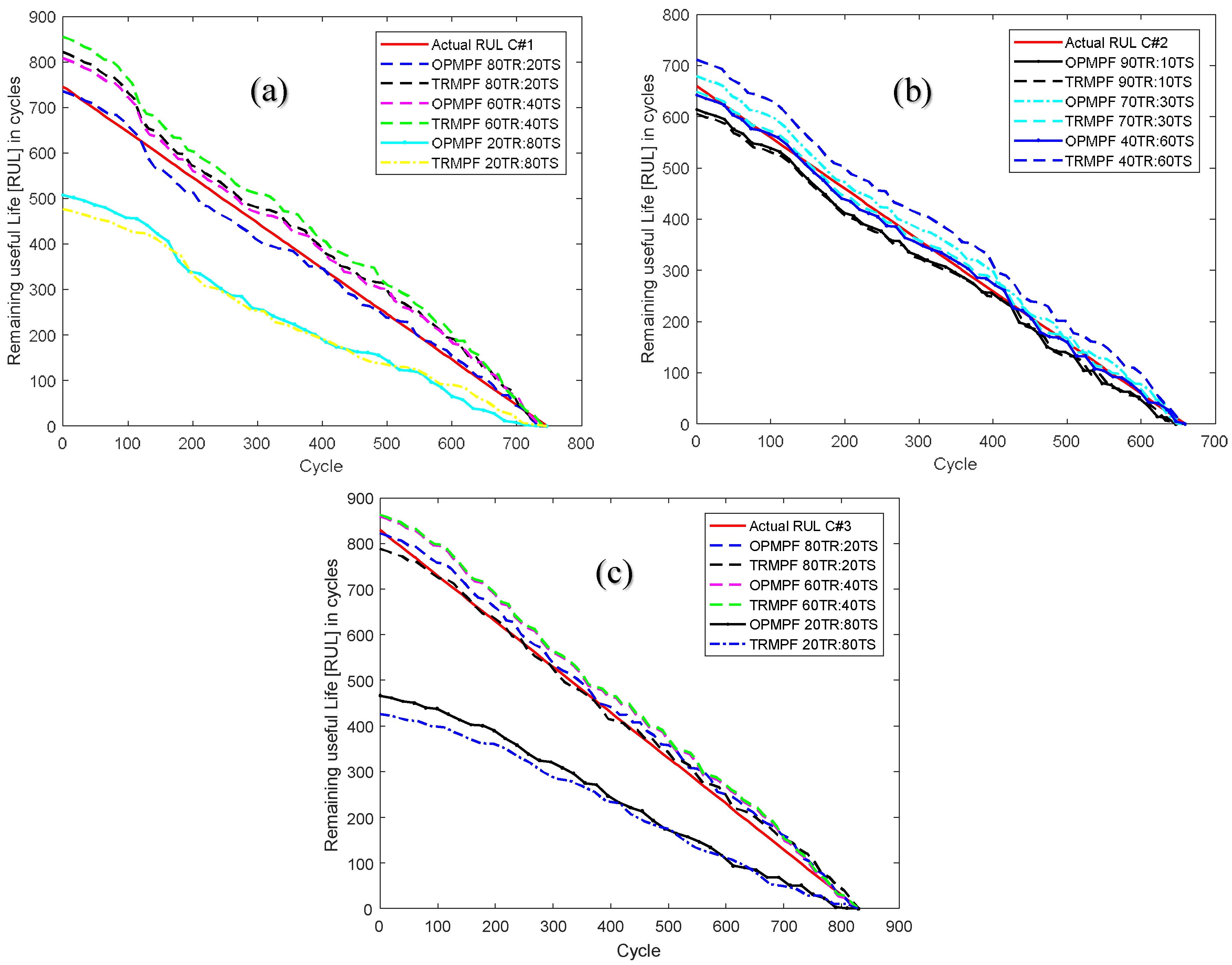
Training/Testing Dataset Partition (TTDP):TR:TS	C#1		C#2		C#3
	OPMPF	TRMPF	OPMPF	TRMPF	OPMPF	TRMPF
90:10	738	630	614	606	822	788
80:20	736	821	626	746	834	n/a
70:30	824	737	679	649	860	863
60:40	808	856	694	666	835	n/a
50:50	790	n/a	700	783	815	n/a
40:60	789	n/a	642	711	823	854
30:70	767	n/a	714	n/a	830	n/a
20:80	508	476	n/a	n/a	466	426
10:90	539	345	500	n/a	n/a	n/a
RULav (cycle)	722	644	646	694	786	733
Standard deviation	110	184	65	60	121	179
Difference	24	102	14	−34	44	97
% variation	3.20%	13.65%	2.10%	−5.08%	5.35%	11.72%

(n/a means that prediction did not converge, and negative signs show cycle beyond the experimental results).

. The information in the table, which depicts the mean RUL of the batteries and the difference between the RUL obtained with TRMPF and OPMPF, indicates the superiority of the OPMPF values over the TRMPF estimates. The better values of the RUL obtained with OPMPF in comparison to those gained with TRMPF, indicates that the evolution of the charge capacities with GA overly influenced the computational results of the MPF. Again, the OPMPF results are highly comparable to most of the PF prognosis results in the literature [46,47,48] because the error inherent in the entire prediction process is minimal judging from the information in Table 4.

6. Conclusions

To better estimate the retained life of C&S, an algorithm that combines MPF and GA optimization was used in an OPMPF to determine the RUL. The study implemented the prognosis and RUL of Li+ batteries by using the charge capacities at the cycling in a TRMPF and OPMPF to predict the capacity fade. The TRMPF was done by using the experimental charge capacities at different charging cycles in a direct MPF at different TTDP, whereas in OPMPF GA helped to optimize the charge capacities at the different generations. The optimized charge capacities at the generations were used for MPF prior to the determination of the expected values.

Three experimental results of Li+ batteries were tested with the technique by implementing a 9-fold cross-validation ensemble that represented a TTDP with training and testing ratios of 10:90, 20:80, 30:70, 40:60, 50:50, 40:60, 30:70, 20:80 and 10:90. At the 80% EOL threshold, the average RMSPE and RUL of the batteries determined with TRMPF were found to be between 8.58~15.51% and 5.08~13.65%, respectively. These values were 4.07~5.60 times and 2.42~2.55 times more than the RMSPE and RUL values of the OPMPF, respectively. The variation in the estimation results of the TRMPF and OPMPF gives a good indication of the superiority of the OPMPF technique over the TRMPF. This advantage, which can be traced to the GA optimization of the charge capacities at the different generations, has helped to enhance the prediction accuracy of MPF that has already been shown to give better predictions of components/systems performance than the particle filter.

It may be important to have the OPMPF technique incorporated into real-time components/systems prognosis architecture since GA optimization has the potential to enhance MPF estimation. The number of generations of the GA can be further improved by increasing the number of GA generations in the optimization framework prior to the MPF to further boost the OPMPF result.