User-Demand-Oriented Healthy Charging Control Strategy for EVs Based on Football Team Training Algorithm
Abstract
1. Introduction
- An EHSBE model is proposed to accurately predict the user’s charging duration. This hybrid framework not only enhances the accuracy of individual models through a boosting module but also maximizes model diversity by integrating a stacking module. As a result, it delivers highly reliable and robust predictions, effectively handling diverse charging demands.
- Distinguished from the existing majority of studies, a user-demand-oriented healthy charging control strategy is developed. Considering users’ charging durations, the strategy employs the FTTA to solve for the optimal charging current through multi-objective equations with constraints. The FTTA intelligently adjusts the charging current based on user demand to complete the charging task. Moreover, this strategy prevents overcharging, reduces heat generation, extends battery life, and avoids low user satisfaction.
- The experiments on the hardware platform confirm the feasibility and effectiveness of the proposed strategy. Simulation and experimental results across various charging durations demonstrate that the proposed healthy charging strategy outperforms fast charging.
2. Research Framework
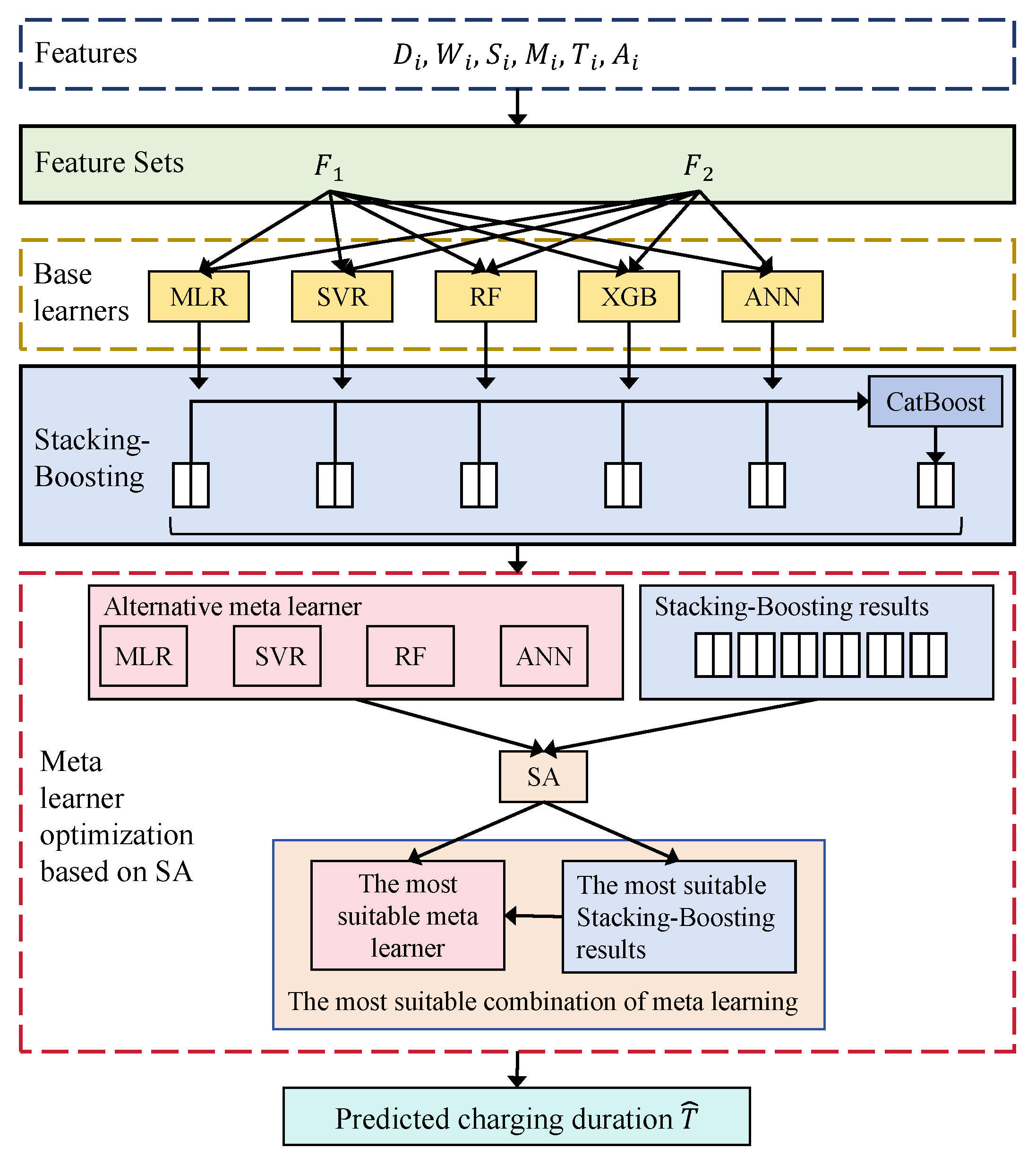
3. Prediction of User Charging Duration
3.1. Extraction and Selection of Charging Features
3.2. Establishment of Charging Duration Prediction Model
3.2.1. Selection of Base Learners
3.2.2. Boosting Module
3.2.3. Hybrid Stacking Module
3.2.4. Meta-Learner Optimization Based on SA
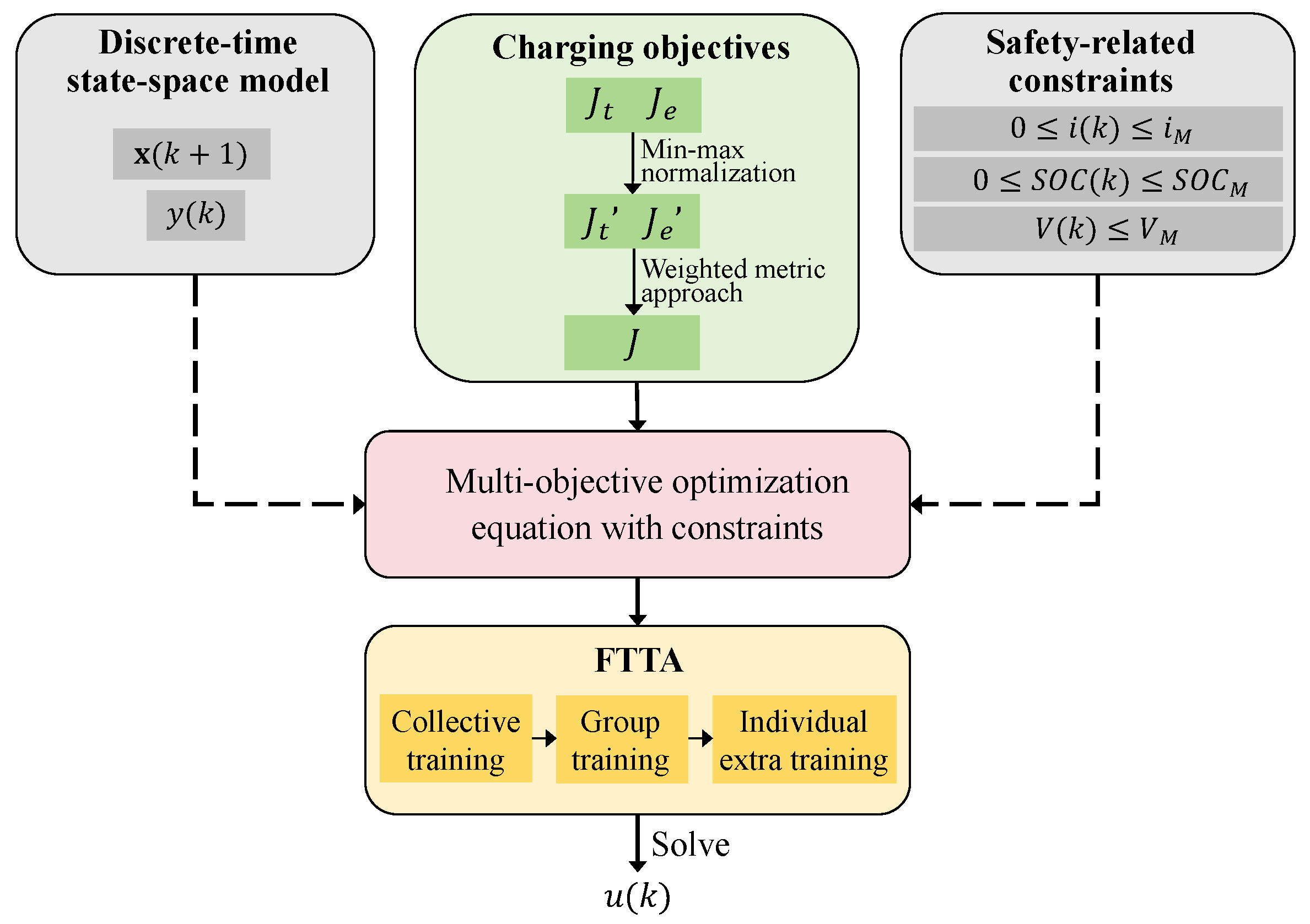
4. Charging Problem Description and Charging Control Strategy Design
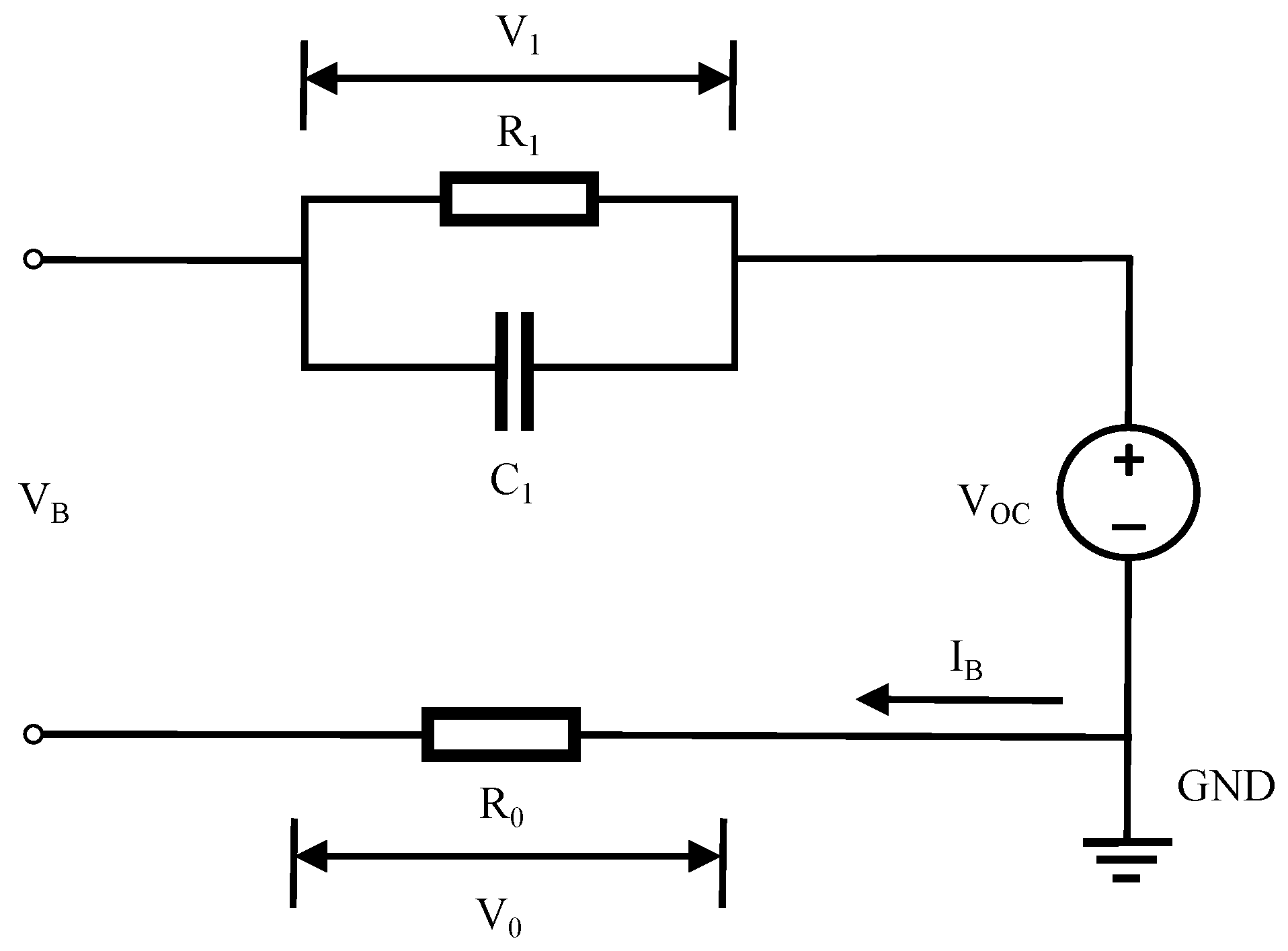
4.1. Battery Model
4.2. Charging Objectives and Safety-Related Constraints
4.2.1. User-Involved Electricity Objective
4.2.2. Energy Loss Reduction Objective
4.2.3. Multi-Objective Equation
4.3. Optimization Problem Establishment
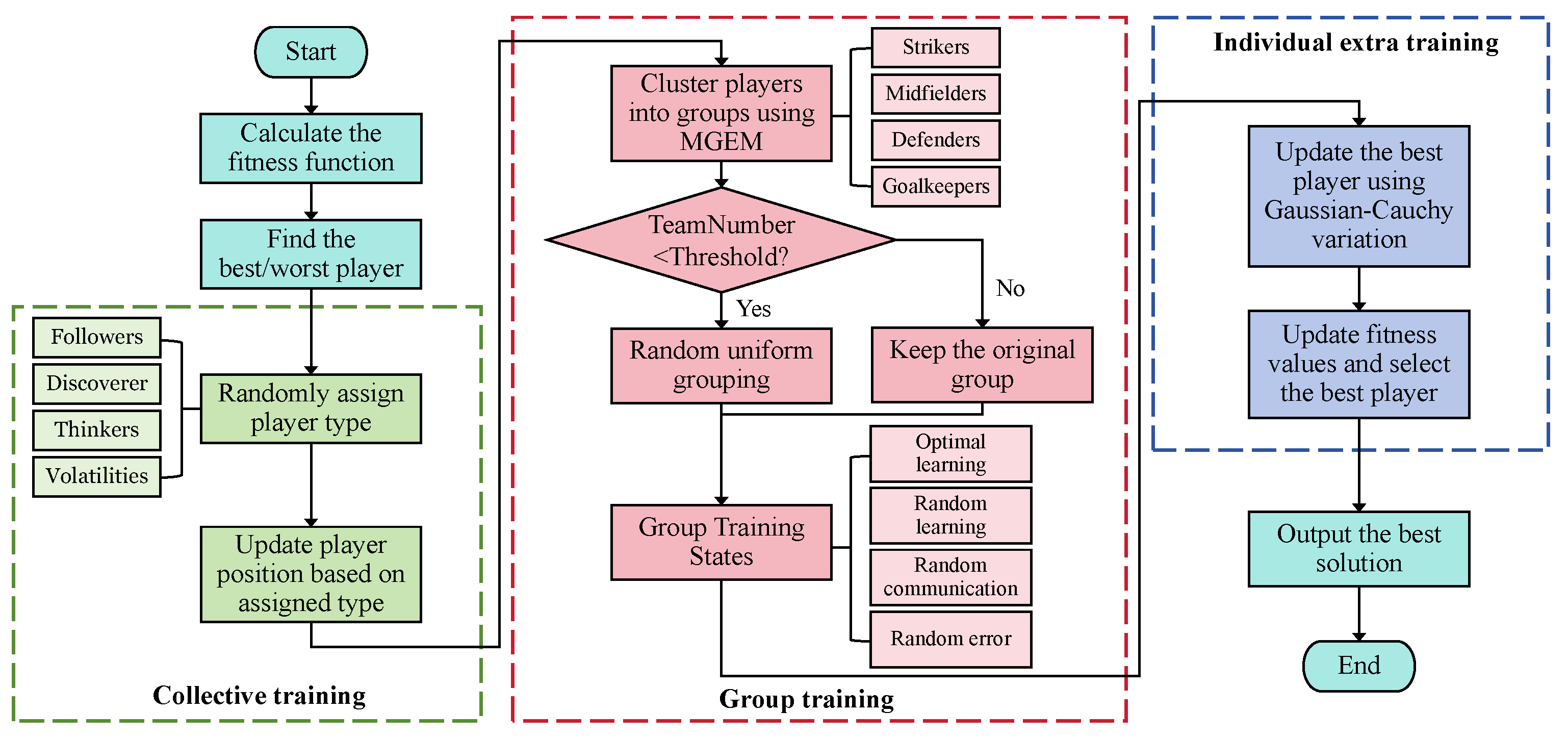
4.4. Design of Charging Control Strategy
5. Results and Discussion
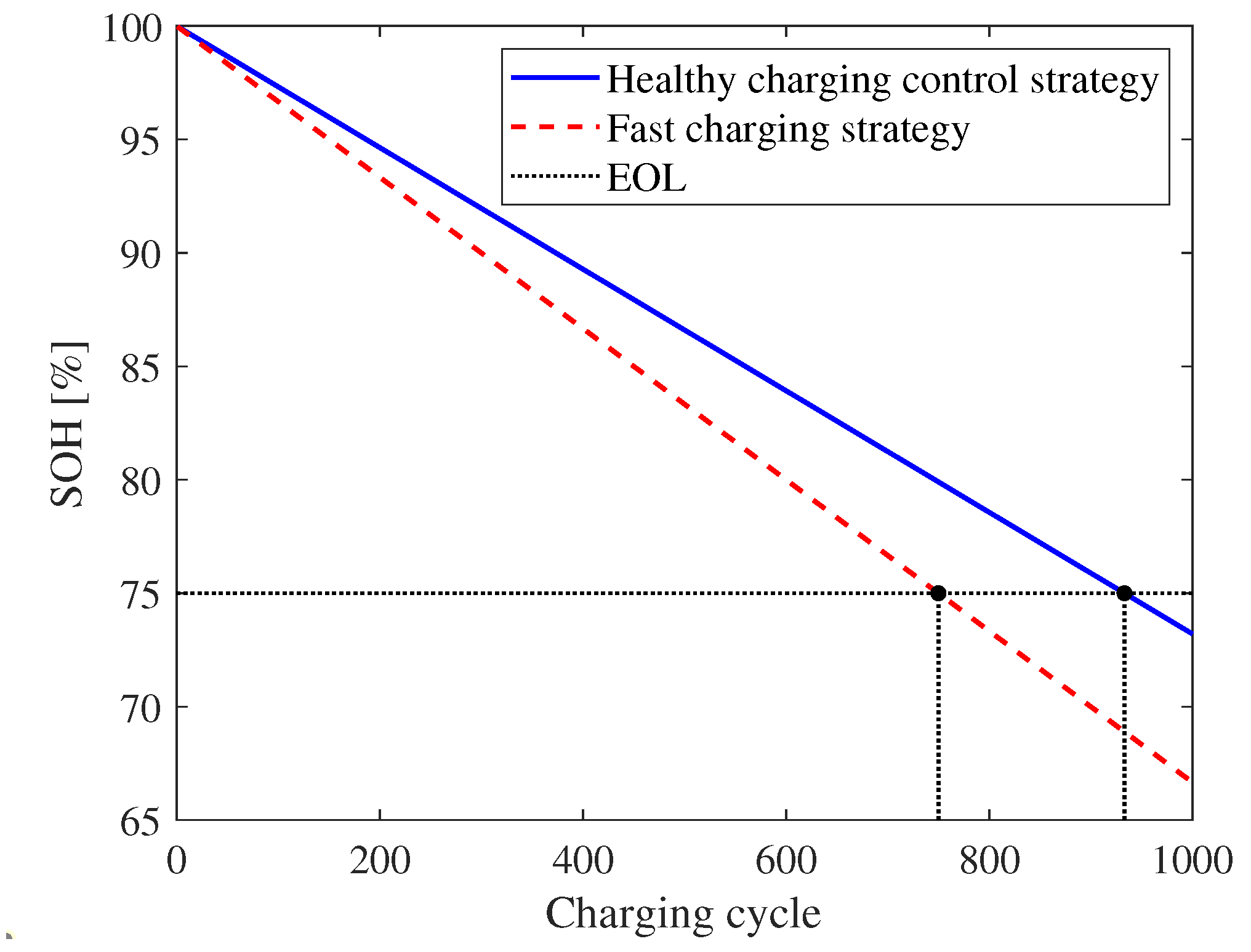
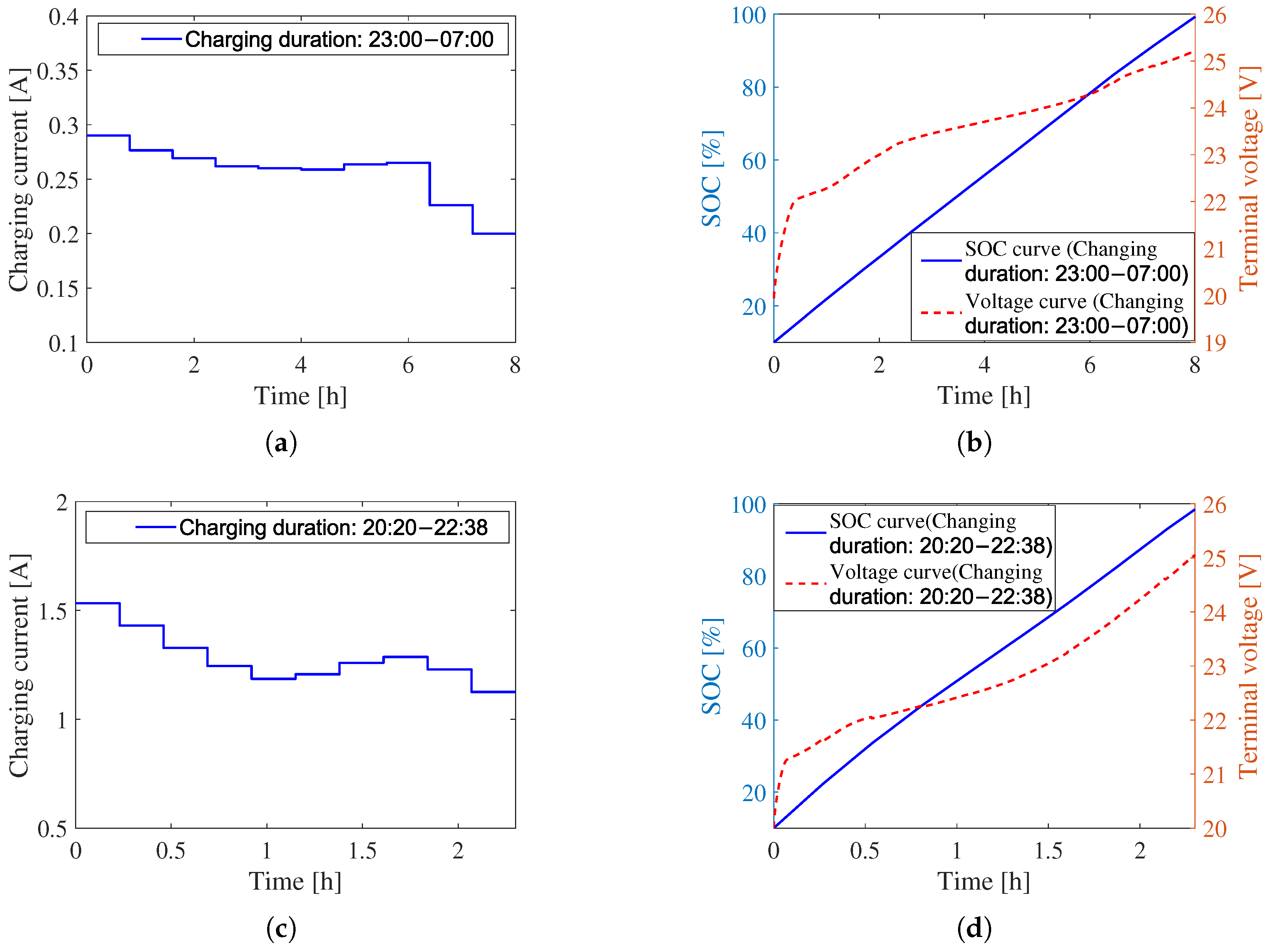
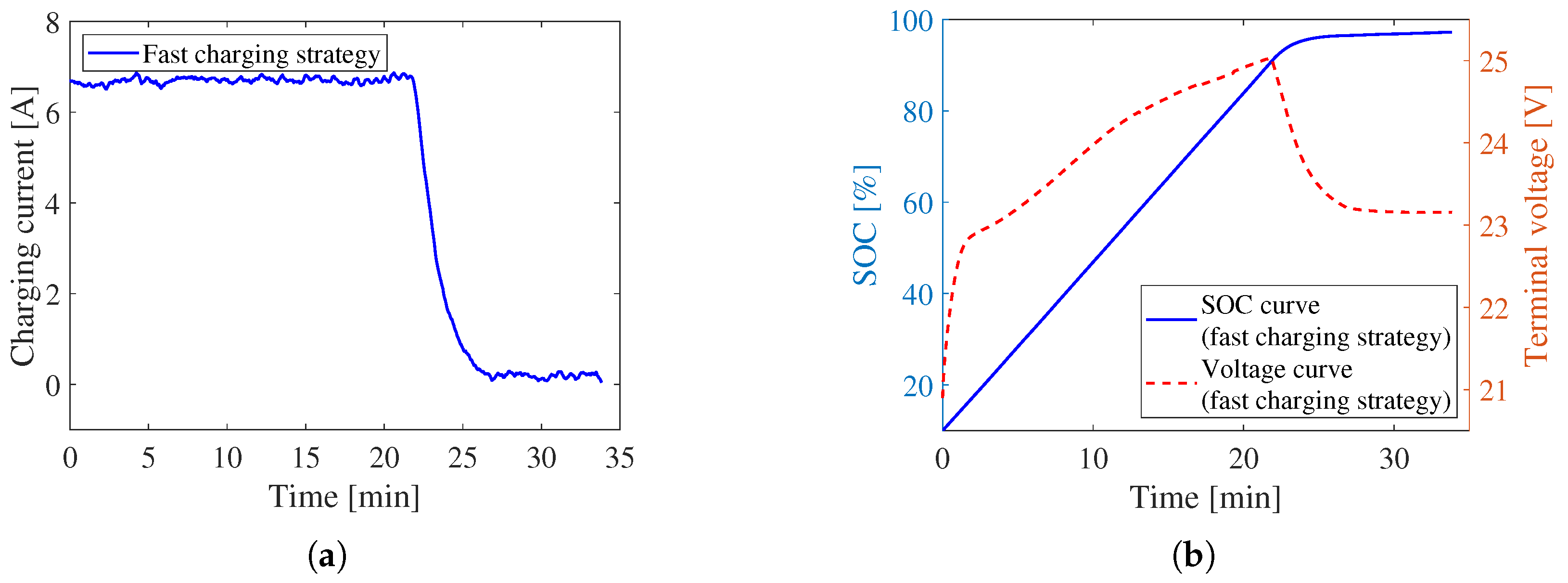
5.1. Comparison with Fast Charging Strategy
5.2. Comparison with Different Optimization Algorithms
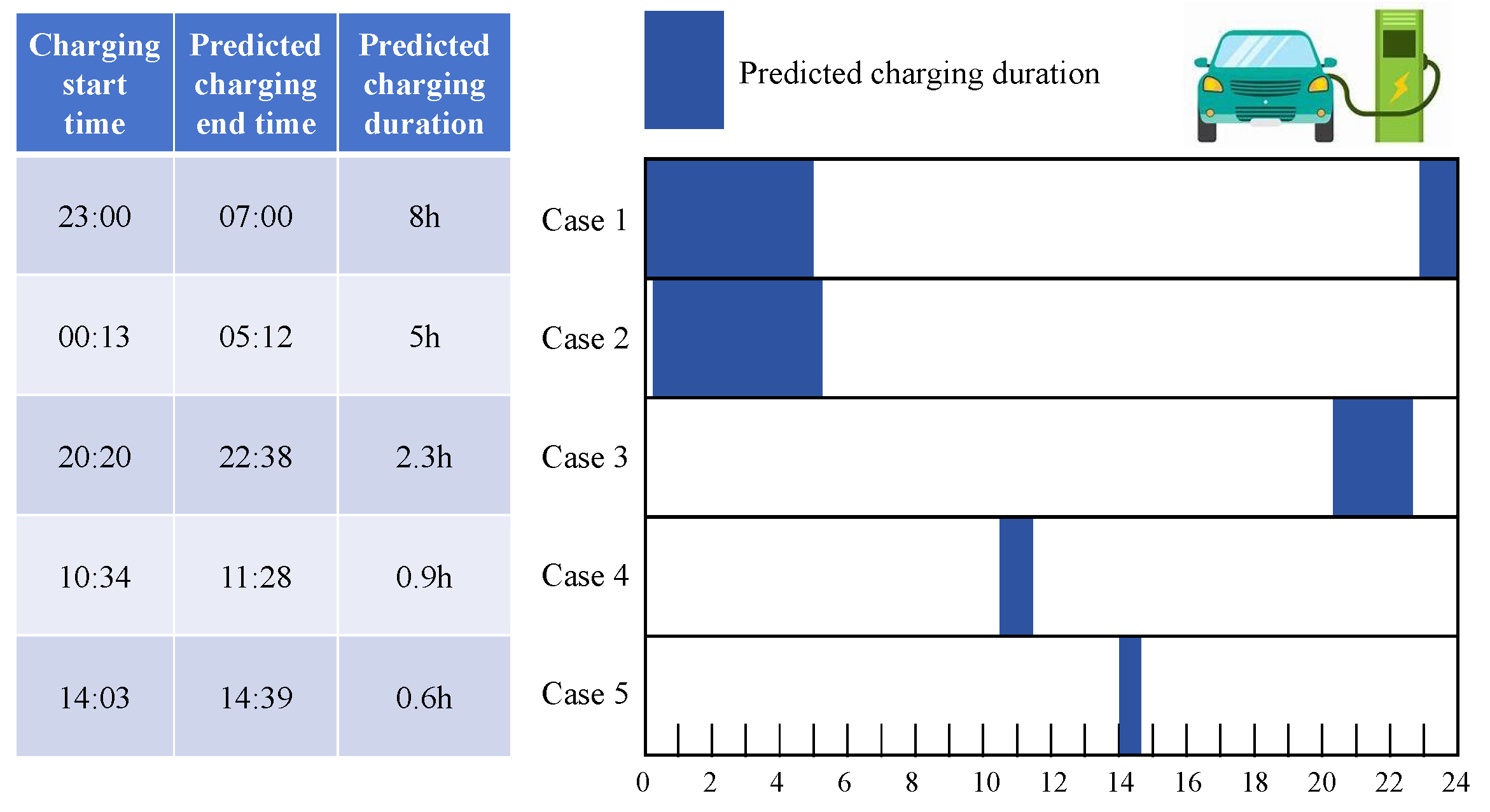
5.3. Comparison with Different Charging Demand
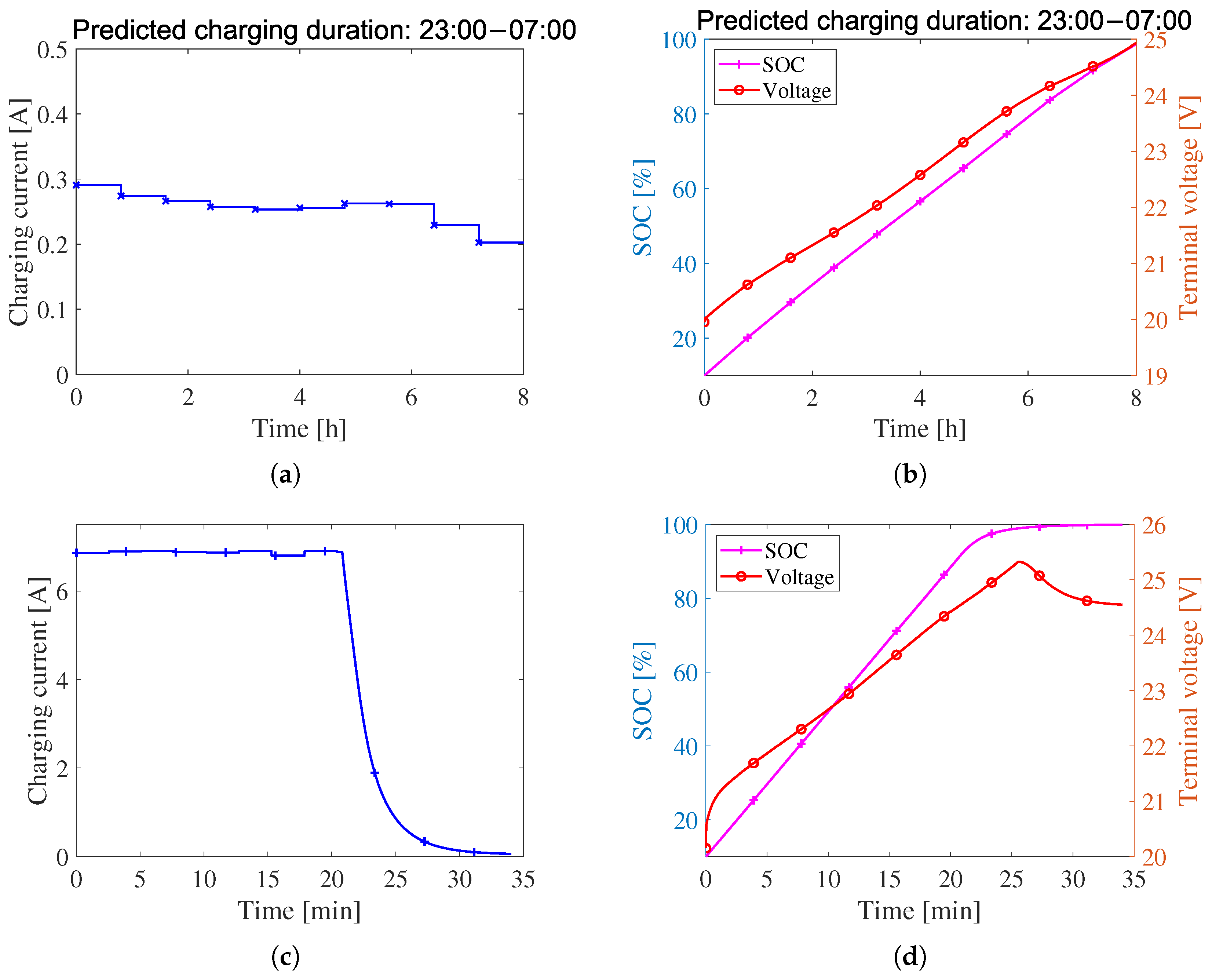
5.4. Charging Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Chen, Y.; Kang, Y.; Zhao, Y.; Wang, L.; Liu, J.; Li, Y.; Liang, Z.; He, X.; Li, X.; Tavajohi, N.; et al. A review of lithium-ion battery safety concerns: The issues, strategies, and testing standards. J. Energy Chem. 2021, 59, 83–99. [Google Scholar] [CrossRef]
- Ronanki, D.; Karneddi, H. Electric vehicle charging infrastructure: Review, cyber security considerations, potential impacts, countermeasures, and future trends. IEEE J. Emerg. Sel. Top. Power Electron. 2023, 12, 242–256. [Google Scholar] [CrossRef]
- Rangarajan, S.; Sunddararaj, S.P.; Sudhakar, A.; Shiva, C.K.; Subramaniam, U.; Collins, E.R.; Senjyu, T. Lithium-ion batteries—The crux of electric vehicles with opportunities and challenges. Clean Technol. 2022, 4, 908–930. [Google Scholar] [CrossRef]
- Arun, V.; Kannan, R.; Ramesh, S.; Vijayakumar, M.; Raghavendran, P.; Siva Ramkumar, M.; Anbarasu, P.; Sundramurthy, V.P. Review on li-ion battery vs nickel metal hydride battery in EV. Adv. Mater. Sci. Eng. 2022, 2022, 7910072. [Google Scholar] [CrossRef]
- Yang, J.; Cai, Y.; Mi, C. Lithium-ion battery capacity estimation based on battery surface temperature change under constant-current charge scenario. Energy 2022, 241, 122879. [Google Scholar] [CrossRef]
- Notten, P.H.; het Veld, J.O.; Van Beek, J. Boostcharging Li-ion batteries: A challenging new charging concept. J. Power Sources 2005, 145, 89–94. [Google Scholar] [CrossRef]
- Pavković, D.; Kasać, J.; Krznar, M.; Cipek, M. Adaptive Constant-Current/Constant-Voltage Charging of a Battery Cell Based on Cell Open-Circuit Voltage Estimation. World Electr. Vehic. J. 2023, 14, 155. [Google Scholar] [CrossRef]
- Lin, Q.; Wang, J.; Xiong, R.; Shen, W.; He, H. Towards a smarter battery management system: A critical review on optimal charging methods of lithium ion batteries. Energy 2019, 183, 220–234. [Google Scholar] [CrossRef]
- Tu, H.; Feng, H.; Srdic, S.; Lukic, S. Extreme fast charging of electric vehicles: A technology overview. IEEE Trans. Transp. Electrif. 2019, 5, 861–878. [Google Scholar] [CrossRef]
- Peng, C.; Yang, L.; Zhang, Q.; Liu, Z.; Guo, W.; Hu, B.; Li, Q.; Li, C.; Li, J. Optimization of fast-charging strategies for lithium-ion batteries with Kriging-Assisted evolution. Int. J. Energy Res. 2022, 46, 24381–24394. [Google Scholar] [CrossRef]
- Zentani, A.; Almaktoof, A.; Kahn, M.T. A Comprehensive Review of Developments in Electric Vehicles Fast Charging Technology. Appl. Sci. 2024, 14, 4728. [Google Scholar] [CrossRef]
- Qu, J.; Jiang, Z.; Zhang, J. Investigation on lithium-ion battery degradation induced by combined effect of current rate and operating temperature during fast charging. J. Energy Storage 2022, 52, 104811. [Google Scholar] [CrossRef]
- Ji, G.; He, L.; Wu, T.; Cui, G. The design of fast charging strategy for lithium-ion batteries and intelligent application: A comprehensive review. Appl. Energy 2025, 377, 124538. [Google Scholar] [CrossRef]
- Tahir, M.U.; Sangwongwanich, A.; Stroe, D.I.; Blaabjerg, F. Multi-objective optimization for multi-stage constant current charging for Li-ion batteries. J. Energy Storage 2024, 86, 111313. [Google Scholar] [CrossRef]
- Chen, Z.; Shu, X.; Xiao, R.; Yan, W.; Liu, Y.; Shen, J. Optimal charging strategy design for lithium-ion batteries considering minimization of temperature rise and energy loss. Int. J. Energy Res. 2019, 43, 4344–4358. [Google Scholar] [CrossRef]
- Lin, R.; Chu, H.; Gao, J.; Chen, H. Charging management and pricing strategy of electric vehicle charging station based on mean field game theory. Asian J. Control 2024, 26, 803–813. [Google Scholar] [CrossRef]
- Han, S. Optimal Charging Current Protocol with Multi-Stage Constant Current Using Dandelion Optimizer for Time-Domain Modeled Lithium-Ion Batteries. Appl. Sci. 2024, 14, 11320. [Google Scholar] [CrossRef]
- Fang, H.; Wang, Y.; Chen, J. Health-Aware and User-Involved Battery Charging Management for Electric Vehicles: Linear Quadratic Strategies. IEEE Trans. Control Syst. Technol. 2017, 25, 911–923. [Google Scholar] [CrossRef]
- Liu, K.; Li, K.; Ma, H.; Zhang, J.; Peng, Q. Multi-objective optimization of charging patterns for lithium-ion battery management. Energy Convers. Manage. 2018, 159, 151–162. [Google Scholar] [CrossRef]
- Shahriar, S.; Al-Ali, A.R.; Osman, A.H.; Dhou, S.; Nijim, M. Prediction of EV Charging Behavior Using Machine Learning. IEEE Access 2021, 9, 111576–111586. [Google Scholar] [CrossRef]
- Ullah, I.; Liu, K.; Yamamoto, T.; Zahid, M.; Jamal, A. Prediction of electric vehicle charging duration time using ensemble machine learning algorithm and Shapley additive explanations. Int. J. Energy Res. 2022, 46, 15211–15230. [Google Scholar] [CrossRef]
- Yapıcı, A.T.; Abut, N.; Erfidan, T. Comparing the Effectiveness of Deep Learning Approaches for Charging Time Prediction in Electric Vehicles: Kocaeli Example. Energies 2025, 18, 1961. [Google Scholar] [CrossRef]
- Hou, J.; Cui, Y.; Rong, M.; Jin, B. An Improved Football Team Training Algorithm for Global Optimization. Biomimetics 2024, 9, 419. [Google Scholar] [CrossRef]
- Ouyang, Q.; Fang, R.; Xu, G.; Liu, Y. User-involved charging control for lithium-ion batteries with economic cost optimization. Appl. Energy 2022, 314, 118878. [Google Scholar] [CrossRef]
- Botsford, C.; Szczepanek, A. Fast charging vs. slow charging: Pros and cons for the new age of electric vehicles. In Proceedings of the International Battery Hybrid Fuel Cell Electric Vehicle Symposium, Stavanger, Norway, 13–16 May 2009; Citeseer: Princeton, NJ, USA, 2009; pp. 1–9. [Google Scholar]
- Miller, C.; Goutham, M.; Chen, X.; Hanumalagutti, P.D.; Blaser, R.; Stockar, S. A Semi-Empirical Approach to a Physically Based Aging Model for Home Energy Management Systems. In Proceedings of the 2022 IEEE Conference on Control Technology and Applications (CCTA), Trieste, Italy, 23–25 August 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 165–170. [Google Scholar]
- Jin, X.; Vora, A.; Hoshing, V.; Saha, T.; Shaver, G.; García, R.E.; Wasynczuk, O.; Varigonda, S. Physically-based reduced-order capacity loss model for graphite anodes in Li-ion battery cells. J. Power Sources 2017, 342, 750–761. [Google Scholar] [CrossRef]
- Tranmer, M.; Elliot, M. Multiple linear regression. Cathie Marsh Cent. Census Surv. Res. (CCSR) 2008, 5, 1–5. [Google Scholar]
- Awad, M.; Khanna, R.; Awad, M.; Khanna, R. Support vector regression. In Efficient Learning Machines: Theories, Concepts, and Applications for Engineers and System Designers; Apress: Berkeley, CA, USA, 2015; pp. 67–80. [Google Scholar]
- Zou, J.; Han, Y.; So, S.S. Overview of artificial neural networks. In Artificial Neural Networks: Methods and Applications; Humana: Totowa, NJ, USA, 2009; pp. 14–22. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Rigatti, S.J. Random forest. J. Insur. Med. 2017, 47, 31–39. [Google Scholar] [CrossRef]
- Tyralis, H.; Papacharalampous, G. Boosting algorithms in energy research: A systematic review. Neural Comput. Appl. 2021, 33, 14101–14117. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2018; Volume 31. [Google Scholar]
- Pavlyshenko, B. Using stacking approaches for machine learning models. In Proceedings of the 2018 IEEE Second International Conference on Data Stream Mining & Processing (DSMP), Lviv, Ukraine, 21–25 August 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 255–258. [Google Scholar]
- Bertsimas, D.; Tsitsiklis, J. Simulated annealing. Stat. Sci. 1993, 8, 10–15. [Google Scholar] [CrossRef]
- Jain, Y.K.; Bhandare, S.K. Min max normalization based data perturbation method for privacy protection. Int. J. Comput. Commun. Technol. 2011, 2, 45–50. [Google Scholar] [CrossRef]
- Vermeer, W.; Mouli, G.R.C.; Bauer, P. A comprehensive review on the characteristics and modeling of lithium-ion battery aging. IEEE Trans. Transp. Electrif. 2021, 8, 2205–2232. [Google Scholar] [CrossRef]
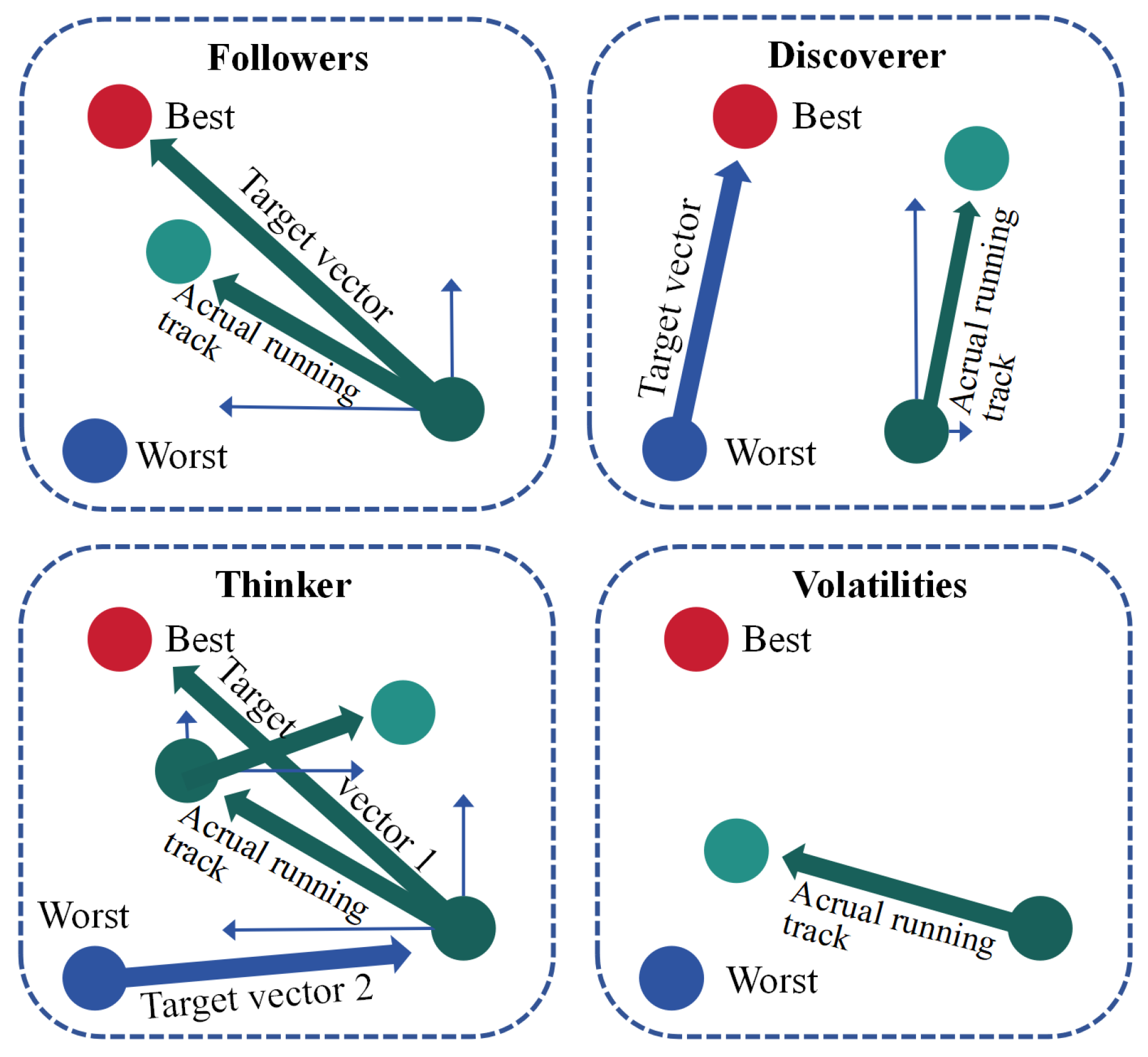
- Tian, Z.; Gai, M. Football team training algorithm: A novel sport-inspired meta-heuristic optimization algorithm for global optimization. Expert Syst. Appl. 2024, 245, 123088. [Google Scholar] [CrossRef]
- Canals Casals, L.; Etxandi-Santolaya, M.; Bibiloni-Mulet, P.A.; Corchero, C.; Trilla, L. Electric vehicle battery health expected at end of life in the upcoming years based on UK data. Batteries 2022, 8, 164. [Google Scholar] [CrossRef]
- Zoltowska, I. Risk Preferences of EV Fleet Aggregators in Day-Ahead Market Bidding: Mean-CVaR Linear Programming Model. Energies 2024, 18, 93. [Google Scholar] [CrossRef]




| Model | Configuration |
|---|---|
| MLR | - The number of CPU cores used for computation: all available cores |
| SVR | - Tolerance: 0.1 |
| RF | - The minimum number of leaves: 5 |
| XGBoost | - The number of basic estimators: 70 - The number of leaf nodes in a single tree model: 5 |
| ANN | - Activation function: tanh - Learning rate: 0.01 |
| CatBoost | - Learning rate: 0.3 |
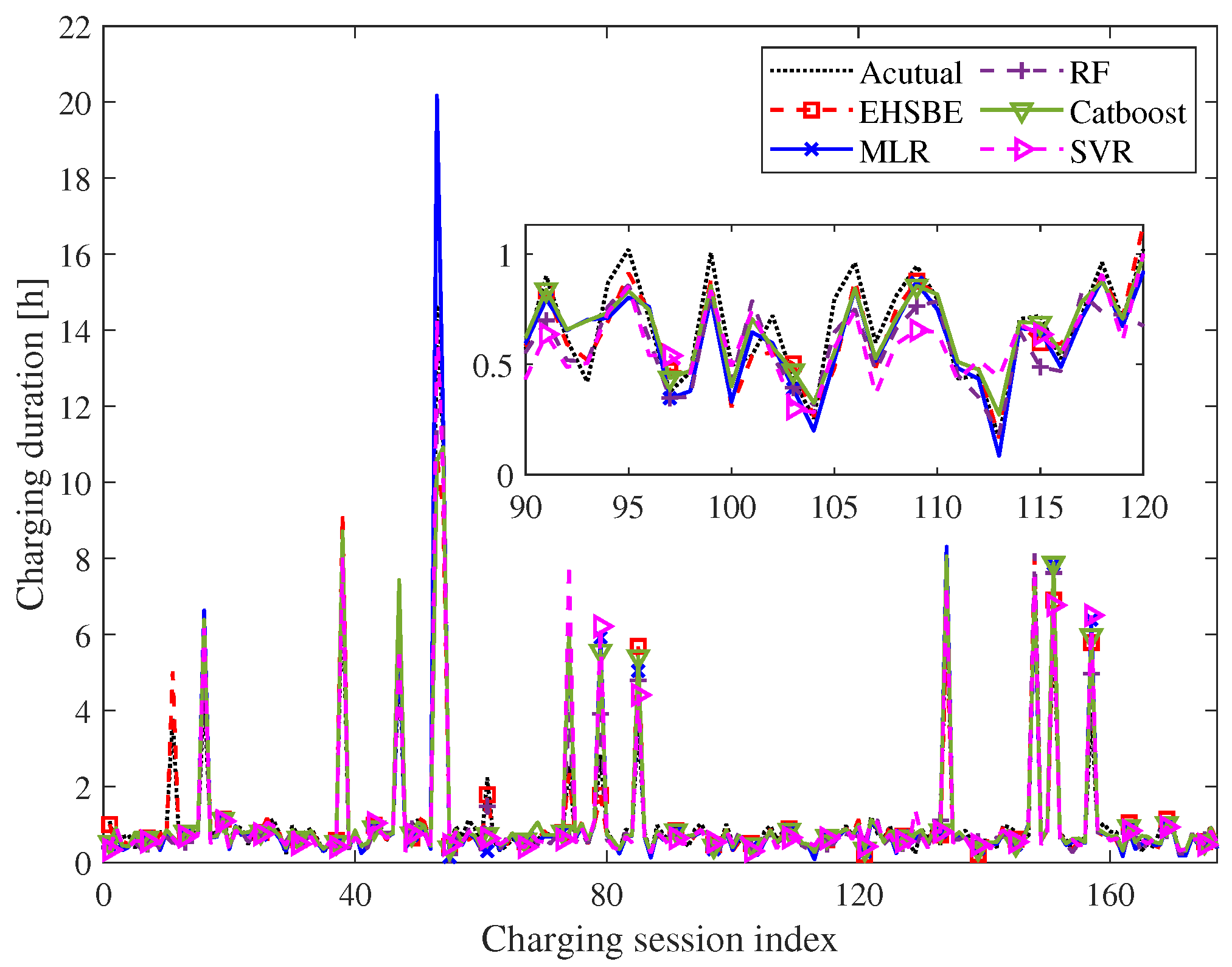
| User 1 | RMSE | MAE | MAPE | SMAPE |
|---|---|---|---|---|
| EHSBE | 0.385 | 0.190 | 16.512% | 16.161% |
| MLR | 0.626 | 0.234 | 20.458% | 18.267% |
| RF | 0.391 | 0.191 | 20.647% | 18.324% |
| CatBoost | 0.540 | 0.224 | 22.278% | 19.432% |
| SVR | 0.598 | 0.284 | 28.640% | 28.028% |
| Charging Strategy | Final Value | Deviation | Energy Loss |
|---|---|---|---|
| Healthy charging | 0.9987 | 0.0013 | 620.0 J |
| Fast charging | 0.9958 | 0.0042 | 10,998.0 J |
| Algorithms | Final Value | Deviation | Energy Loss |
|---|---|---|---|
| FTTA | 0.9988 | 0.0012 | 1029.0 J |
| PSO | 0.9975 | 0.0025 | 1094.4 J |
| GA | 0.9980 | 0.0020 | 1138.2 J |
| Charging Strategy | Final Value | Deviation | Energy Loss |
|---|---|---|---|
| Healthy charging case 1 | 0.9927 | 0.0073 | 614.4 J |
| Healthy charging case 3 | 0.9761 | 0.0239 | 2569.8 J |
| Fast charging | 0.9724 | 0.0276 | 10,549.8 J |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Huang, L.; Ouyang, Q.; Li, Y.; Wan, Y. User-Demand-Oriented Healthy Charging Control Strategy for EVs Based on Football Team Training Algorithm. Batteries 2025, 11, 344. https://doi.org/10.3390/batteries11090344
Liu H, Huang L, Ouyang Q, Li Y, Wan Y. User-Demand-Oriented Healthy Charging Control Strategy for EVs Based on Football Team Training Algorithm. Batteries. 2025; 11(9):344. https://doi.org/10.3390/batteries11090344
Chicago/Turabian StyleLiu, Haoyi, Lianghui Huang, Quan Ouyang, Yujia Li, and Yong Wan. 2025. "User-Demand-Oriented Healthy Charging Control Strategy for EVs Based on Football Team Training Algorithm" Batteries 11, no. 9: 344. https://doi.org/10.3390/batteries11090344
APA StyleLiu, H., Huang, L., Ouyang, Q., Li, Y., & Wan, Y. (2025). User-Demand-Oriented Healthy Charging Control Strategy for EVs Based on Football Team Training Algorithm. Batteries, 11(9), 344. https://doi.org/10.3390/batteries11090344








