Systematic Characterization of Lithium-Ion Cells for Electric Mobility and Grid Storage: A Case Study on Samsung INR21700-50G
Abstract
1. Introduction
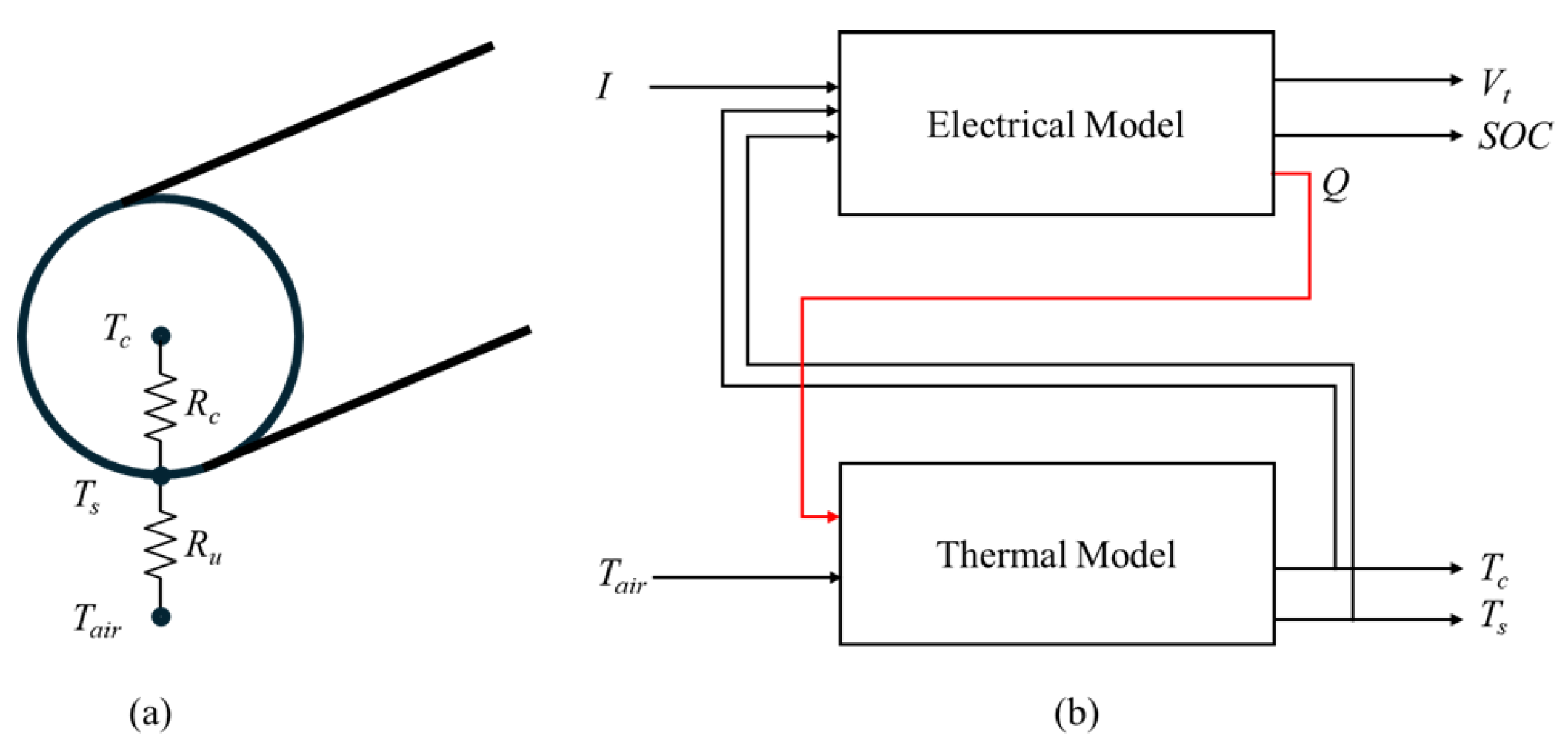
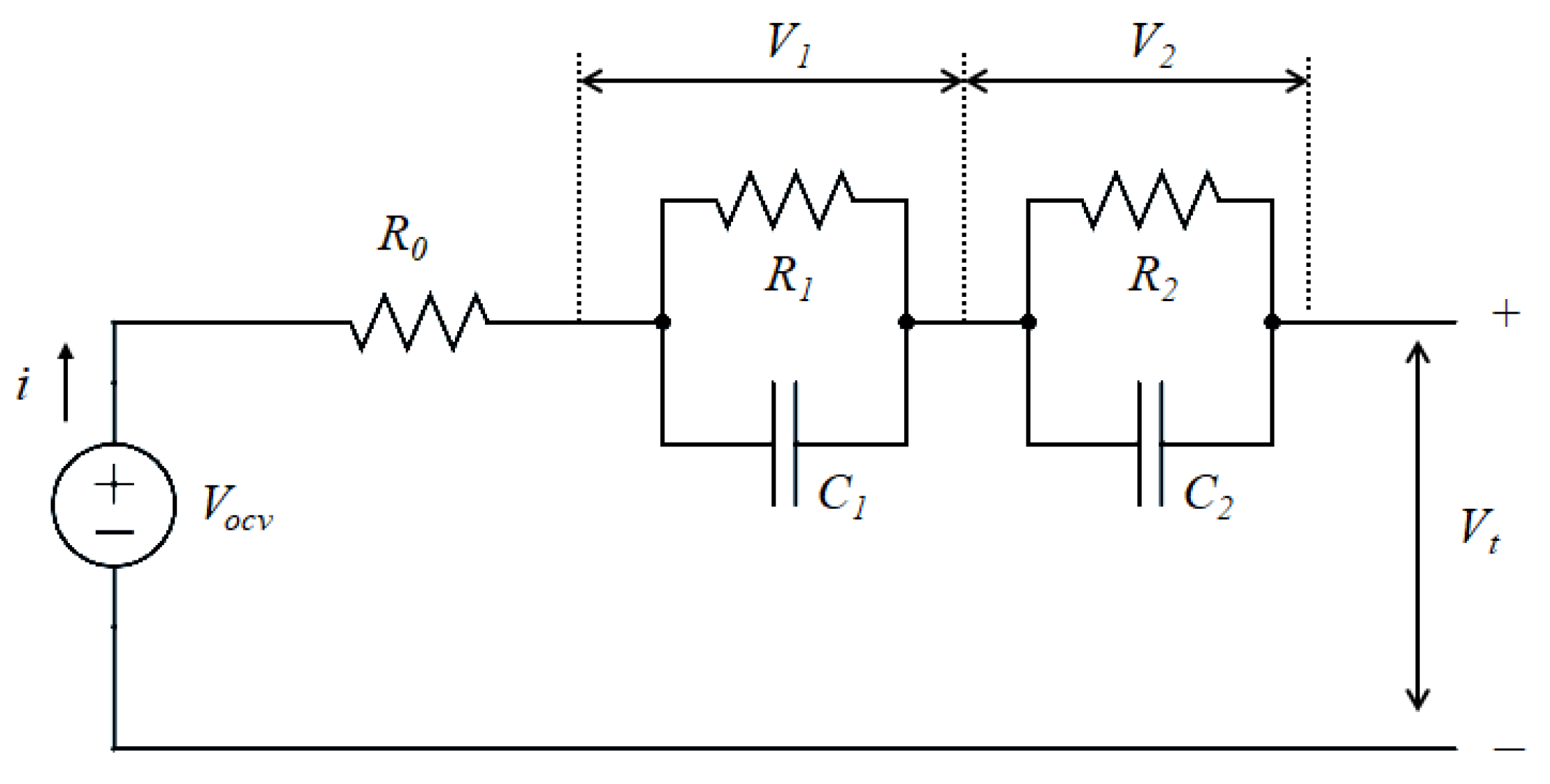
2. Equivalent Circuit Model and Thermal Dynamics
- is the state of charge of the cell;
- Q is the cell capacity in ampere-hours;
- and represent the voltages across the two RC pairs;
- is the applied current, with discharge current defined as negative;
- is the ohmic internal resistance of the cell;
- is the open-circuit voltage as a function of SOC.
- , , and denote the core, surface, and ambient air temperatures, respectively.
- and are the lumped thermal conduction resistances between core-surface and surface-air, respectively.
- and are the lumped thermal capacitance of the core and surface layers, respectively.
- is the instantaneous heat generation rate inside the cell.
3. Test Procedures
3.1. Test Setup
3.2. Test Preparation
3.3. Static Capacity Test
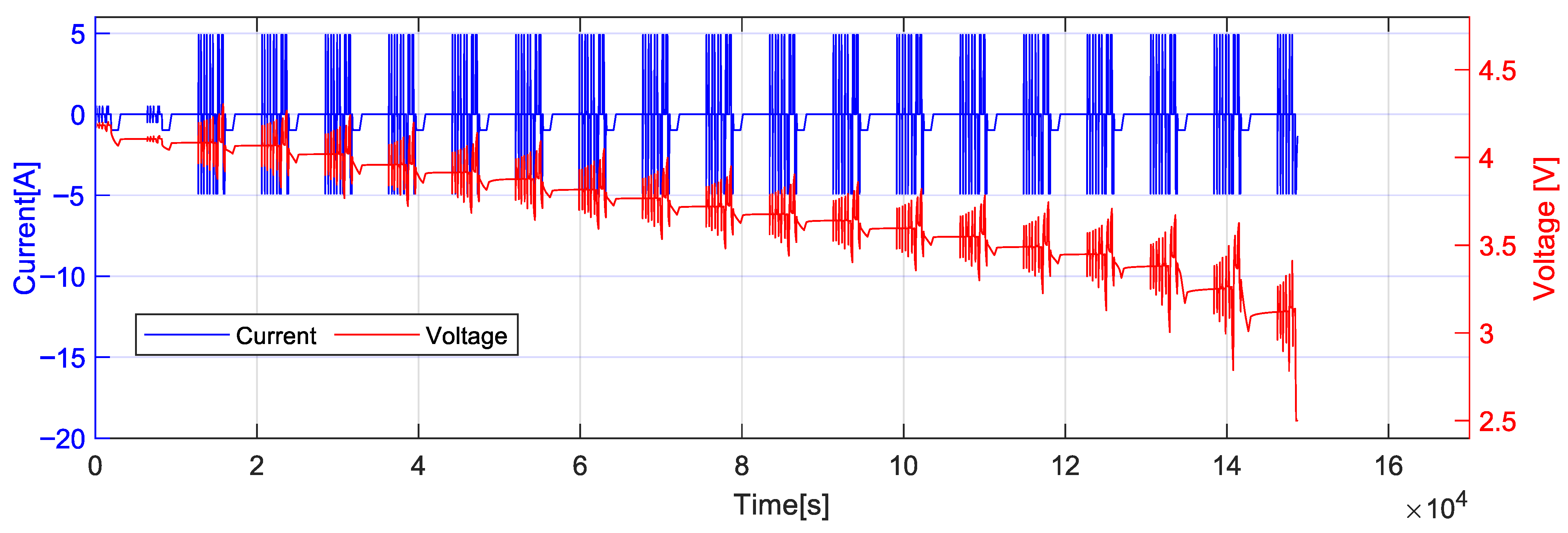
3.4. Hybrid Pulse Power Characterization (HPPC) Test
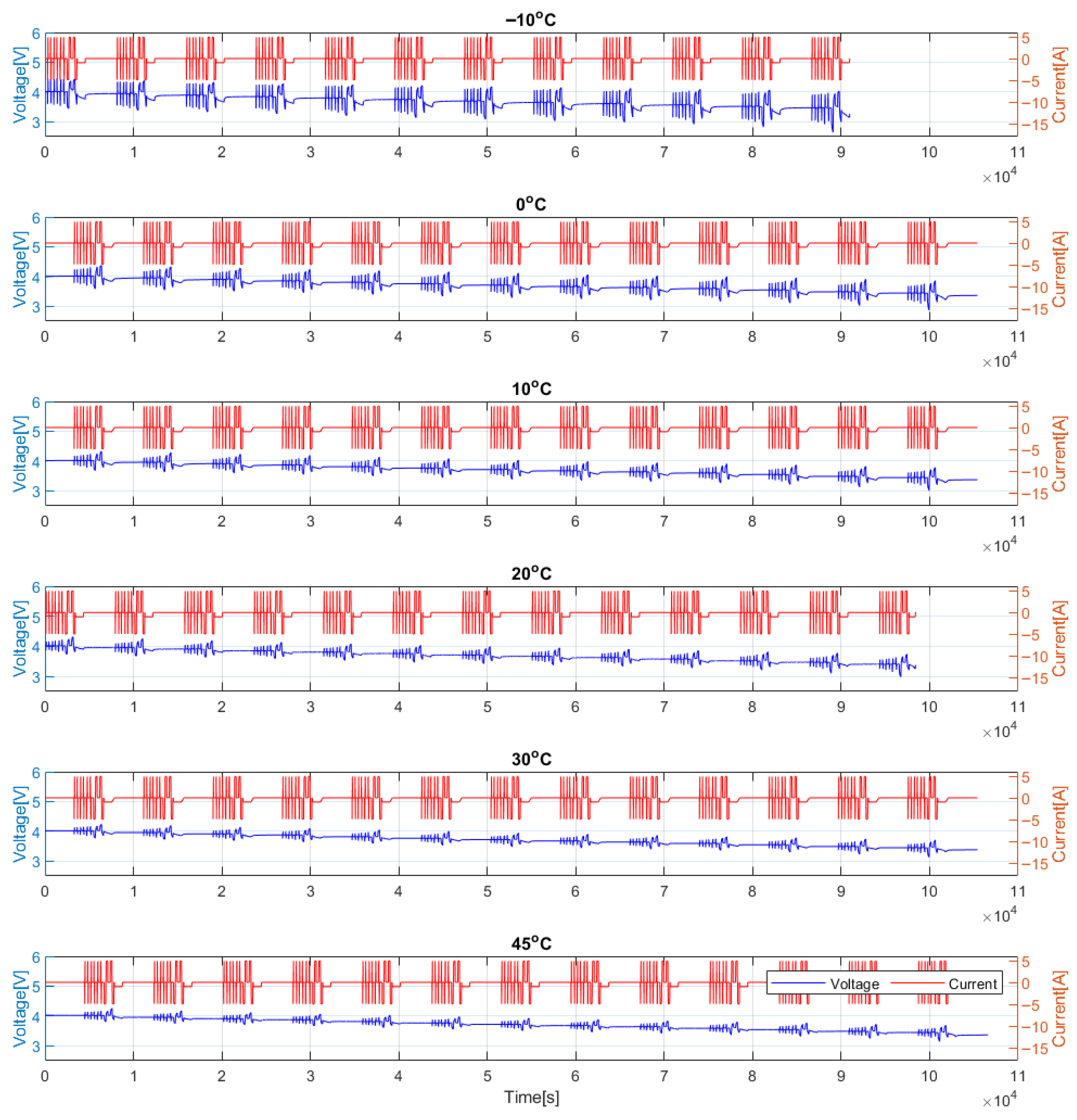
3.5. Test Cases
4. Results
4.1. Static Capacity Test Results
4.2. HPPC Test Results
4.2.1. Open-Circuit Voltage
4.2.2. Charge/Discharge Power Capability
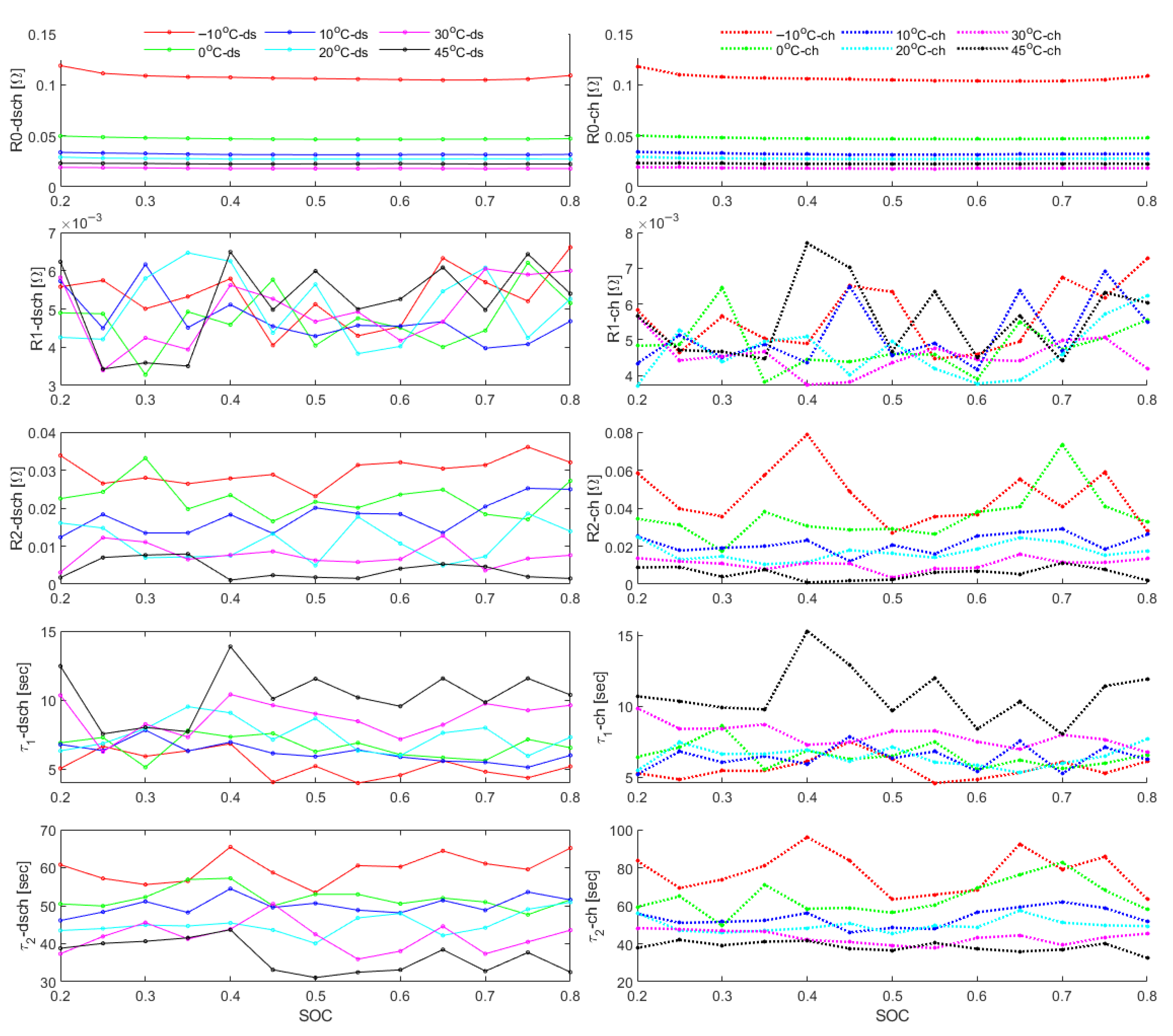
- The internal resistance increases significantly as SOC drops below 30%, and this effect is even more pronounced at sub-zero temperatures. This can be attributed to reduced lithium-ion mobility within the electrolyte [28], slower electrochemical reaction kinetics [29], and increased resistance at the solid-electrolyte interface.
- The DCIR increases with pulse duration for both discharge and regeneration phases, following the trend: . The OCV is a nonlinear function of SOC, and longer discharge pulses result in a greater SOC reduction, lowering the OCV baseline. This leads to a larger terminal voltage drop , and consequently, higher DCIR values. It is worth noting that although the ohmic resistance may decrease slightly during longer pulses due to self-heating, the DCIR is computed from the terminal voltage difference and applied current, and therefore reflects both resistive and dynamic effects.
- Discharge resistance values are generally higher than regeneration (charge) resistance values. This behavior is attributed to intrinsic asymmetries in electrochemical kinetics and internal polarization. During discharge, lithium deintercalation from the anode is more kinetically constrained, particularly at low temperatures, resulting in greater activation and concentration polarization and, consequently, larger voltage drops under load. In contrast, during regeneration, the lithium intercalation process exhibits lower kinetic limitations, leading to comparatively lower observed resistance [30,31].
- The difference between charge and discharge resistance is prominent for longer pulses. The increase in resistance observed during the 180 s pulse at C is primarily attributed to the cumulative effects of sustained high current under low-temperature conditions. At sub-zero temperatures, both ionic conductivity and charge-transfer kinetics are significantly diminished, leading to the formation of a lithium-ion concentration gradient and elevated overpotential during prolonged discharge, thereby increasing the measured resistance [32].
- Discharge power capability consistently decreases with decreasing SOC. At lower SOC levels, the voltage headroom and the effective power output decrease, while the internal resistance increases, resulting in reduced discharge performance.
- Regeneration (charging) power capability increases as SOC decreases. This is attributed to the greater voltage margin between the cell’s open-circuit voltage and the upper voltage limit, particularly at low SOCs.
- Pulse duration significantly affects power capabilities. Shorter pulses (e.g., 2 s and 10 s) result in higher power capabilities due to minimized voltage drop and thermal buildup. In contrast, longer pulses (30 s and 180 s) show reduced power handling, especially under extreme SOC or temperature conditions. This stems directly from Equations (12) and (13) as the power capability is inversely related to the pulse resistance. Under low or high SOC and extreme temperatures, the internal resistance of the cell tends to increase, leading to a reduction in power capability under these conditions.
- Temperature is a dominant influencing factor. Across all pulse durations and SOC levels, both discharge and regeneration capabilities are notably higher at elevated temperatures ( and ). Sub-zero temperatures () lead to severe performance degradation—regeneration power capability, in particular, is significantly reduced due to increased polarization and impedance.
5. Parameter Extraction from HPPC Data
6. Conclusions
- Internal resistance increases sharply at low SOC and sub-zero temperatures due to hindered ion transport and electrochemical kinetics.
- Discharge resistance consistently exceeds regeneration resistance, reflecting the asymmetric nature of charge and discharge processes.
- Longer pulse durations cause higher resistances due to increased polarization and thermal effects.
- Discharge power capability decreases with SOC, while regeneration power capability conversely increases, influenced by voltage margin constraints.
- Elevated temperatures (to a specific limit) significantly enhance power capabilities, whereas cold conditions degrade performance by over two-thirds.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Symbol | Description | Symbol | Description |
| State of charge (dimensionless, 0–1) | Discharge resistance () | ||
| Q | Cell capacity (Ah) | Regeneration resistance () | |
| Applied current (A) | DCIR at respective pulses () | ||
| Terminal voltage (V) | DCIR at respective pulses () | ||
| Open-circuit voltage (V) | Core temperature (°C or K) | ||
| Voltage across first RC pair (V) | Surface temperature (°C or K) | ||
| Voltage across second RC pair (V) | Ambient air temperature (°C or K) | ||
| Ohmic resistance () | Average cell temperature (°C or K) | ||
| Resistances of RC pairs () | Thermal capacitances (J/K) | ||
| Capacitances of RC pairs (F) | Thermal resistances (K/W) | ||
| RC time constants (s) | Voltage drop during discharge pulse (V) | ||
| Sampling time (s) | Voltage rise during charge pulse (V) | ||
| Heat generation rate (W) | Current during discharge pulse (A) | ||
| C-rate | Normalized charge/discharge rate | Current during charge pulse (A) | |
| Minimum voltage in a discharge pulse (V) | Maximum voltage in a charge pulse (V) | ||
| Discharge pulse power capability (W) | Charge pulse power capability (W) | ||
| BMS | Battery management system | LIB | Lithium ion batteries |
| H/BEV | Hybrid/Battery electric vehicle | ECM | Equivalent circuit model |
| ECU | Electronic control unit | EKF | Extended Kalman filter |
| NCA | Nickel Cobalt Aluminum | HPPC | Hybrid Power Pulse Characterization |
| CC-CV | Constant current - Constant voltage | DCIR | Direct current internal resistance |
Appendix A

References
- Chen, J. Recent Progress in Advanced Materials for Lithium Ion Batteries. Materials 2013, 6, 156–183. [Google Scholar] [CrossRef]
- Mallarapu, A.; Çaldichoury, I.; L’Eplattenier, P.; Sunderlin, N.; Santhanagopalan, S. Coupled Multiphysics Modeling of Lithium-Ion Batteries for Automotive Crashworthiness Applications. J. Electrochem. Energy Convers. Storage 2024, 22, 031003. [Google Scholar] [CrossRef]
- Chung, S.H.; Manthiram, A. Lithium–Sulfur Batteries with the Lowest Self-Discharge and the Longest Shelf Life. ACS Energy Lett. 2017, 2, 1056–1061. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, L.; Sun, F.; Wang, Z. An Overview on Thermal Safety Issues of Lithium-ion Batteries for Electric Vehicle Application. IEEE Access 2018, 6, 23848–23863. [Google Scholar] [CrossRef]
- Paudel, S.; De Boever, Q.; Zhang, J.; Ayalew, B.; Pisu, P.; Castanier, M. Design optimization of mobile vehicle-borne microgrids. Sustain. Energy Grids Netw. 2024, 39, 101480. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of Lithium-Ion Battery Equivalent Circuit Models for State of Charge Estimation by an Experimental Approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Di Domenico, D.; Stefanopoulou, A.; Fiengo, G. Lithium-Ion Battery State of Charge and Critical Surface Charge Estimation Using an Electrochemical Model-Based Extended Kalman Filter. J. Dyn. Syst. Meas. Control 2010, 132, 061302. [Google Scholar] [CrossRef]
- Forman, J.C.; Moura, S.J.; Stein, J.L.; Fathy, H.K. Genetic identification and fisher identifiability analysis of the Doyle–Fuller–Newman model from experimental cycling of a LiFePO4 cell. J. Power Sources 2012, 210, 263–275. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Guo, H. Online estimation of model parameters and state-of-charge of LiFePO4 batteries in electric vehicles. Appl. Energy 2012, 89, 413–420. [Google Scholar] [CrossRef]
- Paudel, S.; Zhang, J.; Ayalew, B.; Castanier, M.; Skowronska, A. A Model Predictive Control-Based Operation of Vehicle-Borne Microgrid Considering Battery Degradation. In Proceedings of the Ground Vehicle Systems Engineering and Technology Symposium (GVSETS), NDIA, Novi, MI, USA, 15–17 August 2023. [Google Scholar]
- Moura, S.J. Techniques for Battery Health Conscious Power Management via Electrochemical Modeling and Optimal Control. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2011. [Google Scholar]
- Xu, L.; Lin, X.; Xie, Y.; Hu, X. Enabling high-fidelity electrochemical P2D modeling of lithium-ion batteries via fast and non-destructive parameter identification. Energy Storage Mater. 2022, 45, 952–968. [Google Scholar] [CrossRef]
- Biju, N.; Fang, H. On the Design of An Equivalent Circuit Model for Lithium-Ion Batteries Operating Across Broad Current Ranges. IFAC-PapersOnLine 2023, 56, 7127–7133. [Google Scholar] [CrossRef]
- Paudel, S.; Zhang, J.; Ayalew, B.; Skowronska, A. Charging Load Estimation for a Fleet of Autonomous Vehicles. In Proceedings of the WCX SAE World Congress Experience, Detroit, MI, USA, 16–18 April 2024. [Google Scholar] [CrossRef]
- Zhang, L.; Peng, H.; Ning, Z.; Mu, Z.; Sun, C. Comparative Research on RC Equivalent Circuit Models for Lithium-Ion Batteries of Electric Vehicles. Appl. Sci. 2017, 7, 1002. [Google Scholar] [CrossRef]
- Ding, X.; Zhang, D.; Cheng, J.; Wang, B.; Luk, P.C. An improved Thevenin model of lithium-ion battery with high accuracy for electric vehicles. Appl. Energy 2019, 254, 113615. [Google Scholar] [CrossRef]
- Nejad, S.; Gladwin, D.T.; Stone, D.A. A systematic review of lumped-parameter equivalent circuit models for real-time estimation of lithium-ion battery states. J. Power Sources 2016, 316, 183–196. [Google Scholar] [CrossRef]
- Cheng, Y.S. Identification of parameters for equivalent circuit model of Li-ion battery cell with population based optimization algorithms. Ain Shams Eng. J. 2024, 15, 102481. [Google Scholar] [CrossRef]
- Mishra, D.; Paudel, S.; Zhang, J.; Lawler, B.; Castanier, M.P. Experimental Investigation and Performance Analysis of 21700 Lithium-Ion Batteries for Electric Vehicle Applications. IEEE Trans. Consum. Electron. 2025. submitted. [Google Scholar]
- Lin, X.; Perez, H.E.; Mohan, S.; Siegel, J.B.; Stefanopoulou, A.G.; Ding, Y.; Castanier, M.P. A lumped-parameter electro-thermal model for cylindrical batteries. J. Power Sources 2014, 257, 1–11. [Google Scholar] [CrossRef]
- Smith, K.A.; Rahn, C.D.; Wang, C.Y. Model-Based Electrochemical Estimation and Constraint Management for Pulse Operation of Lithium Ion Batteries. IEEE Trans. Control Syst. Technol. 2010, 18, 654–663. [Google Scholar] [CrossRef]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 2. Modeling and identification. J. Power Sources 2004, 134, 262–276. [Google Scholar] [CrossRef]
- Dey, S.; Biron, Z.A.; Tatipamula, S.; Das, N.; Mohon, S.; Ayalew, B.; Pisu, P. On-board Thermal Fault Diagnosis of Lithium-ion Batteries For Hybrid Electric Vehicle Application. IFAC-PapersOnLine 2015, 48, 389–394. [Google Scholar] [CrossRef]
- Tu, H.; Lin, X.; Wang, Y.; Fang, H. System Identification for Lithium-Ion Batteries with Nonlinear Coupled Electro-Thermal Dynamics via Bayesian Optimization. In Proceedings of the 2024 American Control Conference (ACC), Toronto, ON, Canada, 10–12 July 2024; pp. 1946–1951. [Google Scholar] [CrossRef]
- Plett, G.L. A Linear Method to Fit Equivalent Circuit Model Parameter Values to HPPC Relaxation Data From Lithium-Ion Cells. ASME Lett. Dyn. Syst. Control 2025, 5, 011003. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Battery Test Manual for Electric Vehicles: Revision 3.1; Technical Report; Idaho National Laboratory: Idaho Falls, ID, USA, 2020.
- Białoń, T.; Niestrój, R.; Skarka, W.; Korski, W. HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example. Energies 2023, 16, 6239. [Google Scholar] [CrossRef]
- Xu, K. Nonaqueous Liquid Electrolytes for Lithium-Based Rechargeable Batteries. Chem. Rev. 2004, 104, 4303–4418. [Google Scholar] [CrossRef]
- Zhang, S.S. The effect of the charging protocol on the cycle life of a Li-ion battery. J. Power Sources 2006, 163, 1126–1132. [Google Scholar] [CrossRef]
- Ernst, S.; Heins, T.P.; Schlüter, N.; Schröder, U. Capturing the Current-Overpotential Nonlinearity of Lithium-Ion Batteries by Nonlinear Electrochemical Impedance Spectroscopy (NLEIS) in Charge and Discharge Direction. Front. Energy Res. 2019, 7, 151. [Google Scholar] [CrossRef]
- Mao, Z.; Farkhondeh, M.; Pritzker, M.; Fowler, M.; Chen, Z. Charge/Discharge Asymmetry in Blended Lithium-Ion Electrodes. J. Electrochem. Soc. 2017, 164, A39. [Google Scholar] [CrossRef]
- Jossen, A. Fundamentals of battery dynamics. J. Power Sources 2006, 154, 530–538. [Google Scholar] [CrossRef]
- Safari, M.; Delacourt, C. Modeling of a Commercial Graphite/LiFePO4 Cell. J. Electrochem. Soc. 2011, 158, A562. [Google Scholar] [CrossRef]
- Barai, A.; Uddin, K.; Widanage, W.D.; McGordon, A.; Jennings, P. A study of the influence of measurement timescale on internal resistance characterisation methodologies for lithium-ion cells. Sci. Rep. 2018, 8, 21. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Amini, A.; Özdemir, T.; Ekici, Ö.; Başlamışlı, S.Ç.; Köksal, M. A thermal model for Li-ion batteries operating under dynamic conditions. Appl. Therm. Eng. 2020, 180, 116338. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Nominal Voltage | 3.6 V |
| Maximum Voltage | 4.2 V |
| Nominal Capacity | 4.9 Ah |
| Discharge Cut-off Voltage | 2.5 V |
| Continuous Discharge Rating | 9.8 A |
| Cell Weight | 69 g |
| Cell Dimensions | Height: Max. 70.80 mm |
| Diameter: Max. 21.25 mm |
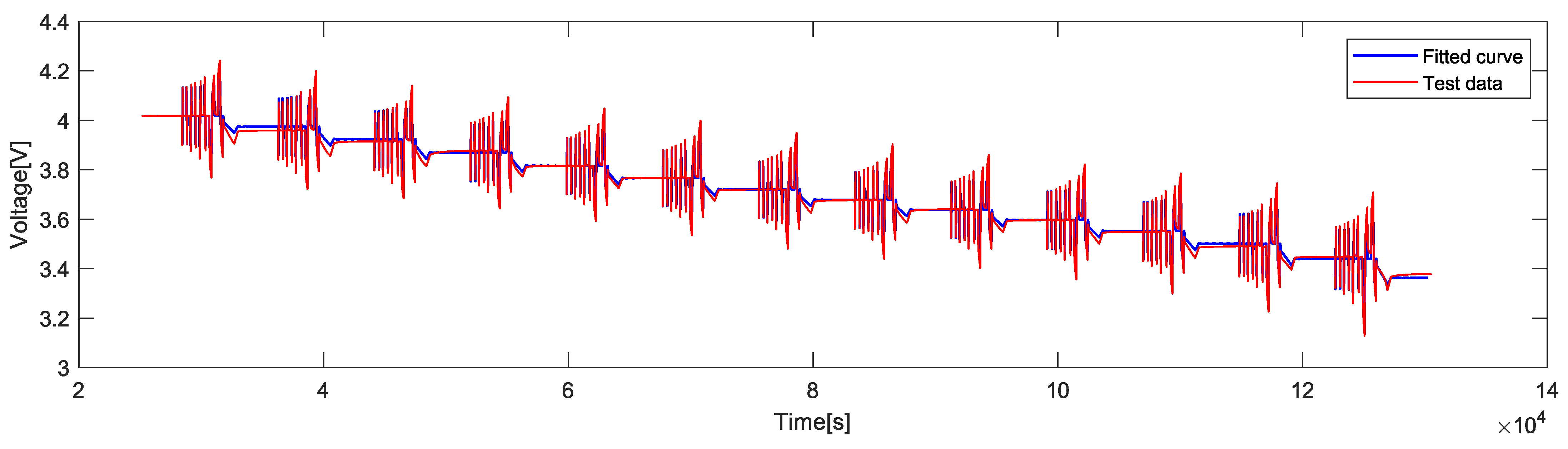
| Temp. (C) | 1C | 0.2C | ||||
|---|---|---|---|---|---|---|
| MAE (V) | RMSE (V) | MAPE (%) | MAE (V) | RMSE (V) | MAPE (%) | |
| 0.032 | 0.038 | 0.876 | 0.036 | 0.044 | 1.003 | |
| 0 | 0.015 | 0.018 | 0.398 | 0.020 | 0.024 | 0.527 |
| 10 | 0.011 | 0.015 | 0.306 | 0.015 | 0.019 | 0.412 |
| 20 | 0.016 | 0.020 | 0.436 | 0.018 | 0.023 | 0.508 |
| 30 | 0.008 | 0.010 | 0.215 | 0.011 | 0.013 | 0.284 |
| 45 | 0.007 | 0.009 | 0.198 | 0.009 | 0.011 | 0.242 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Paudel, S.; Zhang, J.; Ayalew, B.; Singh, R. Systematic Characterization of Lithium-Ion Cells for Electric Mobility and Grid Storage: A Case Study on Samsung INR21700-50G. Batteries 2025, 11, 313. https://doi.org/10.3390/batteries11080313
Paudel S, Zhang J, Ayalew B, Singh R. Systematic Characterization of Lithium-Ion Cells for Electric Mobility and Grid Storage: A Case Study on Samsung INR21700-50G. Batteries. 2025; 11(8):313. https://doi.org/10.3390/batteries11080313
Chicago/Turabian StylePaudel, Saroj, Jiangfeng Zhang, Beshah Ayalew, and Rajendra Singh. 2025. "Systematic Characterization of Lithium-Ion Cells for Electric Mobility and Grid Storage: A Case Study on Samsung INR21700-50G" Batteries 11, no. 8: 313. https://doi.org/10.3390/batteries11080313
APA StylePaudel, S., Zhang, J., Ayalew, B., & Singh, R. (2025). Systematic Characterization of Lithium-Ion Cells for Electric Mobility and Grid Storage: A Case Study on Samsung INR21700-50G. Batteries, 11(8), 313. https://doi.org/10.3390/batteries11080313








