Bayesian Optimization-Based State-of-Charge Estimation with Temperature Drift Compensation for Lithium-Ion Batteries

Abstract

With the widespread application of electric vehicles and electrical energy storage systems, the accurate monitoring of lithium battery states has become crucial for ensuring safety and improving efficiency in terms of the applications. For this reason, this study proposes an algorithm focusing on Bayesian optimization-based adaptive extended Kalman filter (BO-AEKF) to enhance the numerical accuracy and stability of state-of-charge (SOC) estimation for lithium batteries under various operating conditions. By comparing with traditional methods, the proposed algorithm, introducing a temperature-adaptive mechanism and a dynamic parameter updating strategy, can effectively address the estimation limitations under severe temperature variations and initial SOC uncertainties. Experimental results demonstrate that the proposed algorithm exhibits superior estimation performance at different temperatures, including −10 °C, 0 °C, 25 °C, and 50 °C; particularly under dynamic operating conditions, the maximum error (MAX) and root mean square error (RMSE) are reduced by 51.9% and 74.5%, respectively, compared to the extended Kalman filter (EKF) and adaptive extended Kalman filter (AEKF) algorithms. Furthermore, the BO-AEKF achieves rapid convergence even with unknown initial SOC values, demonstrating its robustness and adaptability. These findings provide more reliable technical support for the development of battery management systems, making them suitable for state estimation in electric vehicles and renewable energy storage systems.

1. Introduction

With the global transformation of energy structures and the innovation of energy technologies, lithium-ion batteries (LIBs) have emerged as a highly efficient and clean energy storage solution, finding extensive applications in electric vehicles (EVs), renewable energy storage systems, etc. [1,2]. LIBs are widely regarded as the cornerstone of modern energy storage technologies due to their high energy density, long cycle life, and low self-discharge rate [3,4]. However, the performance and safety of LIBs heavily depend on the accurate monitoring and management of their internal states, particularly under extreme conditions such as high or low temperatures and overloading, which can easily induce overcharging or over-discharging, leading to thermal runaway [5]. There are severe risks due to the thermal runaway, such as overheating, fire, and even explosion [6,7]. Therefore, accurate SOC estimation is a critical measure to prevent such catastrophic events. As one of the core technologies for efficient battery management, precise SOC monitoring enables timely detection of overcharging, over-discharging, or abnormal temperatures, thereby mitigating safety risks, ensuring overall system safety, and extending battery lifespan [8].

Current state-of-charge (SOC) estimation methods primarily include the ampere-hour integration technique [9], open-circuit voltage (OCV) method [10], and data-driven approaches [11,12,13]. Nevertheless, these exhibit severe limitations in practical applications: The accuracy of ampere-hour integration critically depends on initial SOC precision and current-sampling frequency, where accumulated integration errors under significant battery nonlinearity induce substantial deviations between estimated and true SOC values [14]. The OCV method requires offline measurements, inherently compromising real-time performance; moreover, its OCV-SOC relationship deteriorates with battery aging and temperature variations, further reducing estimation accuracy [15]. While data-driven methods achieve high precision and efficiency, they necessitate extensive high-quality datasets, demonstrate limited generalizability across operating conditions, and impose high computational demands, collectively hindering widespread implementation [16,17]. Consequently, equivalent circuit model (ECM)-based methods integrated with Kalman filtering have gained significant traction [18,19].

Recent studies have proposed advanced algorithms to address these challenges. For example, research [20] introduced an improved variable forgetting factor recursive least squares (IVFFRLS) method combined with AEKF for LIB SOC estimation. By eliminating rounding errors in traditional recursive least squares and optimizing parameter boundaries using genetic algorithms, the IVFFRLS method significantly enhanced parameter identification accuracy. Additionally, the incorporation of a covariance matching method in the AEKF enabled adaptive noise parameter updates, improving SOC estimation accuracy and robustness. Research [21] proposed an intelligent adaptive extended Kalman filtering (IAEKF) method, which dynamically updated the covariance matrix by detecting voltage error sequence distribution changes in real time. This approach significantly improved SOC estimation accuracy while maintaining computational efficiency and demonstrated robust performance against model parameter variations, offering a reliable solution for complex operating conditions. Research [22] developed a joint SOC estimation algorithm based on an improved variable forgetting factor recursive least squares method and adaptive square-root unscented Kalman filtering (ASRUKF). By correcting the forgetting factor using multi-step voltage residuals, the algorithm enhanced parameter identification accuracy. The introduction of square-root decomposition in the UKF framework prevented covariance matrix negative definiteness, while the adaptive noise covariance adjustment mechanism dynamically optimized the filtering process. This method exhibited excellent estimation accuracy and robustness across various operating conditions, maintaining reliable SOC tracking even with voltage and current measurement deviations. Research [23] proposed an augmented adaptive extended Kalman filtering (AAEKF) algorithm, which integrated Kalman filtering with adaptive robust control theory to enhance SOC estimation accuracy for EV LIBs. This method innovatively addressed the sensitivity of traditional AEKF to battery model accuracy, demonstrating superior adaptability to system nonlinearity, parameter fluctuations, and environmental temperature variations.

Nevertheless, current methodologies exhibit three interlocked limitations under extreme temperature variations and unknown initial SOC conditions: (1) Pronounced temperature fluctuations induce significant activation energy shifts in lithium-ion diffusion kinetics, while electrolyte conductivity plummets to 15% of its room-temperature value at −20 °C, causing severe model-parameter mismatch and ohmic polarization distortion [24]. (2) The prevalent engineering challenge of unknown initial SOC leads to cumulative error amplification through coulomb counting integration. (3) Critically, most existing models rely on manual parameter calibration. Static parameterization inherently limits adaptive capability by failing to dynamically optimize temperature sensitivity coefficients—as seen in the EKF. Although adaptive variants, including the AEKF, IAEKF, and AAEKF, incorporate dynamic parameters, their adjustment factors still require manual tuning and thus fail to achieve optimal performance. These critical bottlenecks underscore the urgent demand for autonomous parameter identification frameworks, motivating the core contributions of this work:

(1)

A Bayesian optimization-based adaptive extended Kalman filtering (BO-AEKF) algorithm is proposed, which significantly enhances SOC estimation accuracy by incorporating a Bayesian optimization mechanism, enabling adaptability to various operating conditions and environmental disturbances.

(2)

A dynamic parameter adaptive updating strategy is introduced to address model errors caused by temperature variations, effectively improving model stability and estimation accuracy.

(3)

The validation results of the BO-AEKF algorithm under various operating conditions demonstrate that its accuracy and stability outperform traditional methods. With the initial value tracking mechanism, the algorithm achieves rapid convergence under uncertain initial states, further enhancing its robustness.

The remainder of this paper is organized as follows: Section 2 establishes a dual-polarization (DP) model and dynamically updates model parameters through a temperature-adaptive mechanism, completing parameter identification. Section 3 details the construction of the BO-AEKF algorithm and validates its high-precision estimation capabilities and rapid convergence characteristics under varying initial conditions. Section 4 summarizes the findings and proposes potential directions for future research.

2. Materials and Methods

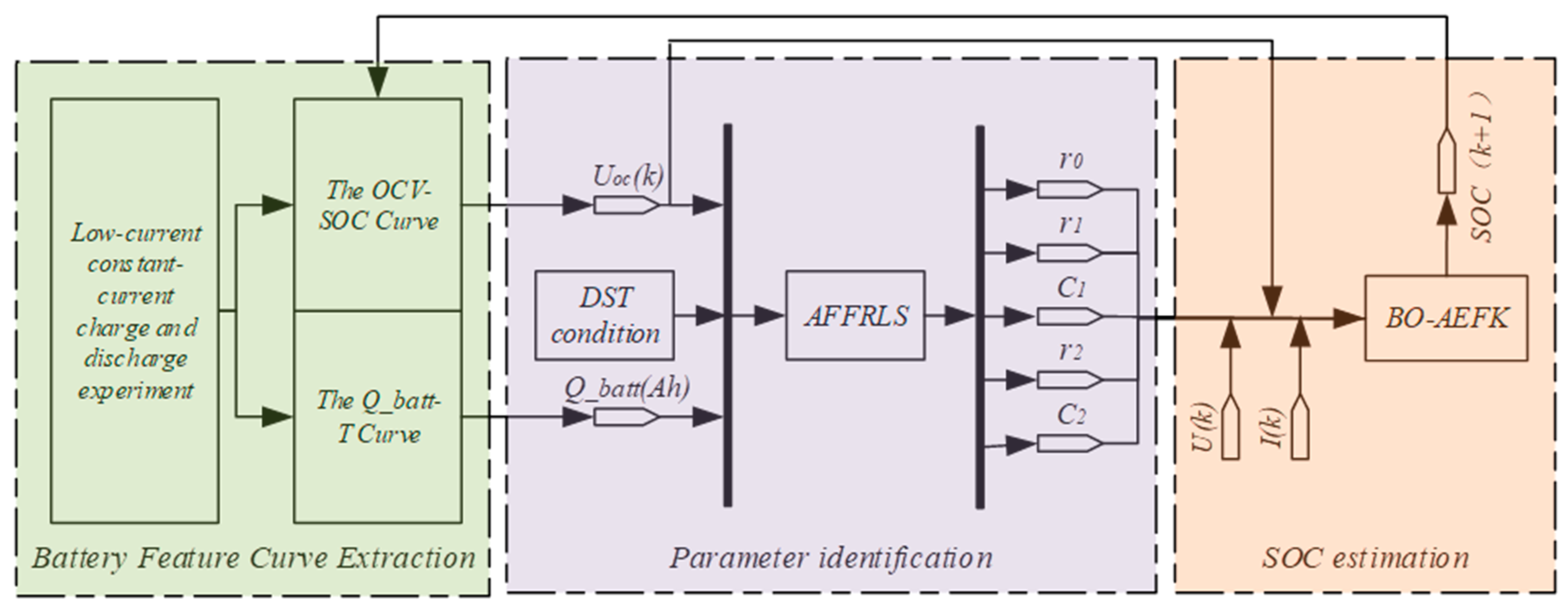
This study constructs a lithium battery state estimation framework with temperature adaptability and enhanced robustness. The implementation procedure is as follows: first, adopt the dual-polarization equivalent circuit model to characterize battery dynamics; then, achieve cross-temperature parameter identification via adaptive RLS incorporating dynamic forgetting factors using public battery datasets, ensuring real-time compensation of temperature-dependent model parameters; finally, the proposed BO-AEKF eliminates manual tuning requirements through intelligent optimization, exhibits rapid convergence characteristics under severe initial state uncertainty, significantly enhances adaptability to initial errors and operational transients, ultimately providing high-accuracy closed-loop solutions for complex scenarios.

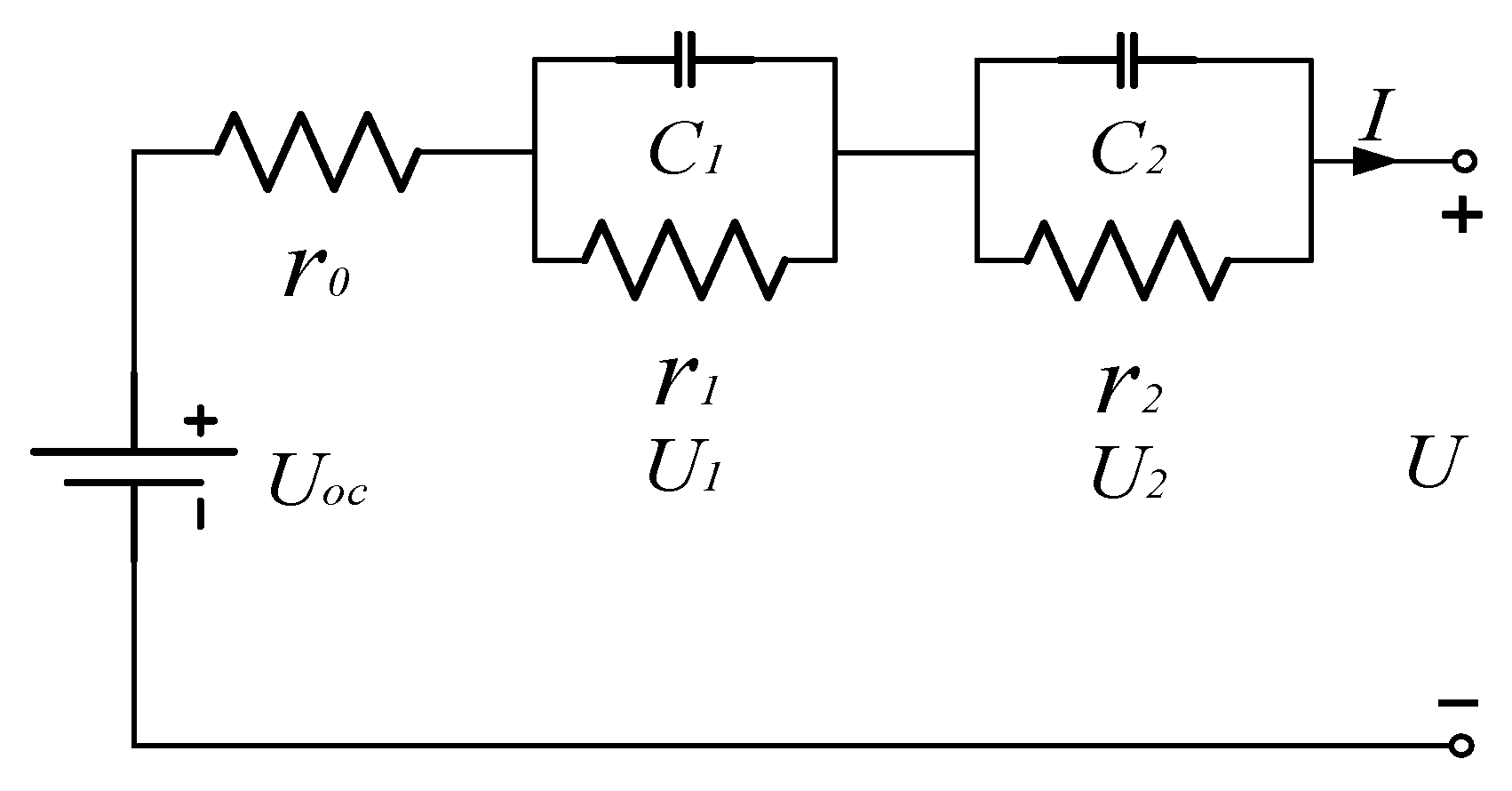
2.1. Establishment of the Equivalent Circuit Model

In the modeling of LIBs, the selection of a model necessitates a balance between accuracy and computational efficiency. The dual-polarization model has been chosen as our primary focus due to its ability to precisely describe the current distribution and voltage response of LIBs, coupled with its concise state-space equation structure [25]. This model achieves high accuracy in characterizing voltage dynamics and facilitates rapid analysis and numerical simulations, providing a reliable theoretical foundation for optimizing LIB performance. Leveraging these advantages, we ultimately adopted the DP model as the subject of our study. The equivalent circuit of the DP model is illustrated in Figure 1. By incorporating two RC (resistor–capacitor) networks, this model accurately captures the dynamic characteristics of LIBs, including ohmic polarization, electrochemical polarization, and concentration polarization phenomena.

Based on the equivalent circuit, the following equations can be established:

$$\left\{\begin{array}{l}U=U_{oc}-U_1-U_2-I{r}_0\\ {\displaystyle \frac{d{U}_1}{dt}}=-{\displaystyle \frac{U_1}{r_1{C}_1}}+{\displaystyle \frac{I}{C_1}}\\ {\displaystyle \frac{d{U}_2}{dt}}=-{\displaystyle \frac{U_2}{r_2{C}_2}}+{\displaystyle \frac{I}{C_2}}\end{array}\right.$$

(1)

among them, $U_{\mathrm{o}\mathrm{c}}$ represents the open-circuit voltage, $r_0$ denotes the ohmic internal resistance, $r_1$ and $C_1$ correspond to the electrochemical polarization resistance and capacitance, respectively, $r_2$ and $C_2$ represent the concentration polarization resistance and capacitance, respectively, $U_1$ and $U_2$ signify the electrochemical polarization voltage and concentration polarization voltage, respectively, and $U$ stands for the terminal voltage.

2.2. Parameter Identification

This study utilizes the publicly available University of Maryland Battery Dataset (UMD Battery Dataset) from the University of Maryland Energy Research Center (UMERC). This high-quality dataset, which focuses on A123 lithium iron phosphate batteries, has been widely employed in research on lithium battery modeling, state estimation, and lifespan prediction [26]. The dataset encompasses comprehensive performance data under various experimental conditions, including dynamic stress tests (DSTs), Federal Urban Driving Schedule (FUDS), Supplemental Federal Test Procedure (US06), and constant current charge–discharge tests, ensuring its representativeness and comprehensiveness. The basic information of the battery is shown in

Table 1. Basic information of the battery.

Model	18650
Nominal Capacity	1.1 Ah
Nominal Voltage	3.3 V
Chemistry	LiFePO4

. The experimental data were collected over a temperature range of −10 °C to 50 °C using multiple cells of the same LiFePO₄ battery model (exact cell quantity unspecified in raw data). The OCV-SOC relationship and capacity characteristics were derived from low-current constant-current charge/discharge tests (0.05 C rate) across all temperature points.

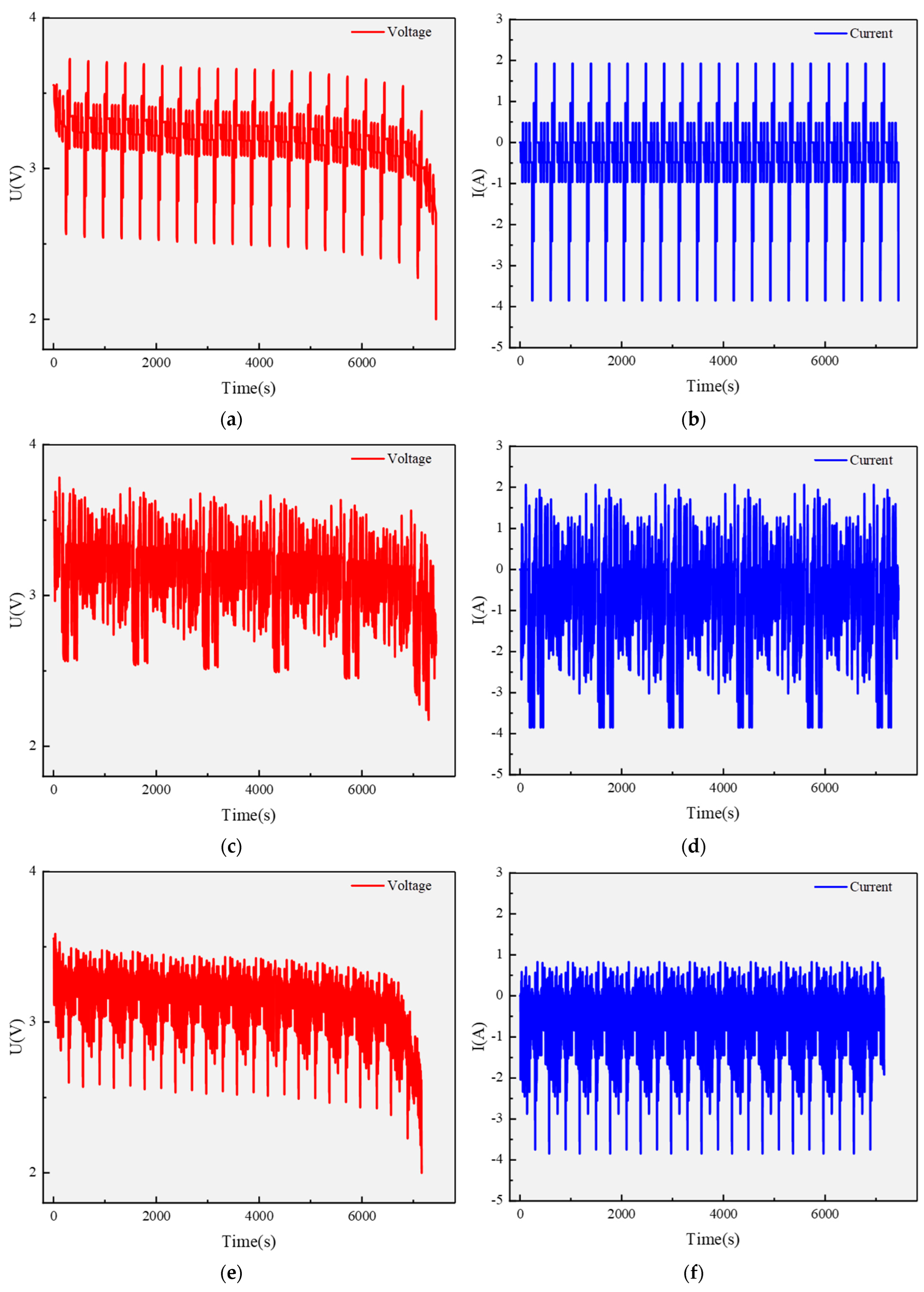
As shown in Figure 2, the DST, FUDS, and US06 driving cycles are displayed, offering a comprehensive visualization of their operational dynamics.

The DST driving cycle, characterized by frequent low-amplitude current fluctuations typical of urban driving, is employed in this study for model parameter calibration due to its suitability for parameter identification and dynamic performance testing. Meanwhile, the FUDS driving cycle, which simulates prolonged urban driving with smoother current variations, is utilized to evaluate system energy efficiency and SOC estimation accuracy. In contrast, the US06 driving cycle, featuring rapid current fluctuations representative of high-speed driving scenarios, is adopted to validate high-power output performance and thermal stability. To comprehensively assess battery performance, this study leverages the DST cycle for parameter identification, while the FUDS and US06 cycles are chosen for SOC estimation validation, as they better reflect real-world operational complexity.

To begin, a low-current constant-current charge–discharge experimental method [27] was employed to obtain the correspondence between OCV and SOC at various temperatures, as well as the corresponding discharge capacity ($Q_{\_batt}$) at different temperatures (T). Subsequently, a 12th-order polynomial fitting method was applied to fit the OCV-SOC curves [28], while a 3rd-order polynomial fitting method was also used for comparison. The corresponding equations are as follows:

$$\left\{\begin{array}{l}OCV=a_0+{\displaystyle \sum _{n=1}^{12}{a}_n}SO{C}^n\\ Q_{\_batt}=b_0+{\displaystyle \sum _{m=1}^3{b}_m}{T}^m\end{array}\right.$$

(2)

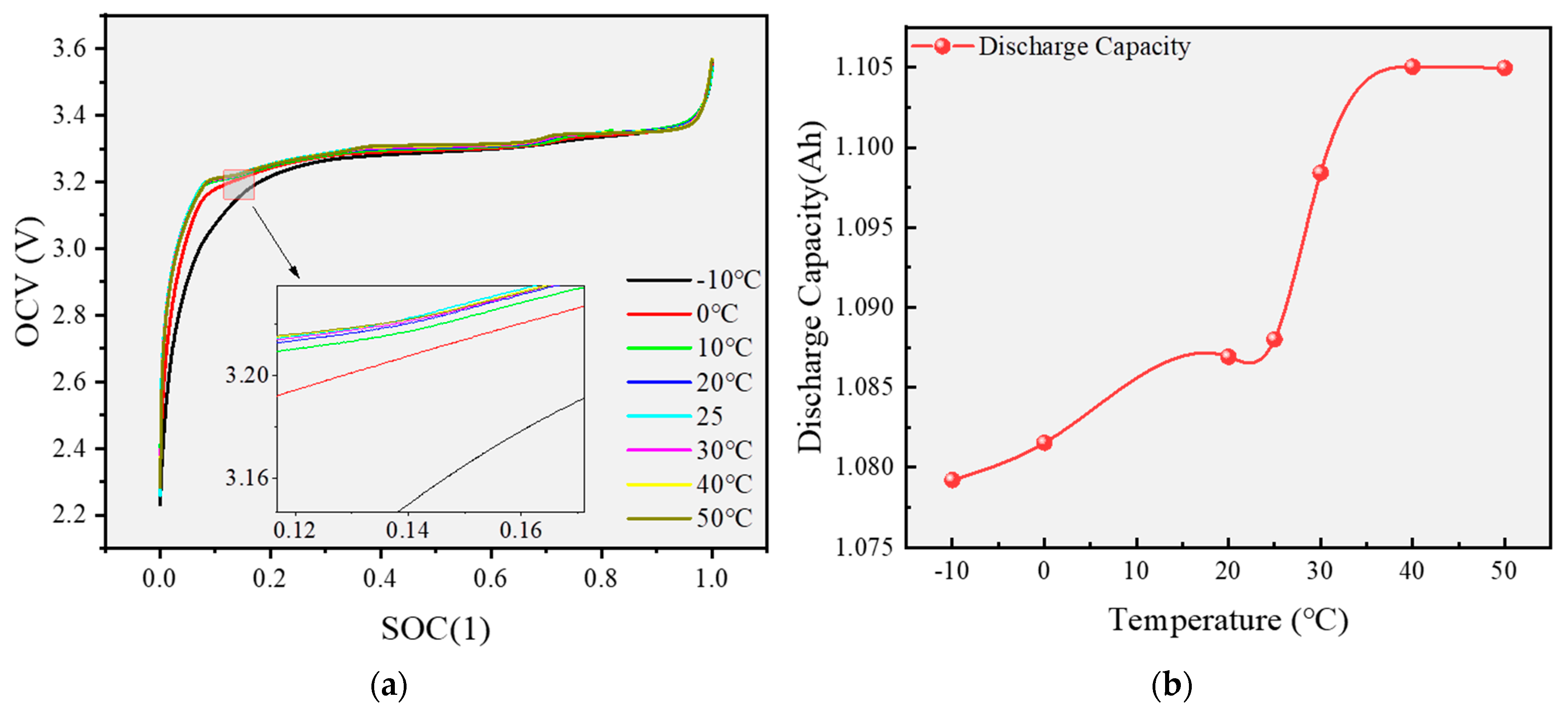
where $a_n$ and $b_m$ are coefficients to be determined. The resulting curves are shown in Figure 3. As illustrated in Figure 3a, under low-temperature conditions (T < 0 °C), the OCV exhibits a significant downward trend as the temperature decreases. Notably, the most pronounced voltage drop occurs within the SOC range of 0 to 0.2, indicating that low temperatures have a substantial impact on the electrochemical performance of the battery, particularly in the low-SOC region. Meanwhile, Figure 3b demonstrates that within a broad temperature range (−10 °C to 50 °C), the battery capacity shows a positive correlation with temperature, with the available capacity gradually increasing as the ambient temperature rises. These findings underscore the importance of incorporating temperature adaptability corrections into the model.

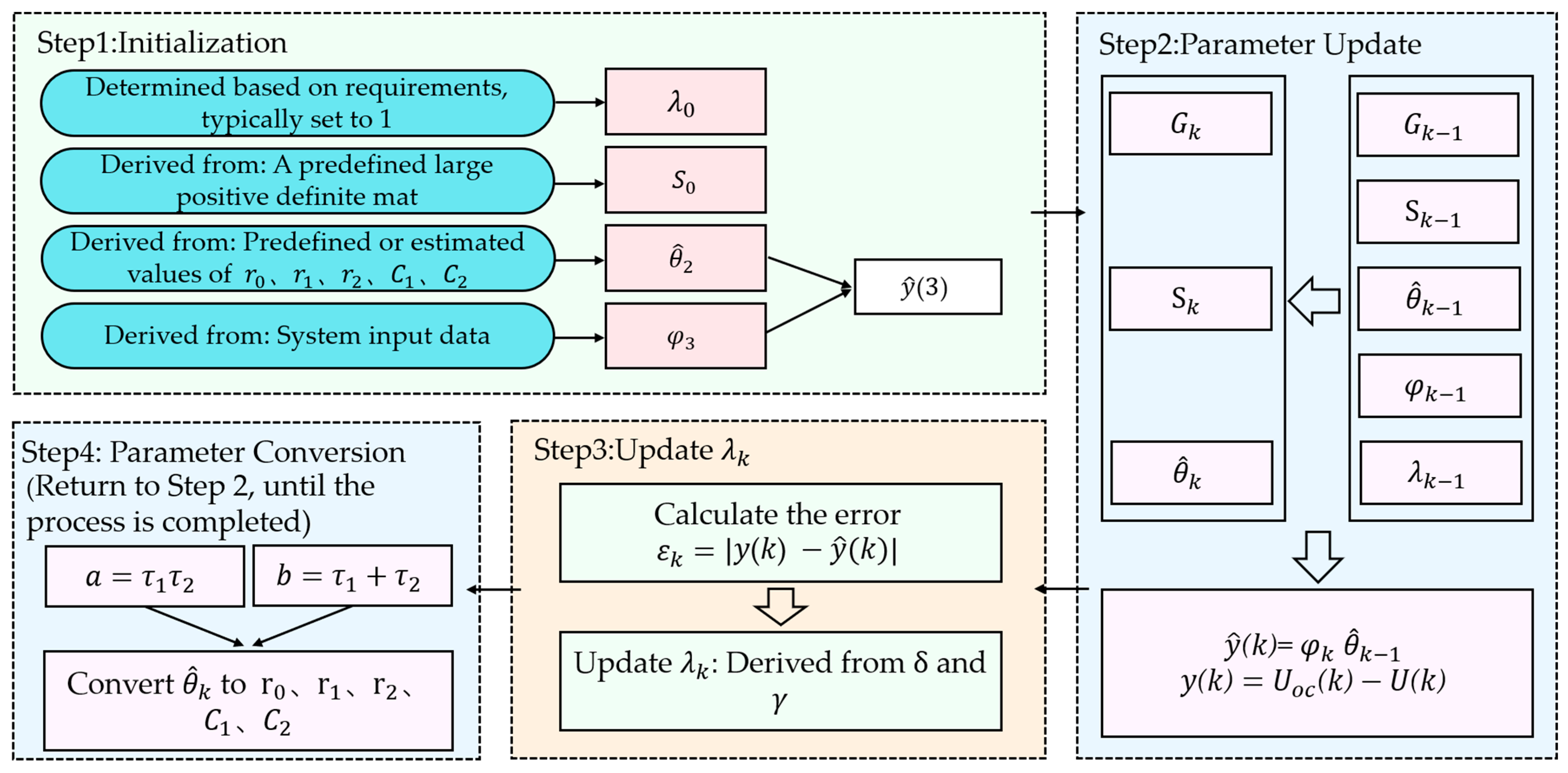
Finally, parameter identification was conducted using data from the DST driving cycle. An adaptive dynamic genetic factor recursive least squares (RLS) method [29,30] was employed for online system parameter identification. The key steps include initialization, predicted output calculation, parameter updating, dynamic genetic factor updating, and parameter transformation, as illustrated in the flowchart in Figure 4.

• Initialization

Set the initial parameter estimates ${\widehat{\theta }}_0$ and the initial covariance matrix $S_0$. The initial parameter estimates ${\widehat{\theta }}_0$ are determined based on the preliminary values of $r_0$, $r_1$, $r_2$, $C_1$, and $C_2$. The initial covariance matrix $S_k$ is typically chosen as a large positive definite matrix.

The initial parameter estimates are given by

$$\widehat{y}(k)={\phi }^T(k){\widehat{\theta }}_{k-1}$$

(3)

The input vector is defined as

$${\phi }_k={[U(k-1)-U_{oc}(k-1)U(k-2)-U_{oc}(k-2)I(k)I(k-1)I(k-2)]}^T$$

(4)

The parameter estimation vector is

$${\widehat{\theta }}_{k-1}={[{\theta }_1{\theta }_2{\theta }_3{\theta }_4{\theta }_5]}^T$$

(5)

• Parameter Update

Compute the gain matrix $K_k$, update the parameter estimates ${\widehat{\theta }}_k$, and update the covariance matrix $S_k$:

$$\left\{\begin{array}{l}{G}_k=S_{k-1}{\phi }_k{({\phi }_k^T{S}_{k-1}{\phi }_k+{\lambda }_k)}^{-1}\hfill \\ {\widehat{\theta }}_k={\widehat{\theta }}_{k-1}+G_k(y(k)-\widehat{y}(k))\hfill \\ S_k={\displaystyle \frac{1}{{\lambda }_k}}\left(I-G_k{\phi }_k^T\right)S_{k-1}\hfill \end{array}\right.$$

(6)

• Update the Dynamic Forgetting Factor ${\lambda }_k$

$$\left\{\begin{array}{l}{\lambda }_k=\delta +(1-\delta )e^{-\gamma {\epsilon }_k}\hfill \\ {\epsilon }_k=|y(k)-\widehat{y}(k)|\hfill \\ y(k)=U_{oc}(k)-U(k)\hfill \end{array}\right.$$

(7)

where $\delta$ is a tunable parameter less than and close to 1, and $\gamma$ is a positive adaptation coefficient.

• Parameter Transformation

Convert ${\widehat{\theta }}_0$ to $r_0$, $r_1$, $r_2$, $C_1$, and $C_2$:

$$\left\{\begin{array}{l}{\theta }_1={\displaystyle \frac{-bTs-2a}{T{s}^2+bTs+a}}\hfill \\ {\theta }_2={\displaystyle \frac{a}{T{s}^2+bTs+a}}\hfill \\ {\theta }_3={\displaystyle \frac{c{t}^2+dTs+a{r}_0}{T{s}^2+bt+a}}\hfill \\ {\theta }_4={\displaystyle \frac{-dTs-2a{r}_0}{T{s}^2+bTs+a}}\hfill \\ {\theta }_5={\displaystyle \frac{a{r}_0}{T{s}^2+bTs+a}}\hfill \end{array}\right.$$

(8)

where $a={\tau }_1{\tau }_2, b={\tau }_1+{\tau }_2$, and $T_{\mathrm{s}}$ the time step. Subsequently, the values can be further transformed according to Equation (9).

$$\left\{\begin{array}{l}{r}_0={\displaystyle \frac{{\theta }_5}{{\theta }_2}}\hfill \\ r_1={\displaystyle \frac{{\tau }_{1}c+{\tau }_2{r}_0-d}{{\tau }_1-{\tau }_2}}\hfill \\ r_2=c-r_0-r_1\hfill \\ C_1={\displaystyle \frac{{\tau }_1}{r_1}}\hfill \\ C_2={\displaystyle \frac{{\tau }_2}{r_2}}\hfill \end{array}\right.$$

(9)

According to the steps outlined above, iteratively executing the procedure allows for the estimation of the values of $r_0$, $r_1$, $r_2$, $C_1$, and $C_2$ at all time instants.

2.3. SOC Estimation

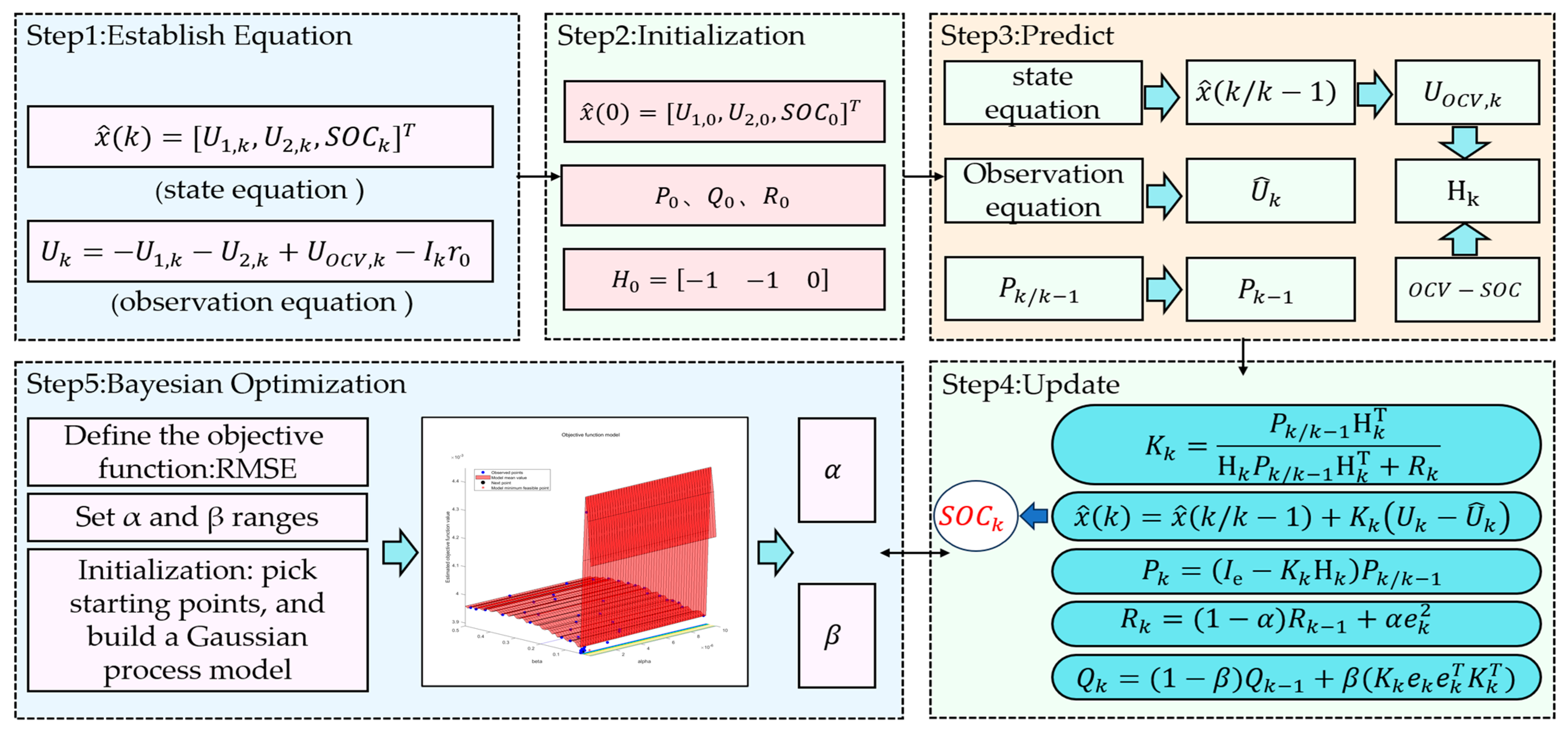
To improve the accuracy and robustness of SOC estimation for lithium-ion batteries, this study proposes a novel BO-AEKF algorithm, which integrates Bayesian optimization with the AEKF [31]. Furthermore, to address model errors induced by environmental temperature variations, dynamic updates are applied to key parameters such as the open-circuit voltage $U_{oc}$ and discharge capacity $Q_{\_batt}$, thereby enhancing the model’s precision and adaptability. The overall estimation framework, incorporating constant current charge–discharge experiments and parameter identification, is illustrated in Figure 5.

EKF estimates the battery SOC by performing local linearization of the nonlinear system dynamics using first-order Taylor expansion, iteratively updating the SOC estimate via state and observation equations; however, its core defect lies in the reliance on preset, fixed process noise covariance matrix and measurement noise covariance matrix, which leads to cumulative estimation bias under dynamic operating conditions due to model mismatch. As an improvement based on the EKF algorithm, the AEKF introduces a sliding-window residual statistics mechanism, enabling self-adjustment of the process noise covariance matrix and measurement noise covariance matrix according to system dynamics; nevertheless, the adjustment factors for scaling these covariance matrices require manual tuning, inherently preventing the identification of an optimal parameter combination. To overcome this limitation, the BO-AEKF framework employs a Bayesian optimization approach, constructing a Gaussian process surrogate model to approximate the black-box relationship between the adjustment factors and SOC estimation accuracy and subsequently performing automatic hyperparameter optimization via acquisition function maximization to enhance SOC estimation precision, with this method proving particularly suitable for practical application scenarios characterized by complex operating conditions and significant parameter variations. The detailed implementation steps are depicted in Figure 6 and described as follows:

• The state and observation equations are established as follows:

$$\left\{\begin{array}{l}\widehat{x}(k)=\left[\begin{array}{c}{U}_{1,k}\\ U_{2,k}\\ SO{C}_k\end{array}\right]=\left[\begin{array}{ccc}{e}^{-{\displaystyle \frac{Ts}{{\tau }_1}}}& 0& 0\\ 0& e^{-{\displaystyle \frac{Ts}{{\tau }_2}}}& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{U}_{1,k-1}\\ U_{2,k-1}\\ SO{C}_{k-1}\end{array}\right]+\left[\begin{array}{c}{r}_1\left(1-e^{-{\displaystyle \frac{Ts}{{\tau }_1}}}\right)\\ r_2\left(1-e^{-{\displaystyle \frac{Ts}{{\tau }_2}}}\right)\\ -\eta {\displaystyle \frac{Ts}{Q_{\_batt}}}\end{array}\right]I_{k-1}\\ U_k=-U_{1,k}-U_{2,k}+U_{OCV,k}-I_k{r}_0\end{array}\right.$$

(10)

where η represents the charge/discharge efficiency.

• Initialization

The state vector is initialized as $\widehat{x}\left(0\right)=[U_{\mathrm{1,0}},U_{\mathrm{2,0}},SO{C}_0{]}^T$, and the covariance matrix $P_0$ is initialized. The process noise covariance matrix $Q_0$ and measurement noise covariance matrix $R_0$ are set, while the Jacobian matrix $H_0=\left[\begin{array}{ccc}-1& -1& 0\end{array}\right]$ is initialized. These matrices can be preliminarily estimated based on the system’s noise characteristics.

• Prediction Step

The prior state $\widehat{x}\left(k\right)$ for the next time step is predicted using the state equation. The open-circuit voltage $U_{OCV,k}$ is calculated using the prior estimate and the OCV-SOC curve at the corresponding temperature. The observation matrix is updated to $H_k=\left[\begin{array}{ccc}-1& -1& U_{OCV,k}\end{array}\right]$, and the terminal voltage ${\widehat{U}}_k$ is estimated using the observation equation. The prior state covariance is predicted as

$$\left\{\begin{array}{l}{P}_{k/k-1}=A_k{P}_{k-1}{A}_k^T+Q_k\\ A_k=\left[\begin{array}{ccc}{e}^{-{\displaystyle \frac{Ts}{{\tau }_1}}}& 0& 0\\ 0& e^{-{\displaystyle \frac{Ts}{{\tau }_2}}}& 0\\ 0& 0& 1\end{array}\right]\end{array}\right.$$

(11)

• Update Step

The Kalman gain is computed as

$$K_k={\displaystyle \frac{P_{k/k-1}{H}_k^T}{H_k{P}_{k/k-1}{H}_k^T+R_k}}$$

(12)

The posterior state is updated using

$$\widehat{x}(k)=\widehat{x}(k/k-1)+K_k(U_k-{\widehat{U}}_k)$$

(13)

where $U_k$ is the measured terminal voltage. The error covariance matrix is updated as

$$P_k=(I_{\mathrm{e}}-K_k{H}_k)P_{k/k-1},$$

(14)

where $I_e$ is the identity matrix. The measurement noise covariance matrix $R_k$ and process noise covariance matrix $Q_k$ are adaptively adjusted using

$$\left\{\begin{array}{l}{R}_k=(1-\alpha )R_{k-1}+\alpha e_k^2\\ Q_k=(1-\beta )Q_{k-1}+\beta (K_k{e}_k{e}_k^T{K}_k^T)\end{array}\right.$$

(15)

where $e_k=U_k-{\widehat{U}}_k$ is the error between the measured and estimated terminal voltages, and $\alpha ,\beta$ are adjustment factors.

• Bayesian Optimization

Bayesian optimization is employed to optimize the adjustment factors $\alpha$ and $\beta$ and output the SOC estimation result. The objective function is defined as the RMSE of the SOC estimation error:

$$f(\alpha ,\beta )=\sqrt{{\displaystyle \frac{1}{N}}\sum _{i=1}^N{\left(SO{C}_{true}(i)-SO{C}_{est}(i)\right)}^2}$$

(16)

where ${SOC}_{true}$ is the true SOC value, ${SOC}_{est}$ is the EKF-estimated SOC value, and N is the number of data points. The optimization variables $\alpha$ and $\beta$ are defined within specific ranges, which can be manually narrowed based on experience to reduce iteration counts.

Initialization involves randomly selecting several initial points, computing the objective function values, and constructing an initial surrogate model. A Gaussian process (GP) surrogate model is employed, which assumes the objective function follows a multivariate Gaussian distribution:

$$f(\alpha ,\beta )\sim \mathcal{G}\mathcal{P}(m(\alpha ,\beta ),k((\alpha ,\beta ),(\alpha \prime ,\beta \prime )))$$

(17)

where $m(\alpha ,\beta )$ is the mean function, and $k(\left(\alpha ,\beta \right),(\alpha \prime \beta \prime )$ is the kernel function. The squared exponential kernel is used:

$$k((\alpha ,\beta ),(\alpha \prime ,\beta \prime ))={\sigma }_f^2\exp \left(-{\displaystyle \frac{{(\alpha -\alpha \prime )}^2}{2l_{\alpha }^2}}-{\displaystyle \frac{{(\beta -\beta \prime )}^2}{2l_{\beta }^2}}\right)$$

(18)

where ${\sigma }_f^2$ is the signal variance, and $l_{\alpha }$ and $l_{\beta }$ are the length scales in the $\alpha$ and $\beta$ dimensions, respectively.

The next evaluation point is selected using the Expected Improvement (EI) acquisition function:

$$\mathrm{EI}(\alpha ,\beta )=\mathbb{E}[\max (f(\alpha ,\beta )-f({\alpha }^{+},{\beta }^{+}),0)]$$

(19)

where $f({\alpha }^{+},{\beta }^{+})$ is the current best objective function value. Iterative optimization proceeds as follows: (1) select the next evaluation point $({\alpha }_{next},{\beta }_{nest})$ using the acquisition function; (2) compute the objective function value ${RMSE}_{next}=f({\alpha }_{next},{\beta }_{nest})$; (3) add the new point $({\alpha }_{next},{\beta }_{nest},{RMSE}_{nest})$ to the observation dataset; (4) update the GP surrogate model based on the new observations; and (5) terminate if the maximum iteration count or convergence criteria are met; otherwise, continue. Finally, the optimal adjustment factors $({\alpha }^{+},{\beta }^{+})$ are output and incorporated into the AEFK to obtain the final results.

3. Results

To validate the effectiveness of the proposed BO-AEKF algorithm, parameter identification was first performed using the AFFRLS algorithm on DST condition data at ambient temperatures of −10 °C, 0 °C, 25 °C, and 50 °C. The results are presented in

Table 2. Parameter Identification Results.

Temperatures (°C)	${\mathit{r}}_0$(Ω)	${\mathit{r}}_1$(Ω)	${\mathit{r}}_2$(Ω)	${\mathit{C}}_1$(F)	${\mathit{C}}_2$(F)
−10	0.291	0.021485	0.19284	20.23	445
0	0.208	0.008135	0.12312	72.13	667
25	0.195	0.002804	0.05913	397.50	1235
50	0.189	0.001646	0.02983	362.10	1342

, with the parameter identification results at 25 °C illustrated in Figure 7.

The parameter identification results in Figure 7 indicate that all parameters exhibit significant fluctuations during the initial phase (approximately 0–2000 s), primarily stemming from algorithmic artifacts—where initial guess deviations cause overcompensation—and model limitations in capturing rapid polarization. Consequently, the observed significant fluctuations and polarity sign jumps in $r_0$/$r_1$/$r_2$ during this period constitute expected phenomena before gradually converging. Specifically, $r_0$ and $r_1$ stabilize after 3000 s, whereas $r_2$ reaches a steady state after 4000 s. Although $C_1$ and $C_2$ exhibit minor fluctuations up to 6000 s, their overall trends maintain stability. Ultimately, all parameters converge to reasonable ranges without divergence, and the terminal voltage estimation error—despite larger initial deviations during early identification—rapidly converges after 20 s and remains maintained below 0.005 V. This confirms that the identification algorithm effectively suppresses noise interference, yielding reliable and robust parameter identification results that establish an accurate basis for lithium battery modeling.

The parameter identification results in Table 2 indicate that both the ohmic resistance $r_0$ and the polarization resistances $r_1$ and $r_2$ exhibit a decreasing trend with increasing temperature. Specifically, $r_0$ decreases from 0.29 Ω at −10 °C to 0.189 Ω at 50 °C, while $r_1$ and $r_2$ decrease from 0.02148 Ω and 0.1928 Ω to 0.001646 Ω and 0.02983 Ω, respectively. This reduction in resistance is attributed to enhanced ionic conductivity and improved reaction kinetics at elevated temperatures. Elevated temperatures significantly reduce both ohmic and polarization resistances, thereby enhancing battery performance and efficiency.

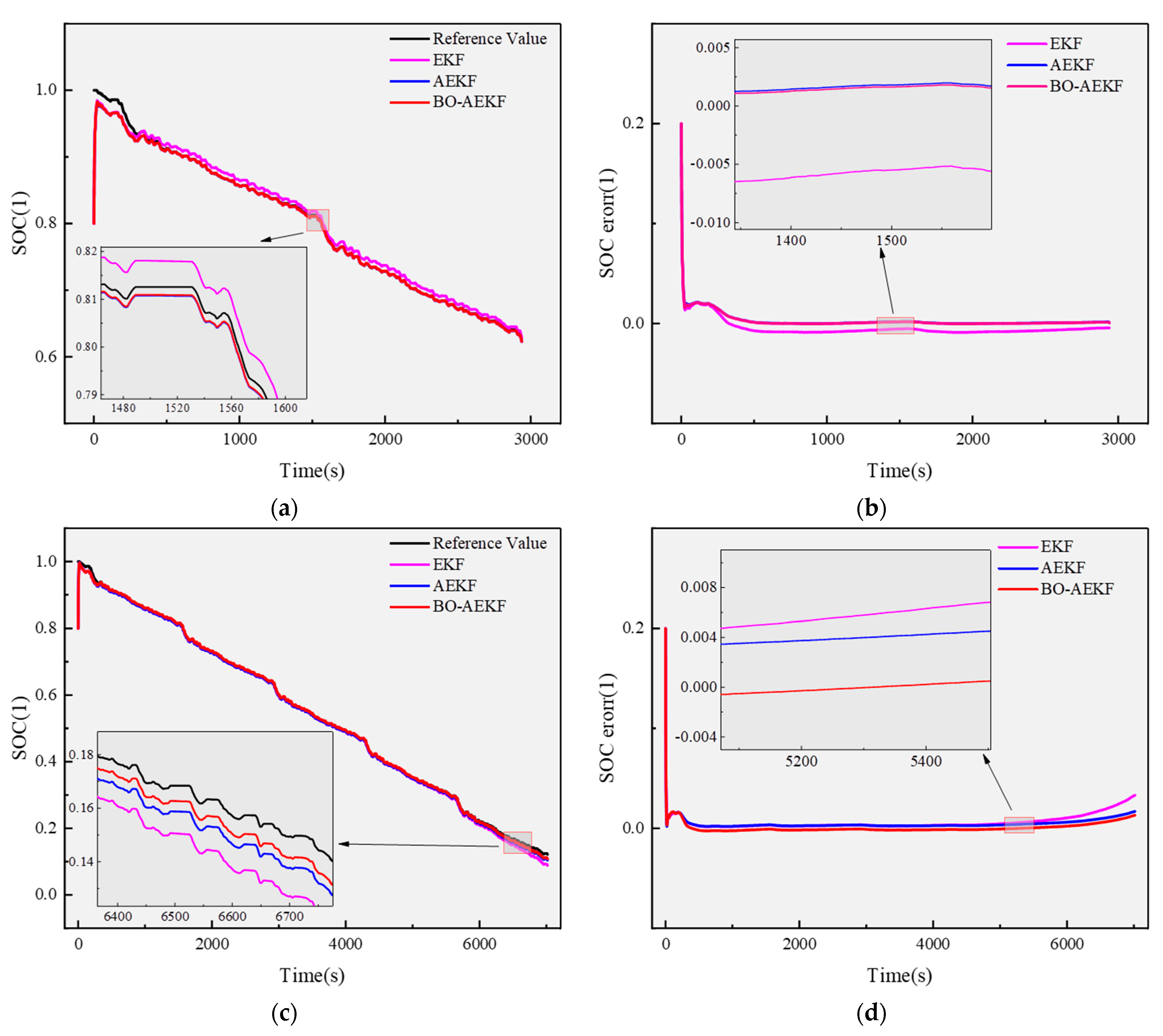
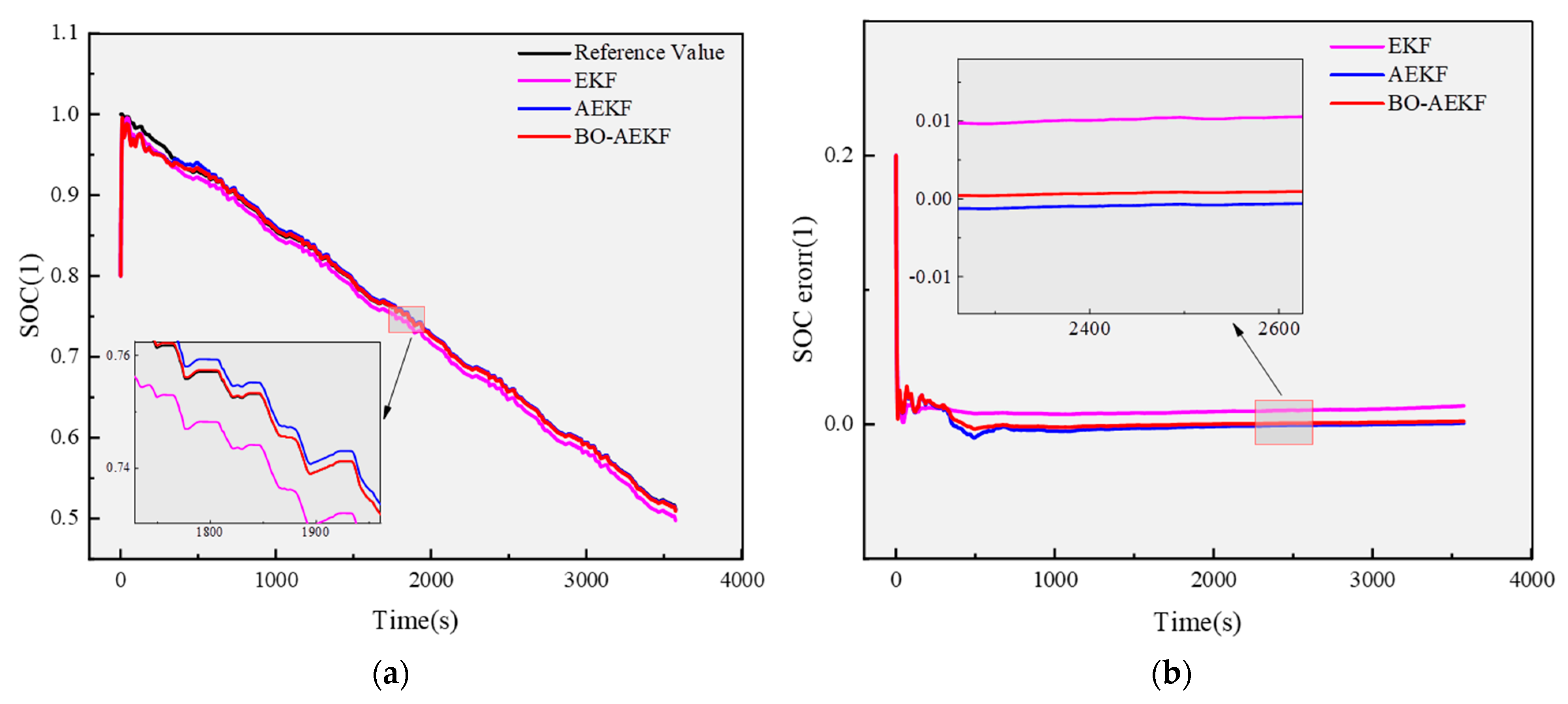
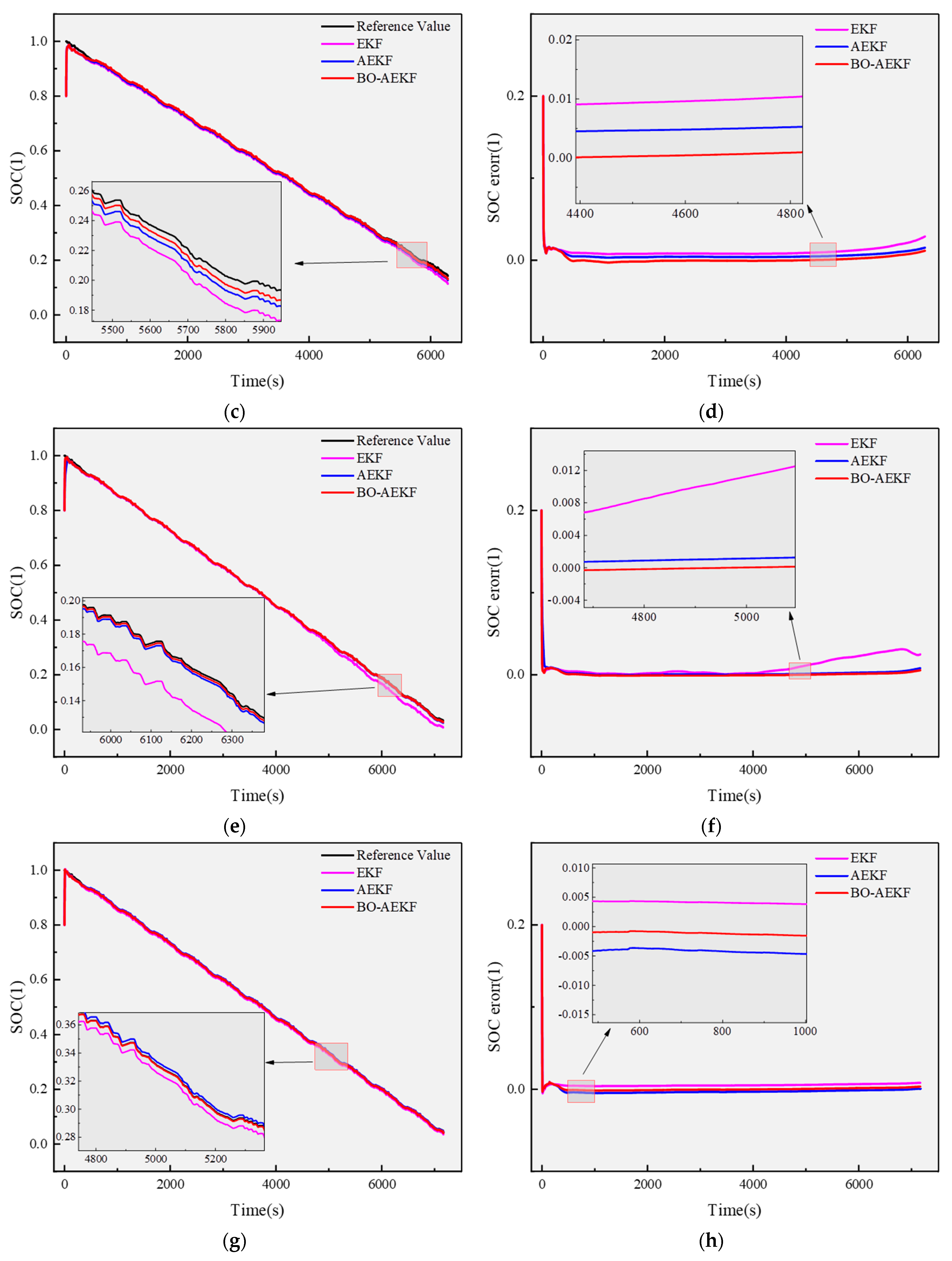
Based on the identified parameters, tests were conducted under FUDS and US06 conditions at ambient temperatures of −10 °C, 0 °C, 25 °C, and 50 °C. To comprehensively evaluate the performance of the BO-AEKF algorithm, it was compared with the traditional EKF and AEKF algorithms, using the SOC calculated by the ampere-hour integration method as the reference [32]. Additionally, the effects of temperature on the open-circuit voltage and battery discharge capacity were fully considered during the testing process. The experimental results are shown in Figure 8 and Figure 9 and

Table 3. Comparison of SOC Estimation by Different Algorithms under Various Temperatures and Operating Conditions.

Temperature (°C)	Algorithm	Operating Condition
		FUDS		US06
		RMSE	MAX	RMSE	MAX
−10	EKF	0.010689	0.0089	0.011343	0.0137
	AEKF	0.008807	0.0020	0.007605	0.0098
	BO-AEKF	0.008706	0.0018	0.007292	0.0035
0	EKF	0.009688	0.0330	0.012020	0.0289
	AEKF	0.006817	0.0169	0.007567	0.0152
	BO-AEKF	0.005564	0.0130	0.005778	0.0115
25	EKF	0.004516	0.0112	0.013841	0.0311
	AEKF	0.003923	0.0058	0.006614	0.0080
	BO-AEKF	0.003886	0.0053	0.004095	0.0054
50	EKF	0.006098	0.0176	0.006172	0.0079
	AEKF	0.005346	0.0192	0.004589	0.0047
	BO-AEKF	0.005283	0.0194	03003665	0.0033

.

From Figure 8 and Figure 9, it is evident that the BO-AEKF algorithm demonstrates superior estimation accuracy and robustness across a wide temperature range under both FUDS and US06 operating conditions, with particularly notable improvements under the more dynamic US06 condition. By integrating Bayesian optimization with adaptive strategies, the BO-AEKF algorithm achieves enhanced SOC estimation accuracy across varying temperatures. As indicated in Table 3, the RMSE and MAX data comparisons reveal that BO-AEKF outperforms both EKF and AEKF in terms of precision and robustness under different temperatures and dynamic conditions. An exception occurs in the FUDS condition at 50 °C, where the inherent thermal drift of the model was not fully mitigated, leading to increased overall error. However, the MAX point shifted toward the direction of reduced error, resulting in a smaller MAX value, while the RMSE remained significantly lower. Thus, from an overall accuracy perspective, BO-AEKF consistently exhibits lower errors across various temperatures. For instance, under the FUDS condition at −10 °C, the RMSE was optimized by 18.5% compared to EKF, while at 25 °C, a 14% improvement in accuracy was maintained. The advantages of BO-AEKF are even more pronounced under the highly dynamic US06 condition, with RMSE reductions of 51.9% at 0 °C and 40.6% at 50 °C, demonstrating its ability to deliver precise state estimations even under conditions of high dynamic uncertainty.

Moreover, BO-AEKF exhibits exceptional stability in extreme temperature environments. For example, under the US06 condition at −10 °C, its MAX value was only 0.0035, representing a 74.5% reduction compared to EKF and a 64.3% reduction compared to AEKF. This robustness stems from its Bayesian optimization layer, which dynamically adjusts the system noise covariance and observation noise covariance to adapt to model uncertainties induced by temperature variations. Although the MAX error in the FUDS condition at 50 °C was slightly higher than that of AEKF, the RMSE remained superior, indicating that BO-AEKF prioritizes maintaining overall accuracy over merely suppressing peak errors in extreme temperatures.

Compared to other algorithms, the core advantage of BO-AEKF lies in its dynamic parameter adaptation. By leveraging Bayesian optimization to adjust noise parameters in real time, it maintains stability across wide temperature ranges and highly dynamic conditions. In conclusion, the BO-AEKF algorithm offers significant advantages for state estimation in photovoltaic and electric vehicle energy storage systems, particularly in complex scenarios involving wide temperature ranges and high dynamics. Overall, BO-AEKF demonstrates higher accuracy and greater adaptability under extreme temperatures and complex operating conditions, providing reliable technical support for the development of lithium battery management systems.

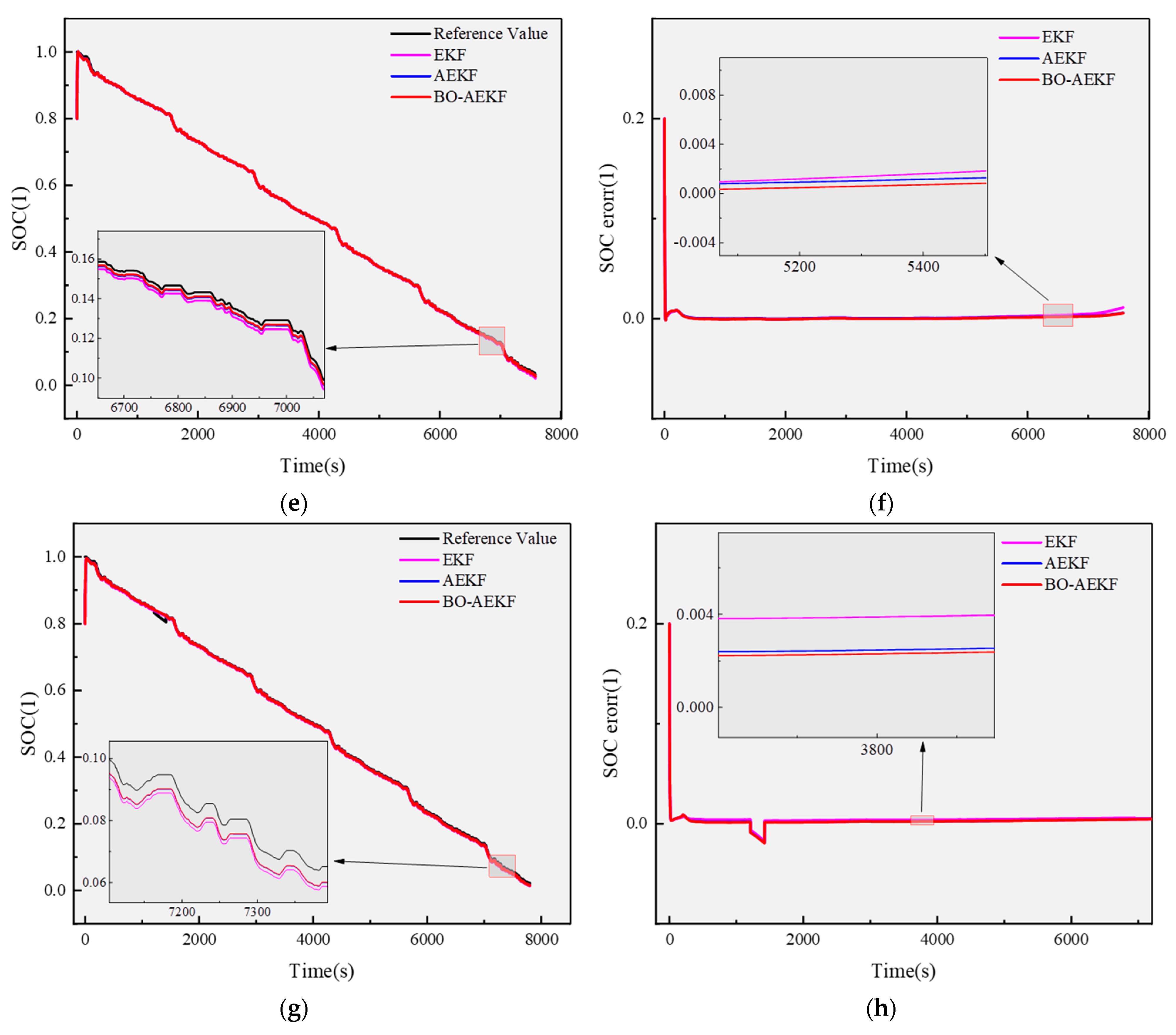
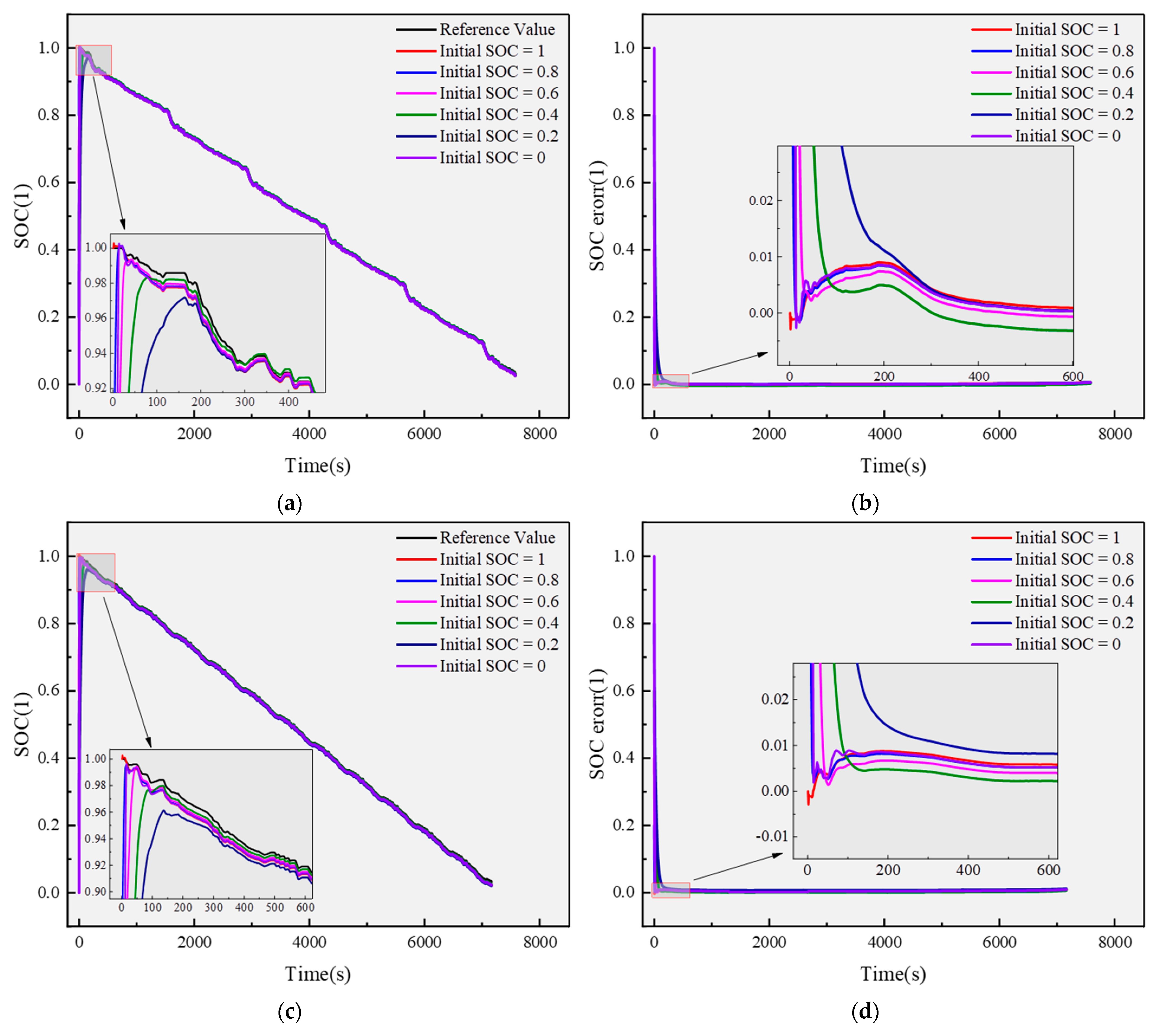
To address the practical engineering challenge of unknown initial SOC in real-world lithium battery operations, this study conducted a series of comparative experiments to systematically evaluate the initial value adaptability and convergence characteristics of the BO-AEKF algorithm. To ensure the algorithm’s robustness and stability across varying initial conditions, the objective function of the Bayesian optimization layer was explicitly defined:

$$RMS{E}_{next}=RMS{E}_1+RMS{E}_{0.8}+RMS{E}_{0.6}+RMS{E}_{0.4}+RMS{E}_{0.2}+RMS{E}_0$$

(20)

The BO-AEKF algorithm was tested under FUDS and US06 driving cycles at 25 °C, with different initial SOC values as inputs. The results, as depicted in Figure 10 and summarized in

Table 4. Error Conditions under Different Initial SOC States at 25 °C.

Operating Conditions	Initial SOC	RMSE
FUDS	1	0.002393
	0.8	0.003932
	0.6	0.010153
	0.4	0.019631
	0.2	0.029458
	0	0.016276
US06	1	0.005635
	0.8	0.006196
	0.6	0.011847
	0.4	0.02267
	0.2	0.034774
	0	0.017793

, demonstrate that the algorithm consistently converges to the true SOC value within a short timeframe, regardless of the initial state. Specifically, the RMSE remained below 3% for the FUDS cycle and within 3.5% for the more dynamic US06 cycle, confirming its high estimation accuracy.

In the initial phase, estimation results exhibited fluctuations due to the uncertainty of the initial SOC value. Notably, the amplitude of these fluctuations increased proportionally with the deviation between the initial state and the true value. However, as the algorithm iterated, these fluctuations gradually diminished and stabilized, highlighting the robust nature of the BO-AEKF algorithm in mitigating the impact of initial errors.

This enhanced robustness and adaptability stem from the algorithm’s adaptive mechanisms and robustness-enhancing design, which effectively address the issue of initial state uncertainty. These features provide reliable SOC estimation support for BMS, offering significant implications for optimizing charging/discharging strategies and extending battery lifespan. Overall, the BO-AEKF algorithm demonstrates superior performance in handling initial state uncertainties, making it a valuable tool for advanced BMS applications.

4. Discussion

Comparative analysis reveals that the BO-AEKF algorithm introduces Bayesian optimization to adjust the parameters of the AEKF, achieving remarkable improvements of up to 74.5% in MAX error and 51.9% in RMSE compared to the traditional EKF. Notably, the algorithm demonstrates the rare and valuable capability to converge within 100 s under large initial SOC error conditions. While the computational complexity of BO-AEKF is higher than that of both EKF and AEKF, it is important to note that this increase is not exponential or multiplicative. The EKF relies on linearizing state and measurement functions, entailing minimal computational overhead. The AEKF adapts process and measurement noise covariances to enhance accuracy, with slightly higher complexity than EKF but still lower than BO-AEKF. BO-AEKF performs iterative calculations via Bayesian optimization to find optimal parameters, but the computational growth is controlled through strategies like adaptive iteration termination and feature dimension reduction—thus avoiding a multiplicative complexity surge. Despite the higher complexity, BO-AEKF achieves superior SOC estimation accuracy while maintaining a feasible computational burden, demonstrating a more balanced trade-off between precision and efficiency in practical applications. Therefore, the BO-AEKF algorithm is highly suitable for computation-constrained environments such as real-time control in electric vehicle BMS and grid energy storage systems.

Although significant progress has been made in the accuracy and robustness of SOC estimation, several research directions warrant further exploration.

Firstly, regarding model adaptability, current studies primarily focus on the impact of temperature as a single factor on SOC estimation models. However, in real-world applications like electric vehicle charging/discharging and grid energy storage peak regulation, battery performance is often influenced by the synergistic effects of multiple factors, such as aging, charge/discharge rates, and battery types. Future research could establish more comprehensive model parameter mapping relationships based on multi-factor coupling experiments, exploring the combined effects of battery degradation, current magnitude, and different lithium battery materials on SOC estimation. This would contribute to the development of a more universal battery state estimation framework.

Secondly, in terms of algorithm optimization, although the BO-AEKF algorithm demonstrates excellent accuracy, its high computational complexity poses a significant burden on onboard computing units. Given the stringent real-time requirements of practical BMS systems, future optimizations could focus on two directions: (1) leveraging the advantages of deep learning algorithms to establish lightweight network structures that replace certain computational modules and (2) investigating simplified model methods based on covariance matrix feature extraction, reducing computational complexity through mathematical techniques such as feature space dimensionality reduction. These approaches aim to achieve an optimal balance between accuracy and efficiency. (3) Based on the Bayesian optimization algorithm, develop a cross-paradigm evaluation framework to achieve joint operation with UKF or PF, enhancing SOC estimation accuracy.

Lastly, in the context of engineering application validation, all current experiments are based on standard test data under laboratory conditions. However, real-world operating conditions impose higher demands on parameter adjustments. Subsequent research could integrate GAN networks for generating and classifying actual operating condition data and constructing adaptive parameter adjustment mechanisms based on condition recognition. Additionally, large-scale empirical studies should be conducted in real-world electric vehicle battery systems and energy storage stations. Long-term operational testing in practical engineering environments would not only further validate the algorithm’s applicability but also provide more reliable practical insights for parameter optimization.

The in-depth exploration of these research directions will facilitate the transition of SOC estimation technology from experimental research to engineering applications, offering technical support for the development of more reliable and efficient battery management systems.

5. Conclusions

In this study, we address the challenges of temperature adaptability and initial value uncertainty in state-of-charge estimation for lithium batteries by proposing an innovative Bayesian optimization-based AEKF algorithm. By introducing a temperature-adaptive update mechanism for dual-polarization model parameters and a Bayesian optimization layer, the algorithm achieves dynamic optimal adjustment of the noise covariance matrix. Experimental results demonstrate that the BO-AEKF algorithm outperforms traditional EKF and AEKF methods under multi-temperature and high-dynamic conditions, with a maximum improvement of 51.9% in RMSE and a 74.5% reduction in maximum error, showcasing its superior temperature adaptability and dynamic tracking capabilities. Furthermore, the algorithm exhibits robust convergence within 100 s under FUDS and US06 driving cycles, even with initial SOC errors of up to ±40%, where the convergence time increases by only 15% and the maximum instantaneous error remains below 5%. Comprehensive evaluations confirm that the BO-AEKF algorithm achieves steady-state estimation accuracy better than 1.5% across various test conditions, providing a reliable SOC estimation solution for BMS.

Future research directions include the following: (1) multi-factor coupling modeling to extend the study to the effects of battery aging, different chemical systems, and mixed operating conditions, thereby establishing a more comprehensive state estimation model; (2) lightweight algorithm design by exploring deep learning-based feature extraction and model compression techniques to enable efficient deployment on resource-constrained embedded systems [33,34]; and (3) real-world vehicle validation and optimization through the construction of an actual operating condition database using onboard data acquisition systems and the development of a digital twin-based online optimization framework to facilitate industrial application. The proposed BO-AEKF algorithm offers a novel technical pathway for enhancing BMS performance, and its design principles can be extended to state estimation in other types of energy storage systems.