Abstract
Accurate prediction of the state of health (SOH) in lithium batteries (LiBs) is essential for ensuring operational safety, extending battery lifespan, and enabling effective second-life applications. However, achieving precise SOH prediction under small-sample conditions remains a significant challenge due to inherent variability among battery cells and capacity recovery phenomena, which result in irregular degradation patterns and hinder effective feature extraction. To overcome these challenges, this study introduces an advanced autoencoder-based method specifically designed for SOH prediction in small-sample scenarios. This method employs a multi-encoder structure—comprising token, positional, and temporal encoders—to comprehensively capture the multi-dimensional characteristics of SOH sequences. Furthermore, a BHTP module is integrated to facilitate feature fusion and enhance the model’s stability and interpretability. By utilizing a pre-training and fine-tuning strategy, the proposed method effectively reduces computational complexity and the number of model parameters while maintaining high prediction accuracy. The validation of the NASA 18650 lithium cobalt oxide battery dataset under various discharge strategies shows that the proposed method achieves fast convergence and outperforms traditional prediction methods. Compared with other models, our method reduces the RMSE by 0.004 and the MAE by 0.003 on average. In addition, ablation experiments show that the addition of the multi-encoder structure and the BHTP module improves the RMSE and MAE by 0.008 and 0.007 on average, respectively. These results highlight the robustness and utility of the proposed method in real battery management systems, especially under data-scarce conditions.
1. Introduction
Battery management systems play a critical role in ensuring the safe and stable operation of lithium batteries and support battery recycling for secondary use. This, in turn, helps to reduce greenhouse gas emissions, mitigate environmental pollution, address the energy crisis, and achieve a carbon peak and a carbon-neutral society. The state of health (SOH) of a battery, as one of the parameters of a battery management system, is a crucial indicator of the continued functioning of the battery. Severe degradation of the SOH of a lithium battery can lead to frequent failures [1,2,3]. Hence, research on SOH can help to identify internal hazards and estimate battery lifecycles so as to avoid further safety issues and facilitate the recycling and reuse of batteries [3,4,5,6,7].
Currently, SOH prediction methods can be categorized into two types: traditional model-based methods, including equivalent circuit models (ECM) [8], electrochemical models [9], and empirical models [10], and data-driven methods. Messing et al. [11,12] demonstrated that electrochemical impedance spectroscopy (EIS) can effectively track the short-term relaxation effects of batteries at different SOHs, and proposed an SOH estimation method combining fractional-order impedance modeling and short-term relaxation effects with EIS characteristics. Luo et al. [13] proposed an EIS-based rapid SOH prediction method by constructing a mathematical model to estimate the SOH of decommissioned batteries. This model combines the constant phase element parameters of EIS-ECM with the state of charge (SOC) and SOH of batteries. Bartlett et al. [14] combined an electrochemical model with an extended Kalman filter to estimate the SOH of lithium-ion batteries with composite electrodes, using a reduced-order electrochemical model to estimate the loss of active materials in batteries to facilitate SOH prediction. However, these methods require specified experimental conditions and are therefore more suitable for battery design and technical improvement.
Among the data-driven methods, Yang et al. [15,16] used four characteristic parameters extracted from the charging curve as the input to a Gaussian process regression model, and then used gray correlation analysis to assess the correlation between the four characteristic parameters and SOH, thus improving the covariance function design and similarity measure to enhance the accuracy of SOH estimation. Tan et al. [17,18] proposed an SOH prediction method based on transfer learning [19]. Zhang et al. [20,21] established a transfer learning model and used the fine-tuning model to conduct SOH estimation by using a small amount of recent historical data of the target battery [22]. Cheng et al. [23] proposed an SOH prediction method that combines empirical mode decomposition with a backpropagation long short-term memory (B-LSTM) neural network [24]. Chang et al. [25,26] proposed an SOH estimation method based on a wavelet neural network combined with a genetic algorithm (GA). After obtaining incremental capacity curves, significant health characteristic variables were extracted using the Pearson correlation coefficient, and the initial parameters of the wavelet neural network were optimized using the GA. Tian et al. [27] proposed a lithium-ion battery SOH estimation method using DT-IC-V health features extracted from a partial charging segment, a DBN-ELM model optimized by SSA, and verified its high accuracy with low errors on Oxford and NASA datasets. Li et al. [28] proposed a SOH prediction method based on neural basis expansion analysis (NBEATS) neural network of hunter and prey optimization (HPO) with variational mode decomposition (VMD). Shi’s [29] SOH prediction of lithium-ion batteries uses automatically extracted features and an IWOA-SVR model.
Due to the highly complex internal mechanisms of batteries and the intricate electrochemical reactions involved in their functioning, it is challenging to directly establish a traditional model for battery SOH prediction based on electrochemical principles [30]. In recent years, data-driven methods have been widely and successfully applied for predicting the SOH of batteries due to their high feasibility [31]. However, data-driven models require extensive training, and their accuracy heavily depends on the quality and quantity of the data used for modeling. Factors such as inconsistent usage scenarios and the long lifecycles of batteries often result in limited acquired data and an imbalanced data distribution. Under these conditions, data-driven models often suffer from low accuracy and generalizability. Under small-sample conditions, the differences between battery cells and the capacity recovery phenomenon will lead to unreasonable SOH degradation, making it difficult for a deep learning model to capture the SOH cycle features of batteries [32].
To tackle the challenges of state-of-health prediction for lithium batteries under small-sample conditions, we propose a multi-encoder and transfer learning empowered method, which leverages a multi-encoder structure. From the perspective of the manifold learning theory, data tend to be distributed on low-dimensional manifold structures in a high-dimensional space, and the manifold structures of different sample sets are essentially similar [33]. Based on this theory, a multi-encoder structure is designed, which includes token, position, and time encoders to comprehensively extract multi-dimensional features from the state of health (SOH) sequences. These features reflect the key information of the data on the manifold structure. The BHTP (battery health temporal prediction) module is integrated, and advanced technologies such as residual connections and hierarchical normalization are utilized to enhance feature fusion and stability. In the pre-training phase of transfer learning [34], the model captures the general characteristics of the manifold structure in large-scale data. When fine-tuning, the similarity of the manifold structures of the large and small sample sets is exploited to enable the model to quickly adapt to small-sample tasks [35]. This effectively solves the problem of overfitting, improves the generalization ability of the model, and thus achieves accurate prediction of the SOH of lithium batteries under the condition of scarce data.
The main contributions of this paper are summarized as follows:
- (1)
- We propose a novel multi-encoder framework for SOH prediction of lithium-ion batteries, which integrates element, positional, and temporal encoders to extract multidimensional features, enabling comprehensive and accurate analysis of SOH sequences under small-sample conditions.
- (2)
- We develop an innovative BHTP module for feature fusion and encoding optimization, incorporating residual connections, convolutional layers, and layer normalization, which significantly enhances the model’s representational capability, mitigates overfitting risks, and improves stability and generalization.
- (3)
- We propose a transfer learning strategy that combines pretraining with fine-tuning, optimizing model parameters for small-sample scenarios, significantly improving prediction accuracy while reducing computational complexity.
- (4)
- The experiments on NASA datasets show that the proposed method excels under small-sample conditions, achieving fast convergence, significant reductions in RMSE and MAE, and accurate SOH predictions, demonstrating its effectiveness and practicality.
This work proceeds as follows: Section 2 reviews related work. Section 3 provides a detailed explanation of the proposed prediction framework, including the multi-encoder structure, BHTP module, and the transfer learning strategy combining pre-training and fine-tuning. Section 4 presents experimental evaluations, including convergence tests, comparative experiments, and ablation studies. Finally, Section 5 concludes the study and discusses future research directions.
2. Related Works
A small sample size refers to a limited number of cases, rather than a small absolute number of cases. Generally, when a sample size (n) is less than 50, it is considered a small sample [36]. In predicting the SOH of lithium batteries under small-sample conditions, existing methods to mitigate challenges brought by small sample sizes include data augmentation and the integration of prior knowledge [37].
Data augmentation: The core idea of data augmentation is to acquire prior knowledge for augmenting the sample size, thereby expanding the sample data [30]. Li et al. [38,39] introduced the concept of mega-trend diffusion (MTD). This method first identifies the sample boundaries and then augments the sample according to the exhibited trend, ultimately augmenting the sample size. Kang et al. [40] improved the original MTD algorithm to ensure that the range of virtual samples is kept under control [41]. Aiming at the problem of insufficient degradation data of lithium-ion battery, a generalized trend diffusion virtual sample generation method based on differential evolution was proposed [42]. Cheng et al. [43] proposed a lithium-ion battery state estimation model based on data augmentation, which augments the existing dataset by generating synthetic data. Experimental results show that the proposed method can achieve accurate prediction under the condition of a small sample size [44]. Liu et al. [45] augmented the existing dataset by training the collected historical charging voltage data with CGAN to generate new data. Experimental results show that the proposed method significantly improves the estimation performance of lithium battery SOH in the case of different degrees of data loss, and shows a good prediction effect under the condition of a small sample size. Ren et al. proposed to utilize CrGAN for data augmentation of all cells in a battery pack [46]. The model fuses shape and time-dependent features by introducing a cross-attention mechanism and delayed spatial encoding. Guo et al. proposed a lithium battery SOH estimation method based on sample data generation and a temporal convolutional neural network for a data-driven model in the case of limited data [47]. The variational autoencoder (VAE) was used to learn the characteristics and distribution of sample data to generate highly similar data and enrich the number of samples.
MTD is based on the sample trend expansion, focusing on the overall distribution. CGAN and other deep learning, or conditional, or re-association. However, data augmentation methods often produce synthetic samples with significant randomness and poor quality, which deviate from the true data distribution [48]. This deviation can adversely impact the model’s predictive accuracy, limiting its reliability and effectiveness [49].
Integrated prior knowledge: Thompson et al. [50] proposed a modeling method combining prior knowledge with neural networks, where prior knowledge is introduced into the neural network with constraints. The prediction results of the constructed network model are credible and consistent with the actual aging process of lithium batteries. Zhao et al. [51] addressed transformer fault issues using a residual back propagation neural network, combining multiple residual modules [52] to ensure that prior knowledge aligns with the needs of the network structure and improves the transformer fault prediction accuracy under small-sample conditions. Aiming at the problem of low accuracy of RUL prediction results under the condition of small samples, Hao Keqing [53] proposed to obtain prior knowledge by drawing the curve relationship between the extracted indirect health factors and the lithium battery capacity. The RUL prediction model [54] of lithium battery with fusion constraints was established. Methods involving the integration of prior knowledge not only adhere to the network convergence conditions but also make full use of existing knowledge. Numerous experiments have achieved improved results when using such methods. Jiang et al. [55] proposed a battery SOH estimation method combining EIS feature extraction and Gaussian process regression. The feature selection was integrated into the prior knowledge of battery electrochemical characteristics, and the model performed well under fixed frequency impedance characteristics. Li et al. [56] proposed a lithium battery internal temperature estimation method based on multi-frequency virtual part impedance and a GPR model. By using an equivalent circuit model, sensitivity analysis, and Pearson coefficient screening features, the prior knowledge of the electrochemical process was introduced.
Different methods for integrating prior knowledge have obvious differences. In terms of the way of introducing knowledge, Thompson et al. introduced prior knowledge into the neural network through constraints, while Zhao et al. made the prior knowledge adapt to the network structure by means of multiple residual modules. Regarding the acquisition of knowledge, Hao Keqing obtained prior knowledge by constructing the curve relationship between the extracted indirect health factors and the battery capacity. Jiang et al. integrated feature selection into the knowledge of battery electrochemical characteristics, and Li et al. introduced the knowledge of the electrochemical process by using the equivalent circuit model and other methods. However, the integration of prior knowledge in the aforementioned methods often depends on domain-specific heuristic rules, limiting their ability to dynamically model complex data relationships [57]. To address these challenges, an innovative approach is proposed, combining a multi-encoder structure, the BHTP module, and a transfer learning strategy. This design significantly improves the accuracy, stability, and generalization capability of lithium battery SOH prediction, effectively addressing the shortcomings of data augmentation methods and prior knowledge-based techniques.
3. Multi-Encoder Architecture and BHTP-Enhanced Feature Fusion
3.1. Task Definitions
The SOH of a battery is defined as the ratio of its current capacity to its rated capacity [58]. The full lifecycle SOH sequence of a battery is denoted as: SOH = {h1, h2, …, hn}, where hn is the SOH value corresponding to the n-th cycle. Based on the top segment of the battery’s SOH sequence, SOH_A = {h1, h2, …, hm|1 < m < n}, the SOH of the battery is predicted, and the full lifecycle SOH sequence is obtained as follows: SOH_B = {hm + 1, hm + 2, …, hn}.
3.2. Sliding Window Prediction
In this study, we used the sliding window technique to predict the SOH sequence of a lithium battery [59]. This technique is used for prediction on temporal datasets. A fixed-size window is applied to the top segment of the SOH sequence, covering the SOH sequence from the 1st to the m-th cycle. The SOH value for the m + 1-th cycle is predicted using the SOH sequence from the 1st to the m-th cycle. The window then slides forward by one step to cover the SOH sequence from the 2nd to the m + 1-th cycle to predict the SOH value for the m + 2-th cycle. This process is repeated iteratively until the SOH value for the n-th cycle is predicted.
3.3. Multi-Encoder Architecture: Overall Structural Design
In this study, we used an autoencoder model to predict the SOH of lithium batteries under small-sample conditions. The overall model design is shown in Figure 1. An autoencoder consists of two components: an encoder and a decoder. It captures data features through the encoding and decoding processes and then outputs the results. Based on the construction of an autoencoder, this study introduced a multi-encoder structure and incorporated a BHTP module. The multi-encoder structure extracts the multi-perspective features of a lithium battery SOH sequence, while the BHTP module integrates and processes the encoded features to generate the codes for the predicted SOH values of the lithium battery.
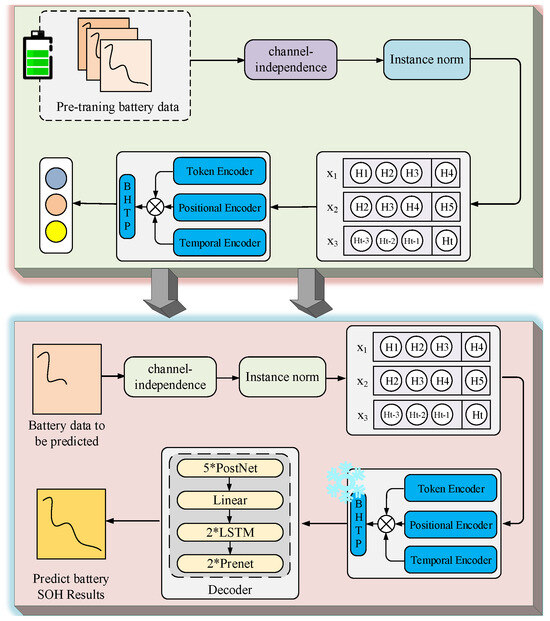
Figure 1.
Autoencoder-based SOH prediction method for lithium batteries.
To prevent model overfitting under small-sample conditions, a combined pre-training and fine-tuning strategy was used to predict the SOH values of lithium batteries. In the pre-training phase, the input data comprises a large dataset of full lifecycle SOH sequences from lithium batteries. In order to ensure the stability of the training model, the data are first normalized by the following formula, where μ and σ are the mean and RMSD of the series, respectively:
where represents the normalized value of , denotes the -th element in the original data sequence, stands for the mean value of the data, and σ represents the standard deviation of the data, with i = 1, 2, ⋯, n. This formula implies that it normalizes the original data element by subtracting the mean and then dividing by the standard deviation .
where represents the mean value of the data, N is the total number of data elements, and stands for the -th data element, with i ranging from 1 to N. This formula shows that the mean is calculated by summing up all N data elements and then dividing by the total number N.
where represents the standard deviation of the data, N is the total number of data elements, denotes the -th data element, and is the mean value of the data, with i ranging from 1 to N. This formula indicates that the standard deviation is obtained by first computing the square of the difference between each data element and the mean , summing these squared differences, dividing by the total number N, and finally taking the square root.
The consistency and reliability of processing different battery SOH sequence data sets are improved by instance normalization. The data are then divided by a sliding window:
where represents the -th sliding window; , , ⋯, denote the elements in the data sequence; and k = 1,2, ⋯, N. This formula indicates that the -th sliding window consists of m consecutive elements starting from the -th element in the data sequence.
Finally, the model is trained using the multi-encoder structure and the BHTP module. After training, the BHTP module is frozen, and the weights are transferred to the fine-tuning phase.
In the fine-tuning phase, the input data comprises the small-sample SOH sequence of the lithium battery being used for prediction. After undergoing instance normalization and channel independence, the data are encoded by the multi-encoder structure and output to the BHTP module. The decoder then decodes the output to generate the predicted SOH values for the time instance. Since the BHTP module is frozen during the pre-training phase, its parameters remain unchanged during the model training phase, and only the encoding and decoding parts are updated. This approach not only leverages the feature representation ability learned by the BHTP module during pre-training but also allows other parts of the model to make adaptive adjustments, thereby achieving more efficient and accurate prediction of the state of health (SOH) of lithium-ion batteries under small-sample conditions. Figure 2 presents the workflow of the proposed battery SOH prediction method under small-sample conditions.
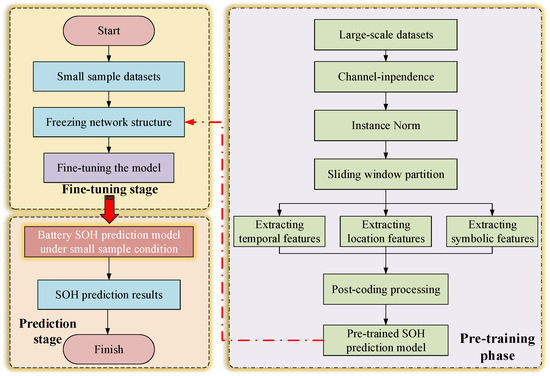
Figure 2.
Workflow design for the proposed prediction approach.
3.4. Advanced Multi-Encoder Architecture
The prediction of a lithium battery’s SOH involves multi-dimensional characteristic information, including the battery’s chemical properties, physical state, usage history, environmental conditions during usage, and its temporal degradation trend. A single type of encoder is unable to capture such comprehensive, multi-dimensional, and multi-perspective data, and therefore will limit the accuracy and generalizability of the prediction model [60,61]. In this study, we used a multi-encoder structure—comprising a token encoder, a positional encoder, and a temporal encoder—to comprehensively analyze and represent the features in the SOH data of lithium batteries. The multi-encoder structure is shown in Figure 3. Through the coordinated processes of these three encoders, the multi-encoder structure proposed in this study extracts the multi-dimensional features from the SOH data to provide feature codes for the subsequent small-sample SOH prediction model for lithium batteries, thus enhancing the accuracy and generalizability of the model. The specific formula is as follows, where Z is the feature information and J is the encoder number:
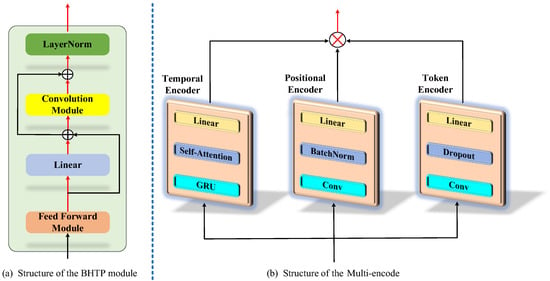
Figure 3.
Multi-encoder structure and BHTP module structure diagram.
Token encoder: The token encoder is a key component of data preprocessing, which is responsible for adapting the dimensions of the input data to the requirements of the subsequent processing module. Due to the diversity and heterogeneity of the original data features, the feature scales are different. Through the transformation and mapping operations such as standardization, normalization, and coding, the various features are unified into a format and scale that can be recognized by the model to ensure that the data can be effectively processed by the model.
where X represents the input data, W denotes the weight matrix, and b represents the bias vector. This formula indicates that the linear layer maps the input features to new features by performing a linear transformation on the input data.
where Z represents the output of the linear layer, M denotes a mask matrix with elements determined by the dropout probability p, and is the probability of an element being kept. This formula indicates that during training, dropout randomly sets some values in Z to 0 to prevent overfitting.
where represents the output of the dropout layer, K denotes the convolutional kernel, and represents the bias of the convolutional layer. This formula indicates that the convolutional layer extracts local features from the input data by convolving with K and adding the bias.
Positional encoder: The positional encoder is used to capture the relative position information between elements in the sequence data. In the time series data type, the order of the elements carries important semantics. It assigns each element a unique vector representation related to its position. The vector contains information about the absolute position of the element in the sequence, and can also imply the relative position relationship by encoding. It can significantly improve the understanding ability and prediction accuracy of the BHTP model for sequence data.
where X represents the input data, denotes the weight matrix, and represents the bias vector. This formula indicates that the linear layer in the positional encoder transforms the input features to prepare for subsequent operations.
where represents the transformed element in the positional encoder’s BatchNorm layer, denotes the normalized element, represents the learnable scaling factor for feature channel j, and denotes the learnable offset factor for feature channel j. This formula indicates that the normalized element is further adjusted by the learnable factors and to help the model’s performance.
where represents the output of the batch normalization layer, denotes the convolutional kernel, and represents the bias of the convolutional layer. This formula indicates that the convolutional layer in the positional encoder extracts position-related features from the normalized input data.
Temporal encoder: The state of health (SOH) of a lithium battery has a timing feature that reflects the changing trend of the battery’s performance over time. Affected by the number of charging and discharging, environmental temperature, and other factors, the battery performance changes dynamically. The time series encoder extracts and represents this time series information by processing the input sequence step by step, learns the time series dependence and dynamic change pattern, and mines the key information in the lithium battery SOH data.
where X represents the input data, denotes the weight matrix, and represents the bias vector. This formula indicates that the linear layer in the temporal encoder maps the input features to a new space to prepare for processing time-series data.
where Q, K, and V are matrices obtained by linearly transforming the input data, and denotes the attention dimension. This formula indicates that the self-attention mechanism captures long-range dependencies in the time-series data by calculating attention scores, normalizing them, and performing a weighted sum on the value matrix.
where represents the input at time step t, denotes the hidden state at the previous time step, calculates the reset gate, calculates the update gate, and calculates the candidate hidden state. This formula indicates that the GRU layer determines how to combine the previous hidden state and the candidate hidden state to form the current hidden state, capturing temporal dependencies in the sequence data.
where , , and represent the outputs of the token encoder, positional encoder, and temporal encoder, respectively. This formula indicates that the final output is obtained by multiplying element-wise the outputs of the three encoders to combine the features they extracted.
3.5. Residual-Fused BHTP Module
To process the SOH codes of a lithium battery, a BHTP module is used to accurately predict SOH under small-sample conditions. The BHTP module is used to process encoded SOH data by first using an encoding layer to pre-process and encode the raw SOH data of the lithium battery. The resulting characteristic data are then passed to the core of the BHTP module for further processing. The core of the BHTP module comprises key modules combined through residual connections. These modules include the FeedForward module, linear layer, convolution module, and LayerNorm module. The specific BHTP model is shown in Figure 3. The residual connections mitigate the vanishing gradient issue during the deep network training, maintaining the stability and efficiency of network learning.
First, the input data dimensions are changed to pass into the FeedForward module, which maps its dimensions into a higher-dimensional space suitable for subsequent processing. The assisting model of the rectified linear unit activation function captures and learns the nonlinear features of the small-sample data during training. The convolution module enables the model to learn broader contextual information about the data. In the convolutional layers, the convolution kernel slides with the local element-by-element multiplication of the input data to extract local features such as edges. Multiple convolution layers are concatenated, and the later layer takes the output of the previous layer as the input to expand the coverage of features. The LayerNorm module normalizes the mean and variance of the inputs for each layer, thus reducing the impact of internal covariate shifts. The final linear module obtains the feature representations output from the FeedForward module through linear transformation. After being processed by the BHTP module, the data are transformed into highly abstract and information-rich feature representations. The formula is as follows:
where signifies the fused feature representation. These feature representations are fed into the decoder part for the final prediction task. According to the relationship between the feature representation and the predicted target, the decoder outputs the predicted value of the SOH of the lithium battery.
3.6. Adaptive and Hybrid Transfer Learning
To better deal with the small sample challenge in a lithium battery’s health state (SOH) prediction, in the above-proposed method, we improved the performance of lithium battery SOH prediction under small sample conditions by the transfer learning method.
Transfer learning is a machine learning method that acquires knowledge in a source task and applies it to a target task. It is particularly suitable for small sample data. It improves the generalization ability of the model by pre-training it on a large dataset and fine-tuning it on a new task. The core idea of transfer learning is that although there are differences between the source and target domains, their underlying feature spaces have certain structural similarities. Therefore, learning the features of large sample data and migrating them to small sample data can effectively learn prior knowledge and improve the prediction ability of the model under small-sample data. The transfer learning model design is shown in Figure 4. In this study, the low-dimensional manifold features learned in large-scale SOH sequences using a multi-encoder structure are transferred by freezing the BHTP module to quickly adapt to the target small-sample task, thereby improving the prediction accuracy of the model.
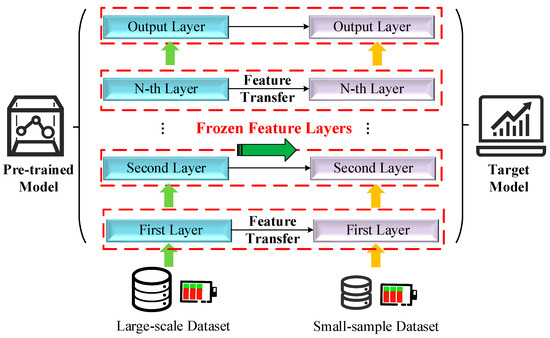
Figure 4.
Adaptive and hybrid transfer learning design.
Firstly, in the pre-training stage containing a large number of lithium battery life cycle SOH sequences, the model preprocesses the data by instance normalization and sliding window division, uses the multi-encoder structure to extract features from multiple perspectives, and performs feature fusion through the BHTP module to obtain a common feature representation. Subsequently, in the fine-tuning phase, the model parameters obtained by pre-training are transferred to the target model, and the pre-trained parameters of the BHTP module are frozen. The formula is as follows:
where represents the initial parameters used in the fine-tuning phase, while denotes the parameters obtained during the pre-training phase. This formula indicates that the parameters learned in the pre-training stage are directly transferred as the initialization parameters for the fine-tuning phase to ensure knowledge reuse.
where refers to the parameters of the BHTP module during the fine-tuning stage, and represents the parameters of the BHTP module trained in the pre-training stage. The encoder, after parameter transfer, is used to extract features to adapt to the prediction requirements of small samples, so as to generate the prediction value through the decoder. The formula is as follows:
where denotes the predicted value, specifically the state of health (SOH) of the lithium batteries. By minimizing the fine-tuning loss function, the weights of the multiple encoders and decoders in the model are optimized to better adapt to the characteristics of small-sample data while keeping the parameters of the BHTP module unchanged.
where represents the actual SOH value of the battery, while corresponds to the predicted SOH value. is the total number of samples in the dataset. This process not only effectively alleviates the overfitting problem caused by small samples, but also enhances the generalization ability of the model, so as to conduct the high-accuracy lithium battery SOH prediction under the condition of limited data.
4. Experiment and Results Analysis
4.1. Dataset and Experimental Setup
The dataset used in this study is the battery cycle life dataset collected from lithium cobalt oxide (LiCoO2) 18650 batteries by the National Aeronautics and Space Administration (NASA) [62]. The data in Table 1 indicate that all batteries were rated 2 Ahr. The aging simulation of a lithium battery involves two processes: charging and discharging. During the charging process, the battery was charged with a constant current (1.5 A) until its voltage reached 4.2 V. Then, charging continued in a constant voltage mode until the current dropped to 20 mA. During the discharge process, the discharge was carried out at a constant current of 2 A until the voltage of B0005 dropped to 2.7 V and the voltage of B0007 dropped to 2.2 V. For B0033, the discharge was carried out at 4 A until its voltage dropped to 2.0 V. The experimental termination condition for batteries B0005 and B0007 is that the rated capacity is reduced to 1.4 Ahr, with a 30% decrease. The experimental termination condition for battery B0033 is that the rated capacity is reduced to 1.6 Ahr, with a 20% attenuation. Different pre-set values were used to simulate different aging degrees.

Table 1.
Introduction to the battery dataset.
In this study, we selected three individual battery cells (B0005, B0007, and B0033) from the dataset for analysis. The charging and discharging experiments were conducted on all three batteries at a room temperature of 24 °C. Since batteries B0005 and B0007 have the same discharge current and contain historical data of 168 charge/discharge cycles, these two cells are placed in the same battery data group. Since batteries B0005 and B0033 have different discharge currents and battery B0033 contains historical data of 197 charge/discharge cycles, B0005 and B0033 are placed in different battery data groups. Due to differences in charge/discharge strategies, the SOH curves of the lithium batteries differ significantly, as shown in Figure 5.
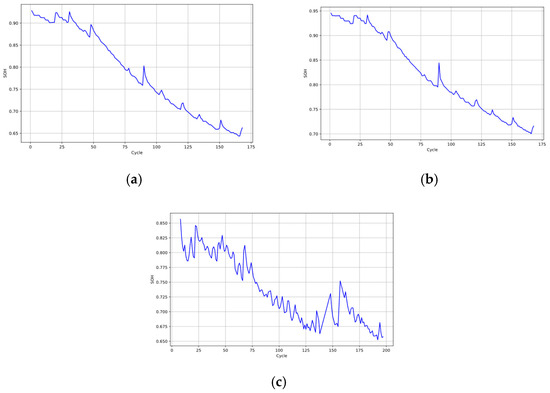
Figure 5.
SOH decline graphs for (a) battery B0005, (b) battery B0007, and (c) battery B0033.
From Figure 5, the following observations can be made: Firstly, it can be seen from the three figures that with the increase of battery operation cycle times, side reactions between electrodes and electrolytes occur, resulting in continuous loss of lithium and active substances, making the SOH of the three batteries show an overall decline trend. Secondly, the overall trend of the battery SOH curve in the figure is decreasing, but it is not monotonically decreasing, and there is an intermittent rise. Since the battery’s SOC, ambient temperature, and circulating current can significantly affect its degradation process, it is difficult to directly measure the theoretical SOH value of the battery. This is shown in Figure 5 as an intermittent rise in the battery’s SOH curve. Finally, the SOH curves of the batteries from the same group (B0005 and B0007) differ only slightly from each other, while those of batteries from different groups (B0005 and B0033) differ significantly from each other.
Table 1 shows that different battery packs have different experimental conditions and different termination conditions, which can be obtained as follows: There is a high degree of similarity in the data of batteries from the same group, and a low degree for batteries in different groups. Therefore, to investigate the results of the proposed algorithm in predicting the SOH values of lithium batteries when the data similarities in the pre-training and the fine-tuning phases differ, the complete B0005 dataset was used for pre-training. For fine-tuning, the SOH values corresponding to the first 20% (i.e., the SOH values within the initial 20% of the battery SOH cycle sequences), the first 30% (i.e., the SOH values within the initial 30% of the battery SOH cycle sequences), and the first 40% (i.e., the SOH values within the initial 40% of the battery SOH cycle sequences) of the battery SOH cycle sequences in the B0007 and B0033 datasets were used. The remaining portions of these datasets served as the test sets. The selection of data for fine-tuning is performed to verify the adaptability of different-sized datasets during the transfer learning process. Smaller-scale datasets (such as the first 20% of the data) can better simulate small-sample scenarios and are used to test the model’s ability to make accurate predictions using pre-trained knowledge with limited information. Medium-scale (the first 30% of the data) and relatively larger-scale (the first 40% of the data) datasets can demonstrate the model’s adaptability under different data richness conditions. The Adam optimizer was used for training with an initial learning rate of 0.003, a batch size of 128, and a number of epochs of 500. The sliding window size is 7.
4.2. Evaluation Indicators
To measure the differences between the predicted and true values and evaluate the prediction results, root mean squared error (RMSE) and mean absolute error (MAE) were used as evaluation indicators of the algorithm’s performance. RMSE and MAE indicate the error between predicted and true values. The lower the RMSE and MAE values, the closer the predicted value is to the true value, and the better the prediction result. RMSE and MAE may obtain values in the range [0, +ꝏ), expressed as follows:
In Equations (1) and (2), n is the total number of samples; is the predicted value; and is the true value.
4.3. Convergence Experiment
Using the proposed method, training was conducted on the top 30% of the B0007 and B0033 datasets. The convergence results are shown in Figure 6. To accurately record the model training curves, both groups of batteries underwent 500 epochs of training. After training, Figure 6 shows that the model achieved convergence on both datasets and was able to reach the convergence values rapidly. Comparing the two curves, it can be observed that on the B0007 dataset, the training and test curves exhibited a more stable overall performance, with relatively smaller initial fluctuations and a smaller gap between the two curves in the later stages. Both curves ultimately converged to lower values, indicating good convergence performance and a lower risk of overfitting. In contrast, for the B0033 dataset, the training curve exhibited larger initial fluctuations and continued to show noticeable minor fluctuations throughout the training process. Similarly, the test curve also had significant initial fluctuations, and in the later training stages, the gap between the training and test curves was slightly larger compared to the B0007 dataset. This suggests that the model’s convergence performance was relatively poorer on the B0033 dataset. The better convergence observed on the B0007 dataset can be attributed to its greater similarity to the B0005 dataset compared to the B0033 dataset.
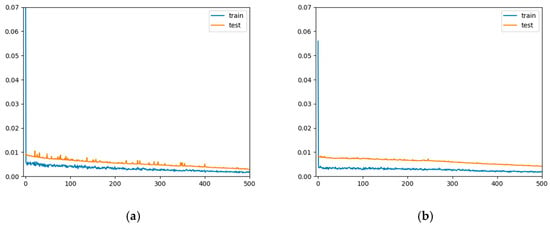
Figure 6.
Convergence experimental results for (a) the 30% training set for B0007 and (b) the 30% training set for B0033.
4.4. Comparative Experiment
To evaluate the ability of the proposed method to predict the SOH values of lithium batteries under small-sample conditions, a comparative experiment was conducted. Using the top 20–40% of the datasets as training sets, we compared the existing mainstream deep learning models for lithium battery SOH predictions, namely, the long short-term memory (LSTM), bidirectional long short-term memory (BiLSTM), gated recurrent unit (GRU), and bidirectional gated recurrent unit (BiGRU) models.
LSTM [63] model: the LSTM model is essentially a special form of recurrent neural network (RNN) designed to address the short-term memory issue present in traditional RNNs by incorporating gates, and enables the RNN to effectively leverage long-term temporal information.
BiLSTM [64] model: the BiLSTM network is an improved LSTM neural network that captures the contextual information in the input sequence by incorporating bidirectionality into the model, thereby enhancing the sequence modeling performance.
GRU [65] model: a GRU is a neural network architecture for sequence modeling, particularly suitable for applications such as natural language processing and time series analysis. It is closely related to LSTM, as both are designed to address the long-term dependency issue. However, compared to LSTM, the GRU model has a simpler structure and fewer parameters.
BiGRU model: BiGRU is an improved RNN architecture and an extension of a GRU. It consists of two GRU models: a forward GRU model that processes the input in the forward direction, and a backward GRU model that processes the input in the reverse direction. The BiGRU model combines a GRU with bidirectionality to capture efficiently the contextual information in the input sequence.
The prediction results using the different methods are shown in Figure 7.
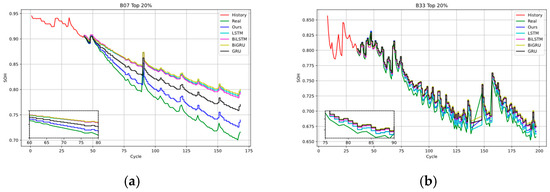
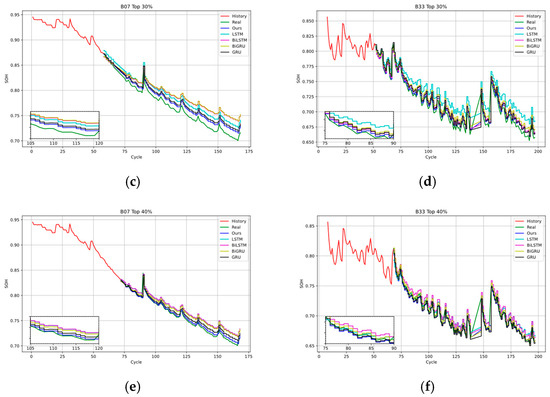
Figure 7.
Comparison of experimental results: (a) the 20% training set of the B0007 dataset, (b) the 20% training set of the B0033 dataset, (c) the 30% training set of the B0007 dataset, (d) the 30% training set of the B0033 dataset, (e) the 40% training set of the B0007 dataset, and (f) the 40% training set of the B0033 dataset.
As shown in Figure 7, across the top 20–40% of the B0007 and B0033 datasets, all of the algorithm models exhibit a good fit with the actual SOH curves of batteries. Compared to the baseline deep learning models, the proposed model exhibits an improved fitting effect due to its utilization of prior knowledge obtained from the B0005 dataset. The specific evaluation indicators for each model are listed in Table 2.

Table 2.
Results of the comparative experiment.
The experimental results in Table 2 show that the proposed model achieved significant reductions in RMSE and MAE compared to LSTM, BiLSTM, BiGRU, and GRU across training samples of different sizes. In the B0007 dataset, both RMSE and MAE dropped by an average of 0.020, while in the B0033 dataset, RMSE and MAE dropped by an average of 0.005 and 0.003, respectively. Additionally, more significant improvements were achieved on the 20% training sets than on the 30% and 40% training sets. The prediction results of the proposed model were more accurate and met the specified prediction requirements, thereby proving the effectiveness and superiority of the proposed method in predicting the SOH of lithium batteries under small-sample conditions.
4.5. Ablation Experiment
To verify the effectiveness of each module in the proposed model, an ablation experiment was conducted by using the top 30% of the B0007 and B0033 datasets as the training sets. The experimental results are shown in Table 3. Moreover, the first 20%, 30%, and 40% training sets of the B0007 and B0033 datasets were used for effectiveness experiments, and the experimental results are shown in Figure 8.

Table 3.
Results of the ablation experiment.
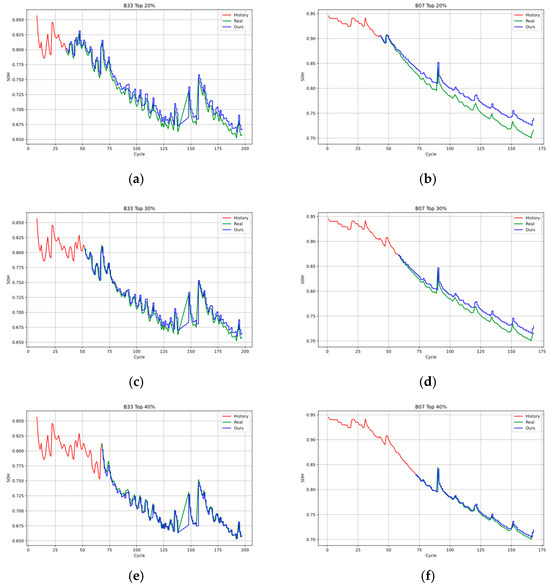
Figure 8.
Comparison results show (a) the 20% training set of the B0033 dataset, (b) the 20% training set of the B0007 dataset, (c) the 30% training set of the B0033 dataset, (d) the 30% training set of the B0007 dataset, (e) the 40% training set of the B0033 dataset, and (f) the 40% training set of the B003 dataset.
This study introduced a multi-encoder structure based on an autoencoder and incorporated a BHTP module. The data were output to the decoder to predict the SOH of lithium batteries. The experimental results in Table 3 indicate that the proposed model significantly outperformed the baseline models in terms of the decrease in RMSE and MAE scores. This improvement can be attributed to the multi-encoder structure, which is capable of effectively extracting relevant information from the SOH sequence from multiple perspectives. In addition, the BHTP module greatly improved the prediction accuracy and the performance of the model under small-sample conditions.
From the experimental results in Table 3, when some encoders are retained or all of them are removed, the RMSE and MAE indicators of the model will deteriorate. Taking the B0007 battery data as an example, when all three encoders are retained, the RMSE is 0.012 and the MAE is 0.010. However, after removing some encoders, the RMSE and MAE increase. This indicates that the multi-encoder structure can comprehensively capture multi-dimensional information such as environmental conditions and time-related degradation trends in the battery SOH sequence. The absence of any encoder will cause the model to fail to fully extract features, thereby reducing the prediction accuracy. When the BHTP module is removed, the model’s performance significantly declines. In the B0033 battery data, when the BHTP module is included, the RMSE is 0.005 and the MAE is 0.004. After removing this module, the RMSE becomes 0.007 and the MAE becomes 0.007. This shows that the BHTP module effectively fuses the features extracted by the multi-encoder through internal techniques such as residual connections and layer normalization, reduces the problem of gradient vanishing, and improves the prediction accuracy and performance of the model under small-sample conditions. Overall, the multi-encoder structure and the BHTP module cooperate with each other to jointly improve the model performance.
4.6. Case Study
To evaluate the differences between the predicted and true values, a case study was conducted using the B0007 and B0033 datasets. For each sized training set, four cycle counts were selected to analyze the differences between the predicted and true values. The results are listed in Table 4, Table 5 and Table 6.

Table 4.
Predicted results for the 20% training set.

Table 5.
Predicted results for the 30% training set.

Table 6.
Predicted results for the 40% training set.
As shown in Table 4, Table 5 and Table 6, the predicted values are generally higher than the true values, and the errors show an increasing trend as the number of cycles increases. However, the predicted values are still relatively close to the true values, demonstrating the feasibility of SOH prediction under small-sample conditions using this model.
5. Conclusions
Accurate SOH prediction under small-sample conditions is challenging due to individual cell variability, capacity recovery effects, and the difficulty of capturing multi-dimensional degradation features. To address these issues, this study proposes an autoencoder-based framework incorporating a multi-encoder structure and a BHTP module, effectively extracting complex SOH features and enhancing stability with a combined pre-training and fine-tuning strategy. The experimental results on the NASA 18650 dataset show that the RMSE and MAE of the B0007 dataset are reduced by 0.020 on average, the RMSE of the B0033 dataset is reduced by 0.005, and the MAE is reduced by 0.003. The method has a significant improvement in RMSE and MAE. The reliability and efficiency of the method are verified.
However, the accuracy of the model for battery SOH prediction will be affected under extreme operating conditions such as high temperature, low temperature, or ultra-fast charging and discharging. In the future, we hope to conduct research in the following key directions. In order to enhance the ability of the model to capture the dynamic characteristics of lithium-ion battery’s SOH, the dynamic feature extraction technology based on VAE will be deeply explored, and the optimized network structure will be constructed to accurately capture the dynamics and track the real-time status. In view of the requirements of few-shot scenarios, MAML-based methods will be deeply studied to accelerate model learning and improve prediction accuracy. In this way, the accuracy of SOH prediction in practical scenarios can be further improved. Through the exploration of these research directions, it is expected to further optimize the method so that it can be better applied to practical scenarios.
Author Contributions
Conceptualization, Z.M.; methodology, S.W.; software, S.G. and C.L.; validation, S.G., C.L. and Z.M.; formal analysis, Y.Q.; investigation, Y.Q.; resources, S.W.; data curation, C.L.; writing—original draft preparation, C.L. and S.G.; writing—review and editing, C.L. and Z.M.; visualization, C.L.; supervision, Z.M.; project administration, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Flying Feather Trail: The Design and Implementation of an Intelligent Cloud System for Wetland Bird Populations, project number 202410128009; Research on the Key Technologies of Dynamically Reconfigurable Battery Modules Based on Digital Twins, project number STZX202307; and Optimization of an Independent Operation DC Microgrid Configuration Scheme and Coordinated Control Study, project number 51867020.
Data Availability Statement
The data that has been used are confidential.
Acknowledgments
All authors thank the editors and reviewers for their attention to the paper. We kindly request the editors and reviewers to provide valuable comments and corrections on this study.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships.
References
- Hong, J.; Li, K.; Liang, F.; Yang, H.; Zhang, C.; Yang, Q.; Wang, J. A novel state of health prediction method for battery system in real-world vehicles based on gated recurrent unit neural networks. Energy 2024, 289, 129918. [Google Scholar] [CrossRef]
- Wei, Y.; Wu, D. State of health and remaining useful life prediction of lithium-ion batteries with conditional graph convolutional network. Expert Syst. Appl. 2024, 238, 122041. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Wu, J.H.; Zhang, L.P.; Dai, H.D.; Bai, W.Q.; Lin, H.J.; Zhang, F.; Yang, Y.X. Research progress of lithiumion battery health state assessment method. Henan Sci. 2024, 42, 1717–1740. [Google Scholar]
- Buchanan, S.; Crawford, C. Probabilistic lithium-ion battery state-of-health prediction using convolutional neural networks and Gaussian process regression. J. Energy Storage 2024, 76, 109799. [Google Scholar] [CrossRef]
- Wang, X.; Hu, B.; Su, X.; Xu, L.; Zhu, D. State of health estimation for lithium-ion batteries using random forest and gated recurrent unit. J. Energy Storage 2024, 76, 109796. [Google Scholar] [CrossRef]
- Che, Y.; Zheng, Y.; Forest, F.E.; Sui, X.; Hu, X.; Teodorescu, R. Predictive health assessment for lithium-ion batteries with probabilistic degradation prediction and accelerating aging detection. Reliab. Eng. Syst. Saf. 2024, 241, 109603. [Google Scholar] [CrossRef]
- Wu, T.Z.; Zhu, J.C.; Cheng, X.F.; Kang, J. SOH estimation method for lithium battery Based on charging phase data and GWO-BiLSTM model. Power Supply Technol. 2024, 48, 2184–2194. [Google Scholar]
- Liu, P.; Li, Z.W.; Cai, Y.S.; Wang, W.; Xia, X.Y. Based on the equivalent circuit model and data driven fusion model of SOC and SOH joint estimation approach. J. Electrotech. 2024, 39, 3232–3243. [Google Scholar]
- Wu, L.X.; Pang, H.; Jin, J.M.; Geng, Y.F.; Liu, K. Review of state-of-charge estimation methods for lithium-ion batteries based on electrochemical models. Trans. China Electrotech. Soc. 2022, 37, 1703–1725. [Google Scholar]
- Jin, J.X.; Yu, R.X.; Liu, G.; Xu, L.B.; Ma, Y.Q.; Wang, H.B.; Hu, C. Research progress on estimation methods for the state of health of lithium-ion batteries. J. Eng. Eng. 2024, 19, 33–48. [Google Scholar]
- Messing, M.; Shoa, T.; Habibi, S. Estimating battery state of health using electrochemical impedance spectroscopy and the relaxation effect. J. Energy Storage 2021, 43, 103210. [Google Scholar] [CrossRef]
- Shi, H.S.; Sun, X.W.; Wang, K. Health state estimation of lithium-ion battery based on electrochemical impedance spectroscopy. Power Gener. Technol. 2024, 1–15. Available online: http://kns.cnki.net/kcms/detail/33.1405.tk.20240716.1502.008.html (accessed on 8 March 2025).
- Luo, F.; Huang, H.; Ni, L.; Li, T. Rapid prediction of the state of health of retired power batteries based on electrochemical impedance spectroscopy. Chin. J. Sci. Instrum. 2021, 42, 172–180. [Google Scholar]
- Wang, Y.; Wei, Q.G.; Sun, P.; Zhang, X.F.; Liu, Y.J. Joint estimation of lithium-battery SOC and SOH based on dual extended kalman filter. In Proceedings of the 2022 China Society of Automotive Engineers Annual Conference, Nantong, China, 20–22 December 2022; pp. 4–9. [Google Scholar]
- Yang, D.; Zhang, X.; Pan, R.; Wang, Y.; Chen, Z. A novel gaussian process regression model for state-of-health estimation of lithium-ion battery using charging curve. J. Power Sources 2018, 384, 387–395. [Google Scholar] [CrossRef]
- Hui, Z.L.; Wang, R.J.; Feng, N.N.; Yang, M. State of health prediction of lithium-ion batteries based on ensemble gaussian process regression. J. Meas. Sci. Instrum. 2024, 15, 397–407. [Google Scholar] [CrossRef]
- Tan, Y.; Zhao, G. Transfer learning with long short-term memory network for state-of-health pre-diction of lithium-ion batteries. IEEE Trans. Ind. Electron. 2019, 67, 8723–8731. [Google Scholar] [CrossRef]
- Li, K.; Hu, L.; Song, T.T. State of health estimation of lithium-ion batteries based on CNN-Bi-LSTM. Shandong Electr. Power Technol. 2023, 50, 66–72. [Google Scholar]
- Ke, H. SOH estimation of lithium battery based on diffusion model and bidirectional long short-term memory network. Ploidy Henan Sci. Technol. 2024, 51, 5–11. [Google Scholar]
- Zheng, W.B.; Zhou, X.Y.; Wu, Y.; Feng, L.; Yin, H.T.; Fu, P. Experimental design for state of health (SOH) estimation of lithium batteries based on transfer learning. Exp. Technol. Manag. 2022, 39. [Google Scholar] [CrossRef]
- Yin, J.; Liu, B.; Sun, G.B.; Qian, X.W. Remaining useful life prediction of lithium-ion batteries based on transfer learning and denoising autoencoder-long short-term memory. Trans. China Electrotech. Soc. 2024, 39, 289–302. [Google Scholar]
- Mo, Y.M.; Yu, Z.H.; Ye, P.; Fan, W.J.; Lin, Y. SOH estimation of lithium battery based on transfer learning and GRU neural network. Acta Sol. Energy 2024, 45, 233–239. [Google Scholar]
- Cheng, G.; Wang, X.; He, Y. Remaining useful life and state of health prediction for lithium batteries based on empirical mode decomposition and a long and short memory neural network. Energy 2021, 232, 121022. [Google Scholar] [CrossRef]
- Zhang, X.F.; Chen, Y.L.; Li, S.Q.; Zeng, X.K.; Lian, X.; Huang, C. LSTM neural network based state estimation of lithium ion battery health. Auto Pract. Technol. 2025, 50, 1–6. [Google Scholar] [CrossRef]
- Chang, C.; Wang, Q.; Jiang, J.; Wu, T. Lithium-ion battery state of health estimation using the incremental capacity and wavelet neural networks with genetic algorithm. J. Energy Storage 2021, 38, 102570. [Google Scholar] [CrossRef]
- Huang, J.Y.; Bai, J.Q.; Xiang, Y.H. SOH estimation method for lithium-ion battery based on DOD-LN-GPR model. Chin. J. Sol. Energy 2025, 46, 60–69. [Google Scholar]
- Tian, A.N.; Yang, C.; Gao, Y.; Li, T.Y.; Wang, L.J.; Chang, C.; Jiang, J.C. A state of health estimation method of lithium-ion batteries based on DT-IC-V health features extracted from partial charging segment. Int. J. Green Energy 2023, 20, 997–1011. [Google Scholar] [CrossRef]
- Li, Z.L.; Qiao, G.Z.; Cui, F.S.; Cai, J.H.; Shi, Y.H.; Wang, B.H. Prediction of state of health of lithium-ion batteries using the VMD-HPO-NBEATS model. China Test 2024, 50, 65–73. [Google Scholar]
- Shi, S.S.; Gao, Z.B. Based on the automatic feature extraction and IWOA—Lithium-ion battery SOH prediction of SVR model. Intern. Combust. Engines Accessories 2024, 22, 10–13. [Google Scholar]
- Li, J.; Chen, X.L.; Xu, L. Li-ion battery health estimation based on multiple health factors and IPSO-LSTM model. Automot. Engine 2025, 1, 39–46. [Google Scholar]
- Zhang, M.; Yang, D.F.; Du, J.X.; Sun, H.L.; Li, L.W.; Wang, L.C.; Wang, K. A Review of SOH prediction of li-ion batteries based on data-driven algorithms. Energies 2023, 16, 3167. [Google Scholar] [CrossRef]
- Dong, X.H.; Dong, J.B.; Wang, M.S.; Zeng, F.; Pan, Y. Rapid estimation method of lithium battery health state Based on new health characteristics. Electr. Power Eng. Technol. 2025, 44, 136–142+206. [Google Scholar]
- Shi, Y.H.; Tian, J.Y.; Liu, J.J.; Yang, S.Q. Research on multi-source adaptive transfer learning algorithm based on manifold structure and its application. Control. Decis. 2023, 38, 797–804. [Google Scholar]
- Li, L.; Yan, X.M.; Zhang, Y.S.; Feng, Y.L.; Hu, H.L.; Duan, Y.J.; Cui, C.H. Lithium battery state of charge estimation method based on transfer learning. J. Xi’an Jiao Tong University 2023, 57, 142–150. [Google Scholar]
- Liu, B.; Yang, J.; Wang, R.G.; Xue, L.X. Memory-based transfer learning for few-shot learning. Comput. Eng. Appl. 2022, 58, 242–249. [Google Scholar]
- Chang, W.; Hu, Z.C.; Pan, D.Z.; Shi, J.W. Application of an improved VAE-GAN model to battery EIS data augmentation. Sci. Technol. Ind. 2024, 24, 258–263. [Google Scholar]
- Zhao, Y.P.; Huang, W.; Zhang, J.F. Lithium battery life prediction based on LSTM-Transformer with hybrid scale health factor. Electron. Meas. Technol. 2024, 11, 112–122. [Google Scholar]
- Li, D.C.; Wu, C.S.; Tsai, T.I.; Lina, Y.S. Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge. Comput. Oper. Res. 2007, 34, 966–982. [Google Scholar] [CrossRef]
- Qiao, J.F.; Guo, Z.H.; Tang, J. Virtual sample generation method based on improved metertrend diffusion and hidden layer interpolation and its application. Chin. Chem. Eng. J. 2020, 71, 5681–5695. [Google Scholar]
- Kang, G.; Wu, L.; Guan, Y.; Peng, Z. A Virtual sample generation method based on differential evolution Al-gorithm for overall trend of small sample data: Used for lithium-ion battery capacity degradation data. IEEE Access 2019, 7, 123255–123267. [Google Scholar] [CrossRef]
- Zhu, H.J.; Lü, Z.G.; Di, R.H.; Sun, X.J.; Hao, K.Q. To improve MD-MTD lithium battery life prediction neural network simulation. J. Xi’an Univ. Technol. 2022, 42, 620–626. [Google Scholar]
- Xu, Z.J.; Zhu, Q.; Xu, S.F.; Mao, Q. Research on parameter identification algorithm of lithium-battery model based on differential evolution method. Electr. Eng. 2021, 7, 35–37. [Google Scholar]
- Zhu, Y.F.; Jiang, G.P.; Gao, H.; Li, W.Z.; Gui, Y.C. Prediction of battery state of charge based on feature selection and data augmentation. Comput. Syst. Appl. 2023, 32, 45–54. [Google Scholar]
- Cui, X.K.; Wang, Q.Z.; Liu, Q.P. State of health prediction of lithium batteries based on data-driven approaches. Complex Syst. Complex. Sci. 2024, 21, 154–159. [Google Scholar]
- Liu, X.H.; Gao, Z.C.; Tian, J.Q.; Wei, Z.B.; Fang, C.Q.; Wang, P. State of health estimation for lithium-ion batteries using voltage curves reconstruction by conditional generative adversarial network. IEEE Trans. Transp. Electrif. 2024, 10, 10557–10567. [Google Scholar] [CrossRef]
- Ren, Y.; Tang, T.; Jiang, F.S.; Xia, Q.; Zhu, X.Y.; Sun, B.; Yang, D.Z.; Feng, Q.; Qian, C. A novel state of health estimation method for lithium-ion battery pack based on cross generative adversarial networks. Appl. Energy 2025, 377, 124385. [Google Scholar] [CrossRef]
- Guo, F.; Huang, G.S.; Zhang, W.C.; Wen, A.; Li, T.T.; He, H.C.; Huang, H.L.; Zhu, S.S. Lithium battery state-of-health estimation based on sample data generation and temporal convolutional neural network. Energies 2023, 16, 8010. [Google Scholar] [CrossRef]
- Lin, C.H.; Kaushik, C.; Dyer, E.L.; Muthukumar, V. The good, the bad and the ugly sides of data augmentation: An implicit spectral regularization perspective. J. Mach. Learn. Res. 2024, 25, 1–85. [Google Scholar]
- Wang, Q.H.; Jia, H.J.; Huang, L.X.; Mao, Q.R. Semantic contrastive clustering with federated data augmentation. J. Comput. Res. Dev. 2024, 61, 1511–1524. [Google Scholar]
- Thompson, M.L.; Kramer, M.A. Modeling chemical processes using prior knowledge and neural networks. Alche J. 1994, 40, 1328–1340. [Google Scholar] [CrossRef]
- Zhao, W.; Yan, H.; Zhou, Z. Transformer fault diagnosis based on a residual BP neural network. Electr. Power Autom. Equip. 2020, 310, 143–148. [Google Scholar]
- Hu, X.Q.; Geng, L.M.; Shu, J.H.; Zhang, W.B.; Wu, C.L.; Wei, X.L.; Huang, D.; Chen, H. Health state estimation of lithium-ion battery using global health factor and residual Model. J. Xi’an Jiaotong Univ. 2025, 59, 105–117. [Google Scholar]
- Hao, K.Q.; Lü, Z.G.; Li, Y.; Di, R.H.; Zhu, H.J. Remaining useful life prediction of lithium-ion batteries using BP neural network incorporating prior knowledge. J. Xi’an Technol. Univ. 2022, 42, 65–73. [Google Scholar]
- Fan, J.H.; Liu, Q.Y.; Ma, L.; Liu, L.H. Life prediction model of lithium-ion batteries for electric vehicles based on deep learning. J. Terahertz Sci. Electron. Inf. Technol. 2025, 23, 182–187. [Google Scholar]
- Jiang, B.; Zhu, J.G.; Wang, X.Y.; Wei, X.Z.; Shang, W.L.; Dai, H.F. A comparative study of different features extracted from electrochemical impedance spectroscopy in state of health estimation for lithium-ion batteries. Appl. Energy 2022, 322, 119502. [Google Scholar] [CrossRef]
- Li, J.H.; Li, T.T.; Qiao, Y.J.; Tan, Z.J.; Qiu, X.H.; Deng, H.; Li, W.; Qi, X.; Wu, W.X. Internal temperature estimation method for lithium-ion battery based on multi-frequency imaginary part impedance and GPR model. J. Energy Storage 2025, 118, 116287. [Google Scholar] [CrossRef]
- Li, Z.H.; Shi, Q.L.; Wang, K.L.; Jiang, K. Research status and prospect of lithium-ion battery health state estimation methods. Autom. Electr. Power Syst. 2024, 48, 109–129. [Google Scholar]
- Zhou, Y.F.; Sun, X.X.; Huang, L.J.; Lian, J. Life cycle oriented health state estimation of lithium battery. J. Harbin Inst. Technol. 2021, 53, 55–62. [Google Scholar]
- Zhang, S.F.; Zhang, Q.Y.; Yang, Y.S.; Su, Y.X.; Xiong, B.Y. Modeling method of lithium-ion battery based on sliding window and LSTM neural network. Energy Storage Sci. Technol. 2022, 11, 228–239. [Google Scholar]
- Chen, M.H.; Wang, T.; Yuan, Y.; Ke, S.T. Study on retinal OCT segmentation with dual-encoder. Opto-Electron. Eng. 2023, 50, 230146. [Google Scholar]
- Ju, F.J.; Wu, Y.C.; Dong, M.J.; Zhao, J.X. MiFDeU: Multi-information fusion network based on dual-encoder for pelvic bones segmentation. Eng. Appl. Artif. Intell. 2025, 147, 110230. [Google Scholar] [CrossRef]
- NASA Ames Prognostics Data Repository. Available online: https://www.nasa.gov/intelligent-systems-division/discovery-and-systems-health/pcoe/pcoe-data-set-repository/ (accessed on 10 April 2025).
- Van Houdt, G.; Mosquera, C.; Nápoles, G. A review on the long short-term memory model. Artif. Intell. Rev. 2020, 53, 5929–5955. [Google Scholar] [CrossRef]
- Huang, Z.; Xu, W.; Yu, K. Bidirectional LSTM-CRF models for sequence tagging. arXiv 2015, arXiv:1508.01991. [Google Scholar]
- Zargar, S. Introduction to Sequence Learning Models: RNN, LSTM, GRU. 2021. Available online: https://www.researchgate.net/profile/Sakib-Zargar-2/publication/350950396_Introduction_to_Sequence_Learning_Models_RNN_LSTM_GRU/links/607b41c0907dcf667ba83ade/Introduction-to-Sequence-Learning-Models-RNN-LSTM-GRU.pdf (accessed on 8 March 2025).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).