Advanced Load Cycle Generation for Electrical Energy Storage Systems Using Gradient Random Pulse Method and Information Maximising-Recurrent Conditional Generative Adversarial Networks †
Abstract
1. Introduction
2. Dataset
3. Methodology
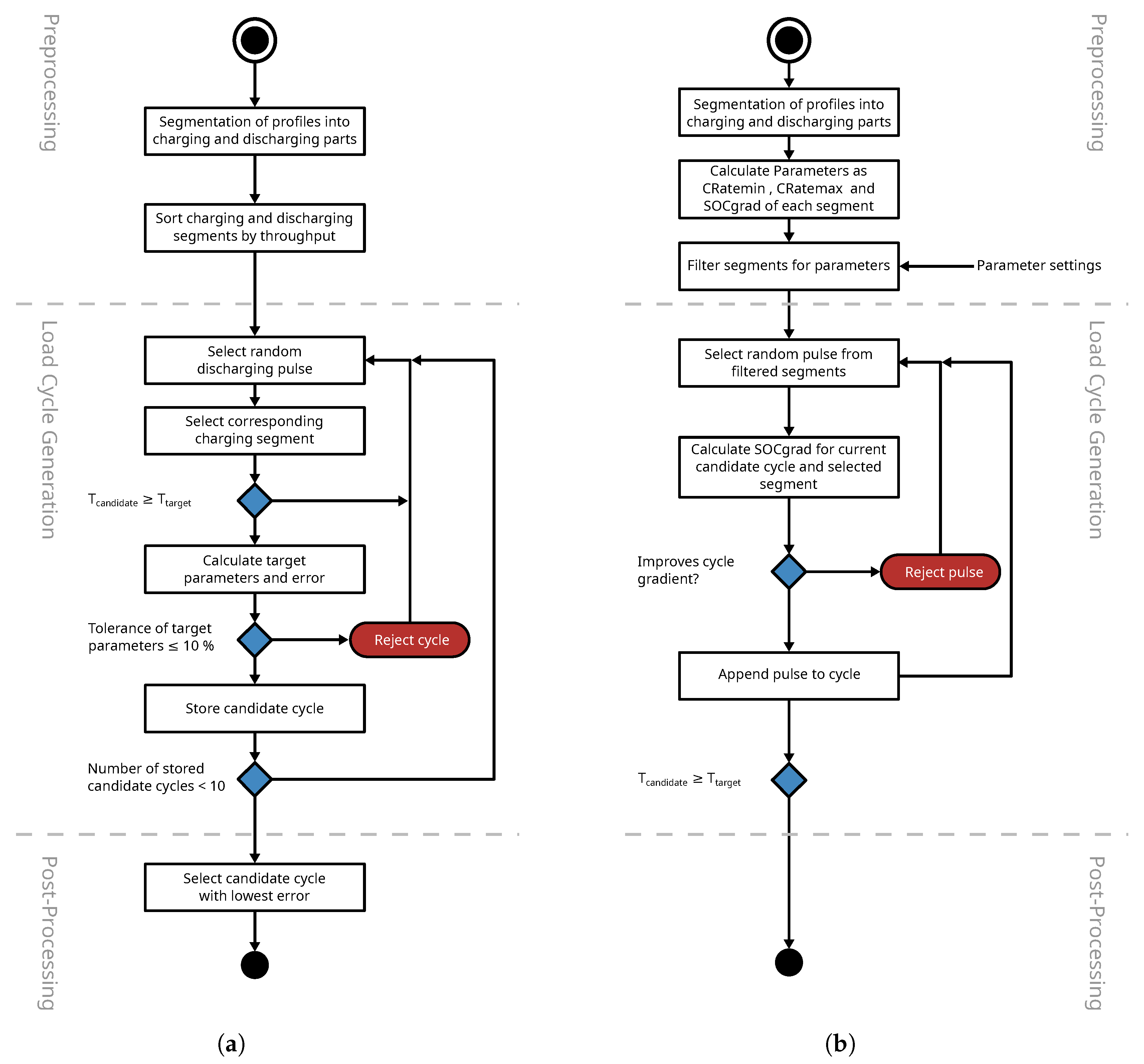
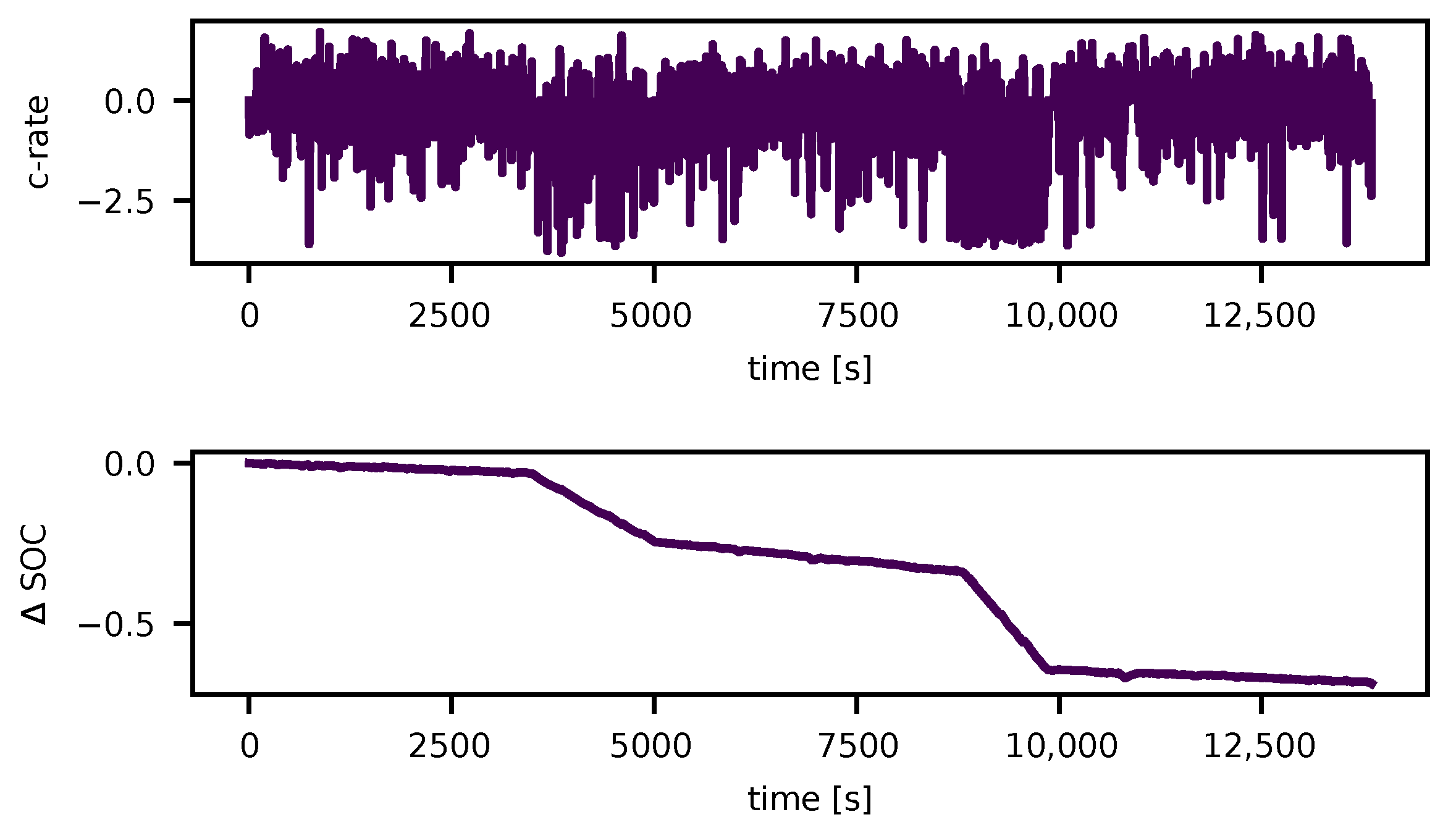
3.1. Gradient Random Pulse Method (gradRPM)
3.2. Process of Analysing Dynamic Load Cycles
- Preprocessing,
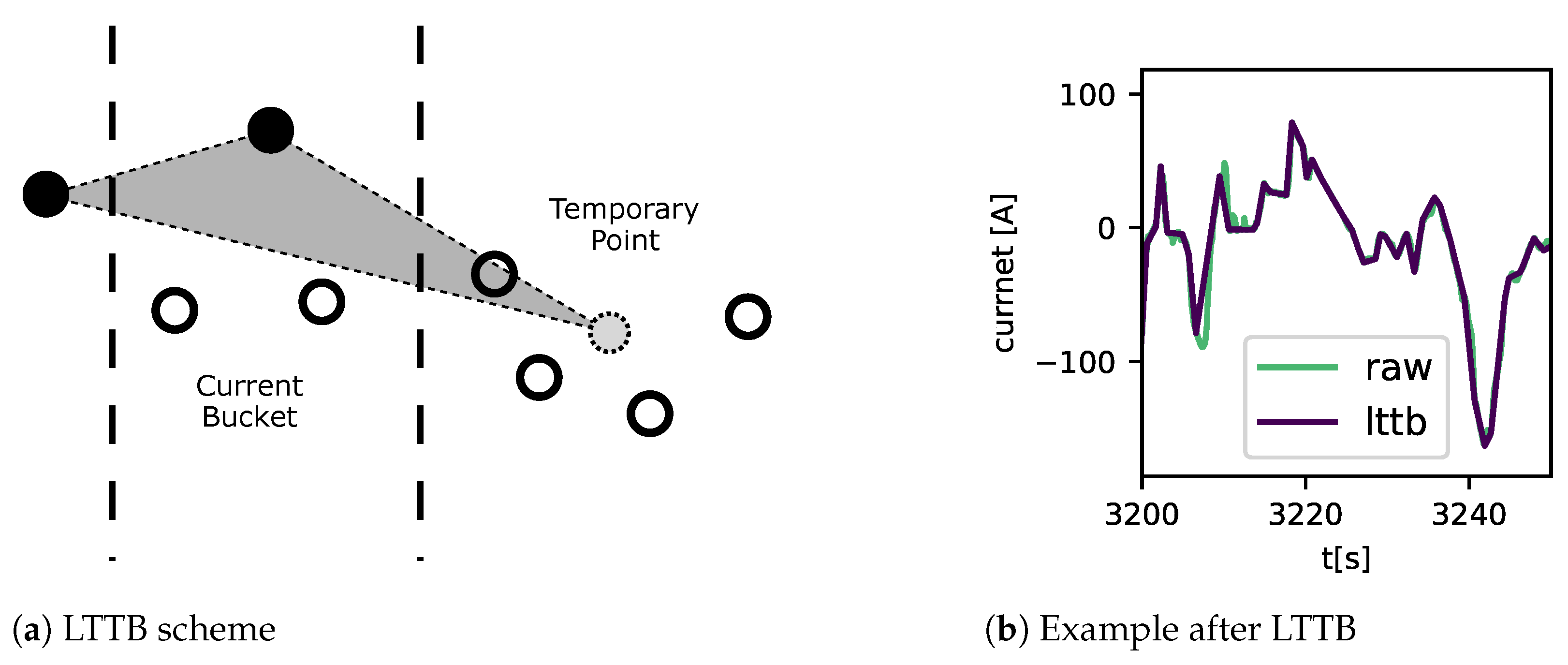
- Downsampling,
- And the analysis.
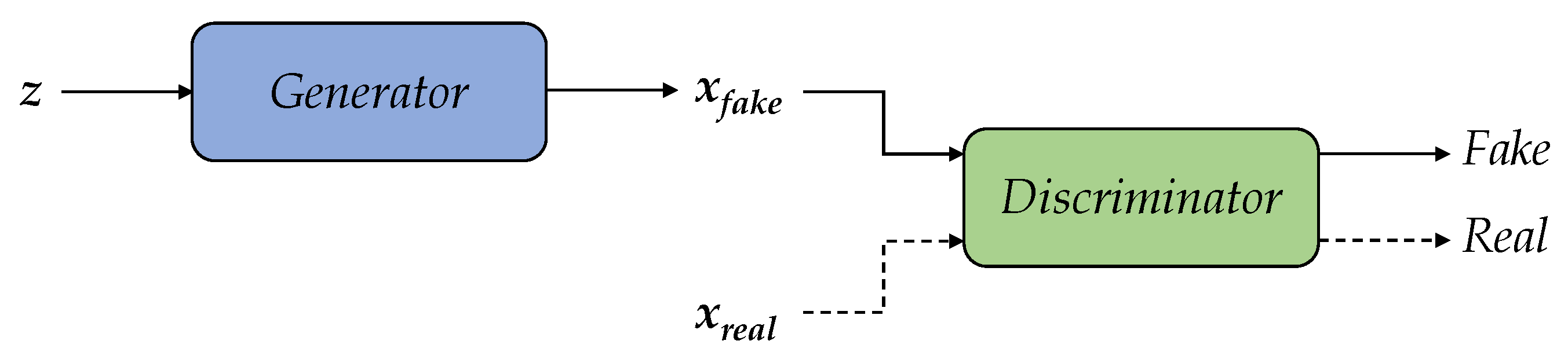
3.3. Data-Driven Approach (Info-RCGAN)
3.3.1. Data Preprocessing
3.3.2. Sequence Processing
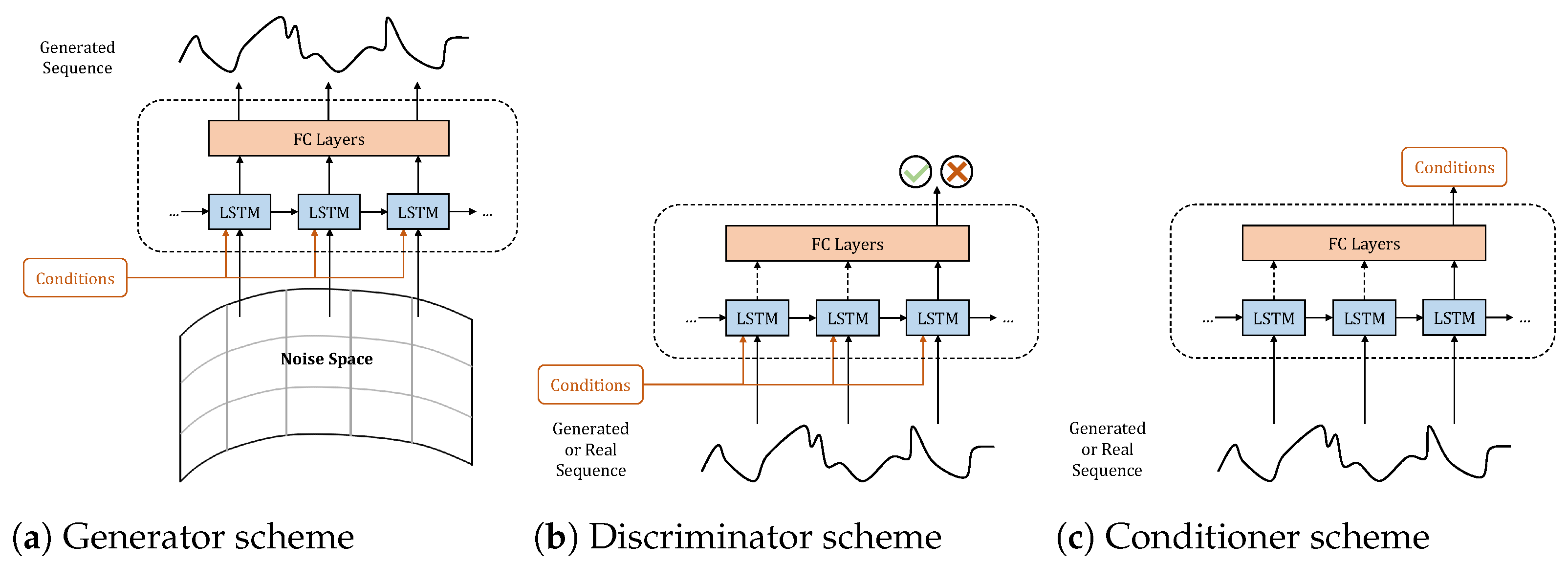
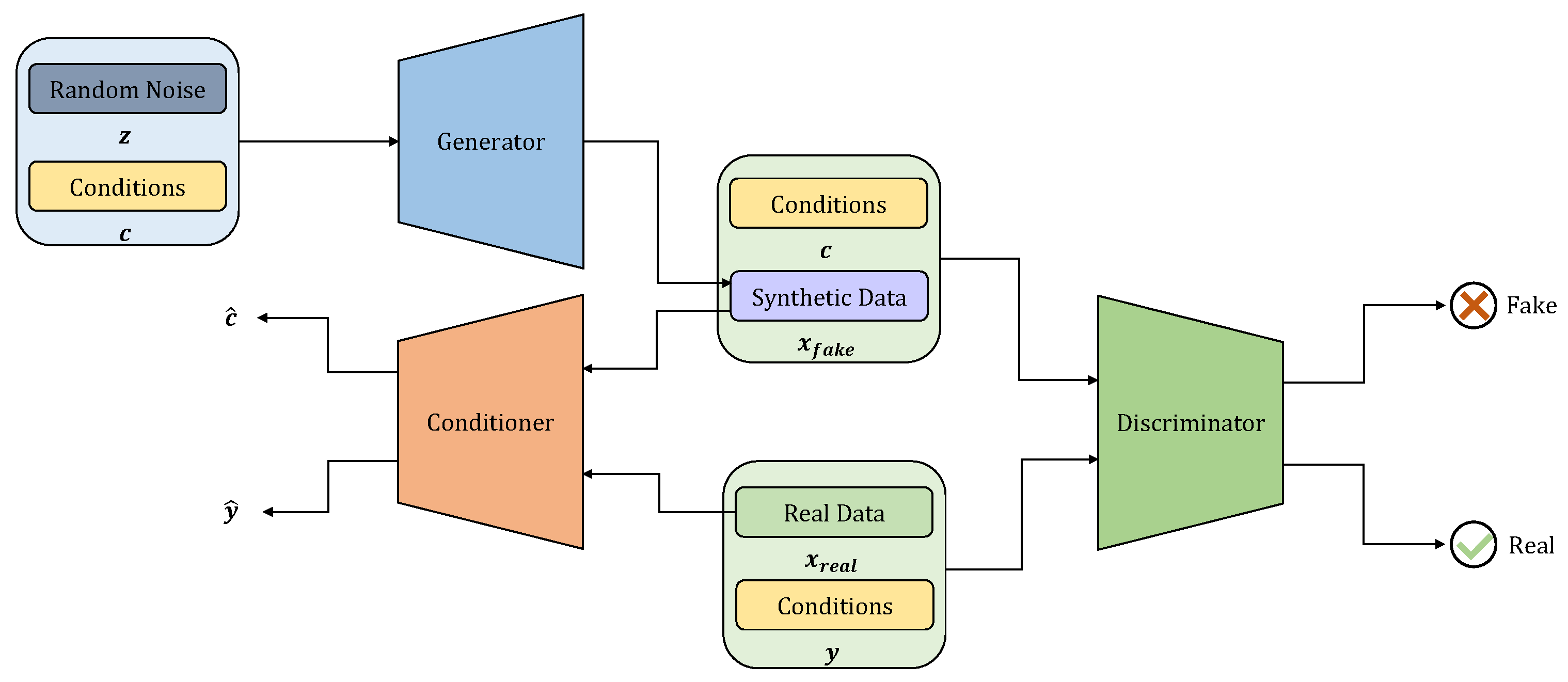
3.3.3. Generative Model
- SOC: the change in SOC after applying the load profile;
- T: the change in temperature of the battery pack;
- (C-rate): the minimum C-rate within the load profile;
- (C-rate): the maximum C-rate within the load profile;
- (U): the minimum voltage change throughout the load profile;
- (U): the maximum voltage change throughout the load profile.
3.3.4. Loss Function Design
- Fake loss : to distinguish fake data with the respective conditional input as fake;
- Real loss : to distinguish real data with the respective real labels as real;
- Unmatched loss : to distinguish real data with the unmatched labels as fake.
- Regression loss : to reconstruct the ground truth labels from the ground truth sequence data.
- Generation loss : to generate data that can fool the discriminator;
- Condition loss : to generate data from which the input conditions can be reproduced by the conditioner.
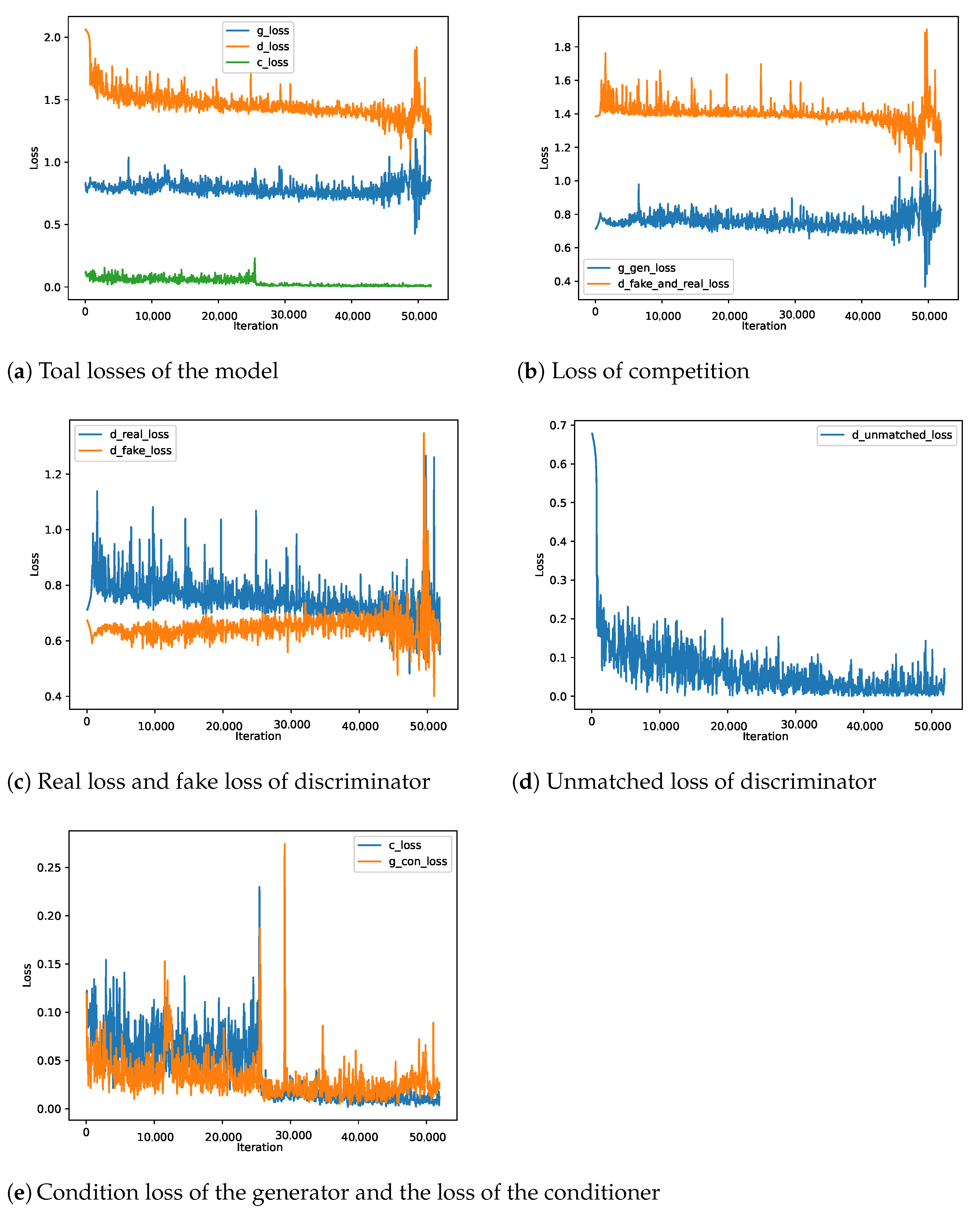
3.3.5. Training of the Model
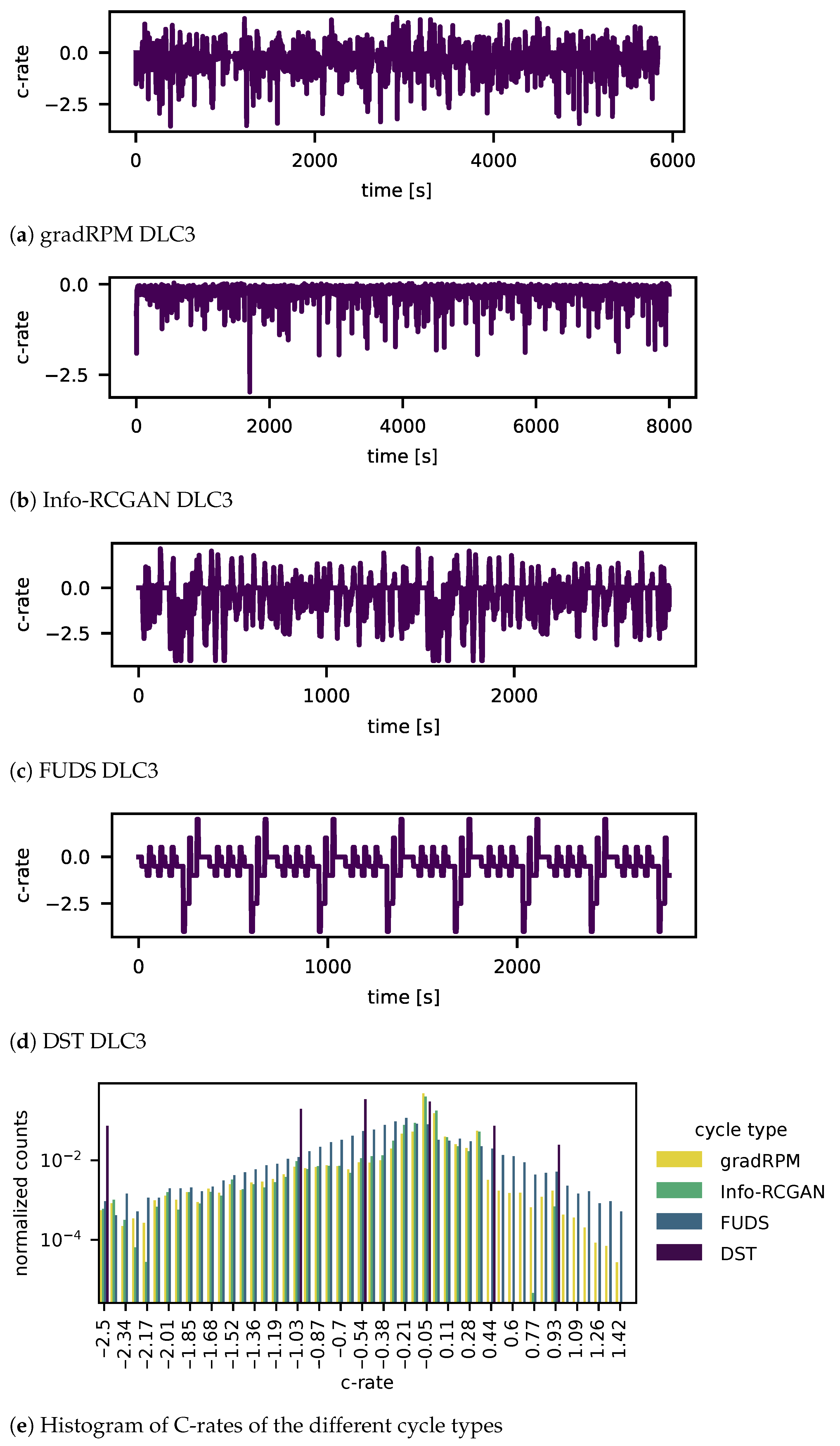
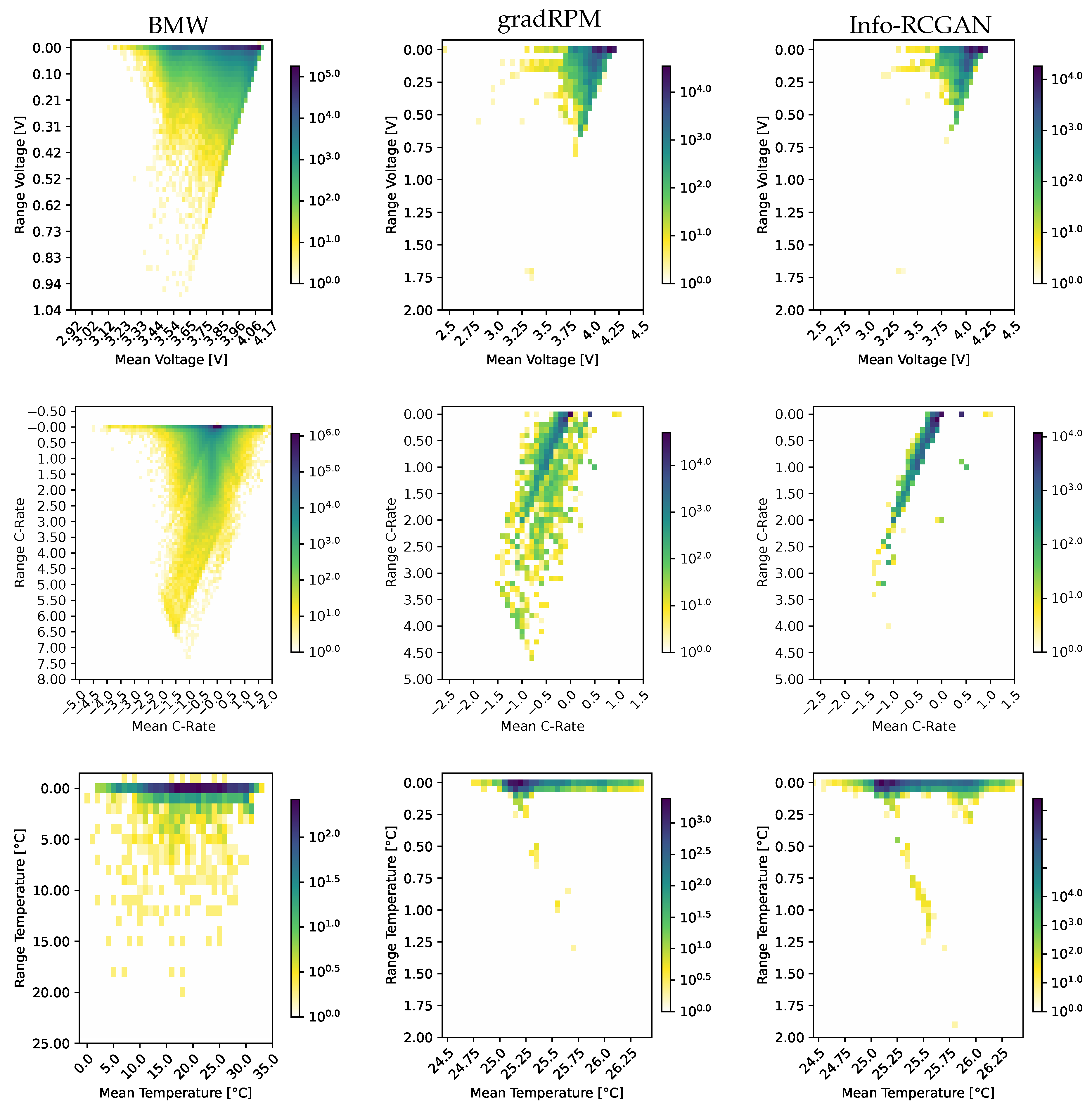
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RPM | Random Pulse Method |
| gradRPM | Gradient-Based Random Pulse Method |
| GAN | Generative Adversarial Network |
| RCGAN | Recurrent Conditional GAN |
| Info-RCGAN | Information Maximizing-RCGAN |
| SOC | State of Charge |
| RNN | Recurrent Neural Network |
| LSTM | Long Short-Term Memory |
| LTTB | Largest-Triangle-Three-Bucket |
| BCE | Binary Cross Entropy |
| MSE | Mean Squared Error |
References
- Geslin, A.; Xu, L.; Ganapathi, D.; Mory, K.; Chueh, W.; Onori, S. Dynamic cycling enhances battery lifetime. Nat. Energy 2025, 10, 172–180. [Google Scholar] [CrossRef]
- Kirkaldy, N.; Samieian, M.; Offer, G.; Marinescu, M.; Patel, Y. Lithium-ion battery degradation: Comprehensive cycle ageing data and analysis for commercial 21,700 cells. J. Power Sources 2024, 603, 234185. [Google Scholar] [CrossRef]
- dos Reis, G.; Strange, C.; Yadav, M.; Li, S. Lithium-ion battery data and where to find it. J. Energy AI 2021, 5, 100081. [Google Scholar] [CrossRef]
- Neupert, S.; Yao, J.; Kowal, J. Load Cycle Design and Analysis for Energy Storage Technologies Utilising Micro-Trip Methods and Machine Learning Approaches. In Proceedings of the Energy Storage Conference 2023 (ESC 2023), Glasgow, UK, 15–16 November 2023; pp. 63–68. [Google Scholar] [CrossRef]
- Gewald, T.; Reiter, C.; Lin, X.; Baumann, M.; Krahl, T.; Hahn, A.; Lienkamp, M. (Eds.) Characterization and Concept Validation of Lithium-Ion Batteries in Automotive Applications by Load Spectrum Analysis; Society of Automotive Engineers of Japan, Inc.: Chiyoda, Japan, 2018. [Google Scholar]
- Barragán-Moreno, A.; Gomez, P.I.; Dragičević, T. Enhancement of Stress Cycle-counting Algorithms for Li-Ion Batteries by means of Fuzzy Logic. In Proceedings of the 2022 IEEE Transportation Electrification Conference & Expo (ITEC), Anaheim, CA, USA, 15–17 June 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar] [CrossRef]
- Fioriti, D.; Scarpelli, C.; Pellegrino, L.; Lutzemberger, G.; Micolano, E.; Salamone, S. Battery lifetime of electric vehicles by novel rainflow-counting algorithm with temperature and C-rate dynamics: Effects of fast charging, user habits, vehicle-to-grid and climate zones. J. Energy Storage 2023, 59, 106458. [Google Scholar] [CrossRef]
- Gundogdu, B.; Gladwin, D.T. A fast battery cycle counting method for grid-tied battery energy storage system subjected to microcycles. In Proceedings of the 2018 International Electrical Engineering Congress (iEECON), Krabi, Thailand, 7–9 March 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar] [CrossRef]
- Nebuloni, R.; Meraldi, L.; Moretti, L.; Ilea, V.; Bovo, C.; Berizzi, A.; Raboni, P. A Real-Time Cycle Counting Method for Battery Degradation Calculation in MILP Models. In Proceedings of the 2023 IEEE International Conference on Environment and Electrical Engineering and 2023 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Madrid, Spain, 6–9 June 2023; IEEE: Piscataway, NJ, USA, 2023. [Google Scholar]
- Saxena, S.; Roman, D.; Robu, V.; Flynn, D.; Pecht, M. Battery Stress Factor Ranking for Accelerated Degradation Test Planning Using Machine Learning. Energies 2021, 14, 723. [Google Scholar] [CrossRef]
- Krause, T.; Nusko, D.; Rittmann, J.; Bauermann, L.; Kroll, M.; Holly, C. Synthetic Data Generation for AI-Informed End-of-Line Testing for Lithium-Ion Battery Production. World Electr. Veh. J. 2025, 16, 75. [Google Scholar] [CrossRef]
- Qiu, H.; Cui, S.; Wang, S.; Wang, Y.; Feng, M. A Clustering-Based Optimization Method for the Driving Cycle Construction: A Case Study in Fuzhou and Putian, China. IEEE Trans. Intell. Transp. Syst. 2022, 23, 18681–18694. [Google Scholar] [CrossRef]
- Wang, T.; Jing, Z.; Zhang, S.; Qiu, C. Utilizing Principal Component Analysis and Hierarchical Clustering to Develop Driving Cycles: A Case Study in Zhenjiang. Sustainability 2023, 15, 4845. [Google Scholar] [CrossRef]
- Kellner, Q.; Hosseinzadeh, E.; Chouchelamane, G.; Widanage, W.D.; Marco, J. Battery cycle life test development for high-performance electric vehicle applications. J. Energy Storage 2018, 15, 228–244. [Google Scholar] [CrossRef]
- Ben-Marzouk, M.; Pelissier, S.; Clerc, G.; Sari, A.; Venet, P. Generation of a Real-Life Battery Usage Pattern for Electrical Vehicle Application and Aging Comparison With the WLTC Profile. IEEE Trans. Veh. Technol. 2021, 70, 5618–5627. [Google Scholar] [CrossRef]
- Etxand-Santolaya, M.; Canals Casals, L.; Corchero, C. Estimation of electric vehicle battery capacity requirements based on synthetic cycles. Transp. Res. Part D 2023, 114, 103545. [Google Scholar] [CrossRef]
- Moy, K.; Beom Lee, S.; Harris, S.; Onori, S. Design and validation of synthetic duty cycles for grid energy storage dispatch using lithium-ion batteries. Adv. Appl. Energy 2021, 4, 100065. [Google Scholar] [CrossRef]
- Lin, J.; Liu, B.; Zhang, L. Autoencoder-based optimization method for driving cycle construction: A case study in Fuzhou, China. J. Ambient. Intell. Humaniz. Comput. 2022, 14, 12635–12650. [Google Scholar] [CrossRef]
- Mohanty, P.; Jena, P.; Padhy, N. imeGAN-based Diversified Synthetic Data Generation Following BERT-based Model for EV Battery SOC Prediction: A State-of-the-Art Approach. IEEE Trans. Ind. Appl. 2025, early acces. [Google Scholar] [CrossRef]
- Steinarsson, S. Downsampling Time Series for Visual Representation. Master’s Thesis, University of Iceland, Faculty of Industrial Engineering, Mechanical Engineering and ComputerScience, Reykjavik, Iceland, 2013. [Google Scholar]
- Sola, J.; Sevilla, J. Importance of input data normalization for the application of neural networks to complex industrial problems. IEEE Trans. Nucl. Sci. 1997, 44, 1464–1468. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Müller, A.; Nothman, J.; Louppe, G.; et al. Scikit-Learn: Machine Learning in Python. arXiv 2018, arXiv:1201.0490. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Vol. 1: Foundations; MIT Press: Cambridge, MA, USA, 1986; pp. 318–362. [Google Scholar]
- Du, X.; Cai, Y.; Wang, S.; Zhang, L. Overview of deep learning. In Proceedings of the 2016 31st Youth Academic Annual Conference of Chinese Association of Automation (YAC), Wuhan, China, 11–13 November 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 159–164. [Google Scholar] [CrossRef]
- Yao, J.; Kowal, J. A Multi-Scale Data-Driven Framework for Online State of Charge Estimation of Lithium-Ion Batteries with a Novel Public Drive Cycle Dataset. J. Energy Storage 2025, 107, 114888. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Goodfellow, I.J.; Pouget-Abadie, J.; Mirza, M.; Xu, B.; Warde-Farley, D.; Ozair, S.; Courville, A.; Bengio, Y. Generative Adversarial Networks. arXiv 2014, arXiv:1406.2661. [Google Scholar] [CrossRef]
- Mirza, M.; Osindero, S. Conditional Generative Adversarial Nets. arXiv 2014. [Google Scholar] [CrossRef]
- Odena, A.; Olah, C.; Shlens, J. Conditional Image Synthesis With Auxiliary Classifier GANs. arXiv 2017, arXiv:1610.09585. [Google Scholar]
- Miyato, T.; Koyama, M. cGANs with Projection Discriminator. arXiv 2018. [Google Scholar] [CrossRef]
- Mogren, O. C-RNN-GAN: Continuous recurrent neural networks with adversarial training. arXiv 2016. [Google Scholar] [CrossRef]
- Esteban, C.; Hyland, S.L.; Rätsch, G. Real-valued (Medical) Time Series Generation with Recurrent Conditional GANs. arXiv 2017. [Google Scholar] [CrossRef]
- Yao, J.; Neupert, S.; Kowal, J. Cross-Stitch Networks for Joint State of Charge and State of Health Online Estimation of Lithium-Ion Batteries. Batteries 2024, 10, 171. [Google Scholar] [CrossRef]
- Ding, X.; Wang, Y.; Xu, Z.; Welch, W.J.; Wang, J. CcGAN: Continuous Conditional Generative Adversarial Networks for Image Generation; The University of British Columbia: Vancouver, BC, Canada, 2021. [Google Scholar]
- Chen, X.; Duan, Y.; Houthooft, R.; Schulman, J.; Sutskever, I.; Abbeel, P. InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets. arXiv 2016. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. arXiv 2019, arXiv:1907.10902. [Google Scholar]

| Characteristic | Value |
|---|---|
| Rated capacity | Ah |
| Typical capacity | Ah |
| Nominal Voltage | |
| Charging cut off voltage | |
| Charging current | |
| Discharging current | 10 |
| Dynamic Load Cycle ID | SOC Start | SOC End | Percent of the Scenario | Repetitions | Load Cycle Duration | SOC per h |
|---|---|---|---|---|---|---|
| DLC1 | 12 | 2520 | SOC/ | |||
| DLC2 | 30 | 1260 | SOC/ | |||
| DLC3 | 2 | 5040 | SOC/ |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neupert, S.; Yao, J.; Kowal, J. Advanced Load Cycle Generation for Electrical Energy Storage Systems Using Gradient Random Pulse Method and Information Maximising-Recurrent Conditional Generative Adversarial Networks. Batteries 2025, 11, 149. https://doi.org/10.3390/batteries11040149
Neupert S, Yao J, Kowal J. Advanced Load Cycle Generation for Electrical Energy Storage Systems Using Gradient Random Pulse Method and Information Maximising-Recurrent Conditional Generative Adversarial Networks. Batteries. 2025; 11(4):149. https://doi.org/10.3390/batteries11040149
Chicago/Turabian StyleNeupert, Steven, Jiaqi Yao, and Julia Kowal. 2025. "Advanced Load Cycle Generation for Electrical Energy Storage Systems Using Gradient Random Pulse Method and Information Maximising-Recurrent Conditional Generative Adversarial Networks" Batteries 11, no. 4: 149. https://doi.org/10.3390/batteries11040149
APA StyleNeupert, S., Yao, J., & Kowal, J. (2025). Advanced Load Cycle Generation for Electrical Energy Storage Systems Using Gradient Random Pulse Method and Information Maximising-Recurrent Conditional Generative Adversarial Networks. Batteries, 11(4), 149. https://doi.org/10.3390/batteries11040149









