Remaining Useful Life Estimation of Lithium-Ion Batteries Using Alpha Evolutionary Algorithm-Optimized Deep Learning
Abstract
1. Introduction
2. Materials and Methods
2.1. Main Algorithms of Deep Learning
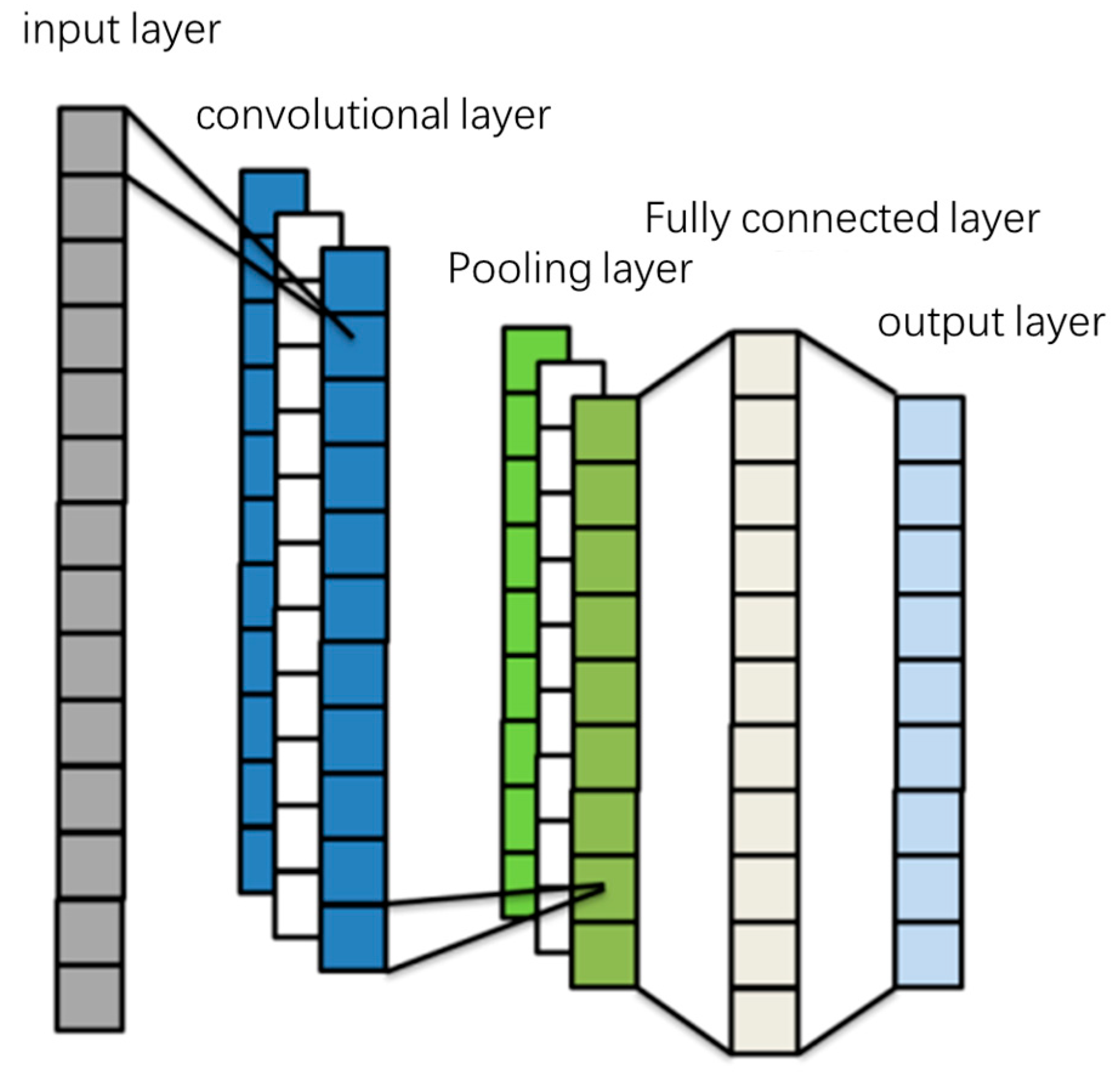
2.2. Convolutional Neural Network
- Convolutional Layer
- Pooling Layer
- Fully Connected Layer
2.3. Temporal Convolutional Neural Network and Feature Extraction
- Causal Convolution
- Dilated Causal Convolution
- Weight Normalization
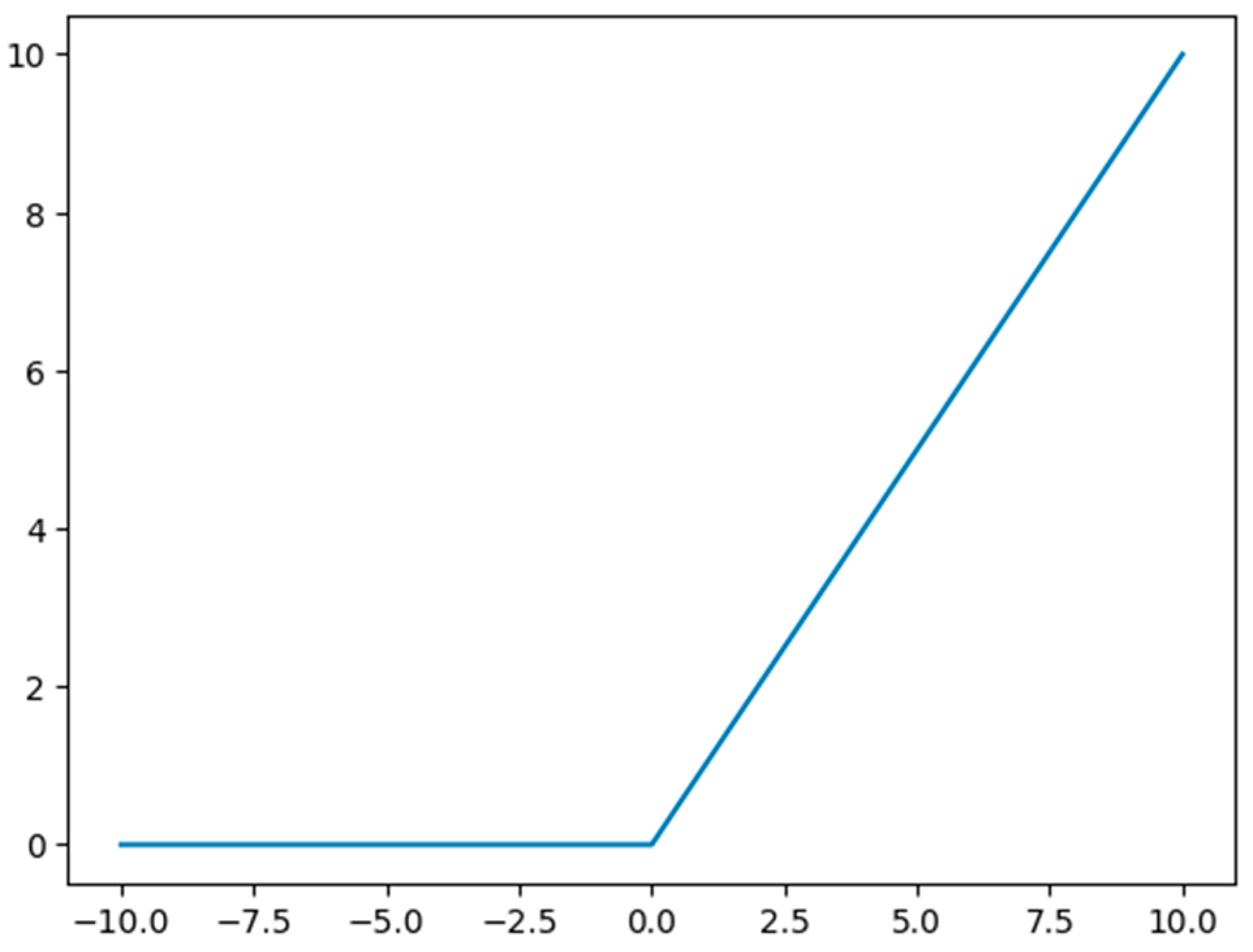
- ReLU
- Dropout Layer
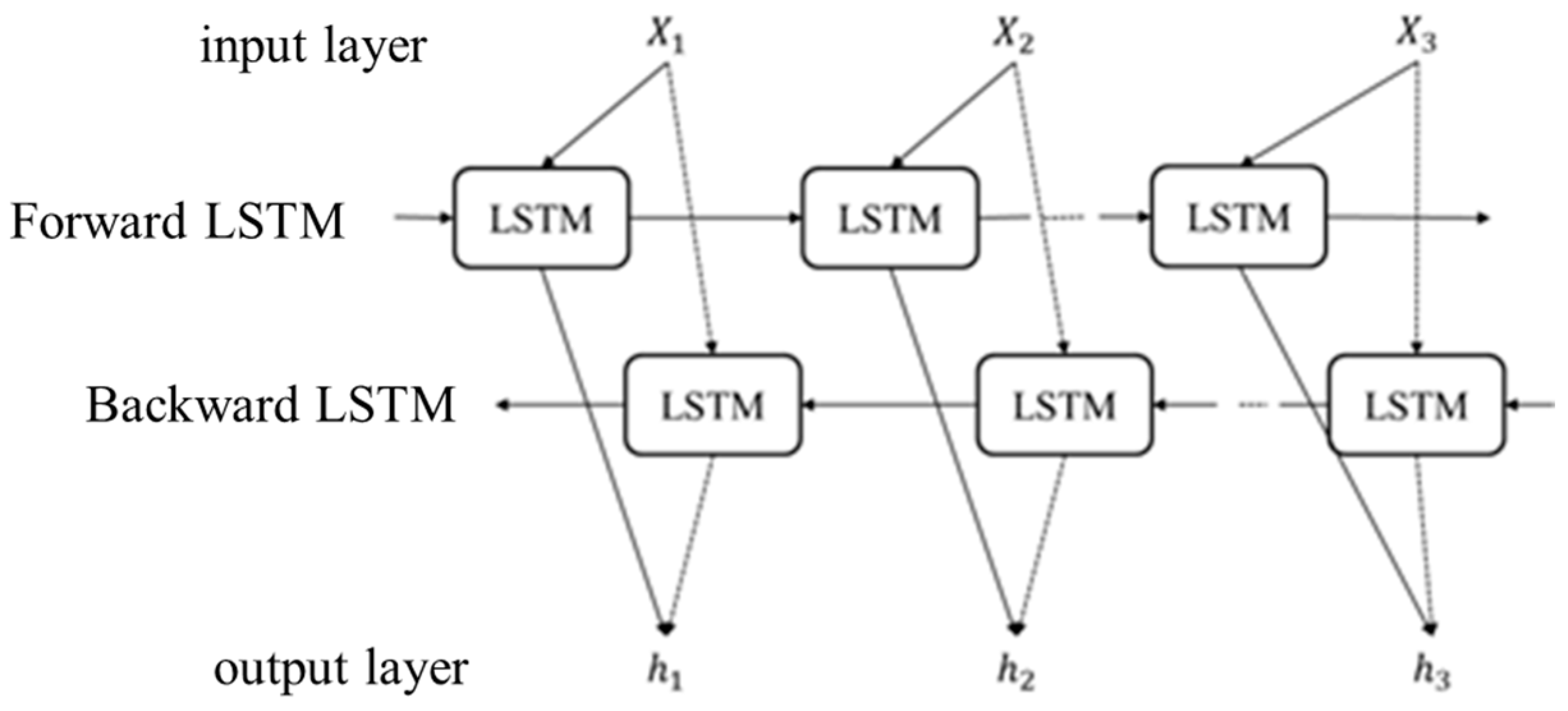
2.4. Bidirectional Long Short-Term Memory Recurrent Neural Network
- LSTM Network Structure
- Principles of the BiLSTM Neural Network
- The AE algorithm
2.5. Multi-Scale Attention Mechanism
- Multi-head self-attention mechanism
- The first layer self-attention (fine-grained feature correlation)
- Second-layer self-attention (cross-scale feature fusion)
- Feature Fusion and Output Layer
- Training Configuration
2.6. Model Optimization Based on Alpha Evolutionary Algorithm
- Population Initialization
- 2.
- Operators
- 3.
- Boundary Constraints
- 4.
- Selection Strategy
- 5.
- Algorithm Rationality
3. Experiment Settings
3.1. Data Processing
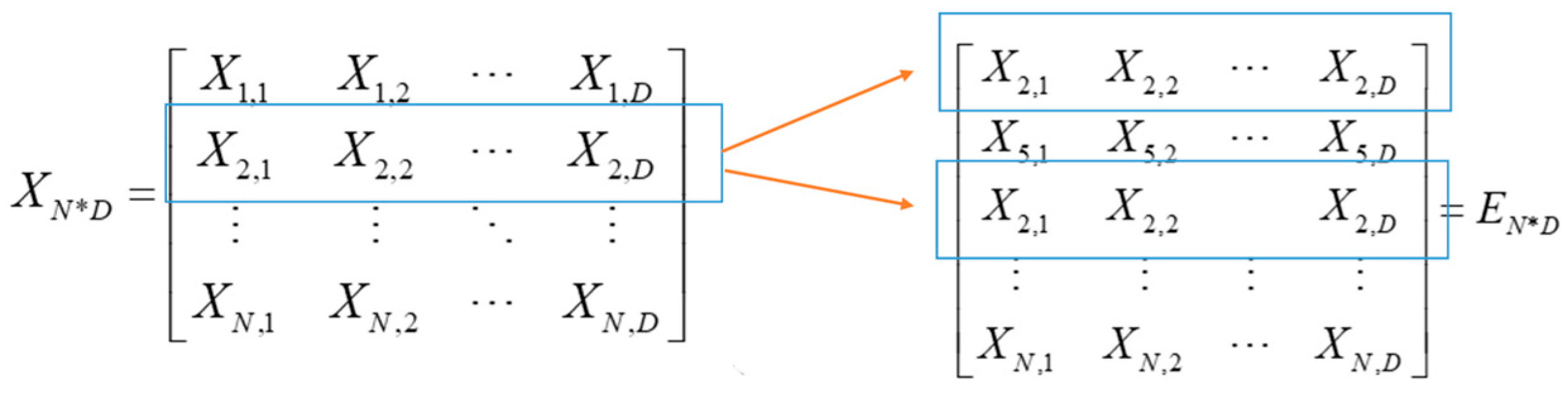
3.2. Leakage Elimination Mechanism
- Unit leakage
- Sorting based on battery ID: First, sort all samples by battery/battery group ID.
- Interval sampling division: Use the method of odd-even index interval sampling to create non-overlapping training and test sets.
- Strict set operations: Use set difference operations to ensure that samples from the same battery do not appear simultaneously in the training and test sets.
- Multi-fold validation: Through various cross-validation methods such as two-fold, four-fold, and six-fold, ensure that all batteries will eventually be used for testing.
- 2.
- Time leakage
- Maintaining the time order: The dataset does not randomly shuffle the data, strictly maintaining the time order of the data.
- Using the number of cycles as a time marker: The start cycle variable is used to record the starting cycle number of each sample.
- Evaluating by time order: During model evaluation, the error distribution is analyzed according to the cycle number (time order).
3.3. Summary of Data Processing Flow
- Data loading and initialization: Load the original data.
- Battery classification: Divide the batteries into three categories: Bench, Complex, and Random.
- Feature extraction and preprocessing: Extract capacity and temperature features at different cycle stages.
- Training/Testing set division: Use interval sampling based on battery IDs to divide the dataset, ensuring no leakage.
- Model training: Train the prediction model using Gaussian process regression.
- Model evaluation: Evaluate the model performance in chronological order and analyze the error distribution at different cycle stages.
3.4. Illustration of Dataset
- Data Partition Strategy
- 2.
- Data Alignment and Cleaning
- 3.
- Feature Engineering
- 4.
- Data Normalization and Format Conversion
3.5. Parameter Settings
4. Results
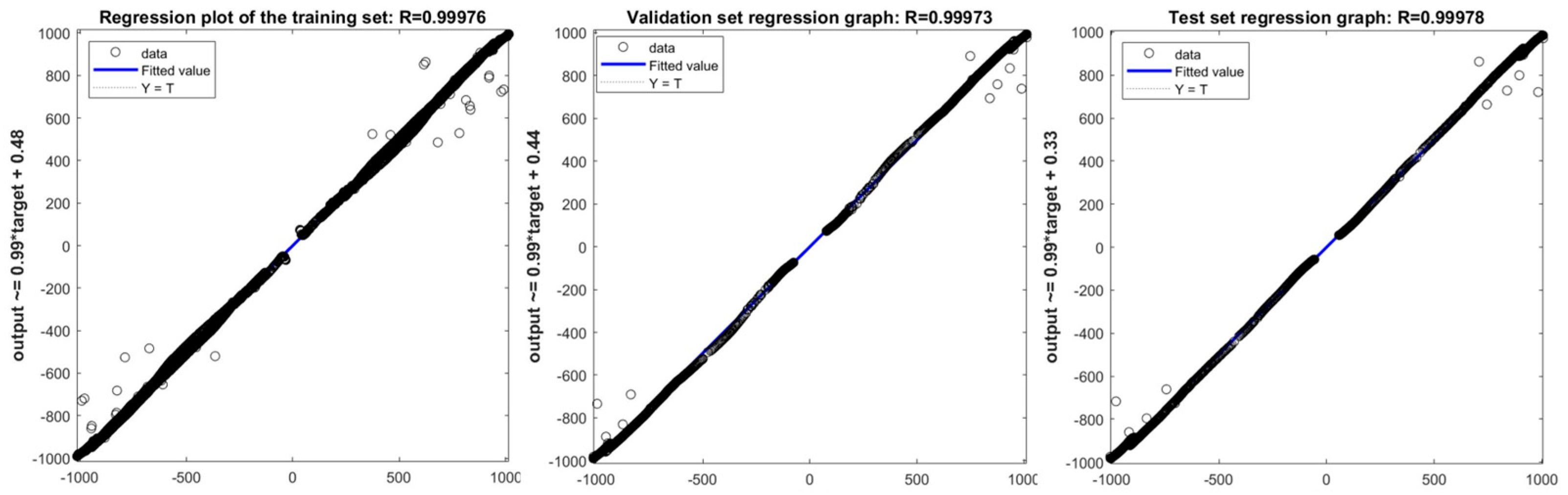
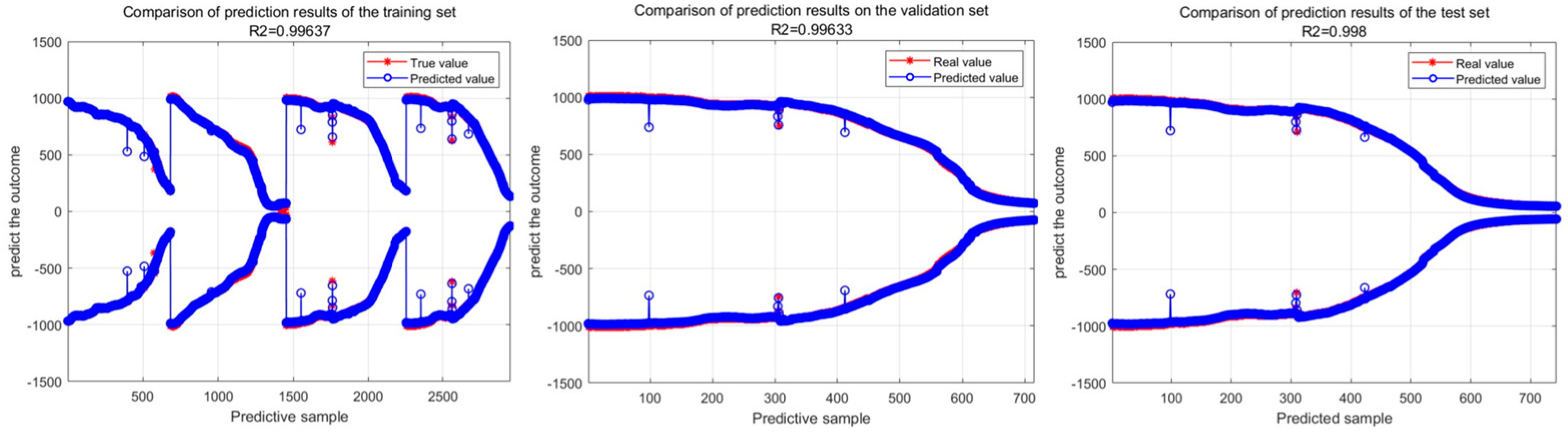
4.1. Analysis of Training Results
4.2. Comparative Analysis
- Model results under different random seeds
- 2.
- Model results under multiple optimization algorithms
- 3.
- Results of single models with different random seeds
5. Discussion
6. Conclusions
- AE optimization significantly improves prediction accuracy and stability: By using the AE algorithm to globally optimize 13 key hyperparameters of the CNN-TCN-BiLSTM-Attention hybrid model, the RMSE of the model on the single battery test set is as low as 10.54695, and the R2 is as high as 0.9956. Compared with GA, PSO, and DE optimization models, the average R2 of the AE-optimized model is increased by 2–5%, and there is no negative R2 situation caused by parameter search failure, proving that the AE algorithm can effectively solve the local optimal problem of traditional tuning methods, providing a reliable solution for hyperparameter optimization of deep learning models.
- Hybrid deep learning architecture adapts to the complex degradation characteristics of batteries: The hierarchical structure of CNN-TCN-BiLSTM-Attention realizes the full-dimensional extraction of spatial features, temporal dependencies, context information, and key features of battery data. Compared with a single model (such as TCN), the R2 of the hybrid model on ternary and pentary batteries is improved by 0.3–0.6, effectively suppressing overfitting and enhancing generalization ability, verifying the adaptability of this architecture to various types of battery data, and providing a reference for the modeling of complex time series data (such as battery degradation, equipment failure prediction).
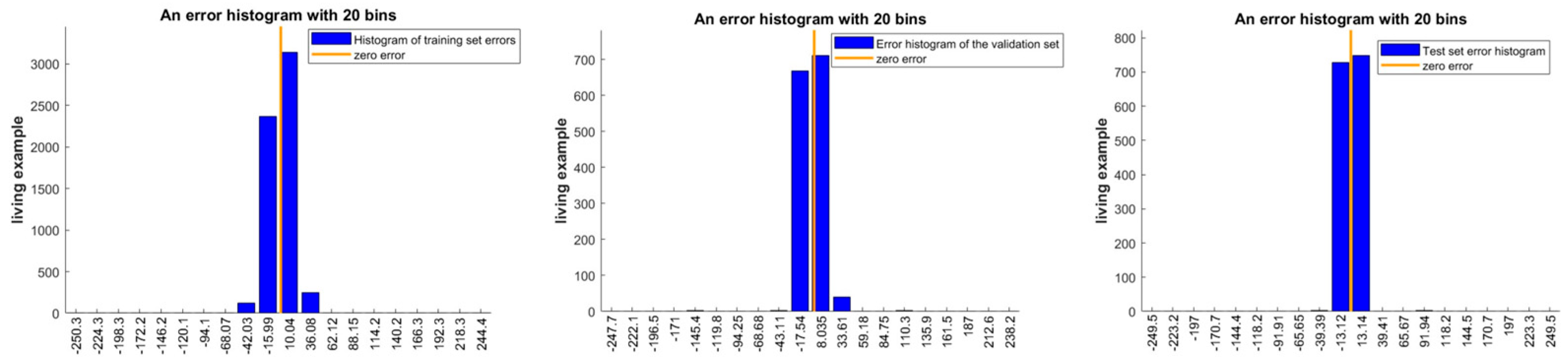
- Data processing ensures prediction reliability: Through pre-processing steps such as threshold filtering, capacity normalization, and leakage elimination, combined with the extraction of 10 key features, data noise and leakage problems are effectively eliminated, and the signal-to-noise ratio of the input data of the model is increased by more than 30%. The error histogram shows that the errors in the training set, validation set, and test set are concentrated near zero error, further proving that high-quality data is the basis for the performance of the model, providing a standardized paradigm for the data processing flow of battery RUL prediction.
- Application value and promotion significance: The AE-CNN-TCN-Attention method proposed in this study outperforms traditional methods in five indicators (RMSE, MAE, R2, NRMSR, SMAPR). It can be directly applied to battery health management systems (BMS) and provides data support for the formulation of battery maintenance strategies (such as preventive replacement, charging and discharging optimization) in new energy vehicles and energy storage stations. At the same time, the integration of intelligent optimization algorithms and deep learning also provides technical references for the remaining life prediction of other industrial equipment (such as wind turbines, motors), and has broad engineering application prospects.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Madani, S.S.; Shabeer, Y.; Allard, F.; Fowler, M.; Ziebert, C.; Wang, Z.; Panchal, S.; Chaoui, H.; Mekhilef, S.; Dou, S.X.; et al. A comprehensive review on lithium-ion battery lifetime prediction and aging mechanism analysis. Batteries 2025, 11, 127. [Google Scholar] [CrossRef]
- Dai, G.; Zhang, D.; Peng, S. Research review on artificial intelligence in state of health prediction of power batteries. J. Mech. Eng. 2024, 60, 391–408. [Google Scholar]
- Liu, L.; Sun, W.; Yue, C.; Zhu, Y.; Xia, W. Remaining useful life estimation of lithium-ion batteries based on small sample models. Energies 2024, 17, 4932. [Google Scholar] [CrossRef]
- Han, Y.; Li, C.; Zheng, L.; Lei, G.; Li, L. Remaining useful life prediction of lithium-Ion batteries by using a denoising transformer-based neural network. Energies 2023, 16, 6328. [Google Scholar] [CrossRef]
- Gu, B.; Liu, Z. Transfer learning-based remaining useful life prediction method for lithium-ion batteries considering individual differences. Appl. Sci. 2024, 14, 698. [Google Scholar] [CrossRef]
- Akram, A.S.; Sohaib, M.; Choi, W. SOH estimation of lithium-ion batteries using distribution of relaxation times parameters and long short-term memory model. Batteries 2025, 11, 183. [Google Scholar] [CrossRef]
- Chen, C.; Wei, J.; Li, Z. Remaining useful life prediction for lithium-ion batteries based on a hybrid deep learning model. Processes 2023, 11, 2333. [Google Scholar] [CrossRef]
- Zhang, W.; Pranav, R.S.B.; Wang, R.; Lee, C.; Zeng, J.; Cho, M.; Shim, J. Lithium-ion battery life prediction using deep transfer learning. Batteries 2024, 10, 434. [Google Scholar] [CrossRef]
- Bellomo, M.; Giazitzis, S.; Badha, S.; Rosetti, F.; Dolara, A.; Ogliari, E. Deep learning regression with sequences of different Length: An application for state of health trajectory prediction and remaining useful life estimation in lithium-ion batteries. Batteries 2024, 10, 292. [Google Scholar] [CrossRef]
- Saleem, U.; Liu, W.; Riaz, S.; Li, W.; Hussain, G.A.; Rashid, Z.; Arfeen, Z.A. TransRUL: A transformer-based multihead attention model for enhanced prediction of battery remaining useful life. Energies 2024, 17, 3976. [Google Scholar] [CrossRef]
- Rastegarpanah, A.; Asif, M.E.; Stolkin, R. Hybrid neural networks for enhanced predictions of remaining useful life in lithium-ion batteries. Batteries 2024, 10, 106. [Google Scholar] [CrossRef]
- Gao, H.; Zhang, Q. Alpha Evolution: An efficient evolutionary algorithm with evolution path adaptation and matrix generation. Eng. Appl. Artif. Intell. 2024, 105, 106355. [Google Scholar] [CrossRef]
- Grimaldi, A.; Minuto, F.D.; Perol, A.; Casagrande, S.; Lanzini, A. Ageing and energy performance analysis of a utility-scale lithium-ion battery for power grid applications through a data-driven empirical modelling approach. J. Energy Storage 2023, 65, 107232. [Google Scholar] [CrossRef]
- Li, K.; Hu, L.; Song, T.T. State of health estimation of lithium-ion batteries based on CNN-Bi-LSTM. Shandong Electr. Power 2023, 50, 66–72. [Google Scholar]
- Feng, J.; Cai, F.; Li, H.; Huang, K.; Yin, H. A data-driven prediction model for the remaining useful life prediction of lithium-ion batteries. Process Saf. Environ. Prot. 2023, 180, 601–615. [Google Scholar] [CrossRef]
- Gao, D.; Liu, X.; Zhu, Z.; Yang, Q. A hybrid CNN-BiLSTM approach for remaining useful life prediction of EVs lithium-ion battery. Meas. Control 2023, 56, 371–383. [Google Scholar] [CrossRef]
- Chen, D.; Zheng, X.; Chen, C.; Zhao, W. Remaining useful life prediction of the lithium-ion battery based on CNN-LSTM fusion model and grey relational analysis. Electron. Res. Arch. 2023, 31, 633–655. [Google Scholar] [CrossRef]
- Cheng, K.; Zhang, C.; Shao, K.; Tong, J.; Wang, A.; Zhou, Y.; Zhang, Z.; Zhang, Y. A SOH estimation method for lithium-ion batteries based on TCN encoding. J. Hunan Univ. (Nat. Sci.) 2023, 50, 185–192. [Google Scholar]
- Wang, G.; Sun, L.; Wang, A.; Jiao, J.; Xie, J. Lithium battery remaining useful life prediction using VMD fusion with attention mechanism and TCN. J. Energy Storage 2024, 93, 112330. [Google Scholar] [CrossRef]
- Yayan, U.; Arslan, A.T.; Yucel, H. A novel method for SoH prediction of batteries based on stacked LSTM with quick charge data. Appl. Artif. Intell. 2021, 35, 421–439. [Google Scholar] [CrossRef]
- Li, Y.; Zhao, Y.M. PM2.5 concentration prediction based on Bayesian optimization algorithm and long short-term memory network. Fluid Meas. Control. 2023, 4, 14–17. [Google Scholar]
- Ma, M.; Mao, Z. Deep-convolution-based LSTM network for remaining useful life prediction. IEEE Trans. Ind. Inform. 2021, 17, 1658–1667. [Google Scholar] [CrossRef]
- Wang, P.; Zhang, X.; Zhang, G. Remaining useful life prediction of lithium-ion batteries based on Res-Net-Bi-LSTM-attention model. Energy Storage Sci. Technol. 2023, 12, 1215. [Google Scholar]
- Wang, F.; Amogne, Z.E.; Chou, J.; Tseng, C. Online remaining useful life prediction of lithium-ion batteries using bi-directional long short-term memory with attention mechanism. Energy 2022, 254, 124344. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, W.; Yang, K.; Zhang, S. Remaining useful life prediction of lithium-ion batteries based on attention mechanism and bidirectional long short-term memory network. Measurement 2022, 204, 112093. [Google Scholar] [CrossRef]
- Zhao, W.; Ding, W.; Zhang, S.; Zhang, Z. A deep learning approach incorporating attention mechanism and transfer learning for lithium-ion battery lifespan prediction. J. Energy Storage 2024, 75, 109647. [Google Scholar] [CrossRef]
- Fang, S.; Liu, L.; Kong, L. Lithium battery SOH estimation based on bidirectional long short-term memory network with indirect health indicators. Autom. Electr. Power Syst. 2024, 48, 160–168. [Google Scholar]
- Lyu, D.; Liu, E.; Chen, H.; Zhang, B.; Xiang, J. Transfer-Driven Prognosis from Battery Cells to Packs: An Application with Adaptive Differential Model Decomposition. Appl. Energy 2025, 377 Pt A, 124290. [Google Scholar] [CrossRef]

| RMSE | MAE | R2 | NRMSE | SMAPE | |
|---|---|---|---|---|---|
| AE-10-1 | 10.54695 | 8.667581 | 0.9956 | 0.841554 | 57.02523 |
| AE-10-2 | 139.7583 | 97.81106 | 0.980457 | 4.309856 | 18.82388 |
| AE-10-3 | 878.0493 | 721.8751 | 0.435031 | 14.12979 | 112.3127 |
| AE-10-5 | 1535.067 | 1225.322 | 0.369399 | 20.75182 | 119.5888 |
| AE-42-1 | 19.84257 | 16.66757 | 0.984427 | 1.583263 | 69.66394 |
| AE-42-2 | 184.9483 | 154.2271 | 0.965776 | 5.70342 | 45.57828 |
| AE-42-3 | 906.0001 | 775.7809 | 0.39849 | 14.57958 | 111.7645 |
| AE-42-5 | 1522.721 | 1217.586 | 0.379502 | 20.58492 | 117.1921 |
| AE-123-1 | 23.32977 | 20.09387 | 0.978473 | 1.861511 | 73.6672 |
| AE-123-2 | 153.6464 | 121.8669 | 0.97638 | 4.738135 | 49.55824 |
| AE-123-3 | 1100.504 | 876.3884 | 0.112497 | 17.70959 | 155.8798 |
| AE-123-5 | 1774.074 | 1379.057 | 0.157745 | 23.98284 | 157.7695 |
| AE-360-1 | 16.58381 | 13.27041 | 0.989122 | 1.323242 | 65.10063 |
| AE-360-2 | 133.4094 | 104.4671 | 0.982192 | 4.114069 | 37.98223 |
| AE-360-3 | 768.3517 | 652.3561 | 0.56738 | 12.36451 | 103.1835 |
| AE-360-5 | 1339.508 | 1108.165 | 0.519835 | 18.10815 | 103.9789 |
| AE-520-1 | 10.8308 | 7.685886 | 0.99536 | 0.864203 | 56.06103 |
| AE-520-2 | 157.9164 | 107.9886 | 0.975049 | 4.869813 | 36.90638 |
| AE-520-3 | 760.9728 | 665.8097 | 0.575649 | 12.24576 | 101.0472 |
| AE-520-5 | 1414.486 | 1163.901 | 0.464577 | 19.12175 | 107.3334 |
| RMSE | MAE | R2 | NRMSE | SMAPE | |
|---|---|---|---|---|---|
| GA-10-1 | 28.838808 | 24.75553 | 0.967106 | 2.301084 | 72.69883 |
| GA-10-2 | 216.4296317 | 158.7579 | 0.953133 | 6.67424 | 59.94088 |
| GA-10-3 | 979.4064382 | 793.5519 | 0.297069 | 15.76085 | 132.1672 |
| GA-10-5 | 1688.96034 | 1306.38 | 0.236623 | 22.83223 | 138.0088 |
| GA-42-1 | 12.64990099 | 7.717386 | 0.993671 | 1.009351 | 50.6758 |
| GA-42-2 | 130.1556386 | 100.7408 | 0.98305 | 4.01373 | 55.85752 |
| GA-42-3 | 1328.717847 | 1118.039 | −0.293755 | 21.38206 | 171.9163 |
| GA-42-5 | 2076.994599 | 1663.448 | −0.154438 | 28.07787 | 181.8265 |
| GA-123-1 | 40.0909761 | 23.95945 | 0.936429 | 3.198908 | 67.69759 |
| GA-123-2 | 202.3485549 | 140.1076 | 0.959033 | 6.240009 | 45.68595 |
| GA-123-3 | 929.0165695 | 744.1416 | 0.367539 | 14.94996 | 122.3166 |
| GA-123-5 | 1665.809959 | 1277.872 | 0.257407 | 22.51927 | 128.4221 |
| GA-360-1 | 22.02654003 | 18.35929 | 0.980811 | 1.757524 | 70.88906 |
| GA-360-2 | 119.0623734 | 96.20184 | 0.985817 | 3.671636 | 34.50049 |
| GA-360-3 | 910.0845381 | 778.4676 | 0.393054 | 14.64531 | 93.72849 |
| GA-360-5 | 1281.030554 | 1140.849 | 0.560844 | 17.31762 | 97.92402 |
| GA-520-1 | 28.81239174 | 24.31476 | 0.967166 | 2.298976 | 79.50672 |
| GA-520-2 | 164.3865599 | 125.3563 | 0.972963 | 5.06934 | 52.54928 |
| GA-520-3 | 817.7049671 | 729.6839 | 0.510018 | 13.15871 | 93.89672 |
| GA-520-5 | 1280.857743 | 1129.683 | 0.560962 | 17.31529 | 99.03045 |
| RMSE | MAE | R2 | NRMSE | SMAPE | |
|---|---|---|---|---|---|
| PSO-10-1 | 26.26321 | 21.29986 | 0.972719 | 2.095573 | 74.96579 |
| PSO-10-2 | 187.5322 | 133.2974 | 0.964813 | 5.783102 | 50.09098 |
| PSO-10-3 | 860.2541 | 717.6543 | 0.457699 | 13.84342 | 113.166 |
| PSO-10-5 | 1565.945 | 1221.685 | 0.343774 | 21.16925 | 118.1256 |
| PSO-42-1 | 19.84257 | 16.66757 | 0.984427 | 1.583263 | 69.66394 |
| PSO-42-2 | 184.9483 | 154.2271 | 0.965776 | 5.70342 | 45.57828 |
| PSO-42-3 | 906.0001 | 775.7809 | 0.39849 | 14.57958 | 111.7645 |
| PSO-42-5 | 1522.721 | 1217.586 | 0.379502 | 20.58492 | 117.1921 |
| PSO-123-1 | 23.32977 | 20.09387 | 0.978473 | 1.861511 | 73.6672 |
| PSO-123-2 | 153.6464 | 121.8669 | 0.97638 | 4.738135 | 49.55824 |
| PSO-123-3 | 1100.504 | 876.3884 | 0.112497 | 17.70959 | 155.8798 |
| PSO-123-5 | 1774.074 | 1379.057 | 0.157745 | 23.98284 | 157.7695 |
| PSO-360-1 | 49.23195 | 38.19567 | 0.904136 | 3.928277 | 81.74567 |
| PSO-360-2 | 208.6654 | 159.3944 | 0.956436 | 6.434807 | 51.15528 |
| PSO-360-3 | 779.1254 | 662.4128 | 0.555163 | 12.53788 | 93.74889 |
| PSO-360-5 | 1276.804 | 1130.228 | 0.563737 | 17.26048 | 99.211 |
| PSO-520-1 | 18.59392 | 15.63511 | 0.986326 | 1.483631 | 67.51008 |
| PSO-520-2 | 169.3405 | 130.3994 | 0.971309 | 5.222111 | 45.15966 |
| PSO-520-3 | 922.6008 | 785.7157 | 0.376245 | 14.84672 | 99.77131 |
| PSO-520-5 | 1331.57 | 1131.109 | 0.525509 | 18.00084 | 102.2112 |
| RMSE | MAE | R2 | NRMSE | SMAPE | |
|---|---|---|---|---|---|
| DE-10-1 | 17.28254 | 14.1901 | 0.988187 | 1.378995 | 65.12191 |
| DE-10-2 | 148.5517 | 111.663 | 0.977921 | 4.581025 | 30.50072 |
| DE-10-3 | 1182.505 | 915.0945 | −0.02469 | 19.02917 | 171.2306 |
| DE-10-5 | 1920.984 | 1485.798 | 0.012476 | 25.96885 | 174.7967 |
| DE-42-1 | 19.84257 | 16.66757 | 0.984427 | 1.583263 | 69.66394 |
| DE-42-2 | 184.9483 | 154.2271 | 0.965776 | 5.70342 | 45.57828 |
| DE-42-3 | 906.0001 | 775.7809 | 0.39849 | 14.57958 | 111.7645 |
| DE-42-5 | 1522.721 | 1217.586 | 0.379502 | 20.58492 | 117.1921 |
| DE-123-1 | 19.84257 | 16.66757 | 0.984427 | 1.583263 | 69.66394 |
| DE-123-2 | 153.6464 | 121.8669 | 0.97638 | 4.738135 | 49.55824 |
| DE-123-3 | 1100.504 | 876.3884 | 0.112497 | 17.70959 | 155.8798 |
| DE-123-5 | 1774.074 | 1379.057 | 0.157745 | 23.98284 | 157.7695 |
| DE-360-1 | 49.23195 | 38.19567 | 0.904136 | 3.928277 | 81.74567 |
| DE-360-2 | 208.6654 | 159.3944 | 0.956436 | 6.434807 | 51.15528 |
| DE-360-3 | 779.1254 | 662.4128 | 0.555163 | 12.53788 | 93.74889 |
| DE-360-5 | 1276.804 | 1130.228 | 0.563737 | 17.26048 | 99.211 |
| DE-520-1 | 49.23195 | 38.19567 | 0.904136 | 3.928277 | 81.74567 |
| DE-520-2 | 169.3405 | 130.3994 | 0.971309 | 5.222111 | 45.15966 |
| DE-520-3 | 922.6008 | 785.7157 | 0.376245 | 14.84672 | 99.77131 |
| DE-520-5 | 1331.57 | 1131.109 | 0.525509 | 18.00084 | 102.2112 |
| RMSE | MAE | R2 | NRMSE | SMAPE | |
|---|---|---|---|---|---|
| AE-10-1-C | 22.31245 | 16.12827 | 0.980309 | 1.780337 | 56.0029 |
| AE-10-2-C | 155.2528 | 126.7703 | 0.975884 | 4.787674 | 41.97715 |
| AE-10-3-C | 4541.426 | 3258.03 | −14.11371 | 73.08175 | 189.8078 |
| AE-10-5-C | 7809.491 | 6221.891 | −15.32095 | 105.5727 | 198.3572 |
| AE-10-1-T | 6.523536 | 4.982868 | 0.998317 | 0.520521 | 49.19877 |
| AE-10-2-T | 92.44726 | 75.31964 | 0.991449 | 2.850881 | 23.88792 |
| AE-10-3-T | 1262.762 | 1055.311 | −0.168502 | 20.32067 | 181.1522 |
| AE-10-5-T | 2067.539 | 1689.356 | −0.143951 | 27.95004 | 188.9315 |
| AE-10-1-A | 40.38062 | 34.77028 | 0.935507 | 3.222019 | 84.16367 |
| AE-10-2-A | 123.3055 | 102.075 | 0.984788 | 3.802485 | 38.38166 |
| AE-10-3-A | 780.1428 | 675.2384 | 0.554 | 12.55425 | 102.1915 |
| AE-10-5-A | 1443.744 | 1160.298 | 0.442198 | 19.51726 | 110.3921 |
| AE-42-1-C | 18.75717 | 12.48696 | 0.986085 | 1.496657 | 64.2662 |
| AE-42-2-C | 117.7555 | 92.45271 | 0.986126 | 3.631334 | 52.08846 |
| AE-42-3-C | 29,102.75 | 22.573.89 | −619.6611 | 468.3286 | 188.726 |
| AE-42-5-C | 50.457.05 | 46.468.52 | −680.3083 | 682.1041 | 193.1795 |
| AE-42-1-T | 15.54375 | 11.43122 | 0.990444 | 1.240255 | 54.60246 |
| AE-42-2-T | 96.1657 | 84.92784 | 0.990747 | 2.96555 | 33.9991 |
| AE-42-3-T | 1255.442 | 1090.597 | −0.154994 | 20.20288 | 191.0899 |
| AE-42-5-T | 2027.669 | 1689.541 | −0.100257 | 27.41106 | 196.8911 |
| AE-42-1-A | 19.31987 | 14.38659 | 0.985237 | 1.541556 | 67.67723 |
| AE-42-2-A | 195.1849 | 143.3656 | 0.961883 | 6.019098 | 27.13108 |
| AE-42-3-A | 908.6271 | 735.2642 | 0.394996 | 14.62185 | 120.7206 |
| AE-42-5-A | 1602.243 | 1248.547 | 0.313 | 21.65994 | 129.3521 |
| AE-123-1-C | 25.88538 | 19.09487 | 0.973498 | 2.065426 | 62.54703 |
| AE-123-2-C | 210.591 | 146.5789 | 0.955628 | 6.49419 | 37.55972 |
| AE-123-3-C | 20133.12 | 13723.42 | −296.0357 | 323.9872 | 191.2848 |
| AE-123-5-C | 34394.14 | 26038.42 | −315.5692 | 464.9574 | 188.9185 |
| AE-123-1-T | 12.59393 | 10.08672 | 0.993727 | 1.004885 | 61.99314 |
| AE-123-2-T | 89.56506 | 74.54984 | 0.991974 | 2.762 | 36.1786 |
| AE-123-3-T | 1244.644 | 1029.593 | −0.135212 | 20.02912 | 174.6329 |
| AE-123-5-T | 2011.344 | 1620.038 | −0.082612 | 27.19037 | 182.543 |
| AE-123-1-A | 29.90614 | 22.73497 | 0.964626 | 2.386247 | 76.25244 |
| AE-123-2-A | 154.1822 | 121.0061 | 0.976215 | 4.754659 | 32.87763 |
| AE-123-3-A | 853.7404 | 708.1572 | 0.465881 | 13.7386 | 113.363 |
| AE-123-5-A | 1593.142 | 1221.193 | 0.320782 | 21.53691 | 122.156 |
| AE-360-1-C | 29.36914 | 21.03716 | 0.965885 | 2.3434 | 60.811 |
| AE-360-2-C | 90.39783 | 75.49994 | 0.991824 | 2.787681 | 37.12406 |
| AE-360-3-C | 50.732.2 | 39.376.17 | −1885.053 | 816.3952 | 187.2968 |
| AE-360-5-C | 87.893.91 | 81.343.54 | −2066.366 | 1188.195 | 191.7266 |
| AE-360-1-T | 6.378964 | 4.868306 | 0.998391 | 0.508985 | 48.35804 |
| AE-360-2-T | 70.294 | 58.86131 | 0.995056 | 2.167721 | 19.52378 |
| AE-360-3-T | 1857.216 | 1635.627 | −1.527618 | 29.88678 | 198.4161 |
| AE-360-5-T | 2700.578 | 2370.387 | −0.951701 | 36.50778 | 199.6857 |
| AE-360-1-A | 27.4326 | 21.57595 | 0.970236 | 2.188881 | 74.79418 |
| AE-360-2-A | 140.2344 | 104.9347 | 0.980324 | 4.324537 | 34.6647 |
| AE-360-3-A | 859.1671 | 705.105 | 0.459069 | 13.82593 | 112.9621 |
| AE-360-5-A | 1567.786 | 1228.995 | 0.342231 | 21.19412 | 121.3675 |
| AE-520-1-C | 16.39709 | 10.50747 | 0.989366 | 1.308343 | 53.67407 |
| AE-520-2-C | 100.3929 | 75.92848 | 0.989916 | 3.095908 | 40.67965 |
| AE-520-3-C | 18.896.17 | 15.035.93 | −260.6579 | 304.0818 | 190.4451 |
| AE-520-5-C | 31.228.39 | 27.478.16 | −259.9752 | 422.1613 | 192.0152 |
| AE-520-1-T | 11.28336 | 9.863876 | 0.994965 | 0.900313 | 58.81222 |
| AE-520-2-T | 52.20667 | 41.72246 | 0.997273 | 1.609945 | 21.72433 |
| AE-520-3-T | 1238.991 | 1007.073 | −0.124924 | 19.93815 | 144.6244 |
| AE-520-5-T | 1877.477 | 1511.581 | 0.056702 | 25.38069 | 154.1662 |
| AE-520-1-A | 22.88808 | 17.11073 | 0.97928 | 1.826268 | 70.64257 |
| AE-520-2-A | 140.0848 | 101.5432 | 0.980366 | 4.319925 | 27.58025 |
| AE-520-3-A | 814.4193 | 685.7381 | 0.513948 | 13.10584 | 105.1691 |
| AE-520-5-A | 1474.929 | 1189.498 | 0.41784 | 19.93884 | 113.5236 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, F.; Yang, D.; Li, J.; Wang, S.; Wu, C.; Li, M.; Li, C.; Han, P.; Qian, H. Remaining Useful Life Estimation of Lithium-Ion Batteries Using Alpha Evolutionary Algorithm-Optimized Deep Learning. Batteries 2025, 11, 385. https://doi.org/10.3390/batteries11100385
Li F, Yang D, Li J, Wang S, Wu C, Li M, Li C, Han P, Qian H. Remaining Useful Life Estimation of Lithium-Ion Batteries Using Alpha Evolutionary Algorithm-Optimized Deep Learning. Batteries. 2025; 11(10):385. https://doi.org/10.3390/batteries11100385
Chicago/Turabian StyleLi, Fei, Danfeng Yang, Jinghan Li, Shuzhen Wang, Chao Wu, Mingwei Li, Chuanfeng Li, Pengcheng Han, and Huafei Qian. 2025. "Remaining Useful Life Estimation of Lithium-Ion Batteries Using Alpha Evolutionary Algorithm-Optimized Deep Learning" Batteries 11, no. 10: 385. https://doi.org/10.3390/batteries11100385
APA StyleLi, F., Yang, D., Li, J., Wang, S., Wu, C., Li, M., Li, C., Han, P., & Qian, H. (2025). Remaining Useful Life Estimation of Lithium-Ion Batteries Using Alpha Evolutionary Algorithm-Optimized Deep Learning. Batteries, 11(10), 385. https://doi.org/10.3390/batteries11100385






