Evaluating Hybridization Potential Using Load Profile Metrics: A Rule-of-Thumb Approach

Abstract

Hybrid battery systems, which combine high-energy and high-power cells, offer a promising solution for electrifying heavy-duty applications by balancing energy density, power capability, and cost. This paper presents a generic methodology for cost-optimal sizing of hybrid battery energy storage systems using a Mixed Integer Nonlinear Programming framework. A large-scale simulation study involving 10,000 load profiles replicating applications varying from road transportation to sea-going vessels is used to derive practical “rules of thumb” that guide when hybridization is beneficial, offering significant reductions in cost, weight, and volume compared to monotype battery configurations. Sensitivity analyses further validate the robustness of the method across varying cell costs and C-rates, making it applicable to a wide range of battery chemistries and use cases.

1. Introduction

The heavy-duty transportation and construction sectors are undergoing significant decarbonization. Battery-powered electric systems are emerging as a viable solution to replace combustion engines, particularly when considering the total cost of ownership. These systems must meet the demanding requirements of high power for heavy loads and high energy for an acceptable range between recharges. Battery hybridization [1], which combines High-Energy (HE) and High-Power (HP) battery technologies within a single pack, presents a promising solution. This approach balances the conflicting demands for energy and power while also reducing cost and weight. Many different applications could benefit from this concept. The authors of [2] give an overview of possible applications when combining batteries with supercapacitors that serve as the High-Power technology. A review of battery-supercapacitor hybrid energy storage systems for electric vehicles is presented in [3]. In [4], the benefits of hybridization for electric marine applications are shown. A model-based evaluation framework investigating the cost, volume, weight, and system complexity reduction benefits of such solutions was established in [5]. The authors of [6] studied a hybrid battery configuration consisting of Lithium Titanate Oxide (LTO) and Lithium Iron Phosphate (LFP) batteries for electric buses, whereas the authors of [7] considered three different energy sources for the sizing of a hybrid battery energy storage system (HBESS) of an electric vehicle. The impact of battery aging on the sizing of hybrid battery systems for electric vehicles was analyzed in [8]. The authors of [9] show that, for an electric race car, the combination of a high-power cell technology (handling traction and regenerative braking) with a high-energy one (reducing the overall battery weight) is able to significantly improve the race time compared to a traditional single chemistry battery pack. Also microgrid applications could benefit from battery hybridization, to provide uninterrupted power to sensitive loads [10,11]. In connection with this, ref. [12] gives an overview of different hybrid energy storage systems for grid applications.

While these studies demonstrate the benefits of hybrid battery systems in specific domains, they often rely on detailed system knowledge, complex optimization routines, or are tailored to narrow use cases. For instance, the bilevel optimization approach to sizing an HBESS system [13] is computationally intensive and requires detailed system knowledge. The framework presented in [5] is computationally intensive and requires strong context knowledge of the systems’ architectural design and its operational scenarios to render optimization results, making it rigid when facing a wide range of scenarios.

There remains a lack of generic, easy-to-apply guidelines that can inform early-stage design decisions across a wide range of applications and cell chemistries. This gap is particularly relevant for system engineers who need to quickly assess whether an HBESS system could be beneficial, without committing to full-scale simulations or prototyping. As electrification efforts accelerate across sectors, system designers are increasingly faced with the challenge of selecting battery configurations that balance performance and cost under diverse operating conditions. In such contexts, fast and intuitive decision-making tools are essential to avoid costly overdesign or underperformance.

In this work, we present a generic method that allows for rapid evaluation of hybridization potential based on load profile characteristics and cell parameters. These rules of thumb could be applied to electric ships, electric construction vehicles (excavators, wheel loaders, dump trucks, etc.), agricultural machinery, etc. The cost-optimal sizing of a hybrid battery pack is first formulated as a Mixed Integer Nonlinear Programming (MINLP) problem. Based on an optimal sizing of 10,000 synthetic load profiles, rules of thumb are derived. Results are demonstrated for hybrid battery packs consisting of Nickel Manganese Cobalt (NMC) and Lithium Titanate Oxide (LTO) cells, and a sensitivity analysis with respect to the cell cost and C-rate is performed, but can be easily generalized to other cells.

The contributions of this work are twofold: (1) Formulation of the optimal sizing of hybrid batteries for a given load profile; (2) Rules of thumb are derived that allow for a quick assessment when hybrid batteries are able to result in a significant cost, volume, and mass reduction compared to monotype battery systems, while meeting the load requirements.

Section 2 describes the hybrid battery concept and the used cell characteristics. In Section 3, the hybrid battery sizing is formulated as an MINLP problem, and an example is given. Section 4 explains the derivation of rules of thumb for the battery sizing, for different costs and C-rates of the cell, based on simulations of 10,000 load profiles for all different combinations of cell cost and C-rate. Section 5 provides a detailed discussion of the results and the benefits of the approach. Finally, Section 6 draws conclusions and describes future work.

2. Material and Methods

2.1. Hybrid Batteries

The hybrid battery considered in this work consists of a combination of Nickel-Manganese-Cobalt (NMC) and LTO cells. NMC cells serve as the high-energy cells in the hybrid battery, whereas the LTO cells have higher charge and discharge rates, and serve as the high-power cells. The downside of LTO cells is that they have a higher cost for the same energy capacity compared to NMC cells. The specifications of each cell are shown in

Table 1. Specifications of the used NMC (high-energy) and LTO (high-power) cells.

Parameter	Unit	NMC	LTO
Capacity	Ah	50	50
Voltage	V	3.65	2.3
C-Rate	C	1.2	5
Resistance	$\mathsf{\Omega }$	0.0006	0.0011
Cost per kWh	€/kWh	120	230
Cost per kW peak	€/kWp	100	46
Energy per kg	Wh/kg	222	99

and are based on data of [14]. The open circuit voltage (OCV) is expressed as a function of the SoC dynamics, and is presented in Figure 1. The considered system configuration of the hybrid battery is a full-active structure with a DC-to-DC converter for the HE battery and the HP battery [15,16].

2.2. Use of Generative AI Tools

During the preparation of this manuscript, Microsoft Copilot (based on OpenAI’s GPT-4 architecture) was used to assist with proofreading and refining the conclusion. All scientific content and data interpretation were developed and verified by the authors without AI assistance.

3. Cost-Optimal Sizing for Hybrid Batteries

The cost-optimal sizing of hybrid batteries can be formulated as a Mixed Integer Nonlinear Programming problem. Several constraints and dynamic equations hold for the hybrid battery system [16].

• SoC Dynamics:

The evolution of the stored energy in the HE and HP branches is tracked through the SoC. Its discrete-time update is:

$$So{C}_{bat}(k+1)=So{C}_{bat}\left(k\right)-{\displaystyle \frac{P_{bat}\left(k\right)·\Delta t}{M_{bat}·N_{bat}·E_{bat}·3.6\times {10}^6}}$$

(1)

Here, $So{C}_{bat}\left(k\right)$ is the SoC for the HE and HP cells at time instance k. $P_{bat}\left(k\right)$ are the power delivered from HE and HP cells [W], $\Delta t$ is the sampling time of the discrete time system. $N_{bat}$ is the number of parallel module strings; $M_{bat}$ is the number of cells connected in series within a string; and $E_{bat}$ is the nominal energy of a single cell.

Remark 1.

The symbol $So{C}_{bat}\left(k\right)$ is a placeholder and must be read separately as $So{C}_{HE}\left(k\right)$ and $So{C}_{HP}\left(k\right)$; the same convention applies to the other battery-indexed quantities below. Any variable using the generic subscript “bat” (e.g., $P_{bat}$, $V_{bat}$, $I_{bat}$, $M_{bat}$, $N_{bat}$, $E_{bat}$) denotes either the HE or the HP quantity.

• Voltage Model:

The voltage of the HE and HP strings varies as a function of the SoC, described by the following model:

$$V_{bat}\left(k\right)=M_{bat}·f_{OC{V}_{bat}}\left(SoC\left(k\right)\right)$$

(2)

where $V_{bat}\left(k\right)$ is the total pack voltage (V) of the HE or HP stack at step k, while $f_{OC{V}_{bat}}$ represent the Open Circuit Voltage (OCV) vs. SoC empirical curve of HE and HP cells. This curve is available in the cell manufacturer’s datasheet or can be experimentally obtained.

• Current Model:

The current through the HE and HP cells is defined based on the power provided by the battery and the battery voltage:

$$I_{bat}\left(k\right)={\displaystyle \frac{P_{bat}\left(k\right)}{V_{bat}\left(k\right)}}$$

(3)

where $I_{bat}\left(k\right)$ are the currents drawn from the HE and HP battery packs [A]. Its admissible range is limited by the cell current capability scaled by the number of parallel strings:

$$-N_{bat}·I_{cel{l}_{max}}\le I_{bat}\left(k\right)\le N_{bat}·I_{cel{l}_{max}}$$

(4)

By allowing both positive and negative current, intercharging is allowed. In certain scenarios, the system could benefit from power flow from one battery to the other battery type, for example, to recharge the high-power battery after providing an amount of peak power for a short duration of time.

For each power profile $P_d$ with a given initial state of charge of the high-power $So{C}_{H{P}_0}$ and high-energy $So{C}_{H{E}_0}$ battery, the optimal sizing problem is defined as:

$$\begin{array}{cc}\underset{N_{HE},M_{HE},N_{HP},M_{HP},P_{HE}\left(k\right),P_{HP}\left(k\right)}{\mathrm{minimize}}& C_{system}=N_{HE}·M_{HE}·C_{HE}+N_{HP}·M_{HP}·C_{HP}\\ & \\ \mathrm{subject}\mathrm{to}:& P_d\left(k\right)=P_{HE}\left(k\right)+P_{HP}\left(k\right),\\ & \left(1\right),\left(2\right),\left(3\right),\left(4\right),\\ & So{C}_{HE}\left(1\right)=So{C}_{H{E}_0}\\ & So{C}_{HP}\left(1\right)=So{C}_{H{P}_0}\\ & So{C}_{HP}\left(k\right)\in [So{C}_{min},So{C}_{max}],\\ & So{C}_{HE}\left(k\right)\in [So{C}_{min},So{C}_{max}],\\ & \forall k\in [1,N_{points}]\\ & N_{HP},M_{HE},N_{HP},M_{HE}\in \mathbb{Z}\ge 0\end{array}$$

(5)

$C_{HE}$ and $C_{HP}$ are the cost of a single high-energy and high-power cell. $P_{HE}\left(k\right)$ and $P_{HP}\left(k\right)$ is the power provided by, respectively, the high-energy and high-power battery at time step k. $So{C}_{min}$ is the minimum allowed SoC, taken to be 10%, whereas $So{C}_{max}$ is the maximum SoC, taken to be 90 %. $N_{points}$ is the number of data points of the load profile. Note that it would be easy to modify the optimization problem to minimize the weight or volume, by replacing $C_{HE}$ and $C_{HP}$ for the mass or volume for a single cell.

This optimization allows to evaluate different hybrid battery sizing scenarios. Based on the evaluation of several thousands of scenarios, rules of thumb can be extracted.

3.1. Example for a Single Load Profile

To demonstrate the effectiveness of the proposed cost-optimal sizing methodology, we consider a representative power demand profile $P_d\left(k\right)$. The profile includes both high-energy and high-power demands, simulating a realistic use case such as for large construction vehicles. The nominal system voltage is considered to be 800 volt. The SoC constraints force the system to stay within 90% SoC and 10% SoC. The optimal system consists of 21 parallel strings of HE-cells ($N_{HE}$), where each string consists of 215 cells ($M_{HE}$), and 9 parallel strings of HP-cells ($N_{HP}$), where each string consists of 347 cells ($M_{HP}$). This results in a cost reduction of approximately 33% compared to a monotype solution.

Figure 2 plots the power profile of both the HE and HP battery. As can be seen, the HE battery provides the base load, whereas the HP battery takes up the peaks. Additionally, it can be seen how the SoC and the battery voltage evolve, and how the current stays under the maximum C-rate of the battery.

As can be seen, the resulting power split between HE and HP batteries ensures that the high-power battery handles short bursts of high demand, while the high-energy battery provides the baseline energy supply. The SoC trajectories remain within the defined bounds, and current constraints are respected throughout the profile.

3.2. Web Application

This code is also implemented in an online web application that performs optimal sizing for different load profiles without excessive waiting time for the user. This web application can be found via the publicly accessible link: https://battery.flandersmake.be/ (accessed on 22 September 2025). To size a hybrid battery in this application, four steps need to be taken, as shown in Figure 3. First, the user needs to select whether they want to size a classic monotype battery system, or a hybrid battery system. In a second step, the user needs to generate or upload a load profile. In a third step, the user needs to select the cell types. Finally, the user can start the optimization. After a few seconds, the optimal sizing is presented. Different figures show how the battery behavior under the given load profile can be selected with a dropdown menu. The results can also be downloaded as an Excel file.

4. Results

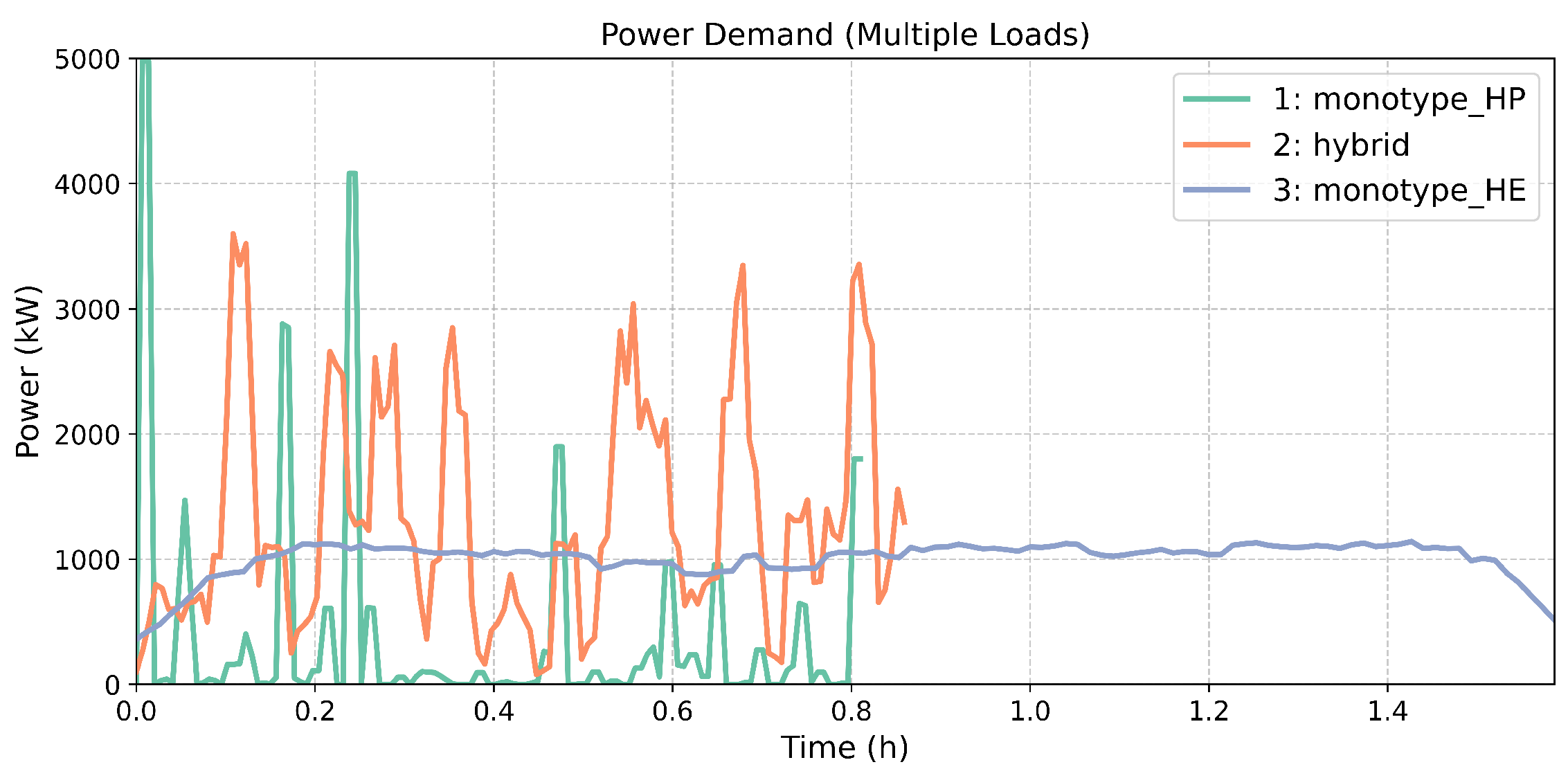
4.1. Load Profiles and Rules of Thumb

To evaluate HBESS sizing under a wide variety of scenarios, a computational framework was developed to generate synthetic load profiles that adhere to predefined energy and peak power targets. The optimal sizing problem defined by (5) was solved for 10,000 load profiles, with an energy content ranging from 10 to 2000 kWh and a peak power from 10 to 6000 kW. The generation process involves randomized sampling of the profile duration, average power, and variability characteristics within specified bounds. For each target combination, the algorithm iteratively constructs candidate profiles by applying Gaussian noise and smoothing operations to emulate realistic load profile behavior. The time vector is dynamically scaled to ensure the total energy content aligns with the target value. Profiles are evaluated against tolerance thresholds for both energy and peak power, and the best-fitting instance is retained after a bounded number of attempts. This method enables the creation of a diverse and controlled dataset of load profiles suitable for evaluating hybrid battery sizing for a wide variety of scenarios.

Figure 4 presents the possible weight, cost, and volume reduction for the cost-optimized HBESS as a function of the load profile energy content and load profile peak power for the 10,000 synthetic load profiles, compared to the best monotype HE or monotype HP solution. The monotype (single chemistry) solutions can also be obtained by solving (5), by constraining the number of cells of one type to zero. It is clear that three different zones can be identified. For load profiles with small energy content and high peak power, the optimal HBESS solution is identical to a monotype solution with HP batteries alone. This zone is marked by number (1). In the second zone (2), where both energy and power requirements are important, a hybrid battery will result in significant cost, mass, and volume savings. In the last zone (3), the energy requirement is dominant, and the optimal HBESS solution will be equal to a monotype HE solution. Further on in this work, equations will be derived to automatically derive these different zones as a function of the cell parameters. Figure 5 shows three different load profiles, one of each zone, that are marked on each of the previous plots. The monotype HP battery use case has high power peaks in the load profile, with limited energy content. The monotype HE use case has high energy content, with limited power peaks. The hybrid battery use case is in between these scenarios.

As can be seen, there are three clear zones in these plots. A zone where a monotype HP battery is favorable, a zone where an HBESS is best, and a zone where a monotype HE is optimal. These zones are separated by a linear line in the plot that is a function of the energy content and peak power of the load profile. The key parameter in evaluating the suitability of hybridization is therefore the peak power-to-energy content ratio (P/E ratio) of the load profile. This ratio, expressed in units of C-rate (1/h), reflects the intensity of power demand relative to the energy capacity required. The following rules of thumb can be derived:

• Load profile C-rate < 1.5 C: The energy requirement is dominant, with relatively low power demands. In such cases, a single HE battery can also efficiently meet the peak power requirements without the need for a high-power supplement. Hybridization will introduce unnecessary complexity and cost. Since the SoC limits are defined between 10% and 90%, only 80% of the battery is effectively used, resulting in a value of 1.2/0.8, which equals 1.5. The generalized equation of the line that approximates the boundary between an optimal monotype HE solution and optimal HBESS solution therefore is:

  $$y_{\mathrm{HE}\mathrm{bound}}=E_{load}·\left({\displaystyle \frac{c_{\mathrm{rate},\mathrm{HE}}}{{\mathrm{SoC}}_{\mathrm{range}}}}\right)$$

  (6)

  with $E_{load}$ the energy content of the load profile, $c_{\mathrm{rate},\mathrm{HE}}$ the C-rate of the HE battery, and ${\mathrm{SoC}}_{\mathrm{range}}$ the useful range of the battery cells, in this work taken as equal to 80%.
• Load profile C-rate > 6.25 C: The load profile is highly power-intensive, often characterized by short-duration, high-current pulses. Here, an HP battery alone will suffice, as the energy demand is minimal and can just be provided by the HP battery. The generalized equation of the line that approximates the boundary between an optimal monotype HP solution and optimal HBESS solution therefore is:

  $$y_{\mathrm{HP}\mathrm{bound}}=E_{load}·\left({\displaystyle \frac{c_{\mathrm{rate},\mathrm{HP}}}{{\mathrm{SoC}}_{\mathrm{range}}}}\right)$$

  (7)

  with $E_{load}$, the energy content of the load profile, $c_{\mathrm{rate},\mathrm{HP}}$, the C-rate of the HP battery, and ${\mathrm{SoC}}_{\mathrm{range}}$, the useful range of the battery cells, in this work taken as equal to 80%.
• Load profile C-rate between 1.5 and 6.25 C: This intermediate regime represents a balanced demand for both energy and power. Hybrid systems excel in this range by dynamically allocating power delivery: the LTO battery handles transient peaks, reducing stress and degradation on the NMC battery, which, in turn, manages the bulk energy supply. The cost reduction of a hybrid battery is at its maximum where the cost of a monotype HP and monotype HE battery would be approximately equal. This can be formulated as:

  $$y_{\min \cos \mathrm{t}}=E_{\mathrm{load}}·\left({\displaystyle \frac{{\cos \mathrm{t}}_{\mathrm{HP},\mathrm{kWh}}}{{\mathrm{SoC}}_{\mathrm{range}}·{\cos \mathrm{t}}_{\mathrm{HE},\mathrm{kWp}}}}\right)$$

  (8)

  with $E_{load}$, the energy content of the load profile, ${\cos \mathrm{t}}_{\mathrm{HP},\mathrm{kWh}}$, the cost of the HP battery per kWh, ${\cos \mathrm{t}}_{\mathrm{HE},\mathrm{kWp}}$, the cost of the HE battery per kWp, and ${\mathrm{SoC}}_{\mathrm{range}}$, the useful range of the battery cells, in this work taken as equal to 80%.

These three lines are shown in Figure 6, which clearly mark the zone where an HBESS system will lead to a cost saving, as a function of the cell parameters. The line that represents the lower bound $y_{\mathrm{HE}\mathrm{bound}}$, defined by (6), is shown by the cross markers in Figure 6. The line that represents the upper bound $y_{\mathrm{HP}\mathrm{bound}}$, defined by (7), is marked by the triangular markers in Figure 6. The line that represents the minimal cost $y_{\min \cos \mathrm{t}}$, as defined by (8), is shown by the dotted line in Figure 6.

These boundaries ($y_{\mathrm{HE}\mathrm{bound}}$ and $y_{\mathrm{HP}\mathrm{bound}}$) enable quick assessment of load profiles, facilitating the identification of cases where hybridization is likely to offer cost advantages, and can serve as a practical rule of thumb for early-stage system evaluation. Next to that, the line $y_{\min \cos \mathrm{t}}$ helps to identify, for a given combination of a HE and HP cells, if we are close to the maximal possible cost reduction compared to a monotype BESS.

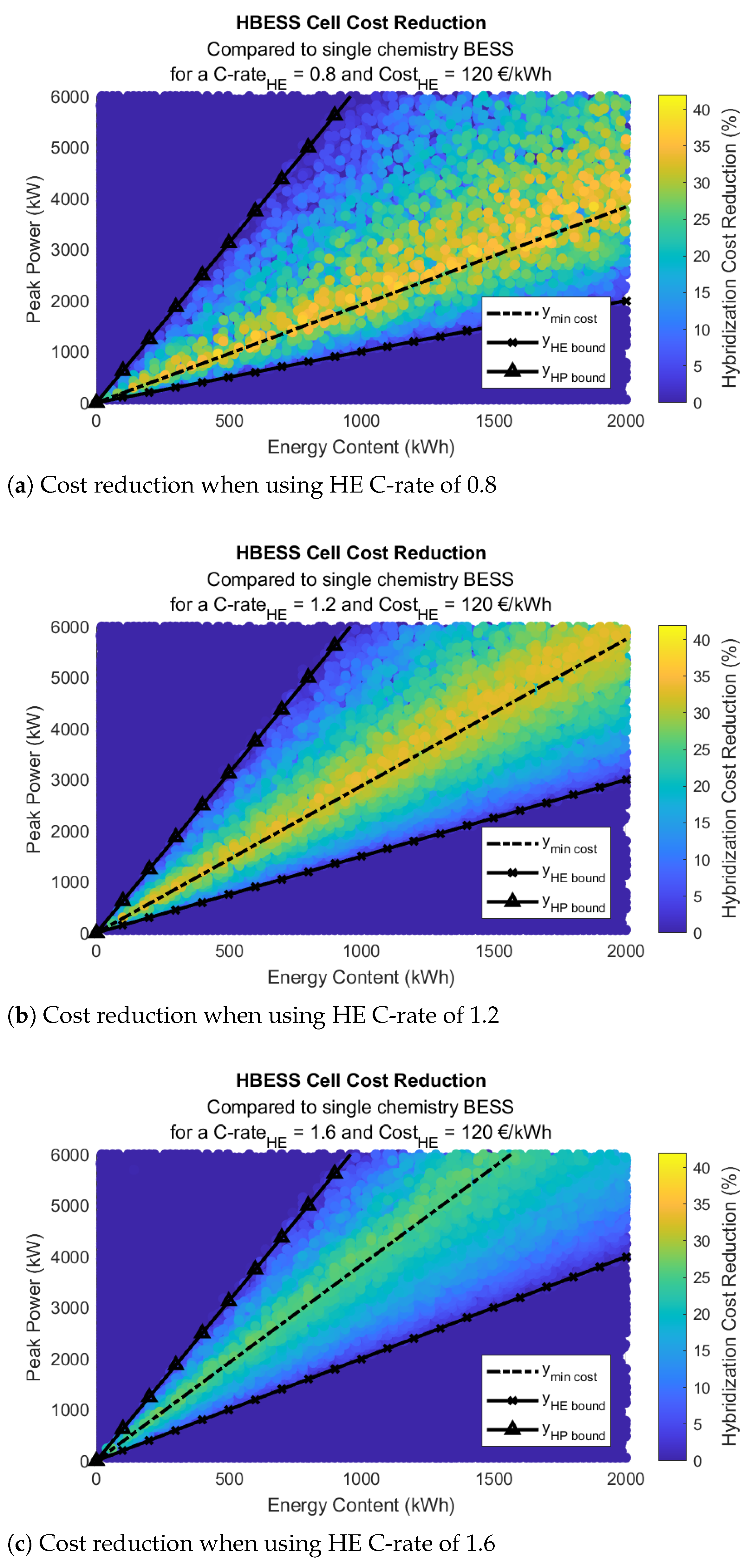
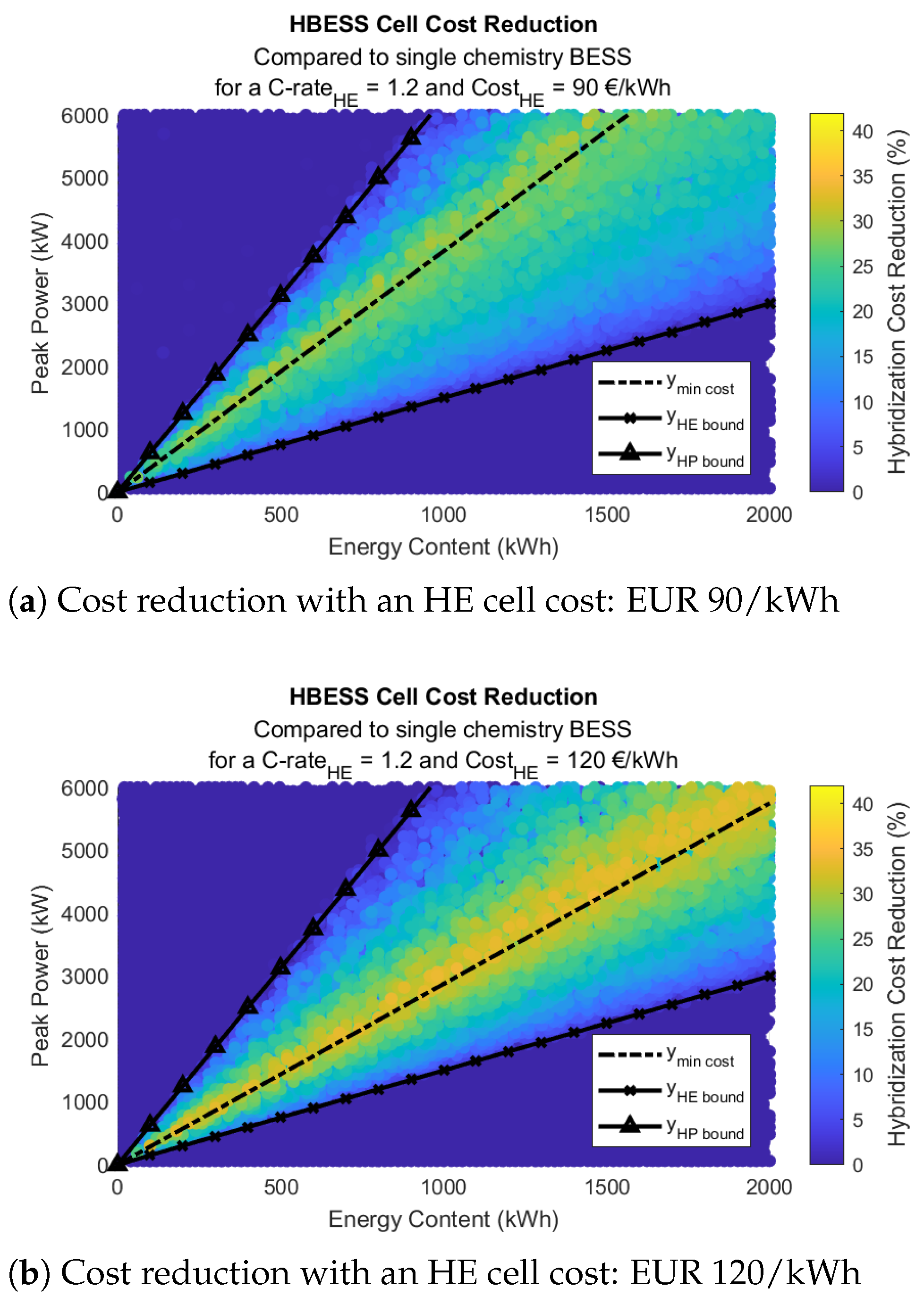
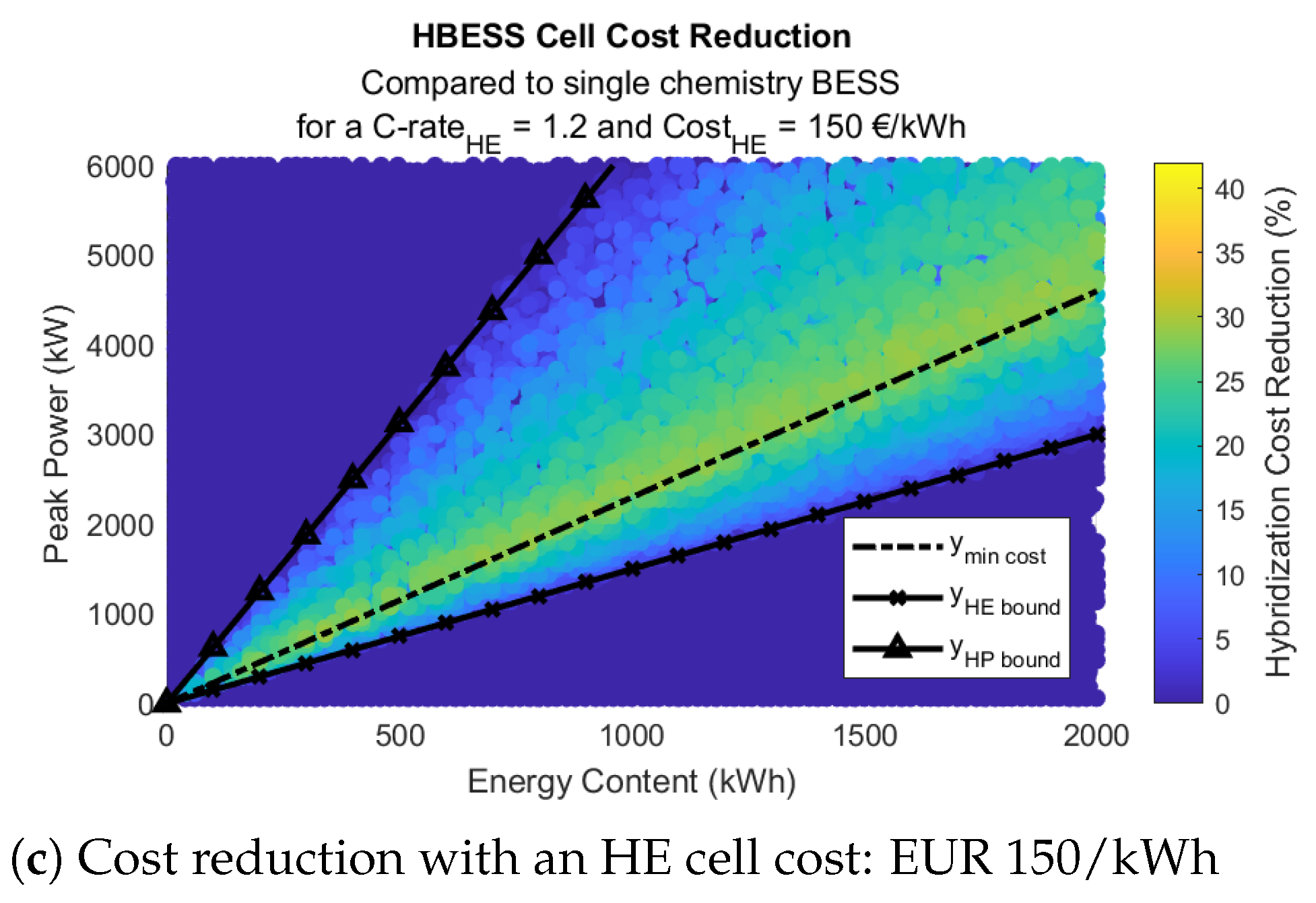
4.2. Sensitivity Analysis

Several cell parameters can affect the optimal sizing of an HBESS. Therefore, we change both the C-rate and the cost of the cells and verify the defined boundaries for different parameters. This also allows to generalize the conclusions to other battery types beyond NMC and LTO that might have different cost or C-rate.

4.2.1. Sensitivity to the C-Rate

To prove the different definitions of $y_{\mathrm{HP}\mathrm{bound}}$, $y_{\mathrm{HE}\mathrm{bound}}$, and $y_{\min \cos \mathrm{t}}$, the simulations are compared for a C-rate of the HE battery of 0.8 C, 1.2 C, and 1.6 C. For each of these C-rates, 10,000 load profiles have been optimized. The cost savings as a function of the load profile energy content and peak power are visualized in Figure 7, for three different HE C-rates. As can be seen, the analytical equations of (6), (7), and (8) remain valid for the different C-rates. Note that the slope of $y_{\mathrm{HE}\mathrm{bound}}$ changes, as could be expected from Equation (6). The C-rate of the HE-battery does not affect the slope of the $y_{\mathrm{HP}\mathrm{bound}}$.

To support early-stage design decisions,

Table 2. Ratio of peak power-to-energy content of a load profile that will lead to a cost reduction by an HBESS battery for varying HE and HP battery C-rates.

C-Rate HE	C-Rate HP	Ratio Peak Power-to-Energy Content for HBESS Cost Reduction
0.8	4.0	1.00–5.00
0.8	5.0	1.00–6.25
0.8	6.0	1.00–7.50
1.2	4.0	1.50–5.00
1.2	5.0	1.50–6.25
1.2	6.0	1.50–7.50
1.6	4.0	2.00–5.00
1.6	5.0	2.00–6.25
1.6	6.0	2.00–7.50

summarizes the sensitivity of HBESS cost-effectiveness to varying C-rates of HE and HP battery cells. The table presents the range of load profile peak power-to-energy content ratios for which hybridization is expected to yield cost benefits, based on the analytical boundary conditions derived. As shown, increasing the C-rate of either battery type shifts the boundaries of the hybridization zone, providing a practical rule of thumb for identifying when a hybrid configuration is likely to outperform monotype solutions. As an example, for an HE battery with a C-rate of 1.2 C and an HP battery with a C-rate of 5 C, hybridization is expected to be cost-effective for load profiles with peak power-to-energy ratios between 1.5 C and 6.25 C. Consider a tug boat with an energy content requirement of 400 kWh and a peak power of 1600 kW. The peak power-to-energy content ratio is 4 C, which lies within the range of 1.5 C to 6.25 C, indicating that a hybrid battery system would provide cost savings over a monotype solution. On the other hand, consider an agricultural vehicle with an energy requirement of 400 kWh, but a peak power limitation by the drivetrain of 200 kW. This results in a ratio of 0.5 C, which is below the lower boundary of 1.5 C. In this case, a monotype HE battery would be more cost-effective than a hybrid system.

4.2.2. Sensitivity to the Cell Cost

To prove the different definitions of $y_{\mathrm{HP}\mathrm{bound}}$, $y_{\mathrm{HE}\mathrm{bound}}$, and $y_{\min \cos \mathrm{t}}$, the simulations are compared for a different cost of the HE battery per kWh for a fixed C-rate of 1.2 C, respectively, a cost of EUR 90/kWh, EUR 120/kWh, and EUR 150/kWh. Because the C-rate is fixed, also the cost per kWp changes. For each of these cost levels, 10,000 load profiles have been optimized. The cost savings of the HBESS compared to a monotype solution as a function of the load profile energy content and peak power are visualized in Figure 8 for the three different cost levels. As can be seen, the analytical equations of (6), (7), and (8) remain valid for the different C-rates. Note that the slope of $y_{\mathrm{HE}\mathrm{bound}}$ changes, as could be expected from Equation (6). The cell costs do not impact the boundaries of the zone in which an HBESS is favorable over a monotype solution, as long as the HE battery remains cheaper per kWh and the HP battery remains cheaper per kW peak.

5. Discussion

The rules of thumb defined by the analytical equations of (6), (7), and (8) offer a practical shortcut for engineers and system designers during the early stages of hybrid battery system development. Instead of running full-scale optimization routines, which can be computationally intensive and require detailed input data, designers can use the derived boundary equations to quickly assess whether hybridization is likely to yield cost benefits for a combination of HE and HP battery cells. By evaluating the peak power-to-energy ratio of a given load profile, one can determine whether a monotype HE, monotype HP, or hybrid configuration is most suitable. This enables rapid screening of candidate applications and supports informed decision-making before committing to detailed simulations or hardware prototyping. The sensitivity analyses further reinforce the robustness of the proposed rules. Varying the C-rate and cost parameters of the cells showed predictable shifts in the hybridization boundaries, confirming the analytical relationships. This shows that the methodology can be extended to other chemistries beyond NMC and LTO, if the relevant cell parameters are known.

6. Conclusions and Future Work

This work introduces a fast and flexible optimization framework for sizing hybrid battery systems, enabling both detailed cost-optimal design and quick feasibility assessments through derived rules of thumb. The study confirms that hybridization is most effective for applications with moderate power-to-energy ratios, where neither HE nor HP batteries alone are optimal. A key contribution is the definition of boundary lines—based on cell parameters—that delineate when a monotype HE, monotype HP, or hybrid battery configuration is most cost-effective. These boundaries allow for rapid evaluation of load profiles, making it easy to determine whether hybridization is likely to yield cost benefits. Future work will focus on extending the methodology to include degradation modeling and integration with hybrid energy management strategies.