A Novel Approach to Day-Ahead Forecasting of Battery Discharge Profiles in Grid Applications Using Historical Daily

Abstract

This paper presents a day-ahead forecasting approach for discharge profiles of a 0.5 MW battery energy storage system connected to the power grid, utilizing historical daily discharge profiles collected over one year to capture key operational patterns and variability. Two forecasting techniques are employed: a Kalman filter for dynamic state estimation and Holt’s exponential smoothing method enhanced with adaptive alpha to capture trend changes more responsively. These methods are applied to generate next-day discharge forecasts, aiming to support better battery scheduling, improve grid interaction, and enhance overall energy management. The accuracy and robustness of the forecasts are evaluated against real operational data. The results confirm that combining model-based and statistical techniques offers a reliable and flexible solution for short-term battery discharge prediction in real-world grid applications.

1. Introduction

Battery energy storage systems (BESSs) play a critical role in modern power grids by providing flexibility, supporting renewable integration, and enhancing grid stability. As electricity generation from intermittent sources like solar and wind continues to grow, the need for dynamic storage solutions becomes increasingly important. BESS can shift energy temporally, mitigate peak demand, and offer ancillary services such as frequency regulation or load balancing [1]. However, the efficient operation of such systems depends heavily on accurate forecasting of their charge and discharge behaviour. In grid-connected scenarios, day-ahead prediction of battery activity is essential for effective scheduling, market participation, and ensuring that storage assets are used optimally. This paper addresses the challenge of day-ahead discharge forecasting by employing historical operational data and adaptive modeling techniques [2]. Accurate day-ahead forecasting of battery discharge is vital for maximizing the economic and operational benefits of energy storage systems within the grid. Precise predictions enable better scheduling of charging and discharging cycles, allowing operators to respond effectively to market price signals, optimize participation in energy and ancillary service markets, and avoid penalties associated with forecast errors. Moreover, accurate forecasts help ensure system reliability by allowing grid operators to plan for demand fluctuations and maintain reserve margins [3,4]. Inaccurate or overly conservative forecasts can lead to suboptimal use of storage capacity, missed revenue opportunities, or even contribute to grid instability. By improving forecast precision, battery operators can enhance system responsiveness, reduce operational costs, and increase the overall efficiency and value of BESS in grid-connected environments [5,6,7]. This study’s primary contribution is not a new forecasting algorithm, but rather a systematic evaluation of two well-established and practically relevant methods under different grid conditions. Unlike previous research that often considers either high-accuracy machine learning models or traditional statistical approaches in isolation, this work emphasizes the balance between accuracy, robustness, and computational efficiency, offering practical insights for real-world BESS operation.

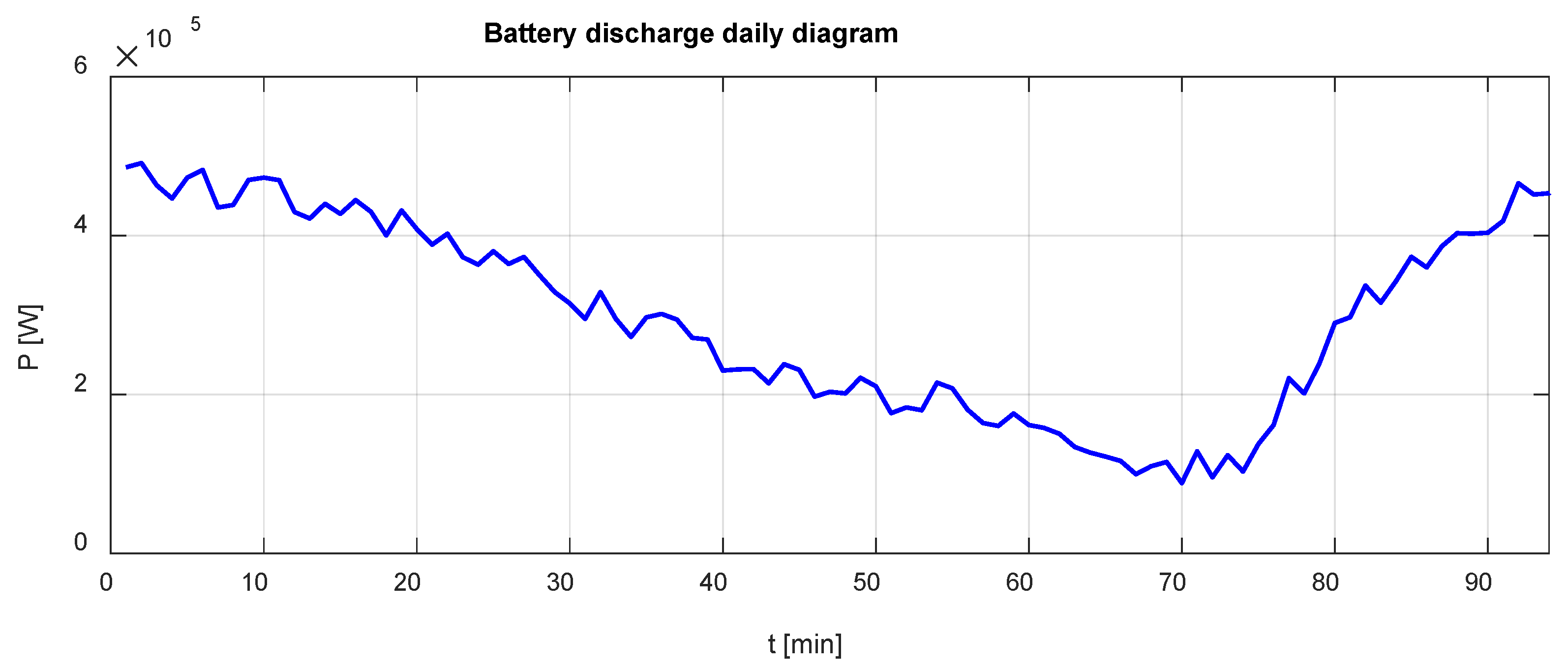
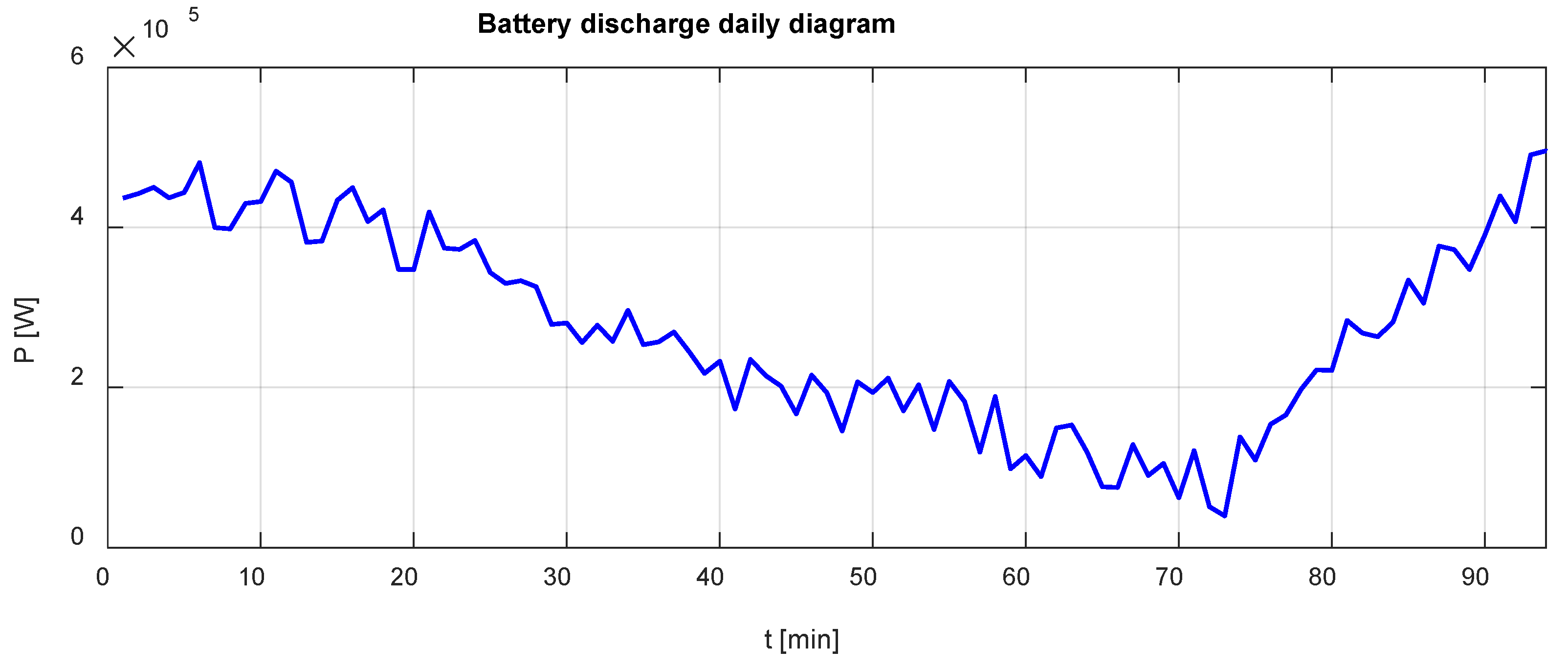
2. Data Description and Preprocessing

The battery system analysed in this study is a grid-connected lithium-ion energy storage unit with a nominal power capacity of 0.5 MW. It is installed at a substation operating at 110 kV, allowing it to interact directly with the high-voltage distribution grid. The system primarily supports local grid stability and optimizes energy flows in response to market and operational signals. The battery is managed through an automated control system that regulates its charging and discharging behaviour based on real-time grid conditions and predefined strategies [8,9,10]. Over the course of one year, the system’s discharge data was recorded at regular intervals, resulting in a comprehensive set of daily discharge profiles. These profiles reflect various operating modes influenced by seasonal demand patterns, grid requirements, and external factors such as energy prices or renewable generation availability. This historical dataset serves as the foundation for developing and validating the forecasting methods presented in this work.

The dataset used in this study consists of daily discharge diagrams representing the battery’s power output over 24 h periods, recorded at fixed time intervals. Each diagram captures the dynamic behaviour of the battery in response to grid demands and control signals throughout the day. The raw data, originally sampled at one-minute resolution, was aggregated into 15 min intervals to reduce noise and computational complexity while preserving key operational patterns. Prior to modelling, the data underwent preprocessing steps including outlier removal, handling of missing values, and normalization to ensure consistency across the dataset. Each day was treated as an individual time series, forming a matrix of daily profiles spanning one full year. These prepared diagrams were then used as input for the forecasting models, enabling the system to learn from historical discharge behaviour and make informed day-ahead predictions [11,12,13,14].

3. Forecasting Methodology

To accurately predict the day-ahead discharge behaviour of battery energy storage systems (BESS), this study employs two complementary time series forecasting approaches: the Kalman filter and Holt’s linear trend method with adaptive smoothing. In the field of time series forecasting, a wide range of methods has been applied, including statistical approaches such as ARIMA and SARIMA, as well as advanced machine learning models like recurrent neural networks (e.g., LSTM, GRU) or hybrid approaches combining state estimation with neural predictors [15,16]. While these methods can achieve high prediction accuracy, they are often computationally demanding, require extensive parameter tuning, and are not always well suited for real-time grid applications where robustness and simplicity are equally important.

Against this background, the Kalman filter and Holt’s model were selected for their ability to model dynamic, time-dependent processes while remaining computationally efficient and relatively easy to implement in practice. The Kalman filter is particularly effective in noisy environments, providing recursive state updates and reliable tracking of system dynamics. Holt’s method, extended with an adaptive smoothing parameter, allows for flexible modelling of linear trends and improves responsiveness to abrupt changes in discharge behaviour. By combining these two approaches, this study aims to achieve a balance between stability, adaptability, and practical applicability, offering a lightweight yet effective solution for day-ahead BESS discharge forecasting in real grid conditions.

3.1. Mathematical Formulation of the Kalman Filter

The Kalman filter is a recursive estimation algorithm widely used for real-time tracking and forecasting of dynamic systems. In the context of BESS discharge forecasting, it enables continuous estimation of the system’s state—specifically, the battery’s capacity or output—by optimally combining prior predictions with noisy measurements. The filter operates in two phases: a prediction step and a correction step, allowing it to adjust to real-world conditions and uncertainties.

Prediction step:

$${\widehat{C}}_{\mathrm{k}|\mathrm{k}-1} = {\widehat{C}}_{\mathrm{k}-1|\mathrm{k}-1} + u_{\mathrm{k}}$$

(1)

$$P_{\mathrm{k}|\mathrm{k}-1}=P_{\mathrm{k}-1|\mathrm{k}-1}+Q$$

(2)

Here, ${\widehat{C}}_{\mathrm{k}|\mathrm{k}-1}$ is the predicted capacity before measurement, $u_{\mathrm{k}}$ is the known change in capacity (e.g., from a control signal or schedule), and $P$ denotes the covariance of the estimation error [17,18].

Correction step:

$$K_{\mathrm{k}} = {\displaystyle \frac{P_{\mathrm{k}|\mathrm{k}-1}}{P_{\mathrm{k}|\mathrm{k}-1} + R}}$$

(3)

$${\widehat{C}}_{\mathrm{k}|\mathrm{k}}={\widehat{C}}_{\mathrm{k}|\mathrm{k}-1}+K_{\mathrm{k}} · (z_{\mathrm{k}}-{\widehat{C}}_{\mathrm{k}|\mathrm{k}-1})$$

(4)

$$P_{\mathrm{k}|\mathrm{k}}=\left(1-K_{\mathrm{k}}\right)\ast P_{\mathrm{k}|\mathrm{k}-1}$$

(5)

In this step, z_k is the observed discharge value, $R$ is the measurement noise covariance, $Q$ is the process noise covariance, and K_k is the Kalman gain, which determines how much the prediction is corrected based on new measurements. This method is particularly effective in systems where both the underlying process and the measurements are affected by noise, and it is well suited for adaptive day-ahead forecasting in dynamic environments [17,18].

3.2. Mathematical Formulation of the Holt’s Linear Model

Holt’s linear trend model is an extension of exponential smoothing that captures both the level and trend components of a time series. To enhance its responsiveness to abrupt changes in discharge behaviour, the model is extended with an adaptive smoothing parameter ${\alpha }_{\mathrm{t}}$, which adjusts based on the forecast error [19,20].

Level component:

$$l_{\mathrm{t}} = \alpha \ast y_{\mathrm{t}} + \left(1 - \alpha \right)\ast (l_{\mathrm{t}-1} + b_{\mathrm{t}-1})$$

(6)

Trend component:

$$b_{\mathrm{t}} = \beta \ast \left(l_{\mathrm{t}} - l_{\mathrm{t}-1}\right)+ \left(1 - \beta \right)\ast b_{\mathrm{t}}-1$$

(7)

Forecast:

$${\hat{\mathrm{y}}}_{\mathrm{t}+1} = l_{\mathrm{t}} + b_{\mathrm{t}}$$

(8)

where:

y_t—is the observed discharge value at time t;

l_t—is the estimated level (smoothed capacity);

b_t—is the estimated trend (rate of change);

ŷ_t+1—is the forecast for the next time step.

To make the model adaptive, the smoothing coefficient ${\alpha }_{\mathrm{t}}$ is dynamically adjusted using a function f based on the current forecast error:

$${\alpha }_{\mathrm{t}} =\max \left( a_{\min } , f\left(|y_{\mathrm{t}} - {\hat{\mathrm{y}}}_{\mathrm{t}}|\right)\right)$$

(9)

This mechanism increases the sensitivity of the model during periods of high prediction error, enabling quicker adaptation to changing battery discharge patterns [19,20,21,22,23,24].

4. Evaluation and Results

To evaluate the performance and robustness of the proposed forecasting methods, simulations were conducted under three controlled variability scenarios, reflecting different levels of daily discharge fluctuations. The simulations aimed to represent realistic operational changes in the battery’s daily discharge profiles while testing the adaptability and accuracy of the Kalman filter and Holt’s adaptive trend model.

4.1. Simulation Setup

The battery system, with a nominal capacity of 0.5 MW, was simulated over a one-year period using historical discharge data, into which artificial day-to-day variability was introduced. Three distinct scenarios were defined to reflect different operating conditions:

• Low Variability (±10 kW): Represents stable grid support with minimal changes in discharge between days.
• Moderate Variability (±50 kW): Simulates moderate fluctuations, possibly driven by seasonal renewable integration or variable load support.
• High Variability (±90 kW): Emulates highly dynamic operational environments such as price-driven arbitrage or response to volatile grid conditions.

Each scenario was constructed by modifying the maximum discharge level of each day by a random value within the defined bounds, relative to the previous day. This approach enabled us to stress-test the forecasting models under different rates of change while maintaining the temporal structure of actual operational data.

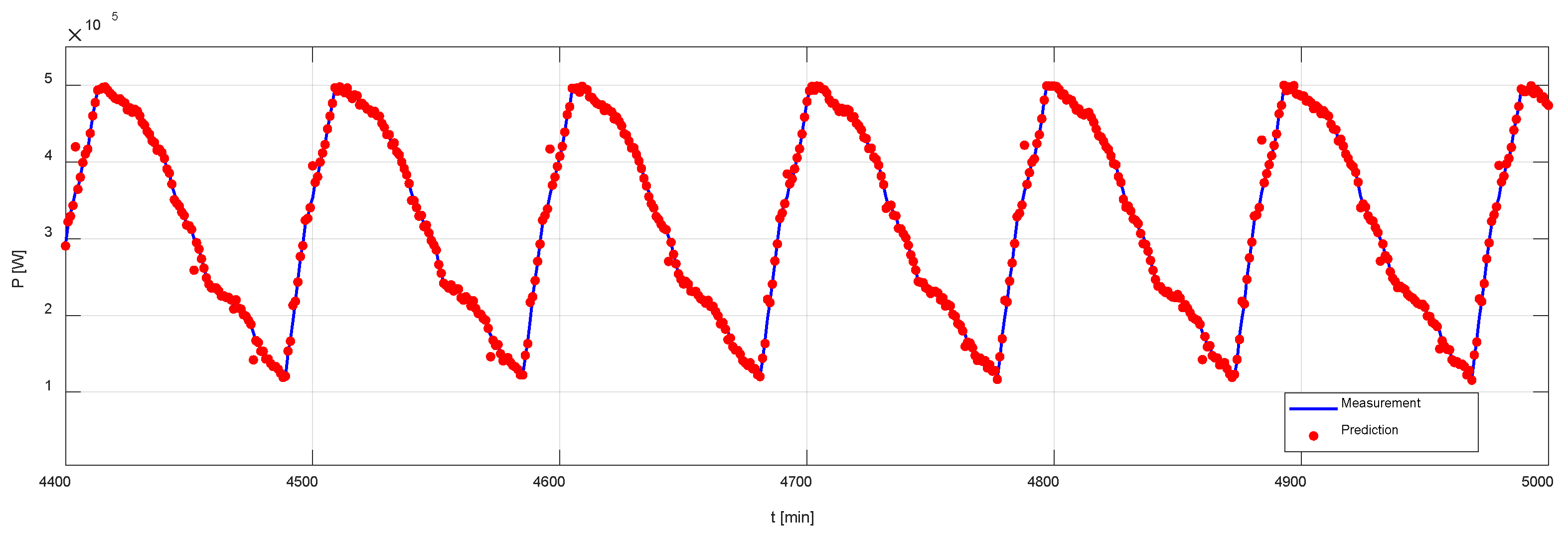
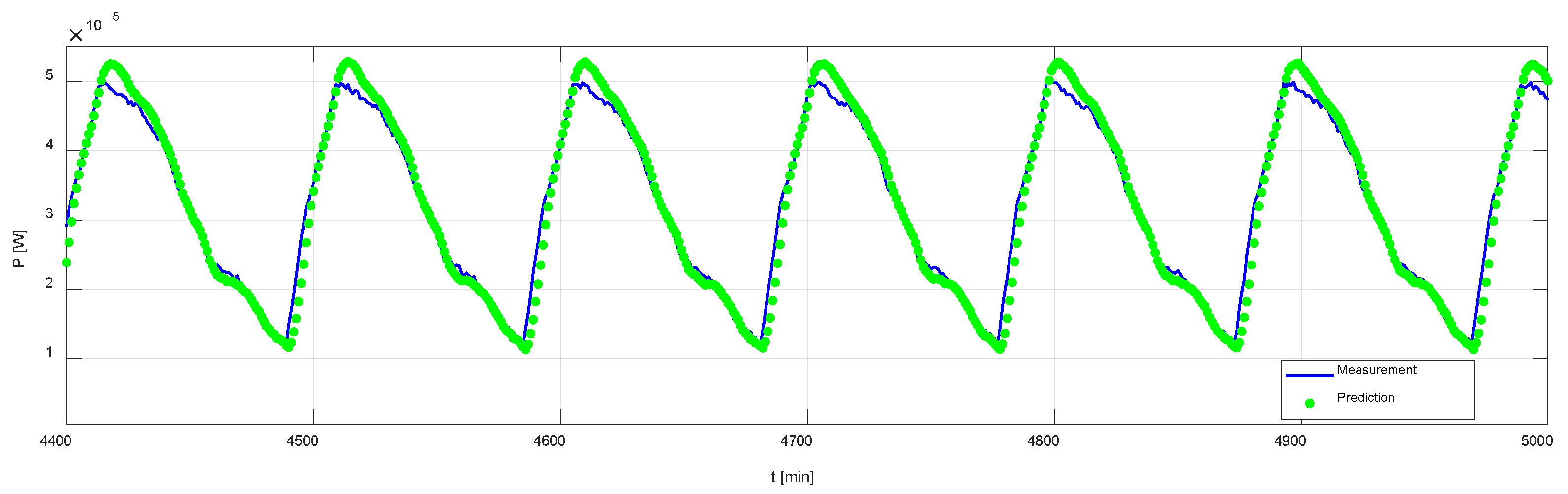
4.2. Simulation Results

To visualize and assess the accuracy of the forecasting models, a set of simulation plots was generated for each variability scenario. These figures present a comparison between the actual measured battery discharge and the predicted values produced by the Kalman filter and Holt’s adaptive trend model. By focusing on selected time intervals, the plots allow for a detailed inspection of model performance under varying operational conditions. The first scenario illustrates a low-variability case, where daily changes in discharge do not exceed ±10 kW. This baseline scenario serves to evaluate how well each model can capture and replicate stable daily discharge patterns with minimal fluctuations.

Figure 1 shows a typical daily battery discharge profile for a 0.5 MW system, where the power output gradually decreases throughout the day and then recovers. This curve illustrates a standard daily charge–discharge cycle under stable operating conditions with only minor fluctuations between days.

Figure 2 compares the actual measured discharge power with the forecast generated by the Kalman filter. The prediction closely follows the measured values, even when zoomed in over multiple consecutive days. This demonstrates that the Kalman filter effectively captures the daily discharge pattern in environments with minimal day-to-day variation.

Figure 3 presents the forecast produced by the Holt’s model with adaptive alpha. Here, as well, the predicted curve aligns very well with the measurements, with only minor deviations or delays occurring occasionally. In this low-variability scenario (±10 kW), Holt’s model also achieves high prediction accuracy.

To evaluate forecasting performance under moderately dynamic conditions, the second scenario introduces daily variations of up to ±50 kW in battery discharge. This level of variability represents a more realistic operating environment, where external factors such as fluctuating grid demand or renewable generation begin to influence the system more significantly. The following figures provide a visual comparison between measured discharge data and predictions from both the Kalman filter and Holt’s adaptive model, highlighting how each method responds to mid-range changes in the battery’s daily discharge pattern.

Figure 4 presents a daily battery discharge profile under moderate variability conditions, where discharge patterns fluctuate up to ±50 kW between consecutive days. The profile still follows a recognizable daily cycle, but includes visible noise and irregularities, reflecting more dynamic grid conditions compared to the low-variability scenario.

Figure 5 shows the performance of the Kalman filter in forecasting daily discharge during this scenario. Despite increased variability, the predicted values (orange) remain closely aligned with the actual measurements (blue), showing that the Kalman filter retains high accuracy and effectively smooths noise while adjusting to moderate changes in the discharge curve.

Figure 6 displays the prediction results using Holt’s adaptive model. Compared to the Kalman filter, Holt’s predictions show slightly larger deviations from the measured values, especially around peak and trough regions. Although the model tracks the general trend, the adaptive smoothing does not fully compensate for the increased variability, resulting in greater forecast errors. Overall, these plots illustrate that while both models can follow the daily discharge pattern under moderate variability, the Kalman filter continues to provide more accurate and stable predictions, whereas Holt’s model begins to show limitations in capturing the full extent of dynamic fluctuations.

To evaluate the robustness of the forecasting models under highly dynamic conditions, the third simulation scenario introduces a ±90 kW change in daily battery discharge values. This scenario simulates a more volatile grid environment, such as during extreme fluctuations in renewable generation or load demand. The following figures illustrate the system’s actual discharge behaviour and compare the prediction accuracy of the Kalman filter and Holt’s adaptive model under this high-variability setting.

Figure 7 shows the daily battery discharge profile with high variability. The discharge curve displays significant fluctuations and irregular dips throughout the day, reflecting rapidly changing system conditions and a more erratic power demand-response behaviour.

Figure 8 presents the Kalman filter’s forecasting performance under this scenario. Despite the increased noise and instability in the discharge profile, the Kalman filter manages to closely track the measured values, maintaining a consistent prediction pattern with minor deviations. Its recursive correction mechanism allows it to remain stable, though slightly conservative in reacting to sharp shifts.

Figure 9 displays the results of Holt’s adaptive model. While it generally follows the trend of the actual measurements, the prediction shows higher error margins compared to the Kalman filter. The model exhibits more noticeable overshooting and lagging, especially during steep changes, as it tries to adjust its smoothing parameters dynamically. These visual differences align with the quantitative evaluation, where Holt’s model produces a significantly higher error rate under high variability.

4.3. Evaluation Metrics

To quantify forecasting accuracy, the following standard time series evaluation metrics were used [2]:

• Mean Absolute Error (MAE);
• Root Mean Squared Error (RMSE);
• Mean Absolute Percentage Error (MAPE).

Table 1. Comparison of charging curve applications for the applied methods.

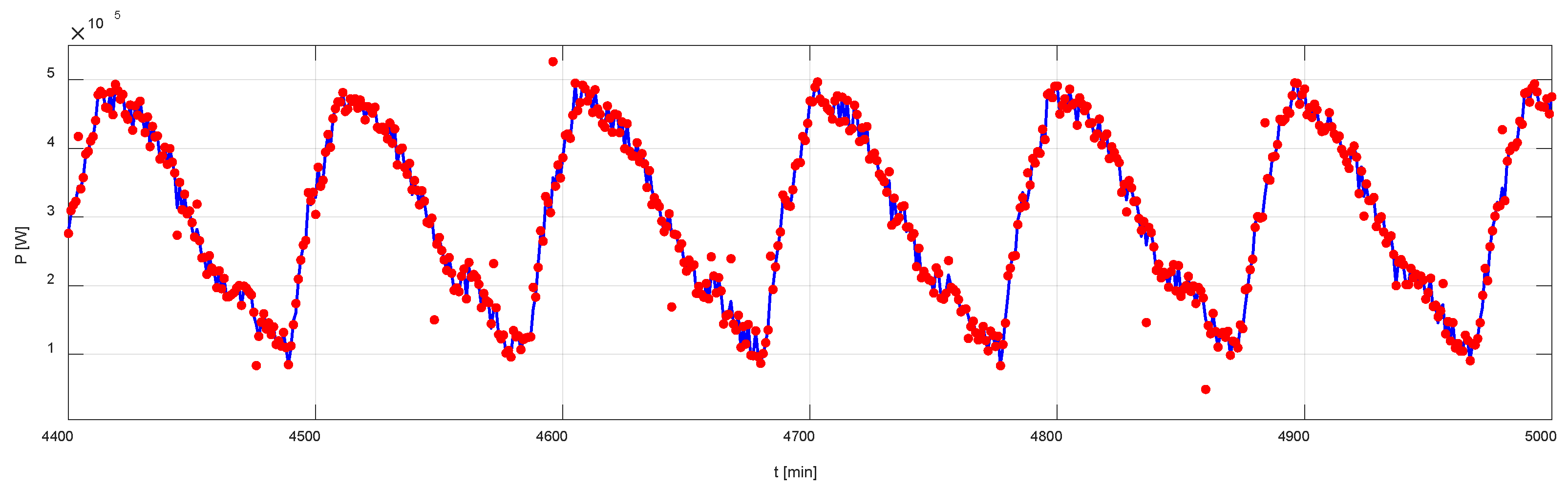
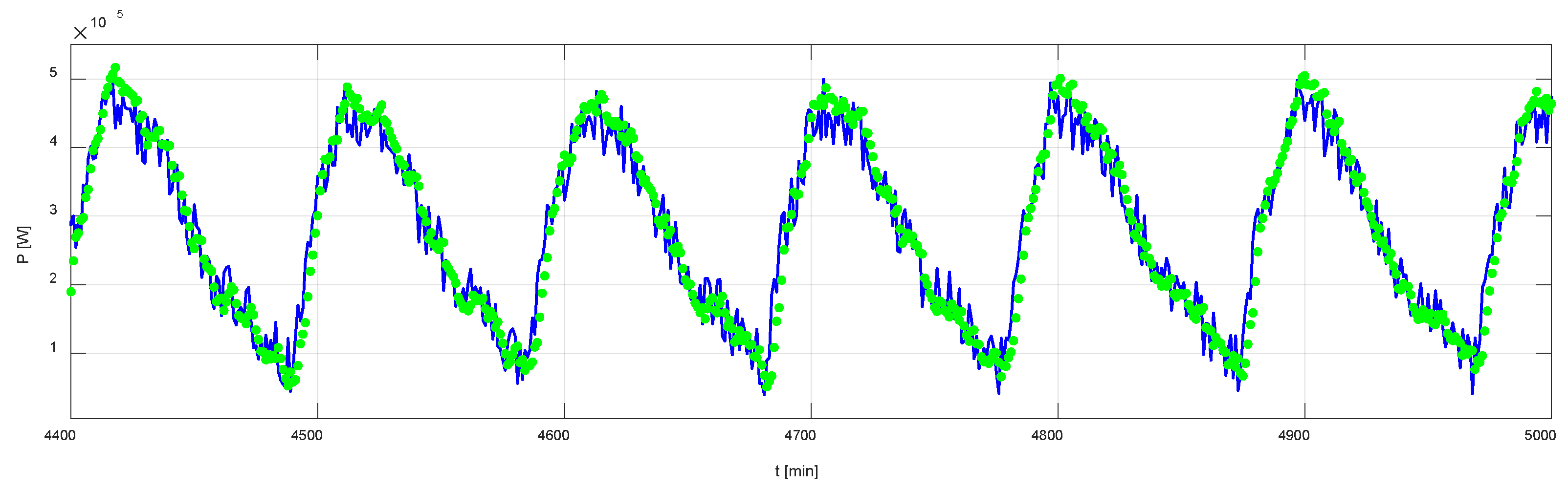
Variability Scenario	Method	MAE (kW)	RMSE (kW)	MAPE (%)
10 kW	Kalman	4.812	8.482	1.82
	Holt’s	15.559	22.205	5.26
50 kW	Kalman	23.146	29.326	8.73
	Holt’s	21.489	27.600	8.56
90 kW	Kalman	44.306	53.527	16.66
	Holt’s	30.389	37.196	14.21

presents a comparison of forecasting accuracy for the Kalman filter and Holt’s adaptive model across three battery discharge variability scenarios. The metrics used to assess performance are Mean Absolute Error ($MAE$), Root Mean Squared Error ($RMSE$) and Mean Absolute Percentage Error ($MAPE$).

$$MAE={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|y_i-\widehat{y_i}\right|$$

(10)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\sum }_{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(11)

$$MAPE={\displaystyle \frac{100}{n}}{\sum }_{i=1}^n\left|{\displaystyle \frac{y_i-\widehat{y_i}}{y_i}}\right|$$

(12)

where $y_i$ are the actual values and ${\widehat{y}}_i$ are the predicted values.

In the low variability scenario (±10 kW), the Kalman filter clearly outperforms Holt’s method, achieving an MAE of 4.812 kW and a MAPE of 1.82%, compared to Holt’s results of 15.559 kW MAE and 5.26% MAPE. This confirms the Kalman filter’s strength in stable operating conditions, where its recursive update process ensures precise tracking with minimal error. In the medium variability case (±50 kW), Holt’s model slightly outperforms the Kalman filter in terms of MAE (21.489 kW vs. 23.146 kW), despite the Kalman filter having a marginally higher MAPE (8.73% vs. 8.56%) and a higher RMSE. This suggests that Holt’s adaptive mechanism was able to slightly better capture the moderate fluctuations in discharge, but both models experienced increased error due to the greater unpredictability. In the high variability scenario (±90 kW), performance diverged more significantly. Kalman’s MAE rose to 44.306 kW and MAPE to 16.66%, while Holt’s MAE was 30.389 kW and MAPE 14.21%. Despite Kalman’s stability in noise handling, it lagged in responding to rapid fluctuations, allowing Holt’s model to better adapt under highly dynamic conditions.

5. Conclusions

This evaluation highlights that forecasting model selection should be based on the expected level of operational variability. The Kalman filter is highly reliable in low-variability environments, providing consistent, accurate predictions with low error margins. However, as variability increases, its conservative nature limits responsiveness, reducing accuracy. Conversely, Holt’s adaptive method becomes more advantageous in highly dynamic scenarios, owing to its flexible trend and level adjustment, enabling it to react more quickly to sudden shifts in discharge patterns. The presented approach improves battery discharge prediction accuracy, which, in turn, supports enhanced power grid stability. By enabling more reliable load balancing and energy storage management, this method contributes to the efficient integration of renewable energy sources and optimization of grid operations, offering practical benefits for modern power systems. An optimal strategy may involve hybrid or switching models that adapt forecasting techniques in real time, depending on recent variability trends—balancing stability with flexibility for improved overall system performance. In conclusion, the presented approach enhances battery discharge prediction accuracy and supports improved power grid stability.