Evaluating the Status of Lithium-Ion Cells Without Historical Data Using the Distribution of Relaxation Time Method

Abstract

In this paper, Distribution of Relaxation Time (DRT) analysis is presented as a powerful tool for understanding the aging mechanisms in lithium-ion batteries, with a focus on its application to estimating the State of Health (SOH). A novel parameter, the characteristic relaxation time, derived from DRT analysis, is introduced to enhance SOH estimation. By analyzing the ratio of the central relaxation time (τ) between the charge transfer and diffusion peaks, the battery status can be determined without the need for historical data. Experimental data from lithium-ion batteries, including 18650 cells and LR2032 coin cells, were examined until the end of their life. Nyquist and DRT plots across various frequency ranges revealed consistent aging trends, particularly in the charge transfer and diffusion processes. These processes appeared as shifting and merging peaks in the DRT plots, signifying progressive degradation. A polynomial equation fitted to the τ ratio graph achieved a high accuracy (Adj. R² = 0.9994), enabling reliable battery lifespan prediction. Validation with a Samsung Galaxy S9+ battery demonstrated that the method could estimate its remaining life, predicting a total lifespan of approximately 2100 cycles (compared to 1000 cycles already completed). These results confirm that SOH estimation is feasible without prior data and highlight the potential of DRT analysis for accurate and quantitative prediction of battery longevity.

1. Introduction

The widespread adoption of electric vehicles (EVs) has fueled extensive research into lithium-ion batteries (LIBs), which serve as their primary power source. Battery degradation is a focal point in this research due to its significant implications. Firstly, as LIBs age, capacity degradation and increased internal resistance diminish both the driving range and power capacity of EVs, leading to suboptimal driving experiences [1]. Secondly, various side reactions occur within LIBs during aging, causing internal structural damage and raising the risk of thermal runaway, ultimately resulting in potential safety hazards [2]. Battery management relies heavily on understanding the aging mechanism and a degradation model to estimate battery health based on historical data, optimize the present operating conditions, and predict future performance.

Beyond lithium-ion batteries, the electrification of transport encompasses a range of technologies, including battery electric vehicles (BEVs), hybrid electric vehicles (HEVs), and fuel cell electric vehicles (FCEVs). While BEVs that rely on LIBs dominate the current market due to their higher energy efficiency and rapidly declining costs, FCEVs have emerged as an alternative solution, offering extended driving ranges and faster refueling times. These two technologies are often considered competitors but can also play complementary roles depending on the application scenarios. BEVs are well suited to passenger cars and urban mobility, whereas FCEVs are particularly attractive for heavy-duty, long-haul transport where refueling speed and energy density are critical factors. Recent studies [3] underscore this complementary relationship and highlight that advances in both LIBs and fuel cell systems are essential for achieving the large-scale adoption of clean transportation. In this context, improving lithium-ion battery aging analysis and state of health estimation remains vital for enhancing the reliability and sustainability of BEVs, which currently represent the mainstream EV technology.

Battery aging analysis encompasses various levels of investigation, including factors influencing degradation, internal side reactions, degradation modes, and external effects [4,5]. Capacity fade and power fade are prominent external indicators of battery degradation and are often the primary focus of aging investigations and modeling [6]. Power fade, however, poses challenges in investigation, with the internal resistance frequently examined as a substitute [7]. Regarding degradation modes, battery aging mechanisms are commonly categorized as Loss of Lithium-Ion Inventory (LLI) and loss of anode/cathode active material (LAM), which are particularly important for battery management and online diagnosis [8,9,10].

Electrochemical Impedance Spectroscopy (EIS) spectra can provide substantial insights into the degradation processes occurring within LiBs [11,12]. By employing appropriate Equivalent Circuit Models (ECMs), which primarily consist of combinations of resistors and constant phase elements with specific physical interpretations [13,14], large volumes of real-time updated EIS data can be utilized effectively. This data can then be applied to various applications, such as predicting the temperature distribution within the battery [15], estimating the State of Charge (SOC) [16,17,18], assessing the State of Health (SOH) [19,20,21], and performing diagnostic assessments [22].

However, Nyquist plots of the EIS spectrum often appear as overlapping semicircles, which can introduce ambiguities into assigning clear physicochemical meaning [23,24]. For accurate analysis, the impedance features must be properly attributed to the corresponding electrode processes [25]. Direct equivalent circuit fitting or geometric estimation of the semicircle diameters can sometimes result in non-unique solutions and obscure important details regarding the underlying electrochemical mechanisms [26,27]. In contrast, Distribution of Relaxation Time (DRT) analysis, although derived from the same EIS data, provides a deconvoluted representation that separates overlapping processes and enhances interpretability.

To gain deeper insights into the internal behaviors of batteries, the Distribution of Relaxation Time (DRT) method has been introduced in several studies [28,29]. This method enables the observation of contact impedance, which is often difficult to describe using fractional-order models. It should be noted that high-frequency features in Nyquist spectra are frequently influenced by contact impedance rather than intrinsic electrochemical processes, as demonstrated in prior studies [30,31,32]. This complicates the interpretation of the equivalent circuit fits and further supports the use of the DRT, which can isolate ohmic and contact contributions from the genuine SEI, charge transfer, and diffusion processes. This paper employs DRT analysis to examine the status of LIBs in detail and further discusses the solution and optimization process for applying DRT to LIBs, addressing aspects that have not been clearly defined in previous research.

Even though DRT analysis is widely used to explain the aging mechanisms of LIBs, methods for estimating the SOH based on DRT analysis are rarely proposed. This limitation may arise because many parameters extracted from DRT analysis in previous studies do not exhibit a clear relationship with SOH. Several recent studies have applied DRT-based indicators for SOH estimation. For example, Iurilli et al. (2022) introduced a physics-based model that combines DRT-derived features to track degradation modes throughout the full lifetime of NMC811/graphite cells [33]. Another recent work, Onboard Health Estimation using DRT, employed DRT curves together with ML models to estimate the SOH across multiple cells and under varied operating conditions [34]. These approaches broadly demonstrate the potential of DRT for SOH estimation but often require either a suite of features or historical baseline data. By contrast, in this work, we propose the τ ratio (τ_ct/τ_diff), which serves as a single, history-independent parameter for SOH estimation, validated across different cell types and without the need for prior cycling history. Beyond the common parameters obtained through traditional DRT analyses, this paper introduces a new parameter called the characteristic relaxation time, which provides additional inputs for SOH estimation. Specifically, the center relaxation time ‘tau’ ratio of the charge transfer peak to the diffusion peak is introduced. Compared to our earlier works [31,32], which examined aging diagnostics and multi-parameter SOH estimation using DRT, the present study introduces a novel single parameter, the τ ratio between the charge transfer and diffusion peaks, that enables SOH estimation without historical data. Data extending up to the end of life (EoL) for LIBs was used to derive the ‘tau’ ratio graph. A polynomial curve was then fitted to this graph, enabling the determination of the battery status at any given time.

The structure of this paper is organized as follows: Section 2 describes the battery specifications and experimental conditions, including the use of Samsung Galaxy S9+ battery (Samsung Electronics Co., Ltd., Suwon, Republic of Korea) data to estimate battery status. The experimental conditions for the 18650 and coin cells are also discussed. Section 3 focuses on the DRT method, explaining how EIS data is deconvoluted and how individual peaks in the DRT plots are obtained. An analysis of DRT plots for the 18650 and two coin cells up to their EoL is examined. Section 4 extracts the DRT parameters and analyzes critical parameters for battery aging. It then compares the results of all cells based on the τ ratio and presents a fitted polynomial curve to determine the battery status without relying on historical data. Section 5 summarizes the findings and explores future research directions.

2. Battery Specifications and Experimental Conditions

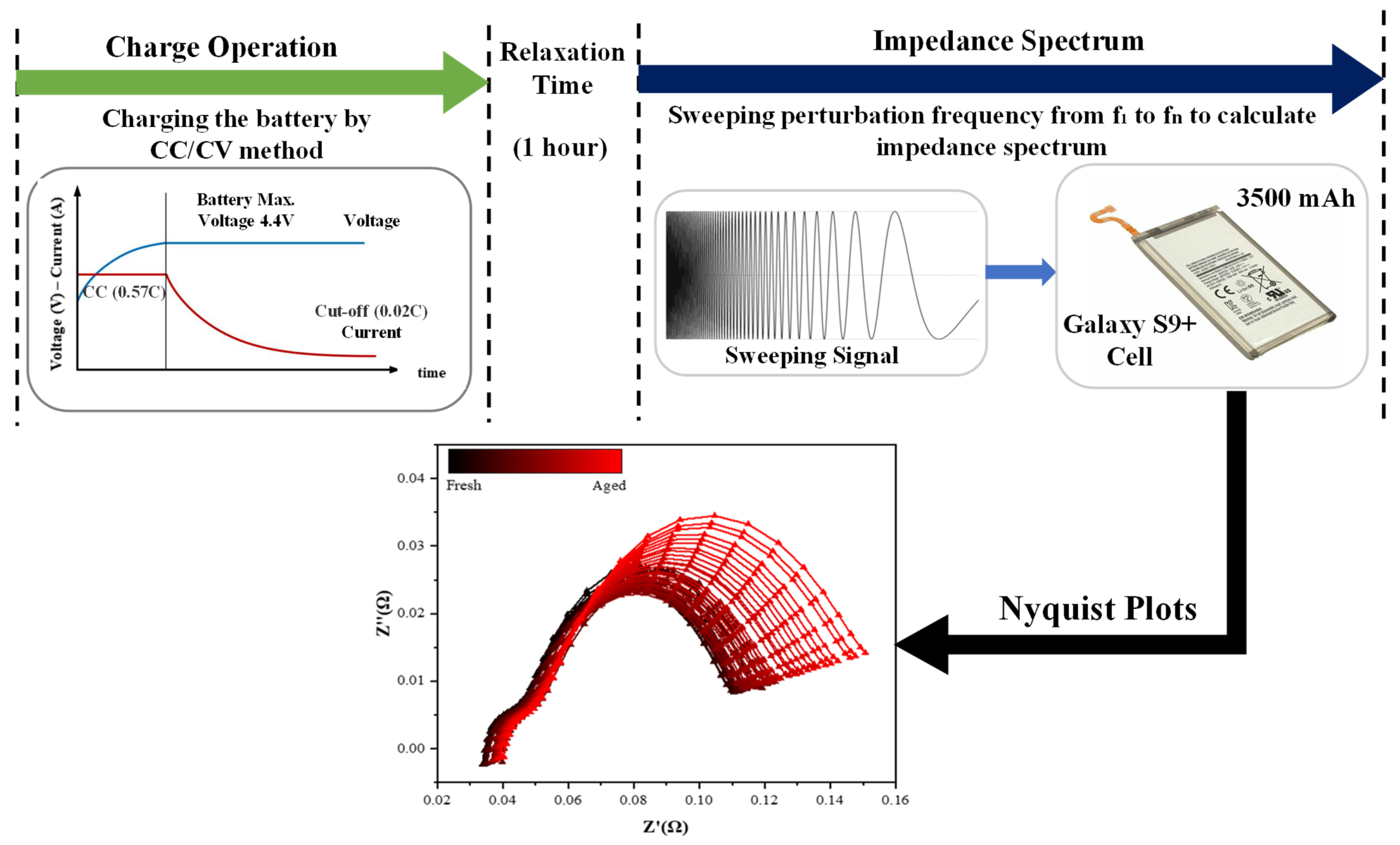
The aging test included LIBs sourced from the Samsung Galaxy S9+ smartphone and subjected to 1000 charge–discharge cycles at 25 °C. Capacity and impedance spectra were recorded every 20 cycles using HYSCLAB environmental chambers (HYSC Co., Ltd., Seoul, Republic of Korea) and WonATech WBCS3000 M2 (WonATech Co., Ltd., Seoul, Republic of Korea) and ZIVE MP2A equipment (WonATech Co., Ltd., Seoul, Republic of Korea). The EIS measurements for the Galaxy S9+ batteries were performed using a 100 mV perturbation in the frequency range of 0.1–4 kHz. The battery specifications are detailed in

Table 1. Specification of Samsung Galaxy battery.

Property	Value
Chemistry	LiNiCoAlO2/graphite
Type	Samsung Galaxy S9+
Capacity. max	3500 mAh
Nominal voltage	3.85 V

, and the aging test conditions are shown in Figure 1. A cylindrical 18650 LIB with a nominal capacity of 2500 mAh and a nominal voltage of 3.7 V was used. The battery was cycled at a constant temperature of 25 °C. Charge–discharge cycles were used with a constant current of 0.5C for both charging and discharging, with a one-hour rest period after each cycle. EIS measurements were conducted every 5 cycles using a 60 mV perturbation in the frequency range of 0.1 Hz to 1 kHz while maintaining the SOC at 100%. The data covered 1035 cycles, continuing until the battery reached its EoL.

The data used in this study was obtained from experiments conducted at the Cavendish Laboratory, the University of Cambridge, Cambridge, CB3 0HE, the UK [35], on 45 mAh Eunicell LR2032 Li-ion (Eunicell International Co., Ltd., Shenzhen, China) coin cells with LiCoO₂/graphite chemistry. A commercially available 45 mAh Eunicell LR2032 Li-ion coin cell was cycled at a constant temperature of 25 °C. Each cycle consisted of a 1 C rate charge up to 4.2 V and a 2 C rate discharge down to 3 V.

Data from three cells, including one 18650 cell and two coin cells, is analyzed up to the end of their operational lives. Additionally, data from a Samsung Galaxy S9+ battery is used to determine its status, as this battery was not cycled to its EoL. The analysis of the Galaxy S9+ battery provides an opportunity to validate the method for assessing battery health without requiring full lifecycle data.

For all datasets, the SOC was maintained at 100% during EIS measurements, and all experiments were conducted at a constant temperature of 25 °C. This included the Samsung Galaxy S9+ smartphone cell, the cylindrical 18650 cell, and the LR2032 coin cells.

To ensure the accuracy of the experimental data, it is essential to confirm that the system under study behaves in a linear and stable manner. Kramers–Kronig (K–K) relations can be utilized to validate complex impedance data. Four fundamental conditions must be satisfied by systems taking impedance measurements: causality, linearity, stability, and finiteness. Causality indicates that there should be no response without excitation, linearity suggests consistency between the excitation and response frequencies, stability means the system should return to its initial state after excitation, and finiteness implies that physical quantities vary with the frequency within finite bounds. Verifying these conditions using K–K relations ensures that the impedance data are stable and interpretable.

$$Z_i{\left(\omega \right)}_{kk}=-\left({\displaystyle \frac{2\omega }{\pi }}\right){\int }_0^{\mathrm{\infty }}{\displaystyle \frac{Z_r\left(x\right)-Z_r\left(\omega \right)}{x^2-{\omega }^2}}dx$$

(1)

$$Z_r{\left(\omega \right)}_{kk}=Z_r\left(\mathrm{\infty }\right)+{\displaystyle \frac{2}{\pi }}{\int }_0^{\mathrm{\infty }}{\displaystyle \frac{{XZ}_i\left(x\right)-{\omega Z}_i\left(\omega \right)}{x^2-{\omega }^2}}dx$$

(2)

Equations (1) and (2) express the K–K relationships between the real and imaginary components of impedance data, providing a mathematical framework for assessing the internal consistency of the experimental results. Using K–K transforms, we calculate the differences between the actual and calculated values for each data point using Equations (3) and (4). For the EIS data to be reliable, these differences (residuals) for both the real and imaginary parts must be less than 1%.

$${∆}_{Re}\left(\omega \right)={\displaystyle \frac{Z_r\left(\omega \right)-{\widehat{Z}}_r\left(\omega \right)}{\left|Z\left(\omega \right)\right|}}$$

(3)

$${∆}_{Im}\left(\omega \right)={\displaystyle \frac{Z_i\left(\omega \right)-{\widehat{Z}}_i\left(\omega \right)}{\left|Z\left(\omega \right)\right|}}$$

(4)

where $\left|Z\left(\omega \right)\right|$ represents the absolute measured impedance at a given $\omega$ and $\widehat{Z}\left(\omega \right)$ the model impedance. The Kramers–Kronig (K–K) relations were applied to examining the real and imaginary components of impedance, specifically for the 18650 Li-ion battery (LiB). To ensure the accuracy of the experimental data, it was crucial that the relative residual difference between the measured values and the impedance spectrum reconstructed using K–K relations stayed within 1% across the entire frequency range. The analysis, as shown in Figure 2, confirmed that the residuals were indeed smaller than 1%, indicating the validity of the experimental data. Consequently, the impedance data, validated through K–K relations, were utilized for subsequent calculations of the Distribution of Relaxation Time (DRT) and the peak analysis.

3. Deconvolution of EIS Data

Deconvolution of the EIS Nyquist plot is essential, as overlapping semicircles make it difficult to distinguish individual electrochemical processes. The Nyquist plot graphically represents the real part of the impedance (Z′) on the x-axis and the imaginary part (Z″) on the y-axis, offering insights into the electrical properties of a system, including the resistance, capacitance, charge transfer kinetics, and Warburg impedance. Each data point corresponds to the impedance of the system at a specific frequency, with distinct regions of the plot providing information about various electrochemical processes. The high-frequency region reflects ohmic resistance, whereas the low-frequency region represents diffusion impedance, as illustrated in Figure 3a.

In comparison, DRT analysis provides a model-free approach to interpreting EIS data by directly examining the relaxation times within the system. Each peak in the DRT spectrum corresponds to a specific electrochemical process, as illustrated in Figure 3b. Unlike the conventional method of fitting Nyquist plots to ECMs, the DRT provides more precise and interpretable insights into the underlying electrochemical processes. Figure 3 demonstrates the relationship between the DRT and Nyquist plots, where the DRT peaks align with distinct features in the Nyquist plot, enabling a clearer understanding of electrochemical processes.

While EIS is a powerful tool for analyzing the internal dynamics of LIBs, traditional Nyquist plots often suffer from overlapping features, obscuring individual processes. The DRT method addresses this limitation by transforming EIS data into a spectrum where each electrochemical process appears as a distinct peak. This transformation facilitates the separation and identification of processes such as ohmic resistance, the Solid Electrolyte Interphase (SEI) layer, charge transfer, and diffusion, thereby providing deeper insights into the internal mechanisms of LIBs.

The DRT curve can be segmented into four peaks (R_Ohm, R_SEI, R_ct, and R_D). These impedance parameters can be derived by integrating the time constants within each interval of the DRT curve, serving as the basis for regrouping criteria. For each interval, the polarization resistance (Rp) can be calculated using the following formula:

$$R_p={\int }_{{\tau }_L}^{{\tau }_U}\gamma \left(\tau \right)d\tau$$

(5)

where ${\tau }_U$ and ${\tau }_L$ are the upper and lower limits of the time constant, respectively.

Analysis of DRT Plots

Integrating frequency-domain and time-domain analysis methods with EIS is vital for comprehensively understanding battery characteristics and diagnosing potential issues in battery research. Although EIS is a powerful tool, its interpretation can be challenging, particularly when overlapping semicircles appear in Nyquist plots. These overlaps make it difficult to distinguish individual electrochemical processes and their corresponding impedance contributions. To address this complexity, the DRT analysis offers a more detailed breakdown of each electrochemical process, providing a clearer understanding than that with frequency-domain analysis alone.

The analysis of the DRT plots for all three cells, as illustrated in Figure 4, revealed consistent relationships among the variations in the observed peaks. The peak located at the far-right end of each DRT plot, corresponding to the diffusion process, showed a steady increase in height as the number of cycles progressed. This trend was consistent across all DRT plots, suggesting a common behavior pattern as the batteries approached EoL conditions. This observation highlights the continuous evolution and intensification of the diffusion process throughout the battery lifespan.

Additionally, the middle peaks in the DRT plots, which are associated with the SEI layer and the charge transfer process, also exhibited increasing trends with cycling. Specifically, the charge transfer peak in both the 18650 battery and the LR2032 coin cells initially appeared at distinct center relaxation time constants. As the batteries underwent further cycling, these peaks gradually shifted towards higher relaxation time values. This shift indicates a dynamic change in the electrochemical processes as the batteries age. Notably, at the end of the battery’s life, the charge transfer and diffusion processes began to merge. This phenomenon is likely attributed to the depletion of lithium ions within the battery, indicating the irreversible degradation of its capacity and performance.

4. Results and Analysis

4.1. Extraction and Analysis of DRT Parameters

To identify polarization processes within LiBs, it is essential to perform multi-peak fitting and analyze the distribution function, γ(lnτ). This approach breaks down complex signals into simpler components, enabling the differentiation of distinct electrochemical processes. Gaussian functions are frequently employed for fitting due to their simplicity and well-defined physical interpretations [36].

The DRT parameters are extracted by fitting Gaussian functions, Gi(τ), to the data, facilitating the identification of electrochemical processes, as illustrated in Figure 5. The parameters of each Gaussian peak provide critical insights and can be extracted from (2).

$$G_i\left(\tau \right)={\displaystyle \frac{A_i}{{\sigma }_i\sqrt{2\pi }}}{e}^{{\displaystyle \frac{{-\left(\tau -{\eta }_i\right)}^2}{2{\sigma }_i^2}}}$$

(6)

In this equation, $A_i$ represents the peak area; ${\eta }_i$ is the characteristic time indicating the position of the peak; and ${\sigma }_i$ controls the peak width, also known as the full width at half maximum (FWHM), approximately $2{\sigma }_i\sqrt{\left(2ln2\right)}$.

The height of the peak, $h_i$, is calculated by

$$h_i={\displaystyle \frac{A_i}{{\sigma }_i\sqrt{2\pi }}}$$

(7)

Peak fitting of the DRTs enables precise separation and identification of electrochemical processes in LIBs. Using Gaussian functions, four DRT peaks are fitted, and four key parameters are calculated for the 18650 and coin cells to track their behavior up to their EoL, as illustrated in Figure 5. These parameters include the peak area, peak height, full width at half maximum (FWHM), and center relaxation time (τ) [37]. The fitted peaks are assigned as follows: G1(τ), representing the ohmic peak; G2(τ), corresponding to the SEI peak; G3(τ), indicating the charge transfer peak; and G4(τ), associated with the diffusion peak, as shown in Figure 6.

Here, the FWHM indicates how the time constants are distributed for a process. Narrow peaks show specific and uniform processes, while broad peaks suggest a wider range of complex processes [36]. The peak area reflects how much a process contributes to the overall impedance, with larger areas indicating a greater role. Peak height represents the intensity of a process, where higher peaks mean a more pronounced electrochemical process. Lastly, the center relaxation time (τ) indicates the speed of a process, with lower ‘τ’ values linked to faster processes like charge transfer and higher ‘τ’ values associated with slower processes such as the diffusion of ions at the EoL. This analysis provides a detailed understanding of a LIB’s electrochemical behavior and its evolution up to the EoL.

From Figure 6, it can be observed that G1(τ) and G2(τ) show minimal variation as the battery approaches its EoL, attributed to the high-quality manufacturing of the anode material and stable SEI layer formation, which increases slightly over time. In contrast, G3(τ) and G4(τ) exhibit significant changes with aging, indicating notable alterations in the LIBs’ electrochemical behavior. Additionally, these peaks gradually converge as the battery nears its EoL.

4.2. Critical Metrics for Assessing Battery Aging

As the battery ages and cycles toward its EoL, the FWHM steadily increases, reflecting the growing complexity of electrochemical processes. This increase in the FWHM indicates reduced uniformity in these processes, driven by material degradation and increased heterogeneity within the battery. At the beginning of the cycles, the FWHM of the G3(τ) peak shows minimal changes, but as the processes approach closer to each other, there is a sharp rise in the FWHM, as shown in Figure 7.

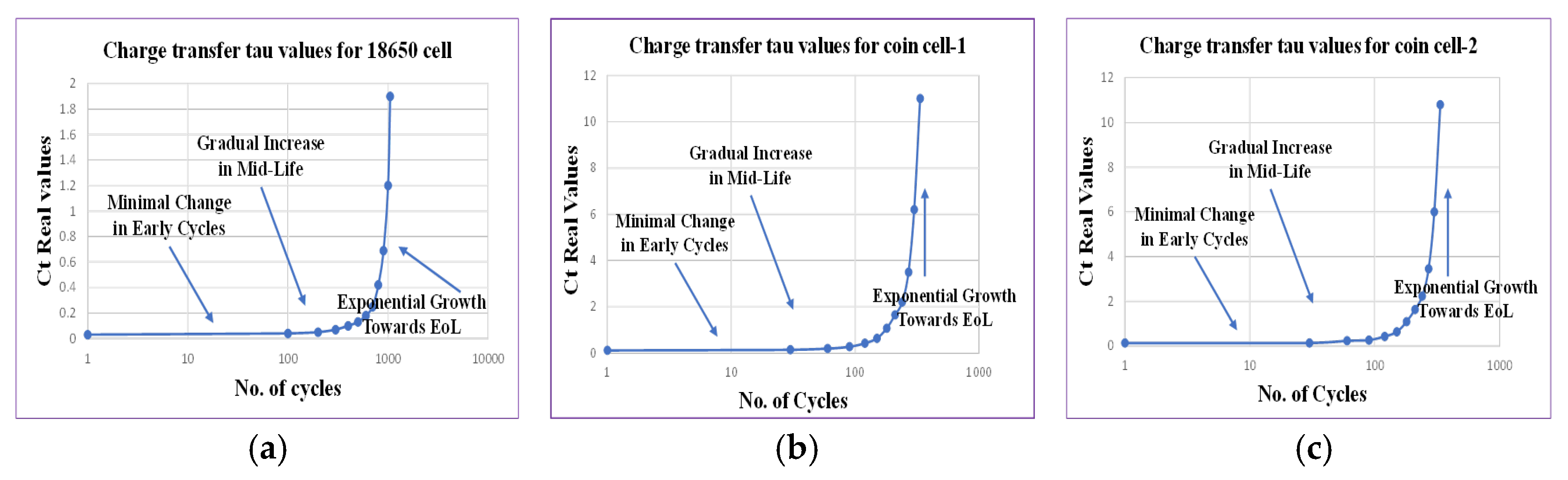
Similarly, the charge transfer process steadily increases with aging, indicating slower electrochemical reactions. Initially, there is minimal change in the early cycles, followed by a gradual increase during the midlife of the battery and exponential growth as the battery approaches its EoL, as shown in Figure 8, where the x-axis (number of cycles) is displayed in logarithmic scale. The cycling and aging of the battery cause degradation of the electrode materials, including structural changes, particle cracking, and the Loss of Active Material (LAM) [37]. This degradation reduces both electronic and ionic conductivity at the electrode–electrolyte interface, leading to an increase in charge transfer resistance.

On the other hand, as the battery approaches its EoL, the diffusion process shifts toward lower relaxation times, signifying faster diffusion. There is a stable diffusion process at the start of the cycle and a rapid decline in the midlife of the battery, as well as indicators of failure points when both processes G3(τ) and G4(τ) become close to each other, as shown in Figure 9 [37].

This change occurs as microscopic pores form in the electrode materials, particularly in the SEI layer, increasing the overall resistance but facilitating faster ion diffusion. The accelerated diffusion, especially near the EoL, suggests instability in the SEI layer, leading to rapid ion migration.

The FWHM parameter of the charge transfer peak and the center relaxation time (τ) for G3(τ) and G4(τ) are critical indicators of aging. These parameters are plotted as shown in Figure 7, Figure 8 and Figure 9.

4.3. Computation of the Central Relaxation Time

From the DRT graphs obtained for all cells, a noticeable trend emerges in the charge transfer process, which shifts towards higher relaxation times as the number of cycles increases. The movement of the charge transfer peak, highlighted by arrows, indicates this progression towards higher relaxation times. As the battery approaches its EoL cycles, the diffusion process slightly shifts towards lower relaxation times, eventually merging with the charge transfer process. This merging results in both processes sharing the same relaxation time in the final cycle, forming a single peak. This phenomenon is consistently observed across the DRT plots for all cells, exhibiting a similar pattern.

To gain deeper insights, the ratio of the charge transfer process to the diffusion process was calculated for each cell. Initially, this ratio was computed for the 18650 cell using a specific formula, and the same calculation was then applied to both coin cells.

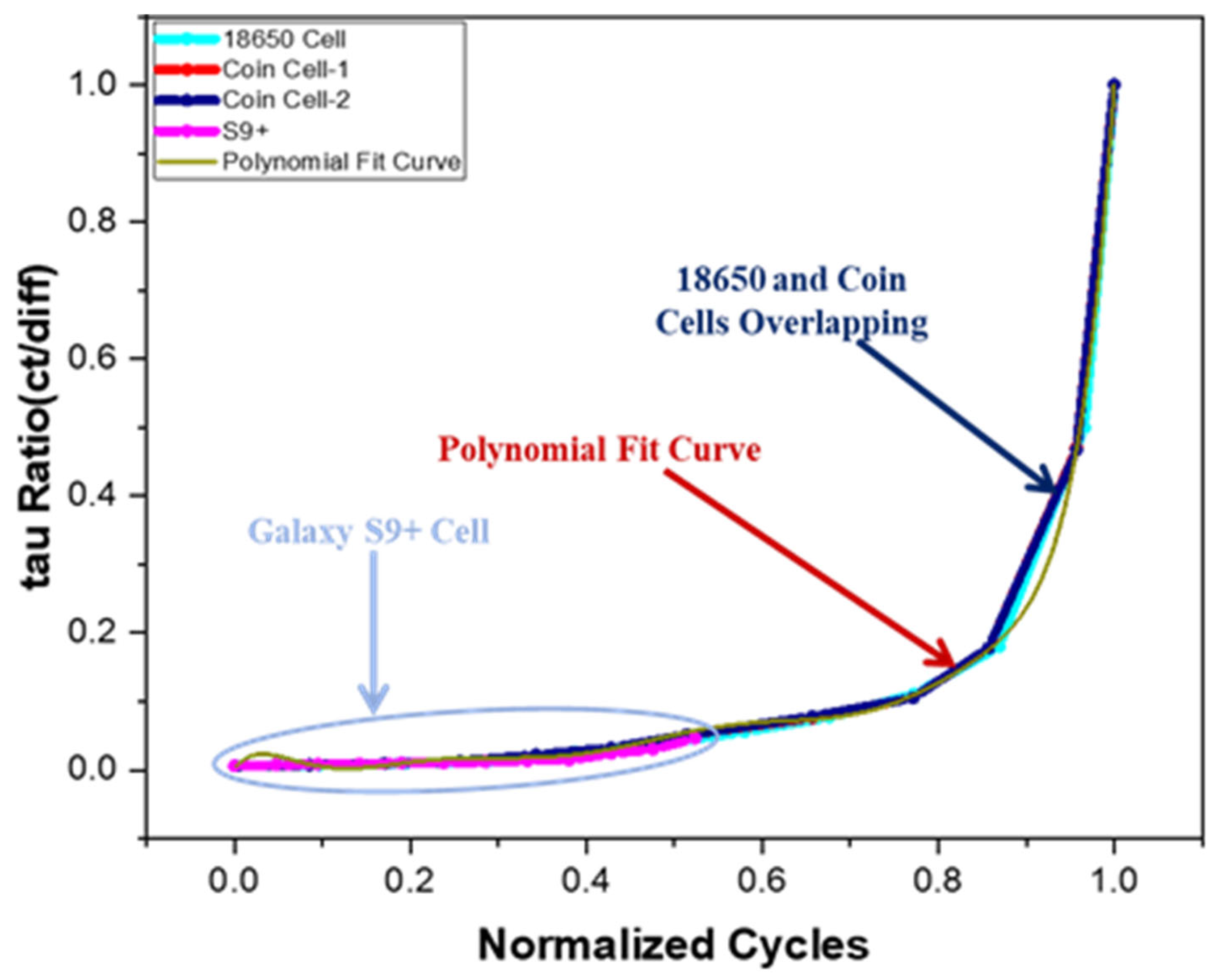
Analysis of the ratios for all three cells revealed a consistent pattern, with bar graphs shown in Figure 10, illustrating low variation in the ‘tau’ ratios, which are very close to each other. Among all of the parameters extracted from the DRT analysis, only the tau ratio exhibits a consistent trend across all cells. This trend is expected because as the battery undergoes repeated cycling, the charge transfer process shifts towards higher relaxation times, indicating a slowdown in the process due to the LLI in the battery. This phenomenon is consistently observed in all LIBs, making the tau ratio a critical parameter for evaluating battery status.

Following this analysis, the ‘tau’ ratios for all cells were calculated and plotted as shown in Figure 11. The resulting graph was then best fitted using a polynomial equation, as depicted in Figure 11. The polynomial equation derived from the data fitting process, including its intercepts and coefficients, is provided in

Table 2. Fitted polynomial curve equation with coefficients.

Equation	y = Intercept + B1 × x1 + B2 × x2 + B3 × x3 + B4 × x4 + B5 × x5 + B6 × x6 + B7 × x7 + B8 × x8 + B9 × x9
Intercept	0.00116 ± 0.00814
B1	1.67162 ± 1.10211
B2	−42.4958 ± 24.79537
B3	428.05814 ± 223.68722
B4	−2221.26036 ± 1050.45838
B5	6607.51524 ± 2846.14195
B6	−11,687.56268 ± 4611.76551
B7	12,142.34403 ± 4408.06719
B8	−6840.2013 ± 2290.91638
B9	1612.92962 ± 498.94644
Adj. R-Square	0.99943

, along with the corresponding R-squared value.

The errors reported for each coefficient in Table 2 represent the standard errors obtained from the least-squares polynomial regression fitting. These errors were derived from the covariance matrix of the fitted parameters, which accounts for the residual variance in the experimental data. The very small error magnitudes, combined with the high adjusted R² value (0.9994), confirm the reliability and robustness of the polynomial fitting approach.

For completeness, it is noted that Nyquist plots also reveal aging-related changes, with the growth of the mid-frequency semicircle reflecting increased charge transfer resistance and the extension of the low-frequency tail indicating diffusion polarization. However, these features often overlap, and equivalent circuit fitting can yield non-unique parameter values. In contrast, the DRT approach separates these contributions into distinct peaks, allowing the τ ratio between the charge transfer and diffusion processes to be quantified robustly. This highlights why the τ ratio derived from the DRT offers advantages over direct a Nyquist/ECM analysis for SOH estimation.

The Samsung Galaxy S9+ battery data was used to assess battery status and estimate lifespan. Initially, EIS Nyquist plots were generated and subsequently deconvoluted to differentiate each electrochemical process. This deconvolution enabled the derivation of DRT plots, from which the ratio of charge transfer to diffusion processes was calculated.

To evaluate the status of a LIB, the ‘tau’ ratio is calculated from the DRT plots and plotted onto the same graph. For verification in this study, Samsung Galaxy S9+ battery data was analyzed, and its transformation into the DRT is shown in Figure 12. The ‘tau’ ratio graph for the Samsung Galaxy S9+ battery aligned closely with the main ‘tau’ ratio graph up to its midpoint, indicating that the battery had completed approximately half of its life, which was 1000 cycles. By analyzing this segment of the graph, it was concluded that approximately half of the battery’s health or lifespan had been depleted. Based on these findings, it was estimated that the Samsung Galaxy S9+ battery would require an additional 1100 cycles to reach its EoL, giving it a total lifespan of approximately 2100 cycles. This approach illustrates that by generating a DRT plot for any LIB, its current status can be accurately assessed without depending on historical data. Furthermore, the total lifespan of the battery can be predicted using the ‘tau’ ratio parameter, providing valuable insights into battery performance and longevity.

5. Conclusions

In this paper, a novel approach to estimating the SOH of LIBs is introduced using DRT analysis, with a specific focus on the characterization of the central relaxation time (τ) ratio between charge transfer and diffusion processes. This method distinguishes itself from conventional DRT parameters by offering a more direct and data-independent approach to assessing battery health and predicting overall lifespan. The experimental results reveal consistent and observable trends in the shifting and merging of the DRT peaks as the batteries undergo aging, which are effectively captured and quantified by the proposed τ ratio. A polynomial model derived from the τ ratio data further enhances the analysis, enabling accurate predictions of battery status and lifespan over time. The practicality and robustness of this approach are validated through its application to a commercial Samsung Galaxy S9+ battery, which, although not cycled to the EoL, still shows consistent behavior in line with the model predictions. Additionally, the ability of the method to deliver insights into battery performance degradation without relying on extensive historical data sets it apart from traditional SOH estimation techniques, thereby advancing our broader understanding of battery aging mechanisms and contributing to more efficient and predictive battery health management. Limitations of this study are the relatively small sample size and the absence of replicates, which prevent full quantification of between-cell variability. Nevertheless, the consistent τ ratio trends observed across the three distinct cell formats indicate the robustness of the proposed method. The statistical reliability of the polynomial fit (Adj. R² = 0.9994 with low coefficient errors) supports these findings further. Future work will expand this analysis to larger datasets, including multiple replicates of 18650 and automotive-grade cells, to establish confidence intervals and assess variability across batches.