Numerical Simulation Study and Stress Prediction of Lithium-Ion Batteries Based on an Electrochemical–Thermal–Mechanical Coupled Model
Abstract
1. Introduction
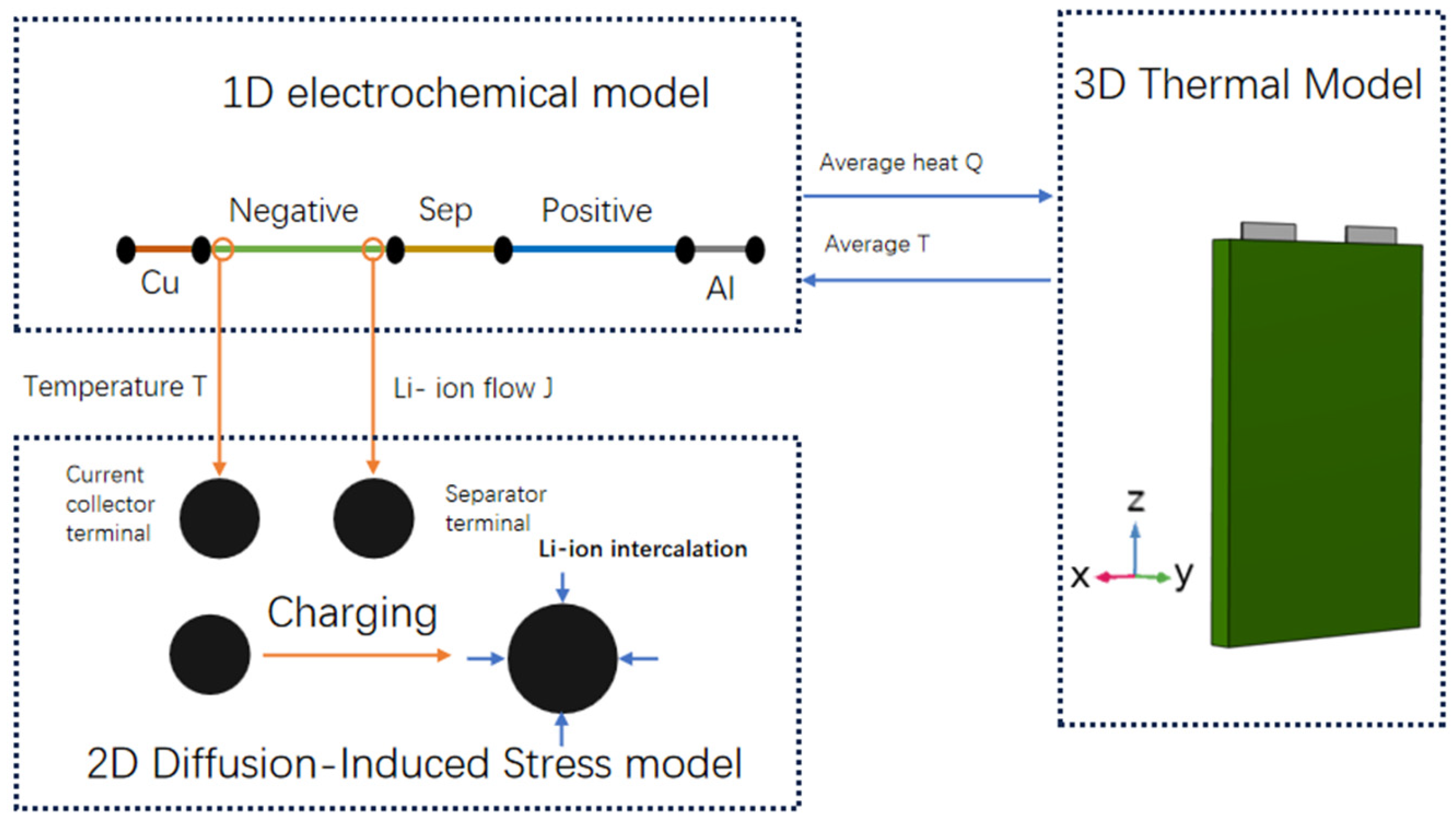
2. Establishment of Electrochemical–Thermal–Mechanical Coupling Model
2.1. Electrochemical Model
2.2. Thermal Model
2.3. Mechanical Model
| Parameter | Definition/Unit | Aluminum | Cathode | Separator | Anode | Copper |
|---|---|---|---|---|---|---|
| L | Electrode thickness/μm | 21 | 150 | 30 | 120 | 18 [16] |
| r | Particle radius/μm | 8 [30] | 12.5 [30] | |||
| Cs,max | Max. Li-ion concentration In the solid phase/mol·m−3 | 22,860 [30] | 26,390 [30] | |||
| Cs,0 | Initial Li-ion concentration in the solid phase/mol·m−3 | 3800 | 21,061 | |||
| Cl,0 | Initial Li-ion concentration in the liquid phase/mol·m−3 | 1000 [29] | ||||
| εs | Solid-phase volume fraction | 0.297 [30] | 0.471 [30] | |||
| εl | Liquid-phase volume fraction | 0.44 [30] | 0.35 [30] | |||
| Ds | Solid-phase diffusion coefficient/m2·s−1 | Equation (2) | Equation (3) | |||
| Dl | Liquid-phase diffusion coefficient/m2·s−1 | Equation (4) | ||||
| σs | Solid-phase conductivity/S·m−1 | 3.8 [29] | 100 [29] | |||
| σl | Liquid-phase conductivity/S·m−1 | Equation (5) | ||||
| Kref | Reference reaction rate constant/m·s−1 | 2 × 10−11 [29] | 2 × 10−11 [29] | |||
| EaD | Activation energy for diffusion/J·mol−1 | 35,000 [16] | 31,000 [16] | |||
| γ | Bruggeman coefficient | 1.5 | 1.5 | 1.5 | ||
| EaR | Activation energy for reaction/J·mol−1 | |||||
| Tref | Reference temperature/°C | 25 [31] | ||||
| α | Charge transfer coefficient | 0.5 [29] | 0.5 [29] | |||
| t+ | Li-ion transference number | 0.363 [30] | ||||
| F | Faraday constant/C·mol−1 | 96,487 | ||||
| K | Thermal conductivity/W·(m·K)−1 | 238 | 1.48 | 1.33 | 1.04 | 398 |
| Cp | Specific heat capacity/J·(kg·K)−1 | 903 | 700 | 1978 | 1437 | 385 |
| ρ | Density/kg·m−3 | 2700 | 1500 | 492 | 2660 | 8900 |
2.4. Coupling Process
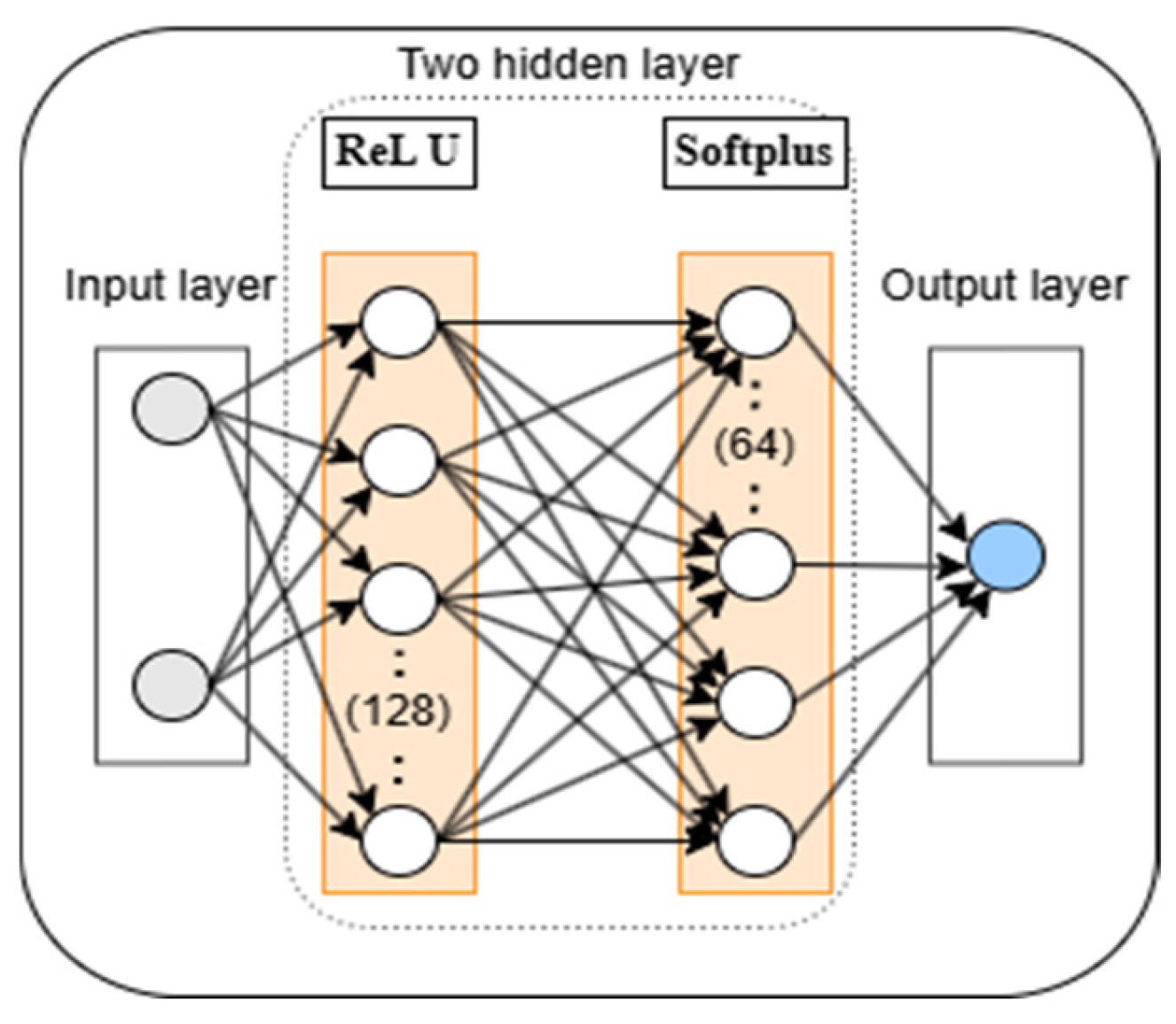
2.5. DNN Algorithm
3. Results and Discussion
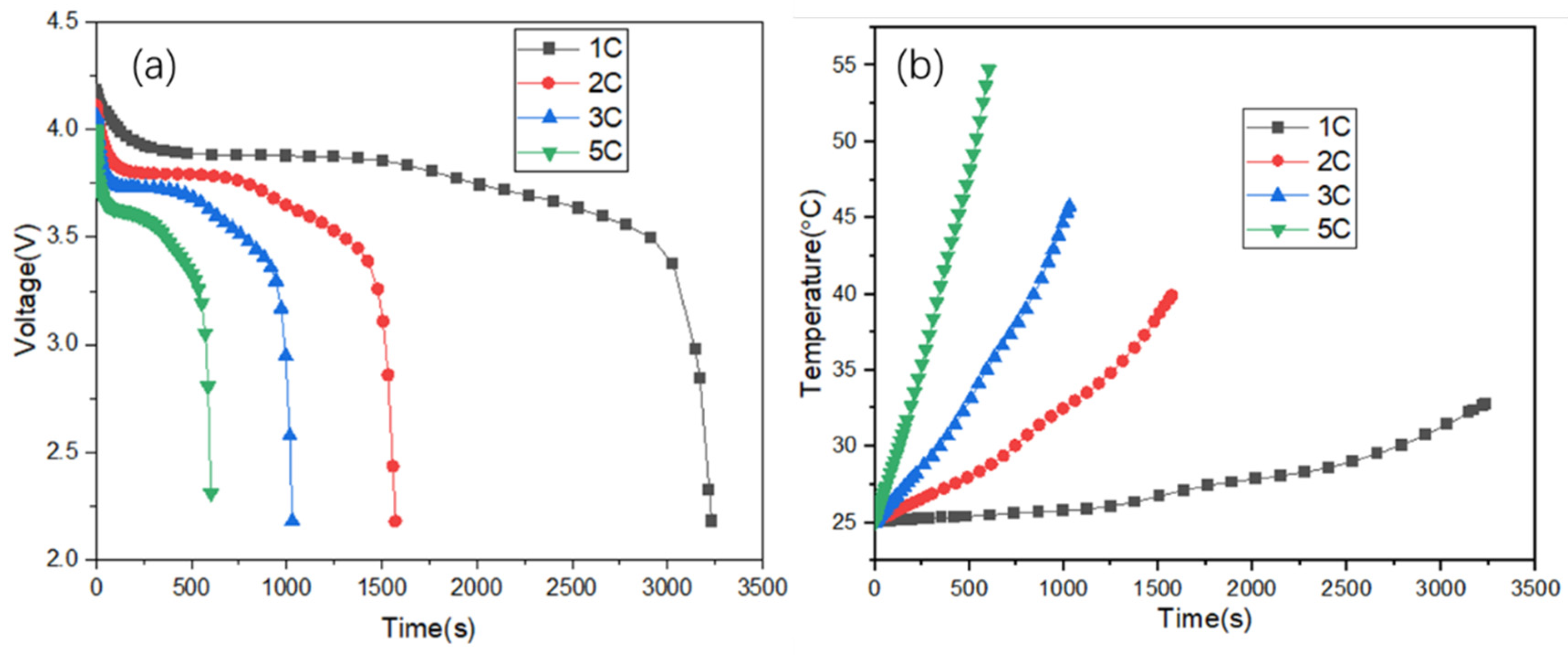
3.1. Research on Battery Discharge Characteristics
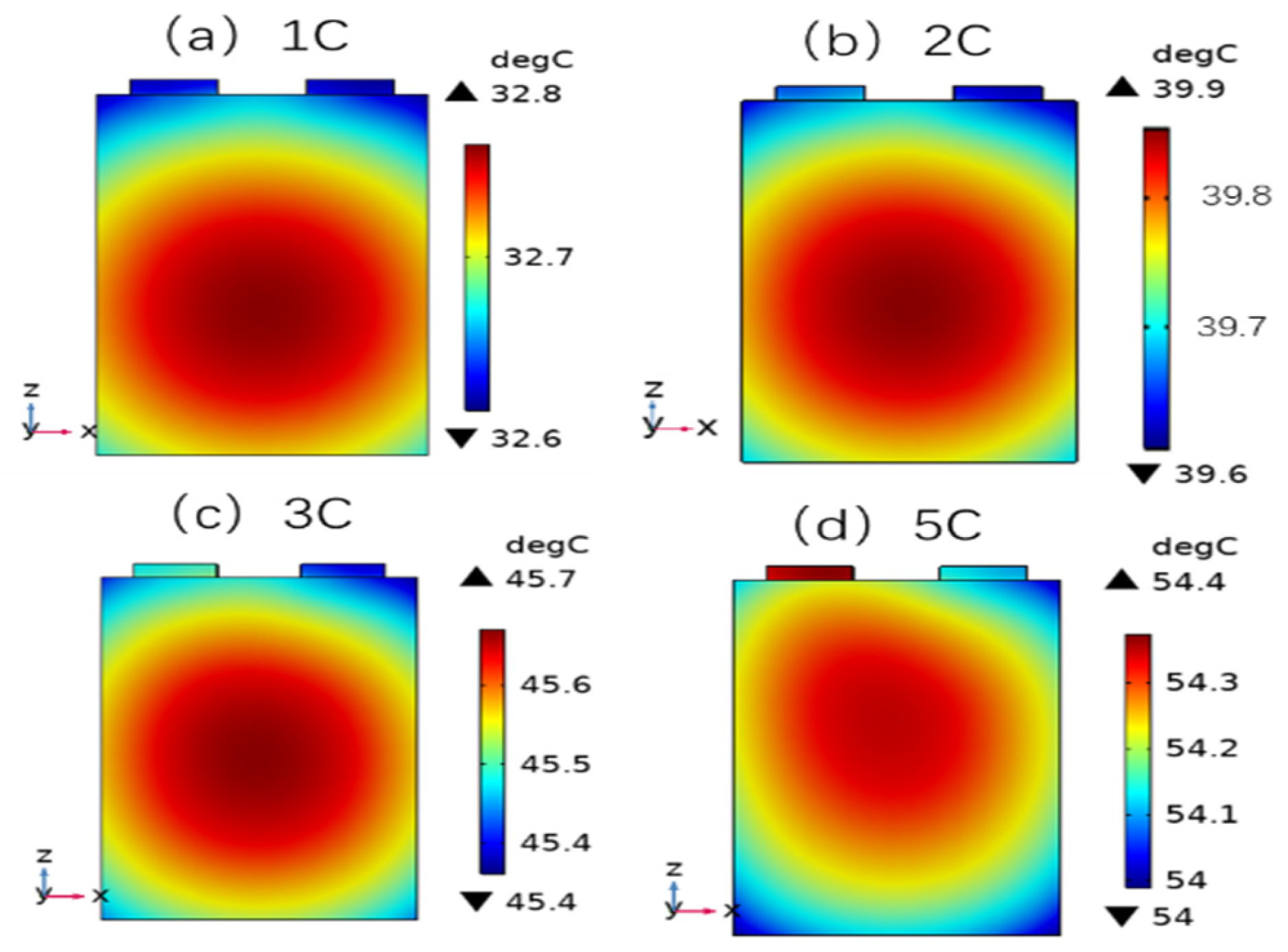
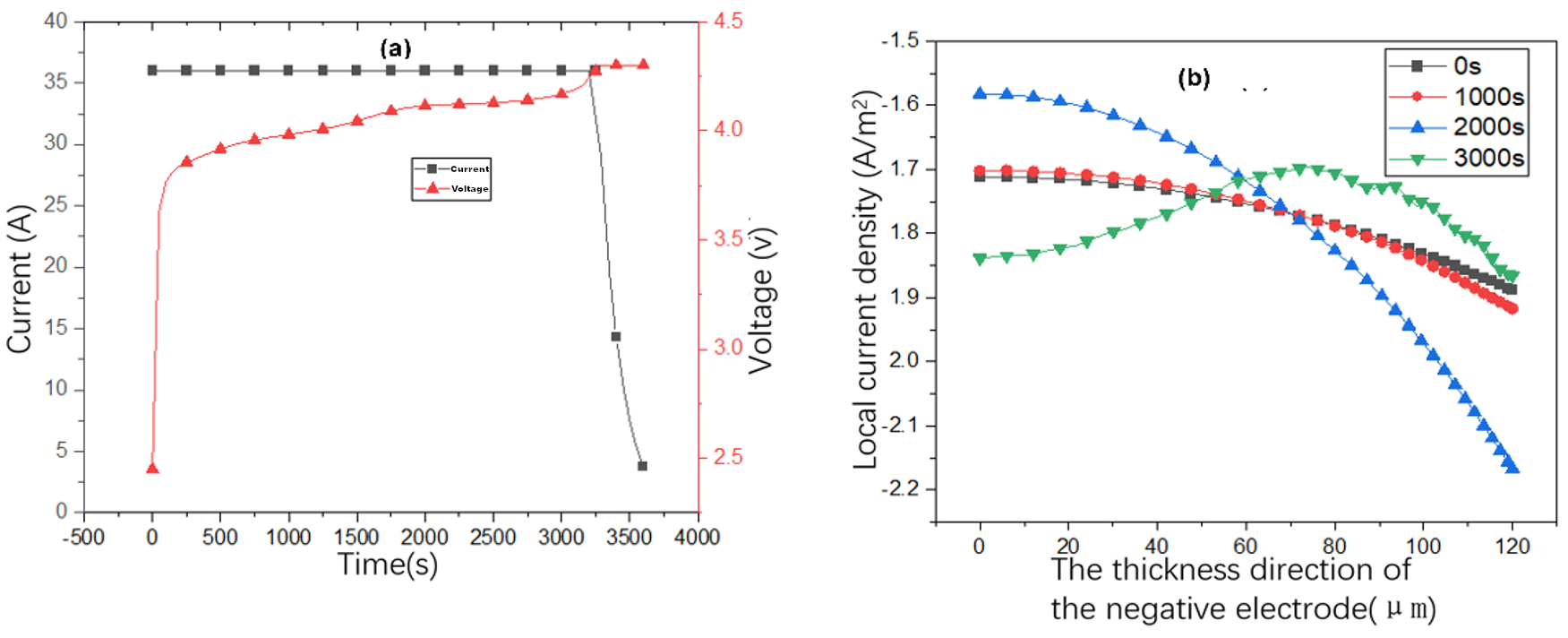
3.2. Research on Battery Charge Characteristics
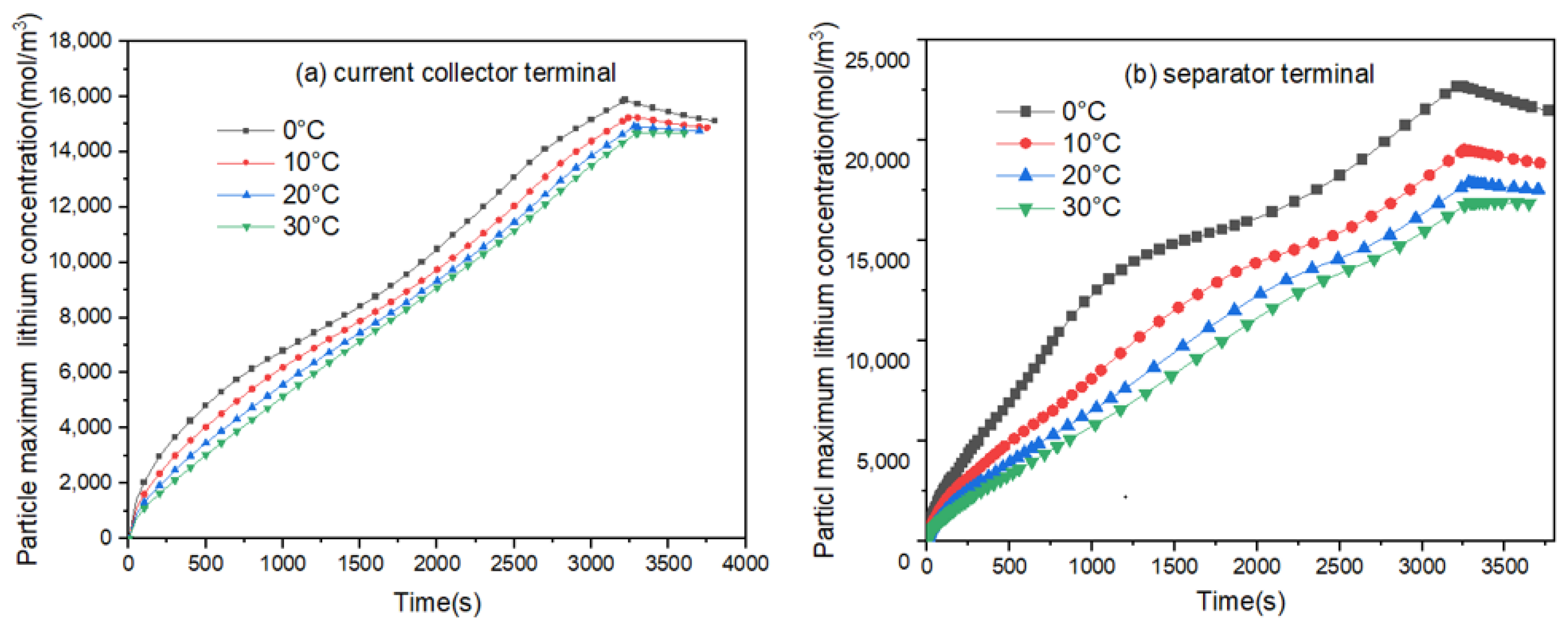
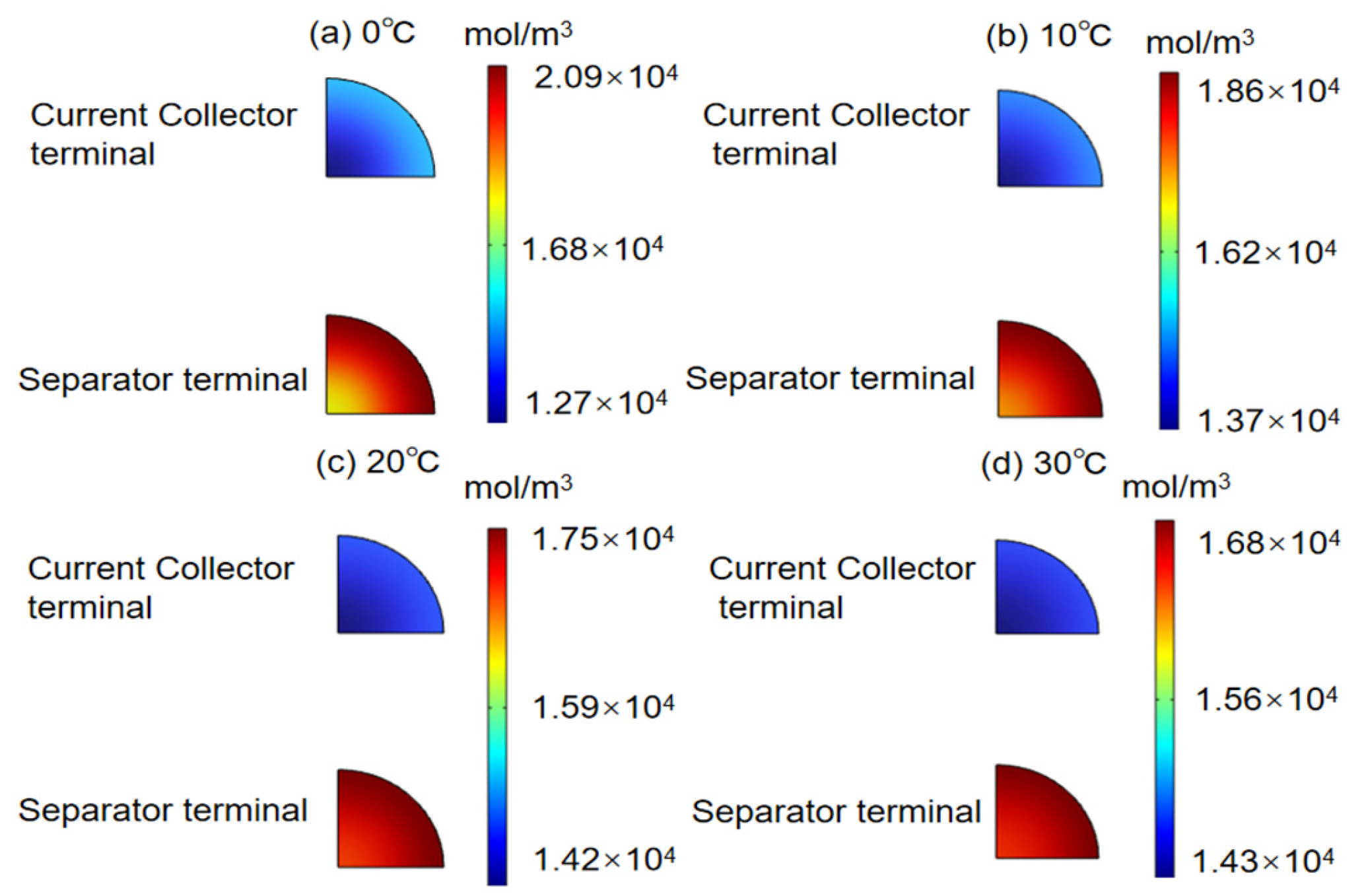
3.3. Influence of Different Charging Temperatures on the Concentration and Stress of Active Particles
- (i)
- The lithium concentration on the surface of particles (both on the current collector side and separator side) is higher than that at the center of the particles.
- (ii)
- The overall concentration of anode active particles near the separator side is higher than that on the current collector side.
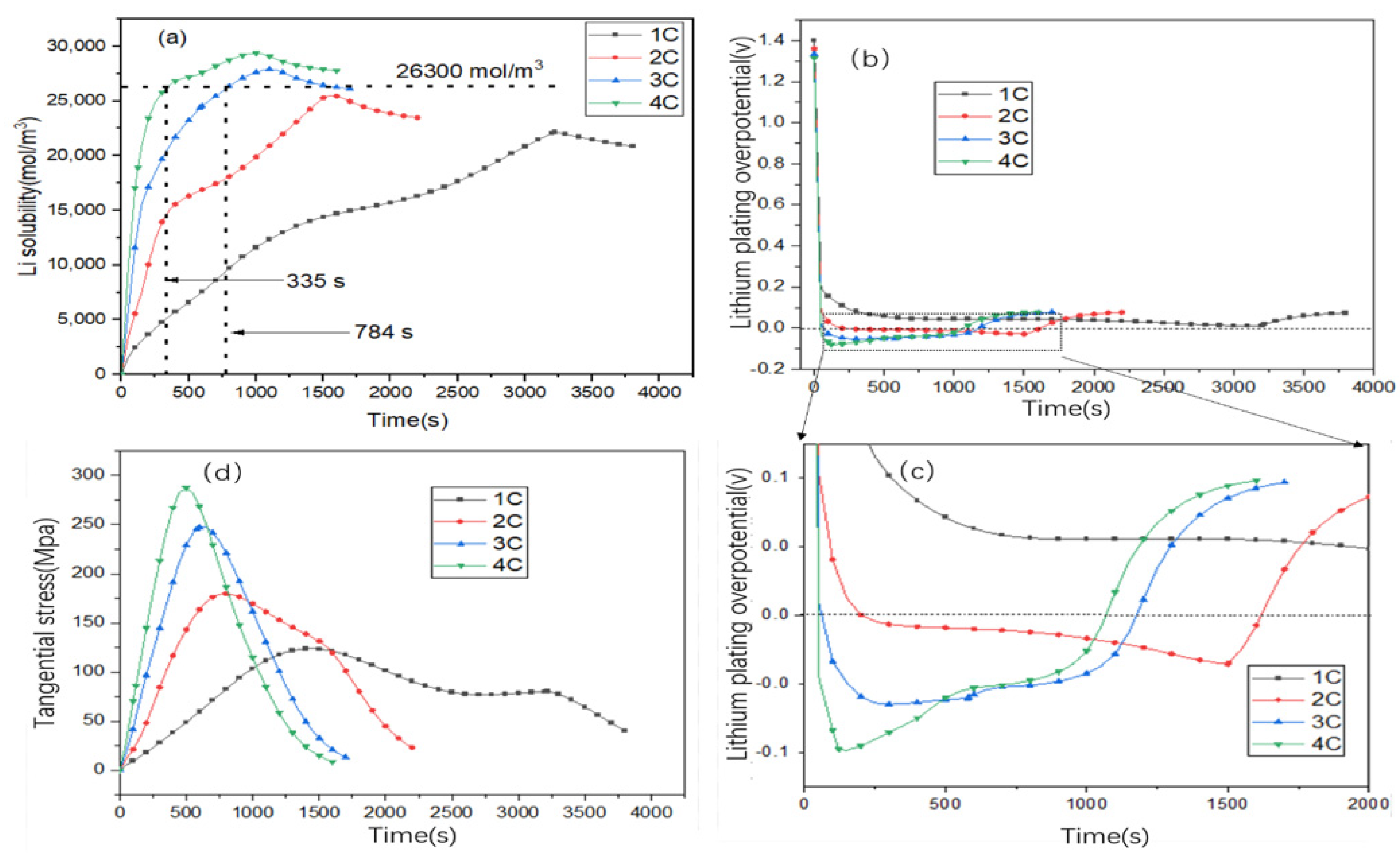
3.4. Influence of Different Charging Rates on Solubility, Stress, and Lithium Plating of Active Particles
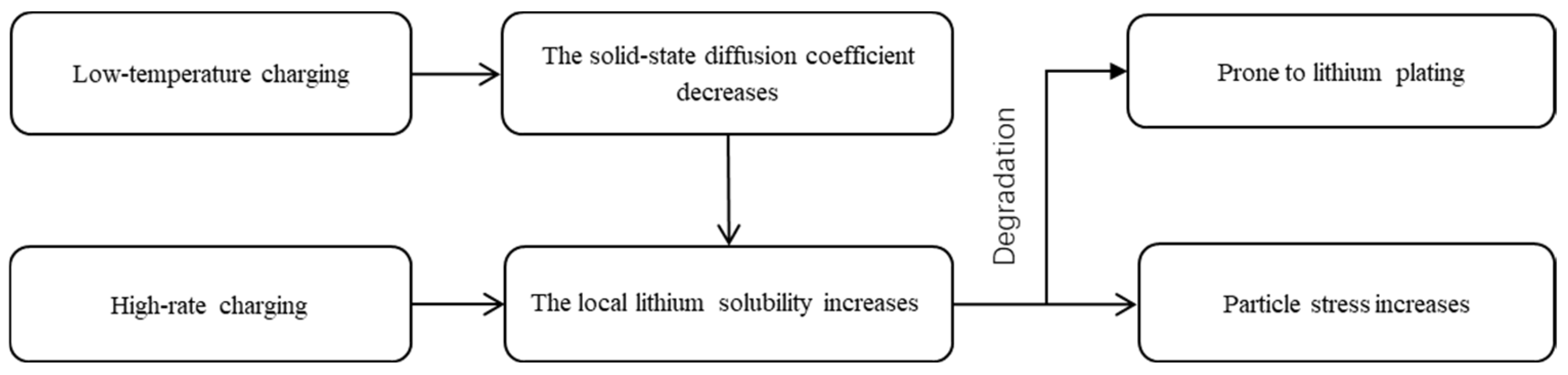
3.5. Potential Relationships Between Different Factors and Degradation Mechanism
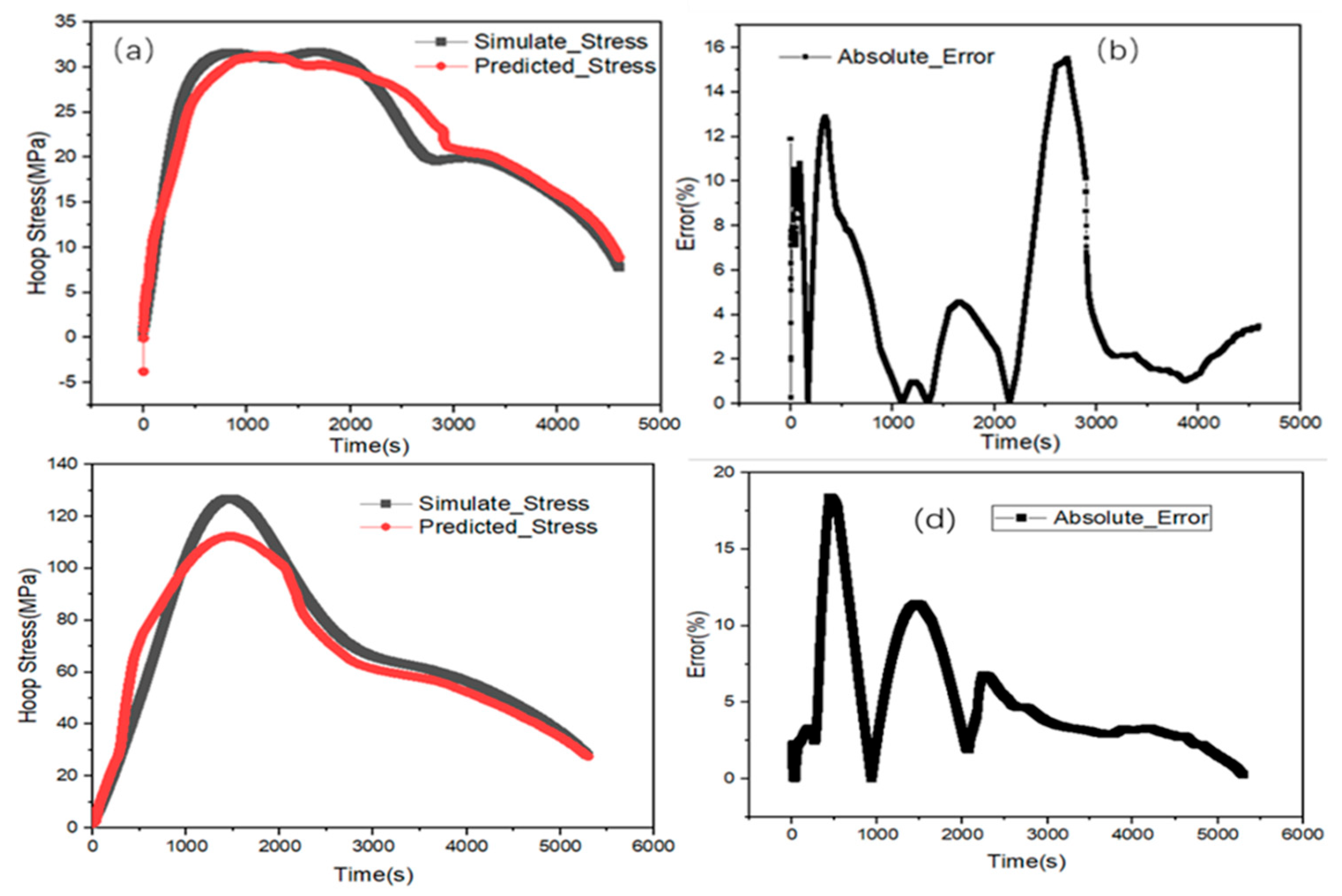
3.6. Stress Estimation
4. Conclusions
- During the charging process, the intercalation of lithium ions along the thickness direction of the negative electrode shows an uneven distribution. The lithium-ion concentration in the negative electrode particles near the separator is higher than that in the particles near the current collector. This is because the local current density at the separator terminal is higher, while the current density at the current collector terminal is lower.
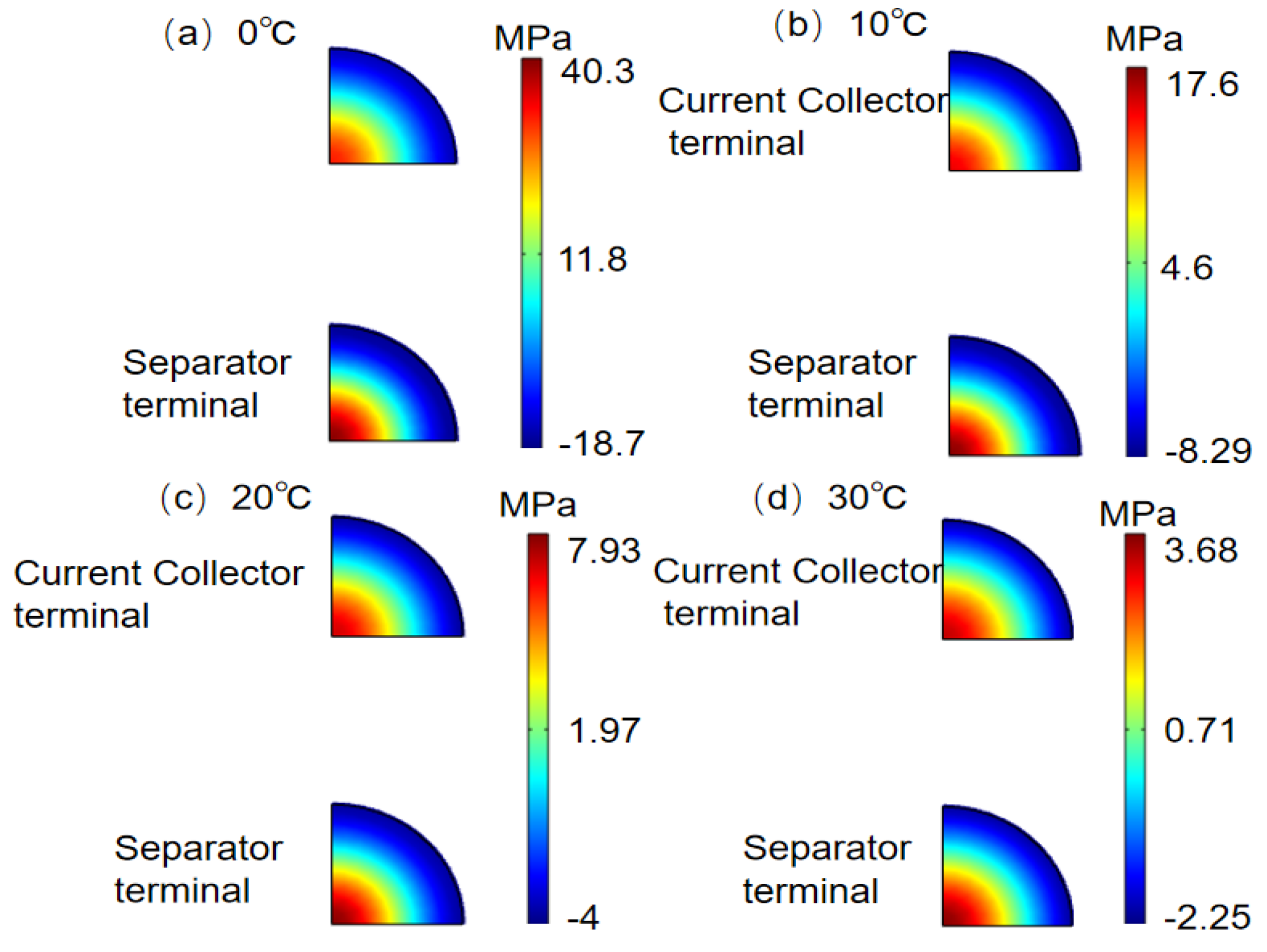
- The stress of active particles increases with the increase in charging rate and decreases with the increase in charging temperature. When charging at a rate of 1C and 0 °C, the maximum stress of the particles at the negative electrode–separator interface reaches 123.7 MPa, while when charging at 30 °C, the maximum particle stress is 24.3 MPa. Cloud image analysis shows that the stress at the particle center is tensile stress, while the stress on the surface is compressive stress, indicating that cracks may initiate from the center of the particles.
- The DNN algorithm is used to predict the stress of active particles during charging, with MAE and RMSE values of 0.034 and 0.046, respectively. The prediction results are in good agreement with the simulation results.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| As | Heat transfer area, m2 |
| αa, αc | Transfer coefficients, dimensionless |
| cs, cl | Lithium-ion concentrations in solid and liquid phases, respectively, mol/m3 |
| cp | Specific heat capacity at constant pressure, mol/m3 |
| Ds, Dl | Diffusion coefficients of solid and liquid phases, respectively, m2/s |
| E | Activation energy, J/mol |
| F | Activation energy, C/mol |
| h | Convective heat transfer coefficient, W/(m2·K) |
| i0 | Exchange current density, A/m2 |
| j | Local current density, A/m2 |
| k | Reaction rate constant, m/s |
| R | Ideal gas constant, J/(mol·K) |
| r | Radius of active particles, m |
| T | Battery temperature, K |
| Ta | Ambient temperature, K |
| t+ | Transference number of lithium ions, dimensionless, 1 |
| t | Battery discharge time, s |
| σs, σl | Electrical conductivities of solid and liquid phases, respectively, S/m |
| Φs, Φl | Potentials of solid and liquid phases, respectively, V |
| εs, εl | Volume fractions of solid and liquid phases, respectively, dimensionless, 1 |
| ρ | Density, kg/m3 |
| η | Overpotential, V |
| E | Elastic modulus, GPa |
| ν | Poisson’s ratio, dimensionless |
| Ω | Partial molar volume, m3(mol)−1 |
References
- Wang, S.; Ren, D.; Xu, C.; Han, X.; Liu, X.; Lu, L.; Ouyang, M. Lithium plating induced volume expansion overshoot of lithium-ion batteries: Experimental analysis and modeling. J. Power Sources 2024, 593, 233946. [Google Scholar] [CrossRef]
- Liu, Y.; Mao, Y.; Cao, J.; Wang, H.; Liu, B. Adjustment of swelling stress ranges to control internal short circuit behavior of high-energy lithium metal batteries. Chem. Eng. J. 2025, 517, 164403. [Google Scholar] [CrossRef]
- Yu, C.; Huang, S.; Xu, H.; Yan, J.; Rong, K.; Sun, M. Optimal charging of lithium-ion batteries based on lithium precipitation suppression. J. Energy Storage 2024, 82, 110580. [Google Scholar] [CrossRef]
- Shin, H.R.; Lee, J.-W. Electrochemistry-based method for determining Li plating-induced degradation of fast-charging Li-ion batteries. Electrochim. Acta 2025, 523, 145959. [Google Scholar] [CrossRef]
- Sandherr, J.; Bolsinger, M.; Kleefoot, M.-J.; Knoblauch, V. A combined electrochemical and microscopical analysis on the effect of laser structuring on Li plating of graphite anodes for lithium-ion batteries. J. Energy Storage 2024, 102, 114187. [Google Scholar] [CrossRef]
- Chen, Y.; Ding, L.; Zeng, Q.; Dong, Y.; Yue, X.; Si, X.; Zhang, D.; Qu, Q.; Liang, Z.; Hao, W. Investigating the gas generation during Li plating in fast-charging Li-ion batteries. Chin. Chem. Lett. 2025, in press, journal pre-proof. [Google Scholar]
- Clerici, D.; Mocera, F.; Somà, A. Analytical Solution for Coupled Diffusion Induced Stress Model for Lithium-Ion Battery. Energies 2020, 13, 1717. [Google Scholar] [CrossRef]
- Clerici, D.; Mocera, F. Micro-scale modeling of Lithium-ion battery. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1038, 012007. [Google Scholar] [CrossRef]
- Verbrugge, M.W.; Cheng, Y.-T. Stress and Strain-Energy Distributions within Diffusion-Controlled Insertion-Electrode Particles Subjected to Periodic Potential Excitations. J. Electrochem. Soc. 2009, 156, A927–A937. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, Y.; Chen, H.; Luan, W. The diffusion induced stress and cracking behaviour of primary particle for Li-ion battery electrode. Int. J. Mech. Sci. 2020, 178, 105608. [Google Scholar] [CrossRef]
- Korsunsky, A.M.; Sui, T.; Song, B. Explicit formulae for the internal stress in spherical particles of active material within lithium ion battery cathodes during charging and discharging. Mater. Des. 2015, 69, 247–252. [Google Scholar] [CrossRef]
- Zhao, K.; Pharr, M.; Vlassak, J.J.; Suo, Z. Fracture of electrodes in lithium-ion batteries caused by fast charging. J. Appl. Phys. 2010, 108, 073517. [Google Scholar] [CrossRef]
- Pistorio, F.; Clerici, D.; Mocera, F.; Somà, A. Coupled electrochemical–mechanical model for fracture analysis in active materials of lithium ion batteries. J. Power Sources 2023, 580, 233378. [Google Scholar] [CrossRef]
- Zhu, X.; Xie, Y.; Chen, H.; Luan, W. Numerical analysis of the cyclic mechanical damage of Li-ion battery electrode and experimental validation. Int. J. Fatigue 2021, 142, 105915. [Google Scholar] [CrossRef]
- Chen, Y.; Chen, H.; Luan, W. Shakedown, ratcheting and fatigue analysis of cathode coating in lithium-ion battery under steady charging-discharging process. J. Mech. Phys. Solids 2021, 150, 104366. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Wang, K.; Zhang, H.; Huang, H. Numerical investigation on the elastoplastic behavior and fatigue life of the current collector of lithium-ion batteries based on the electrochemical-thermal-mechanical coupling model. J. Energy Storage 2023, 68, 107792. [Google Scholar] [CrossRef]
- Chen, L.R.; Wei, S.H.; Hsieh, H.Y.; Shen, H.Y.; Wu, C.H. Comparison of battery internal temperature using electrochemical impedance spectroscopy. Int. J. Electrochem. Sci. 2025, 20, 101070. [Google Scholar] [CrossRef]
- Zafar, M.H.; Mansoor, M.; Abou Houran, M.; Khan, N.M.; Khan, K.; Moosavi, S.K.R.; Sanfilippo, F. Hybrid deep learning model for efficient state of charge estimation of Li-ion batteries in electric vehicles. Energy 2023, 282, 128317. [Google Scholar] [CrossRef]
- Zhou, Z.; Ryan, Z.J.; Sharma, U.; Anh, T.T.; Mehrotra, S.; Greco, A.; West, J.; Prasad, M. Deep Learning Approaches for Battery Capacity and State of Charge Estimation with the NASA B0005 Dataset. Comput. Mater. Contin. 2025, 83, 4795–4813. [Google Scholar] [CrossRef]
- Su, T.-W.; Ko, C.-J.; Chen, K.-C. Estimation of battery temperature during drive cycle operation by the time evolution of voltage and current. J. Energy Storage 2024, 91, 112075. [Google Scholar] [CrossRef]
- Li, Z.; Yu, H.; Fan, G.; Zhang, J.; Xu, J. Energy-efficient offloading for DNN-based applications in edge-cloud computing: A hybrid chaotic evolutionary approach. J. Parallel Distrib. Comput. 2024, 187, 104850. [Google Scholar] [CrossRef]
- Ahn, J.; Lee, Y.; Han, B.; Lee, S.; Kim, Y.; Chung, D.; Jeon, J. A highly effective and robust structure-based LSTM with feature-vector tuning framework for high-accuracy SOC estimation in EV. Energy 2025, 325, 136134. [Google Scholar] [CrossRef]
- Mustaffa, Z.; Sulaiman, M.H.; Isuwa, J. State of charge estimation of lithium-ion batteries in an electric vehicle using hybrid metaheuristic—Deep neural networks models. Energy Storage Sav. 2025, 4, 111–122. [Google Scholar] [CrossRef]
- Ma, L.; Li, Y.; Zhang, T.; Tian, J.; Guo, Q.; Guo, S.; Hu, C.; Chung, C.Y. Trustworthy battery state of charge estimation enabled by multi-task deep learning. Energy 2025, 326, 136264. [Google Scholar] [CrossRef]
- Fuller, T.F.; Doyle, M.; Newman, J. Simulation and Optimization of the Dual Lithium ion Insertion Cell. J. Electrochem. Soc. 1994, 141, 1. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium Polymer Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Yousefi, E.; Ramasamy, D.; Kadirgama, K.; Talele, V.; Najafi, H.; Olyaei, M.; Miljkovic, N.; Panchal, S. Electrochemical-thermal modeling of phase change material battery thermal management systems: Investigating mesh types for accurate simulations. Int. J. Heat Mass Transf. 2025, 247, 127107. [Google Scholar] [CrossRef]
- Bahiraei, F.; Ghalkhani, M.; Fartaj, A.; Nazri, G.-A. A pseudo 3D electrochemical-thermal modeling and analysis of a lithium-ion battery for electric vehicle thermal management applications. Appl. Therm. Eng. 2017, 125, 904–918. [Google Scholar] [CrossRef]
- Ali, Y.; Iqbal, N.; Lee, S. Role of SEI layer growth in fracture probability in lithium-ion battery electrodes. Int. J. Energy Res. 2021, 45, 5293–5308. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. The effects of electrode thickness on the electrochemical and thermal characteristics of lithium ion battery. Appl. Energy 2015, 139, 220–229. [Google Scholar] [CrossRef]
- An, Z.; Jia, L.; Wei, L.; Dang, C.; Peng, Q. Investigation on lithium-ion battery electrochemical and thermal characteristic based on electrochemical-thermal coupled model. Appl. Therm. Eng. 2018, 137, 792–807. [Google Scholar] [CrossRef]
- Christensen, J.; Newman, J. Stress generation and fracture in lithium insertion materials. J. Solid State Electrochem. 2006, 10, 293–319. [Google Scholar] [CrossRef]
- Iqbal, N.; Ali, Y.; Lee, S. Analysis of mechanical failure at the interface between graphite particles and polyvinylidene fluoride binder in lithium-ion batteries. J. Power Sources 2020, 457, 228019. [Google Scholar] [CrossRef]
- Iqbal, N.; Lee, S. Mechanical Failure Analysis of Graphite Anode Particles with PVDF Binders in Li-Ion Batteries. J. Electrochem. Soc. 2018, 165, A1961–A1970. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, Z.; Wang, X.; Jia, L.; Yang, L. Two-dimensional electrochemical–thermal coupled modeling of cylindrical LiFePO4 batteries. J. Power Sources 2014, 256, 233–243. [Google Scholar] [CrossRef]
- Bahiraei, F.; Fartaj, A.; Nazri, G.-A. Electrochemical-thermal Modeling to Evaluate Active Thermal Management of a Lithium-ion Battery Module. Electrochim. Acta 2017, 254, 59–71. [Google Scholar] [CrossRef]

| Parameter | Definition | Anode |
|---|---|---|
| Elastic modulus/GPa | 15 [32,33] | |
| Poisson’s ratio | 0.3 [32,33] | |
| Partial molar volume/m3·mol−1 | 3.64 × 10−6 [34] |
| Hyperparameter | Value |
|---|---|
| Number of epochs | 80 |
| Batch size | 16 |
| Learning rate | 0.001 |
| Optimizer | Adam |
| Dropout | 0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Zhang, Y. Numerical Simulation Study and Stress Prediction of Lithium-Ion Batteries Based on an Electrochemical–Thermal–Mechanical Coupled Model. Batteries 2025, 11, 360. https://doi.org/10.3390/batteries11100360
Cao J, Zhang Y. Numerical Simulation Study and Stress Prediction of Lithium-Ion Batteries Based on an Electrochemical–Thermal–Mechanical Coupled Model. Batteries. 2025; 11(10):360. https://doi.org/10.3390/batteries11100360
Chicago/Turabian StyleCao, Juanhua, and Yafang Zhang. 2025. "Numerical Simulation Study and Stress Prediction of Lithium-Ion Batteries Based on an Electrochemical–Thermal–Mechanical Coupled Model" Batteries 11, no. 10: 360. https://doi.org/10.3390/batteries11100360
APA StyleCao, J., & Zhang, Y. (2025). Numerical Simulation Study and Stress Prediction of Lithium-Ion Batteries Based on an Electrochemical–Thermal–Mechanical Coupled Model. Batteries, 11(10), 360. https://doi.org/10.3390/batteries11100360





