Sensor Fusion-Based Pulsed Controller for Low Power Solar-Charged Batteries with Experimental Tests: NiMH Battery as a Case Study
Abstract
1. Introduction
1.1. Background and Motivation
1.2. Contributions and Novelties
- (1)
- A literature review on the existing pulse controller for battery chargers is provided, and their performance and shortcomings are analyzed.
- (2)
- A sensor-fusion-based pulse charging technique is proposed for the battery charger that minimizes charging losses and battery degradations to increase battery lifetime.
- (3)
- With the aid of sensor fusion, the charge controller is disconnected and reconnects the battery during battery overcharging and deep discharging conditions using sensors with relays.
- (4)
- A prototype solar-powered battery charger with the proposed technique is developed and tested using a less expensive PV panel, battery, and digital signal processor (DSP) controller.
- (5)
- The comparative study is presented by comparing the charging performance of the solar-powered PWM charge controller with the constant current-constant voltage method. The proposed method is pertinent for minimizing energy issues in impoverished places at a reasonable price.
2. Revolution of Pulse Charging (Current) Mode Technique
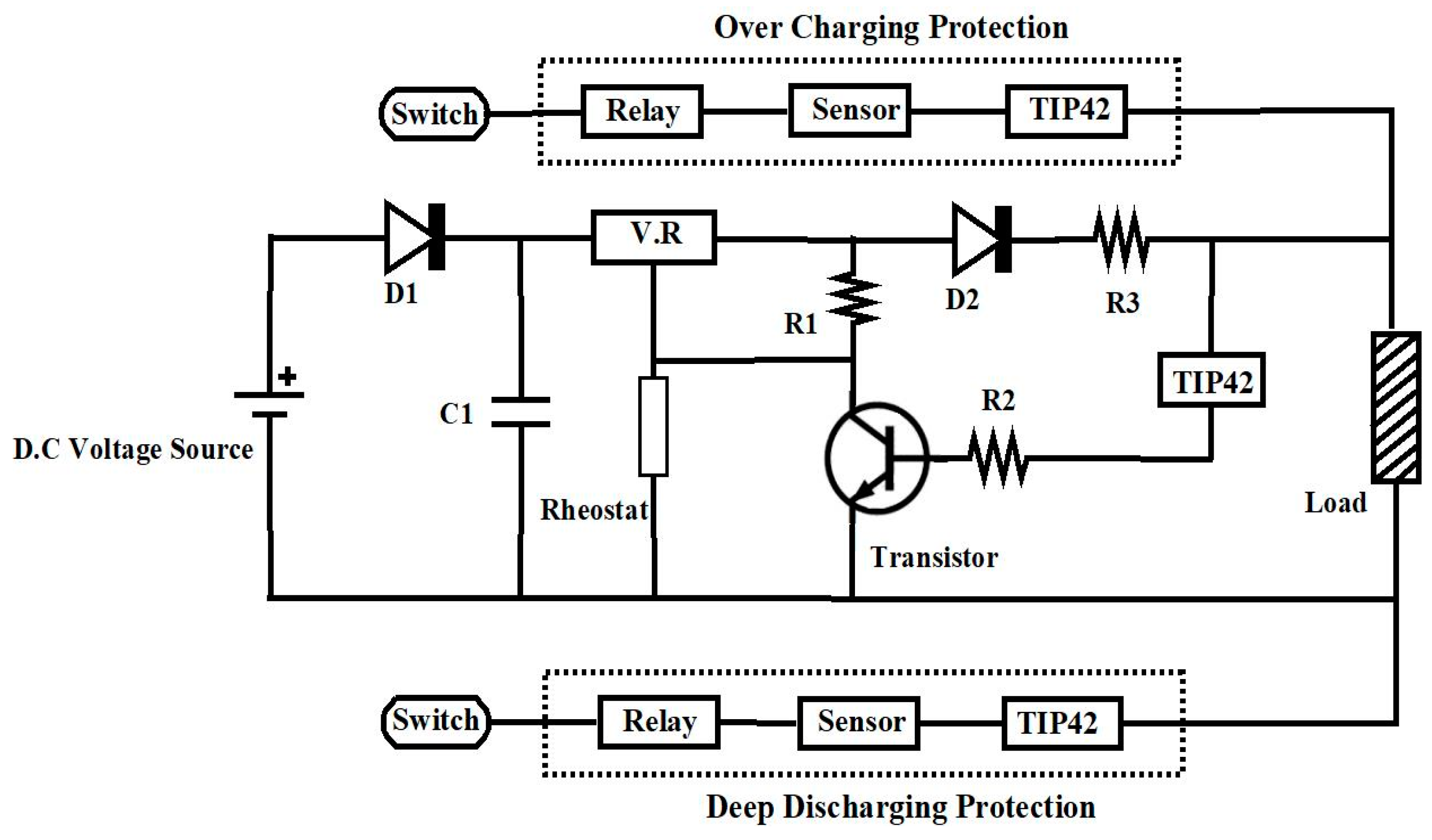
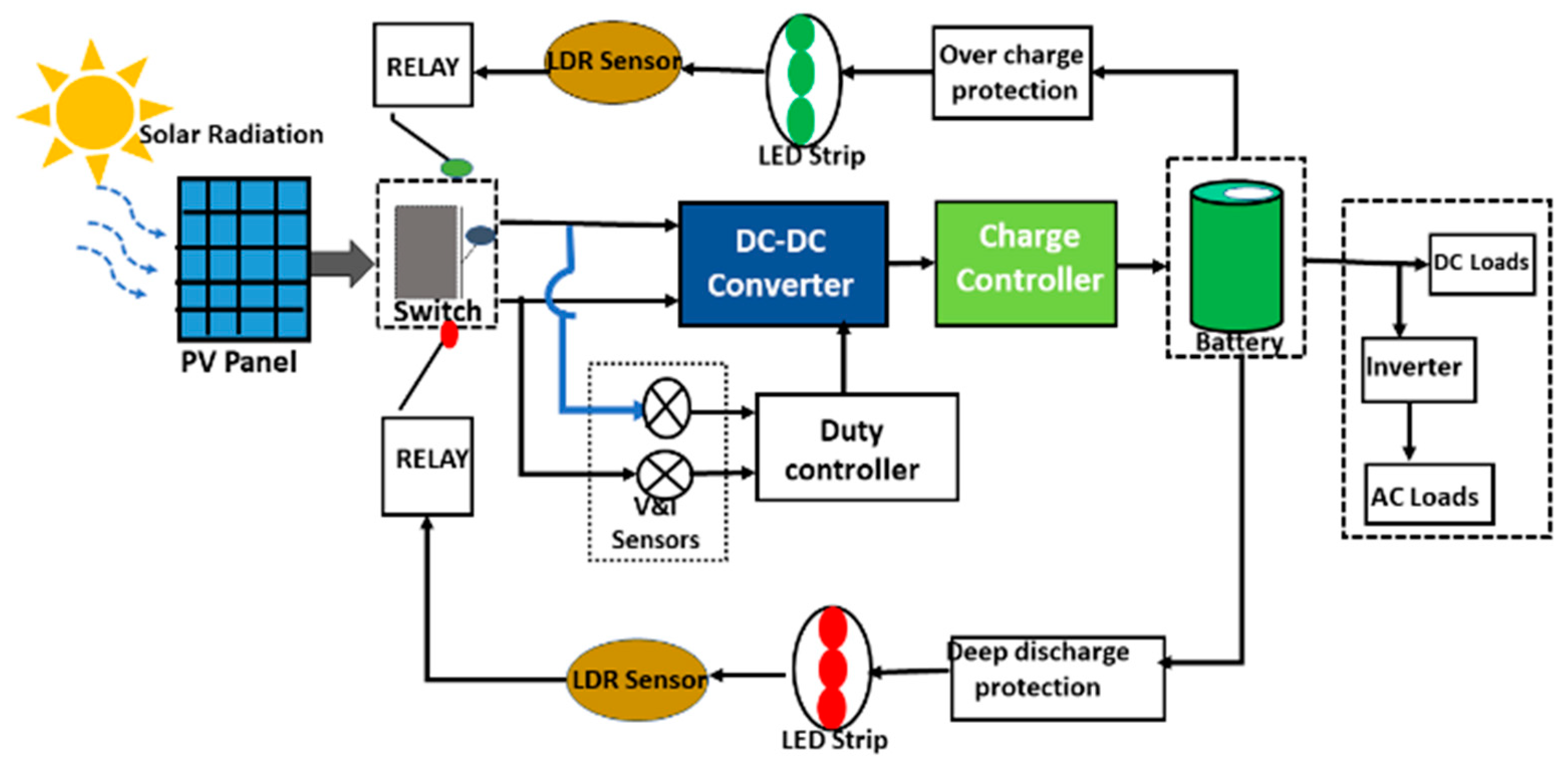
3. The Proposed Pulse Charging Protocol
3.1. PV Equivalent Circuit Analysis
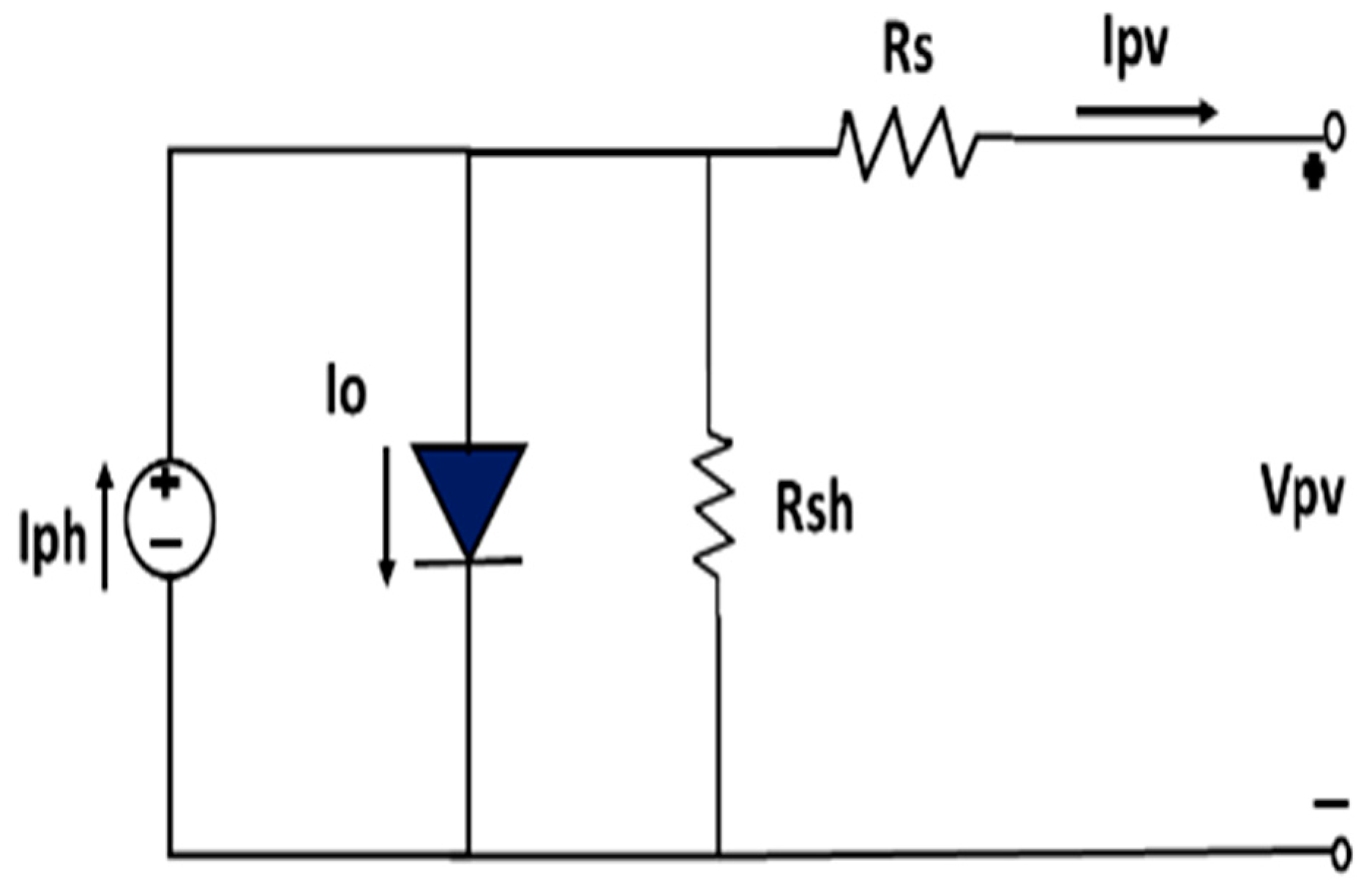
| PV Module Electrical Parameters and Ratings: 5 W/12 V | |
|---|---|
| Maximum Power (MPmax) | 5 W/12 V |
| Potential at Ultimate. Power (Vmp) | 17.40 V |
| Current at Optimum Power (Imp) | 0.26 A |
| The voltage at Open Circuit (Voc) | 21.50 V |
| Panel current at short circuit (Isc) | 0.32 A |
| Tolerance | +5% |
| Specifications are at STC 1000 W/m Irradiance AM 1.5, Cell Temp 25 °C | |
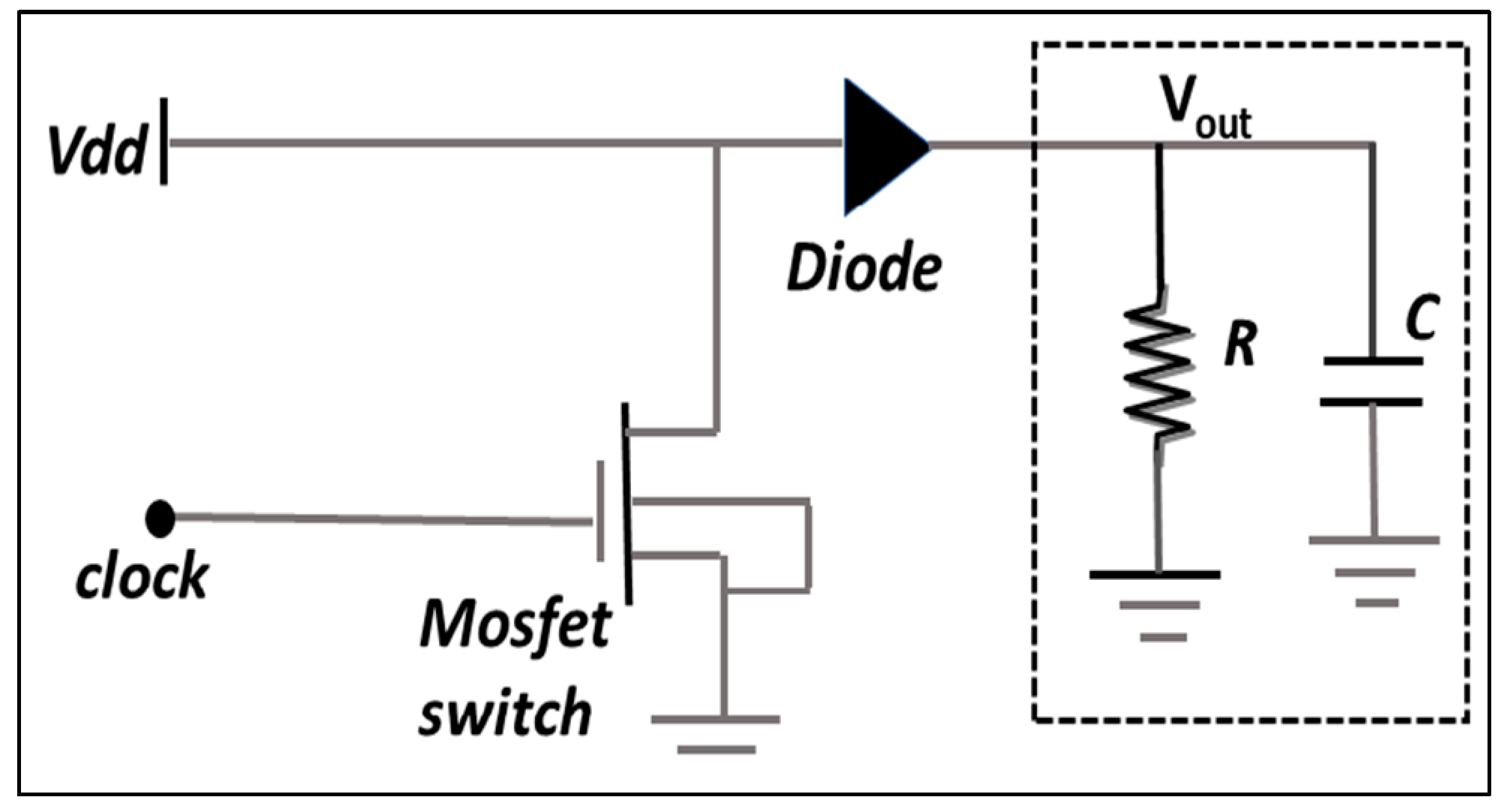
3.2. DC-DC Converter and Power Stage Design
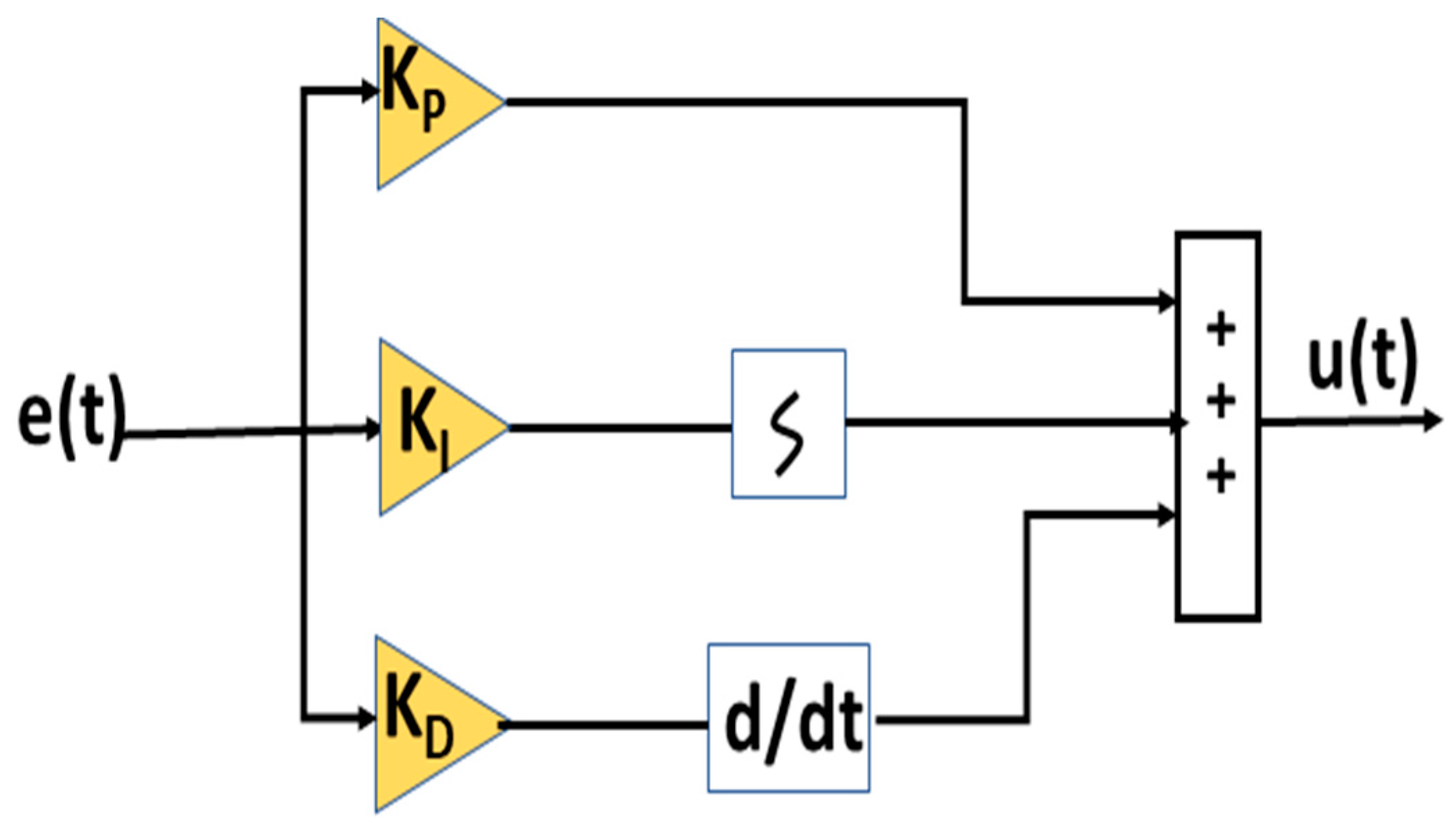
3.3. Control System Based on PID
3.4. Solar Charge Regulator
3.5. Sensor Fusion Process
4. Assessment of the Experiment and Test Results
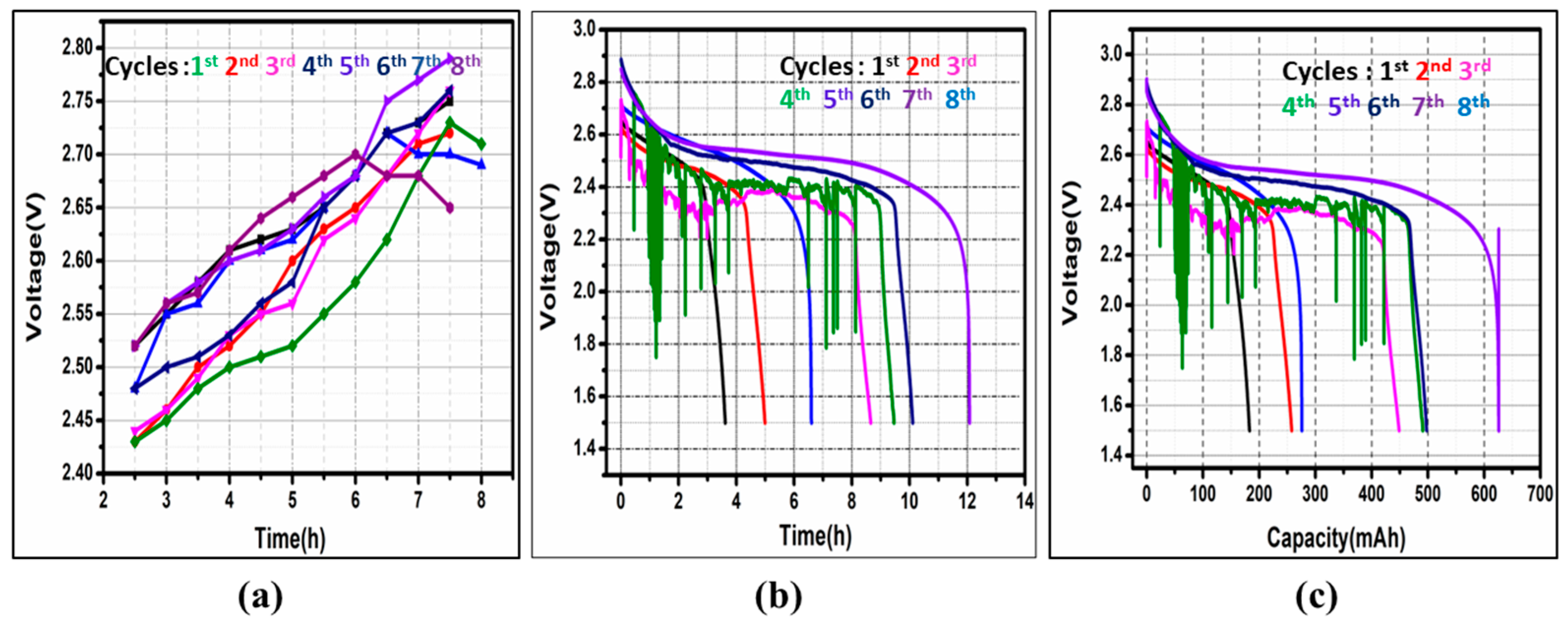
4.1. Traditional Charging Strategy
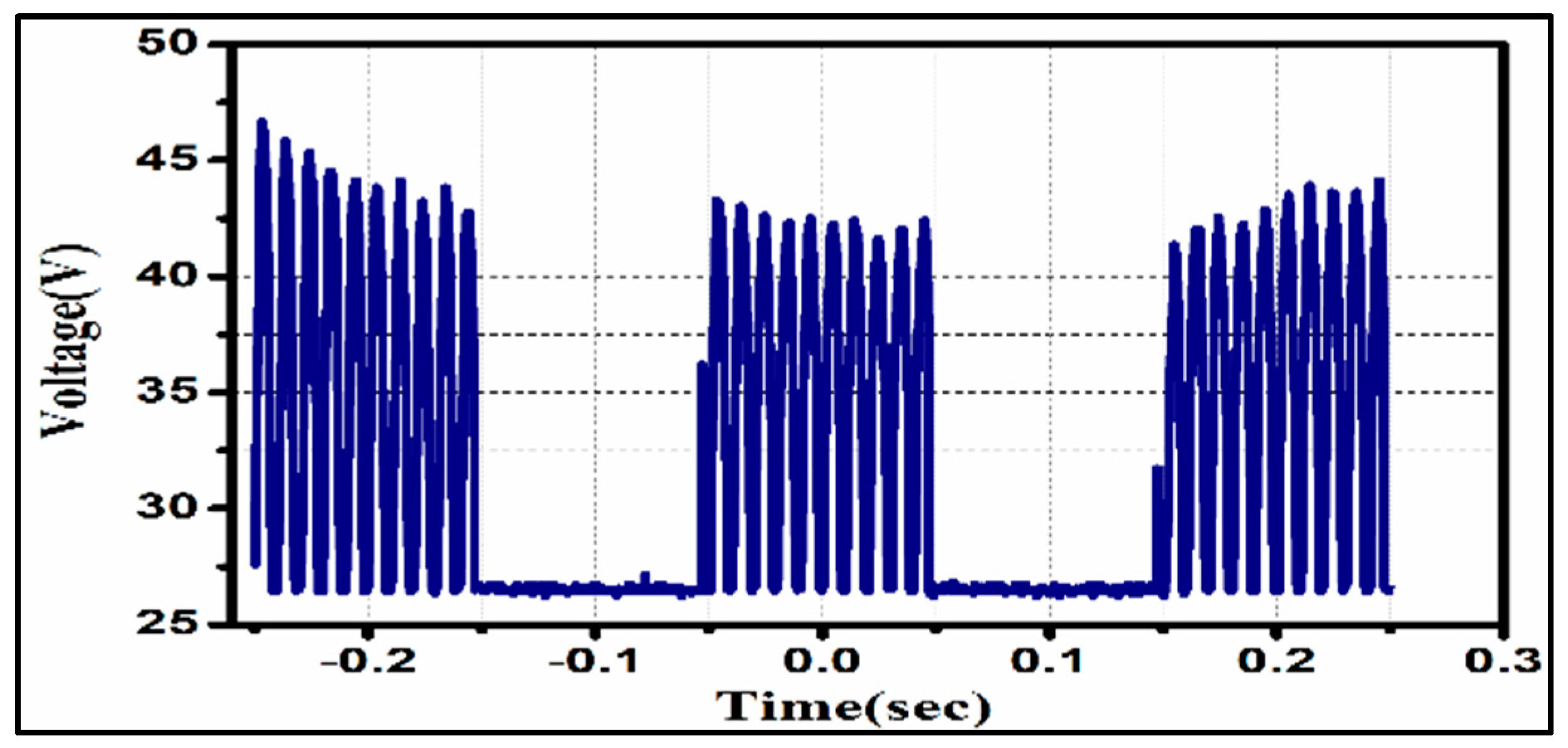
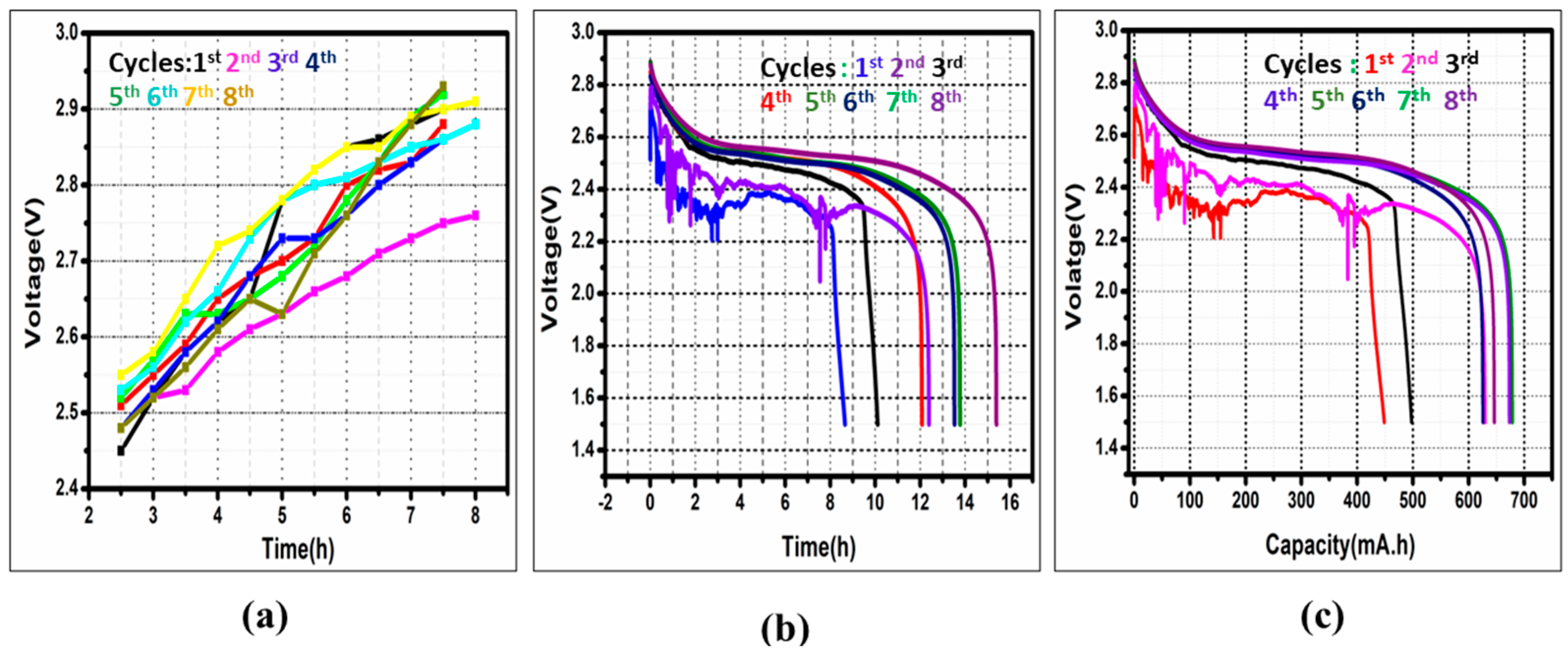
4.2. Proposed Efficient Pulse Charging Protocol
5. Comparative Evaluation and Results with Discussions
5.1. Impedance Study
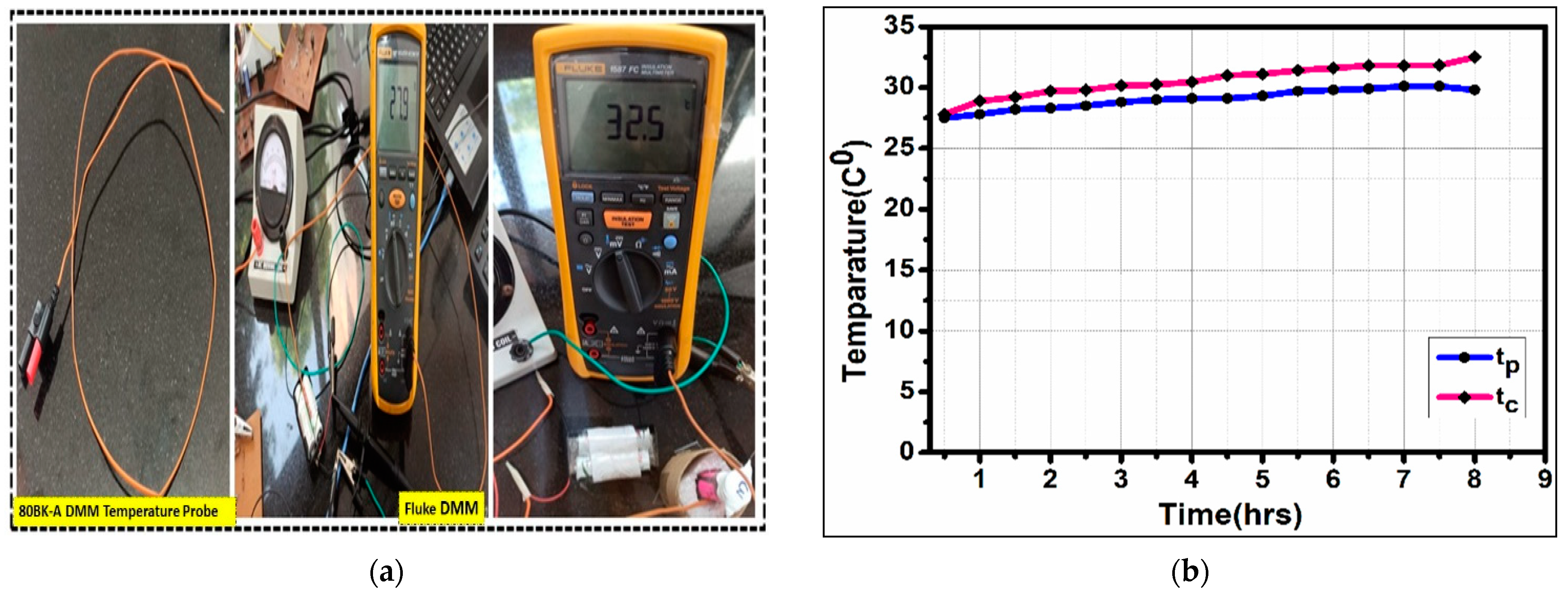
5.2. Thermal Study
5.3. Theoretical Analysis and Numerical Results
5.4. Discussions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Asadi, Y.; Eskandari, M.; Mansouri, M.; Moradi, M.H.; Savkin, A.V. A universal model for power converters of battery energy storage systems utilizing the impedance-shaping concepts. Int. J. Electr. Power Energy Syst. 2023, 149, 109055. [Google Scholar] [CrossRef]
- Chetan Singh, S. Solar Photovoltaics: Fundamentals, Technologies and Applications; PHI Learning Private Limited: Delhi, India, 2015. [Google Scholar]
- Sun, Z.; Eskandari, M.; Zheng, C.; Li, M. Handling Computation Hardness and Time Complexity Issue of Battery Energy Storage Scheduling in Microgrids by Deep Reinforcement Learning. Energies 2023, 16, 90. [Google Scholar] [CrossRef]
- Zheng, C.; Eskandari, M.; Li, M.; Sun, Z. GA–Reinforced Deep Neural Network for Net Electric Load Forecasting in Microgrids with Renewable Energy Resources for Scheduling Battery Energy Storage Systems. Algorithms 2022, 15, 338. [Google Scholar] [CrossRef]
- Bouselham, L.; Hajji, M.; Hajji, B.; Bouali, H. A new MPPT-based ANN for photovoltaic system under partial shading conditions. Energy Procedia 2017, 111, 924–933. [Google Scholar] [CrossRef]
- Chhipa, A.A.; Kumar, V.; Joshi, R.R.; Chakrabarti, P.; Jasinski, M.; Burgio, A.; Leonowicz, Z.; Jasinska, E.; Soni, R.; Chakrabarti, T. Adaptive neuro-fuzzy inference system-based maximum power tracking controller for variable speed WECS. Energies 2021, 14, 6275. [Google Scholar] [CrossRef]
- Alzayed, M.; Chaoui, H.; Farajpour, Y. Maximum power tracking for a wind energy conversion system using cascade-forward neural networks. IEEE Trans. Sustain. Energy 2021, 12, 2367–2377. [Google Scholar] [CrossRef]
- Tian, X.; Chau, K.T.; Liu, W.; Pang, H.; Lee, C.H. Maximum Power Tracking for Magnetic Field Editing-Based Omnidirectional Wireless Power Transfer. IEEE Trans. Power Electron. 2022, 37, 12901–12912. [Google Scholar] [CrossRef]
- LokeshReddy, M.; Kumar, P.P.; Chandra, S.A.M.; Babu, T.S.; Rajasekar, N. Comparative study on charge controller techniques for solar PV system. Energy Procedia 2017, 117, 1070–1077. [Google Scholar] [CrossRef]
- Osaretin, C.A.; Edeko, F.O. Design and implementation of a solar charge controller with variable output. Electr. Electron. Eng. 2015, 12, 40–50. [Google Scholar]
- Koehler, U. General overview of non-lithium battery systems and their safety issues. In Electrochemical Power Sources: Fundamentals, Systems, and Applications; Garche, J., Brandt, K., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 21–46. [Google Scholar]
- Eskandari, M.; Rajabi, A.; Savkin, A.V.; Moradi, M.H.; Dong, Z.Y. Battery energy storage systems (BESSs) and the economy-dynamics of microgrids: Review, analysis, and classification for standardization of BESSs applications. J. Energy Storage 2022, 55, 105627. [Google Scholar] [CrossRef]
- Chao, K.-H.; Huang, B.-Z. Quantitative Design for the Battery Equalizing Charge/Discharge Controller of the Photovoltaic Energy Storage System. Batteries 2022, 8, 278. [Google Scholar] [CrossRef]
- Yin, M.D.; Cho, J.; Park, D. Pulse-based fast battery IoT charger using dynamic frequency and duty control techniques based on multi-sensing of polarization curve. Energies 2016, 9, 209. [Google Scholar] [CrossRef]
- Eltawil, M.A.; Zhao, Z. MPPT techniques for photovoltaic applications. Renew. Sustain. Energy Rev. 2013, 25, 793–813. [Google Scholar] [CrossRef]
- Chen, K.; Tian, S.; Cheng, Y.; Bai, L. An improved MPPT controller for photovoltaic system under partial shading condition. IEEE Trans. Sustain. Energy 2014, 5, 978–985. [Google Scholar] [CrossRef]
- Bhandari, B.; Lee, K.T.; Lee, C.S.; Song, C.K.; Maskey, R.K.; Ahn, S.H. A novel off-grid hybrid power system comprised of solar photovoltaic, wind, and hydro energy sources. Appl. Energy 2014, 133, 236–242. [Google Scholar] [CrossRef]
- Taslimi, M.S.; Maleki Dastjerdi, S.; Bashiri Mousavi, S.; Ahmadi, P.; Ashjaee, M. Assessment and multi-objective optimization of an off-grid solar based energy system for a Conex. Energy Equip. Syst. 2021, 9, 127–143. [Google Scholar]
- Chen, L.R.; Chen, J.J.; Ho, C.M.; Wu, S.L.; Shieh, D.T. Improvement of Li-ion battery Discharging Performance by pulse and Sinusoidal current strategies. IEEE Trans. Ind. Electron. 2013, 60, 5620–5628. [Google Scholar] [CrossRef]
- Kwak, B.; Kim, M.; Kim, J. Add-on type pulse charger for quick charging Li-ion batteries. Electronics 2020, 9, 227. [Google Scholar] [CrossRef]
- Amanor-Boadu, J.M.; Guiseppi-Elie, A. Improved performance of li-ion polymer batteries through improved pulse charging algorithm. Appl. Sci. 2020, 10, 895. [Google Scholar] [CrossRef]
- Goldammer, E.; Kowal, J. Determination of the distribution of relaxation times by means of pulse evaluation for offline and online diagnosis of lithium-ion batteries. Batteries 2021, 7, 36. [Google Scholar] [CrossRef]
- Yadasu, S.; Jetti, V.R.; Awaar, V.K.; Gorle, M. Development of Novel Pulse Charger for Next-Generation Batteries. Energy Technol. 2023, 11, 2200894. [Google Scholar] [CrossRef]
- Amanor-Boadu, J.M.; Guiseppi-Elie, A.; Sánchez-Sinencio, E. The impact of pulse charging parameters on the life cycle of lithium-ion polymer batteries. Energies 2018, 11, 2162. [Google Scholar] [CrossRef]
- Serhan, H.A.; Ahmed, E.M. Effect of the different charging techniques on battery life-time. In Proceedings of the 2018 International Conference on Innovative Trends in Computer Engineering (ITCE), Aswan, Egypt, 19–21 February 2018; pp. 421–426. [Google Scholar]
- Praisuwanna, C.; Khomfoi, S. A pulse frequency technique for a quick charger. In Proceedings of the 2013 10th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Krabi, Thailand, 15–17 May 2013; pp. 1–6. [Google Scholar]
- Gumera, X.D.G.; Caberos, A.B.; Huang, S.C.; Liou, W.R.; Lin, J.C. A Variable Duty Cycle Pulse Train Charger for Improving Lead-Acid Battery Performance. In Proceedings of the 2017 Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 24–26 October 2017; pp. 1–4. [Google Scholar]
- Chu, Y.; Chen, R.; Liang, T.; Changchien, S.; Chen, J. Positive/negative pulse battery charger with energy feedback and power factor correction. In Proceedings of the Twentieth Annual IEEE Applied Power Electronics Conference and Exposition, Austin, TX, USA, 6–10 March 2005; Volume 2, pp. 986–990. [Google Scholar]
- Shen, W.; Vo, T.T.; Kapoor, A. Charging algorithms of lithium-ion batteries: An overview. In Proceedings of the 2012 7th IEEE Conference on Industrial Electronics and Applications (ICIEA), Singapore, 18–20 July 2012; pp. 1567–1572. [Google Scholar]
- Chen, L.R. A design of an optimal battery pulse charge system by frequency-varied technique. IEEE Trans. Ind. Electron. 2007, 54, 398–405. [Google Scholar] [CrossRef]
- Chen, L.R. Design of duty-varied voltage pulse charger for improving Li-ion battery-charging response. IEEE Trans. Ind. Electron. 2008, 56, 480–487. [Google Scholar] [CrossRef]
- Keil, P.; Jossen, A. Charging protocols for lithium-ion batteries and their impact on cycle life—An experimental study with different 18650 high-power cells. J. Energy Storage 2016, 6, 125–141. [Google Scholar] [CrossRef]
- Shaoqing, L.; Wu, Q.; Zhang, D.; Liu, Z.; He, Y.; Wang, Z.L.; Sun, C. Effects of pulse charging on the performances of lithium-ion batteries. Nano Energy 2019, 56, 555–562. [Google Scholar]
- Franco, F.L.; Ricco, M.; Mandrioli, R.; Viatkin, A.; Grandi, G. Current pulse generation methods for li-ion battery chargers. In Proceedings of the 2020 2nd IEEE International Conference on Industrial Electronics for Sustainable Energy Systems (IESES), Cagliari, Italy, 1–3 September 2020; IEEE: Piscataway, NJ, USA, 2020; Volume 1. [Google Scholar]
- Li, J.; Murphy, E.; Winnick, J.; Kohl, P.A. The effects of pulse charging on cycling characteristics of commercial lithium-ion batteries. J. Power Sources 2001, 102, 302–309. [Google Scholar] [CrossRef]
- Purushothaman, B.K.; Morrison, P.W.; Landau, U. Reducing mass-transport limitations by application of special pulsed current modes. J. Electrochem. Soc. 2005, 152, J33. [Google Scholar] [CrossRef]
- Jampeethong, P.; Khomfoi, S. An EV Quick Charging Station Using a Pulse Frequency Current Control Technique. In Proceedings of the 2015 12th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Hua Hin, Thailand, 24–27 June 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–5. [Google Scholar]
- Huang, X.; Liu, W.; Acharya, A.B.; Meng, J.; Teodorescu, R.; Stroe, D.I. Effect of pulsed current on charging performance of lithium-ion batteries. IEEE Trans. Ind. Electron. 2021, 69, 10144–10153. [Google Scholar] [CrossRef]
- Zhao, X.; Mu, G.; Tang, X.; Chen, M. Mid-IR Intraband Photodetectors with Colloidal Quantum Dots. Coatings 2022, 12, 467. [Google Scholar] [CrossRef]
- Al-Ezzi, A.S.; Ansari, M.N.M. Photovoltaic Solar Cells: A Review. Appl. Syst. Innov. 2022, 5, 67. [Google Scholar] [CrossRef]
- Carrasco, M.; Laudani, A.; Lozito, G.M.; Mancilla-David, F.; Riganti Fulginei, F.; Salvini, A. Low-cost solar irradiance sensing for pv systems. Energies 2017, 10, 998. [Google Scholar] [CrossRef]
- Bayod-Rújula, A.A. Solar photovoltaics (PV). In Solar Hydrogen Production; Academic Press: Cambridge, MA, USA, 2019; pp. 237–295. [Google Scholar]
- Zhang, T.; Fan, S.; Zhao, J.; Jiang, L.; Liu, H. Design and control of a multisensory five-finger prosthetic hand. In Proceedings of the 11th World Congress on Intelligent Control and Automation, Shenyang, China, 29 June–4 July 2024; IEEE: Piscataway, NJ, USA, 2014. [Google Scholar]
- Eldahab, Y.E.A.; Saad, N.H.; Zekry, A. Enhancing the design of battery charging controllers for photovoltaic systems. Renew. Sustain. Energy Rev. 2016, 58, 646–655. [Google Scholar] [CrossRef]
- Al-Quraan, A.; Al-Qaisi, M. Modelling, design, and control of a standalone hybrid PV-wind microgrid system. Energies 2021, 14, 4849. [Google Scholar] [CrossRef]
- Marinho, F.; Carvalho, C.M.; Apolinário, F.R.; Paulucci, L. Measuring light with light-dependent resistors: An easy approach for optics experiments. Eur. J. Phys. 2019, 40, 035801. [Google Scholar] [CrossRef]
- Fetcenko, M.A.; Ovshinsky, S.R.; Reichman, B.; Young, K.; Fierro, C.; Koch, J.; Zallen, A.; Mays, W.; Ouchi, T. Recent advances in NiMH battery technology. J. Power Sources 2007, 165, 544–551. [Google Scholar] [CrossRef]
- Xiong, X.; Wang, S.L.; Fernandez, C.; Yu, C.M.; Zou, C.Y.; Jiang, C. A novel practical state of charge estimation method: An adaptive improved ampere-hour method based on composite correction factor. Int. J. Energy Res. 2020, 44, 11385–11404. [Google Scholar] [CrossRef]
- Nichols, D. Arduino-based data acquisition into Excel, LabVIEW, and MATLAB. Phys. Teach. 2017, 55, 226–227. [Google Scholar] [CrossRef]
- Arabsalmanabadi, B.; Tashakor, N.; Javadi, A.; Al-Haddad, K. Charging techniques in lithium-ion battery charger: Review and new solution. In Proceedings of the IECON2018—44th Annual Conference of the IEEE Industrial Electronics Society, Washington, DC, USA, 21–23 October 2018; IEEE: Piscataway, NJ, USA, 2018. [Google Scholar]
- Berliner, M.D.; Jiang, B.; Cogswell, D.A.; Bazant, M.Z.; Braatz, R.D. Fast charging of lithium-ion batteries by mathematical reformulation as mixed continuous-discrete simulation. In Proceedings of the 2022 American Control Conference (ACC), Atlanta, GA, USA, 8–10 June 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Heidari, S.; Hatami, A.; Eskandari, M. An intelligent capacity management system for interface converter in AC-DC hybrid microgrids. Appl. Energy 2022, 316, 119112. [Google Scholar] [CrossRef]
- Asadi, Y.; Eskandari, M.; Mansouri, M.; Savkin, A.V.; Pathan, E. Frequency and Voltage Control Techniques through Inverter-Interfaced Distributed Energy Resources in Microgrids: A Review. Energies 2022, 15, 8580. [Google Scholar] [CrossRef]
- Nerubatskyi, V.; Plakhtii, O.; Hordiienko, D. Efficiency analysis of DC-DC converter with pulse-width and pulse-frequency modulation. In Proceedings of the IEEE 41st International Conference on Electronics and Nanotechnology (ELNANO), Kyiv, Ukraine, 10–14 October 2022; IEEE: Piscataway, NJ, USA, 2022. [Google Scholar]
- Vedith, S.; Bhanu Tej, J.N.; Sampath, S.; Usha Sree, M.; Nithin Rao, P.; Neelima, K. Review on Pulse Width Modulation and Optimization Techniques for Multilevel Inverters. In International Conference on Artificial Intelligence and Sustainable Engineering: Select Proceedings of AISE 2020; Sanyal, G., Travieso-Gonzáles, C.M., Awasthi, S., Purushothama, B.R., Eds.; Springer Nature: Singapore, 2022; Volume 1, p. 1. [Google Scholar]
- Tushar, W.; Yuen, C.; Huang, S.; Smith, D.B.; Poor, H.V. Cost minimization of charging stations with photovoltaics: An approach with EV classification. IEEE Trans. Intell. Transp. Syst. 2015, 17, 156–169. [Google Scholar] [CrossRef]
- Single, F.; Horstmann, B.; Latz, A. Theory of impedance spectroscopy for lithium batteries. J. Phys. Chem. C 2019, 123, 27327–27343. [Google Scholar] [CrossRef]
- Song, S.; Zhang, X.; Li, C.; Wang, K.; Sun, X.; Huo, Q.; Wei, T.; Ma, Y. Equivalent circuit models and parameter identification methods for lithium-ion capacitors. J. Energy Storage 2019, 24, 100762. [Google Scholar] [CrossRef]
- Chang, W.Y. The State of Charge Estimating Methods for Battery: A Review. ISRN Appl. Math. 2013, 24, 100762. [Google Scholar] [CrossRef]
- Onda, K.; Ohshima, T.; Nakayama, M.; Fukuda, K.; Araki, T. Thermal behavior of small lithium-ion battery during rapid charge and discharge cycles. J. Power Sources 2006, 158, 535–542. [Google Scholar] [CrossRef]
- Khan, M.R.; Swierczynski, M.J.; Kær, S.K. Towards an ultimate battery thermal management system: A review. Batteries 2017, 3, 9. [Google Scholar] [CrossRef]
- Zhu, W.H.; Zhu, Y.; Tatarchuk, B.J. Self-discharge characteristics and performance degradation of Ni-MH batteries for storage applications. Int. J. Hydrogen Energy 2014, 39, 19789. [Google Scholar] [CrossRef]
- Eskandari, M.; Savkin, A.V.; Fletcher, J. Convolutional Neural Network with Reinforcement Learning for Trajectories Boundedness of Fault Ride-Through Transients of Grid-Feeding Converters in Microgrids. IEEE Trans. Ind. Inform. 2024, 20, 4906–4918. [Google Scholar] [CrossRef]
- Eskandari, M.; Savkin, A.V.; Fletcher, J. A Deep Reinforcement Learning-Based Intelligent Grid-Forming Inverter for Inertia Synthesis by Impedance Emulation. IEEE Trans. Power Syst. 2023, 38, 2978–2981. [Google Scholar] [CrossRef]

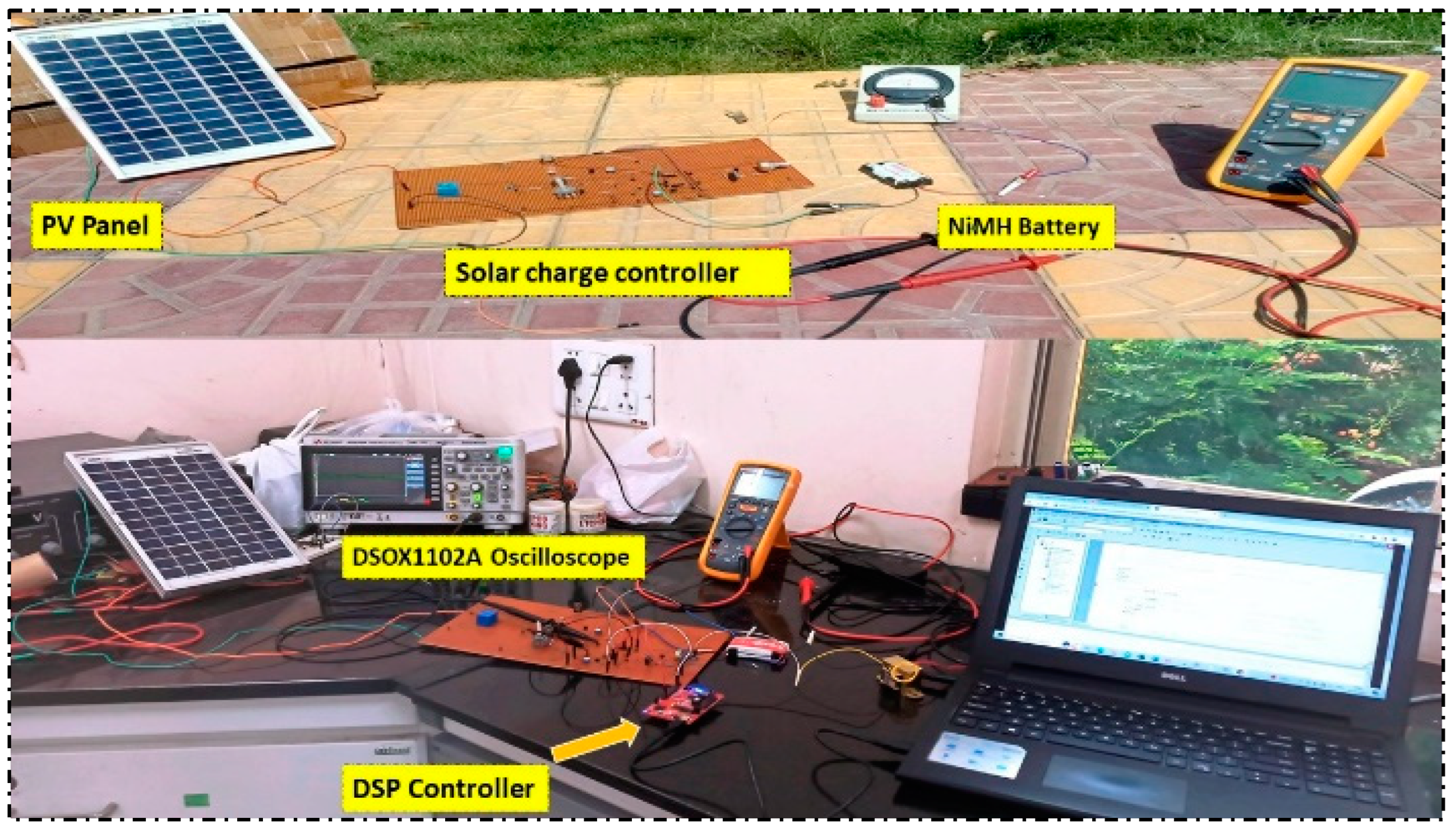



| Circuit Parameters for a Prototype Solar Charge Controller | |
|---|---|
| Steady Input voltage | 16.5 V |
| Input current | 60 mA |
| Output voltage | 14.3 V |
| Output stable current | 50 mA |
| Resistors | 100, 180, 470, 1 k ohms |
| Diode | IN4007 |
| Rheostats | 1 k, 2 k, 5 k ohms |
| Switching Frequency | 25 KHz |
| LDR | 6 |
| Relays | 1 |
| Transistors | BC 541, TL431, TIP42C |
| Battery Specifications | Traditional Mode Charging | Pulse Charging |
|---|---|---|
| Total charging period (h) | 7:30 | 7:30 |
| Total discharging period (h) | 10:06 | 13:45 |
| Battery Capacity (mAh) | 498 | 678 |
| Battery Cell Voltage (V) | 2.7 | 2.9 |
| Battery Cycle Life (cycles) | 270 | 339 |
| S. No | Parameters | CCCV Mode Charging | Pulse Mode Charging |
|---|---|---|---|
| 1 | Start voltage (V) | 2.4 | 2.4 |
| 2 | End voltage (V) | 2.7 | 2.9 |
| 3 | Start temperature(0 °C) | 26 °C | 26 °C |
| 4 | End temperature(0 °C) | 32.5 °C | 29 °C |
| 5 | Total charge time (h) | 7:30 | 7:30 |
| 6 | Total discharge time (h) | 10:06 | 13:45 |
| 7 | Charging Speed improvements (%) | 66.4 | 90.4, i.e., (24%) |
| 8 | Total discharge capacity (mAh) | 498 | 678 |
| 9 | Total Capacity improvement (%) | 498 | 678 i.e., (36.14%) |
| 10 | Cycle life improvements | 270 | 339, i.e., (+69 cycles) |
| 11 | Temperature Rise (∆TMAX) | 6.5 °C | 3 °C |
| 12 | Impedance Rise | 1.8 Ω | 1.3 Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadasu, S.; Awaar, V.K.; Jetti, V.R.; Eskandari, M. Sensor Fusion-Based Pulsed Controller for Low Power Solar-Charged Batteries with Experimental Tests: NiMH Battery as a Case Study. Batteries 2024, 10, 335. https://doi.org/10.3390/batteries10090335
Yadasu S, Awaar VK, Jetti VR, Eskandari M. Sensor Fusion-Based Pulsed Controller for Low Power Solar-Charged Batteries with Experimental Tests: NiMH Battery as a Case Study. Batteries. 2024; 10(9):335. https://doi.org/10.3390/batteries10090335
Chicago/Turabian StyleYadasu, Shyam, Vinay Kumar Awaar, Vatsala Rani Jetti, and Mohsen Eskandari. 2024. "Sensor Fusion-Based Pulsed Controller for Low Power Solar-Charged Batteries with Experimental Tests: NiMH Battery as a Case Study" Batteries 10, no. 9: 335. https://doi.org/10.3390/batteries10090335
APA StyleYadasu, S., Awaar, V. K., Jetti, V. R., & Eskandari, M. (2024). Sensor Fusion-Based Pulsed Controller for Low Power Solar-Charged Batteries with Experimental Tests: NiMH Battery as a Case Study. Batteries, 10(9), 335. https://doi.org/10.3390/batteries10090335







