Design and Implementation of a Non-Destructive AC Heating System for Lithium-Ion Battery Modules
Abstract
1. Introduction
- An AC thermoelectric heating model for electric bicycles is established, and the experimental results verify the effectiveness of this model at different AC heating frequencies and currents.
- In the case of considering the normal working scenario, a creative low-temperature heating application of the electric bicycle lithium-ion battery is considered in the battery swapping scenario.
- A prototype AC heating system is designed for an electric bicycle lithium-ion battery module. It is of great significance to solve the problem of low-temperature heating of electric bicycles in cold regions.
2. Mathematical Model and Design Requirement Analysis
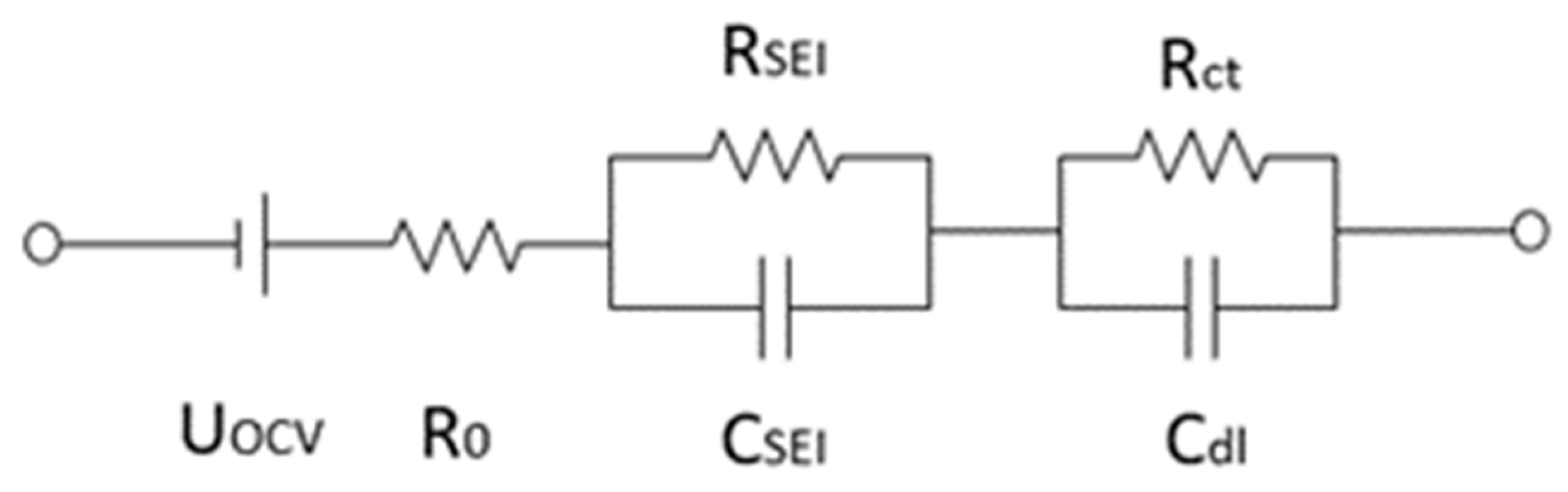
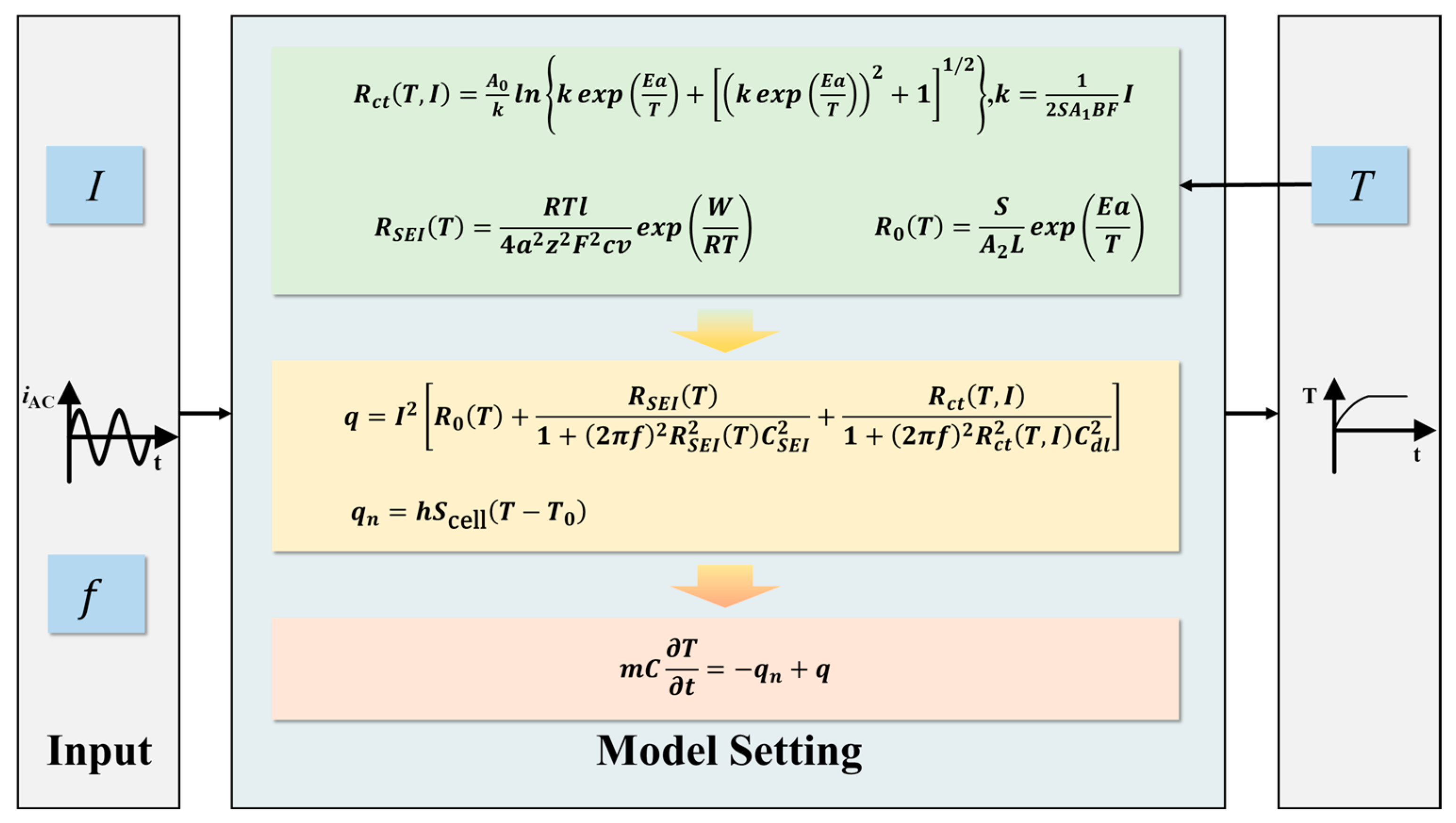
2.1. Modeling
2.2. Model Simulation
3. System Design
3.1. Design Requirement Analysis
3.2. Topological Structure and Hardware Design
3.3. Determination of Main Parameters
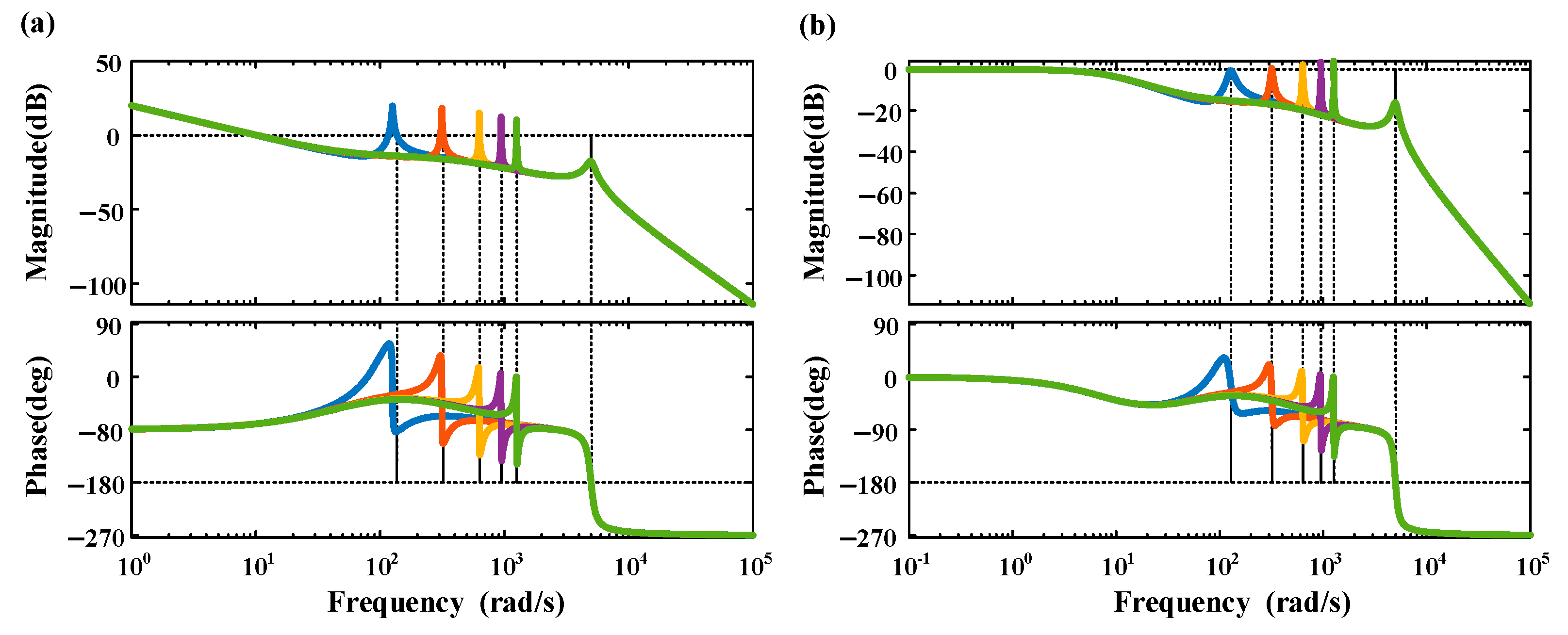
3.4. Full-Bridge Topology Modeling
3.5. System Control Strategy
3.6. System Simulation
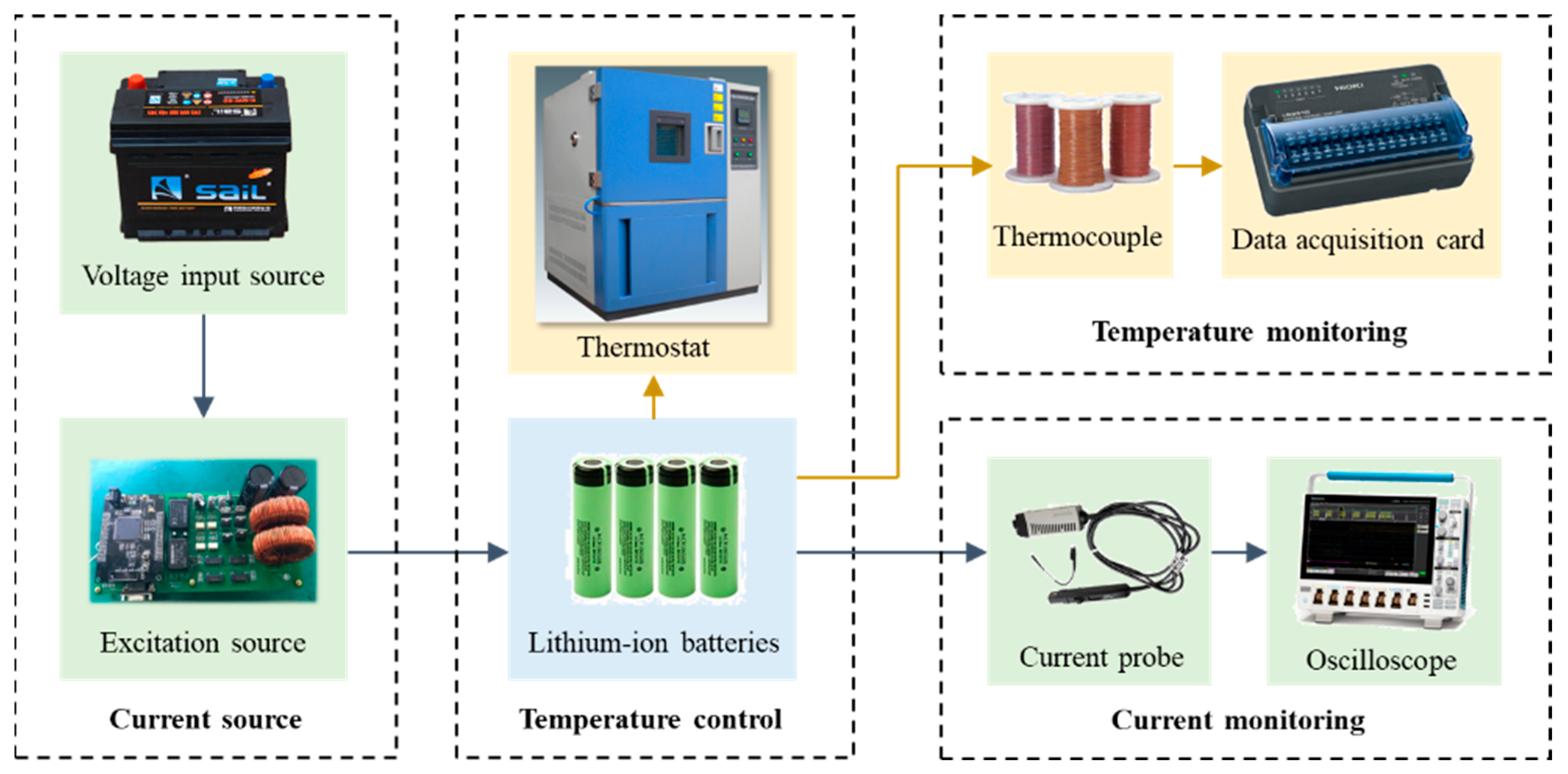
4. Experimental Section
5. Results and Discussion
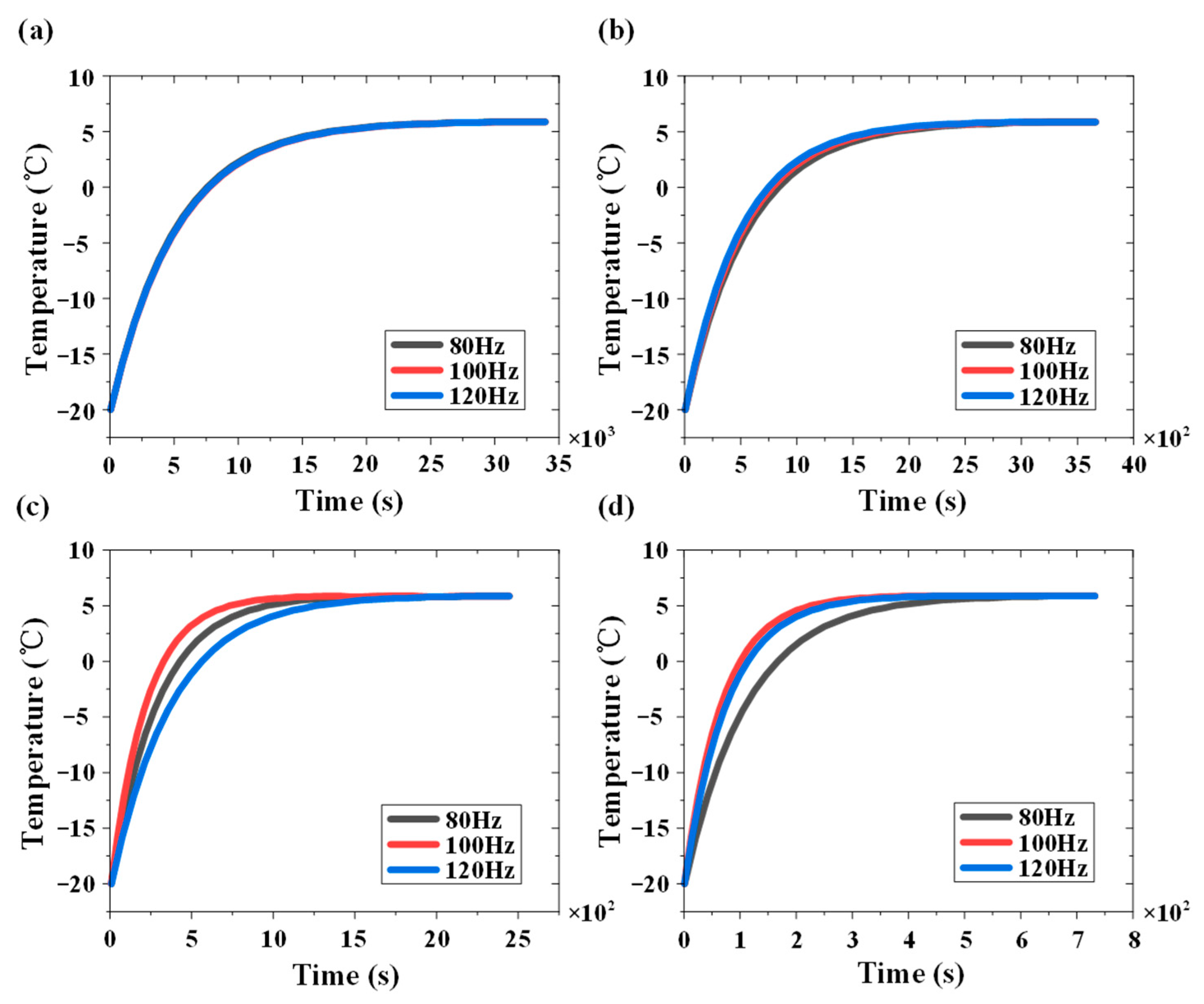
5.1. System Verification
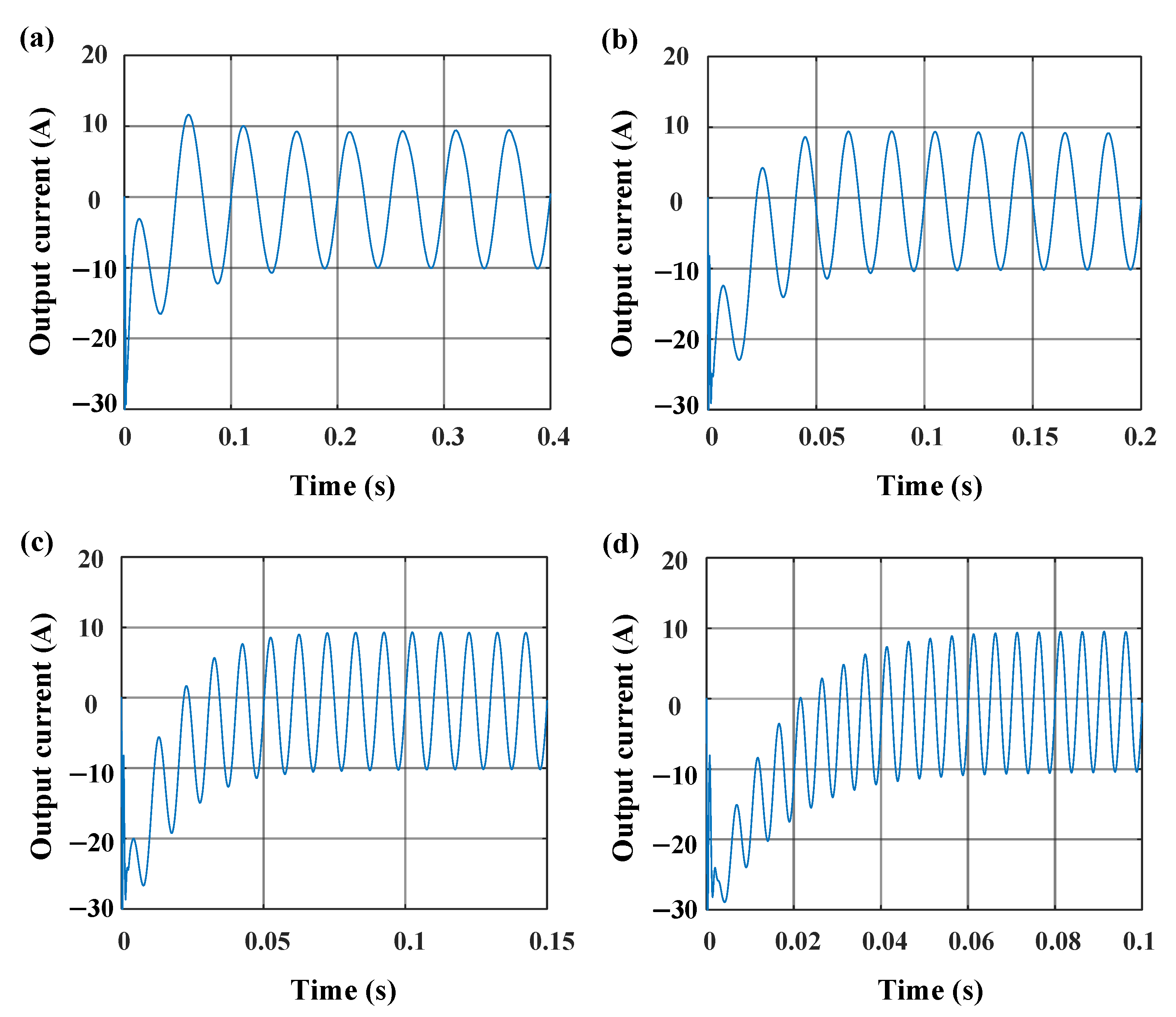
5.1.1. Verification of Current Control Effect
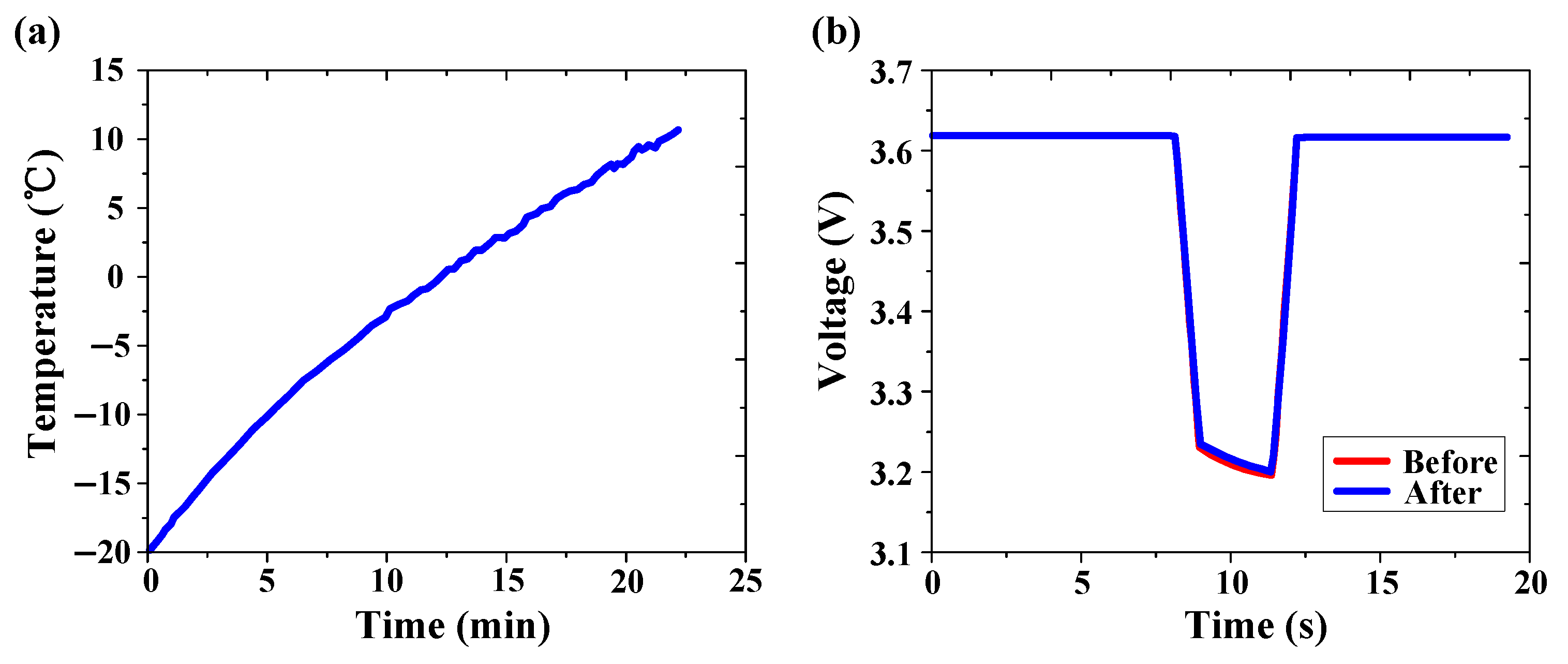
5.1.2. Heating Effect Verification
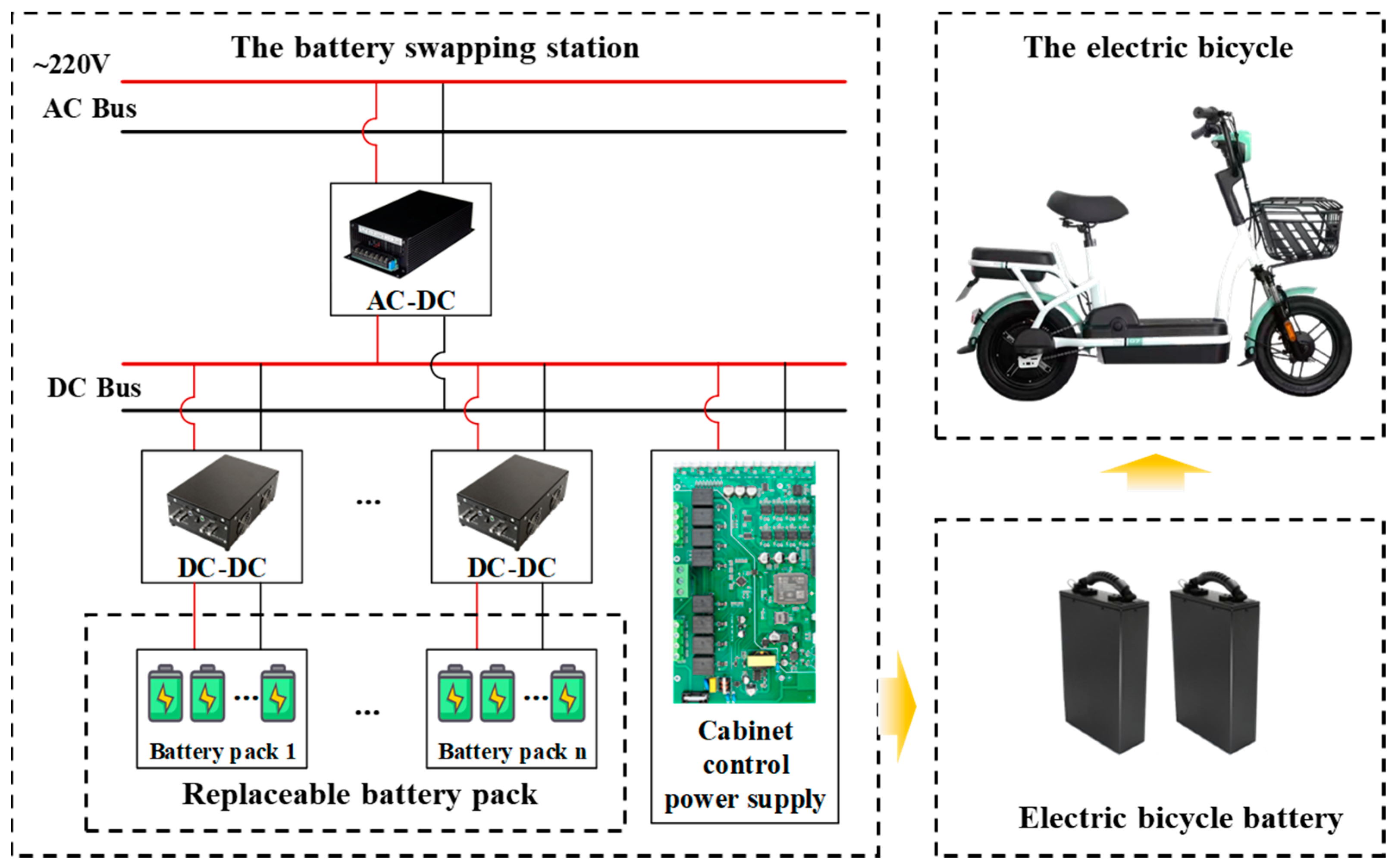
6. System Implementation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhao, L.; Shen, S.; Zhao, Z. Planning decentralized battery-swapping recharging facilities for e-bike sharing systems. Sustain. Cities Soc. 2024, 101, 105118. [Google Scholar] [CrossRef]
- Xie, X.; Dai, X.; Pei, Z. Empowering the Capillary of the Urban Daily Commute: Battery Deployment Analysis for the Locker-Based E-bike Battery Swapping. Transp. Sci. 2024, 58, 176–197. [Google Scholar] [CrossRef]
- Ahmad, F.; Alam, M.S.; Alsaidan, I.S.; Shariff, S.M. Battery Swapping Station for Electric Vehicles: Opportunities and Challenges. Iet Smart Grid 2020, 3, 280–286. [Google Scholar] [CrossRef]
- Zhang, S.S.; Xu, K.; Jow, T.R. Charge and Discharge Characteristics of a Commercial LiCoo2-Based 18650 Li-ion Battery. J. Power Sources 2006, 160, 1403–1409. [Google Scholar] [CrossRef]
- Sun, B.; Qi, X.; Song, D.; Ruan, H. Review of Low-Temperature Performance, Modeling and Heating for Lithium-Ion Batteries. Energies 2023, 16, 7142. [Google Scholar] [CrossRef]
- Elbuluk, M.E.; Hammoud, A.; Gerber, S.; Patterson, R.L. Low Temperature Performance Evaluation of Battery Management Technologies. In Proceedings of the 34th Intersociety Energy Conversion Engineering Conference, Vancouver, BC, Canda, 2–5 August 1999; pp. 313–318. [Google Scholar]
- Zhang, S.S.; Xu, K.; Jow, T.R. The Low Temperature Performance of Li-Ion Batteries. J. Power Sources 2003, 115, 137–140. [Google Scholar] [CrossRef]
- Fan, W.; Zhu, J.; Qiao, D.; Jiang, B.; Wang, X.; Wei, X.; Dai, H. Low-Temperature Charging Strategy Optimization Based on Electrochemical-Aging-Thermal Coupling Model. IEEE Trans. Transp. Electrif. 2024, 1, 35. [Google Scholar] [CrossRef]
- Wankhede, S.; More, K.; Kamble, L. A Review of Li-ion Battery Temperature Control and A Key Future Perspective on Cutting-Edge Cooling Methods For Electrical Vehicle Applications. Energy Storage 2024, 6, e572. [Google Scholar] [CrossRef]
- Kulova, T.L.; Skundin, A.M.; Nizhnikovskii, E.A.; Fesenko, A.V. Temperature Effect on the Lithium Diffusion Rate in Graphite. Russ. J. Electrochem. 2006, 42, 259–262. [Google Scholar] [CrossRef]
- Hein, S.; Latz, A. INFLUENCE of Local Lithium Metal Deposition in 3D Microstructures on Local and Global Behavior of LITHIUM-ion Batteries. Electrochim. Acta 2016, 201, 354–365. [Google Scholar] [CrossRef]
- Janakiraman, U.; Garrick, T.R.; Fortier, M.E. Review-Lithium Plating Detection Methods in Li-Ion Batteries. J. Electrochem. Soc. 2020, 167, 160552. [Google Scholar] [CrossRef]
- Suthar, B.; Sonawane, D.; Braatz, R.D.; Subramanian, V.R. Optimal Low Temperature Charging of Lithium-ion Batteries. In Proceedings of the 9th IFAC Symposium on Advanced Control of Chemical Processes ADCHEM 2015, Whistler, CA, USA, 7–10 June 2015; pp. 1216–1221. [Google Scholar]
- Huang, R.; Wei, G.; Zhou, X.; Zhu, J.; Pan, X.; Wang, X.; Jiang, B.; Wei, X.; Dai, H. Targeting the Low-Temperature Performance Degradation of Lithium-Ion Batteries: A Non-Destructive Bidirectional Pulse Current Heating Framework. Energy Storage Mater. 2024, 65, 103173. [Google Scholar] [CrossRef]
- Jaguemont, J.; Boulon, L.; Venet, P.; Dubé, Y.; Sari, A. Lithium-Ion Battery Aging Experiments at Subzero Temperatures and Model Development for Capacity Fade Estimation. IEEE Trans. Veh. Technol. 2016, 65, 4328–4343. [Google Scholar] [CrossRef]
- Kim, R.; Kim, Y.; Lee, D.H.; Kim, S.; Kim, D.K. Thermal-Electrochemical Effect on the Degradation of Lithium-Ion Batteries During the Charging Process. Int. Commun. Heat Mass Transf. 2024, 158, 107855. [Google Scholar] [CrossRef]
- Wei, G.; Zhang, G.; Chen, S.; Jiang, B.; Zhu, J.; Han, G.; Wei, X.; Dai, H. Experimental Study on Effect of State of Charge on Thermal Runaway Characteristics of Commercial Large-Format NCM811 Lithium-Ion Battery; SAE International: Warrendale, PA, USA, 2023. [Google Scholar]
- Thakur, A.K.; Sathyamurthy, R.; Velraj, R.; Saidur, R.; Pandey, A.K.; Ma, Z.; Singh, P.; Hazra, S.K.; Sharshir, S.W.; Prabakaran, R.; et al. A State-of-the Art Review on Advancing Battery Thermal Management Systems for Fast-charging. Appl. Therm. Eng. 2023, 226, 120303. [Google Scholar] [CrossRef]
- Siruvuri, S.D.V.S.S.V.; Budarapu, P.R. Studies on Thermal Management of Lithium-Ion Battery Pack Using Water as the Cooling Fluid (Article). J. Energy Storage 2020, 29, 101377. [Google Scholar] [CrossRef]
- Amy, C.; Pishahang, M.; Kelsall, C.C.; LaPotin, A.; Henry, A. High-temperature Pumping of Silicon for Thermal Energy Grid Storage. Energy 2021, 233, 121105. [Google Scholar] [CrossRef]
- Yao, J.; Wang, Z.; Ma, J. Dehydration Method for Lithium ion Battery Core, Involves Pulsating High-Temperature Gas Circulating via Circulation Device Connected With Sealed Container and Extracting High-Temperature Gas for Reducing Internal Pressure of Container; Shandong Sacred Sun Power Sources Co., Ltd. (SHAN-Non-standard): Yantai, China, 2016. [Google Scholar]
- Ross, M.; Lin, T.Y.; Wicoff, I.; Sieh, B.; Sabharwall, P.; McEligot, D.E.; Bindra, H. Passive Heat Removal in Horizontally Oriented Micro-HTGRs. Prog. Nucl. Energy 2023, 156, 104530. [Google Scholar] [CrossRef]
- Lei, Z.; Zhang, C.; Dong, Y.; Lin, Z. Low-Temperature Performance and Heating Method of Lithium Battery in Electric Vehicles. Beijing Gongye Daxue Xuebao/J. Beijing Univ. Technol. 2013, 39, 1399. [Google Scholar]
- Zhang, S.; Li, T.; Chen, L. Fuzzy Logic Control of External Heating System for Electric Vehicle Batteries at Low Temperature. World Electr. Veh. J. 2023, 14, 99. [Google Scholar] [CrossRef]
- Nolte, O.; Heim, U. Temperature Control Element for Battery, Which Drives Electric Vehicle, Has Ptc Heating Element for Heating Element, and Base Surface Provided in Element, Which Transfers Heat between Element and Battery Module of Battery; Porsche Ag F (Pors-C) Volkswagen Ag (Vols-C): Wolfsburg, DE, USA, 2018. [Google Scholar]
- Sarvar-Ardeh, S.; Rashidi, S.; Rafee, R.; Karimi, N. A Review on the Applications of Micro-/Mini-Channels for Battery Thermal Management. J. Therm. Anal. Calorim. 2023, 148, 7959–7979. [Google Scholar] [CrossRef]
- Zhang, L.; Zhao, H.; Liang, S.; Liu, C. Heat Transfer in Phase Change Materials for Integrated Batteries and Power Electronics Systems. Appl. Therm. Eng. 2023, 232, 120997. [Google Scholar] [CrossRef]
- Gao, C.; Sun, K.; Song, K.; Zhang, K.; Hou, Q. Performance Improvement of a Thermal Management System for Lithium-Ion Power Battery Pack by the Combination of Phase Change Material and Heat Pipe. J. Energy Storage 2024, 82, 110512. [Google Scholar] [CrossRef]
- Sevugan, P.A.; Pradeep, M.; Krishnaswamy, A.; Karunamurthy, K. Battery Thermal Management System for electric vehicles using Phase Change Materials. In Proceedings of the 2nd International Conference on Sustainable Energy Solutions for a Better Tomorrow (SESBT), Vellore Inst Technol, Chennai, India, 23–24 July 2021; pp. 1604–1611. [Google Scholar]
- Upadhyay, D.; Mujadia, V.; Daruwala, R.; Lakdawala, A.; Shah, D.V. Investigation on Performance of Composite Phase Change Material Based Thermal Management of Electrical Battery. Int. J. Interact. Des. Manuf. 2024, 1, 1–10. [Google Scholar] [CrossRef]
- Huang, R.; Wei, G.; Jiang, B.; Zhu, J.; Pan, X.; Wang, X.; Zhou, X.; Ye, J.; Wei, X.; Dai, H. Investigating the Effect of Different Bidirectional Pulsed Current Parameters on the Heat Generation of Lithium-Ion Battery at Low Temperatures. Batteries 2023, 9, 457. [Google Scholar] [CrossRef]
- Ruan, H.; Jiang, J.; Sun, B.; Zhang, W.; Gao, W.; Wang, L.; Ma, Z. A Rapid Low-Temperature Internal Heating Strategy with Optimal Frequency Based on Constant Polarization Voltage for Lithium-Ion Batteries. Appl. Energy 2016, 177, 771–782. [Google Scholar] [CrossRef]
- Stuart, T.A.; Hande, A. HEV Battery Heating Using AC Currents. J. Power Sources 2004, 129, 368–378. [Google Scholar] [CrossRef]
- Qu, Z.; Jiang, Z.; Wang, Q. Experimental Study on Pulse Self–Heating of Lithium–ion Battery at Low Temperature. Int. J. Heat Mass Transf. 2019, 135, 696–705. [Google Scholar] [CrossRef]
- Arvind, S.; Naik, S.; Sirisha, T.; Madhavi, P.; Ogeti, P.S.; Tharun, O.; Praneeth, D.; Uday, B.; Rakesh, P.; Satyanarayana, S.V. Electric Tricycle I.E. Hybrid Tricycle for Used by Physically-Handicapped People, Has Smart Starter System Comprising Hub Motor Kit, Battery Pack, Li-Ion Battery Charger Pack, Arduino Uno, Lm35 Sensor, Cooling Fans and Sine Wave Controller; Hyderabad Technology & Management Inst. (HYDE-Non-standard): Hyderabad, India, 2024. [Google Scholar]
- Geun, P.J. Charger Air Cooling Structure of Portable Terminal for Two-Wheeled Vehicle E.G. Motorcycle, Has Heat Dissipation Fins That Are Attached to Substrate of Circuit Structure and Positioned in Second Air Chamber; GEUN P J. (GEUN-Individual): Seoul, Republic of Korea, 2022. [Google Scholar]
- Ok, K.K.; Kim, K.S. Charger for Electric Transport Device E.G. Electric Bicycle, Has Cooling Fan That Is Provided inside Main Portion to Cool First Charging Unit and Second Charging Unit, and Vent Hole through Which Air Moves by Cooling Fan Is Formed Outside Main Portion; HYUNDAI EVC. (HYUN-Non-standard): Seoul, Republic of Korea, 2022. [Google Scholar]
- Meyers, J.P.; Doyle, M.; Darling, R.M.; Newman, J.S. The Impedance Response of a Porous Electrode Composed of Intercalation Particles. J. Electrochem. Soc. 2000, 147, 2930–2940. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.M. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.F.; Newman, J. Modelling the Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1992, 140, 1526–1533. [Google Scholar] [CrossRef]
- Chung, K.-i.; Chung, M.-W.; Kim, W.-S.; Kim, S.-K.; Sung, Y.-E.; Choi, Y.-K. Studies of the Passivation Film as a Function of the Concentration of Electrolyte in Lithium-Ion Battery. Bull. Korean Chem. Soc. 2001, 22, 189–193. [Google Scholar]
- Kim, G.-H.; Pesaran, A.; Spotnitz, R. A Three-Dimensional Thermal Abuse Model for Lithium-Ion Cells. J. Power Sources 2007, 170, 476–489. [Google Scholar] [CrossRef]
- Panasonic Ncr18650b. Available online: https://batterybro.com/products/panasonic-b-ncr18650b-3400mah-4-8a (accessed on 4 December 2023).
- Hatchard, T.D.; MacNeil, D.D.; Basu, A.; Dahn, J. Thermal Model of Cylindrical and Prismatic Lithium-Ion Cells. J. Electrochem. Soc. 2001, 148, A755–A761. [Google Scholar] [CrossRef]
- Momma, T.; Matsunaga, M.; Mukoyama, D.; Osaka, T. AC Impedance Analysis of Lithium Ion Battery Under Temperature control (Article). J. Power Sources 2012, 216, 304–307. [Google Scholar] [CrossRef]
- Han, X.; Ouyang, M.; Lu, L.; Li, J. Simplification of Physics-Based Electrochemical Model for Lithium Ion Battery on Electric Vehicle. Part i: Diffusion Simplification and Single Particle Model. J. Power Sources 2015, 278, 802–813. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Chen, D.; Wang, X.; Chen, S.; Zhu, J.; Dai, H. Thermal Characteristic Evolution of Lithium–Ion Batteries during the Whole Lifecycle. J. Energy Chem. 2024, 92, 534–547. [Google Scholar] [CrossRef]
- Zhuang, Q.; Yang, Z.; Zhang, L.; Cui, Y. Diagnosis of Electrochemical Impedance Spectroscopy in Lithium Ion Batteries. Prog. Chem. 2020, 32, 761–791. [Google Scholar] [CrossRef]



| Parameter | Value | Unit | Description |
|---|---|---|---|
| 90 [38] | pm | the ion jumping half distance | |
| 0.421 [39] | -- | pre-exponential factor | |
| 0.392 [40] | -- | pre-exponential factor | |
| 0.450 [40] | -- | pre-exponential factor | |
| 1000 [41] | mol/m3 | the lithium-ion concentration function in the battery | |
| 1500 [40] | mol/m3 | the ion concentration | |
| 1319.9 [42] | J/(kg∙K) | the specific heat capacity of the lithium-ion battery | |
| 2.94 [43] | C | the maximum charge C-rate | |
| 3.4 [43] | Ah | the capacity of the lithium-ion battery | |
| 3.168 [38] | kJ/mol | activation energy | |
| 96,487 | C/mol | Faraday’s constant | |
| 16 [44] | W/(m2·K) | the equivalent heat transfer coefficient | |
| 120 [44] | nm | the thickness of the SEI | |
| 49.5 [43] | g | the mass of the lithium-ion battery | |
| 21 [45] | mΩ | the resistance of the lithium-ion battery | |
| 8.314 | J/(mol∙K) | the ideal gas constant | |
| 0.05 [46] | m2 | the effective area of the electrode | |
| 0.0043 * | m2 | the battery surface area | |
| 279.15 * | K | the target Kelvin’s temperature | |
| 1013 [40] | Hz | the lattice vibration frequency | |
| 3.6 [40] | V | the nominal voltage of the lithium-ion battery | |
| 1.12 [40] | eV | an ion jumping energy barrier | |
| 1 | C | the ionic charge |
| Target Parameters | Value and Unit |
|---|---|
| input voltage | 36 V |
| output voltage | 25 V |
| maximum output current value | 10 A |
| output current frequency range | 20~200 Hz |
| output current waveform | Sine |
| switching frequency | 10 kHz |
| Component | Model | Parameter |
|---|---|---|
| switching devices | IRF540N MOSFET | = 10 kHz |
| the filter circuit at the output end | LCL filter | input voltage = 36 V output current = 10 A switching frequency = 10 kHz rated output voltage = 20 V |
| input-side inductance | -- | = 300 μH |
| input filter capacitor | -- | = 470 μF |
| output-side inductance | -- | = 75 μH |
| input capacitance | -- | = 75 V = 1000 μF |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Wang, X.; Fan, W.; Wei, X.; Dai, H. Design and Implementation of a Non-Destructive AC Heating System for Lithium-Ion Battery Modules. Batteries 2024, 10, 300. https://doi.org/10.3390/batteries10090300
Xu Q, Wang X, Fan W, Wei X, Dai H. Design and Implementation of a Non-Destructive AC Heating System for Lithium-Ion Battery Modules. Batteries. 2024; 10(9):300. https://doi.org/10.3390/batteries10090300
Chicago/Turabian StyleXu, Qian, Xueyuan Wang, Wenjun Fan, Xuezhe Wei, and Haifeng Dai. 2024. "Design and Implementation of a Non-Destructive AC Heating System for Lithium-Ion Battery Modules" Batteries 10, no. 9: 300. https://doi.org/10.3390/batteries10090300
APA StyleXu, Q., Wang, X., Fan, W., Wei, X., & Dai, H. (2024). Design and Implementation of a Non-Destructive AC Heating System for Lithium-Ion Battery Modules. Batteries, 10(9), 300. https://doi.org/10.3390/batteries10090300









