Abstract
The methodology presented in this work allows for the creation of a real-time adjustment of Kalman Filter process noise for lithium battery state-of-charge estimation. This work innovates by creating a methodology for adjusting the process () and measurement () Kalman Filter noise matrices in real-time. The filter algorithm with this adaptative mechanism achieved an average accuracy of 99.56% in real tests by comparing the estimated battery voltage and measured battery voltage. A cell-balancing strategy was also implemented, capable of guaranteeing the safety and efficiency of the battery pack in all conducted tests. This work presents all the methods, equations, and simulations necessary for the development of a battery management system and applies the system in a practical, real environment. The battery management system hardware and firmware were developed, evaluated, and validated on a battery pack with eight LiFePO4 cells, achieving excellent performance on all conducted tests.
1. Introduction
The extended Kalman filter for state-of-charge estimation is one of the most used methods due to its accuracy and ability to be implemented in an embedded microprocessor environment. Furthermore, the Kalman filter algorithm for estimating the state of charge (SOC) can include the coulomb counting method and the open circuit voltage (OCV) method in its structure, making it very efficient for estimating a battery’s SOC. This is a method that requires dynamic battery knowledge, making use of estimators, but that has many challenges in incorporating the effects of nonlinearities and other phenomena, as well as identifying and classifying the parameters of its constituent models.
One of the biggest challenges in Kalman filter implementation is defining the process and measurement noise matrices. These matrices can be defined in different ways and must consider the entire system in which it will be applied. Some works were found in the literature that used fixed values in the process and measurement noise matrices without an explanation regarding this definition, as well as an offline tuning procedure [1,2,3]. However, if these matrices are defined in any way, the accuracy of the extended Kalman filter will be affected. A common way to describe the measurement noise covariance is using available physical sensors; the authors of [4] presented a dynamic perception of measurement noise, modeling the measurement noise as a Gaussian mixture model. Regarding the process noise, an optimization procedure is commonly carried out in a heuristic manner, that is, either by trial and error or by means of regulation metrics, such as the L curve [5].
If and are exceedingly small, the uncertainty range will be small, resulting in a biased estimation, and if and are high, it may cause divergence in the filter [6,7]. The extended Kalman filter considers that these matrices are constant; however, in some applications, it is necessary to consider that noise may vary under operating conditions. To improve the estimation accuracy, adaptive Kalman filters were developed with the aim of adjusting noise variances in real time [8,9]. These strategies can be classified into four main categories [9], namely Bayesian [10], maximum-likelihood estimation [11], correlation [12,13,14,15], and covariance matching [16] methods. These approaches are typically characterized by excessive computational costs, as they describe generic adaptive filtering schemes. They are generally based on searching for the most suitable process and steady-state measurement noise estimates rather than their current ideal values [9]. In [6], matrices and were updated in real time using the sliding-window method, considering the error between the model output value () and the measured value (). During tests of the SOC estimator, this method proved capable of adapting to different temperature conditions and different cell states of health (SOHs), in addition to achieving greater precision and better robustness compared to other filtering algorithms. The authors of [17] presented a similar method; however, it uses a forgetting factor in conjunction with the sliding window. Simulations and experimental results showed that the algorithm proposed in [17] was able to estimate the SOC accurately, even when the statistical noise characteristic deviated from the nominal values. In [18], an approach was developed that also considers the error between the model output value () and the measured value () using the sliding-window method but updating the matrix considering the Kalman gain (), while the update of matrix considers the covariance matrix (). This approach achieved 43.34% higher SOC accuracy than the traditional approach and resulted in only a 4.59% increase in computational time. Several other strategies have been found for calculating the and matrices in real time; however, all the process noise approaches found in the literature are similar in considering the error between the model output value () and the measured value (). The authors of [19] correlated the process noise end the measurement noise, and the system noise matrix was estimated and updated in real-time according to measurement data; the process noise is related to measurement noise form the frequency-domain perspective, and the measurement noise changes with time. Also correlating the process and measurement noise, in [20], variance component estimation was proposed by tuning the variance of process and observation noise together. A unified system model was constructed by a time window of multiple historical epochs. A noise with distribution equivalence strategy was proposed to make the unified system model a standard linear mixed-effects model.
A very interesting approach was proposed in [9] for adaptive process noise covariance matrix tuning for joint input–state estimation; in this paper, both shaping of states and unknown input uncertainties are considered for optimization. Moreover, the covariance matrix process noise is time-variant, since the modeling uncertainty and the dynamic characteristics of the input may vary over time.
In this paper, a measurement noise time-varying method is presented, and the modeling uncertainty is used to define the process noise, but unlike the strategies found in the literature, this work considers the uncertainty of each model parameter individually, bringing a practical understanding to the definition of process noise.
1.1. Objectives and Contributions
This work applies a methodology for developing the adaptive extended Kalman filter algorithm for state-of-charge estimation that is able to define the process noise and measurement noise matrices, considering the individual cell voltage and current measurement, in real time. A cell-balancing strategy was also developed, enabling safe and efficient system operation. To corroborate the results of this work, the system was applied to a real battery pack with a specially developed battery management system (in hardware and software) to test and verify the functionalities, validating the contributions of this work. To achieve this purpose, the work previously done in [21,22] was used as a basis for this work. Mathematical modeling and the parameter identification were presented in these previous works and used to achieve the results presented in this paper.
1.2. Paper Organization
Section 2 presents the basic concepts of the Kalman filter and the methodology for multidimensional models. Section 3 presents the state-of-charge methodology and the Kalman filter process noise methodology, which constitute the contribution of this paper. Section 4 presents the state-of-charge algorithm. Section 5 presents the algorithm validation, and Section 6 presents the conclusions.
2. Kalman Filtering Revisited
In a stricter context, the Kalman filter can be understood as a learning process that uses an estimation problem model that distinguishes between what is capable of being observed and what is happening. In this “learning process”, the state of knowledge about what is really happening can be deduced from what is capable of being observed. This state of knowledge is characterized by probabilistic distributions, which represent real-world knowledge, while the cumulative processing of this knowledge is the learning process [23].
From the Kalman gain, it is possible to determine the measurements precision and the estimation accuracy. If the Kalman gain value is closer to 1, the algorithm will consider that the measurements are accurate and the model estimates are unstable; in this case, the algorithm will give greater weight to the measurements and less weight to the estimates. However, if the Kalman gain value is closer to 0, the algorithm will consider that the measurements are imprecise and the model estimates are stable; in this case, the algorithm will give greater weight to the model estimates and less weight to measurements.
For the Kalman filter to be carried out computationally and with different state variables, it is necessary to represent the dynamic system in the form of state-space equations according to Equations (1) and (2).
where: is the state vector, is the state matrix, is the input vector, is the output vector, is the input matrix, is the output matrix, and is the direct transmission matrix.
In this way, it is possible to represent a linear dynamic system mathematically and compare its estimated output with a measured output of that system to then estimate its state. Then, by comparing the actual output () and the estimated output , the Kalman gain () is calculated by adjusting the estimated state () so that the estimated output is as close as possible to the real output () and, consequently, the estimated state () is as close as possible to the real state (). Therefore, the mathematical model must be as close as possible to the real system for the estimated output to be close to the real output and the state estimation to be accurate.
To better understand the logic of the Kalman filter in a state space, it is important to know some concepts. If the measurement noise matrix () is close to 0, then the Kalman gain () will be close to 1. This means that the updated state () will be adjusted first by considering the updated measurement data (). Otherwise, the updated state () will be adjusted first considering the predicted state (). If the covariance matrix () is close to 0, then the state update () will be performed through the predicted state (), practically ignoring the measurement data ().
As seen in the literature, the Kalman filter is commonly applied to battery state-of-charge estimation [1,6,24,25] because, through a mathematical model, it is possible to compare the estimated battery voltage with the actually measured battery voltage. It is also possible to estimate the battery state of charge without carrying out direct measurements in relation to its electrochemical states. Furthermore, despite involving matrix calculations, depending on the model order, implementing the filter is viable and computationally possible. Therefore, the Kalman filter can result in good accuracy and reliable performance when used in BMS-embedded electronic systems. However, its application requires modifications due to nonlinearities (such as the use of extended filter techniques), in addition to procedures for inference (identification), parameterization, model adjustment, covariances, and initial estimates, which are discussed later in this work.
3. State-of-Charge Estimation Methodology
In this work, the extended Kalman filter presented in Section 2 is used to estimate the battery charge state. The model presented in [22] must be applied to the filter; however, for this, its conversion to the discrete time domain is necessary. The model in the discrete state space is represented by Equations (3) and (4).
where matrices , , , and are matrices , , , and of the system in the discrete sample space. These matrices, in continuous time, were presented in [22]. To discretize the model, the backward Euler method was chosen, as it results in very simple and elementary arithmetic to represent numerical integration.
The discrete extended Kalman filter system is shown in Equations (5) and (6).
where is the system state variable; is the system observation variable; is the system input; is the nonlinear state function; is the nonlinear measurement function; and and are the white noise Gaussians with mean 0 and covariance for and , respectively.
The extended Kalman filter uses Taylor series expansion to perform a linear approximation of a nonlinear function, which, in this case, is found in the total battery voltage equation, that is, at the output of the battery system presented in [22]. To define the total battery voltage, it is necessary to determine the battery’s open-circuit voltage , which has a nonlinear relationship with the battery’s state of charge . In this context, Taylor series expansion must be performed on the battery open circuit voltage equation, which can be represented by a polynomial of order n, as described in [21]. In this way, fixed nominal trajectory linearization is performed.
The battery nonlinearities are approximated using linearization through Taylor series expansion, which is represented by matrices and .
Matrix F is a Jacobian matrix of partial derivatives of , where and . Matrix has a relationship with the previous states () and the entry () and is expressed as follows:
Therefore, matrix is expressed as follows:
To solve Equation (15), discretization using the Euler method is performed considering the states presented in Equations (9) and (10). This equation approach was detailed in [21].
where ;
where .
Matrix is a Jacobian matrix of partial derivatives of , where and . Matrix is related to the states of the system and is expressed as follows:
Therefore, matrix is expressed as follows:
where is expressed as follows:
Taylor series expansion for the SOC–OCV relationship must be carried out to the necessary order. In this case, using piecewise linearized functions, as presented in [21], the approximation to the first order is sufficient, that is,
where is the SOC. Therefore, the output equation becomes
One of the biggest challenges in implementing the Kalman filter is defining the measurement noise () and process noise () matrices.
Kalman Filter Process Noise Methodology
The definitions of process and measurement noise matrices are very important for the performance and accuracy of the Kalman Filter. The process noise matrix () represents the entire mathematical noise variance inherent to the system (including approximations and truncations), and the measurement noise matrix () represents the system measurement noise variance.
In this work, the system measurement noise considers current and voltage noise. To calculate voltage measurement noise variance, voltage sensor accuracy is considered, together with noise variance due to EMI (Electromagnetic Interference)/EMC (Electromagnetic Compatibility) of conditioning circuits. This calculation is performed every three iterations of the algorithm. In this context, Equation (16) represents the voltage measurement noise variance.
where is the variance of the voltage measurement noise calculated every three iterations of the algorithm, and is the voltage measurement accuracy of the sensor reported by the manufacturer.
Thus, we have the measurement noise covariance matrix, as represented by Equation (17).
In an equivalent way, for current measurement, Equation (18) is obtained for the measurement noise variance.
where is the current measurement noise variance calculated every three iterations of the algorithm, and is the current sensor accuracy, as reported by the manufacturer.
However, the algorithm must be able to differentiate between what is actually noise and what is just a change or a transient signal in the voltage or current amplitude. For this purpose, the standard variance (observed under steady-state operation) of the measurement noise was calculated through a laboratory test. In the embedded algorithm, the variance is calculated every three interactions; if this variance is greater than the standard variance, the algorithm ignores this value, as it represents a variation in the amplitude of the voltage or current and does not truly represent noise.
The process noise covariance matrix () is calculated considering the data flow itself as a process to identify the parameters, where each one has its standard deviation, that is, its uncertainty. In this context, the process noise covariance matrix is represented by Equation (19), where the first term of the matrix is related to the derivative of the first state of the system () and the second term of the matrix is related to the derivative of the second state of the system (.
The calculation of Equation (19) is conducted based on the uncertainty combination of the parameters in Equations (20) and (21).
The uncertainty combination calculation must consider the algebraic relationship between the quantities and whether they are statistically independent or correlated; this methodology is presented in [26], and more detail is presented in [27].
To calculate the uncertainty combination, we consider that all variables are correlated.
To calculate the uncertainty of Equation (20), we have the following:
where: is the variance of parameter , is the variance of parameter , is the variance of the current noise determined in Equation (18), and is the variance of the calculation of voltage () determined in Equation (26).
Solving Equation (22), we have the following sequence of equations:
By analyzing the equivalent circuit model presented in [27], the RC circuit voltage is calculated by Equation (25).
where is the total battery voltage.
Therefore, the RC circuit voltage variance presented in Equation (35) is calculated according to Equation (39).
Next, using Equations (23), (24), and (26), it is possible to calculate Equation (22).
And to calculate the uncertainty in Equation (21), we have:
where is the variance of the parameter, and is the variance of the current noise described by Equation (18).
Solving Equation (27), we have the following sequence of equations.
Therefore, using Equations (23), (24), (26), and (28), it is possible to determine the process covariance matrix () given by Equation (19). It is important to highlight that this approach is dependent on the accuracy of the battery’s mathematical model parameters, in addition to the current and voltage measurement noise variance. Therefore, this definition of the and matrices must be associated with the model parameter identification approach.
This approach can also be used as a self-diagnosis of the BMS itself, indicating possible hardware problems in the cells, in signal conditioning, in analog filtering, etc. Since this method is linked to the real-time current measurement noise and voltage measurement noise, at times, when there are abrupt changes in any of their coefficients, it can be determined whether a serious failure is in progress, allowing protection and security measures to be taken.
4. State-of-Charge Estimation Algorithm
In this paper, all the tests were conducted with the same battery cell used in [21,22], which is a cylindrical LiFePO4 battery with 6 Ah of capacity. The current profile used in this work is the same as that presented in detail in [21], which represents the use of an electric forklift, as an application used for practical validation.
The state of charge was estimated using the adaptive extended Kalman filter according to the methodology presented in Section 3. To apply the extended Kalman filter, it is necessary to discretize the model in the state space in continuous time, as presented in [22]. Thus, applying discretization, it is possible to obtain the following model matrices in the domain of samples. It should be noted that a sampling time () of 10 ms was used.
Matrices and are Jacobian matrices necessary for the discretization of the system using the Euler method, with linearization through Taylor series expansion. In this way, by applying Equations (7)–(15) as detailed in Section 3, it is possible to obtain the following Jacobian matrices.
A real oscillography record obtained with the BMS hardware allows for observation of the battery voltage measurement noise, as shown in Figure 1, where a noise characteristic of a digitization and quantization process is noted, in addition to a slightly decreasing behavior, since the battery is in the process of discharging at that moment. Only the noise resulting from the conditioning, analog filtering, and quantization process is of interest in this analysis.
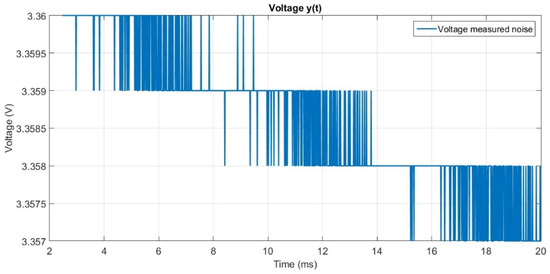
Figure 1.
Voltage measurement noise.
In another record, it is possible to observe the battery current measurement noise, as shown in Figure 2, where, in addition to noises related to conditioning, filtering, and quantization, other components and influences on the measured signal are noted. It is important to emphasize that the battery was subjected, on this occasion, to a constant current discharge regime, which comes from the BMS’s own consumption.
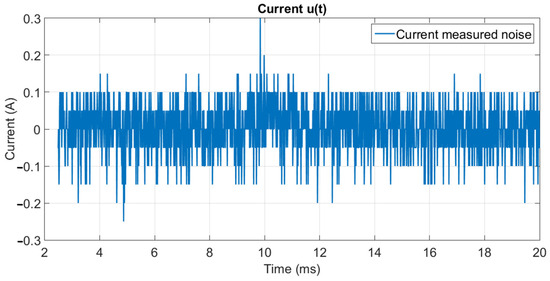
Figure 2.
Current measurement noise.
The covariances of voltage () and current () measurement noise, calculated through the analysis of Figure 1 and Figure 2, are presented in Equations (35) and (36), respectively; however, it is important to highlight that these values are updated every three software iterations (30.0 ms) for better result accuracy.
To validate the extended Kalman filter algorithm in a computational environment, the “30 s high 30 s low” experiment described in [21] was used, as this represents an average use condition of a forklift, in addition to being sufficient to validate the algorithm before applying it to the BMS for validation in a real environment. In this case, an initial estimation error with a standard deviation of 33.33% (or 2 V, considering the cell used) was inserted for the voltage (, ()), and an initial estimation error with a standard deviation of 10% was considered for the (). The initial values were set quite high, but they must be corrected by the algorithm itself at run time, converging to the observed values for these uncertainties. Therefore, the initial covariance matrix is presented in Equation (37).
The values of Equation (37) are defined through the variance of each parameter, which is calculated by Equation (38).
where is the variance of the parameter, and is the standard deviation of the parameter.
In the initial state matrix, 0 V was admitted for the voltage , (), and 100% was considered for the (). Thus, we have the initial state matrix presented in Equation (39).
The adaptive extended Kalman filter algorithm was created as presented in Section 3. Figure 3 presents a summary of calculations necessary for its execution. Where the measurements were presented in blue and the outputs were presented in green.
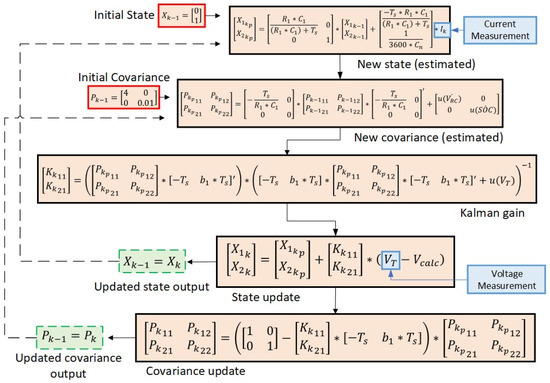
Figure 3.
Adaptive extended Kalman filter algorithm equations.
The result of the coefficients of the covariance matrix ( and ) related to state over time is presented in Figure 4.
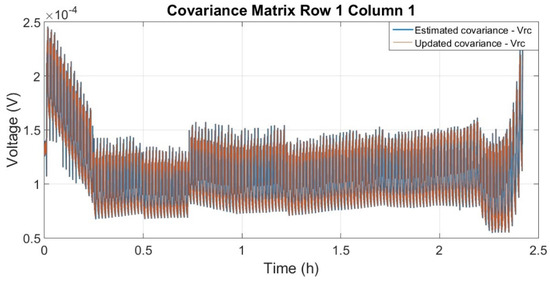
Figure 4.
Estimated and updated state-related covariance ().
Figure 4 shows the estimated covariance in blue and the updated covariance in red. In this Figure, it is possible to conclude that the two covariances (estimated and updated) have a very similar characteristic, with an average value of around . The covariance matrices ( and ) related to state are shown in Figure 5.
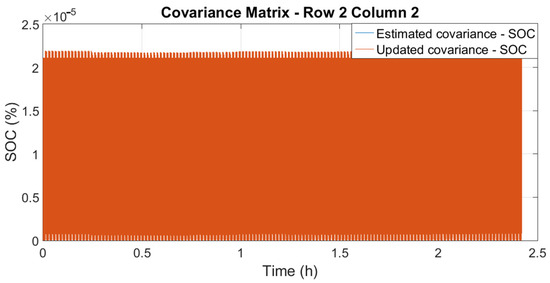
Figure 5.
Estimated and updated state-related covariance ().
Analyzing Figure 5, it is also possible to conclude that the two covariances (estimated and updated) have similar characteristics, with an average value of around . To facilitate visualization of the difference between the two signals, Figure 6 presents an enlarged view.
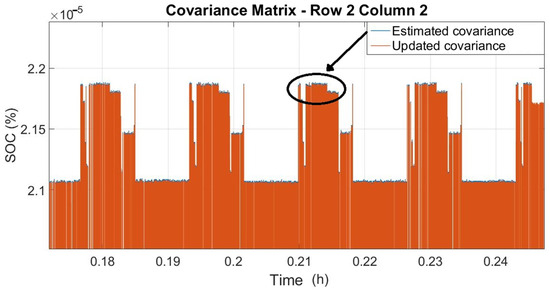
Figure 6.
Estimated and updated covariance, related to state —extended signal.
Analyzing Figure 6, it is possible to verify that the updated covariance is always smaller than the estimated covariance, that is, the error in estimating the SOC state decreases throughout the algorithm’s execution. Furthermore, the covariance is low—on the order of —which indicates that the error in estimating the state of charge is small, as desired for an estimator under these conditions.
The Kalman gain matrix related to state is shown in Figure 7.
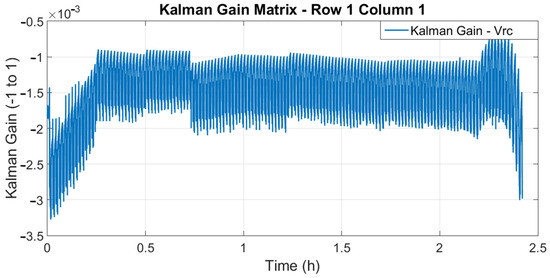
Figure 7.
State-related Kalman gain ().
The Kalman gain matrix related to state is shown in Figure 8.
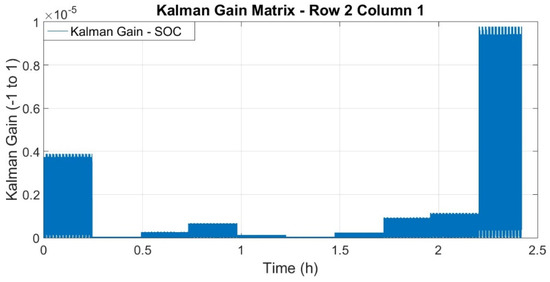
Figure 8.
State-related Kalman gain ().
Analyzing Figure 8, it is possible to observe that the greatest gains occur at the beginning and end of the test, when the battery presents greater nonlinearity. At these points, the Kalman filter give the battery voltage measurement greater weight in estimating the state. However, the central points of the test indicate that the Kalman filter gives the estimate of the previous state more weight in the estimation of the current state than the measurement of the battery voltage, as these are the points of lowest nonlinearity of the battery.
The estimated battery voltage (through this mathematical model) and the measured voltage are presented in Figure 9. The Kalman filter algorithm makes a comparison between the two values to estimate the battery states ().
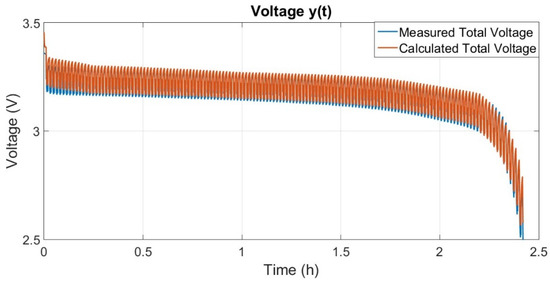
Figure 9.
Measured and estimated total voltage.
Analyzing Figure 9, it is possible to observe that the measured and calculated values are remarkably similar.
The percentage difference between the measured voltage and the estimated voltage is a maximum of 5.4% at the point of greatest nonlinearity of the cell, as shown in Figure 10. However, on average, the percentage difference is 0.44%, achieving an accuracy of 99.56%, on average.
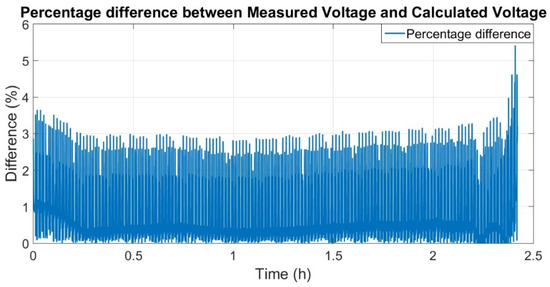
Figure 10.
Percentage difference between measured and calculated voltage.
The difference between the measured voltage and the estimated voltage is shown in Figure 11 and is used in the filter algorithm to calculate the Kalman gain.
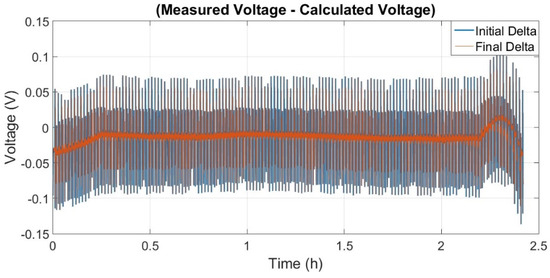
Figure 11.
Difference between measured voltage and estimated voltage.
In Figure 11, it is possible to observe the initial difference (initial delta) in blue, which is used to calculate the Kalman gain, and the final difference (final delta) in red, which is calculated at the end of each iteration of the algorithm. It is known that the initial difference must always be greater than the final difference. The largest final difference was 0.10 V, with an average of −0.01 V. The results and information presented in Figure 9, Figure 10 and Figure 11 are capable of completely validating the mathematical model used to describe the battery dynamics, presenting an average difference of just 0.44% between the measured voltage and the voltage estimated by the model. The voltage in the RC circuit , represented by state and calculated at the end of the Kalman filter algorithm, is shown in Figure 12.
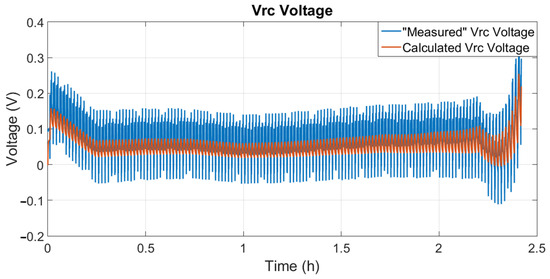
Figure 12.
“Measured” voltage (, blue) and calculated voltage (, red).
Figure 12 presents the “measured” voltage (, blue), which is calculated using Equation (38), and the calculated voltage (, red), which is calculated at the end of the Kalman algorithm. It is possible to observe that the two values are remarkably close and have similar behavior, validating the Kalman algorithm and the battery model.
The state of charge of the battery was validated by making a comparison between the state of charge calculated using the coulomb counting algorithm (SOC CC BMS) implemented in the BMS and the state of charge estimated using the extended Kalman filter algorithm (SOC Kalman). Therefore, the state of charge estimated by both is presented in Figure 13.
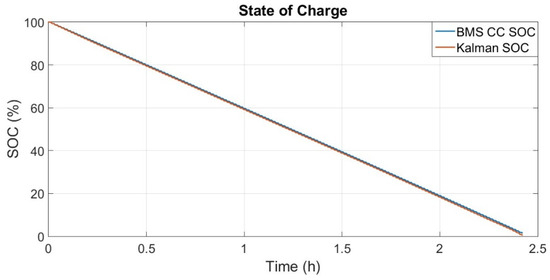
Figure 13.
State of charge calculated by the coulomb counting algorithm and state of charge estimated by the Kalman algorithm.
The result presented in Figure 13 indicates that the Kalman filter algorithm was successfully implemented and fully validated in the computational environment with digital simulations. It is important to highlight that the state of charge estimated by the Kalman Filter algorithm has a more coherent final value than the coulomb counting algorithm, as in the test carried out in this study, the cell was discharged until the end, and the SOC should present a value of 0%; however, the final value presented by the coulomb counting algorithm was 1.56% SOC, and the final value presented by the Kalman filter algorithm was 0.59% SOC.
Therefore, the accuracy of the algorithm was calculated according to the difference between the voltage measured through the sensor and the voltage estimated through the mathematical model inserted in the adaptive Kalman filter algorithm; this percentage difference is presented in Figure 10. Evaluation of the algorithm’s accuracy was carried out in this way, since the measured battery voltage is the only information taken from a sensor; therefore, if the accuracy evaluation is carried out in comparison with the state of charge estimated by the coulomb counting algorithm, the result will be inaccurate because coulomb counting is also an estimator and accumulates errors during its execution.
5. Algorithm Validation
The entire state-of-charge state estimation algorithm was properly embedded in a BMS specially designed for this work. In addition to several auxiliary components, the BMS hardware is based on the following components:
- An integrated circuit called AFE (analogic front end) whose main function is to measure individual cell voltages;
- A microcontroller capable of receiving and sending information to the AFE, controlling and configuring all necessary parameters, and executing the algorithms developed for all desired functionalities;
- A current sensor with adequate accuracy.
The complete printed circuit board for this hardware is shown in Figure 14.

Figure 14.
BMS printed hardware circuit board.
With this hardware and a set of eight lithium cells connected in series, it was possible to validate the mathematical battery model presented in [22] and the state-of-charge estimation algorithm presented in this paper. The results of this implementation, testing, and validation are presented in the next sections.
To fully validate the algorithm, it was implemented on real BMS hardware. Figure 15 presents a comparison between the algorithm executed in a simulation environment (MATLAB) and in the embedded environment. In the embedded environment, C language was used, with double precision floating point arithmetic and all routines developed in an authorial manner, including all calculations with matrices and vectors. In this way, it was possible to avoid ready-made routines with functions that are often unused, which would result in large unnecessary computational costs. This figure shows the SOC outputs of both implementations.
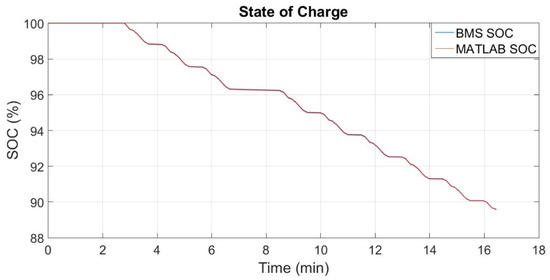
Figure 15.
Comparison between the algorithm executed with computer simulation (red) and the algorithm embedded in the BMS (blue).
To validate the algorithm, the battery current data were artificially inserted into the embedded code using an external computer, which sent the synchronized data to the BMS so that it was possible to insert a large amount of information without resulting in extra computational time for the BMS. The entered data were the same as those used in the simulation environment (MATLAB), thus guaranteeing the same inputs for both algorithms, hoping to produce the same outputs. Analyzing Figure 15, it is possible to observe that the two signals are the same; thus, it was possible to completely validate the implementation of the Kalman filter algorithm embedded in the BMS.
Figure 16 shows the time that the BMS needs to perform a complete cycle of the algorithm and estimate the cell’s charge state. Computational time is the high-logic period shown in the square wave.
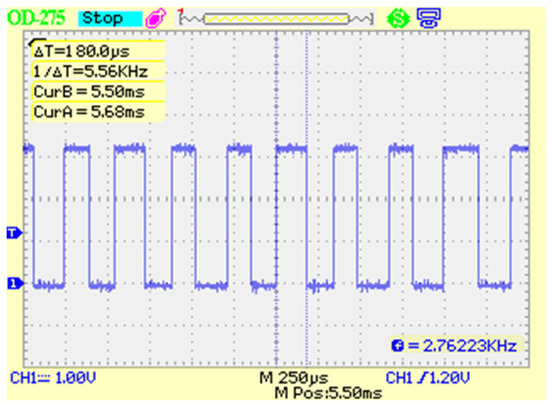
Figure 16.
Computational time of the algorithm in the BMS.
As shown in Figure 16, the time required for a complete cycle of the algorithm was 180 μs, using a microcontroller clocked at 240 MHz. This algorithm is the complete extended Kalman filter, including the implementation of the adaptive strategy for the readjustment of process noise and measurement noise. This adaptive strategy alone corresponds to approximately 30% of this computational time. In any case, the result of 180 μs is enough for the microcontroller to be able to calculate the state of charge of each cell in a set of several cells in series, guaranteeing enough time to implement all other necessary BMS functions.
It is also important to highlight that this specific filter algorithm can be heavily optimized in the future using simpler arithmetic (single precision, fixed point, or integer arithmetic), with the ability to be executed on smaller microcontrollers and DSPs (digital signal processors), achievinglower costs. It is also possible to envisage the creation of an ASIC (application-specific integrated circuit) for this purpose, synthesizing hardware dedicated to this function.
The charge state estimation algorithm was validated on a real set of eight cells in series. However, for the charge and discharge tests of this set of cells to be conducted safely, it was necessary to develop a balancing algorithm. In this context, a simple algorithm was created that consists of recognizing which cell has the highest voltage and activating an FET-type transistor connected in parallel to that cell, discharging its energy into a resistor. This balancing scheme, known as “dissipative passive”, is carried out in the cell until another cell becomes the cell with the highest voltage. An adjustable hysteresis band is used in the voltage classifier so that the balancing process is only activated if a certain voltage level is detected in a cell. Through this strategy, it is possible to guarantee a minimum balance of all cells during algorithm validation tests.
Algorithm validation was carried out through a complete charge and discharge cycle in the eight cells, as shown in Figure 17 and Figure 18.
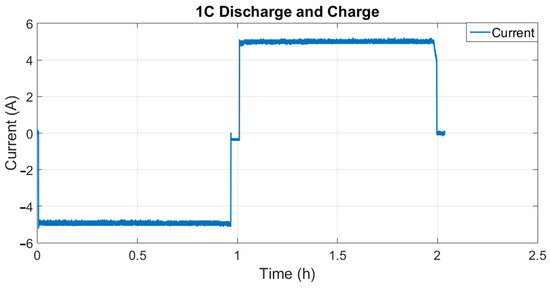
Figure 17.
Current used in the complete charge and discharge cycle test.
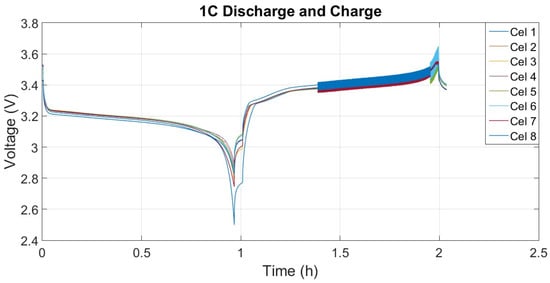
Figure 18.
Cell voltage in the full cycle test.
Analyzing Figure 18, it is possible to verify the moment of cell balancing. Balancing begins in the charge cycle, close to the voltage of 3.4 V, as this is the moment when the difference in voltage between the cells is the greatest. During balancing, it is possible to visualize the change in a cell’s voltage value because when one cell is balanced, its voltage decreases and another becomes the cell with the highest voltage.
In this context, it is possible to understand that the state of charge is directly affected by balancing, as the energy of the cells changes at these moments. The state of charge of each cell during the validation test is shown in Figure 19.
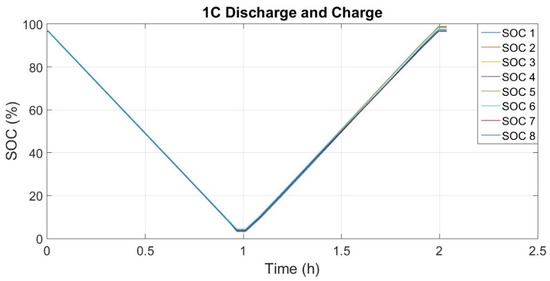
Figure 19.
State of charge during the complete battery charge and discharge cycle.
It is possible to notice that at the end of the validation test, the individual state of charge is different; this is due to the type of balancing used. Through a better balancing strategy, it is possible to minimize this difference and ensure that all cells have the same state of charge at the end of a charging cycle. Table 1 presents the SOC of each cell and the total SOC of the battery at the end of the validation test.

Table 1.
Total state of charge and states of charge of individual cells.
The battery’s total state of charge is calculated considering the average of the individual states of charge, resulting in a value of 98.02%. Analyzing Table 1, it is possible to observe that all SOCs are remarkably close; in this case, the calculated standard deviation was only 0.92%.
Based on what has been presented, the state-of-charge algorithm can be considered validated, as it is capable of estimating the state of charge of each cell individually, considering the energy exchange between them at balancing moments. With this, it is possible to evaluate the state-of-charge algorithm embedded in hardware, reading several different cells, and responding appropriately to each of them. In this case, balancing was used to validate the state-of-charge algorithm for different situations at the same time.
Through this test, it was possible to commission the BMS hardware and firmware, which operated properly, corroborating the choices adopted for this research and its development, including the functioning of the mathematical model and the adaptive extended Kalman filter algorithm for state-of-charge estimation.
6. Conclusions
The adaptive extended Kalman filter algorithm was developed using a different strategy with real-time process noise and measurement noise matrices. These matrices are calculated in real time by the algorithm using battery voltage and current measurements. The process noise matrix uses the parameters’ standard deviation identified through the mathematical model. Combining the parameter identification strategy with the adaptability of the process noise matrix, the state-of-charge estimation algorithm can achieve an average accuracy of 99.56%.
The presented strategy uses the uncertainty combination method, which can simplify the understanding of the process noise matrix, considering that it is composed of the modeling process itself and model parameter identification. Without computational optimizations, this strategy adds 30% processing time to the developed BMS and performs a complete iteration in 180 μs, in addition to being able to consider all system uncertainties together with the battery current and voltage measurement noises calculated in real time, becoming a robust and reliable algorithm. The advantages of the method presented in this paper are the low computational cost for an embedded system and the correlation of noise with uncertainty in identifying parameters. Furthermore, it is a physically easy method to understand, as process noise directly depends on the uncertainties in the method of identifying model parameters. It is important to emphasize that these process and measurement noise matrices can be used, in the future, for self-diagnosis of the BMS itself, indicating incipient hardware problems (in cells, analog conditioning, filtering, etc.) at times when there are abrupt changes in their coefficients. On such an occasion, it can determined be whether any serious failure is in progress, allowing protection and safety actions and measures to be implemented. This should be investigated in future work, as it also addresses advanced monitoring of the battery and its health status.
The BMS hardware and firmware were developed to guarantee the operation of all tasks and functionalities in real time. The battery charge state estimation algorithm was duly embedded in the BMS and validated on a battery pack with eight cells in series. For the tests on this battery pack to be carried out ensuring the integrity of the cells, a simple balancing strategy was developed. With this approach, it was possible to evaluate the performance of the state-of-charge algorithm in each cell, considering the energy exchange between them during its balancing and validating the accuracy of the algorithm throughout the test.
Author Contributions
Conceptualization, R.E.A., E.L.P. and C.T.d.S.; methodology, C.T.d.S., R.E.A. and E.L.P.; software, B.M.d.A.D.; validation, R.E.A., E.L.P. and A.A.M.L.; formal analysis, E.L.P. and R.E.A.; investigation, C.T.d.S. and B.M.d.A.D.; resources, R.E.A., E.L.P. and A.A.M.L.; data curation, B.M.d.A.D.; writing—original draft preparation, C.T.d.S.; writing—review and editing, E.L.P. and R.E.A.; visualization, B.M.d.A.D.; supervision, R.E.A. and E.L.P.; project administration, A.A.M.L.; funding acquisition, A.A.M.L. All authors have read and agreed to the published version of the manuscript.
Funding
This study was financed in part by the “Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brazil (CAPES)—Finance Code 001”. This paper was partially supported by the “Fundação de Desenvolvimento da Pesquisa (FUNDEP) Rota 2030/Linha V” under grant 27192/27. The participation of Rui Esteves Araújo in this work was financed by National Funds through the Portuguese funding agency, FCT—Fundação para Ciência e a Tecnologia, within project LA/P/0063/2020 (https://doi.org/10.54499/LA/P/0063/2020).
Data Availability Statement
The data presented in this study are available on request from the first author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jokie, I.; Zarko, Z.; Bozo, K. State of charge estimation of lithium-ion batteries using extended Kalman filter and unscented Kalman filter. In Proceedings of the 2018 23rd International Scientific-Professional Conference on Information Technology, Zabljak, Montanegro, 19–24 February 2018; pp. 1–4. [Google Scholar]
- Yuan, S.; Hongjie, W.; Chengliang, Y. State of charge estimation using the extended Kalman filter for battery management systems based on the ARX battery model. Energies 2013, 6, 444–470. [Google Scholar] [CrossRef]
- Dertimanis, V.K.; Chatzi, E.N.; Azam, S.E.; Papadimitriou, C. Input-state-parameter estimation of structural systems from limited output information. Mech. Syst. Signal Process 2019, 126, 711–746. [Google Scholar] [CrossRef]
- Zhong, S.; Peng, B.; He, J.; Feng, Z.; Li, M.; Wang, G. Kalman filtering based on dynamic perception of measurement noise. Mech. Syst. Signal Process. 2024, 213, 111343. [Google Scholar] [CrossRef]
- Hansen, P.C.; O’Leary, D.P. The use of the L-curve in the regularization of discrete ill-posed problems. SIAM J. Sci. Comput. 1993, 14, 1487–1503. [Google Scholar] [CrossRef]
- Shi, N.; Chen, Z.; Niu, M.; He, Z.; Wang, Y.; Cui, J. State of charge estimation for the lithium-ion battery based on adaptive extended Kalman filter using improved parameter identification. J. Energy Storage 2021, 45, 103518. [Google Scholar] [CrossRef]
- Li, L.; Hu, M.; Xu, Y.; Fu, C.; Jin, G.; Li, Z. State of charge estimation for lithium-ion power battery based on H-infinity filter algorithm. Appl. Sci. 2021, 10, 6371. [Google Scholar] [CrossRef]
- Tatsis, K.E.; Dertimanis, V.K.; Chatzi, E.N. Adaptive process and measurement noise identification for recursive Bayesians estimation. In Model Validation and Uncertainty Quantification; Springer: Berlin/Heidelberg, Germany, 2020; Volume 3, pp. 361–364. [Google Scholar]
- Vettori, S.; Di Lorenzo, E.; Peeters, B.; Luczak, M.M.; Chatzi, E. An adaptive-noise Augmented Kalman Filter approach for input-state estimation in structural dynamics. Mech. Syst. Signal Process. 2023, 184, 109654. [Google Scholar] [CrossRef]
- Hilborn, C.G.; Lainiotis, D.G. Optimal estimation in the presence of unknown parameters. IEEE Trans. Syst. Cybern. 1969, 5, 38–43. [Google Scholar] [CrossRef]
- Kashyap, R. Maximum likelihood identification of stochastic linear systems. IEEE Trans. Autom. Control 1970, 15, 25–34. [Google Scholar] [CrossRef]
- Mehra, R. On the identification of variances and adaptive Kalman filtering. IEEE Trans. Autom. Control 1970, 15, 175–184. [Google Scholar] [CrossRef]
- Mehra, R. On-line identification of linear dynamic systems with applications to Kalman filtering. IEEE Trans. Autom. Control 1971, 16, 12–21. [Google Scholar] [CrossRef]
- Odelson, B.J.; Rajamani, J.B.R. A new autocovariance least-squares method for estimating noise covariances. Automatica 2006, 42, 303–308. [Google Scholar] [CrossRef]
- Wernitz, S.; Chatzi, E.; Hofmeister, B.; Wokniak, M.; Shen, W.; Rolfes, R. On noise covariance estimation for Kalman filter-based damage localization. Mech. Syst. Signal Process 2022, 170, 108808. [Google Scholar] [CrossRef]
- Rutan, S.C. Adaptive Kalman filtering. Anal. Chem. 1991, 63, 1103–1109. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, L.; Zhang, L.; Huang, C. State of charge estimation of lithium-ion battery pack by using an adaptive extended Kalman filter for electric vehicles. J. Energy Storage 2021, 37, 102457. [Google Scholar] [CrossRef]
- Sun, D.; Yu, X.; Wang, C.; Zhang, C.; Huang, R.; Zhou, Q.; Amietszajew, T.; Bhagat, R. State of charge estimation for lithium-ion battery based on an intelligent adaptive extended Kalman filter with improved noise estimator. Energy 2021, 214, 119025. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, K.; Cao, Z. System noise variance matrix adaptive Kalman filter method for AUV INS/DVL navigation system. Ocean Eng. 2023, 267, 113269. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhang, Z.; Zhu, S. Adaptive Kalman filtering with uncertain system noises based on variance component estimation theory. IEEE Sens. J. 2024, 24, 17896–17906. [Google Scholar] [CrossRef]
- Da Silva, C.T.; Dias, B.M.d.A.; Araújo, R.E.; Pellini, E.L.; Laganá, A.A.M. Battery model identification approach for electric forklift application. Energies 2021, 14, 6221. [Google Scholar] [CrossRef]
- Da Silva, C.T.; Dias, B.M.d.A.; Araújo, R.E.; Pellini, E.L.; Laganá, A.A.M. Two-outputs nonlinear grey box model for lithium-ion batteries. Energies 2023, 16, 2218. [Google Scholar] [CrossRef]
- Mohinder, S.G.; Angus, P.A. Kalman Filtering Theory and Practice Using MATLAB, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008; ISBN 0-471-26638-8. [Google Scholar]
- Costa, S.C.L. Análise e desenvolvimento de um método de estimação de estado da carga de baterias baseado em filtro de Kalman. Master’s Thesis, Faculdade de Engenharia, Universidade do Porto, Porto, Portugal, 2014; 128p. [Google Scholar]
- Peng, J.; Luo, J.; He, H.; Lu, B. An improved state of charge estimation method based on cubature Kalman filter for lithium-ion batteries. Appl. Energy 2019, 253, 113520. [Google Scholar] [CrossRef]
- Kirkup, L.; Frekel, R.B. An Introduction to Uncertainty in Measurement; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Da Silva, C.T. Lithium Battery Management System with State Estimation with Adaptive Extended Kalman Filter. Ph.D. Thesis, University of São Paulo, São Paulo, Brazil, 2022; 146p. (In Portuguese). [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).