Development of a Fast Running Equivalent Circuit Model with Thermal Predictions for Battery Management Applications
Abstract
1. Introduction
2. Experimental Data Source and Details
3. Numerical Model
3.1. Coupled Thermal–Electrochemical Model Development
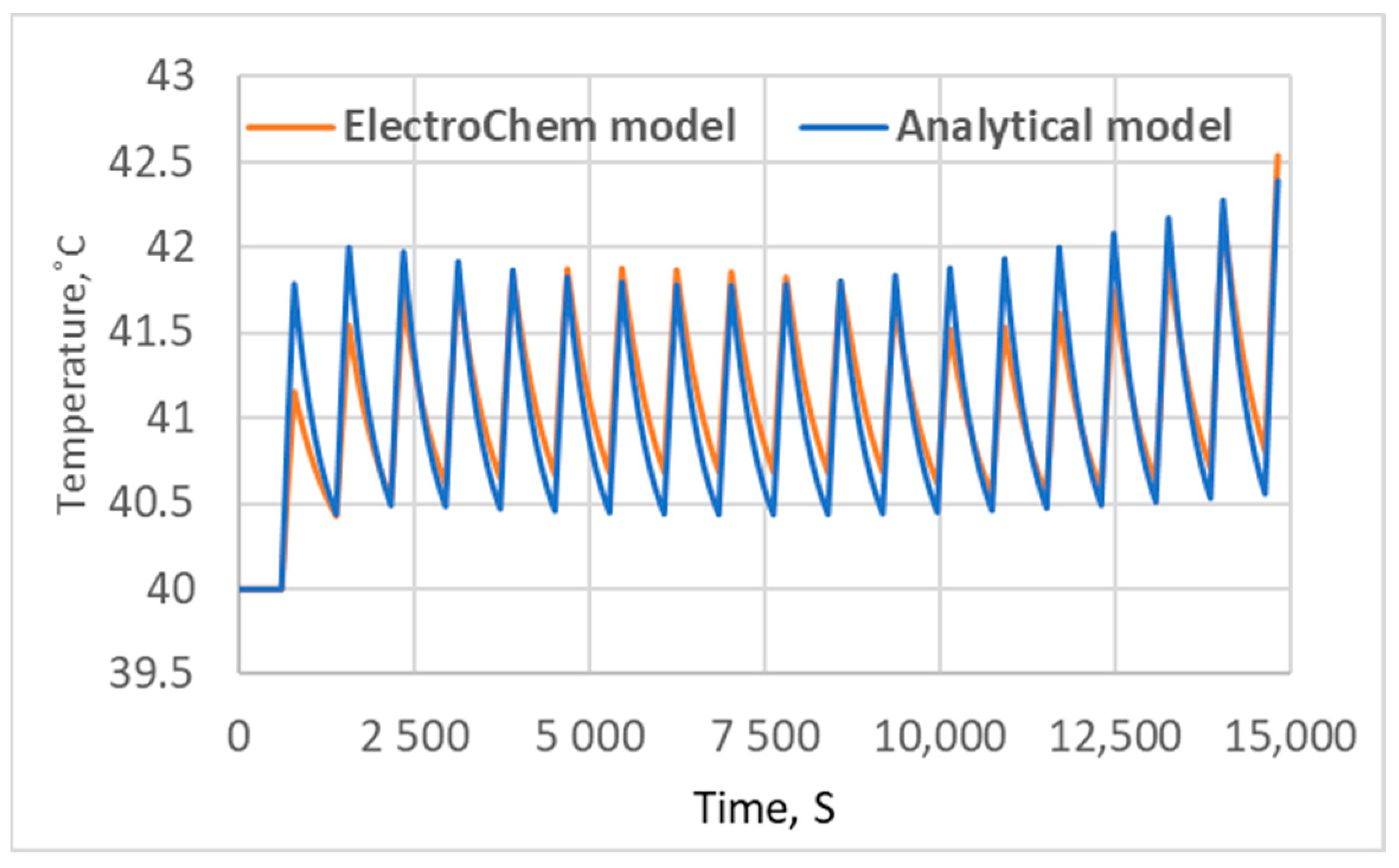
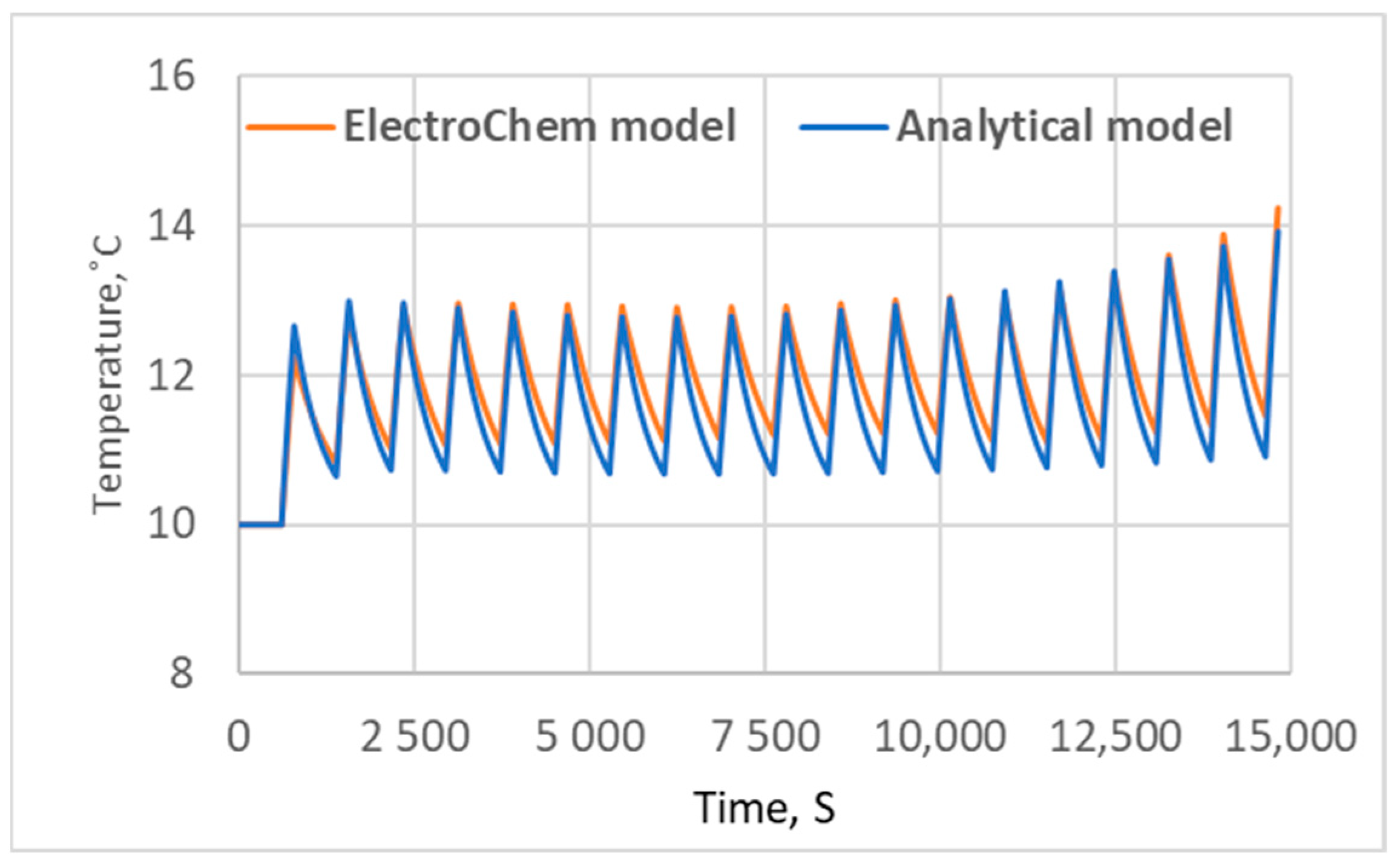
3.2. Electrochemical Model Validation
4. Simplified Battery Analytical Model Development
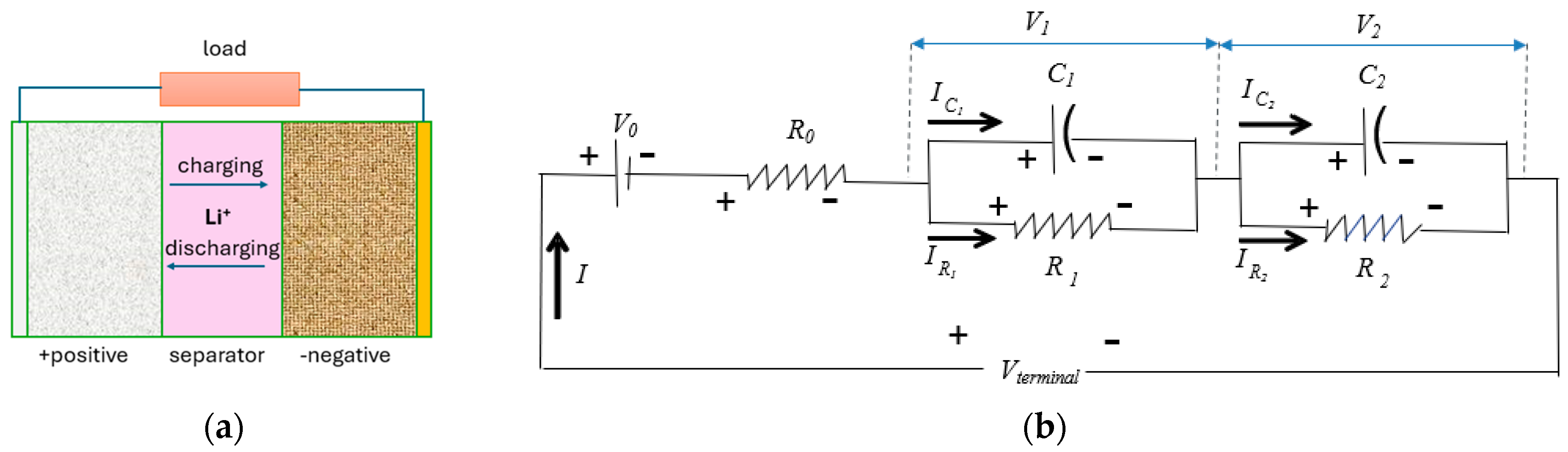
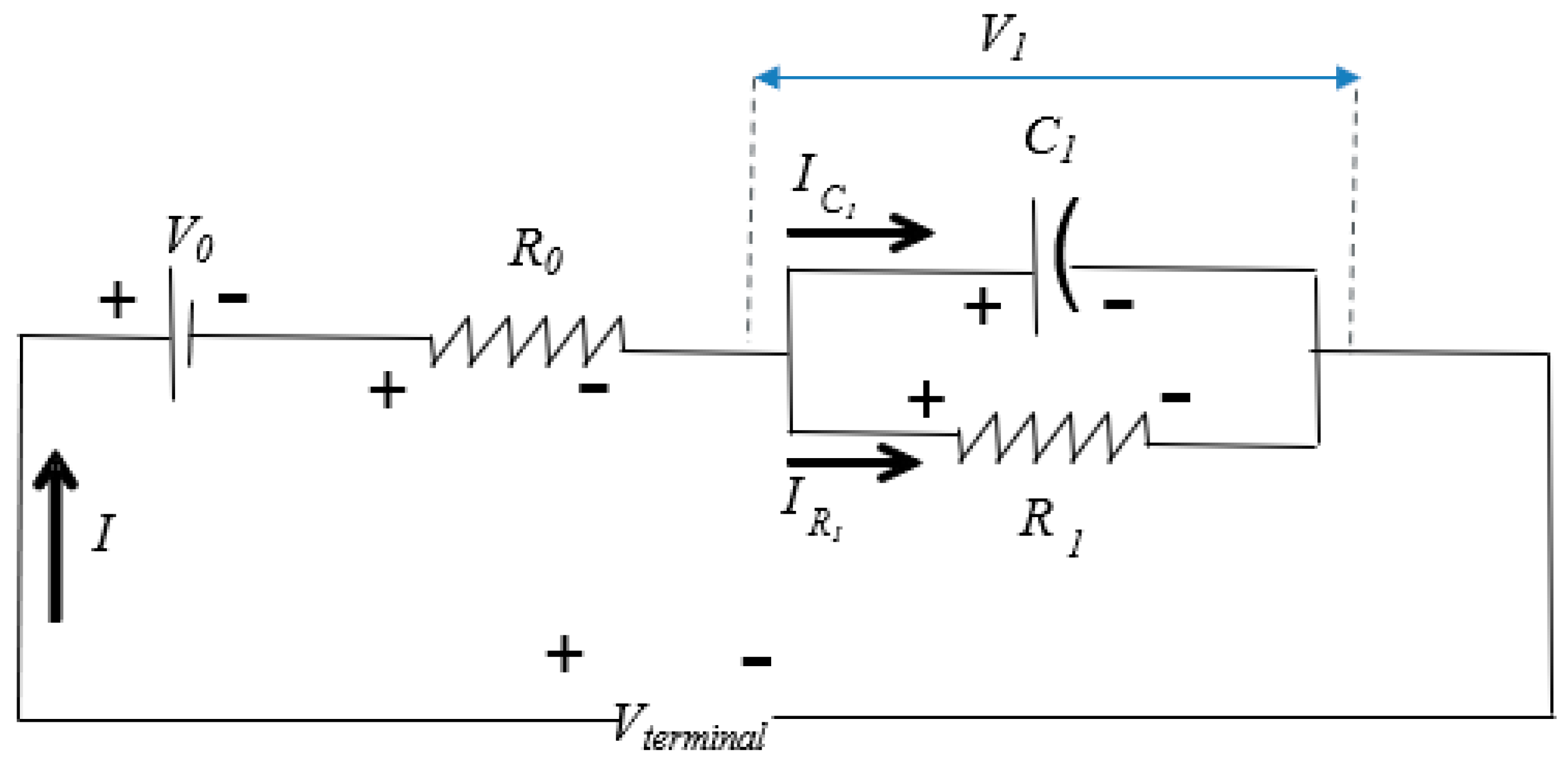
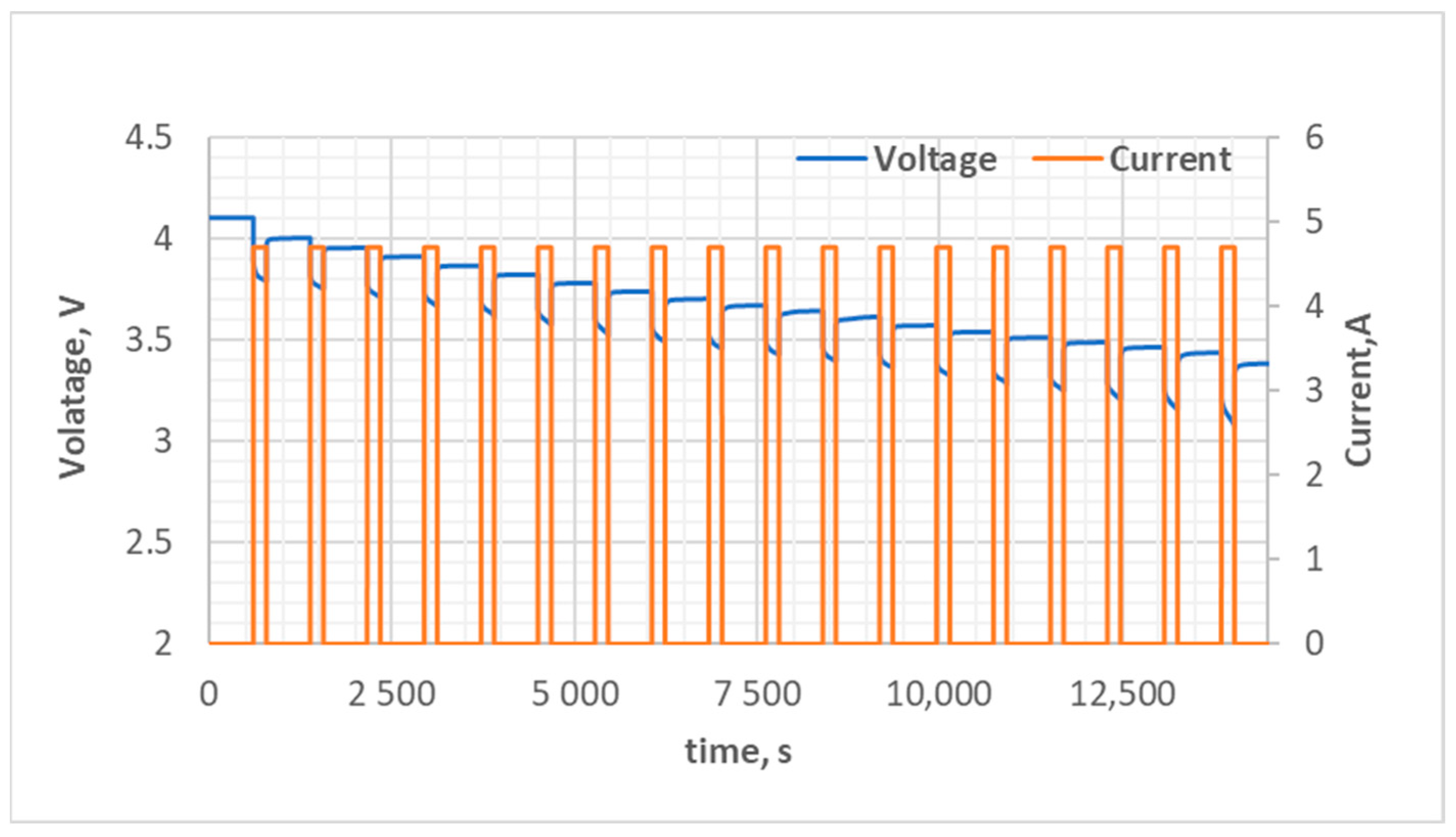
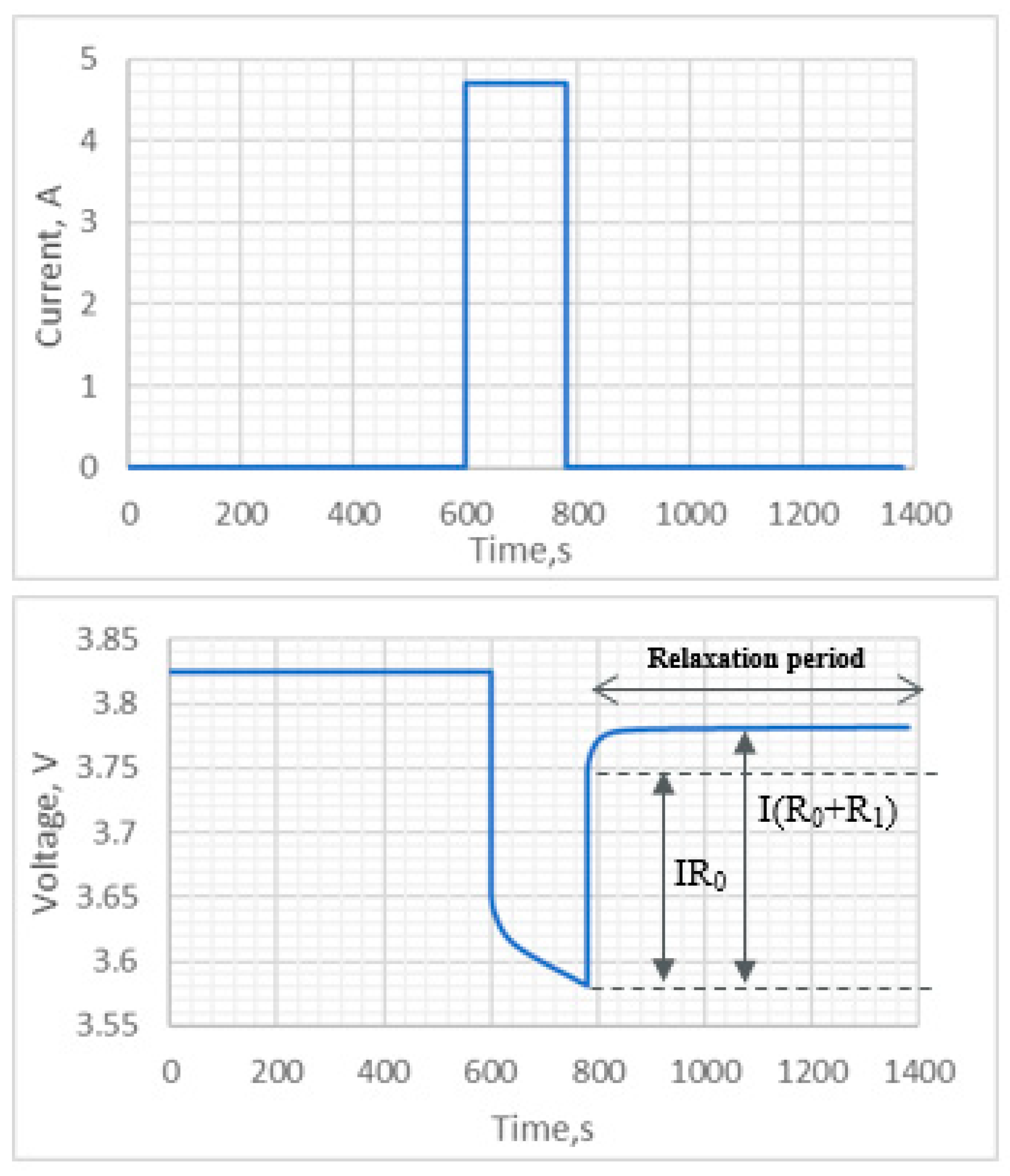
4.1. Electrical Equivalent Circuit Model Development and HPPC Testing
4.2. Identification of Parameters
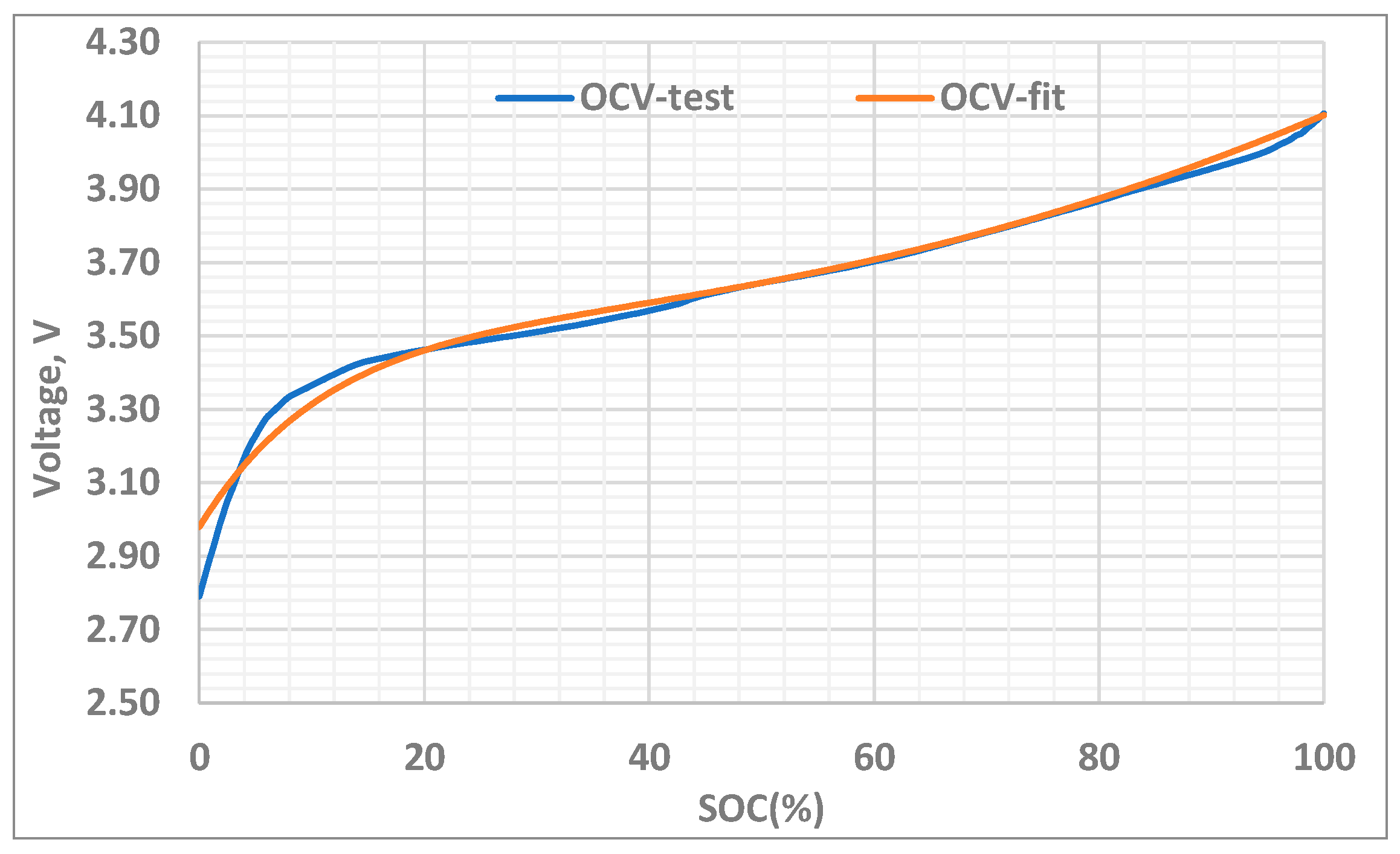
4.2.1. Identification of Open Circuit Voltage (OCV)
4.2.2. Identification of Ohmic Resistance R0
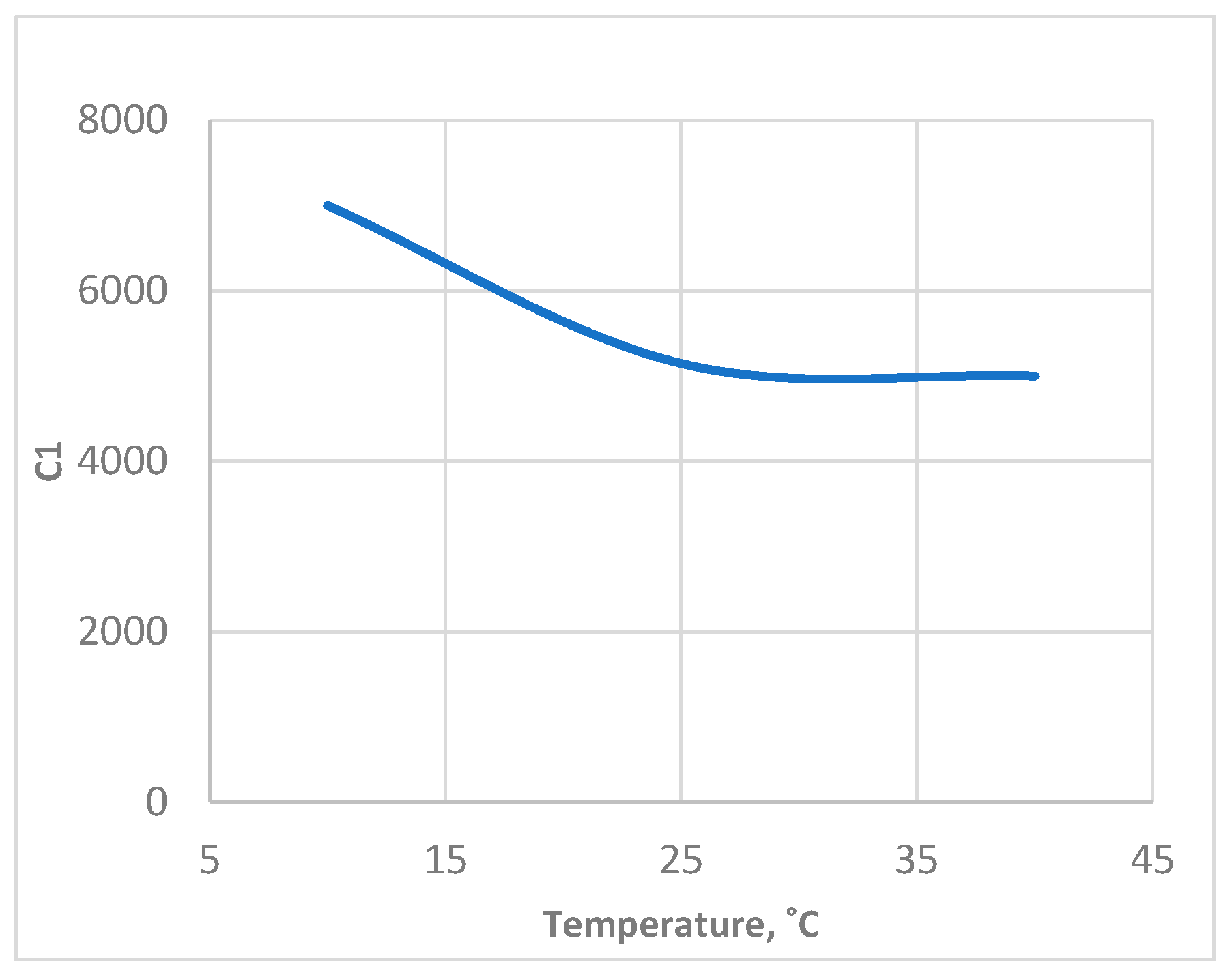
4.2.3. Identification of R1 and C1
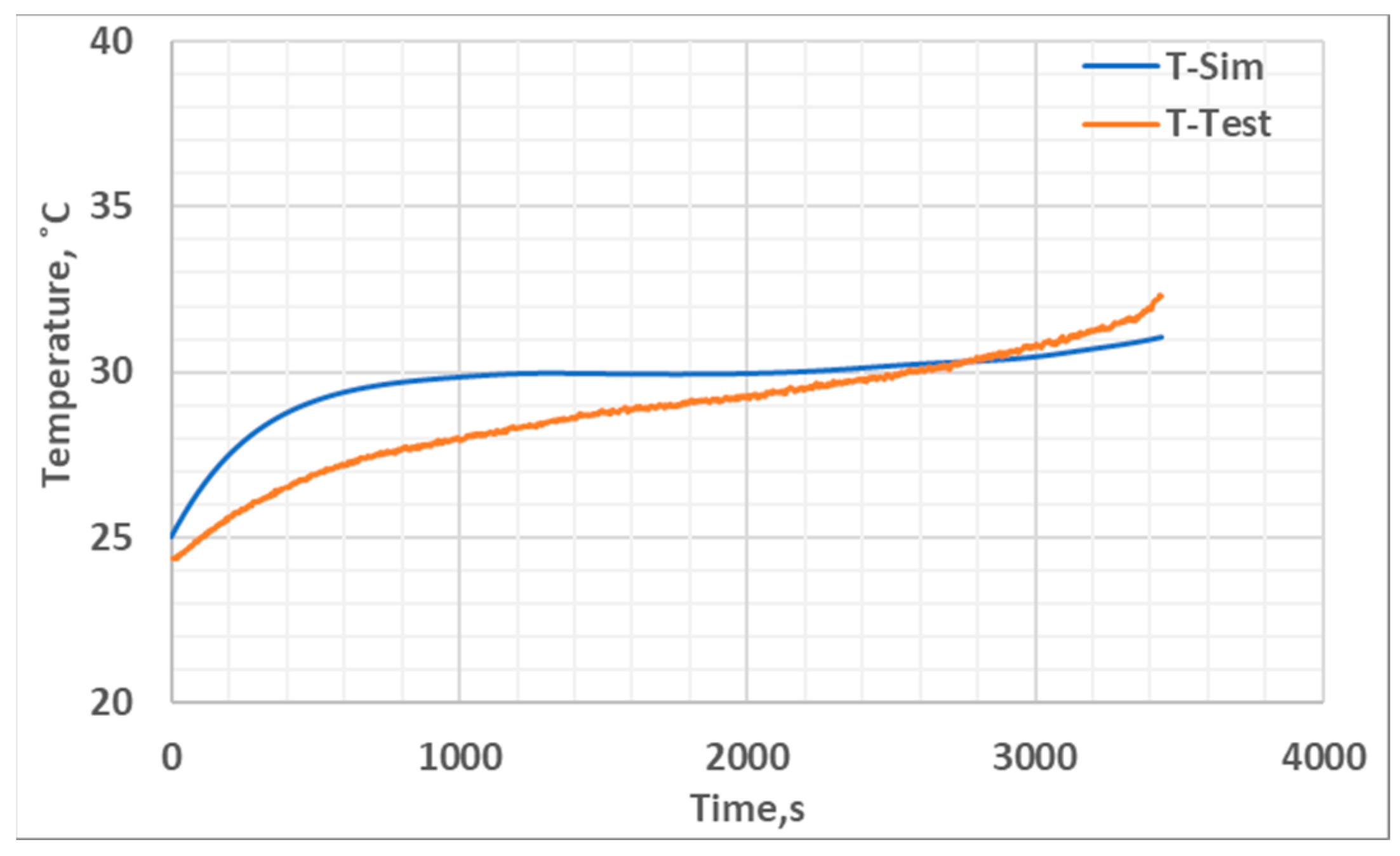
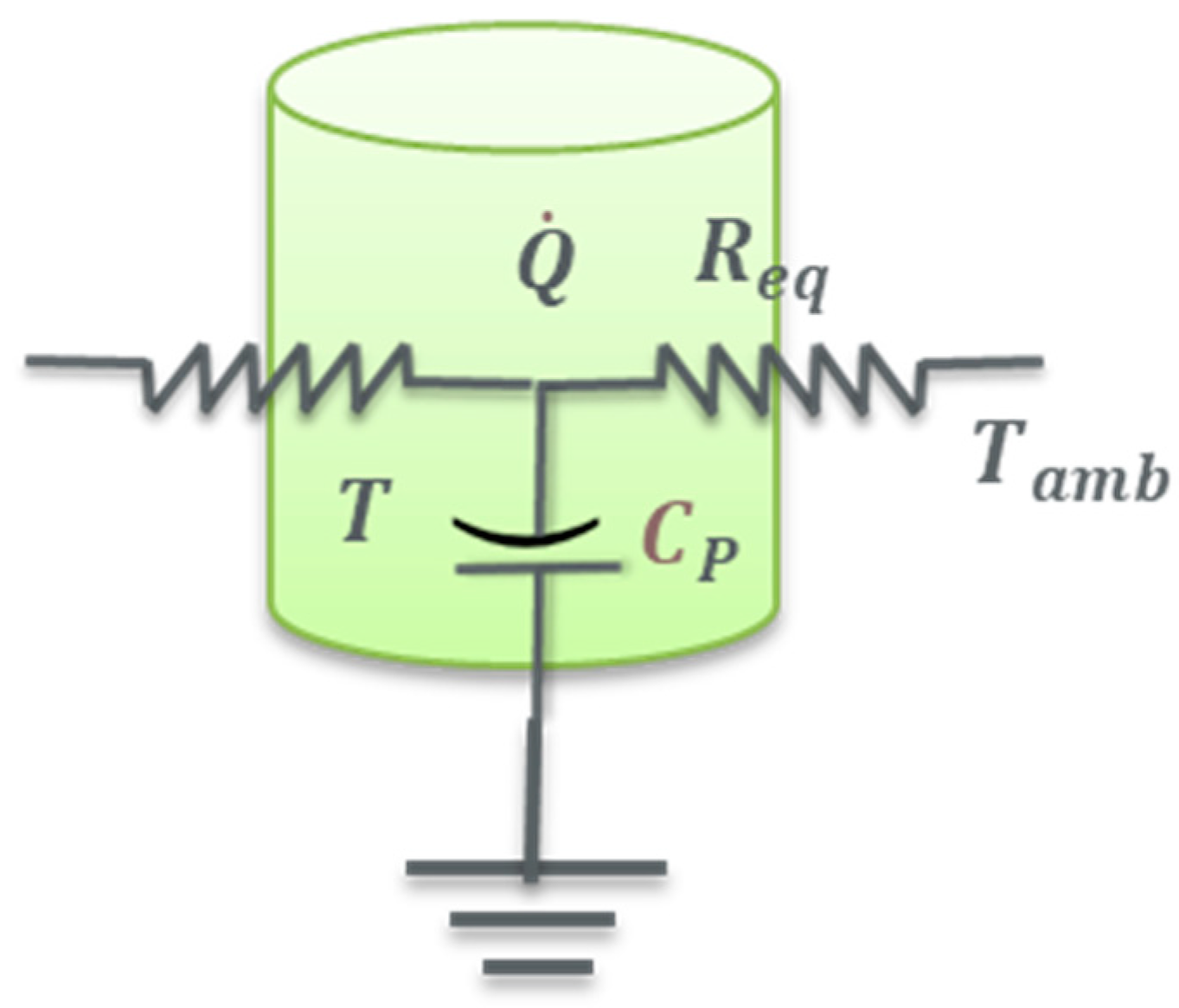
4.3. Thermal Model Development
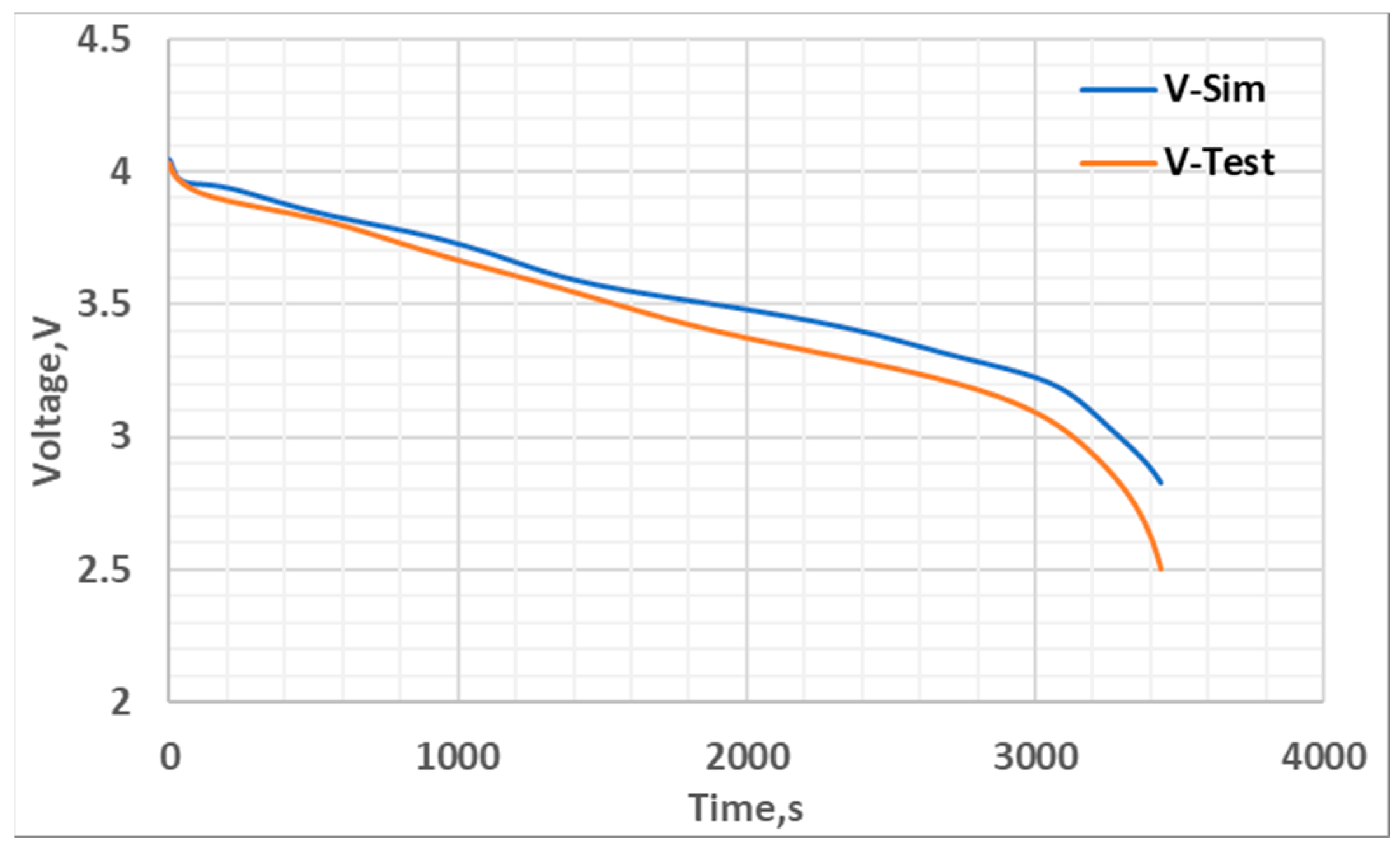
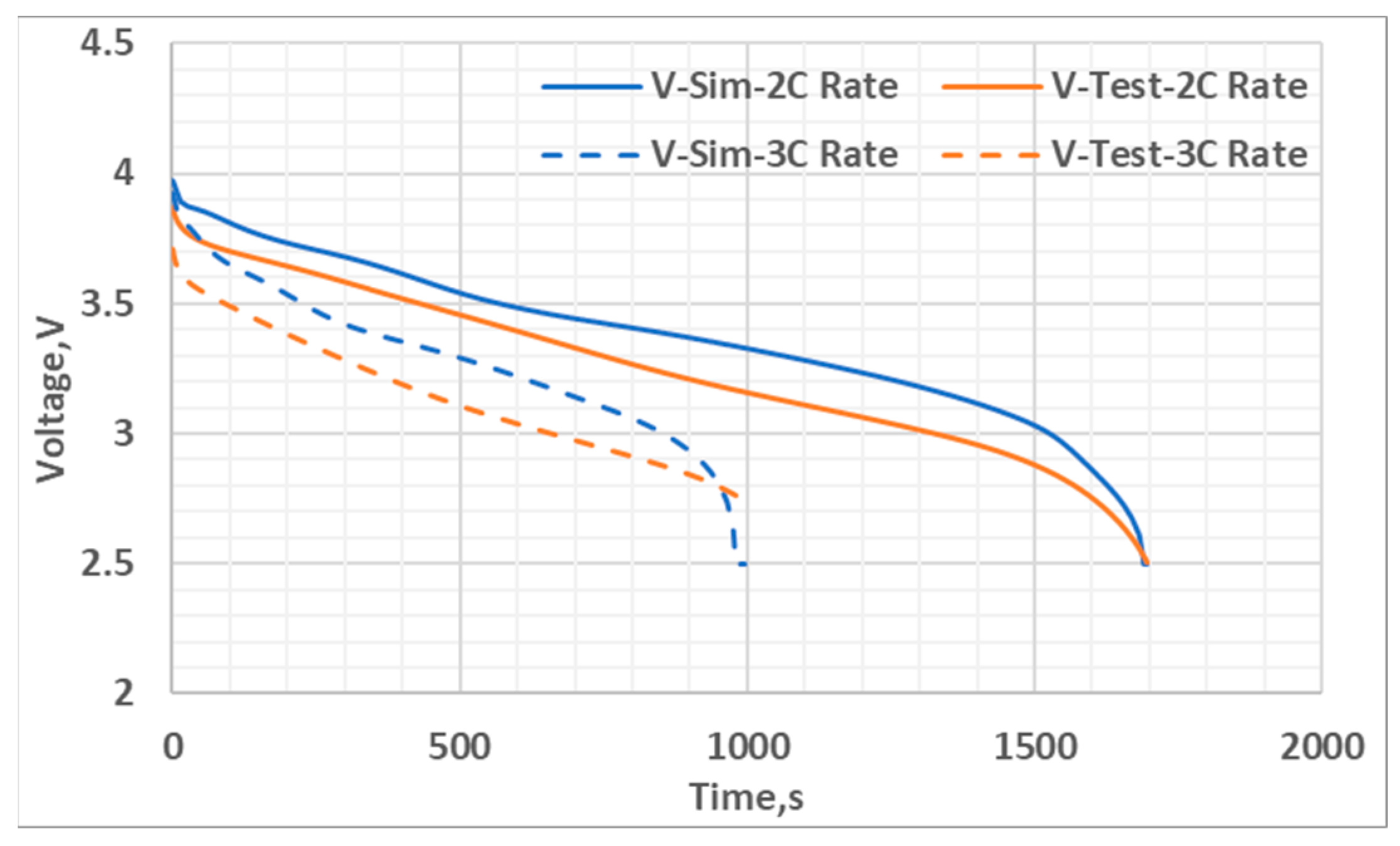
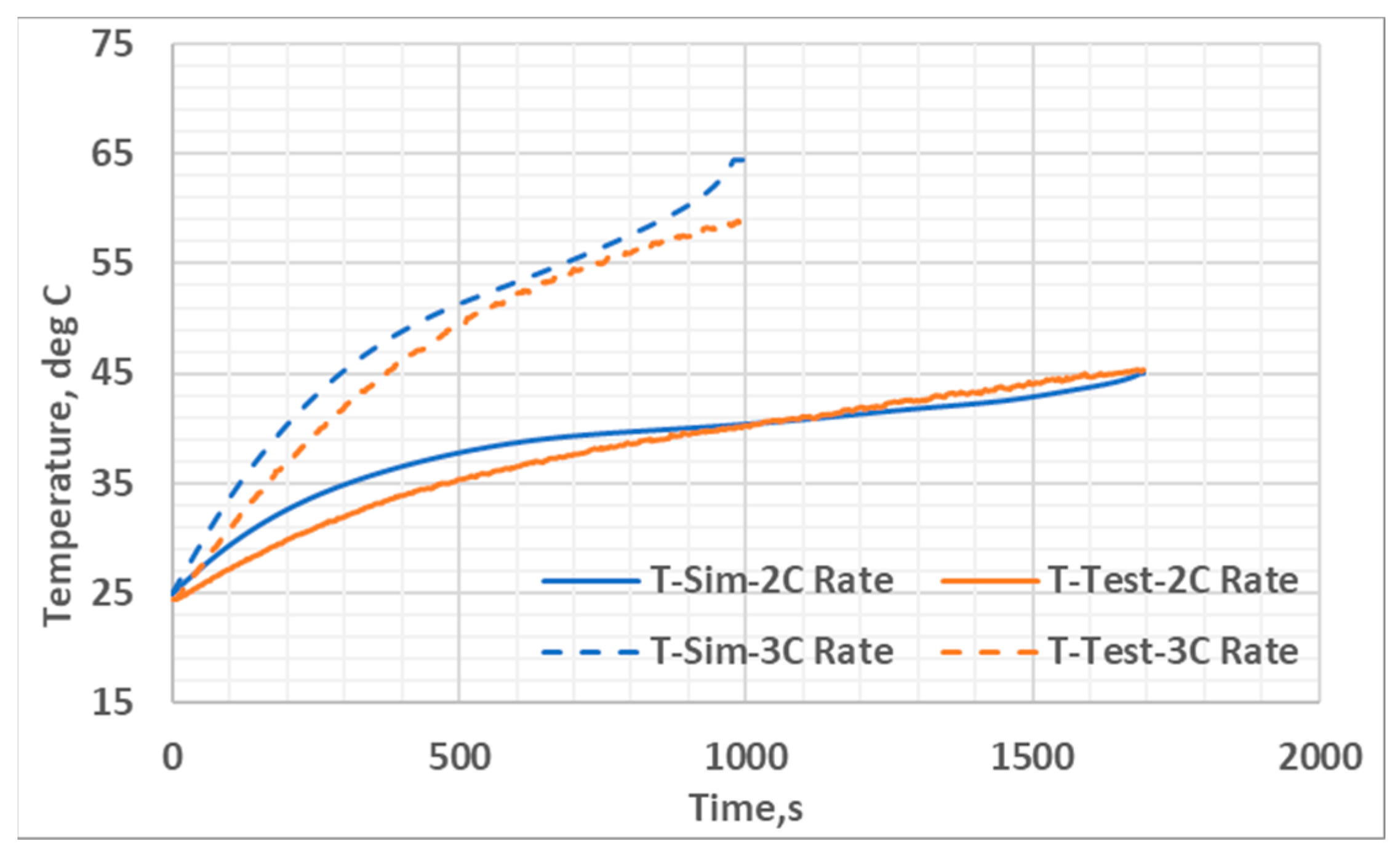
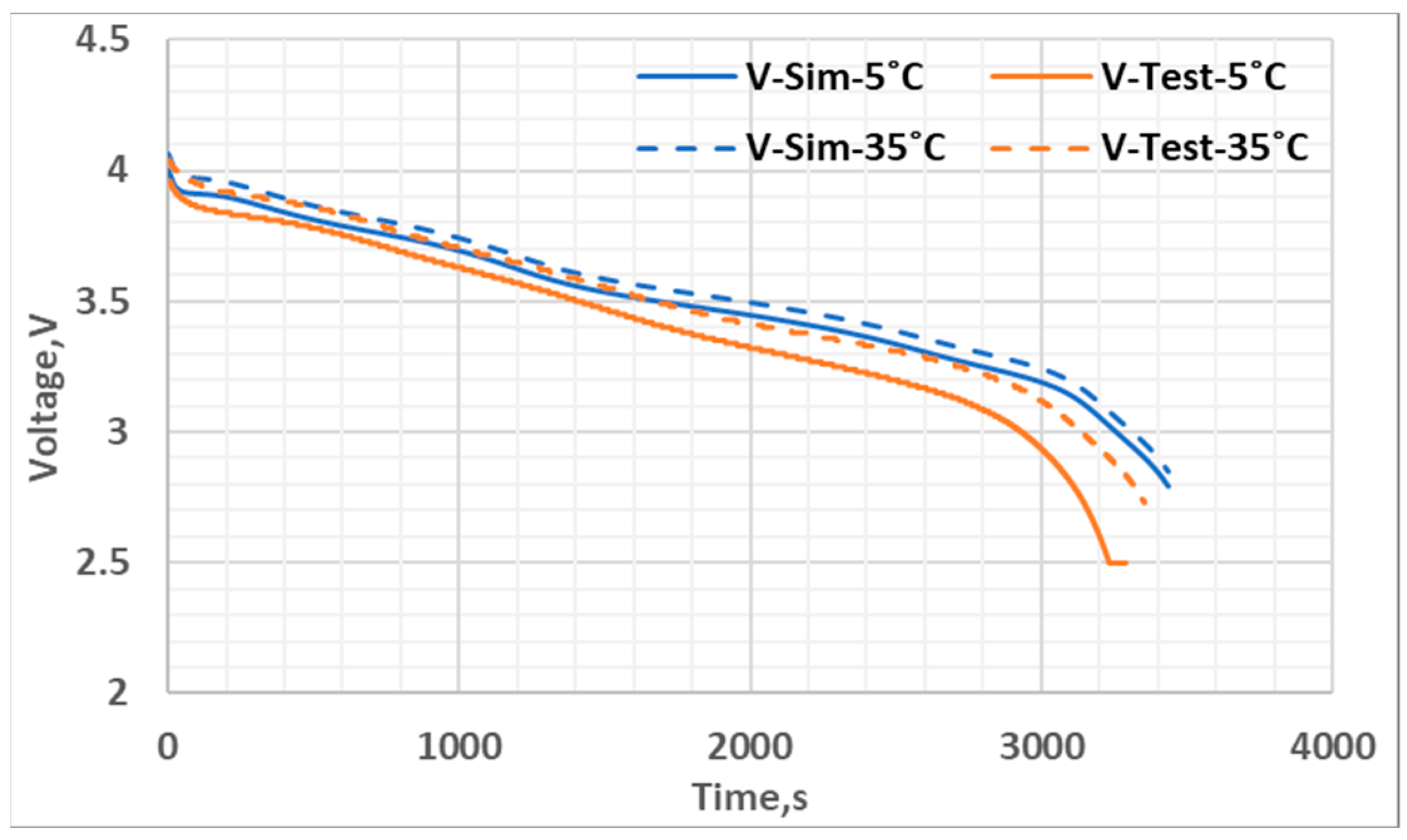
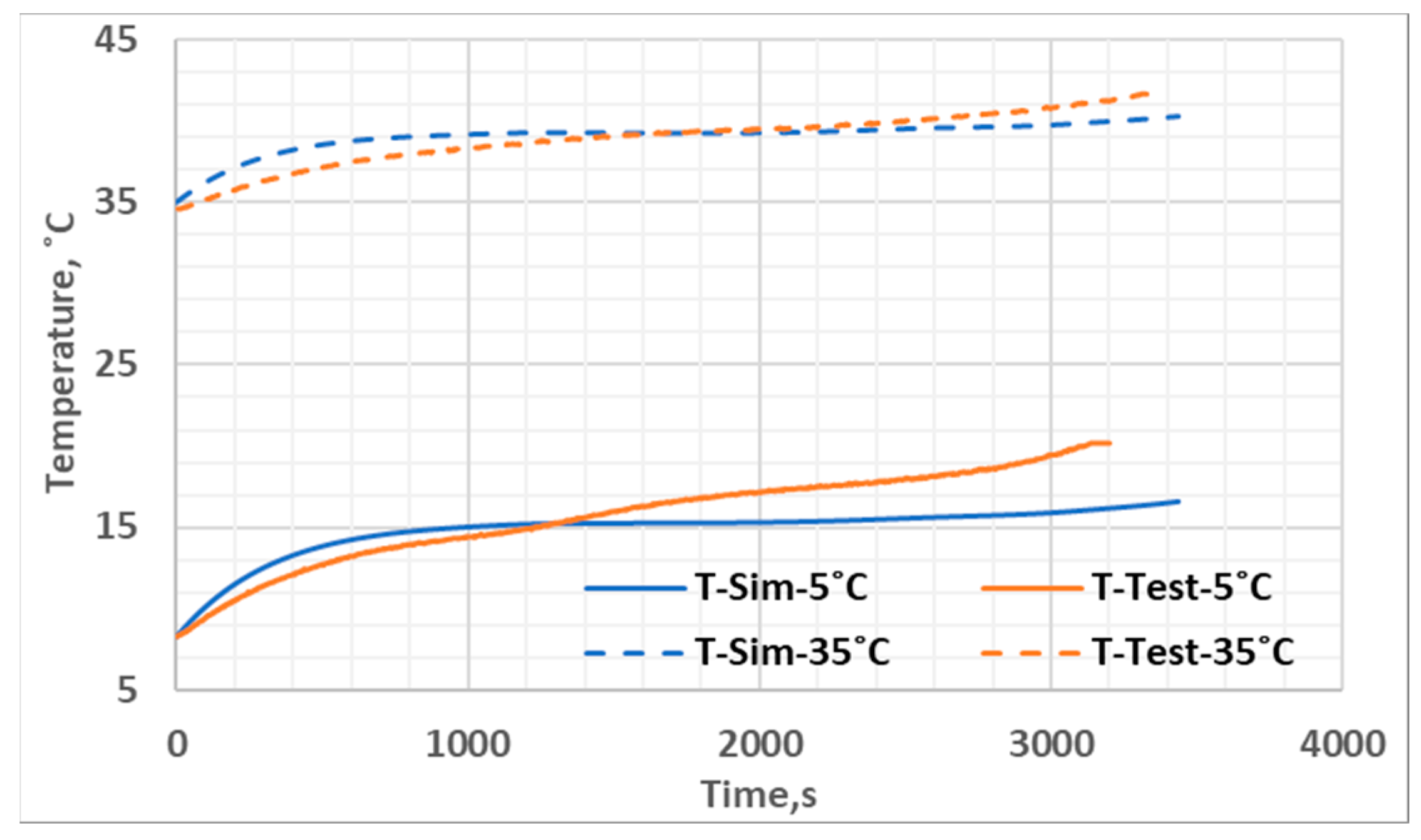
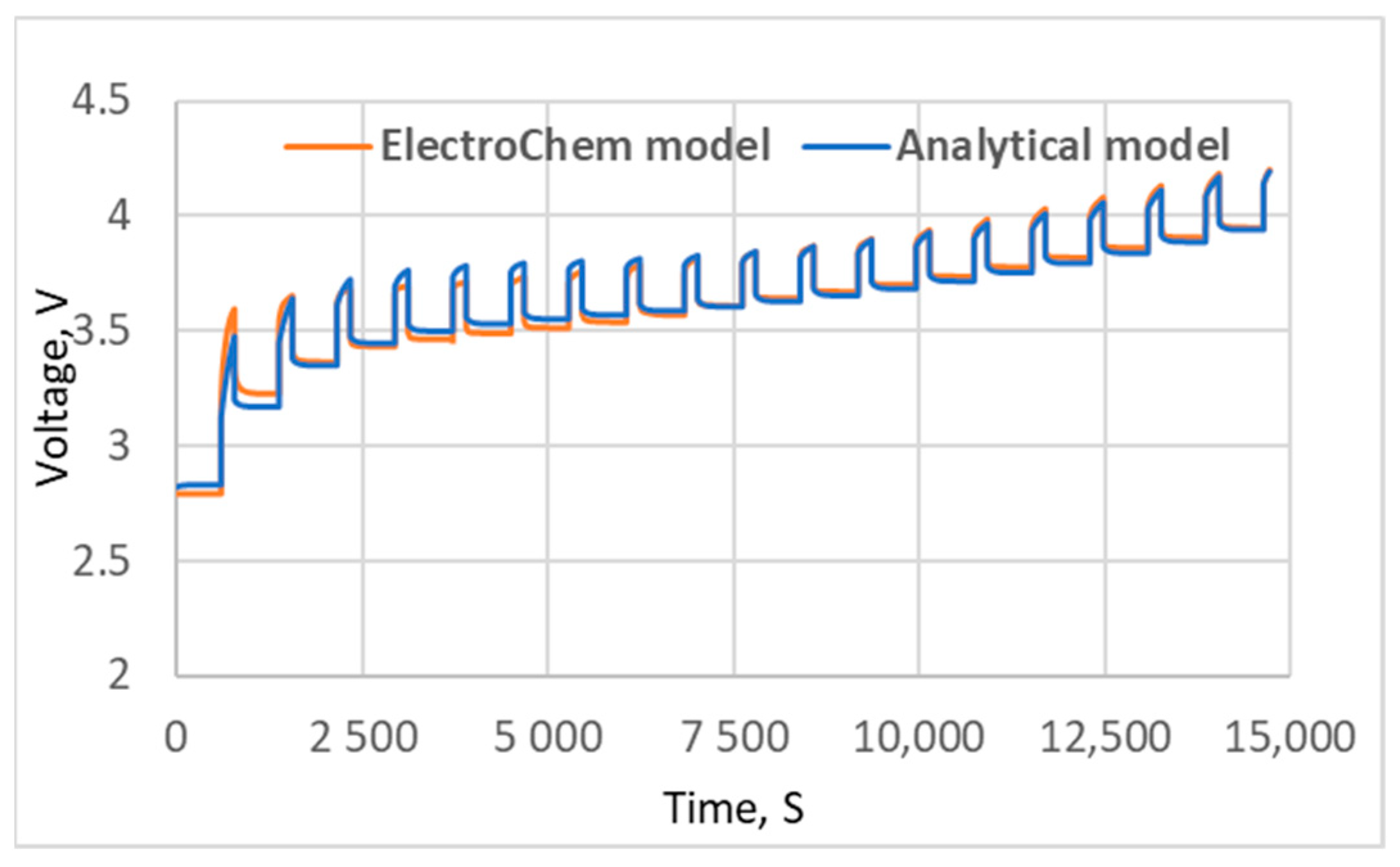
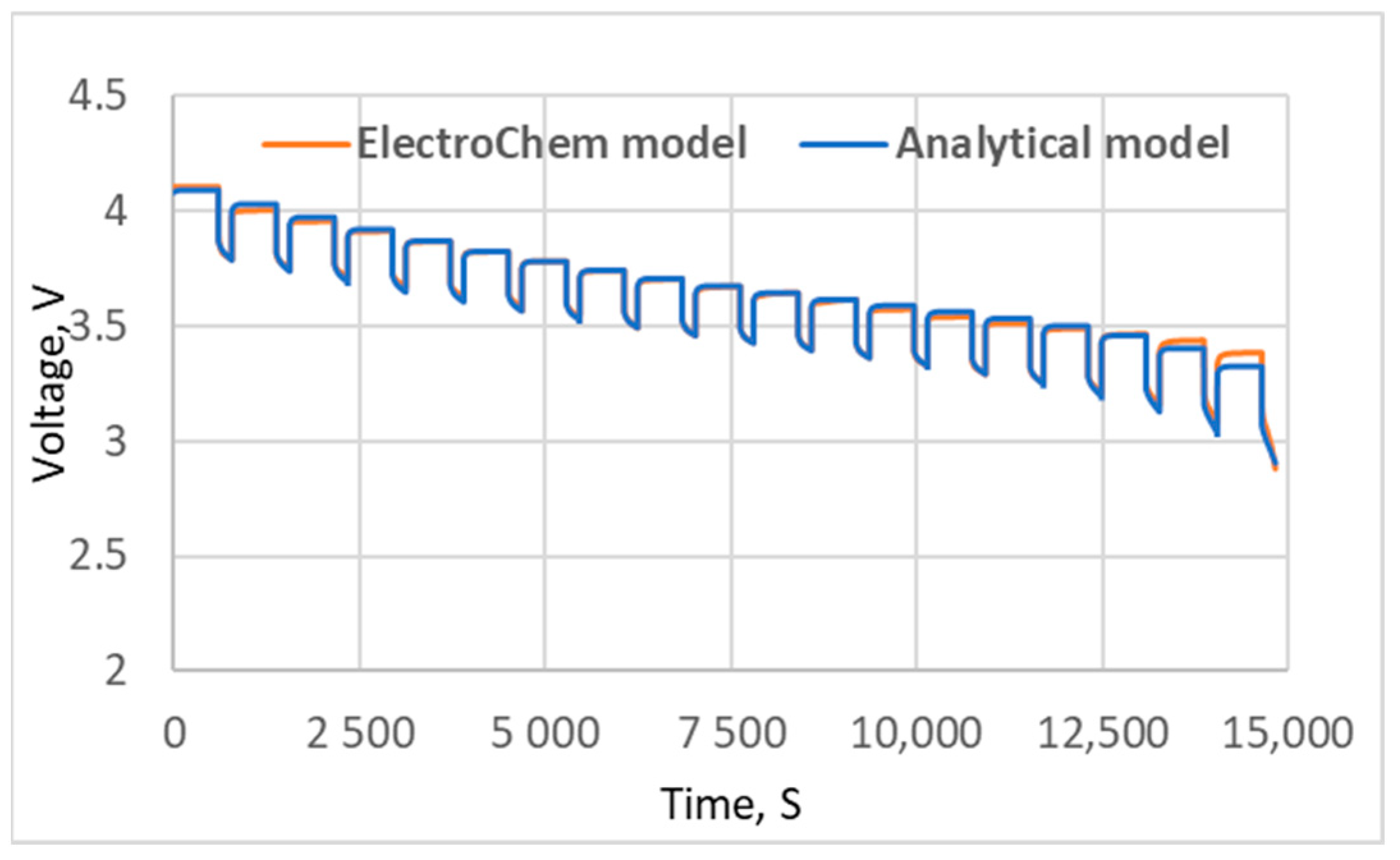
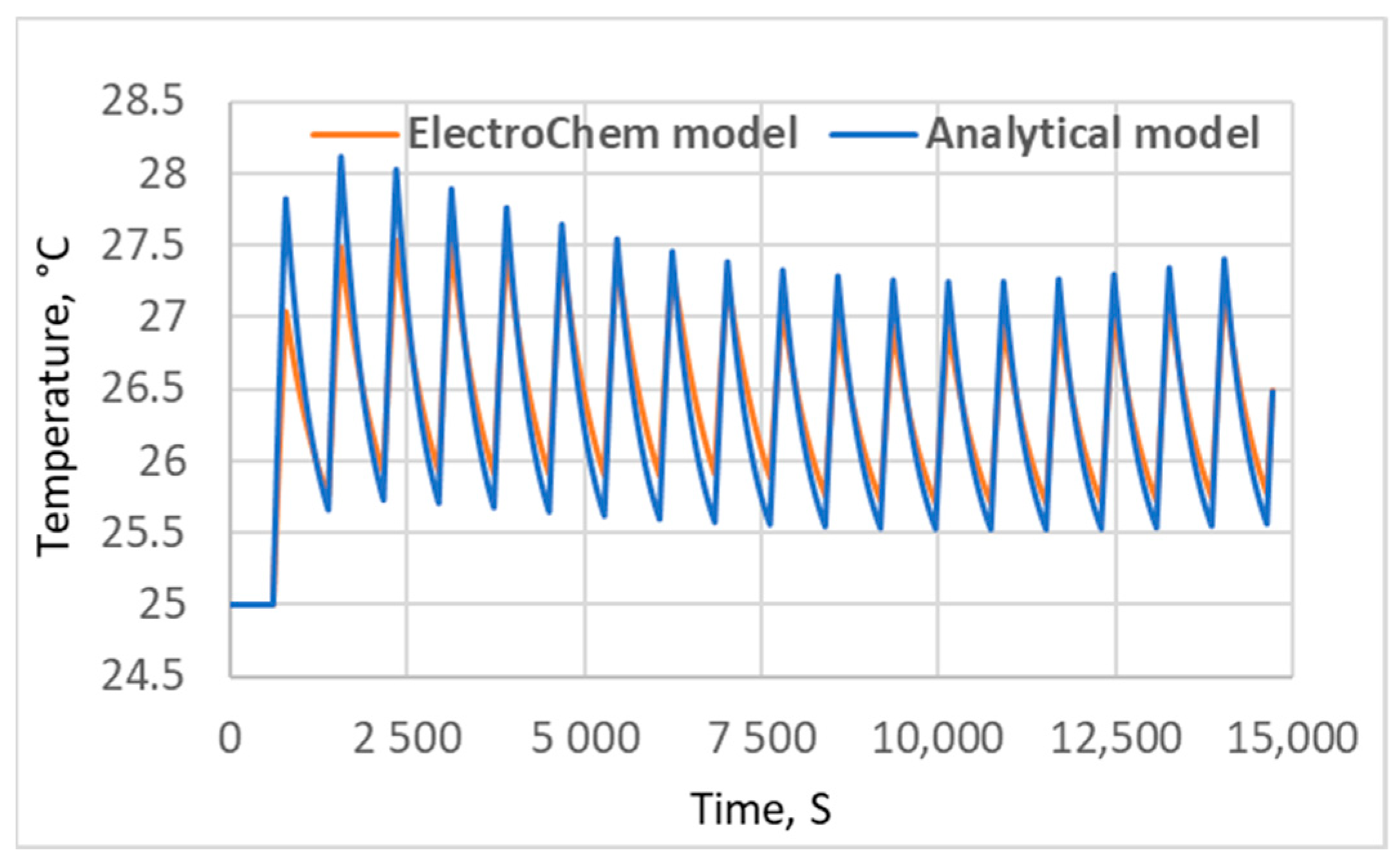
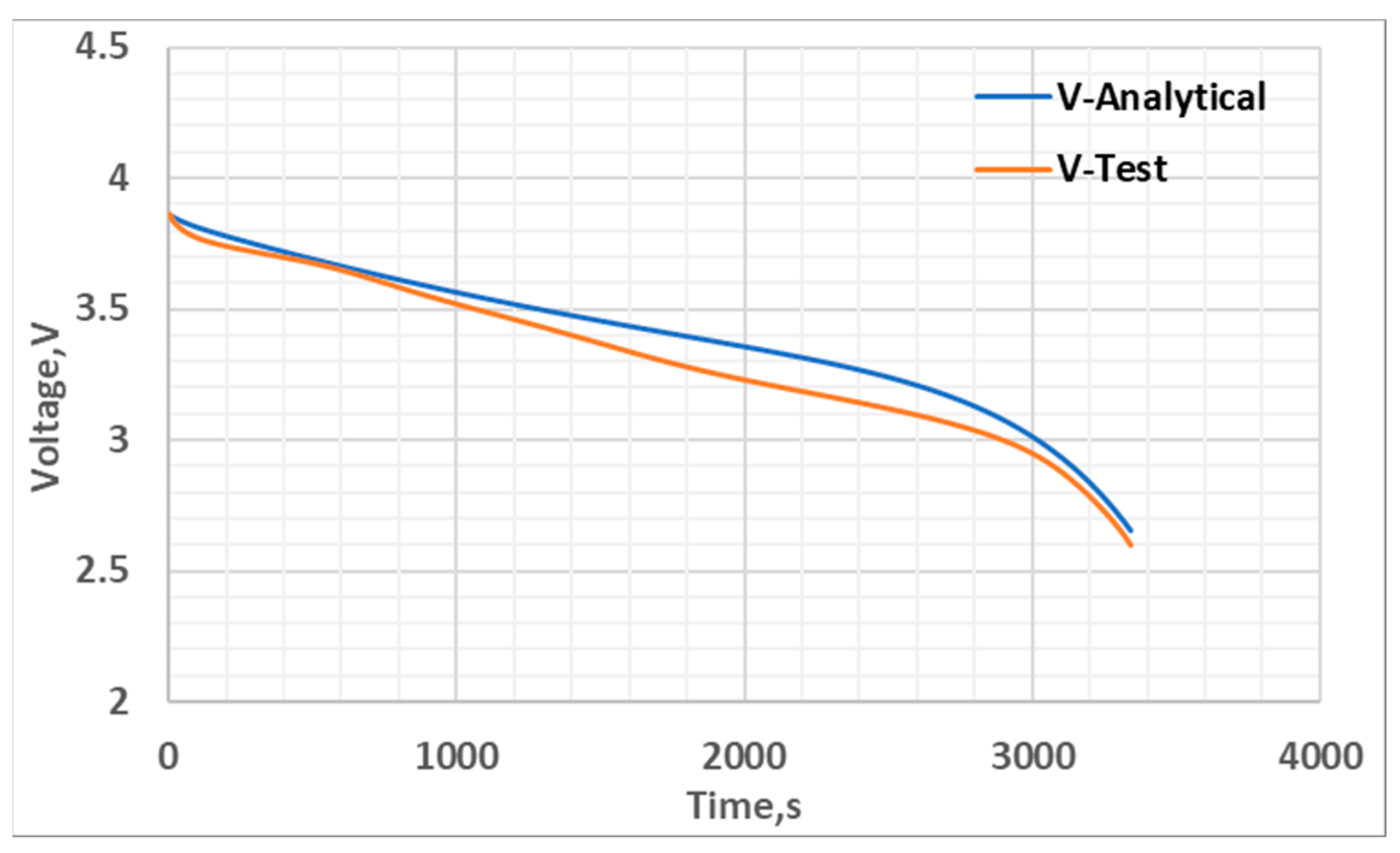
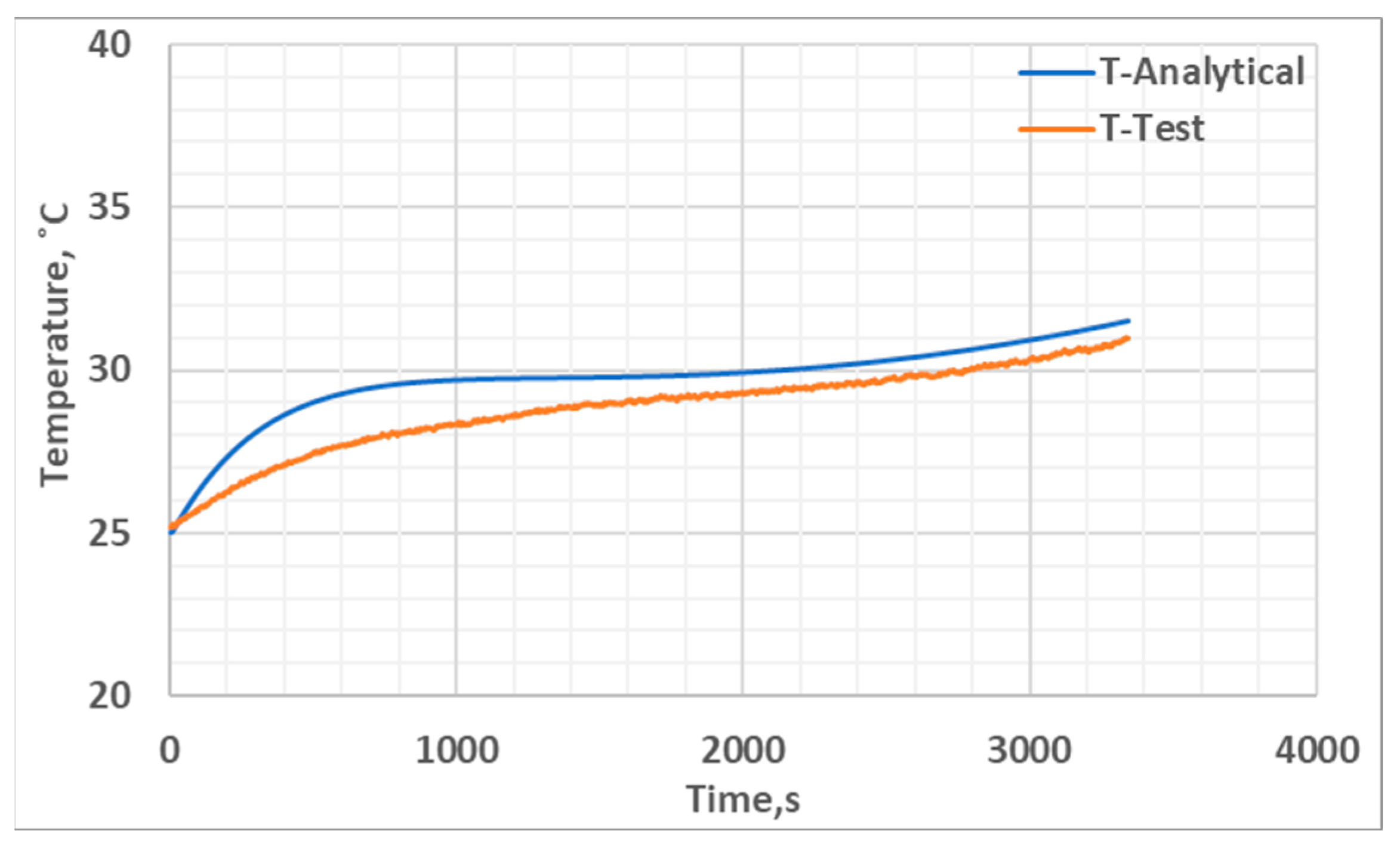
5. Results and Discussion
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| n | Number of electrons transferred |
| IC | Current through capacitance circuit |
| IR | Current through resistance circuit |
| Charge across capacitance | |
| Voltage at previous time step | |
| r | Radius of spherical electrode particle |
| F | Faraday’s constant |
| Transference number | |
| R | Universal constant |
| VOC | Open circuit voltage, Volts |
| Vt | Terminal voltage, Volts |
References
- Hariharan, K.; Tagade, P.; Ramachandran, S. Mathematical Modeling of Lithium Batteries: From Electrochemical Models to State Estimator Algorithms; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Plett, G.L. Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs: Part 3. State and parameter estimation. J. Power Sources 2004, 134, 277–292. [Google Scholar] [CrossRef]
- Xu, Y.; Hu, M.; Fu, C.; Cao, K.; Su, Z.; Yang, Z. State of Charge Estimation for Lithium-Ion Batteries Based on Temperature-Dependent Second-Order RC Model. Electronics 2019, 8, 1012. [Google Scholar] [CrossRef]
- Xiong, R.; Cao, J.; Yu, Q.; He, H.; Sun, F. Critical Review on the Battery State of Charge Estimation Methods for Electric Vehicles. IEEE Access 2018, 6, 1832–1843. [Google Scholar] [CrossRef]
- Zhang, C.; Allafi, W.; Dinh, Q.; Ascencio, P.; Marco, J. Online estimation of battery equivalent circuit model parameters and state of charge using decoupled least squares technique. Energy 2018, 142, 678–688. [Google Scholar] [CrossRef]
- Aditya, K. Simulation and Validation of a Precise 2RC Model of Lithium-Ion cell Incorporating Wire-bond Losses. In Proceedings of the 2023 International Conference on Control, Communication and Computing (ICCC), Thiruvananthapuram, India, 19–21 May 2023; pp. 1–4. [Google Scholar] [CrossRef]
- Dai, H.; Xu, T.; Zhu, L.; Wei, X.; Sun, Z. Adaptive model parameter identification for large capacity Li-ion batteries on separated time scales. Appl. Energy 2016, 184, 119–131. [Google Scholar] [CrossRef]
- Jiang, S. A Parameter Identification Method for a Battery Equivalent Circuit Model; SAE Technical Paper; 2011-01-1367; SAE International: Warrendale, PA, USA, 2011; Available online: https://saemobilus.sae.org/papers/a-parameter-identification-method-a-battery-equivalent-circuit-model-2011-01-1367 (accessed on 10 October 2023).
- Dagci, O.H.; Chandrasekaran, R. Li-Ion Battery Pack Characterization and Equivalent Electrical Circuit Model Development; SAE Technical Paper; 2014-01-1839; SAE International: Warrendale, PA, USA, 2014; Available online: https://saemobilus.sae.org/papers/li-ion-battery-pack-characterization-equivalent-electrical-circuit-model-development-2014-01-1839 (accessed on 10 October 2023).
- Chen, C. Parameter Determination for the Battery Equivalent Circuit Model Using a Numerical Integro-Differential Method; SAE Technical Paper; 2020-01-1179; SAE International: Warrendale, PA, USA, 2020; Available online: https://saemobilus.sae.org/papers/parameter-determination-battery-equivalent-circuit-model-using-a-numerical-integro-differential-method-2020-01-1179 (accessed on 10 October 2023).
- Hussein, A.A.-H.; Batarseh, I. An Overview of Generic Battery Models. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, L.; Hu, X.; Xiong, N.; Hu, G.-D. H∞-Based Nonlinear Observer Design for State of Charge Estimation of Lithium-Ion Battery with Polynomial Parameters. IEEE Trans. Veh. Technol. 2017, 66, 10853–10865. [Google Scholar] [CrossRef]
- Barbieri, M.; Ceraolo, M.; Lutzemberger, G.; Scarpelli, C. An Electro-Thermal Model for LFP Cells: Calibration Procedure and Validation. Energies 2022, 15, 2653. [Google Scholar] [CrossRef]
- Surya, S.; Samanta, A.; Marcis, V.; Williamson, S. Smart Core and Surface Temperature Estimation Techniques for Health-Conscious Lithium-Ion Battery Management Systems: A Model-to-Model Comparison. Energies 2022, 15, 623. [Google Scholar] [CrossRef]
- Guo, J.; Guo, Q.; Liu, J.; Wang, H. The Polarization and Heat Generation Characteristics of Lithium-Ion Battery with Electric–Thermal Coupled Modeling. Batteries 2023, 9, 529. [Google Scholar] [CrossRef]
- Zhang, R.; Xia, B.; Li, B.; Cao, L.; Lai, Y.; Zheng, W.; Wang, H.; Wang, W.; Wang, M. A Study on the Open Circuit Voltage and State of Charge Characterization of High Capacity Lithium-Ion Battery under Different Temperature. Energies 2018, 11, 2408. [Google Scholar] [CrossRef]
- Catenaro, E.; Onori, S. Experimental data of three lithium-ion batteries under galvanostatic discharge tests at different C-rates and operating temperatures. Data Brief 2021, 35, 106894. [Google Scholar] [CrossRef]
- Miguel, E.; Plett, L.G.; Trimboli, M.S.; Oca, L.; Iraola, U.; Bekaert, E. Review of computational parameter estimation methods for electrochemical models. J. Energy Storage 2021, 44, 103388. [Google Scholar] [CrossRef]
- Chen, C.-H.; Planella, F.B.; O’Regan, K.; Gastol, D.; Widanage, W.D.; Kendrick, E. Development of Experimental Techniques for Parameterization of Multi-scale Lithium-ion Battery Models. J. Electrochem. Soc. 2020, 167, 080534. [Google Scholar] [CrossRef]
- Doyle, M.; Fuller, T.; Newman, J. Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell. J. Electrochem. Soc. 1993, 140, 1526–1533. [Google Scholar] [CrossRef]
- Newman, J.; Thomas-Alyea, K. Electrochemical Systems, 3rd ed.; Wiley-Interscience: Hoboken, NJ, USA, 2004. [Google Scholar]
- Sulzer, V.; Marquis, S.; Timms, R.; Robinson, M.; Chapman, S.J. Python battery mathematical modelling (PyBaMM). J. Open Res. Softw. 2021, 9, 14. [Google Scholar] [CrossRef]
- Seals, D.; Ramesh, P.; D’Arpino, M.; Canova, M. Physics-Based Equivalent Circuit Model for Lithium-Ion Cells via Reduction and Approximation of Electrochemical Model. SAE Int. J. Adv. Curr. Prac. Mobil. 2022, 4, 1154–1165. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Positive electrode active material volume fraction | 0.65 |
| Positive electrode porosity | 0.35 |
| Negative electrode active material volume fraction | 0.75 |
| Negative electrode porosity | 0.25 |
| Positive electrode thickness, m | 7.56 × 10−5 |
| Negative electrode thickness, m | 8.52 × 10−5 |
| Open circuit voltage, V | 4.2 |
| Parameter | Final Optimized Value |
|---|---|
| Contact resistance, Ohm | 0.001 |
| Heat transfer coefficient, W/m2K | 25 |
| Bruggeman exponents | 1.25 |
| Parameter | Fitted Equation with Parameter Values |
|---|---|
| V0 | |
| R0 | |
| R1 | 0.0065 |
| C1 |
| Parameter | Values |
|---|---|
| Contact Resistance—Rcontact (Ω) | 1.2427 × 10−4 |
| Area—A (m2) | 0.1616 |
| Heat Transfer Coefficient—h (W/(m2K)) | 20 |
| Cell thermal mass—m (kg) | 0.06 |
| Correction factor—Cf | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Damodaran, V.; Paramadayalan, T.; Natarajan, D.; Kumar C, R.; Kanna, P.R.; Taler, D.; Sobota, T.; Taler, J.; Szymkiewicz, M.; Ahamed, M.J. Development of a Fast Running Equivalent Circuit Model with Thermal Predictions for Battery Management Applications. Batteries 2024, 10, 215. https://doi.org/10.3390/batteries10060215
Damodaran V, Paramadayalan T, Natarajan D, Kumar C R, Kanna PR, Taler D, Sobota T, Taler J, Szymkiewicz M, Ahamed MJ. Development of a Fast Running Equivalent Circuit Model with Thermal Predictions for Battery Management Applications. Batteries. 2024; 10(6):215. https://doi.org/10.3390/batteries10060215
Chicago/Turabian StyleDamodaran, Vijayakanthan, Thiyagarajan Paramadayalan, Diwakar Natarajan, Ramesh Kumar C, P. Rajesh Kanna, Dawid Taler, Tomasz Sobota, Jan Taler, Magdalena Szymkiewicz, and Mohammed Jalal Ahamed. 2024. "Development of a Fast Running Equivalent Circuit Model with Thermal Predictions for Battery Management Applications" Batteries 10, no. 6: 215. https://doi.org/10.3390/batteries10060215
APA StyleDamodaran, V., Paramadayalan, T., Natarajan, D., Kumar C, R., Kanna, P. R., Taler, D., Sobota, T., Taler, J., Szymkiewicz, M., & Ahamed, M. J. (2024). Development of a Fast Running Equivalent Circuit Model with Thermal Predictions for Battery Management Applications. Batteries, 10(6), 215. https://doi.org/10.3390/batteries10060215









