A Novel Reaction Rate Parametrization Method for Lithium-Ion Battery Electrochemical Modelling
Abstract
1. Introduction
2. Model Presentation
2.1. Model Types
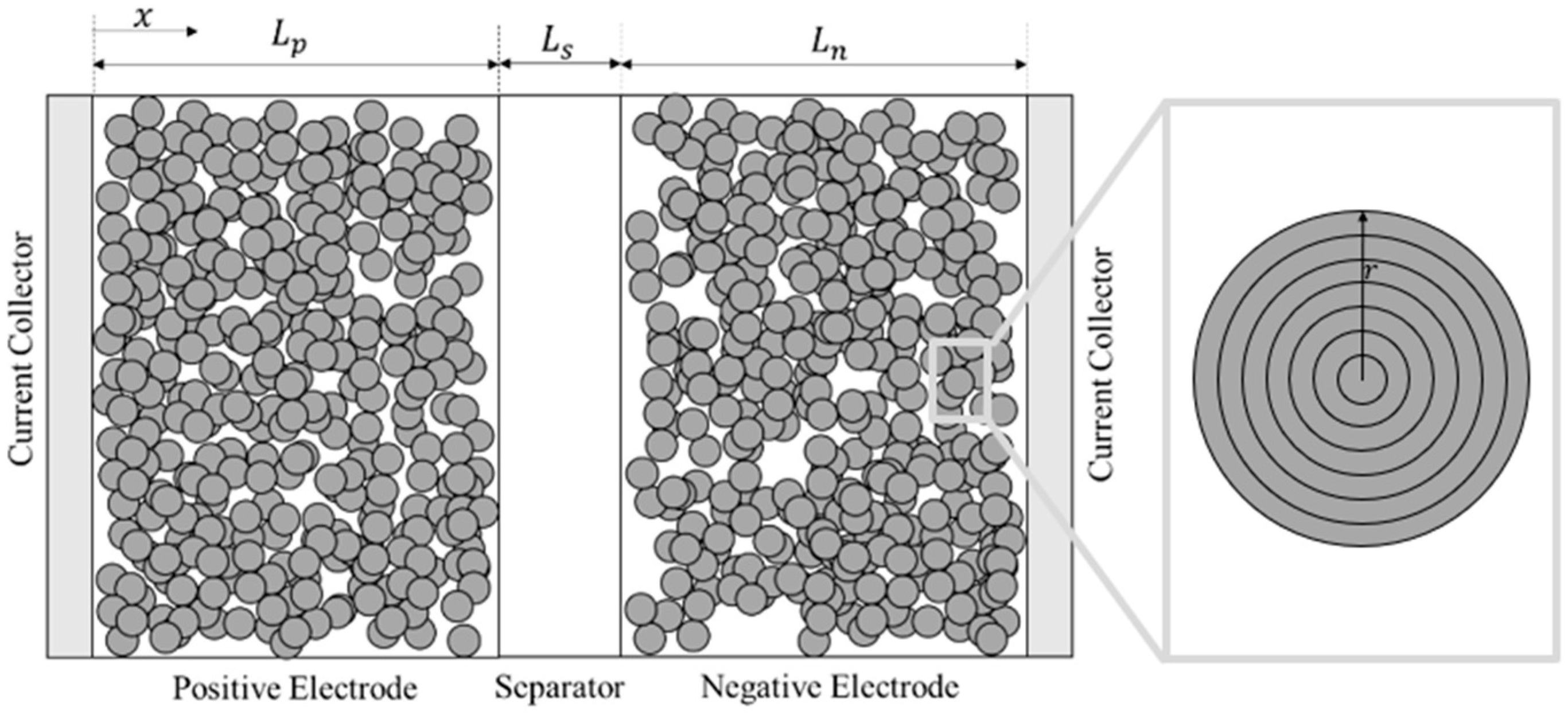
2.2. Chosen Model Description
2.3. Coefficient Convention and Units
- Variables: These represent the actual state of a physical quantity such as —the ionic flux, —the normalized ion concentration on the surface of a particle, —the overpotential, —the temperature, and —the electrolyte concentration (for P2D models).
- Constants: is the Faraday constant, is the ideal gas constant, and is the electrode maximum concentration that is known via material selection.
- Coefficient: is the reaction rate constant.
3. Experimental Protocol
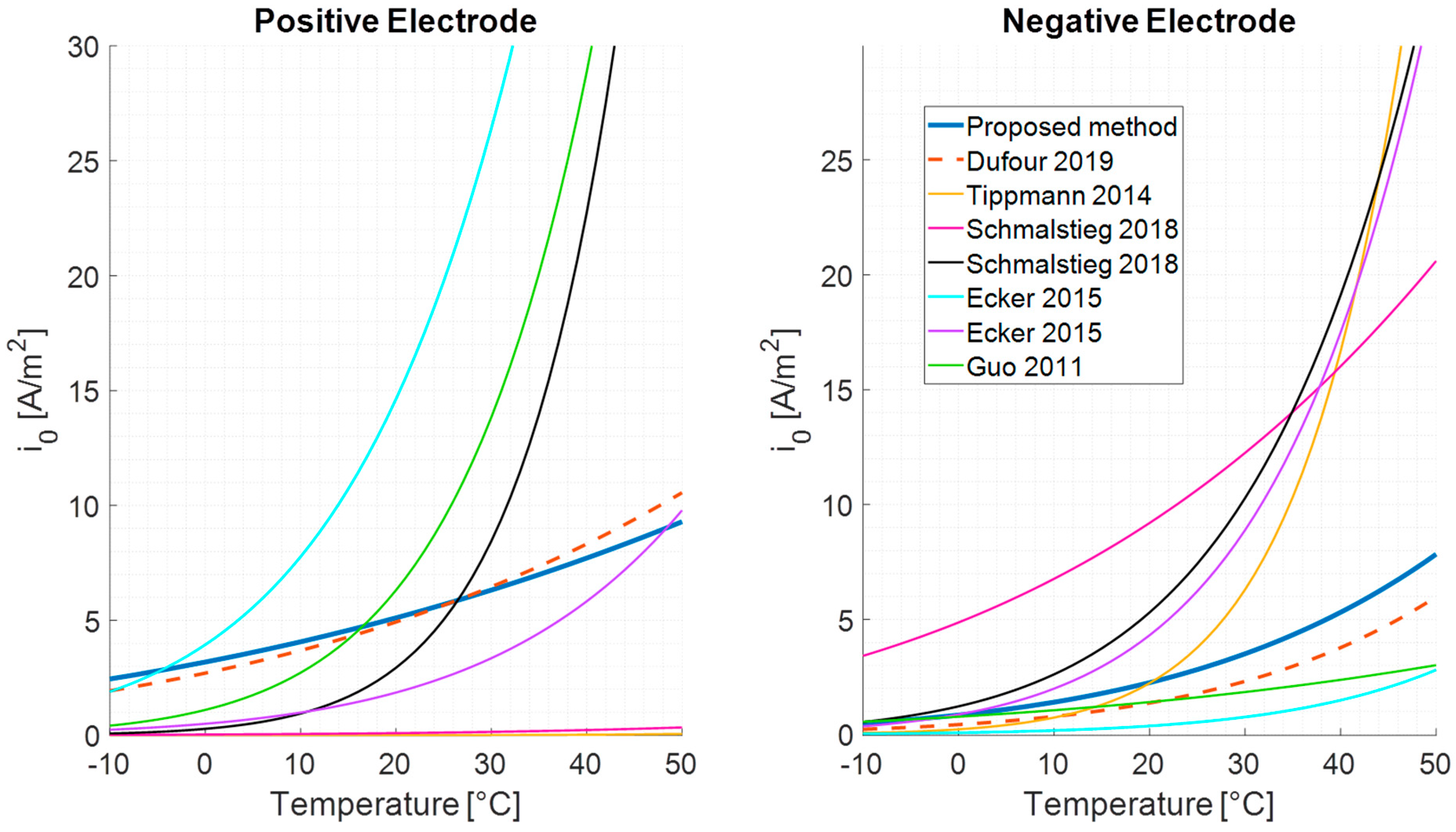
4. State of the Art of the Identification Methods for the BV Kinetic Parameter
5. Method
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Krewer, U.; Roeder, F.; Harinath, E.; Braatz, R.D.; Beduerftig, B.; Findeisen, R. Review-Dynamic Models of Li-Ion Batteries for Diagnosis and Operation: A Review and Perspective. J. Electrochem. Soc. 2018, 165, A3656–A3673. [Google Scholar] [CrossRef]
- Meng, J.; Luo, G.; Ricco, M.; Swierczynski, M.; Stroe, D.-I.; Teodorescu, R. Overview of Lithium-Ion Battery Modeling Methods for State-of-Charge Estimation in Electrical Vehicles. Appl. Sci. 2018, 8, 659. [Google Scholar] [CrossRef]
- Cai, L.; White, R.E. Mathematical modeling of a lithium ion battery with thermal effects in COMSOL Inc. Multiphysics (MP) software. J. Power Sources 2011, 196, 5985–5989. [Google Scholar] [CrossRef]
- Botte, G.G.; Subramanian, V.R.; White, R.E. Mathematical modeling of secondary lithium batteries. Electrochim. Acta 2000, 45, 2595–2609. [Google Scholar] [CrossRef]
- Fan, G.; Pan, K.; Canova, M.; Marcicki, J.; Yang, X.G. Modeling of Li-Ion Cells for Fast Simulation of High C-Rate and Low Temperature Operations. J. Electrochem. Soc. 2016, 163, A666–A676. [Google Scholar] [CrossRef]
- Jokar, A.; Rajabloo, B.; Désilets, M.; Lacroix, M. Review of simplified Pseudo-two-Dimensional models of lithium-ion batteries. J. Power Sources 2016, 327, 44–55. [Google Scholar] [CrossRef]
- Mai, W.; Colclasure, A.; Smith, K. A Novel Reformulation of the Pseudo2D Battery Model Coupling Large Deformations at Particle and Electrode Levels; National Renewable Energy Lab (NREL): Golden, CO, USA, 2019.
- Liu, B.; Li, Q.; Engelhard, M.H.; He, Y.; Zhang, X.; Mei, D.; Wang, C.; Zhang, J.-G.; Xu, W. Constructing Robust Electrode/Electrolyte Interphases to Enable Wide Temperature Applications of Lithium-Ion Batteries. ACS Appl. Mater. Interfaces 2019, 11, 21496–21505. [Google Scholar] [CrossRef] [PubMed]
- Ramadesigan, V.; Northrop, P.W.C.; De, S.; Santhanagopalan, S.; Braatz, R.D.; Subramanian, V.R. Modeling and Simulation of Lithium-Ion Batteries from a Systems Engineering Perspective. J. Electrochem. Soc. 2012, 159, R31–R45. [Google Scholar] [CrossRef]
- Doyle, C.M. Design and Simulation of Lithium Rechargeable Batteries; University of California, Berkeley: Berkeley, CA, USA, 1995. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J. The use of mathematical modeling in the design of lithium/polymer battery systems. Electrochim. Acta 1995, 40, 2191–2196. [Google Scholar] [CrossRef]
- Dao, T.-S.; Vyasarayani, C.P.; McPhee, J. Simplification and order reduction of lithium-ion battery model based on porous-electrode theory. J. Power Sources 2012, 198, 329–337. [Google Scholar] [CrossRef]
- Guo, M.; Sikha, G.; White, R.E. Single-Particle Model for a Lithium-Ion Cell: Thermal Behavior. J. Electrochem. Soc. 2011, 158, A122–A132. [Google Scholar] [CrossRef]
- Cai, l.; White, R.E. Mathematical Modeling of a Lithium Ion Battery; University of South Carolina: Columbia, SC, USA, 2009; p. 5. [Google Scholar]
- Li, X.; Fan, G.; Rizzoni, G.; Canova, M.; Zhu, C.; Wei, G. A simplified multi-particle model for lithium ion batteries via a predictor-corrector strategy and quasi-linearization. Energy 2016, 116, 154–169. [Google Scholar] [CrossRef]
- Schmitt, J.; Kraft, B.; Schmidt, J.P.; Meir, B.; Elian, K.; Ensling, D.; Keser, G.; Jossen, A. Measurement of gas pressure inside large-format prismatic lithium-ion cells during operation and cycle aging. J. Power Sources 2020, 478, 228661. [Google Scholar] [CrossRef]
- Cheng, Y.-T.; Verbrugge, M.W. The influence of surface mechanics on diffusion induced stresses within spherical nanoparticles. J. Appl. Phys. 2008, 104, 083521. [Google Scholar] [CrossRef]
- Zhao, Y.; Stein, P.; Bai, Y.; Al-Siraj, M.; Yang, Y.; Xu, B.-X. A review on modeling of electro-chemo-mechanics in lithium-ion batteries. J. Power Sources 2019, 413, 259–283. [Google Scholar] [CrossRef]
- Ender, M. An extended homogenized porous electrode model for lithium-ion cell electrodes. J. Power Sources 2015, 282, 572–580. [Google Scholar] [CrossRef]
- Kashkooli, A.G.; Farhad, S.; Lee, D.U.; Feng, K.; Litster, S.; Babu, S.K.; Zhu, L.; Chen, Z. Multiscale modeling of lithium-ion battery electrodes based on nano-scale X-ray computed tomography. J. Power Sources 2016, 307, 496–509. [Google Scholar] [CrossRef]
- Torchio, M.; Magni, L.; Gopaluni, R.B.; Braatz, R.D.; Raimondo, D.M. LIONSIMBA: A Matlab Framework Based on a Finite Volume Model Suitable for Li-Ion Battery Design, Simulation, and Control. J. Electrochem. Soc. 2016, 163, A1192–A1205. [Google Scholar] [CrossRef]
- Namor, E.; Torregrossa, D.; Cherkaoui, R.; Paolone, M. Parameter identification of a lithium-ion cell single-particle model through non-invasive testing. J. Energy Storage 2017, 12, 138–148. [Google Scholar] [CrossRef]
- Doyle, M.; Newman, J.; Gozdz, A.S.; Schmutz, C.N.; Tarascon, J.-M. Comparison of Modeling Predictions with Experimental Data from Plastic Lithium Ion Cells. J. Electrochem. Soc. 1996, 143, 1890. [Google Scholar] [CrossRef]
- Ecker, M.; Tran, T.K.D.; Dechent, P.; Käbitz, S.; Warnecke, A.; Sauer, D.U. Parameterization of a Physico-Chemical Model of a Lithium-Ion Battery: I. Determination of Parameters. J. Electrochem. Soc. 2015, 162, A1836–A1848. [Google Scholar] [CrossRef]
- Edouard, C.; Petit, M.; Forgez, C.; Bernard, J.; Revel, R. Parameter sensitivity analysis of a simplified electrochemical and thermal model for Li-ion batteries aging. J. Power Sources 2016, 325, 482–494. [Google Scholar] [CrossRef]
- Dufour, N. Modélisation Multi-Physique de L’électrode de Graphite au Sein d’une Batterie Lithium-Ion: Etude des Hétérogénéités et des Mécanismes de Vieillissement. Ph.D. Thesis, Université Grenoble-Alpes, Saint-Martin-d’Hères, France, 2019. Available online: https://theses.hal.science/tel-02148211 (accessed on 1 February 2020).
- Tippmann, S.; Walper, D.; Balboa, L.; Spier, B.; Bessler, W.G. Low-temperature charging of lithium-ion cells part I: Electrochemical modeling and experimental investigation of degradation behavior. J. Power Sources 2014, 252, 305–316. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Rahe, C.; Ecker, M.; Sauer, D.U. Full Cell Parameterization of a High-Power Lithium-Ion Battery for a Physico-Chemical Model: Part I. Physical and Electrochemical Parameters. J. Electrochem. Soc. 2018, 165, A3799–A3810. [Google Scholar] [CrossRef]
- Schmalstieg, J.; Sauer, D.U. Full Cell Parameterization of a High-Power Lithium-Ion Battery for a Physico-Chemical Model: Part II. Thermal Parameters and Validation. J. Electrochem. Soc. 2018, 165, A3811–A3819. [Google Scholar] [CrossRef]




| Parameter | Symbol | Unit |
|---|---|---|
| Ionic flux | ||
| Maximum concentration | ||
| Local concentration | ||
| Electrolyte concentration | ||
| Normalized surface concentration | % | |
| Faraday constant | ||
| Perfect gas constant | ||
| Temperature | ||
| Overpotential | ||
| Solid phase potential | ||
| Liquid phase potential | ||
| Open circuit potential | ||
| Anodic and cathodic charge transfer coefficients | - | |
| Applied current | ||
| Active material surface | ||
| Reaction rate constant | ||
| SoL-dependent reaction rate | ||
| Arranged reaction rate constant | ||
| Exchange current density | ||
| Internal cell resistance | ||
| Voltage drops |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goussian, A.; Assaud, L.; Baghdadi, I.; Nouillant, C.; Franger, S. A Novel Reaction Rate Parametrization Method for Lithium-Ion Battery Electrochemical Modelling. Batteries 2024, 10, 205. https://doi.org/10.3390/batteries10060205
Goussian A, Assaud L, Baghdadi I, Nouillant C, Franger S. A Novel Reaction Rate Parametrization Method for Lithium-Ion Battery Electrochemical Modelling. Batteries. 2024; 10(6):205. https://doi.org/10.3390/batteries10060205
Chicago/Turabian StyleGoussian, Alain, Loïc Assaud, Issam Baghdadi, Cédric Nouillant, and Sylvain Franger. 2024. "A Novel Reaction Rate Parametrization Method for Lithium-Ion Battery Electrochemical Modelling" Batteries 10, no. 6: 205. https://doi.org/10.3390/batteries10060205
APA StyleGoussian, A., Assaud, L., Baghdadi, I., Nouillant, C., & Franger, S. (2024). A Novel Reaction Rate Parametrization Method for Lithium-Ion Battery Electrochemical Modelling. Batteries, 10(6), 205. https://doi.org/10.3390/batteries10060205