Modelling Li-V₂O₅ Batteries Using Galvanostatic Intermittent Titration Technique and Electrochemical Impedance Spectroscopy: Towards Final Applications

Abstract

Given the relevance of lithium and post-lithium batteries as electrochemical energy storage systems, the peculiar crystalline structure of V₂O₅ and its doping capacity play key roles in lithium-ion battery technology. To integrate them in high-efficiency modules, systematic methodologies are required to estimate the state of charge in a reliable way and predict the Li-V₂O₅ battery’s performance according to their electrochemical phenomena, including two plateaus in the galvanostatic cycling curves and the dynamic behavior governed by the energy demand. Most state of charge estimation and battery modeling procedures are focused on conventional Li-batteries that show a unique plateau. In this work, we propose a systematic methodology based on the galvanostatic intermittent titration technique and electrochemical impedance spectroscopy to study battery performance in the time and frequency domains, respectively. The proposed methodology, with a time–frequency correlation, promotes a deeper understanding of the electrochemical phenomena and general behavior of Li-V₂O₅ batteries, allowing for its subsequent extrapolation to more complex and higher-capacity lithium and post-lithium batteries used in high-power applications with a minimum error.

1. Introduction

The global energy demand has significantly increased in recent years, and this trend is expected to continue. The main energy supply sources mostly rely on the use of fossil fuels, limited resources whose use is controversial, given their associated environmental impacts. A renewable energy transition is, therefore, needed to ensure a clean supply chain, respecting the environment while preserving the level of development and quality of life of the present and future generations [1]. In this sense, electrochemical storage systems, specifically batteries, are considered to be the alternative of choice, mainly due to their large storage capacity, high energy density, low self-discharge, and lack of memory effect when compared with other technologies [2,3,4].

Within the advances in lithium-ion battery technology, the peculiar crystalline structure of vanadium pentoxide (V₂O₅) has made it a notable contributor to improving the performance and durability of batteries, mitigating the problems associated with electrode degradation and capacity fading [5]. This is because the intricate atomic lattice, characterized by an ordered arrangement of vanadium and oxygen atoms, favors ionic diffusion, facilitating the efficient intercalation and de-intercalation of Li⁺ during the charging and discharging cycles of the batteries. In addition to these features, the crystalline structure of V₂O₅ can be adjusted and optimized to improve its electrochemical properties, so it is possible to modify the lattice spacing and incorporate various dopants to enhance the Li⁺ storage capabilities [6,7]. This adaptability makes Li-V₂O₅ batteries a potential candidate for the development of high-performance lithium-ion batteries with a higher energy density, longer cycle life, and faster charging capabilities. These improvements could promote Li-V₂O₅ batteries’ emergence, as current and future energy needs require innovative contenders in a new era of lithium-ion energy storage, with potential use in fully developed and mature applications such as electric vehicles (EVs) [8,9], hybrid electric vehicles (HEVs) [10], and smart grids [11], among others [12,13]. Despite the Li batteries commonly used in these applications presenting typical electrochemical behavior with simple galvanostatic charge and discharge curves [14,15], Li-V₂O₅ batteries exhibit more complex electrochemical behavior with two plateaus in their galvanostatic cycling [16]. Guaranteeing the optimal integration of Li-V₂O₅ batteries in high-performance applications requires determining and even predicting their behavior by estimating the state of charge (SoC) [17,18,19] and obtaining an accurate battery model [15], which allows for reproducing both the behavior defined by the electrochemical phenomena taking place and the dynamic behavior defined by the current changes experienced during the charge and discharge cycles governed by the energy demand.

In this work, we propose a systematic methodology based on the galvanostatic intermittent titration technique (GITT) [20,21] and electrochemical impedance spectroscopy (EIS) [22,23,24] to study battery performance in the time and frequency domains, respectively. The proposed methodology, with a time–frequency correlation, provides a deeper understanding of the electrochemical phenomena taking place in Li-V₂O₅ batteries, as well as an insight into its their behavior in terms of energy demand. A deep understanding of the complex phenomena taking place in Li-V₂O₅ cells would enable the subsequent extrapolation of the proposed methodology to more complex and higher-capacity lithium and post-lithium batteries used in high-power applications with a minimum error.

2. Experimental Procedure

2.1. Galvanostatic Charge/Discharge Curves

The studied VL2020 coin cell, manufactured by Panasonic (Moriguchi, Japan), has a vanadium oxide (V₂O₅) cathode, lithium alloy anode, and non-aqueous liquid electrolyte. With a nominal capacity of 20 mA and a maximum current rate of C/13 (1.5 mA), this cell can be considered as a low-capacity power cell whose main application relies on memory backup power supplies for automation equipment (personal computers and fax machines), audio–video equipment (video tape recorders), communications equipment (mobile phones), and hybrid systems with solar batteries as remote controllers. The main specifications of this battery are summarized in

Table 1. VL2020 coin cell technical specifications.

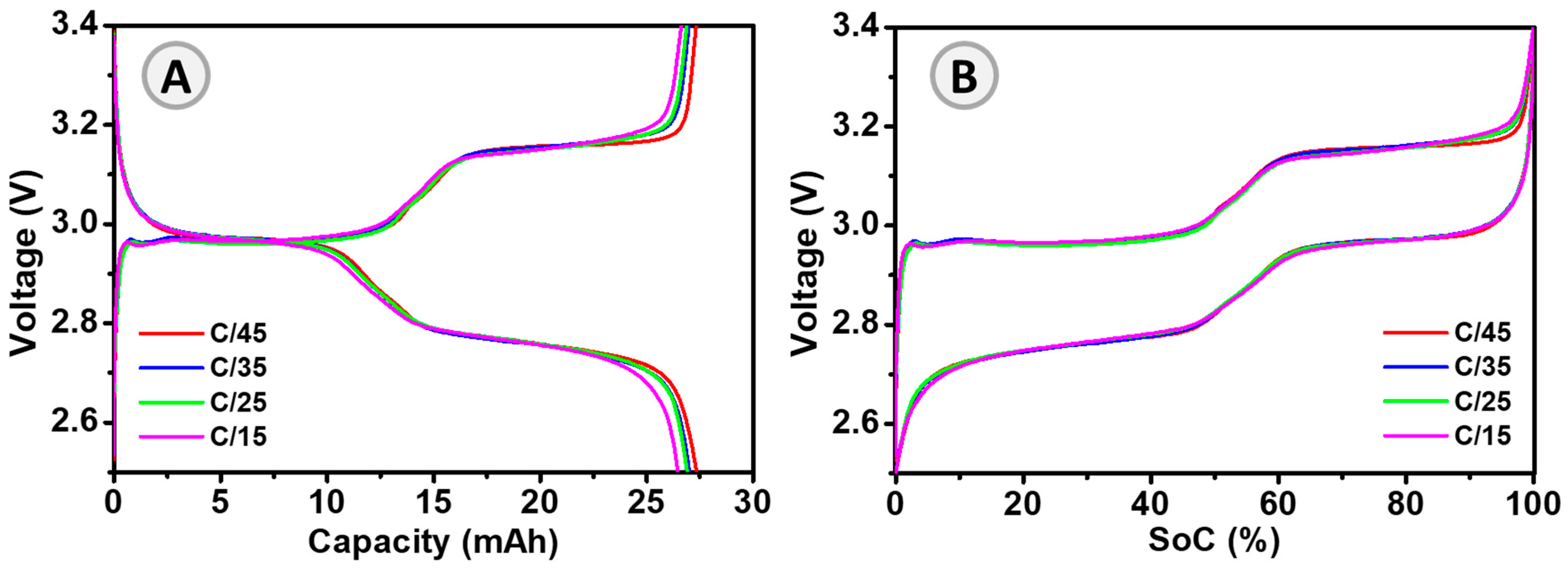
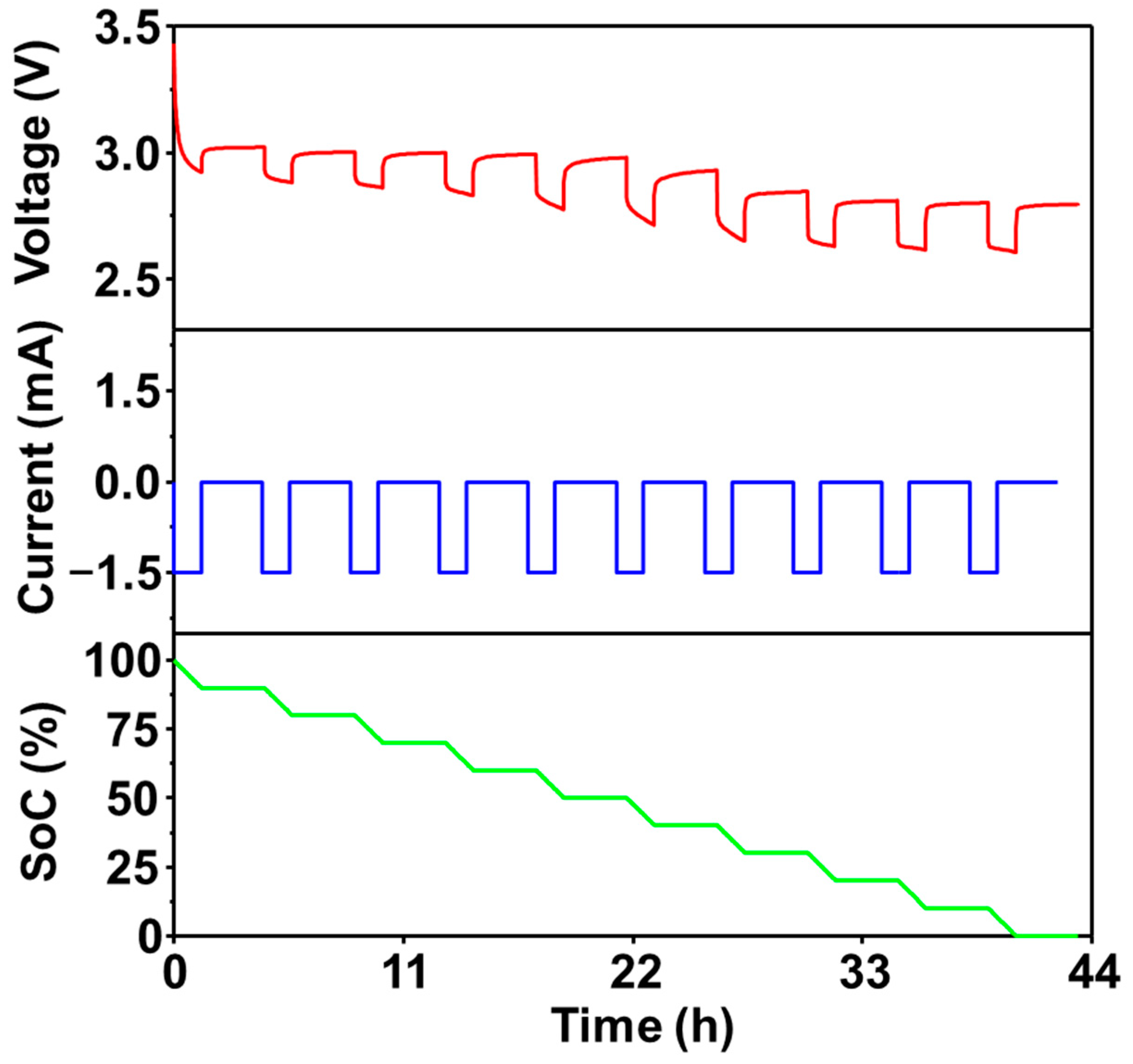
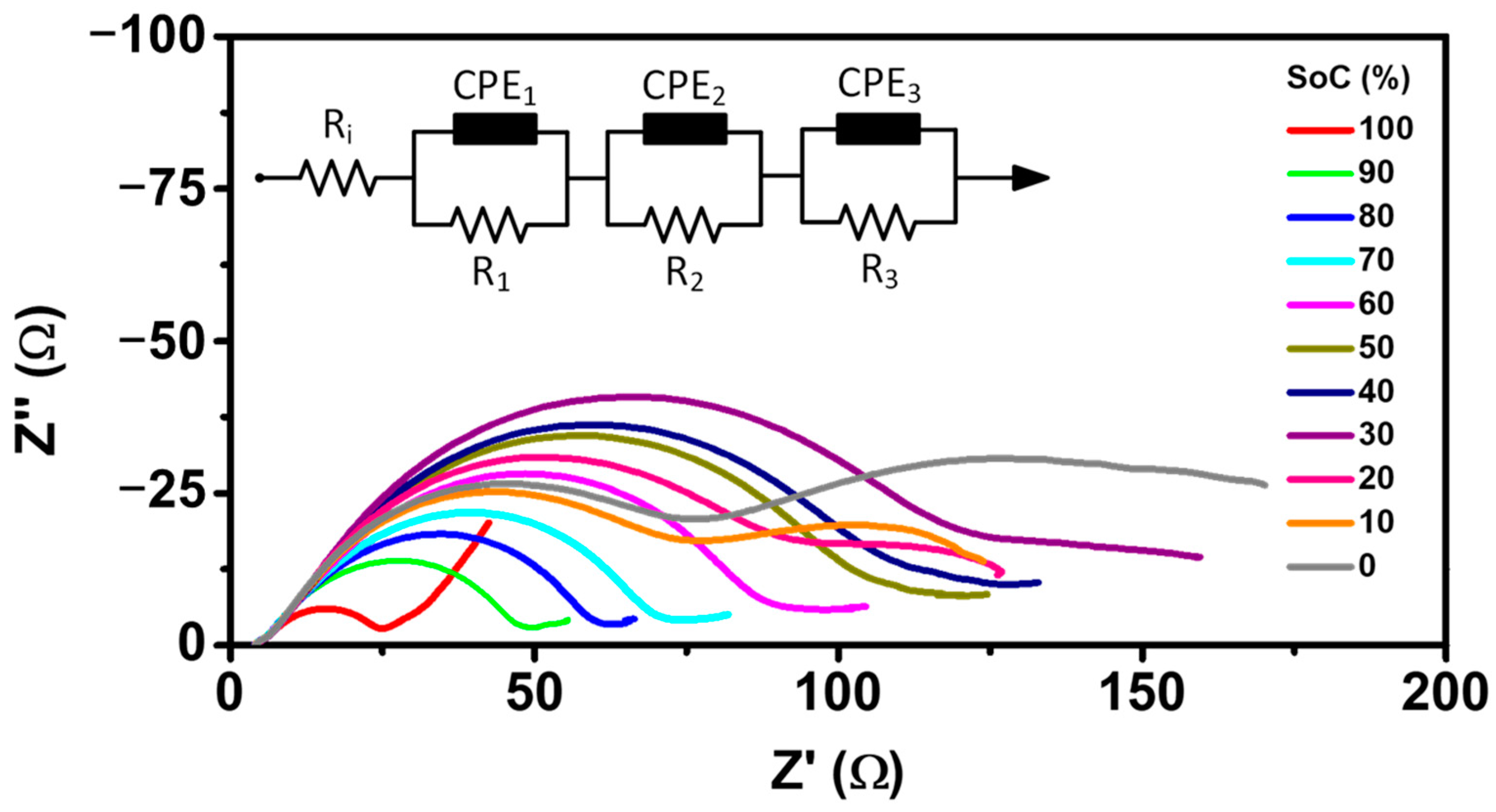
Parameter	Value
Nominal Capacity	20~22.5 mAh
Nominal Voltage	3 V
Open Circuit Voltage (OCV)	2.95 V to 3.55 V
Maximum Voltage	3.4 V ± 0.15 V
Cut-off Voltage	2.5 V
Current Charge to 3 V	Maximum 1.5 mA (C/13)

.

The galvanostatic charge and discharge curves of the VL2020 cell are experimentally obtained at different C-rates (C/13, C/25, C/35, and C/45), as shown in Figure 1A, by setting the Neware (Shenzhen, China) BTS-4000 potentiostat to the constant current (CC) cycling mode. The lower the C-rate, the higher the capacity, reaching values up to 27.5 mAh. According to the experimental data obtained (Figure S1), the polarization effects become more significant as the charge/discharge rate increases, which implies a higher impedance in the cell and, therefore, a slower rate of ion transfer, which hinders intercalation reactions. Two plateaus are observed at approximately 3 V and 3.2 V during charge and 3 V and 2.8 V during discharge, which are attributed to the phase transitions experienced by the cathode material during discharge, i.e., from α-V₂ to ε-Li_0.5V₂O₅ and from ε-Li_0.5V₂O₅ to δ-LiV₂O₅ [5,6,7,16]. This shows a clear difference regarding the electrochemical behavior of most widely used lithium batteries, which typically present simpler behavior with a unique plateau [8,14,25,26]. In this case, the presence of two plateaus might complicate the modeling process of the cell, jeopardizing the accuracy when applying methods typically used for conventional lithium cells, including the mathematical models of Shepherd [11,27] and Nernst [12,28]. Therefore, here, we propose a systematic methodology based on the application of the GITT and EIS that, being able to fulfil complex electrochemical behavior, can be later extrapolated to the electrochemical characterization and modeling of new cathode materials towards novel lithium and post-lithium batteries.

2.2. Estimation of State of Charge (SoC)

The state of charge is the proportion of the available charge at a point compared to the total available charge when the cell is fully charged. Therefore, an SoC value of 100% is considered when the battery is fully charged and a value of 0% is considered when it is fully discharged. In many applications where lithium batteries are used as an energy storage system, the SoC is calculated using the basic Coulombic counting method or its variations, since it has an acceptable accuracy and involves a simple computational implementation [17,29,30,31].

This method consists of periodically calculating the current flowing out of and into the cell, estimating the SoC by subtracting or adding the accumulated net charge. In this case, since the cell capacity is always known and the current flow can be accurately measured, the SoC is estimated by the ampere-hour integral Expression (1)

$$\mathrm{SoC}={\mathrm{SoC}}_0+\frac{1}{{\mathrm{Q}}_{\mathrm{n}}}·{\int }_{{\mathrm{t}}_0}^{\mathrm{t}}{\mathrm{I}}_{\mathrm{b}}·\mathrm{dt},$$

(1)

where SoC₀ is the initial value of the state of charge, I_b is the current flowing through the cell during charging and discharging, and Q_n is the nominal capacity [30,31].

The curves obtained from the SoC estimation by applying (1) to the experimental data obtained in Figure 1A are shown in Figure 1B. In this case, to increase the fitting and accuracy, the maximum capacity values obtained experimentally during charging and discharging are taken as nominal values (Figure 1A). On the other hand, both the cell current and charge/discharge times are obtained from the potentiostat used to control the cycling process (Neware BTS-4000).

2.3. Battery Modeling Considerations

To model the battery, two approaches are considered, the conventional Thevenin model (Figure 2A) and the SoC-dependent Thevenin model (Figure 2B). The main difference between them relies on the variability of the latter in the values of the elements of the electrical circuit. R_i corresponds to the internal resistance, the R_nC_n grids reproduce the dynamic behavior corresponding to the polarization effect in the cell, and the power supply, referred to as OCV, corresponds to the open-circuit voltage.

In general, increasing the number of RC elements is considered to improve the fitting, increasing the accuracy of the Thevenin model when reproducing the cell behavior. However, the use of more than four RC grids to implement the electrical circuit considerably increases the computational demand, without any significant improvement in the model’s accuracy, especially in SoC-dependent models [32]. Therefore, the criterion we follow to set the number of RC elements is, according to the literature [33], increasing the number of RC networks until the difference between the experimental charge/discharge curves and simulated curves reaches a steady state. Following this approach, the number of RC grids chosen is three.

2.4. Modeling Techniques

2.4.1. Galvanostatic Intermittent Titration Technique (GITT)

The galvanostatic intermittent titration technique, or the GITT, is one of the most widely used in the time domain and consists of applying a train of controlled continuous current pulses to discharge a cell, in such a way that each current pulse decreases a percentage of the state of charge (Figure 3).

The duration of the discharge pulses (t_p) is calculated by using Expression (2), as indicated in [34,35,36,37],

$${\mathrm{t}}_{\mathrm{p}}=\frac{\Delta \mathrm{SoC}·{\mathrm{Q}}_{\mathrm{n}}}{{\mathrm{I}}_{\mathrm{b}}·100},$$

(2)

where I_b is the discharge current of each pulse, Q_n is the nominal capacity, and ΔSoC is the percentage of the state of charge to vary with each pulse.

Although I_b should typically be about 0.2 C [34,37], in this case, the cell is discharged at the maximum current, according to the specifications given in Table 1. The nominal capacity is obtained from the cell data sheet, amounting to 20 mAh. The value of ∆SoC is set considering that, the lower the percentage, the higher the resolution obtained from the voltage curve, and, therefore, the lower the error after implementing the Thevenin model. In this case, ∆SoC is set to 10%, reducing the SoC value from 100% (fully charged cell) to 0% (fully discharged cell), as shown in Figure 3. According to these guidelines, the duration of the calculated discharge current pulse time is 1.33 h.

2.4.2. Electrochemical Impedance Spectroscopy (EIS)

To enrich the electrochemical study, the cells are also investigated in the frequency domain by using electrochemical impedance spectroscopy (EIS) with a BioLogic (Seyssinet-Pariset, France) VMP3 Multichannel Potentiostat. In this sense, taking advantage of the GITT, impedance measurements are performed at the instant before the cell starts discharging and the voltage reaches a steady state (purple dots in Figure S2). Each measurement corresponds to the SoC value obtained as it decreases by 10% in each pulse. Figure 4 presents the results of the EIS measurements carried out over the whole SoC range (from 100% to 0% SoC), where four different regions, related to different processes, can be distinguished in the impedance spectra (Figure S3). The first region is located at the intersection with the real impedance axis (x-axis), corresponding to the internal resistance of the cell (R_i); the second region is represented by a small semicircle, related to the electrode–electrolyte interface and the emergence of the SEI (solid–electrolyte interface); the third region is defined by a larger semicircle and is related to the charge transfer processes and double-layer capacitance; and finally, the fourth region, at low frequencies, corresponds to the diffusion processes [12,22,38,39]. Normally, the last semicircle is represented by a Warburg resistor in most models for Li batteries. However, in this case, the more complex behavior of the Li-V₂O₅ cell is best reproduced when a constant phase element (CPE) is used.

According to the EIS data obtained (Figure 4), the intersection with the x-axis in the high-frequency zone does not vary significantly (region 1 in Figure S3), suggesting that the internal resistance only slightly increases as the SoC decreases. Only negligible variations are observed regarding the small semicircle at high frequencies (region 2 in Figure S3), suggesting a stable electrode–electrolyte interface. The main differences in the spectra are seen in regions 3 and 4. Regarding region 3, the semicircle shifts to the right and increases in diameter as the SoC decreases, whereas the semicircle in region 4 not only shifts to the right, but also increases in size and begins to become better defined as the SoC decreases. These two semicircles could be associated with the processes of charge transfer and the diffusional effects of the lithium-ion on the host material, respectively. Thus, it can be inferred that a decrease in the state of charge produces an increase in the impedance in the cell, hindering the intercalation and diffusion phenomena of the lithium battery. Although the spectra corresponding to the SoC from 20% to 0% clearly present the four regions mentioned above, there is not a clear trend. This could be associated with the low charge in the battery, being outside of the limits recommended by the manufacturer, who suggests cycling from 20% to 80% of the SoC. A different trend can also be observed in the semicircle at low frequencies when the cell is fully charged (100% SoC), as is observed in Figure S13. The steep slope of almost 45° may suggest that the cathode material has all vacancies free, favoring lithium diffusion [12,38,39].

2.5. Identification and Estimation of Parameters

2.5.1. Galvanostatic Intermittent Titration Technique (GITT)

The cell discharge curve (Figure 3) shows the voltage relaxation processes once the discharge current is no longer applied, resulting in a pulsed discharge curve. The changes experienced by the voltage amplitude can be attributed to the slope and plateau changes observed in the charge and discharge curves previously observed in Figure 1A. This dynamic voltage response allows for the identification and estimation of the elements of the equivalent electrical circuit according to the Thevenin models (Figure 2) by using general-purpose software tools, such as MATLAB^®/Simulink (R2022b).

The procedure performed is depicted in Figure S14 and consists of: (1) obtaining the identification data, in this case, the pulsed current and voltage curve of the cycled cell using the GITT; (2) implementing the equivalent electrical circuits of the conventional Thevenin and SoC-dependent models in Simulink; (3) importing the identification data to the implemented models and choosing the parameters to be estimated, that is, the circuit elements whose value needs to be known; and finally (4) calculating the error. As previously shown in Figure S2, the experimental voltage curve presents three zones where different amplitudes are exhibited. Therefore, to reproduce such dynamic behavior more accurately, electrical circuits are implemented by using three RC grids. These amplitude changes can be attributed to the phase transitions experienced by the cathode material, which cause the voltage curve to exhibit two plateaus (Figure 1A).

After applying the identification and estimation process, the values of the electrical circuit elements used to implement the conventional model and SoC-dependent model are shown in

Table 2. Estimated values of the equivalent electrical circuit elements of the conventional and SoC-dependent Thevenin models with GITT.

Parameters	Conventional	SoC-Dependent Model
		0%	10%	20%	30%	40%	50%	60%	70%	80%	90%	100%
Ri (Ω)	4.2	4.2	4.2	4.2	4.2	4.2	4.2	4.2	4.2	4.0	4.1	4.1
R1 (Ω) C1 (mF)	2.1	2.3	2.3	2.3	1.5	2.2	2.1	2.3	1.8	1.7	1.8	1.9
	0.2	0.047	0.052	0.046	0.073	0.045	0.286	0.046	0.070	0.448	0.427	0.103
R2 (kΩ) C2 (mF)	33.3	0.027	0.028	0.027	0.033	0.030	0.250	0.067	0.067	0.105	0.254	0.346
	0.2	0.346	0.254	0.105	0.067	0.067	0.255	0.030	0.033	0.027	0.028	0.027
R3 (kΩ) C3 (mF)	62.2	0.075	0.072	0.069	0.086	0.090	0.086	0.070	0.053	0.051	0.056	0.098
	12.8	13.1	13.9	14.4	9.8	10.1	11.1	13.0	17.3	16.1	16.8	10.0

. While the conventional model uses only one value to reproduce the cell behavior in each state of charge, the SoC-dependent model uses one value for the SoC using a lookup table (LUT). In general, the values obtained by both methods are in the same order of magnitude, with some differences mainly observed in the capacitance. Nevertheless, since the SoC-dependent model gives place to one value for each element corresponding to each SoC, a higher accuracy would be expected while modeling the battery and, therefore, a reduced error.

2.5.2. Electrochemical Impedance Spectroscopy (EIS)

From the EIS data, analogous to the time-domain electrical model (Figure 2), the behavior of the cell in the frequency domain is modeled by obtaining an equivalent electrical circuit. As can be seen in the inset of Figure 4, the three RC elements are maintained, in which the capacitors used in the time domain are replaced by constant phase elements (CPE) in the frequency domain [40].

In this case, modeling in the frequency domain is carried out by using the ZView^® software (4.0C). The adjustments made are shown in the Supplementary Materials from Figures S3–S13, while the estimated values for the electrical circuits are given in

Table 3. Estimated values of the equivalent electrical circuit elements of the conventional and SoC-dependent Thevenin models with EIS.

Parameters	Conventional	SoC-Dependent Model
		0%	10%	20%	30%	40%	50%	60%	70%	80%	90%	100%
Ri (Ω)	4.0	4.0	3.9	4.1	4.2	4.2	4.2	4.1	3.9	3.9	3.8	3.9
R1 (Ω) C1 (mF)	2.2	1.8	2.5	2.5	2.5	2.5	2.5	2.4	2.1	2.1	1.7	1.4
	13.4	11.6	12.9	97.7	12.9	12.9	12.9	16.7	15.5	15.5	13.9	12.5
R2 (kΩ) C2 (mF)	70.4	80	62	78	106	100	92	83	61	51	42	19
	0.3	0.3	0.3	0.3	0.3	0.3	0.3	0.3	0.2	0.3	0.3	0.3
R3 (kΩ) C3 (mF)	158.5	82.0	80	65	95	48	50	74	55	55	164	492
	38.8	0.3	13.3	0.1	0.3	0.3	0.4	12.4	58.6	58.6	258.2	24.3

. It is worth mentioning that the values of the equivalent capacitors to the CPEs are calculated, since, in order to obtain a similar electrical circuit and compare the curves obtained from it with the experimental curves obtained from the VL2020 cell, it is necessary that the elements of the model are in the time domain.

In general, the values obtained by both methods are in the same order of magnitude. The main differences are observed in the case of the third RC grid (R₃ and C₃), where a significant increase in values is observed when using the conventional model.

3. Results and Discussion

The modeling of Li-V₂O₅ batteries, characterized by both conventional dynamic behavior due to changes in the current profiles and complex chemical behavior due to phase transition processes, reflected as two plateaus in the charge and discharge curves (Figure 1), is carried out using the GITT and EIS technique, similar to how conventional lithium-ion battery modeling is performed, which exhibits a single plateau in the charge/discharge curves. The electrical model obtained facilitates the implementation and future integration of Li-V₂O₅ batteries into end-use applications where they are required. This is different from the existing literature, which focuses on obtaining analytical models to study thermodynamic and kinetic properties through intercalation mechanisms in V₂O₅ electrodes [41,42,43].

3.1. Thevenin Models and Galvanostatic Intermittent Titration Technique

Figure 5 shows the experimental pulsed discharge curve obtained by cycling the Li-battery and that simulated by the Thevenin models, together with the difference between both curves represented as the relative error. A clear difference is observed between the curves in the conventional Thevenin model, especially in the abrupt voltage changes, which means that this model is not able to faithfully reproduce the dynamic behavior of the cell, leading to an error in the range of about ±0.6 V (Figure S15).

On the other hand, the SoC-dependent Thevenin model presents a more accurate approximation of the experimental behavior, with only negligible differences and an error of about ±0.2 V (Figure S15). Although the difference between the relative errors of the two models does not seem to be significant, in terms of the relative error, a percentage error with respect to the real cell voltage value of 16% is obtained with the conventional model (Figure 5A) vs. the 6% obtained for the SoC-dependent model (Figure 5B).

In general, the maximum acceptable error limit for a model is about 10% [44,45,46,47,48], with the SoC-dependent model having this limit. Moreover, this model can better represent the dynamic behavior of the cell, which is very important when reproducing current profiles, since the energy demand of the cell will not always be the same.

The main merits of the electric model obtained through the GITT include providing detailed information about phase transition processes, offering a comprehensive profile of the Li-V₂O₅ battery’s response to different currents and states of charge, and preventing overheating during testing. It also allows for the development of an adaptable and versatile procedure that can be applied to different types of batteries and under a variety of conditions, depending on their integration into the final applications. However, drawbacks include a prolonged testing time, requirements for specialized equipment, and sensitivity to temperature, which affects the accuracy of the results.

3.2. Thevenin Models and Electrochemical Impedance Spectroscopy

To compare the results of the GITT and EIS measurements, the values obtained in Table 3 from the impedance spectra are replaced in the equivalent electrical circuits considered in Simulink and the pulsating voltage curve is simulated. In the conventional Thevenin model, which does not depend on the SoC of the cell, the values of the circuit elements are calculated by averaging them all, whereas in the SoC-dependent Thevenin model, an LUT (lookup table) is used to represent the variability of the values of the electrical circuit elements with the SoC.

The simulation results show that both models tend to follow the pulsating trend of the voltage curve, but neither are able to faithfully reproduce the abrupt voltage changes. Hence, the dynamic behavior of the cell cannot be accurately reproduced by using this approach. Figure 5C shows how the conventional model follows the voltage more accurately during discharging, while Figure 5D shows how the SoC-dependent model tends to follow the voltage more accurately when the cell is at rest.

The error percentage achieved with the conventional model (16%) is twice the value obtained with the SoC-dependent model (6%), and, as mentioned before, is far from the error considered as acceptable (10%) for a model to be reliable [44,45,46,47,48]. Consequently, the SoC-dependent Thevenin equivalent electrical circuit offers a better fitting. In terms of the absolute error (Figure S15), the difference between the two models is quite small, with 0.6 V obtained with the conventional model and 0.2 V with the SoC-dependent model.

The electric model obtained through EIS provides a comprehensive understanding of the electrochemical properties of Li-V₂O₅ batteries, facilitating their accurate modeling. It allows for real-time data collection without interrupting the battery operation and covers a wide range of frequencies to obtain a detailed electrochemical response. However, challenges include interpreting complex data, requirements for specialized equipment, and sensitivity to experimental conditions that can lead to variability, which affects the accuracy of the results.

When comparing the GITT and EIS method, the advantage of the GITT in reliably and accurately reproducing the behavior of Li-V₂O₅ batteries is revealed, with an acceptable error margin of less than 10%, which falls within battery modeling standards [44,45,46,47,48]. The electrical model obtained in the time domain through the GITT is direct, simple, precise, reproducible, reliable, and robust, facilitating the integration of Li-V₂O₅ batteries into their final applications where required. In contrast, the EIS technique provides a model in the frequency domain, which may lack reproducibility due to the high sensitivity of the technique to changes in the test parameters or conditions. Additionally, it requires the transformation of the model into the time domain to allow for the practical implementation and integration of Li-V₂O₅ batteries into their final applications, making it less suitable for the direct acquisition of the battery model.

4. Conclusions

The modeling and simulation of Li-batteries with complex electrochemical behavior was successfully accomplished by applying two complementary techniques: galvanostatic intermittent titration (GITT) and electrochemical impedance spectroscopy (EIS). In both cases, the equivalent electrical circuit was obtained by using two approaches, the conventional Thevenin model and SoC-dependent Thevenin model. The obtained results and subsequent error analysis demonstrated that the model estimated by the GITT better met all the criteria required to represent, with confidence and a high accuracy, the dynamic behavior of the cell, especially abrupt voltage changes. The model had a fairly linear error of 6% (±0.2 V) and a high accuracy when comparing the voltage curve simulated by the electrical circuit implemented in Simulink and the experimental curve obtained by cycling the cell. It also better fit the pulsating trend of the real voltage curve compared to the model based on the application of electrochemical impedance spectroscopy.

Despite the complexity associated with unconventional charge/discharge curves, which Li-V₂O₅ cell exhibit, showing two plateaus associated with the different phase transitions experienced by the cathode material, the systematic methodology proposed allows for accurately reproducing this dynamic electrochemical behavior. It was, thus, demonstrated that the galvanostatic intermittent titration technique allows for finding the electrical model of a cell quickly and reliably, even when it presents complex dynamic behavior. This is contrary to the impedance spectroscopy technique, which requires a longer analysis time, since it makes it necessary to fit each impedance spectrum to an equivalent electrical circuit in the frequency domain in order to obtain similar results when compared to the SoC-dependent Thevenin electrical model parameterized by the GITT.

Further work is ongoing in order to extrapolate the proposed methodology to more complex systems based on new electrode materials for solid-state batteries, including those based on the electrochemistry of sodium, paving the way for the next generation of all-solid-state post-lithium batteries [49,50,51].