Abstract
In large-capacity energy storage systems, instructions are decomposed typically using an equalized power distribution strategy, where clusters/modules operate at the same power and durations. When dispatching shifts from stable single conditions to intricate coupled conditions, this distribution strategy inevitably results in increased inconsistency and hastened system aging. This paper presents a novel differentiated power distribution strategy comprising three control variables: the rotation status, and the operating boundaries for both depth of discharge (DOD) and C-rates (C) within a control period. The proposed strategy integrates an aging cost prediction model developed to express the mapping relationship between these control variables and aging costs. Additionally, it incorporates the multi-colony particle swarm optimization (Mc-PSO) algorithm into the optimization model to minimize aging costs. The aging cost prediction model consists of three functions: predicting health features (HFs) based on the cumulative charge/discharge throughput quantity and operating boundaries, characterizing HFs as comprehensive scores, and calculating aging costs using both comprehensive scores and residual equipment value. Further, we elaborated on the engineering application process for the proposed control strategy. In the simulation scenarios, this strategy prolonged the service life by 14.62%, reduced the overall aging cost by 6.61%, and improved module consistency by 21.98%, compared with the traditional equalized distribution strategy. In summary, the proposed strategy proves effective in elongating service life, reducing overall aging costs, and increasing the benefit of energy storage systems in particular application scenarios.
1. Introduction
Battery energy storage systems (BESSs) with varying capacities consist of several battery modules or clusters, each made up of multiple modules that further comprise individual cells [1]. Large-scale energy storage stations are usually equipped with numerous battery cabins corresponding to the installed capacity, and each battery cabin is formed by multiple clusters. The typical topology is illustrated in Figure 1.
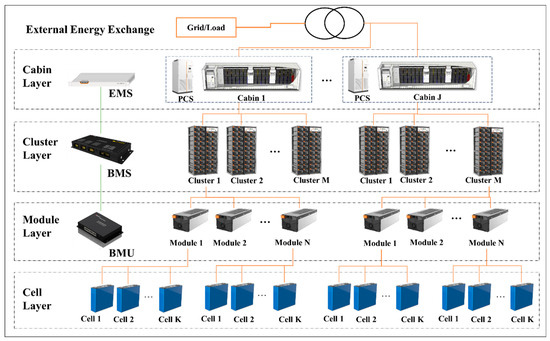
Figure 1.
Typical topology of energy storage station.
Battery cabins typically receive dispatching instructions individually. Inside a cabin, control instructions are decomposed into clusters following the traditional control approach of equalized distribution, where all cells operate at the same power and durations. This dispatching method reduces the software and hardware configuration requirements of the control system. However, due to inconsistencies among battery cells and modules [2], maintaining the same operational intensity exacerbates their inconsistency [3]. To enhance benefits, energy storage stations have evolved from traditional single-application scenarios to new composite application scenarios, resulting in a transition from stable single operating conditions—such as peak shaving, renewable energy consumption, and emergencies—to more intricate coupled operating conditions [4]. The inconsistency trend becomes more apparent in these new scenarios, due to the accelerated aging rate of “inferior batteries”, thus adversely affecting the system’s overall aging and safety [5]. As energy storage stations with inadequate integration during the early stages of the energy storage industry approach and surpass the halfway point of their service lives, coupled with the rising number of decommissioned batteries recycled for energy storage applications in recent years [6], the traditional equalized power distribution strategy is likely to pose progressively significant safety concerns [7].
Many scholars have studied control strategies for mitigating aging under power system scenarios. Zhao et al. [8] established the semi-empirical life model of the battery based on throughput, state of charge (SOC), and injected/output power of a BESS, applied to an aging rate equalization strategy for microgrid-scale battery energy storage systems. Xu et al. [9] developed a mapping relationship between system capacity losses and aging costs to optimize and support dispatching in the service market, ultimately boosting profits and prolonging battery longevity. However, energy storage systems were considered as a whole in the majority of previous research, primarily due to the unavailability of separate control over battery clusters/modules. In the traditional topological structure shown in the cabin layer of Figure 1, one power conversion system (PCS) corresponds to one battery cabin, where power is simply distributed to clusters and modules in an equalized manner. Ci et al. [10] proposed the dynamic reconfigurable battery energy storage technology. Han et al. [11] provides an overview of a next-generation battery management system (BMS) featuring dynamic reconfiguration. In comparison to the conventional norm of fixed series–parallel connections, the DRB networks use new program-controlled connections between battery cells/modules.
Limited literature have explored differentiated control modes in the context of batteries. Yan et al. [12] primarily concentrated on investigating the impact of DOD, establishing a control strategy for frequency regulation scenarios aimed at enhancing battery lifetimes. Furthermore, Karunathilake et al. [13] developed a multi-objective optimization control strategy that takes into account aging and is based on multiple features reflecting energy and power performance. However, they focused on multiple independent cells as the subjects of research. These studies emphasized the state of health (SOH) as the primary optimization objective, rather than considering the enhancement of overall operational performance. According to the findings of the literature [14], with the increasing complexity of energy storage conditions in power system applications and the coupled and variable aging mechanisms, additional health indicators are essential for assessing the performance of energy storage systems.
In conclusion, implementing a differentiated control strategy for battery systems that consider the combined influence of multiple HFs is crucial to efficiently address inconsistency amplification and extend service life. In Section 2, the primary algorithm and its application process are introduced. In Section 3, the experiment is detailed, and both the multi-dimensional HFS extraction method and the prediction technique are introduced. In Section 4, the mapping of aging costs is delineated, incorporating comprehensive scoring and health status. Finally, a simulation comparison is presented for an industrial park scenario in Section 5.
2. Control Strategy
2.1. Optimization Control Strategy to Minimize Aging Cost in a Single Operational Period
Theoretically, optimization control strategy can be applied to any level that integrates circuitry that supports differentiated control, such as battery clusters, a single battery cluster, a battery module, or multiple cells. Among the controllers in Figure 1, Battery management units (BMU) are not yet available because the hardware cost of controlling each cell individually is too high. For the BMS, it depends on whether it could control each module separately. However, the batteries in one module undergo similar operating conditions and are more consistent, so the benefits are not obvious. Therefore, to simplify the discussion process, multiple clusters are considered as the independently controlled objects to elucidate optimization control. The rotation status (RS) of all battery clusters and their operating boundaries are determined within an operational period, aiming to minimize the predicted aging cost through optimization. The framework of the optimization algorithm is shown in Figure 2.
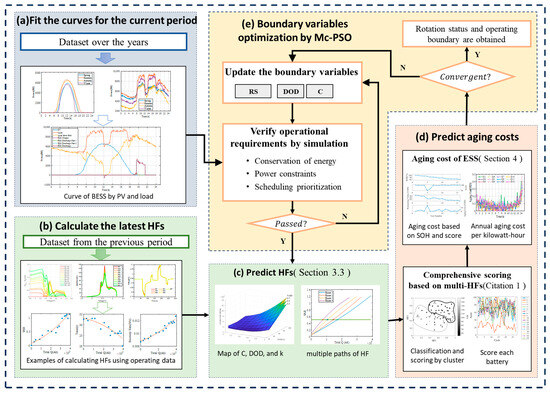
Figure 2.
Framework of optimization algorithm.
(a) A period of time with similar conditions is defined as a study period. (b) Input data collected over this period across multiple years are utilized to create a typical dispatching curve with the latest data gathered, through a fitting process. (c) By employing boundary parameters that ensure effective responses to dispatching instructions, multiple HFs are predicted at the end of an operational period. (d) Subsequently, a comprehensive score is calculated to evaluate aging costs. (e) The Mc-PSO algorithm is then utilized to adjust control variables until operating boundaries are identified that lead to the lowest aging cost.
The optimization model is described as follows:
Optimization objective: minimize predicted aging cost in current period.
where, m denotes the number of clusters within one battery cabin, taken as m = 1, 2, …, M; denotes the predicted aging cost of cluster m.
The constraints are as follows:
The most important constraint is to ensure that performance does not fall below the expectation. Specifically, the execution of dispatching instructions signals the realization of anticipated performance. In simulation operations, the completion of the most rigorous instructions serves as the benchmark, forming the verification module for simulation operations as illustrated in Figure 2. In addition, it is assumed that no rigorous instructions would remain unfulfilled in real dispatching, based on the principle of negotiating the dispatchable range with the upper-level dispatching system by the energy management system (EMS) of energy storage stations one day in advance: The State of Power (SOP) upper limits reported by the EMS would be acknowledged by the upper-level dispatching system, and dispatching curve instructions issued from the upper-level system would not surpass the reported upper limits.
The accumulated maximum available power of all battery clusters at any given time (t) is greater than or equal to the dispatching power required to be responded to by the corresponding battery cabin.
where j denotes the battery cabin number, taken as j = 1, 2, …, J, indicating the number of battery cabins at an energy storage station.
The maximum power does not exceed the C-rate boundary obtained from a solving process:
where denotes the rated power at a C-rate of 1C.
is constrained by DOD boundaries:
denotes the maximum state of charge (SOC) value after charging, generally taken as 100%, to ensure that the energy storage station can serve for emergencies in most cases. SOC is subjected to correction using the ampere-hour integral method:
where denotes the effective value of current at a given time (t), with a positive value indicating discharge and a negative value indicating charge. denotes the time interval and denotes the rated capacity.
The simulation scenarios in this paper involve SOC calculations based on data with high precision and granularity, to ensure the SOC is error free. However, the SOC may be corrected in engineering applications.
The operational process fulfills the law of energy conservation:
where denotes the power generation from renewable energy sources (RESs); denotes the power consumption of loads from a direct RES supply; denotes the power energy of the energy storage system by charge from the grid; denotes the battery discharge efficiency; and denotes the power supply from batteries to loads.
and operating boundaries are the variables to be optimized. However, each battery cluster covers the whole optional range, resulting in an intricate solving process. To reduce the solving difficulty and control complexity, the following two methods are applied for simplification. The first method involves taking C-rate values as 0.25, 0.5, …, 1.75 and 2, and the DOD as discrete points of 20%, 30%, …, 100%, to simplify the solution domain space dimensionality. The second method is to introduce a new variable, Rotation Status, in operation to preliminarily define the range of boundary parameters and narrow the search scope. RS includes stable operation (S), dynamic operation (D), and emergency operation (E). Each rotation status imposes specific constraints on the maximum values of the operating boundaries, as outlined in Table 1.

Table 1.
Correlation between rotation status and operating boundaries.
The correlation assumes D1 > D2 > D3, C1 < C2 < C3. For instance, when a high C-rate value is used for emergency operation (E), it is crucial to limit the DOD to prevent the undervoltage of certain cells at a low SOC.
Moreover, the rotation status influences the priority of power distribution. The priorities, based on ΔC (absolute value of C-rate change between two scheduling time intervals), are presented below:
where represents the steady-state operating battery that has been started, and represents those that have not been started. Ca indicates the threshold to determine significant power changes, generally taken as of E.
The general principle is to minimize the frequency of startups by preventing inactive batteries from being enabled frequently. In the case of load increasing, batteries are raised first, up to the maximum permissible power. If the demand cannot be satisfied, D batteries take precedence to respond if they remain in operation, before enabling other S batteries. During load shedding, E and D batteries are successively reduced in priority for transition into standby mode.
The following additional operating rules are followed:
- (1)
- In the case of emergency batteries enabled, when other batteries are sufficient to take the place of E batteries, they will be reduced in power at a rate of 2%/s for transition into standby mode.
- (2)
- If other batteries reach the lower limit of the DOD, D and E will be enabled to fill the vacancy successively, to meet the requirements of charging and discharging instructions.
Solving method:
The initial values of RS, , and generally follow the values in the previous operational period to further speed up the solving process. The reasons include: (1) there is not much difference between the dispatching curves in two consecutive periods, and (2) aging costs arising from changes in HFs increase slowly under circumstances without safety concerns.
It is required to solve multiple boundary parameters of multiple batteries, and the solution domain is large. The traditional exhaustive method is time-consuming and resource-intensive, so it is necessary to introduce a swarm intelligence algorithm for solving. Particle swarm optimization (PSO) is a swarm intelligence algorithm, which has an obvious premature convergence phenomenon and tends to fall into a local optimum [15]. In this paper, The Mc-PSO algorithm is used for solving, with the swarm divided into three sub-swarms evenly, which are evolved according to PSO, ω Adjustment Particle Swarm Optimization, and Cloud Adaptive Particle Swarm Optimization [16]. The particle richness is increased, so that the computation speed is effectively increased, and the probability of falling into a local optimum is reduced.
2.2. Rolling Optimization Process for Long-Time Operational Scenarios
Under the constraints of boundary parameters and adhering to actual dispatching curves, the ultimate aging levels of battery packs typically do not match the predicted values precisely. However, the relative magnitude relationship among the aging levels closely mirrors the predictions. To eliminate the estimation errors of HFs after long-term operation, a rolling optimization process is proposed. The EMS integrated with this strategy at energy storage stations, performs periodic control based on boundaries derived from the solving process. Following each period, the multi-dimensional HFs are updated using actual operational data, serving as the algorithm’s initial input for the next period. Since the operating conditions are generally one to two charge/discharge cycles per day, the HFs usually change slowly. The length of each data collection period can be set to one month or more. However, if the HF is strongly related to safety, daily monitoring is required. It also depends on the battery life and the complexity of the operating conditions. The proposed strategy contributes to minimizing the total aging cost of energy storage systems after extended operational durations, as shown in Figure 3.
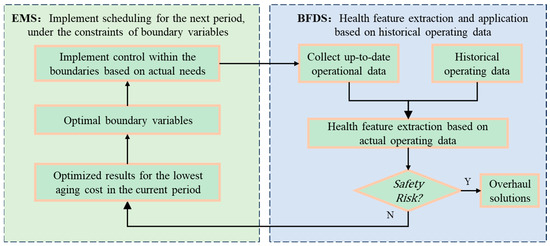
Figure 3.
Application process based on EMS and BFDS.
At the end of each operational period, actual data are imported into the battery fault diagnosis system (BFDS) specially developed for energy storage stations, as shown in Figure 4. The author’s team spent over two years developing the platform, which integrates multiple functional modules for energy storage stations such as operational data preprocessing, fault diagnosis, health assessment, and inconsistency analysis. BFDS extracts real HFs as input for a new period and identifies any safety concerns based on these HFs. Any safety concerns identified lead to the suspension of control to initiate the inspection and maintenance process.
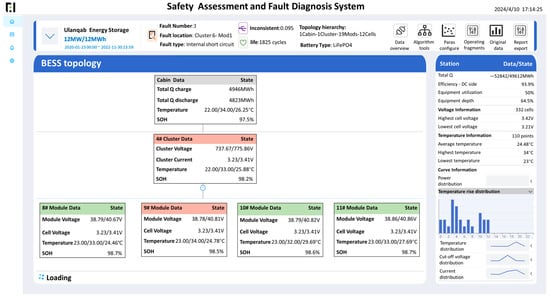
Figure 4.
BFDS homepage (The original page is in Chinese).
The key HFs to be considered include the “capacity diving” risk [17], temperature rise rate [18], and internal short-circuit resistance [19], all of which are strongly linked to the risk of thermal runaway. When safety risks escalate, batteries are prone to exhibiting “capacity diving” [20]. Other common fault diagnosis studies, such as sensor fault [21], overcharge/discharge [22], actuator fault [23], external short circuit [24], overheat [25], et al., have also been studied by many scholars. If an HF deteriorates but is not yet sufficient to cause safety accidents, the aging costs will sharply rise due to the significant decrease in comprehensive scores, leading to stricter control constraints. This mechanism helps to integrate safety into the control strategy to some extent. In the absence of any hidden dangers identified, the solving process for optimization control in subsequent periods is initiated.
3. Extraction and Prediction of Multi-Dimensional HFs
3.1. Aging Experiment
50 Ah NCM622 square pouch batteries, with a rated capacity of 50 Ah, and upper and lower cut-off voltages of 2.75 V and 4.2 V, respectively, manufactured by China Aviation Lithium Battery Technology Co., Ltd. (CALB, Changzhou, Jiangsu.) were selected for the experiment, as shown in Figure 5a. The experimental instruments included the charge–discharge instrument manufactured by Neware, as shown in Figure 5b, and the temperature and humidity test chamber manufactured by Doaho, as shown in Figure 5c.

Figure 5.
Experiment equipment: (a) NCM622 lithium-ion battery; (b) Neware charge–discharge instrument; (c) Doaho temperature and humidity test chamber.
There are many operating parameters that contribute to the difference in aging rates. Among them, DOD, C-rate, and temperature have the greatest impact. However, almost all energy storage battery compartments are already equipped with temperature management systems, such as air conditioning, air cooling, and liquid cooling, which the result that the uneven effect of temperature is no longer obvious and significant [26]. Therefore, combined aging experiments were conducted using the chosen batteries at varying DODs and C-rates, as shown in Table 2:

Table 2.
Battery numbers for aging tests under different operating conditions.
The batteries were charged and discharged based on the preset boundary conditions and were evaluated for their performance and capacity every calendar month. Taking the No. 1 battery as an example, partial cycles are shown in Figure 6:
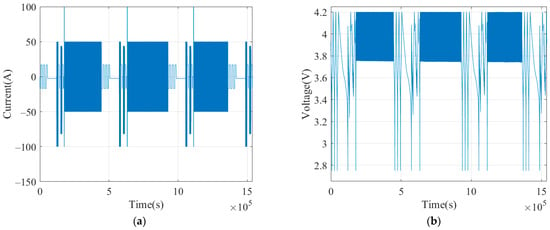
Figure 6.
Partial experimental cycles of No. 1 battery: (a) current; (b) voltage.
The battery operation for one cycle is shown in Figure 7, where the areas a–e indicate the performance evaluation, including capacity, low-rate discharge, dynamic stress test (DST), Federal Urban Driving Schedule (FUDS), and hybrid pulse power characterization (HPPC), respectively, and f indicates the cyclic aging.
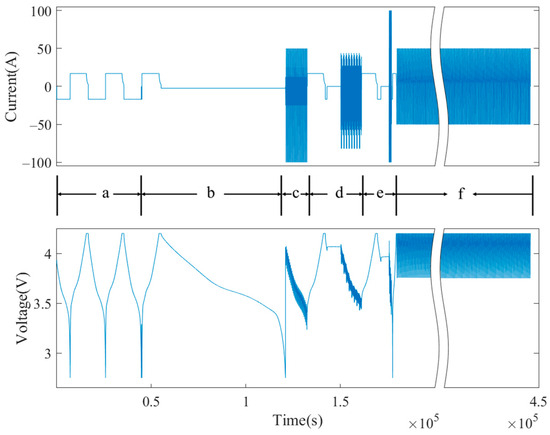
Figure 7.
One experimental cycle of No. 1 battery.
The experimental procedure is described as follows:
- Actual capacity test: Discharge the batteries at a constant current of 1/3C to the lower cut-off voltage of 2.75 V. Charge them at a constant current of 1/3C to 4.2 V, and subsequently charge at a constant voltage until the current drops below C/20. Next, discharge them at a constant current of 1/3C to the lower cut-off voltage of 2.75 V. Repeat this charge and discharge procedure two times. Refer to Figure 8a.
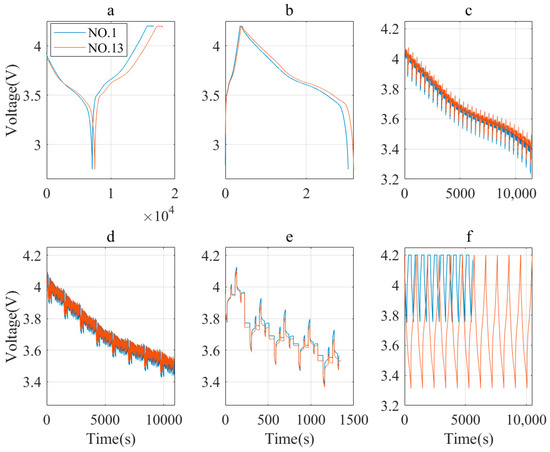 Figure 8. Items within a test cycle for No. 1 and No. 13 battery: (a) capacity; (b) low-rate discharge; (c) DST; (d) FUDS; (e) HPPC; (f) aging cycles.
Figure 8. Items within a test cycle for No. 1 and No. 13 battery: (a) capacity; (b) low-rate discharge; (c) DST; (d) FUDS; (e) HPPC; (f) aging cycles. - Low-current discharge curve: Charge the batteries at a current of 1/3C to the cut-off voltage and discharge them at a current of C/20 to 2.75 V after standing, as shown in Figure 8b.
- DST and FUDS conditions: Set the batteries according to the FreedomCAR test manual [27], as shown in Figure 8c,d.
- HPPC: Perform tests at varying SOC levels [28]. After the batteries are fully charged, gradually discharge them to 80%, 60%, 50%, 40%, and 20% SOC for evaluations. Specifically, discharge them at a current of 2C for 18 s, after setting them aside to stand for 40 s, charge them at 1C for 10 s, and then set them aside again to stand for 40 s. Then charge the batteries with a current of 2C for 18 s, after setting them aside to stand for 40 s, discharge them at a current of 1C for 10 s, and finally set them aside to stand for 40 s. Refer to Figure 8e.
- Cyclic aging: Cyclic aging is performed according to the set DOD and C. No. 1 and No. 13 battery are plotted together to show the difference in performance between different batteries. Refer to Figure 8f.
The battery experiments are terminated when the battery capacity diminishes to 80% of the rated capacity, and the end of the battery life is recorded. Should any experimental battery exhibit significant bulging and leakage, the corresponding experiment should be halted promptly. The aging curves of all batteries are depicted in Figure 9a, and those derived from polynomial fitting are illustrated in Figure 9b.
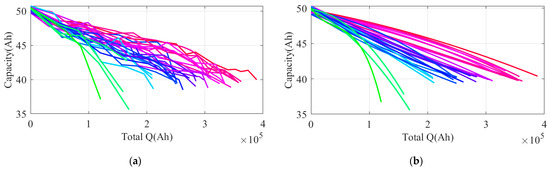
Figure 9.
(a) Aging curves of all batteries between capacity and cumulative throughput quantity (Total Q); (b) aging curves of all batteries after polynomial fitting.
The cycle life of No. 3 battery was more than 40% shorter than that of No. 4 battery under the same conditions due to manufacturing defects. No. 30 battery experienced bulging and leakage at an SOH of 0.844, leading to the termination of the experiment. These two batteries were excluded from subsequent analysis.
3.2. Extraction of HFs
A health feature system for battery cells adaptable to various conditions has been developed from summarizing research findings over many years, as shown in Table 3.

Table 3.
HF system.
The extraction methods of features can be found in publications of relevant research as cited in Table 3. It is important to note that calculating all features in the table is not necessary; selections should be made based on actual data quality, operating conditions, and computing power configuration. In Section 4, a comprehensive performance scoring method is introduced to support analysis using available HFs. Comparative evaluation can be achieved in parallel by ensuring the input of the same HFs and the same application scenario, without specifying the number and type of HFs.
Taking the No. 1 battery in the above experiment as an example, several features are described as follows:
- Capacity variance (VAR). As shown in Figure 10, the available discharge capacity at identical ΔV decreases with aging progression, resulting in steeper curves of differences from the initial test. Figure 11 shows a strong correlation between VAR and SOH.
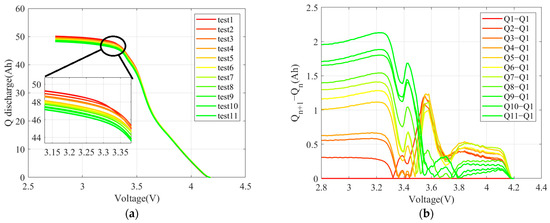 Figure 10. Calculation process of VAR: (a) original V-Q curve; (b) discharge difference curve based on test 1.
Figure 10. Calculation process of VAR: (a) original V-Q curve; (b) discharge difference curve based on test 1.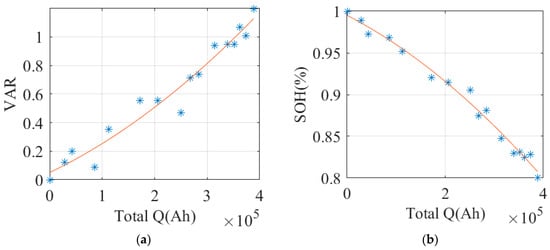 Figure 11. Strong correlation between VAR and SOH: (a) scatter plot and fitting curve of VAR; (b) scatter plot and fitting curve of SOH.
Figure 11. Strong correlation between VAR and SOH: (a) scatter plot and fitting curve of VAR; (b) scatter plot and fitting curve of SOH. - Resistance. The ohmic and polarization internal resistances can be calculated through the HPPC test according to the literature [54]. Refer to Figure 12a and Formula (8). Figure 12b displays the HPPC curves for multiple tests of No. 1 battery, illustrating that voltage changes intensify under the same current excitation with aging progression. Figure 13 shows the change curves of ohmic and polarization internal resistances.
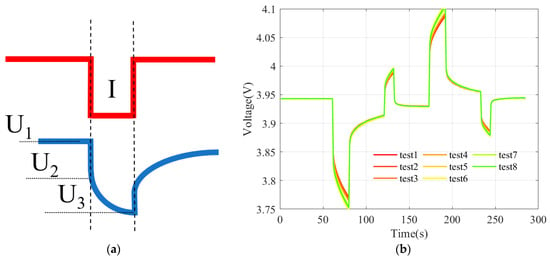 Figure 12. (a) Partial enlarged view of HPPC; (b) HPPC data from multiple tests.
Figure 12. (a) Partial enlarged view of HPPC; (b) HPPC data from multiple tests.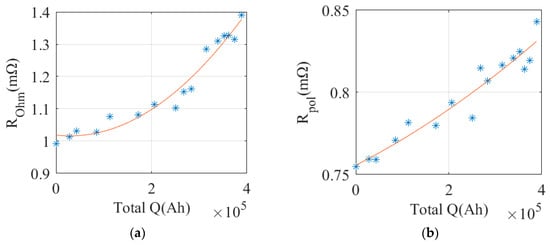 Figure 13. Resistance: (a) scatter plot and fitting curve of ohmic resistance; (b) scatter plot and fitting curve of polarization resistance.
Figure 13. Resistance: (a) scatter plot and fitting curve of ohmic resistance; (b) scatter plot and fitting curve of polarization resistance.
- 3.
- ICA. Figure 14a shows the original IC curve of a single test, subjected to smoothing. Figure 14b shows the IC curves of multiple tests, indicating decreasing peak values, rightward shifting peak positions, and narrowed peak areas with aging progression. Figure 15 shows the variation curves of peak values and peak areas, respectively.
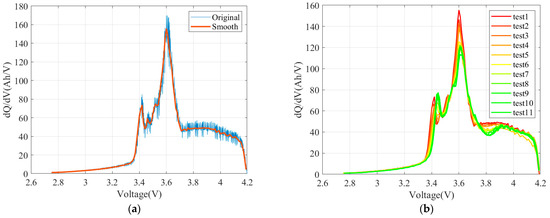 Figure 14. IC curves: (a) original IC curve and smoothed IC curve; (b) a set of IC curves from multiple tests.
Figure 14. IC curves: (a) original IC curve and smoothed IC curve; (b) a set of IC curves from multiple tests.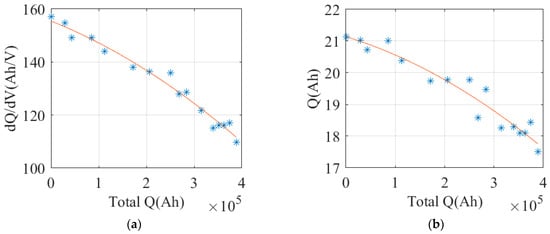 Figure 15. IC features: (a) scatter plot and fitting curve of peak value; (b) scatter plot and fitting curve of peak area.
Figure 15. IC features: (a) scatter plot and fitting curve of peak value; (b) scatter plot and fitting curve of peak area. - 4.
- Relaxation. Relaxation refers to the process in which voltage slowly returns to a specific stationary stage upon the conclusion of excitation. The recovery to 3.91 V upon the conclusion of excitation was considered for current calculations. Figure 16 illustrates the recovery process following the removal of excitation during multiple HPPC tests. As shown, the recovery process is prolonged with aging progression. Figure 17 shows the variation curves of relaxation time and slope.
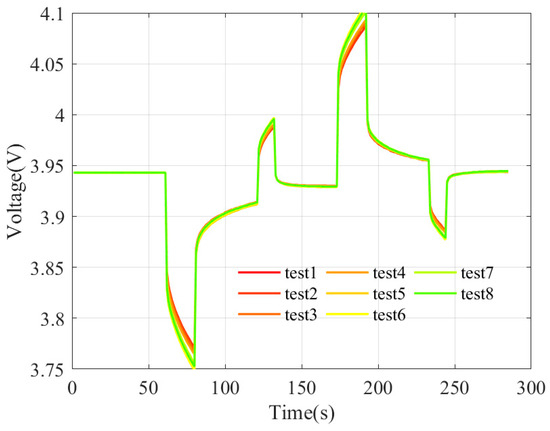 Figure 16. Enlarged view of relaxation during multiple tests.
Figure 16. Enlarged view of relaxation during multiple tests.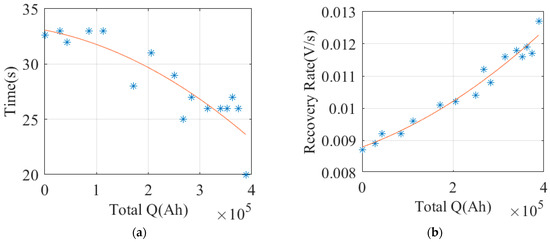 Figure 17. Relaxation features: (a) scatter plot and fitting curve of recovery time; (b) scatter plot and fitting curve of maximum recovery slope.
Figure 17. Relaxation features: (a) scatter plot and fitting curve of recovery time; (b) scatter plot and fitting curve of maximum recovery slope.
3.3. Prediction of HFs
A prediction method is proposed, which integrates modeling based on experimental data to generate the aging rates of HFs along their respective paths, and incorporates the projection of cumulative throughput quantity for predicting HF values in the end-of-period phase. The main idea is shown in Figure 18.
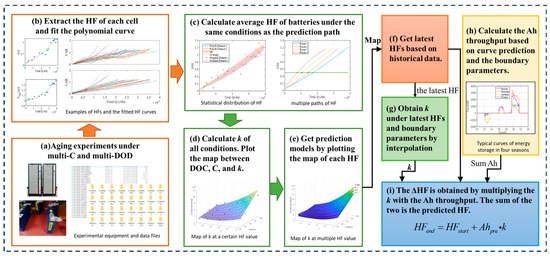
Figure 18.
HF prediction procedure.
Sets of mean HF curves under all conditions were plotted, as seen in Figure 19a, with VAR taken as an example. The curves were then subjected to polynomial interpolation fitting. Two rounds of tests were carried out for identical conditions, and the calculated mean values of VAR represent the averages of a normal distribution, as shown in Figure 19b. Experimental curves representing the 95% confidence interval were used to simulate inconsistent changes during the simulation process, as illustrated in Section 5.2, rather than being incorporated here. For the abnormal No. 3 and 30 batteries, average values were derived from the data of normal cells from the same test, and rational confidence intervals were chosen for them based on two rounds of tests with similar conditions. For the convenience of illustration, several curves were taken for explanation, as shown in Figure 19c.
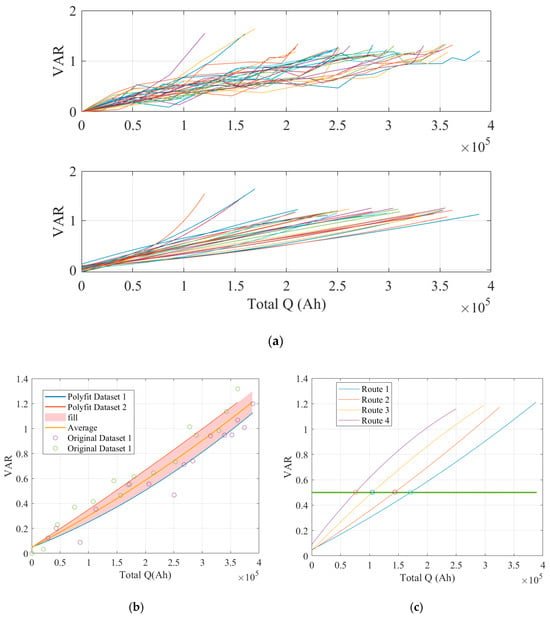
Figure 19.
(a) Original and fitted VAR curves; (b) statistical distribution of calculated VARs for two batteries; (c) schematic diagram of multiple paths with VAR = 0.5 (Green Line).
Subsequent aging paths vary depending on variations in the DOD and C and in association with the current VAR. Calculations of slope changes in curves at a specific VAR value yielded 16 slopes as a function of DOD and C. Three-dimensional scatter plots were created and later integrated into Figure 20a using two-dimensional interpolation. It is evident that with larger C and DOD values, the change in the slope of VAR will increase accordingly. Change slopes beyond the scope of scatter points can be acquired through interpolation using the map. As slope changes vary at different HFs, it is essential to account for the current actual HF value in calculations. Figure 20b displays the map with three VAR values. In this figure, as VAR increases, ΔVAR exhibits a greater increase under identical charge/discharge capacities.
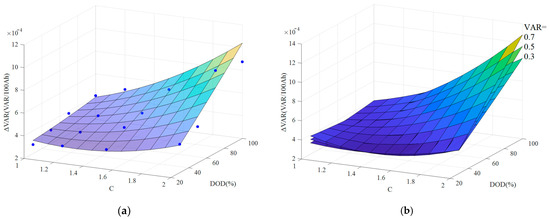
Figure 20.
(a) Map of C, DOD, and k with VAR = 0.5; (b) map of C, DOD, and k with VAR = 0.3, 0.5, and 0.7.
With actual HFs at the period outset, the variation rate (k) corresponding to and is derived through interpolation using the respective map. The alteration in Ah throughput is projected based on typical curves of the next period. Subsequently, the HFs following a period of operation are predicted using the formula below:
where denotes HF at the closure of the specific timeframe for prediction, denotes the current HF, and denotes the approximated total charge/discharge.
This calculation method is applicable for predicting results for operation at constant DOD and C values throughout the full lifetime, using the initial feature values as the starting point. Nevertheless, there are varying DOD and C values in actual operation, making it almost impossible to maintain consistent conditions. Hence, it is theoretically appropriate to modify the DOD and C values after a specific aging phase before conducting further experiments, and calculate slope changes using the experimental data acquired in the subsequent phase. However, conducting such experiments involves numerous combinations that may be impractical, not to mention the limited practical significance. The following two assumptions are proposed, which are adequate to underpin the solving process of the optimization model.
Hypothesis 1:
The DOD and C values of the current operation predominantly influence the subsequent aging process, irrespective of the historical operating conditions’ contribution to underlying failures. That is to say, attention should solely be focused on k values resulting from values of DOD and C for subsequent phases.
Hypothesis 2:
All daily conditions in the next period are regarded as the most severe, and all batteries function based on the maximum boundaries established through optimization. The predicted results for operation under such circumstances serve as a reference for the optimization model.
In a majority of cases, the most severe conditions rarely occur in actual control. Consequently, the actual aging status tends to be worse compared with the predicted values. Nonetheless, multiple batteries at the same layer generate identical operating curves, and performance differences emerge irrespective of whether they function at extremes. Additionally, this simplified method significantly enhances calculation efficiency. Figure 21 shows exemplary maps for several HFs:
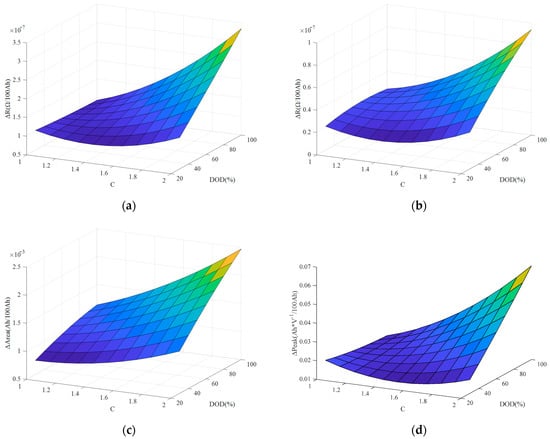
Figure 21.
Map of (a) Ro, (b) Rp, (c) IC area, and (d) IC peak.
4. Prediction Method of Aging Cost for Energy Storage System
In traditional energy application scenarios, regular charge and discharge processes with constant currents were prevalent, where battery charge/discharge capacities were considered as the primary performance indicator. As a result, conventional methods for determining battery residual value often involve calculating the capacity SOH. SOH represents the lifetime value including cascade utilization subsequent to decommissioning [55]. However, as applications expand to encompass more intricate scenarios, integrating multiple performance indicators crucial for energy and power applications becomes imperative. Evaluating battery functionality can no longer rely solely on capacity SOH. Two batteries with identical SOHs may exhibit varying performances despite following the same operating curve. From this standpoint, the authors established a comprehensive performance scoring system based on multi-dimensional HFs. The calculation methods have been detailed in our prior research [1]. This system primarily seeks to reveal distinctions in overall operational performance among batteries at the same layer.
In that study, an unsupervised learning-based multi-appraiser model was proposed, incorporating multiple clustering algorithms for categorization into “good” and “bad”, subsequently converting these classification outcomes into scores via statistical methods. Figure 22 illustrates a comparison of comprehensive performance scores utilizing data from the initial 100 cycles and accumulations (numbers of cells have been reordered based on score, which is different from the experimental numbers in Table 2), showcasing an obvious correlation between them, particularly for batteries that were prematurely terminated from the experiments.
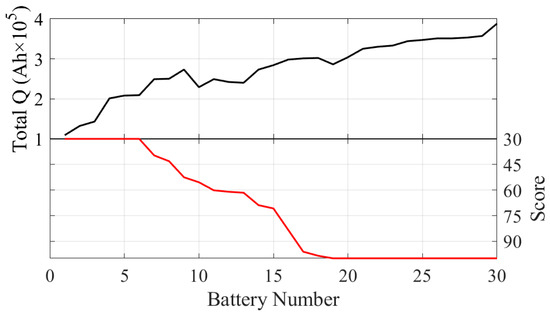
Figure 22.
Correlation between Score and Total Q.
This method not only effectively sidesteps the possible challenges associated with excluding features in calculations but also eradicates the necessity for feature selection. The exclusion of features in calculations due to conditions or data quality is consistent across all batteries.
After multiple batteries have been operating under the same operating conditions for a period of time, the degradation cost of each battery is different. This varied degradation can be effectively quantified using the comprehensive performance scoring system. Lower scores indicate higher aging costs due to inferior performance compared to other batteries in one or more aspects. Without optimization in the control strategies, battery performance is prone to continuous degradation, resulting in a continuous decline in actual commercial value within current operating scenarios. In summary, SOH reflects the objective depreciation of batteries over time and the scoring system incorporates variances from other batteries under current operating scenarios. The strategy proposed in this paper still utilizes SOH as the main criterion for residual value calculation, subjected to weighting using comprehensive scoring. The resulting calculation formula for residual values is expressed as follows:
where denotes the initial value, denotes the recovery value, and denotes the SOH recommended for decommissioning. The initial cost is calculated by spreading out the total cost of integrated modules across individual cells through amortization.
Taking into account the potential recovery of battery capacity, which can lead to increasing scores due to optimization within the operational domain, it is possible to generate higher residual values compared to the preceding operational period. The consequent negative aging costs may introduce anomalies in the solving process aimed at minimizing aging costs through optimization. A zero aging cost suggests that the battery’s operating boundaries have been rationally optimized. The formula for calculating aging costs is expressed as follows:
where denotes the equipment residual value at the end of the preceding period (or at the beginning of the current period), which is obtained by calculating the latest HFs using actual operational data. denotes the equipment residual value at the end of the current period. According to Section 3.3, is approximated in accordance with boundary parameters, and k is deduced accordingly, resulting in the prediction of . For example, the aging cost curve of the No. 1 experimental battery is not linearly related to SOH variations in the prediction based on SOH and scoring, as shown in Figure 23.
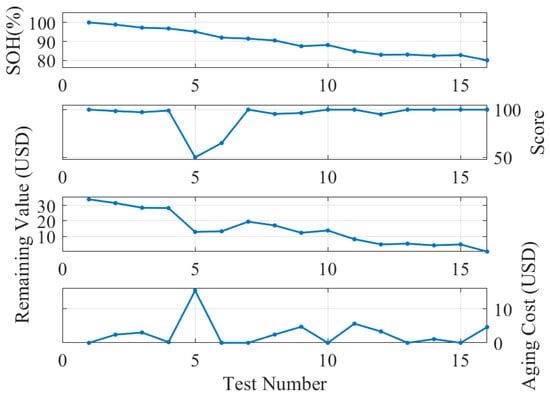
Figure 23.
Case of aging cost based on SOH and score.
The aging costs of battery clusters can be predicted by accumulation according to their topological relationships. If inconsistencies escalate among cells within a cluster, the count of cells with low scores rises, leading to elevated aging costs for the cluster. Consequently, less power is assigned to the cluster to impede the advancement of these inconsistencies.
5. Case Study
5.1. Description of Application Scenario
At a “Source-Grid-Load-Storage park” including PV, industrial load, and citizen load, factories within the park are supplied by a 10 kV medium-voltage line with a rated capacity of 10 MW via a dedicated transformer, as shown in Figure 24a. The annual PV output of the geographical region is shown in Figure 24b. Additionally, the surrounding residential areas are supplied also by this line via a public transformer. Data concerning industrial loads in this park were gathered and used to plot seasonal production load curves as shown in Figure 25a and the typical output curves fitted for four seasons are shown in Figure 25b.
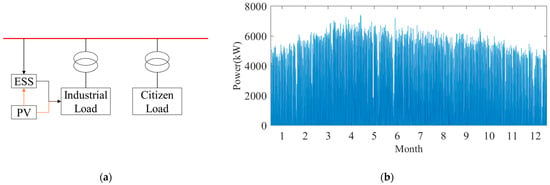
Figure 24.
(a) Schematic diagram of power supply and consumption structure in the park; (b) annual PV output.
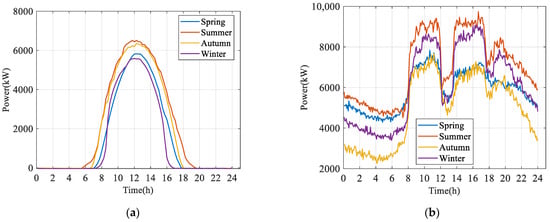
Figure 25.
(a) Typical curves of PV output in four seasons; (b) typical curves of industrial loads in four seasons.
The energy storage station follows the following operational rules: PV power is to be primarily consumed locally, with surplus power stored in cases where immediate consumption is not feasible. To prevent overloading of the dedicated transformer within the park, any surplus loads should be served from the energy storage system. In addition, to prioritize ensuring power supply to residential loads during nighttime hours, the local power grid company enforces a time-of-day tariff system aimed at incentivizing the reduction of nighttime loads within the park. Consequently, every day from 19:30 to 21:30, the energy storage system discharges to maintain loads below 5000 kW for the dedicated transformer serving industrial loads. Figure 26 showcases the process of deriving energy storage operation curves during the summer months: PV power is first consumed by loads, and any excess is absorbed by the energy storage system, referred to as “ESS Charge”. The curve labeled “Load from Grid” represents loads obtained directly from the grid without involving the energy storage system. The curve labeled “ESS Discharge Part 1” illustrates the energy storage system’s supply to prevent line overloading, while “ESS Discharge Part 2” denotes the capacity reserved for residential nighttime consumption.
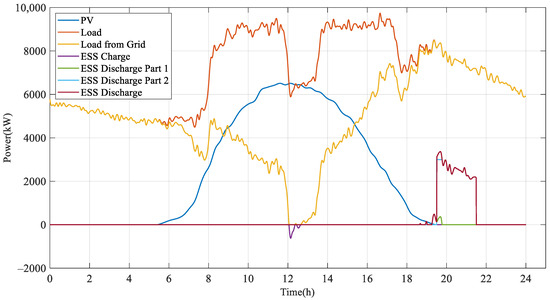
Figure 26.
Schematic diagram of energy storage output in summer.
Similarly, the typical output curves in four seasons are plotted as shown in Figure 27:
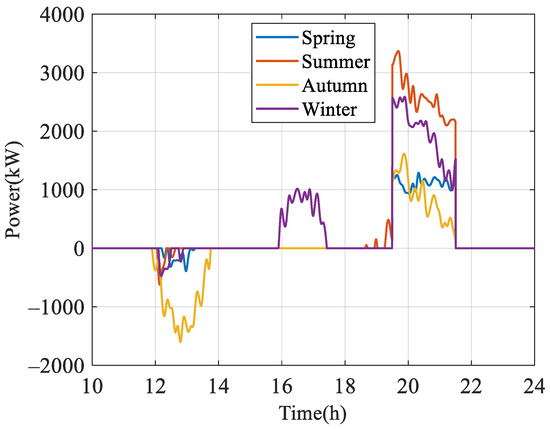
Figure 27.
Typical curves of energy storage output in four seasons.
The resulting energy imbalance can be compensated by adjusting the nighttime charging power. Considering the plentiful wind power resources in the region, the energy storage station leverages lower nighttime tariffs to charge to the desired SOC. To simplify the processing, it was assumed that all energy storage units could be charged at a reduced rate during nighttime, which is omitted in subsequent steps for the convenience of plotting.
5.2. Simulation Model of Energy Storage System
The energy storage system consists of a total of 20 cabins, and dispatching instructions are first evenly distributed among them, as shown in Figure 27. Each cabin comprises 12 clusters, with each under independent control by PCS. As the energy storage station was in the initial stage of the trial operation, it has not been verified for prolonged operational durations. Therefore, Simulink was used to simulate a battery cabin for algorithm verification. The simplified electrochemical model, as outlined in our prior article [52], underwent parameter identification through experimental data before being incorporated into Simulink for operational simulation. The overall simulation model is shown in Figure 28.
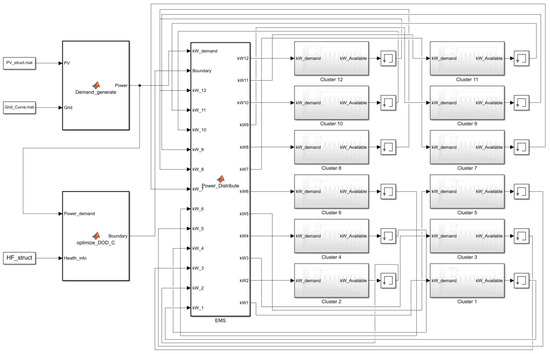
Figure 28.
Overall Simulink model.
It was challenging to simulate each cell individually, especially considering the extensive computing power required. Each cluster within the energy storage system contained 162 cells distributed among nine modules, with each module being treated as a simulation unit, assuming cells within a module are identical, as illustrated in Figure 29. Distinct initial SOH values were assigned to these battery modules; the SOH of a cluster was determined by selecting the lowest SOH among the modules within the cluster following the “buckets effect” [56].
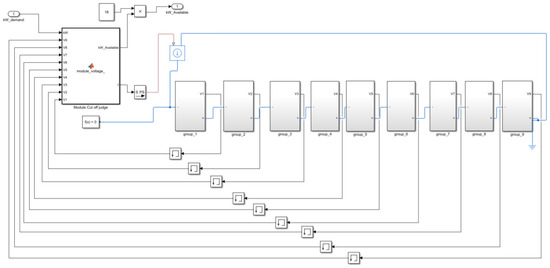
Figure 29.
Simulation model within a cluster.
For aging evaluation, variations of HFs were calculated using the average DOD and C values during real operation. To simulate inconsistencies linked to manufacturing level, system integration, ambient temperature distribution within battery cabins, etc. under actual operating environments, the simulated HFs were randomly updated according to a normal distribution. As shown in Figure 30a, with point A assumed to represent the calculated mean HF, and points B and C to delineate the upper and lower boundaries of the 95% confidence interval, random updates were confined within the shaded area shown in Figure 30b.
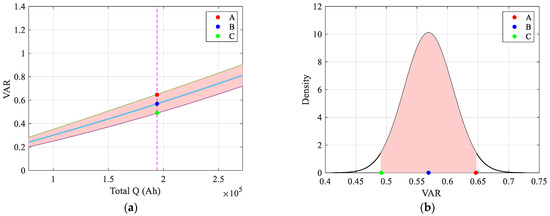
Figure 30.
Schematic diagram of HF calculation based on normal distribution: (a) average value and calculated value according to total Q; (b) probability density distribution.
It is important to note that HFs can be calculated synchronously with real data without introducing artificial inconsistencies in engineering applications.
5.3. Comparative Analysis of Results
For comparative analysis, simulations were conducted for the battery cabin utilizing two strategies, which are, respectively, the traditional equalized dispatching strategy and the differentiated dispatching strategy proposed in this paper. The simulations incorporated the following conditions: any battery clusters with an SOH lower than 80% are suspended from responding to dispatching instructions; the unit cost of the battery system is assumed at 0.3667 USD/Wh and is 0 after retirement; η is 95%; and [D1, D2, D3, C1, C2, C3] = [100%, 70%, 50%, 1, 1.25, 1.5].
Under the differentiated dispatching strategy proposed in this paper, the operation profile under typical conditions in summer is shown in Figure 31.
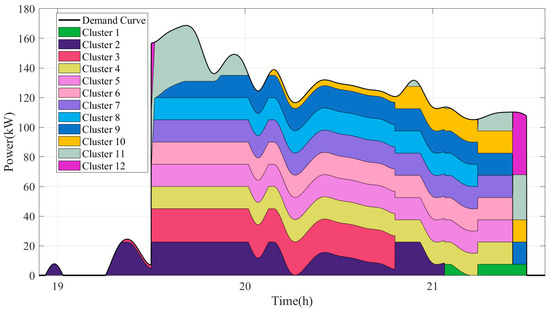
Figure 31.
Stack graph of typical output in summer under differentiated dispatching strategy.
Under the equalized distribution strategy, the operational profile at evenly distributed power levels is shown in Figure 32:
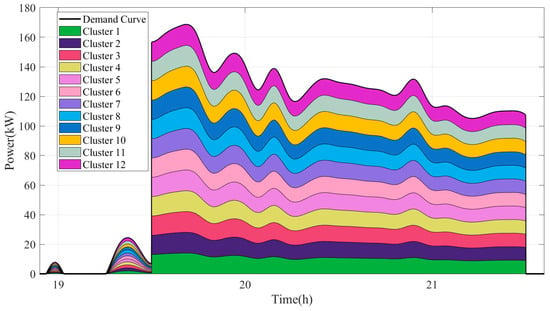
Figure 32.
Stack graph of typical output in summer under equalized dispatching strategy.
To avoid unexpected results stemming from operating procedures with random inconsistencies, three rounds of operation simulations were conducted alongside solving for optimization, using the same SOH initialization values of 0.94, 0.982, 0.981, 0.986, 0.983, 0.974, 0.973, 0.975, 0.977, 0.972, 0.997, and 0.998 for respective clusters. The following typical integration defects were considered in initialization: abnormal cells in cluster 1, slight aging in clusters 2 to 5, consistencies in clusters 6 to 10 along with slight aging, and clusters 11 and 12 in good status. The nine groups of cells in each cluster are randomly distributed according to the above assumptions. The SOH of each module is continuously updated, and the worst SOH in all modules is set as the SOH of the cluster based on the “bucket effect”. For comparison, under the differentiated scheduling strategy, we use Linear decreasing weight-Particle Swarm Optimization (Ldw_PSO) [34] as the optimization algorithm. The comparison of results is presented in Table 4:

Table 4.
Comparison of results from three rounds of simulation calculations.
Obviously, the proposed differentiated method is superior to the traditional equalized strategy, with a longer life, lower aging cost, and better consistency. Because the particle population of the Ldw_PSO is not diverse enough, it may sometimes be easy to fall into the local optimal solution. In the subsequent analysis, we mainly compare differentiated dispatching strategy with Mc_PSO and equalized dispatching strategy. The first round of the solving process is meticulously outlined. Figure 33 presents a comparison of aging curves among the 12 clusters under the proposed method. These clusters using the proposed method halt in responding in summer with peak demands, after a nine-and-a-half-year operational duration, due to serious aging, as shown in Figure 34. With DOD and C constraints removed in summer, the clusters continue to operate with equalized distribution, yielding identical operating curves as shown in Figure 32. Furthermore, the differentiated dispatching strategy is sustained in other seasons, as exemplified in the winter operation shown in Figure 35. In the first quarter of the 14th year, cluster 1 is decommissioned but the remaining 11 clusters remain available in responding to instructions. In the next quarter, with the decommissioning of cluster 6, the battery cabin becomes incapable of responding to dispatching instructions, signaling its end-of-life stage.
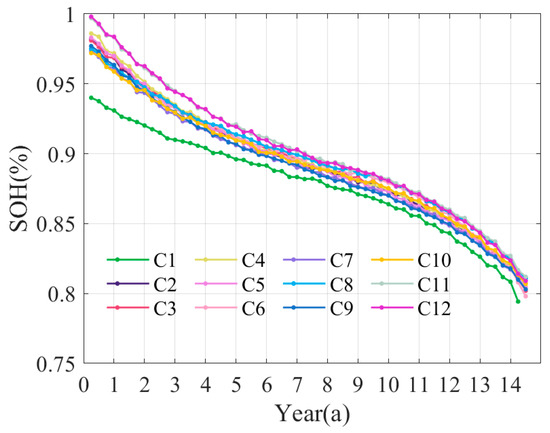
Figure 33.
SOH variations under differentiated dispatching strategy.
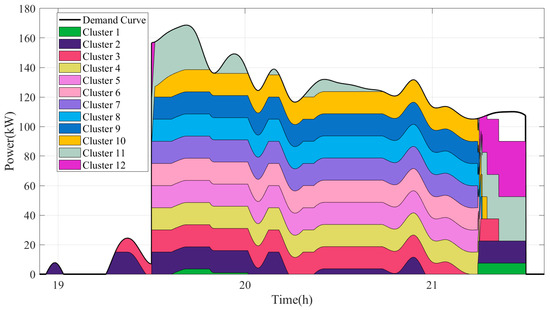
Figure 34.
Stack graph of output insufficiency in summer under differentiated dispatching strategy.
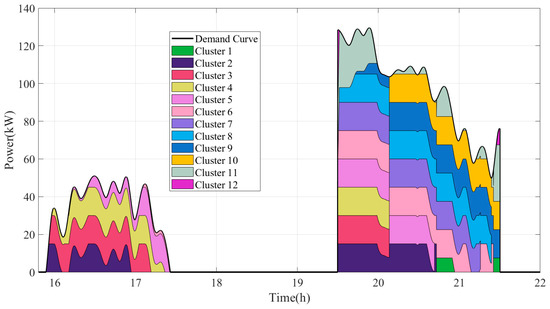
Figure 35.
Stack graph of output in winter under differentiated dispatching strategy.
In this example, cluster 12 is initially defined as E and cluster 11 as D. There is an exchange between clusters 12 and 11 in their rotation status in the third quarter of the fourth year, and another exchange occurs in the first quarter of the eighth year. The rest of the clusters retain their status as S throughout the operational timeframe, exhibiting reductions in and elevations in . Figure 36 shows the boundary comparison between the initial state (Parameters 1) and transition threshold towards the equalized dispatching (Parameters 2):
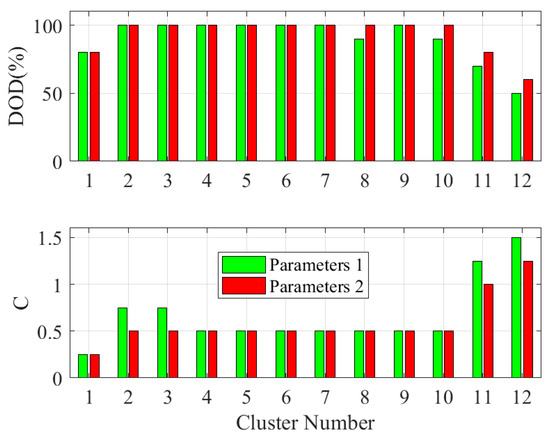
Figure 36.
Comparison of boundary parameters.
Figure 37 shows the aging curves of the 12 clusters under the equalized method. When a cluster with inferior performance is disconnected upon reaching the cut-off voltage, power is redistributed equally among the others. Cluster 1 is decommissioned after the first quarter of the 12th year, followed by cluster 10 in the next quarter. Although the other batteries remain in good health, the cabin can no longer respond to instructions, as shown in Figure 38. Compared with the differential strategy in Figure 33, the life of high-performance batteries in early operation is sacrificed, resulting in an increase in the downward slope of their life curves. However, the overall result is that the aging rates are not the same; nevertheless, the aim is to achieve the convergence of the aging curves, and finally obtain balanced aging curves.
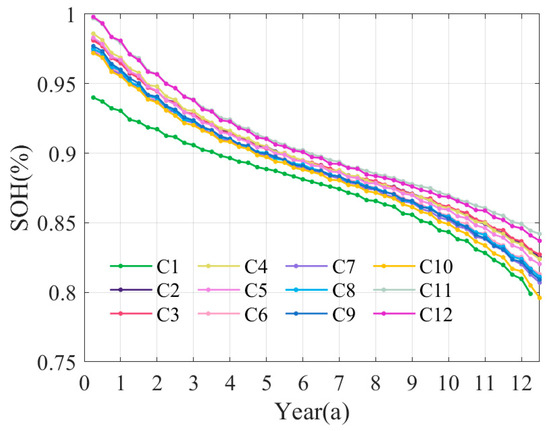
Figure 37.
SOH variations under equalized dispatching strategy.
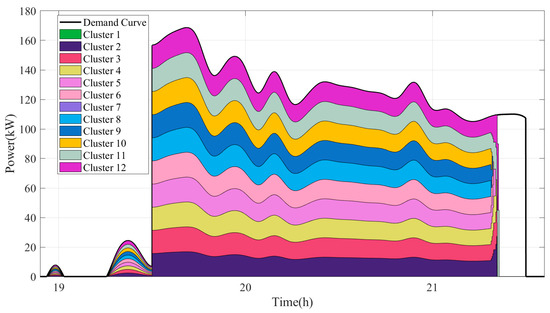
Figure 38.
Stack graph of output before decommissioning under equalized dispatching strategy.
Under the differentiated strategy, aging exhibited a slower rate and tended to converge, whereas the equalized strategy led to contrasting trends. The former resulted in a 16% extension in service duration. Variances in SOH across clusters were calculated as an inconsistency indicator, and Figure 39 shows a comparison of cluster SOHs after decommissioning. The sums of variances were 2.1821 × 10−4 and 2.8150 × 10−4, respectively, amounting to a 22.48% decline.
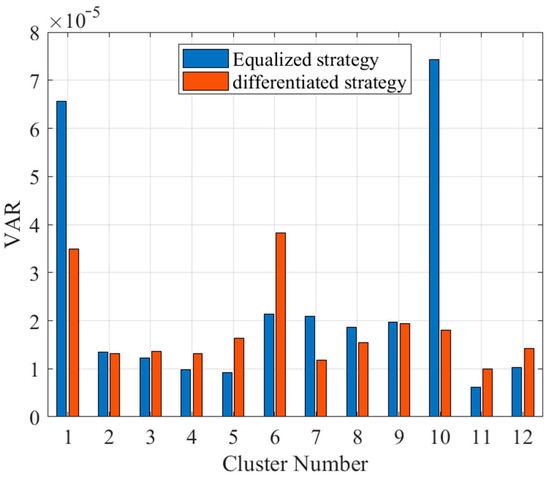
Figure 39.
Comparison of SOH variances after decommissioning under two strategies.
The aging costs per kilowatt-hour of clusters resulting from the proposed method is shown in Figure 40a, and those from the equalized method are shown in Figure 40b. Significant differences emerge among clusters in the initial phases under the proposed method. The aging progression of lower-quality batteries is decelerated by leveraging the presence of high-quality batteries, leading to a convergence in aging costs during the later stages. The total aging cost per kilowatt-hour is 0.0759 USD and 0.0819 USD, respectively, with a reduction of 7.33%.
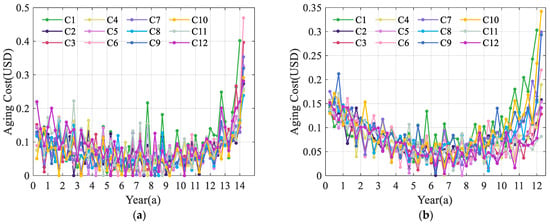
Figure 40.
(a) Annual aging cost per kilowatt-hour under differentiated dispatching strategy; (b) annual aging cost per kilowatt-hour under equalized dispatching strategy.
In summary, the three rounds of simulation verification illustrated in Table 4 demonstrated an average extension of service life by 14.62%, a decrease in aging costs by 6.61%, and a reduction in inconsistencies by 21.98%.
6. Conclusions
To tackle the challenges posed by composite energy storage applications with escalating complexities in operating conditions, this paper presents a novel control strategy integrating an objective function to minimize aging costs, supplemented by the corresponding application procedure. With a focus on enhancing consistency and extending service life, this research accomplished the following tasks:
- The optimization control strategy presented, along with its solving process, helps in reducing aging costs and extending the service life of energy storage systems. Furthermore, it improves module consistency, offering advantages for cascade utilization following module recombination.
- The periodic rolling optimization mode proposed for integrating this strategy into engineering operation benefits not only from reducing the computational power needed for each optimization control but also from enabling iterative adjustments based on the actual operational status.
- The aging cost evaluation introduced incorporates multi-dimensional features, rather than solely considering capacity SOH.
This study was conducted through experiments and simulations, and the findings were verified to some extent. It is still essential to conduct further research and application exploration from the following aspects in the future:
- Due to time and equipment limitations, the comparative experiments were not sufficient. Variable intervals may be refined in the future, to establish a more accurate aging prediction model. Additionally, data collected during long-term operation revealed that batteries with high SOC and low operating frequency exhibited noticeable storage aging. In the subsequent strategy optimization, it may be beneficial to optimize SOC points after charging instead of performing a full charge each time.
- Utilizing the universality of the proposed approach, models can be developed with a small amount of experimental data in scenarios involving other types of batteries. These models can then be used for simulations of aging under multiple variables to provide a reference. This approach can help in reducing the cost associated with long-term aging experiments.
- Shortening the time span of each period allows for more refined optimization control in engineering applications. At the same time, we continue to explore other data-driven models to improve the effectiveness of the solution.
Author Contributions
Conceptualization, W.X. and J.J.; methodology, J.J., W.L., C.J. and W.Z.; software, J.J. and C.J.; validation, Z.W., W.X. and W.Z.; formal analysis, W.L. and B.L.; investigation, W.X., J.J., B.L. and Z.W.; resources, Z.W., W.X. and W.L.; writing—original draft preparation, J.J. and W.X.; writing—review and editing, W.X., J.J., W.Z. and W.L.; visualization, C.J., J.J. and B.L.; supervision, W.X. and Z.W.; funding acquisition, Z.W. and W.X. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Key R&D Program of China, grant number 2021YFB2400700.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Thanks to the many masters, doctors, and teachers from Chongqing University who have participated in the experiment for more than three years. Thanks to the trial operation scenario provided by the Three Gorges Source-Grid-Load-Storage Demonstration Base in Ulanqab, Inner Mongolia. Thanks to the scholars mentioned in the references for their research results on health feature extraction.
Conflicts of Interest
Zhuoyan Wu and Binke Li were employed by the company China Three Gorges Corporation. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Jia, J.; Hu, X.; Deng, Z.; Xiao, W.; Xu, H.; Han, F. Data-Driven Comprehensive Evaluation of Lithium-Ion Battery State of Health and Abnormal Battery Screening. J. Mech. Eng. 2021, 57, 141–149, 159. [Google Scholar] [CrossRef]
- Feng, F.; Hu, X.; Hu, L.; Hu, F.; Li, Y.; Zhang, L. Propagation Mechanisms and Diagnosis of Parameter Inconsistency within Li-Ion Battery Packs. Renew. Sustain. Energy Rev. 2019, 112, 102–113. [Google Scholar] [CrossRef]
- Hu, X.; Zhang, K.; Liu, K.; Lin, X.; Dey, S.; Onori, S. Advanced Fault Diagnosis for Lithium-Ion Battery Systems: A Review of Fault Mechanisms, Fault Features, and Diagnosis Procedures. IEEE Ind. Electron. Mag. 2020, 14, 65–91. [Google Scholar] [CrossRef]
- Jiang, X.; Jin, Y.; Zheng, X.; Hu, G.; Zeng, Q. Optimal Configuration of Grid-Side Battery Energy Storage System under Power Marketization. Appl. Energy 2020, 272, 115242. [Google Scholar] [CrossRef]
- Hu, X.; Xu, L.; Lin, X.; Pecht, M. Battery Lifetime Prognostics. Joule 2020, 4, 310–346. [Google Scholar] [CrossRef]
- Hassan, A.; Khan, S.A.; Li, R.; Su, W.; Zhou, X.; Wang, M.; Wang, B. Second-Life Batteries: A Review on Power Grid Applications, Degradation Mechanisms, and Power Electronics Interface Architectures. Batteries 2023, 9, 571. [Google Scholar] [CrossRef]
- Han, W.; Zou, C.; Zhou, C.; Zhang, L. Estimation of Cell SOC Evolution and System Performance in Module-Based Battery Charge Equalization Systems. IEEE Trans. Smart Grid 2019, 10, 4717–4728. [Google Scholar] [CrossRef]
- Zhao, Q.; Liao, K.; Yang, J.; He, Z.; Xu, Y. Aging Rate Equalization Strategy for Battery Energy Storage Systems in Microgrids. IEEE Trans. Smart Grid 2024, 15, 136–148. [Google Scholar] [CrossRef]
- Xu, B.; Zhao, J.; Zheng, T.; Litvinov, E.; Kirschen, D.S. Factoring the Cycle Aging Cost of Batteries Participating in Electricity Markets. IEEE Trans. Power Syst. 2018, 33, 2248–2259. [Google Scholar] [CrossRef]
- Luo, Y.; Tian, P.; Yan, X.; Xiao, X.; Ci, S.; Zhou, Q.; Yang, Y. Energy Storage Dynamic Configuration of Active Distribution Networks—Joint Planning of Grid Structures. Processes 2023, 12, 79. [Google Scholar] [CrossRef]
- Han, W.; Wik, T.; Kersten, A.; Dong, G.; Zou, C. Next-Generation Battery Management Systems: Dynamic Reconfiguration. IEEE Ind. Electron. Mag. 2020, 14, 20–31. [Google Scholar] [CrossRef]
- Yan, G.; Liu, D.; Li, J.; Mu, G. A Cost Accounting Method of the Li-Ion Battery Energy Storage System for Frequency Regulation Considering the Effect of Life Degradation. Prot. Control Mod. Power Syst. 2018, 3, 4. [Google Scholar] [CrossRef]
- Karunathilake, D.; Vilathgamuwa, D.; Mishra, Y.; Corry, P.; Farrell, T.; Choi, S.S. Degradation-Conscious Multiobjective Optimal Control of Reconfigurable Li-Ion Battery Energy Storage Systems. Batteries 2023, 9, 217. [Google Scholar] [CrossRef]
- Collath, N.; Tepe, B.; Englberger, S.; Jossen, A.; Hesse, H. Aging Aware Operation of Lithium-Ion Battery Energy Storage Systems: A Review. J. Energy Storage 2022, 55, 105634. [Google Scholar] [CrossRef]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Xiao, W.; Xu, H.; Jia, J.; Feng, F.; Wang, W. State of Health Estimation Framework of Li-on Battery Based on Improved Gaussian Process Regression for Real Car Data. IOP Conf. Ser. Mater. Sci. Eng. 2020, 793, 012063. [Google Scholar] [CrossRef]
- Liu, K.; Xiaopeng, T.; Teodorescu, R.; Gao, F.; Meng, J. Future Ageing Trajectory Prediction for Lithium-Ion Battery Considering the Knee Point Effect. IEEE Trans. Energy Convers. 2022, 37, 1282–1291. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, X.; Tang, X.; Zhu, J.; Chen, S.; Dai, H. Internal Short Circuit Mechanisms, Experimental Approaches and Detection Methods of Lithium-Ion Batteries for Electric Vehicles: A Review. Renew. Sustain. Energy Rev. 2021, 141, 110790. [Google Scholar] [CrossRef]
- Zheng, Y.; Lu, Y.; Gao, W.; Han, X.; Feng, X.; Ouyang, M. Micro-Short-Circuit Cell Fault Identification Method for Lithium-Ion Battery Packs Based on Mutual Information. IEEE Trans. Ind. Electron. 2021, 68, 4373–4381. [Google Scholar] [CrossRef]
- Xiao, W.; Miao, S.; Jia, J.; Zhu, Q.; Huang, Y. Lithium-Ion Batteries Fault Diagnosis Based on Multi-Dimensional Indicator. In Proceedings of the 2021 Annual Meeting of CSEE Study Committee of HVDC and Power Electronics (HVDC 2021), Beijing, China, 28–30 December 2021; Volume 2021, pp. 96–101. [Google Scholar]
- Doostmohammadian, M.; Meskin, N. Sensor Fault Detection and Isolation via Networked Estimation: Full-Rank Dynamical Systems. IEEE Trans. Control Netw. Syst. 2021, 8, 987–996. [Google Scholar] [CrossRef]
- Gan, N.; Sun, Z.; Zhang, Z.; Xu, S.; Liu, P.; Qin, Z. Data-Driven Fault Diagnosis of Lithium-Ion Battery Overdischarge in Electric Vehicles. IEEE Trans. Power Electron. 2022, 37, 4575–4588. [Google Scholar] [CrossRef]
- Wu, C.; Zhu, C.; Ge, Y. A New Fault Diagnosis and Prognosis Technology for High-Power Lithium-Ion Battery. IEEE Trans. Plasma Sci. 2017, 45, 1533–1538. [Google Scholar] [CrossRef]
- Xia, B.; Chen, Z.; Mi, C.; Robert, B. External Short Circuit Fault Diagnosis for Lithium-Ion Batteries. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–7. [Google Scholar]
- Wang, H.; Shi, W.; Hu, F.; Wang, Y.; Hu, X.; Li, H. Over-Heating Triggered Thermal Runaway Behavior for Lithium-Ion Battery with High Nickel Content in Positive Electrode. Energy 2021, 224, 120072. [Google Scholar] [CrossRef]
- Gao, Y.; Gao, Q.; Zhang, X. Study on Battery Direct-Cooling Coupled with Air Conditioner Novel System and Control Method. J. Energy Storage 2023, 70, 108032. [Google Scholar] [CrossRef]
- Doughty, D.H.; Crafts, C.C. FreedomCAR: Electrical Energy Storage System Abuse Test Manual for Electric and Hybrid Electric Vehicle Applications; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2006. [Google Scholar]
- Białoń, T.; Niestrój, R.; Skarka, W.; Korski, W. HPPC Test Methodology Using LFP Battery Cell Identification Tests as an Example. Energies 2023, 16, 6239. [Google Scholar] [CrossRef]
- R-Smith, N.A.-Z.; Moertelmaier, M.; Gramse, G.; Kasper, M.; Ragulskis, M.; Groebmeyer, A.; Jurjovec, M.; Brorein, E.; Zollo, B.; Kienberger, F. Fast Method for Calibrated Self-Discharge Measurement of Lithium-Ion Batteries Including Temperature Effects and Comparison to Modelling. Energy Rep. 2023, 10, 3394–3401. [Google Scholar] [CrossRef]
- Wu, L.; Liu, K.; Liu, J.; Pang, H. Evaluating the Heat Generation Characteristics of Cylindrical Lithium-Ion Battery Considering the Discharge Rates and N/P Ratio. J. Energy Storage 2023, 64, 107182. [Google Scholar] [CrossRef]
- Steger, F.; Krogh, J.T.; Meegahapola, L.G.; Schweiger, H.-G. Calculating Available Charge and Energy of Lithium-Ion Cells Based on OCV and Internal Resistance. Energies 2022, 15, 7902. [Google Scholar] [CrossRef]
- Messing, M.; Shoa, T.; Habibi, S. Lithium-Ion Battery Relaxation Effects. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019; pp. 1–6. [Google Scholar]
- Yu, P.; Wang, S.; Yu, C.; Shi, W.; Li, B. Study of Hysteresis Voltage State Dependence in Lithium-Ion Battery and a Novel Asymmetric Hysteresis Modeling. J. Energy Storage 2022, 51, 104492. [Google Scholar] [CrossRef]
- Wu, Z.; Yin, L.; Xiong, R.; Wang, S.; Xiao, W.; Liu, Y.; Jia, J.; Liu, Y. A Novel State of Health Estimation of Lithium-Ion Battery Energy Storage System Based on Linear Decreasing Weight-Particle Swarm Optimization Algorithm and Incremental Capacity-Differential Voltage Method. Int. J. Electrochem. Sci. 2022, 17, 220754. [Google Scholar] [CrossRef]
- Feng, X.; Merla, Y.; Weng, C.; Ouyang, M.; He, X.; Liaw, B.Y.; Santhanagopalan, S.; Li, X.; Liu, P.; Lu, L.; et al. A Reliable Approach of Differentiating Discrete Sampled-Data for Battery Diagnosis. eTransportation 2020, 3, 100051. [Google Scholar] [CrossRef]
- Noelle, D.J.; Wang, M.; Le, A.V.; Shi, Y.; Qiao, Y. Internal Resistance and Polarization Dynamics of Lithium-Ion Batteries upon Internal Shorting. Appl. Energy 2018, 212, 796–808. [Google Scholar] [CrossRef]
- Xiao, J.; Li, Q.; Bi, Y.; Cai, M.; Dunn, B.; Glossmann, T.; Liu, J.; Osaka, T.; Sugiura, R.; Wu, B.; et al. Understanding and Applying Coulombic Efficiency in Lithium Metal Batteries. Nat. Energy 2020, 5, 561–568. [Google Scholar] [CrossRef]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-Driven Prediction of Battery Cycle Life before Capacity Degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef]
- Maity, J.; Dutta, S.; Khanra, M. Constant Voltage Charging Curve Based Features and State of Health Estimation of Li-Ion Batteries: A Comprehensive Study. In Proceedings of the 2022 International Conference on Smart Generation Computing, Communication and Networking (SMART GENCON), Bangalore, India, 23–25 December 2022; pp. 1–7. [Google Scholar]
- Zheng, Y.; Han, X.; Lu, L.; Li, J.; Ouyang, M. Lithium Ion Battery Pack Power Fade Fault Identification Based on Shannon Entropy in Electric Vehicles. J. Power Sources 2013, 223, 136–146. [Google Scholar] [CrossRef]
- Gateman, S.M.; Gharbi, O.; Gomes de Melo, H.; Ngo, K.; Turmine, M.; Vivier, V. On the Use of a Constant Phase Element (CPE) in Electrochemistry. Curr. Opin. Electrochem. 2022, 36, 101133. [Google Scholar] [CrossRef]
- Xiong, R.; Sun, Y.; Wang, C.; Tian, J.; Chen, X.; Li, H.; Zhang, Q. A Data-Driven Method for Extracting Aging Features to Accurately Predict the Battery Health. Energy Storage Mater. 2023, 57, 460–470. [Google Scholar] [CrossRef]
- Zhang, K.; Xiong, R.; Qu, S.; Zhang, B.; Shen, W. Electrochemical Impedance Spectroscopy: A Novel High-Power Measurement Technique for Onboard Batteries Using Full-Bridge Conversion. IEEE Trans. Transp. Electrif. 2024. early access. [Google Scholar] [CrossRef]
- Tian, J.; Xiong, R.; Shen, W.; Lu, J. State-of-Charge Estimation of LiFePO4 Batteries in Electric Vehicles: A Deep-Learning Enabled Approach. Appl. Energy 2021, 291, 116812. [Google Scholar] [CrossRef]
- Mawonou, K.S.R.; Eddahech, A.; Dumur, D.; Beauvois, D.; Godoy, E. State-of-Health Estimators Coupled to a Random Forest Approach for Lithium-Ion Battery Aging Factor Ranking. J. Power Sources 2021, 484, 229154. [Google Scholar] [CrossRef]
- Jia, X.; Wang, S.; Cao, W.; Qiao, J.; Yang, X.; Li, Y.; Fernandez, C. A Novel Genetic Marginalized Particle Filter Method for State of Charge and State of Energy Estimation Adaptive to Multi-Temperature Conditions of Lithium-Ion Batteries. J. Energy Storage 2023, 74, 109291. [Google Scholar] [CrossRef]
- Lai, X.; Yuan, M.; Tang, X.; Zheng, Y.; Zhu, J.; Sun, Y.; Zhou, Y.; Gao, F. State-of-Power Estimation for Lithium-Ion Batteries Based on a Frequency-Dependent Integer-Order Model. J. Power Sources 2024, 594, 234000. [Google Scholar] [CrossRef]
- Liu, W.; Hu, X.; Lin, X.; Yang, X.-G.; Song, Z.; Foley, A.M.; Couture, J. Toward High-Accuracy and High-Efficiency Battery Electrothermal Modeling: A General Approach to Tackling Modeling Errors. eTransportation 2022, 14, 100195. [Google Scholar] [CrossRef]
- Zhou, H.; Gao, L.T.; Li, Y.; Lyu, Y.; Guo, Z.-S. Electrochemical Performance of Lithium-Ion Batteries with Two-Layer Gradient Electrode Architectures. Electrochim. Acta 2024, 476, 143656. [Google Scholar] [CrossRef]
- Jha, V.; Krishnamurthy, B. Modeling the SEI Layer Formation and Its Growth in Lithium-Ion Batteries (LiB) during Charge–Discharge Cycling. Ionics 2022, 28, 3661–3670. [Google Scholar] [CrossRef]
- Liu, D.; He, Y.; Chen, Y.; Cao, J.; Zhu, F. Electrochemical Modeling, Li Plating Onsets and Performance Analysis of Thick Graphite Electrodes Considering the Solid Electrolyte Interface Formed from the First Cycle. Electrochim. Acta 2023, 439, 141651. [Google Scholar] [CrossRef]
- Gu, Y.; Wang, J.; Chen, Y.; Xiao, W.; Deng, Z.; Chen, Q. A Simplified Electro-Chemical Lithium-Ion Battery Model Applicable for in Situ Monitoring and Online Control. Energy 2023, 264, 126192. [Google Scholar] [CrossRef]
- Luo, G.; Zhang, Y.; Tang, A. Capacity Degradation and Aging Mechanisms Evolution of Lithium-Ion Batteries under Different Operation Conditions. Energies 2023, 16, 4232. [Google Scholar] [CrossRef]
- Naylor Marlow, M.; Chen, J.; Wu, B. Degradation in Parallel-Connected Lithium-Ion Battery Packs under Thermal Gradients. Commun. Eng. 2024, 3, 2. [Google Scholar] [CrossRef]
- Liu, K.; Shang, Y.; Ouyang, Q.; Widanage, W. A Data-Driven Approach with Uncertainty Quantification for Predicting Future Capacities and Remaining Useful Life of Lithium-Ion Battery. IEEE Trans. Ind. Electron. 2021, 68, 3170–3180. [Google Scholar] [CrossRef]
- Fan, T.-E.; Liu, S.-M.; Yang, H.; Li, P.-H.; Qu, B. A Fast Active Balancing Strategy Based on Model Predictive Control for Lithium-Ion Battery Packs. Energy 2023, 279, 128028. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).