AI-Based Nano-Scale Material Property Prediction for Li-Ion Batteries
Abstract
1. Introduction
1.1. Database
1.2. Molecular Representation
1.3. AI Model
2. Materials and Methods
2.1. Database Generation
2.2. Data Preprocessing
2.2.1. Curve Fitting
2.2.2. Clustering
2.3. AI Model and Training
2.3.1. Fingerprint
2.3.2. Training
2.3.3. Algorithm
2.3.4. MD Simulations
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MD | Molecular dynamics |
| QM | Quantum mechanics |
| ML | Machine learning |
| CCS | Chemical compound space |
| DFT | Density functional theory |
| DL | Deep learning |
| AI | Artificial intelligence |
| LMO | Lithium manganese oxide |
| HOIPs | Hybrid organic-inorganic perovskites |
| OQMD | Open quantum materials database |
| ICSD | Inorganic crystal structure database |
| ANNs | Artificial neural networks |
| SVR | Support vector regression |
| QE | Quantum Espresso |
| EC | Ethylene carbonate |
References
- von Lilienfeld, O.A. First principles view on chemical compound space: Gaining rigorous atomistic control of molecular properties. Int. J. Quantum Chem. 2013, 113, 1676–1689. [Google Scholar] [CrossRef]
- Huang, B.; von Lilienfeld, O.A. Ab Initio Machine Learning in Chemical Compound Space. Chem. Rev. 2021, 121, 10001–10036. [Google Scholar] [CrossRef] [PubMed]
- Lemonick, S. Exploring chemical space: Can AI take us where no human has gone before? Chem. Eng. News 2020, 98, 30–35. [Google Scholar]
- Ruddigkeit, L.; van Deursen, R.; Blum, L.C.; Reymond, J.L. Enumeration of 166 Billion Organic Small Molecules in the Chemical Universe Database GDB-17. J. Chem. Inf. Model. 2012, 52, 2864–2875. [Google Scholar] [CrossRef] [PubMed]
- Moradi, Z.; Heydarinasab, A.; Shariati, F.P. First-principle study of doping effects (Ti, Cu, and Zn) on electrochemical performance of Li2MnO3 cathode materials for lithium-ion batteries. Int. J. Quantum Chem. 2021, 121, e26458. [Google Scholar] [CrossRef]
- Moradi, Z.; Lanjan, A.; Srinivasan, S. Multiscale Investigation into the Co-Doping Strategy on the Electrochemical Properties of Li2RuO3 Cathodes for Li-Ion Batteries. ChemElectroChem 2021, 8, 112–124. [Google Scholar] [CrossRef]
- Tyagi, R.; Lanjan, A.; Srinivasan, S. Co-Doping Strategies to Improve the Electrochemical Properties of LixMn2O4 Cathodes for Li-Ion Batteries. ChemElectroChem 2022, 9, e202101626. [Google Scholar] [CrossRef]
- Moradi, Z.; Lanjan, A.; Srinivasan, S. Enhancement of Electrochemical Properties of Lithium Rich Li2RuO3 Cathode Material. J. Electrochem. Soc. 2020, 167, 110537. [Google Scholar] [CrossRef]
- Xia, W.; Sakurai, M.; Balasubramanian, B.; Liao, T.; Wang, R.; Zhang, C.; Sun, H.; Ho, K.M.; Chelikowsky, J.R.; Sellmyer, D.J.; et al. Accelerating the discovery of novel magnetic materials using machine learning–guided adaptive feedback. Proc. Natl. Acad. Sci. USA 2022, 119, e2204485119. [Google Scholar] [CrossRef]
- Lanjan, A.; Srinivasan, S. An Enhanced Battery Aging Model Based on a Detailed Diffusing Mechanism in the SEI Layer. ECS Adv. 2022, 1, 030504. [Google Scholar] [CrossRef]
- Lanjan, A.; Moradi, Z.; Srinivasan, S. Multiscale Investigation of the Diffusion Mechanism within the Solid–Electrolyte Interface Layer: Coupling Quantum Mechanics, Molecular Dynamics, and Macroscale Mathematical Modeling. ACS Appl. Mater. Interfaces 2021, 13, 42220–42229. [Google Scholar] [CrossRef] [PubMed]
- Lanjan, A.; Choobar, B.G.; Amjad-Iranagh, S. First principle study on the application of crystalline cathodes Li2Mn0.5TM0.5O3 for promoting the performance of lithium-ion batteries. Comput. Mater. Sci. 2020, 173, 109417. [Google Scholar] [CrossRef]
- Lanjan, A.; Choobar, B.G.; Amjad-Iranagh, S. Promoting lithium-ion battery performance by application of crystalline cathodes LiXMn1-zFezPO4. J. Solid State Electrochem. 2020, 24, 157–171. [Google Scholar] [CrossRef]
- Stanev, V.; Choudhary, K.; Kusne, A.G.; Paglione, J.; Takeuchi, I. Artificial intelligence for search and discovery of quantum materials. Commun. Mater. 2021, 2, 105. [Google Scholar] [CrossRef]
- Aykol, M.; Herring, P.; Anapolsky, A. Machine learning for continuous innovation in battery technologies. Nat. Rev. Mater. 2020, 5, 725–727. [Google Scholar] [CrossRef]
- Ye, C.; Tan, R.; Wang, A.; Chen, J.; Comesaña Gándara, B.; Breakwell, C.; Alvarez-Fernandez, A.; Fan, Z.; Weng, J.; Bezzu, C.G.; et al. Long-Life Aqueous Organic Redox Flow Batteries Enabled by Amidoxime-Functionalized Ion-Selective Polymer Membranes. Angew. Chem. Int. Ed. 2022, 61, e202207580. [Google Scholar] [CrossRef]
- Spotte-Smith, E.W.C.; Blau, S.M.; Xie, X.; Patel, H.D.; Wen, M.; Wood, B.; Dwaraknath, S.; Persson, K.A. Quantum chemical calculations of lithium-ion battery electrolyte and interphase species. Sci. Data 2021, 8, 203. [Google Scholar] [CrossRef]
- Chattopadhyay, J.; Pathak, T.S.; Santos, D.M.F. Applications of Polymer Electrolytes in Lithium-Ion Batteries: A Review. Polymers 2023, 15, 3907. [Google Scholar] [CrossRef]
- Chan, H.; Narayanan, B.; Cherukara, M.J.; Sen, F.G.; Sasikumar, K.; Gray, S.K.; Chan, M.K.Y.; Sankaranarayanan, S.K.R.S. Machine Learning Classical Interatomic Potentials for Molecular Dynamics from First-Principles Training Data. J. Phys. Chem. C 2019, 123, 6941–6957. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, T.; Ji, H.; Zhou, J.; Wang, Z.; Qian, T.; Yan, C. Boosting the Optimization of Lithium Metal Batteries by Molecular Dynamics Simulations: A Perspective. Adv. Energy Mater. 2020, 10, 2002373. [Google Scholar] [CrossRef]
- Behler, J. Perspective: Machine learning potentials for atomistic simulations. J. Chem. Phys. 2016, 145, 170901. [Google Scholar] [CrossRef]
- Lanjan, A.; Moradi, Z.; Srinivasan, S. A computational framework for evaluating molecular dynamics potential parameters employing quantum mechanics. Mol. Syst. Des. Eng. 2023, 8, 632–646. [Google Scholar] [CrossRef]
- Sandhu, S.; Tyagi, R.; Talaie, E.; Srinivasan, S. Using neurocomputing techniques to determine microstructural properties in a Li-ion battery. Neural Comput. Appl. 2022, 34, 9983–9999. [Google Scholar] [CrossRef]
- Raccuglia, P.; Elbert, K.C.; Adler, P.D.F.; Falk, C.; Wenny, M.B.; Mollo, A.; Zeller, M.; Friedler, S.A.; Schrier, J.; Norquist, A.J. Machine-learning-assisted materials discovery using failed experiments. Nature 2016, 533, 73–76. [Google Scholar] [CrossRef]
- Lu, S.; Zhou, Q.; Ouyang, Y.; Guo, Y.; Li, Q.; Wang, J. Accelerated discovery of stable lead-free hybrid organic-inorganic perovskites via machine learning. Nat. Commun. 2018, 9, 3405. [Google Scholar] [CrossRef]
- Meredig, B.; Agrawal, A.; Kirklin, S.; Saal, J.E.; Doak, J.W.; Thompson, A.; Zhang, K.; Choudhary, A.; Wolverton, C. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B 2014, 89, 094104. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. NSF Efforts to Achieve the Nation’s Vision for the Materials Genome Initiative: Designing Materials to Revolutionize and Engineer Our Future (DMREF); The National Academies Press: Washington, DC, USA, 2023. [Google Scholar]
- Belsky, A.; Hellenbrandt, M.; Karen, V.L.; Luksch, P. New developments in the Inorganic Crystal Structure Database (ICSD): Accessibility in support of materials research and design. Acta Crystallogr. Sect. B Struct. Sci. 2002, 58, 364–369. [Google Scholar] [CrossRef] [PubMed]
- Kirklin, S.; Saal, J.E.; Meredig, B.; Thompson, A.; Doak, J.W.; Aykol, M.; Rühl, S.; Wolverton, C. The Open Quantum Materials Database (OQMD): Assessing the accuracy of DFT formation energies. Npj Comput. Mater. 2015, 1, 15010. [Google Scholar] [CrossRef]
- Groom, C.R.; Bruno, I.J.; Lightfoot, M.P.; Ward, S.C. The Cambridge Structural Database. Acta Crystallogr. Sect. B Struct. Sci. Cryst. Eng. Mater. 2016, 72, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Hachmann, J.; Olivares-Amaya, R.; Atahan-Evrenk, S.; Amador-Bedolla, C.; Sánchez-Carrera, R.S.; Gold-Parker, A.; Vogt, L.; Brockway, A.M.; Aspuru-Guzik, A. The Harvard Clean Energy Project: Large-Scale Computational Screening and Design of Organic Photovoltaics on the World Community Grid. J. Phys. Chem. Lett. 2011, 2, 2241–2251. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- Curtarolo, S.; Setyawan, W.; Wang, S.; Xue, J.; Yang, K.; Taylor, R.H.; Nelson, L.J.; Hart, G.L.; Sanvito, S.; Buongiorno-Nardelli, M.; et al. AFLOWLIB.ORG: A distributed materials properties repository from high-throughput ab initio calculations. Comput. Mater. Sci. 2012, 58, 227–235. [Google Scholar] [CrossRef]
- Zhang, Y.; Ling, C. A strategy to apply machine learning to small datasets in materials science. Npj Comput. Mater. 2018, 4, 25. [Google Scholar] [CrossRef]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. Npj Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- Schütt, K.T.; Glawe, H.; Brockherde, F.; Sanna, A.; Müller, K.R.; Gross, E.K.U. How to represent crystal structures for machine learning: Towards fast prediction of electronic properties. Phys. Rev. B 2014, 89, 205118. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Himanen, L.; Jäger, M.O.; Morooka, E.V.; Canova, F.F.; Ranawat, Y.S.; Gao, D.Z.; Rinke, P.; Foster, A.S. DScribe: Library of descriptors for machine learning in materials science. Comput. Phys. Commun. 2020, 247, 106949. [Google Scholar] [CrossRef]
- Sanchez-Lengeling, B.; Aspuru-Guzik, A. Inverse molecular design using machine learning: Generative models for matter engineering. Science 2018, 361, 360–365. [Google Scholar] [CrossRef] [PubMed]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; von Lilienfeld, O.A. Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef]
- Hansen, K.; Biegler, F.; Ramakrishnan, R.; Pronobis, W.; von Lilienfeld, O.A.; Müller, K.R.; Tkatchenko, A. Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space. J. Phys. Chem. Lett. 2015, 6, 2326–2331. [Google Scholar] [CrossRef]
- Akbarpour, H.; Mohajeri, M.; Moradi, M. Investigation on the synthesis conditions at the interpore distance of nanoporous anodic aluminum oxide: A comparison of experimental study, artificial neural network, and multiple linear regression. Comput. Mater. Sci. 2013, 79, 75–81. [Google Scholar] [CrossRef]
- Serra, J.M.; Baumes, L.A.; Moliner, M.; Serna, P.; Corma, A. Zeolite Synthesis Modelling with Support Vector Machines: A Combinatorial Approach. Comb. Chem. High Throughput Screen. 2007, 10, 13–24. [Google Scholar] [CrossRef]
- Fang, S.; Wang, M.; Qi, W.; Zheng, F. Hybrid genetic algorithms and support vector regression in forecasting atmospheric corrosion of metallic materials. Comput. Mater. Sci. 2008, 44, 647–655. [Google Scholar] [CrossRef]
- The classical equation of state of gaseous helium, neon and argon. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1938, 168, 264–283. [CrossRef]
- Wei, J.; Chu, X.; Sun, X.; Xu, K.; Deng, H.; Chen, J.; Wei, Z.; Lei, M. Machine learning in materials science. InfoMat 2019, 1, 338–358. [Google Scholar] [CrossRef]
- Giannozzi, P.; Baroni, S.; Bonini, N.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Chiarotti, G.L.; Cococcioni, M.; Dabo, I.; et al. QUANTUM ESPRESSO: A modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 2009, 21, 395502. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef] [PubMed]
- Giannozzi, P.; Baseggio, O.; Bonfà, P.; Brunato, D.; Car, R.; Carnimeo, I.; Cavazzoni, C.; de Gironcoli, S.; Delugas, P.; Ruffino, F.F.; et al. Quantum ESPRESSO toward the exascale. J. Chem. Phys. 2020, 152, 154105. [Google Scholar] [CrossRef] [PubMed]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
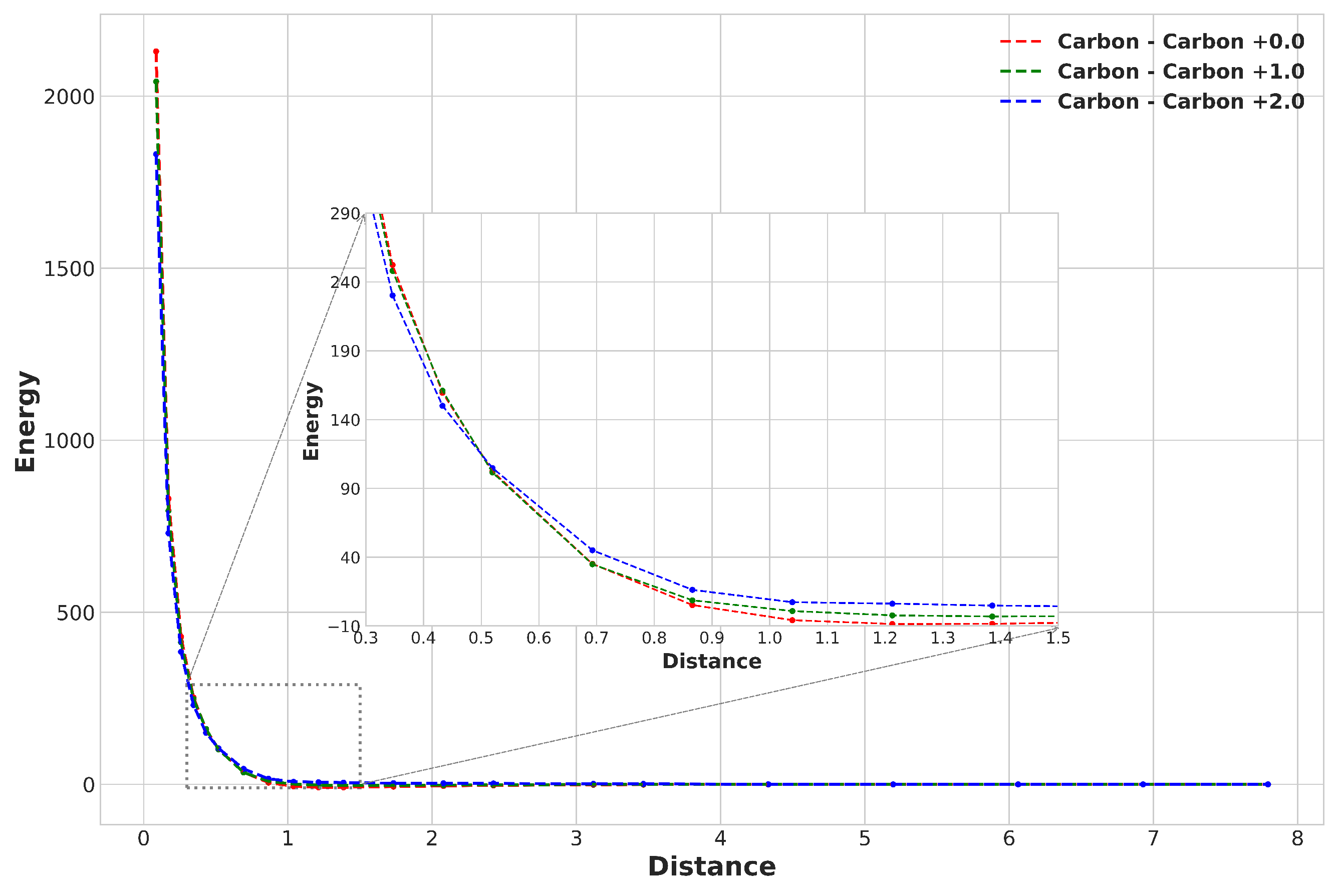
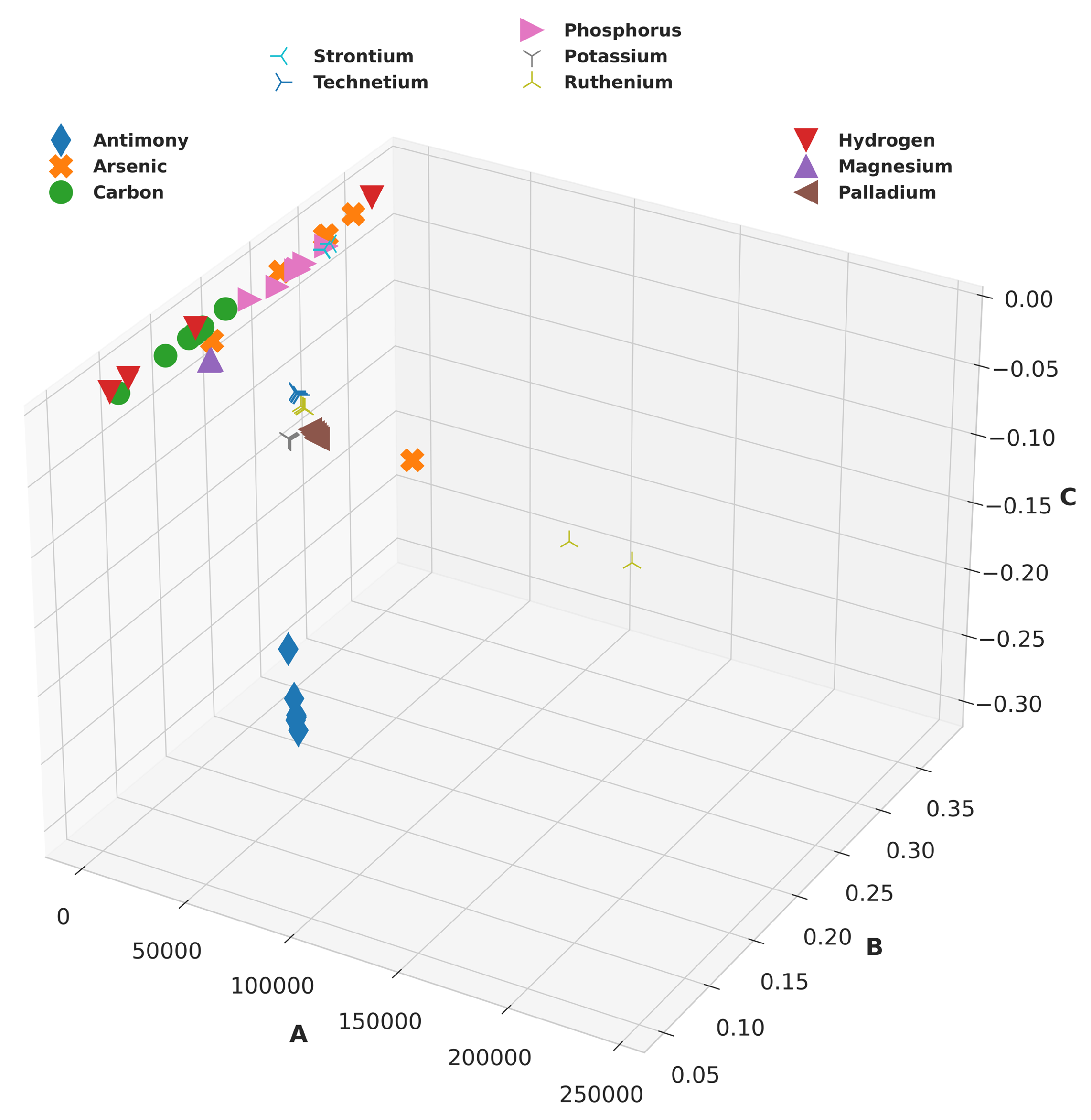
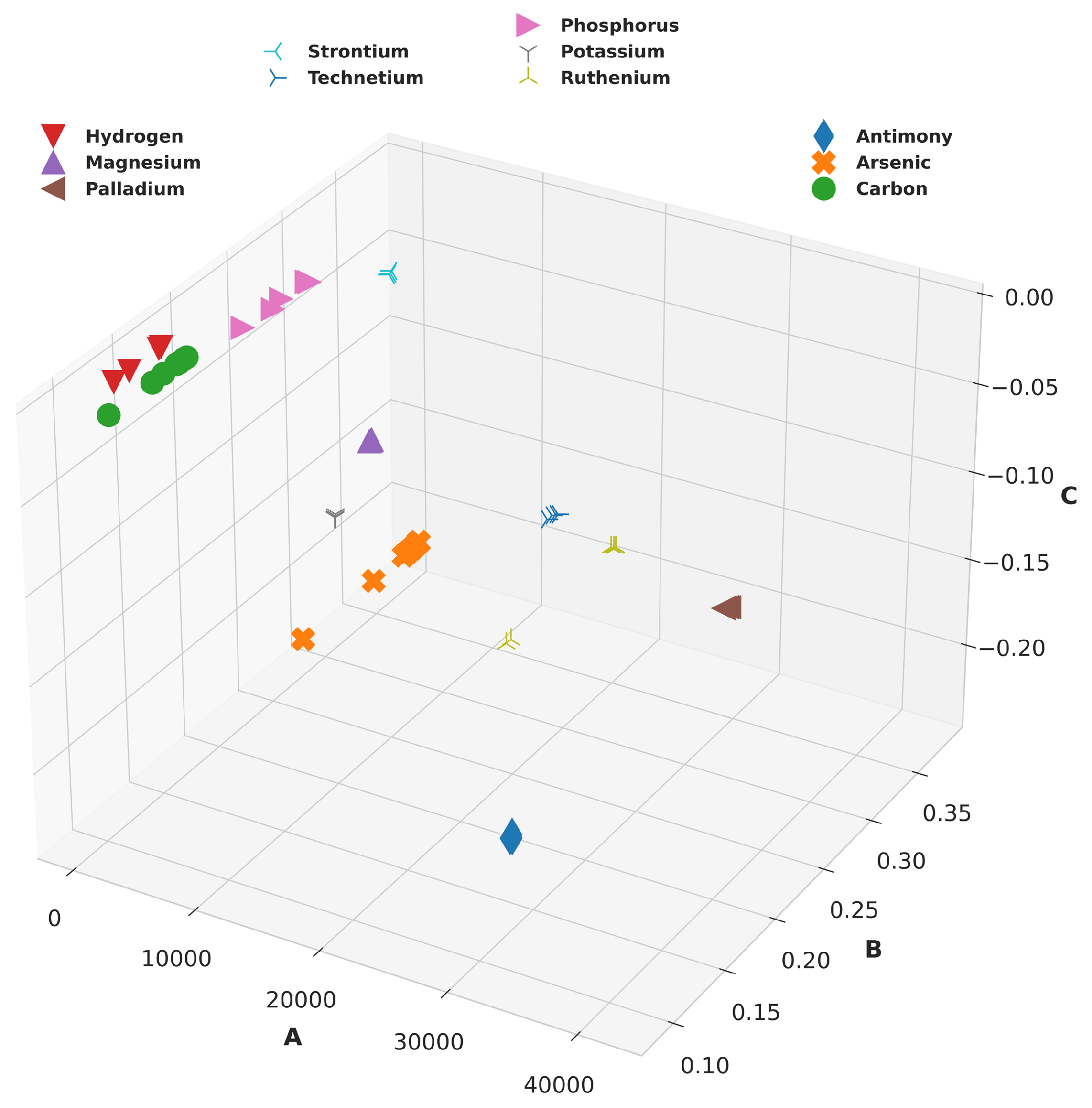
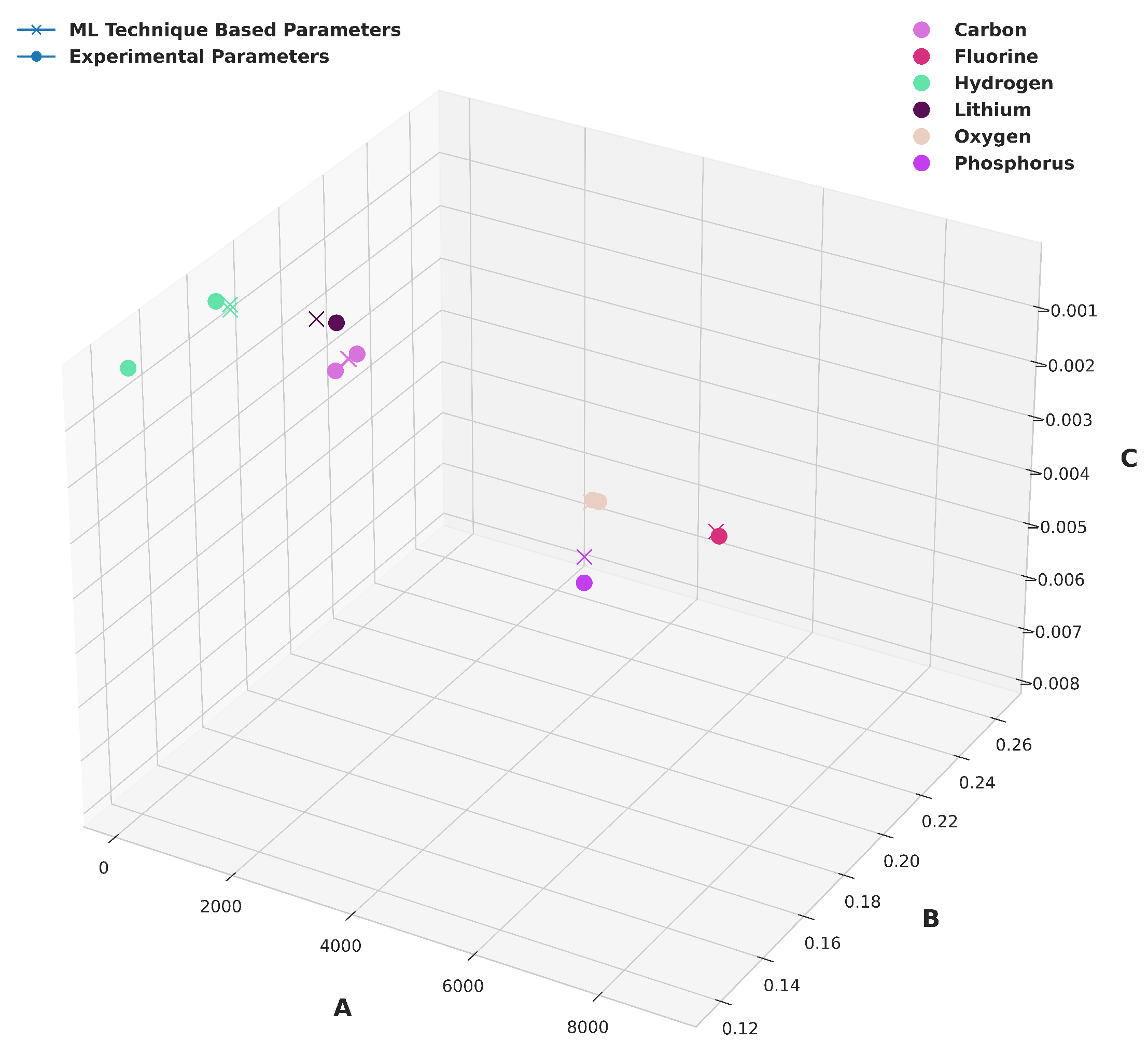
| Properties | Value Method |
|---|---|
| XC Functional | PBE |
| Convergence Tolerance | |
| W.F. Cutoff | |
| Charge Cutoff | |
| Maximum Force | |
| Smearing Factor | |
| K-Point Mesh Size |
| Properties | Description or Specification |
|---|---|
| Energy minimization | Conjugate gradient for steps |
| Equilibrium | 1 ns NVT run and 10 ns NPT run |
| Production run | 10 ns |
| Motions integrator | Stoermer–Verlet, 1 fs time step |
| Temperature coupling | 25 °C, Nose–Hoover thermostat |
| Pressure coupling | 1 bar, Parrinello–Rahman barostat |
| Constraint solver | Constraining all bonds |
| Periodic boundary | x, y and z directions |
| Long-range interactions | Ewald summation with accuracy |
| Trajectory output | Every 1000 time step (fs) |
| Neighbor list updating | Every 10 fs |
| Dynamic load balance | Yes |
| Interaction Type | Potential Style | Equation |
|---|---|---|
| Non-bonded | Buckingham or Coulombic | |
| Bonded | Harmonic | |
| Angle | Harmonic | |
| Dihedral | Quadratic | |
| Improper | Harmonic |
| Element Name | Partial Charge | R2 (A) | R2 (B) | R2 (C) |
|---|---|---|---|---|
| Carbon | −0.4656 | 100.00% | 97.75% | 94.18% |
| Carbon | −0.0257 | 100.00% | 97.75% | 94.18% |
| Carbon | 0.7305 | 99.15% | 96.15% | 94.18% |
| Carbon | −0.3101 | 100.00% | 97.75% | 94.18% |
| Carbon | −0.0714 | 100.00% | 97.75% | 94.18% |
| Hydrogen | 0.222 | 37.19% | 76.07% | 47.82% |
| Hydrogen | 0.4053 | 31.15% | 99.83% | 11.42% |
| Hydrogen | 0.1899 | 37.19% | 76.07% | 47.82% |
| Hydrogen | 0.1968 | 37.19% | 76.07% | 47.82% |
| Hydrogen | 0.4153 | 31.15% | 99.83% | 11.42% |
| Hydrogen | 0.1783 | 37.19% | 76.07% | 47.82% |
| Oxygen | −0.3745 | 99.75% | 98.94% | 98.04% |
| Oxygen | −0.711 | 98.91% | 98.94% | 98.04% |
| Oxygen | −0.5357 | 98.91% | 98.94% | 98.04% |
| Oxygen | −0.2865 | 99.75% | 98.94% | 98.04% |
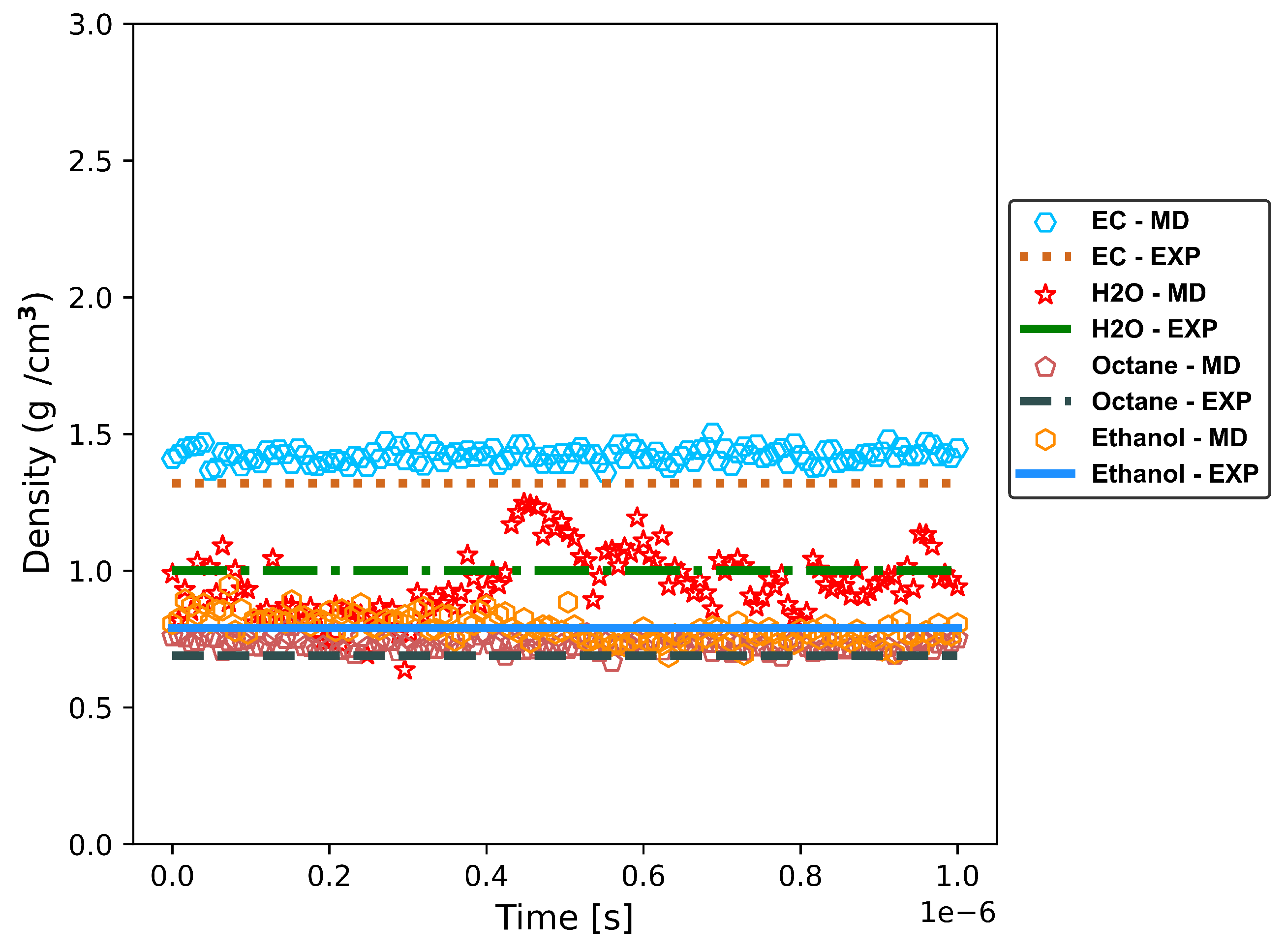
| Density | Experimental | This Work | Error |
|---|---|---|---|
| H2O | 0.99 | 0.95 | 4.04% |
| Octane | 0.7 | 0.73 | 4.29% |
| Ethanol | 0.79 | 0.78 | 1.27% |
| EC | 1.33 | 1.42 | 6.77% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lal, M.A.; Singh, A.; Mzik, R.; Lanjan, A.; Srinivasan, S. AI-Based Nano-Scale Material Property Prediction for Li-Ion Batteries. Batteries 2024, 10, 51. https://doi.org/10.3390/batteries10020051
Lal MA, Singh A, Mzik R, Lanjan A, Srinivasan S. AI-Based Nano-Scale Material Property Prediction for Li-Ion Batteries. Batteries. 2024; 10(2):51. https://doi.org/10.3390/batteries10020051
Chicago/Turabian StyleLal, Mohit Anil, Akashdeep Singh, Ryan Mzik, Amirmasoud Lanjan, and Seshasai Srinivasan. 2024. "AI-Based Nano-Scale Material Property Prediction for Li-Ion Batteries" Batteries 10, no. 2: 51. https://doi.org/10.3390/batteries10020051
APA StyleLal, M. A., Singh, A., Mzik, R., Lanjan, A., & Srinivasan, S. (2024). AI-Based Nano-Scale Material Property Prediction for Li-Ion Batteries. Batteries, 10(2), 51. https://doi.org/10.3390/batteries10020051






